A Comparative Study of Continuum and Structural Modelling Approaches to Simulate Bone Adaptation in the Pelvic Construct
Abstract
1. Introduction
2. Methods
2.1. Musculoskeletal Modelling
2.2. Finite Element Modelling
2.2.1. Base Model
2.2.2. Ligaments
2.2.3. Loading and Boundary Conditions
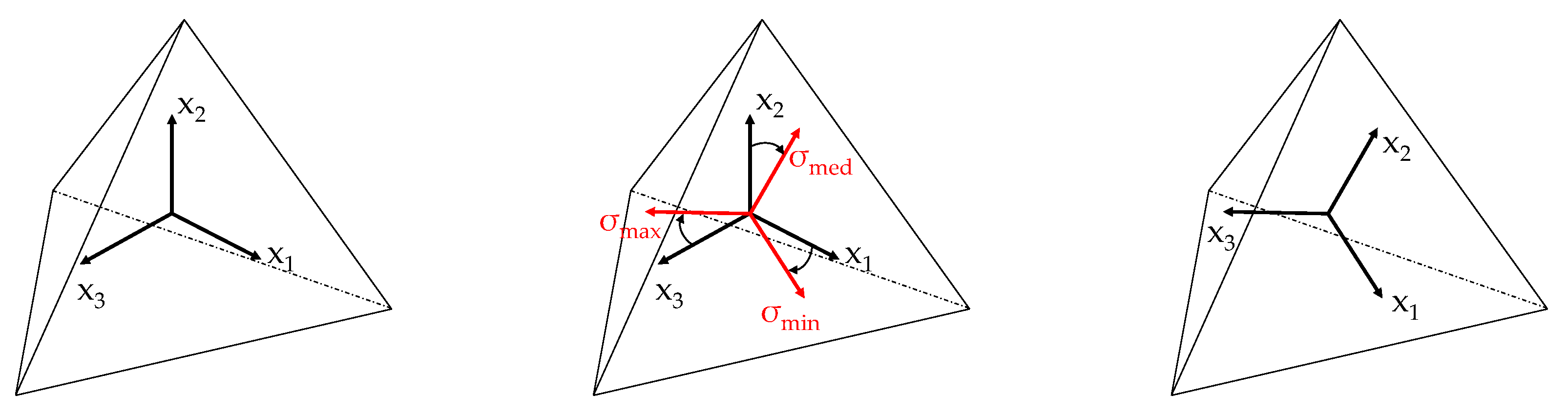
2.3. Bone Adaptation
2.4. Comparison with CT Scan Derived Model
3. Results
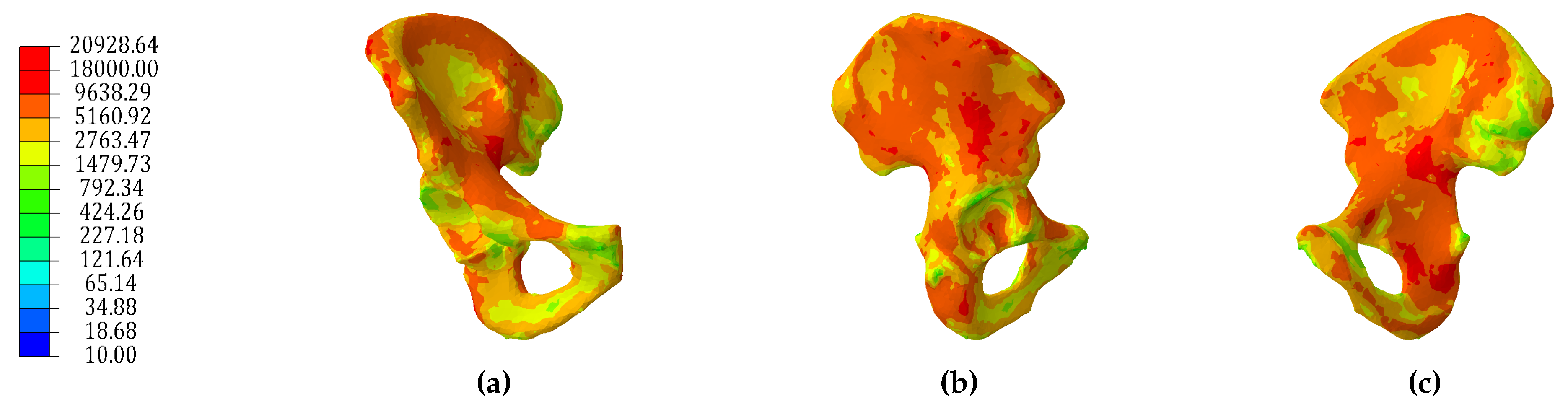
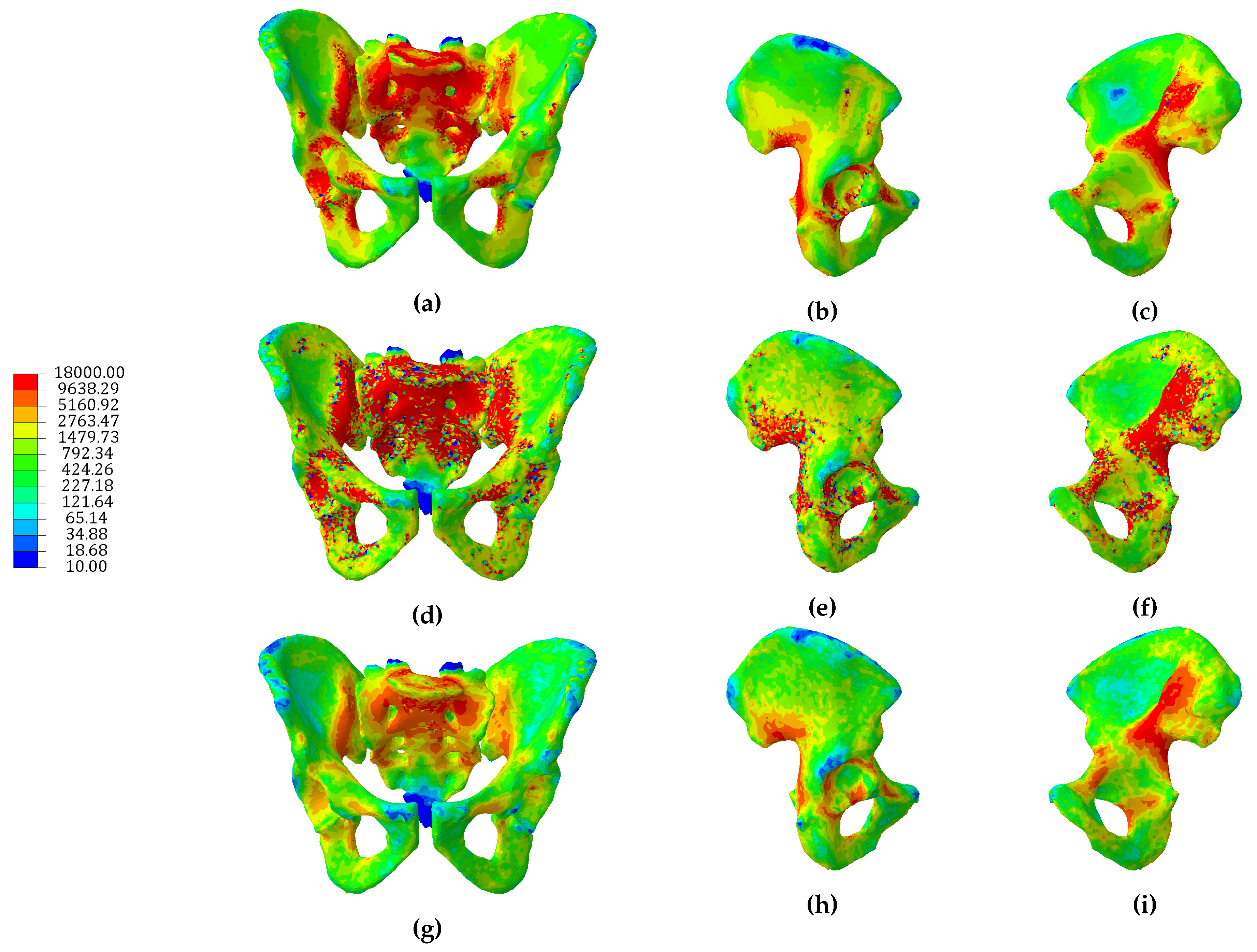
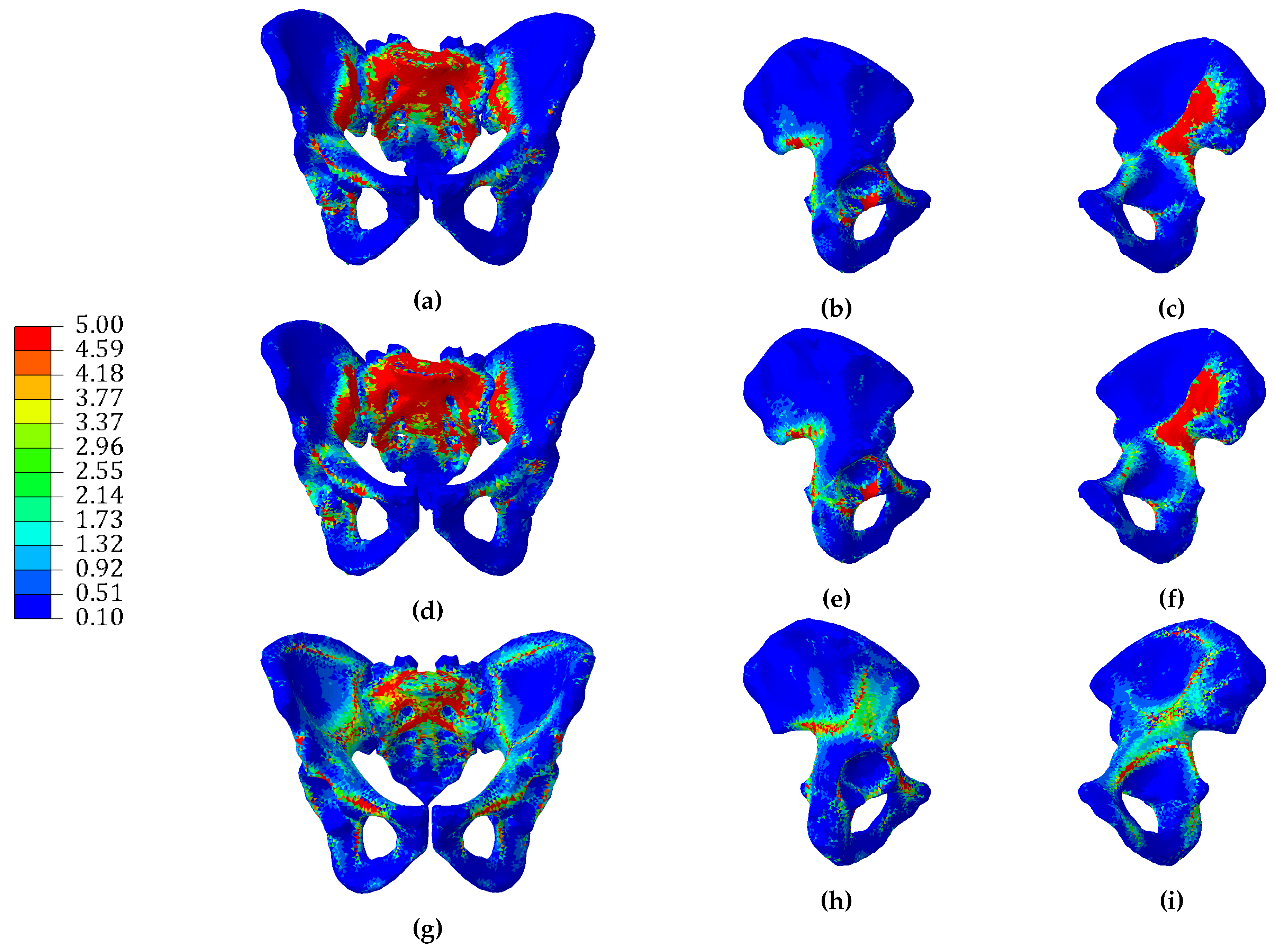
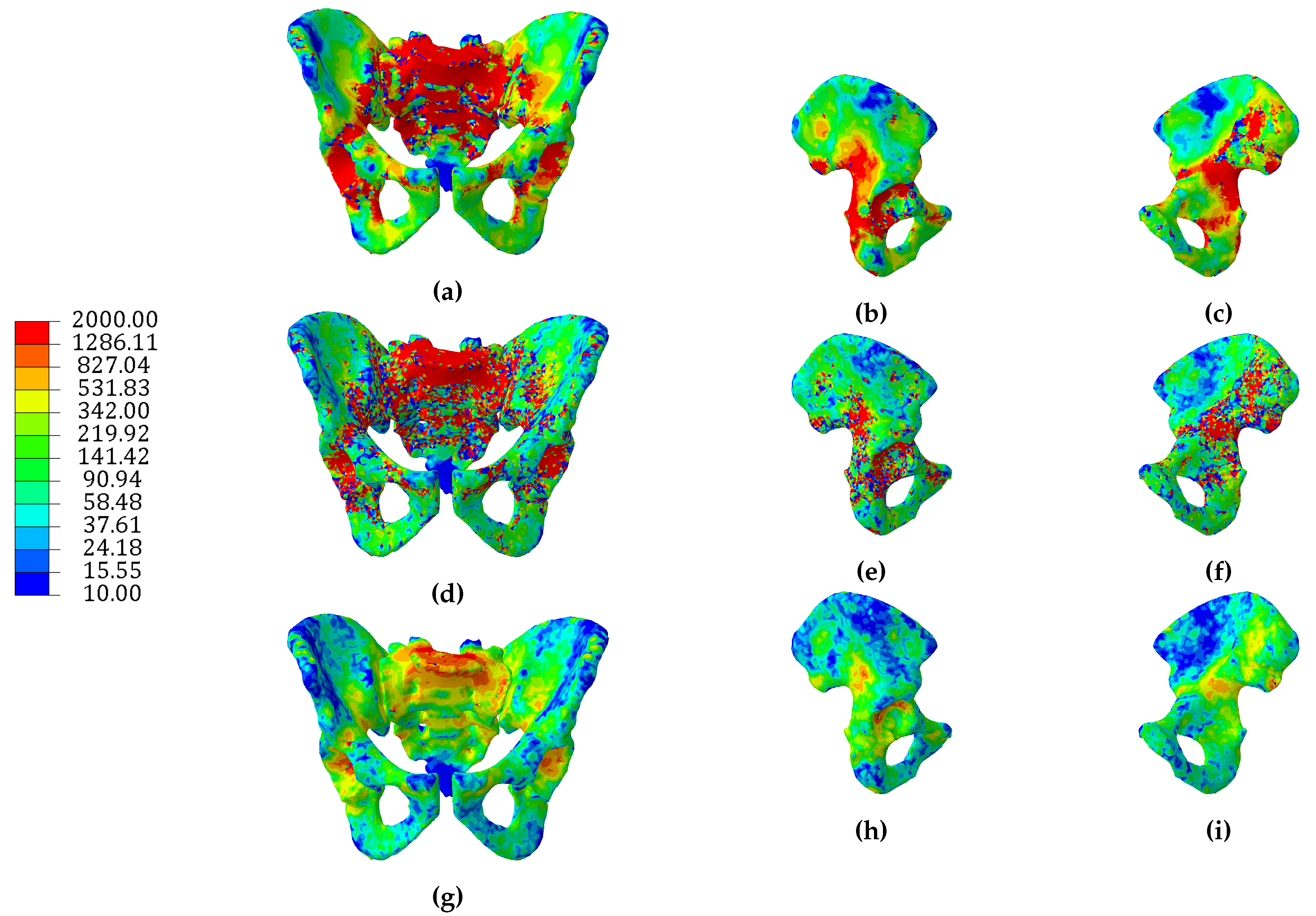
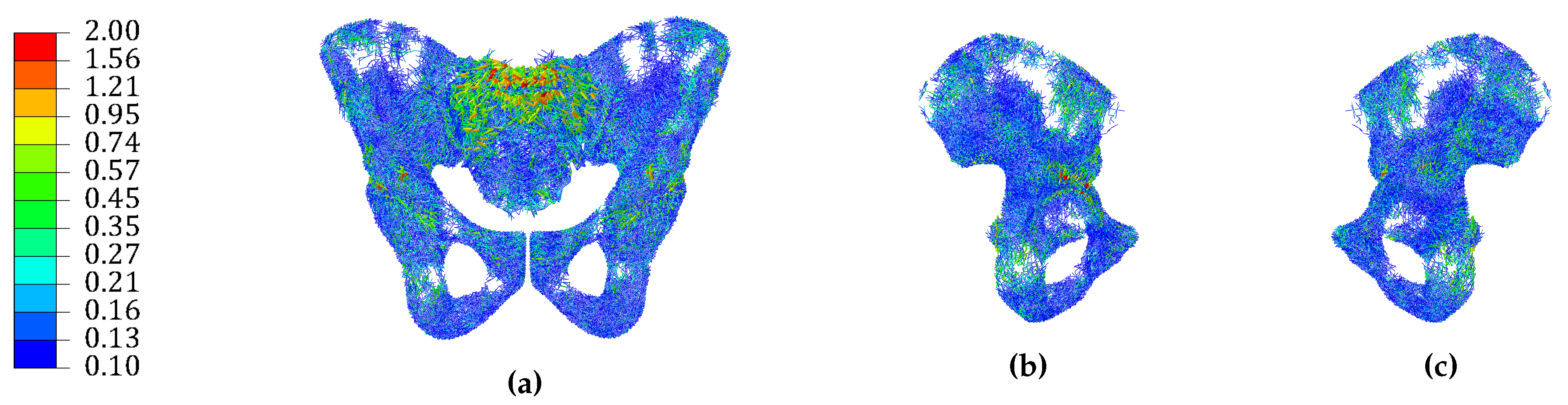
3.1. Continuum Models
3.2. Hybrid Continuum Models
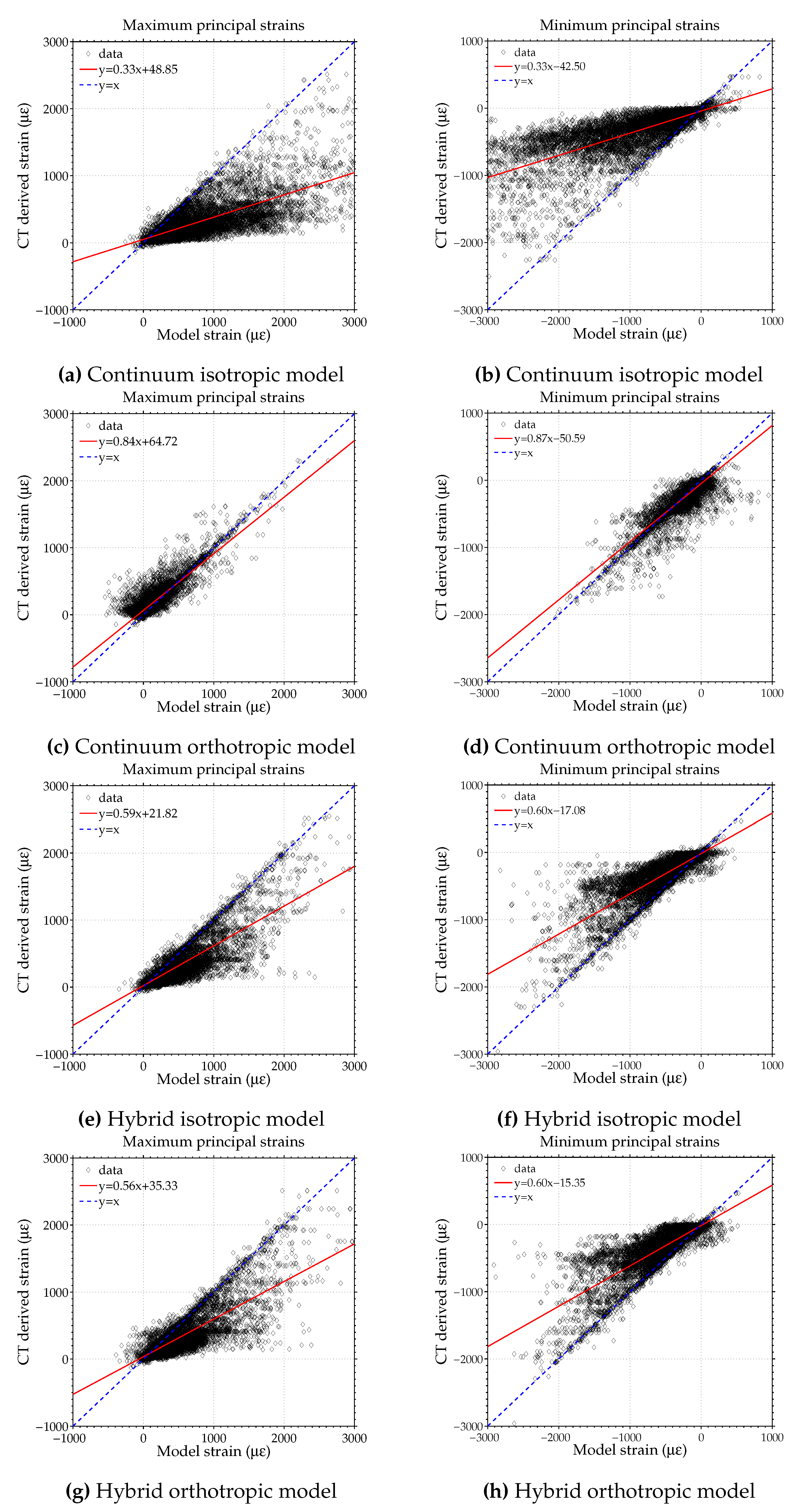
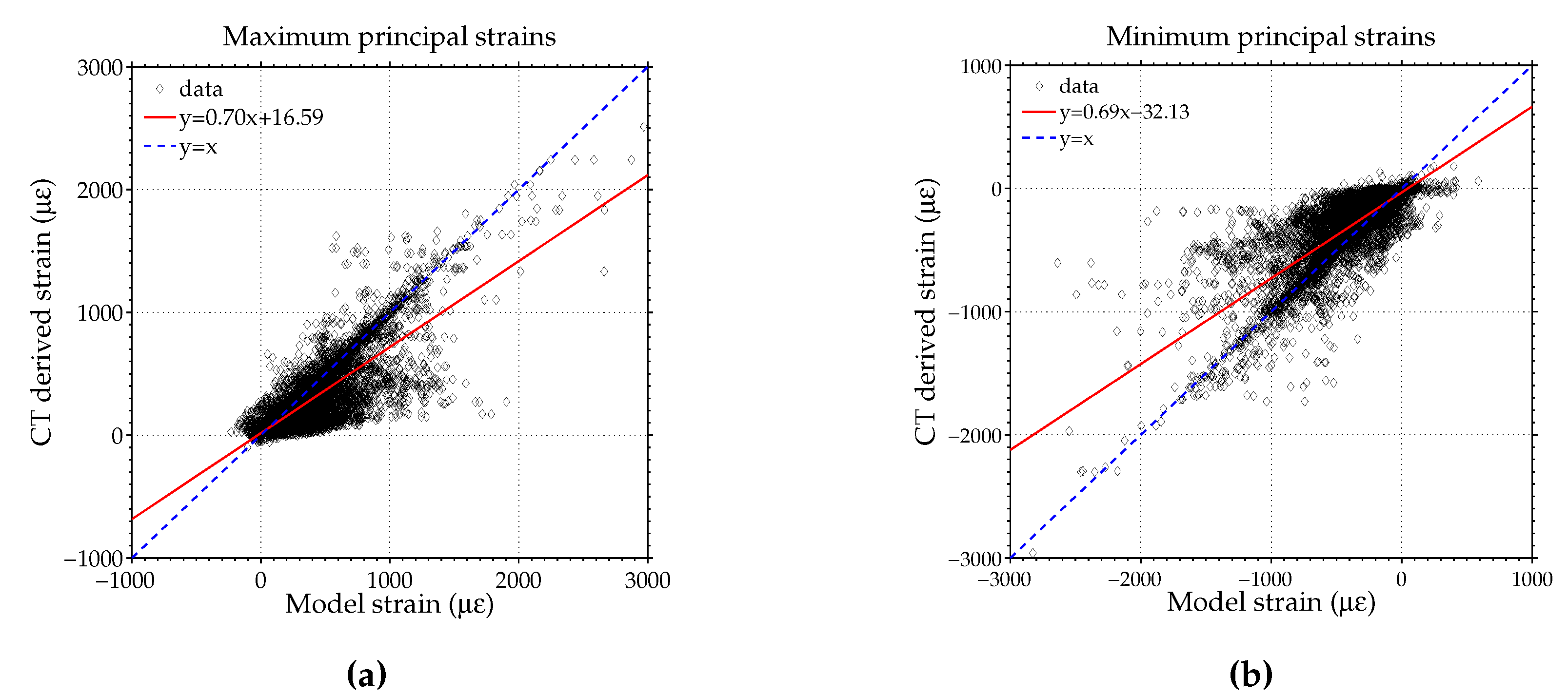
3.3. Comparison to CT Scan Derived Model
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Michaeli, D.A.; Murphy, S.B.; Hipp, J.A. Comparison of predicted and measured contact pressures in normal and dysplastic hips. Med. Eng. Phys. 1997, 19, 180–186. [Google Scholar] [CrossRef]
- van den Bogert, A.J.; Read, L.; Nigg, B.M. An analysis of hip joint loading during walking, running, and skiing. Med. Sci. Sports Exerc. 1999, 31, 131–142. [Google Scholar] [CrossRef] [PubMed]
- Bergmann, G.; Deuretzabacher, G.; Heller, M.; Graichen, F.; Rohlmann, A.; Strauss, J.; Duda, G.N. Hip forces and gait patterns from rountine activities. J. Biomech. 2001, 34, 859–871. [Google Scholar] [CrossRef]
- Frost, H.M. Bone’s mechanostat: A 2003 update. Anat. Rec. Part A Discov. Mol. Cell. Evolut. Biol. 2003, 275, 1081–1101. [Google Scholar] [CrossRef] [PubMed]
- Treece, G.M.; Gee, A.H.; Mayhew, P.M.; Poole, K.E.S. High resolution cortical bone thickness measurement from clinical CT data. Med. Image Anal. 2010, 14, 276–290. [Google Scholar] [CrossRef]
- Phillips, A.T.M.; Villette, C.C.; Modenese, L. Femoral bone mesoscale structural architecture prediction using musculoskeletal and finite element modelling. Int. Biomech. 2015, 2, 43–61. [Google Scholar] [CrossRef]
- Jacob, H.A.C.; Huggler, A.H.; Dietschi, C.; Schreiber, A. Mechanical function of subchondral bone as experimentally determined on the acetabulum of the human pelvis. J. Biomech. 1976, 9, 625–627. [Google Scholar] [CrossRef]
- Dalstra, M.; Huiskes, R.; Odgaard, A.; van Erning, L. Mechanical and textural properties of pelvic trabecular bone. J. Biomech. 1993, 26, 523–535. [Google Scholar] [CrossRef]
- Anderson, A.E.; Peters, C.L.; Tuttle, B.D.; Weiss, J.A. Subject-Specific Finite Element Model of the Pelvis: Development, Validation and Sensitivity Studies. J. Biomech. Eng. 2005, 127, 364. [Google Scholar] [CrossRef]
- Giorgi, M.; Verbruggen, S.W.; Lacroix, D. In silico bone mechanobiology: Modeling a multifaceted biological system. Wiley Interdiscip. Rev. Syst. Biol. Med. 2016, 8, 485–505. [Google Scholar] [CrossRef]
- Wang, L.; Dong, J.; Xian, C.J. Computational modeling of bone cells and their biomechanical behaviors in responses to mechanical stimuli. Crit. Rev. Eukaryot. Gene Expr. 2019, 29, 51–67. [Google Scholar] [CrossRef] [PubMed]
- Tsubota, K.I.; Suzuki, Y.; Yamada, T.; Hojo, M.; Makinouchi, A.; Adachi, T. Computer simulation of trabecular remodeling in human proximal femur using large-scale voxel FE models: Approach to understanding Wolff’s law. J. Biomech. 2009, 42, 1088–1094. [Google Scholar] [CrossRef] [PubMed]
- Geraldes, D.; Phillips, A. A novel 3d strain-adaptive continuum orthotropic bone remodelling algorithm: prediction of bone architecture in the femur. In Proceedings of the 6th World Congress of Biomechanics (WCB 2010), Singapore, 1–6 August 2010; Springer: Berlin, Germany, 2010; pp. 772–775. [Google Scholar]
- Geraldes, D.M.; Phillips, A. A comparative study of orthotropic and isotropic bone adaptation in the femur. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 873–889. [Google Scholar] [CrossRef] [PubMed]
- Geraldes, D.M.; Modenese, L.; Phillips, A.T. Consideration of multiple load cases is critical in modelling orthotropic bone adaptation in the femur. Biomech. Model. Mechanobiol. 2016, 15, 1029–1042. [Google Scholar] [CrossRef] [PubMed]
- Marzban, A.; Nayeb-Hashemi, H.; Vaziri, A. Numerical simulation of load-induced bone structural remodelling using stress-limit criterion. Comput. Methods Biomech. Biomed. Eng. 2015, 18, 259–268. [Google Scholar] [CrossRef] [PubMed]
- Villette, C.C.; Phillips, A.T. Informing phenomenological structural bone remodelling with a mechanistic poroelastic model. Biomech. Model. Mechanobiol. 2016, 15, 69–82. [Google Scholar] [CrossRef] [PubMed]
- Villette, C.; Phillips, A. Microscale poroelastic metamodel for efficient mesoscale bone remodelling simulations. Biomech. Model. Mechanobiol. 2017, 16, 2077–2091. [Google Scholar] [CrossRef]
- Goel, V.K.; Valliappan, S.; Svensson, N.L. Stresses in the normal pelvis. Comput. Biol. Med. 1978, 8, 91–104. [Google Scholar] [CrossRef]
- Oonishi, H.; Isha, H.; Hasegawa, T. Mechanical analysis of the human pelvis and its application to the artificial hip joint–by means of the three-dimensional, finite element method. J. Biomech. 1983, 16, 427–444. [Google Scholar] [CrossRef]
- Landjerit, B.; Jacquard-Simon, N.; Thourot, M.; Massin, P. Physiological loadings on human pelvis: A comparison between numerical and experimental simulations. Proc. ESB 1992, 8, 195. [Google Scholar]
- Schuller, H.; Dalstra, M.; Huiskes, R.; Marti, R. Total hip reconstruction in acetabular dysplasia. A finite element study. J. Bone Joint Surg. Br. 1993, 75B, 468–474. [Google Scholar] [CrossRef]
- Pedersen, D.R.; Crowninshield, R.D.; Brand, R.A.; Johnston, R.C. An axisymmetric model of acetabular components in total hip arthroplasty. J. Biomech. 1982, 15, 305–315. [Google Scholar] [CrossRef]
- Huiskes, R. Finite element analysis of acetabular reconstruction. Noncemented threaded cups. Acta Orthop. Scand. 1987, 58, 620–625. [Google Scholar] [CrossRef] [PubMed]
- Vasu, R.; Carter, D.R.; Harris, W.H. Stress distributions in the acetabular region-I. Before and after total joint replacement. J. Biomech. 1982, 15, 155–157. [Google Scholar] [CrossRef]
- Carter, D.R.; Vasu, R.; Harris, W.H. Stress distributions in the acetabular region-II. Effects of cement thickness and metal backing of the total hip acetabular component. J. Biomech. 1982, 15, 165–170. [Google Scholar] [CrossRef]
- Rapperport, D.; Carter, D.; Schurman, D. Contact finite element stress analysis of the hip joint. J. Orthop. Res. 1985, 3, 435–446. [Google Scholar] [CrossRef] [PubMed]
- Oonishi, H.; Tatsumi, M.; Kawaguchi, A. Biomechanical studies on fixations of an artificial hip joint acetabular socket by means of 2D-FEM. In Biological and Biomechanical Performance of Biomaterials; Christel, P., Meunier, A., Lee, A.J.C., Eds.; Elsevier: Amsterdam, The Netherlands, 1986; pp. 513–518. [Google Scholar]
- Phillips, A.T.M.; Pankaj, P.; Usmani, A.S.; Howie, C.R. Numerical modelling of the acetabular construct following impaction grafting. In Proceedings of the International Symposium on Computer Methods in Biomechanics and Biomedical Engineering, Madrid, Spain, 25–28 February 2004. [Google Scholar]
- Dalstra, M.; Huiskes, R.; van Erning, L. Development and validation of a three-dimensional finite element model of the pelvic bone. J. Biomech. Eng. 1995, 117, 272–278. [Google Scholar] [CrossRef]
- Li, Z.; Kim, J.E.; Davidson, J.S.; Etheridge, B.S.; Alonso, J.E.; Eberhardt, A.W. Biomechanical response of the pubic symphysis in lateral pelvic impacts: a finite element study. J. Biomech. 2007, 40, 2758–2766. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.H.; Wang, J.Y.; Lupton, C.; Heaton-Adegbile, P.; Guo, Z.X.; Liu, Q.; Tong, J. A subject-specific pelvic bone model and its application to cemented acetabular replacements. J. Biomech. 2010, 43, 2722–2727. [Google Scholar] [CrossRef]
- Pankaj, P. Patient-specific modelling of bone and bone-implant systems: the challenges. Int. J. Numer. Methods Biomed. Eng. 2013, 29, 233–249. [Google Scholar] [CrossRef]
- Ashman, R.; Cowin, S.; Van Buskirk, W.; Rice, J. A continuous wave technique for the measurement of the elastic properties of cortical bone. J. Biomech. 1984, 17, 349–361. [Google Scholar] [CrossRef]
- Morlock, M.; Schneider, E.; Bluhm, A.; Vollmer, M.; Bergmann, G.; Müller, V.; Honl, M. Duration and frequency of every day activities in total hip patients. J. Biomech. 2001, 34, 873–881. [Google Scholar] [CrossRef]
- Modenese, L.; Gopalakrishnan, A.; Phillips, A. Application of a falsification strategy to a musculoskeletal model of the lower limb and accuracy of the predicted hip contact force vector. J. Biomech. 2013, 46, 1193–1200. [Google Scholar] [CrossRef] [PubMed]
- Horsman, M.D.K.; Koopman, H.; der Helm, F.C.T.; Prosé, L.P.; Veeger, H.E.J. Morphological muscle and joint parameters for musculoskeletal modelling of the lower extremity. Clin. Biomech. 2007, 22, 239–247. [Google Scholar] [CrossRef] [PubMed]
- Delp, S.; Anderson, F.; Arnold, A.; Loan, P.; Habib, A.; John, C.; Guendelman, E.; Thelen, D. OpenSim: Open source to create and analyze dynamic simulations of movement. IEEE Trans. Biomed. Eng. 2007, 54, 1940–1950. [Google Scholar] [CrossRef]
- Zaharie, D.T.; Phillips, A.T. Pelvic construct prediction of trabecular and cortical bone structural architecture. J. Biomech. Eng. 2018, 140, 091001. [Google Scholar] [CrossRef] [PubMed]
- Barre, A.; Armand, S. Biomechanical ToolKit: Open-source framework to visualize and process biomechanical data. Comput. Methods Programs Biomed. 2014, 114, 80–87. [Google Scholar] [CrossRef]
- Dumas, R.; Chèze, L.; Verriest, J.P. Adjustments to McConville et al. and Young et al. body segment inertial parameters. J. Biomech. 2007, 40, 543–553. [Google Scholar] [CrossRef]
- Lu, T.W.; O’Connor, J.J. Bone position estimation from skin marker co-ordinates using global optimisation with joint constraints. J. Biomech. 1999, 32, 129–134. [Google Scholar] [CrossRef]
- van Arkel, R.J.; Modenese, L.; Phillips, A.T.; Jeffers, J.R. Hip abduction can prevent posterior edge loading of hip replacements. J. Orthop. Res. 2013, 31, 1172–1179. [Google Scholar] [CrossRef]
- Steele, K.M.; DeMers, M.S.; Schwartz, M.H.; Delp, S.L. Compressive tibiofemoral force during crouch gait. Gait Posture 2012, 35, 556–560. [Google Scholar] [CrossRef]
- Phillips, A.; Pankaj, P.; Howie, C.; Usmani, A.; Simpson, A. Finite element modelling of the pelvis: Inclusion of muscular and ligamentous boundary conditions. Med. Eng. Phys. 2007, 29, 739–748. [Google Scholar] [CrossRef]
- Hammer, N.; Steinke, H.; Slowik, V.; Josten, C.; Stadler, J.; Böhme, J.; Spanel-Borowski, K. The sacrotuberous and the sacrospinous ligament—A virtual reconstruction. Ann. Anat. Anat. Anz. 2009, 191, 417–425. [Google Scholar] [CrossRef]
- Hammer, N.; Steinke, H.; Böhme, J.; Stadler, J.; Josten, C.; Spanel-Borowski, K. Description of the iliolumbar ligament for computer-assisted reconstruction. Ann. Anat. Anat. Anz. 2010, 192, 162–167. [Google Scholar] [CrossRef]
- Moore, K.L.; Agur, A.M.R.; Dalley, A.F.; Moore, K.L. Essential Clinical Anatomy; Wolters Kluwer Health: Alphen aan den Rijn, The Netherlands, 2015. [Google Scholar]
- Modenese, L.; Phillips, A.T.M.; Bull, A.M.J. An open source lower limb model: Hip joint validation. J. Biomech. 2011, 44, 2185–2193. [Google Scholar] [CrossRef]
- Phillips, A.T.M. Structural optimisation: Biomechanics of the femur. Proc. ICE Eng. Comput. Mech. 2012, 165, 147–154. [Google Scholar] [CrossRef]
- Taddei, F.; Schileo, E.; Helgason, B.; Cristofolini, L.; Viceconti, M. The material mapping strategy influences the accuracy of CT-based finite element models of bones: An evaluation against experimental measurements. Med. Eng. Phys. 2007, 29, 973–979. [Google Scholar] [CrossRef]
- Les, C.; Keyak, J.; Stover, S.; Taylor, K.; Kaneps, A. Estimation of material properties in the equine metacarpus with use of quantitative computed tomography. J. Orthop. Res. 1994, 12, 822–833. [Google Scholar] [CrossRef]
- Keller, T.S. Predicting the compressive mechanical behavior of bone. J. Biomech. 1994, 27, 1159–1168. [Google Scholar] [CrossRef]
- Teo, J.C.; Si-Hoe, K.M.; Keh, J.E.; Teoh, S.H. Relationship between CT intensity, micro-architecture and mechanical properties of porcine vertebral cancellous bone. Clin. Biomech. 2006, 21, 235–244. [Google Scholar] [CrossRef]
| Model | Cortical Bone | Trabecular Bone |
|---|---|---|
| Orthotropic | Tetrahedral elements | |
| Isotropic | Tetrahedral elements | |
| Hybrid orthotropic | Shell elements | Tetrahedral elements |
| Hybrid isotropic | Shell elements | Tetrahedral elements |
| Structural | Shell elements | Truss elements |
| CT Scan Model | Isotropic Model | Orthotropic Model | Orthotropic Model | Orthotropic Model | Orthotropic Model | Orthotropic Model | |
|---|---|---|---|---|---|---|---|
| 10–1000 MPa | 26.32 | 63.83 | 86.33 | 91.45 | 89.37 | 71.89 | 81.79 |
| 10–2000 MPa | 47.37 | 77.88 | 89.64 | 93.89 | 92.27 | 78.85 | 87.56 |
| 10–3000 MPa | 59.48 | 84.23 | 91.44 | 95.10 | 93.74 | 82.57 | 90.43 |
| 10–5000 MPa | 73.74 | 91.01 | 93.53 | 96.39 | 95.38 | 86.82 | 93.57 |
| 10–10,000 MPa | 90.43 | 96.78 | 95.93 | 97.81 | 97.14 | 91.63 | 99.42 |
| 10–15,000 MPa | 98.51 | 98.27 | 97.14 | 98.50 | 98.01 | 94.06 | 99.97 |
| 10–18,000 MPa | 99.91 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Mean (MPa) | 3727.6 | 1688.7 | 1059.4 | 616.4 | 781.9 | 2161.3 | 819.2 |
| Std. dev. (MPa) | 3817.5 | 3076.9 | 3411.5 | 2559.7 | 2898.7 | 4646.9 | 1841.8 |
| Isotropic Model | Orthotropic Model | Orthotropic Model | Orthotropic Model | Orthotropic Model | Orthotropic Model | |
|---|---|---|---|---|---|---|
| 10–100 MPa | 33.87 | 80.06 | 87.98 | 83.05 | 59.76 | 69.44 |
| 10–200 MPa | 45.01 | 83.56 | 90.62 | 86.42 | 66.88 | 76.33 |
| 10–300 MPa | 52.78 | 85.56 | 91.99 | 88.24 | 70.84 | 80.16 |
| 10–500 MPa | 63.33 | 88.00 | 93.58 | 90.41 | 75.71 | 84.84 |
| 10–1000 MPa | 76.30 | 91.22 | 95.45 | 93.28 | 82.13 | 98.02 |
| 10–1500 MPa | 83.79 | 93.04 | 96.42 | 94.80 | 85.75 | 99.86 |
| 10–2000 MPa | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Mean (MPa) | 585.5 | 213.3 | 121.0 | 171.0 | 422.8 | 168.5 |
| Std. dev. (MPa) | 689.1 | 522.4 | 389.1 | 461.9 | 685.9 | 281.4 |
| Isotropic Model (%) | Orthotropic Model (%) | Structural Model (%) | |
|---|---|---|---|
| 0.1–0.3 mm | 47.33 | 45.51 | 37.46 |
| 0.1–0.5 mm | 62.21 | 58.99 | 56.30 |
| 0.1–1 mm | 75.60 | 72.27 | 76.61 |
| 0.1–2 mm | 83.68 | 81.06 | 88.72 |
| 0.1–3 mm | 86.91 | 85.00 | 93.38 |
| 0.1–4 mm | 88.81 | 87.10 | 95.66 |
| 0.1–5 mm | 100.00 | 100.00 | 100.00 |
| Mean (mm) | 1.1 | 1.2 | 0.9 |
| Std. dev. (mm) | 1.5 | 1.6 | 1.1 |
| Model | εmin (R2) | εmax (R2) | εmin (Slope) | εmax (Slope) |
|---|---|---|---|---|
| Isotropic | 0.64 | 0.63 | 0.33 | 0.33 |
| Orthotropic | 0.78 | 0.79 | 0.87 | 0.84 |
| Hybrid isotropic | 0.71 | 0.72 | 0.60 | 0.59 |
| Hybrid orthotropic | 0.70 | 0.69 | 0.60 | 0.59 |
| Structural | 0.66 | 0.65 | 0.69 | 0.70 |
| Model | Isotropic | Orthotropic | Hybrid Isotropic | Hybrid Orthotropic | Structural |
|---|---|---|---|---|---|
| Isotropic | N/A | 0.35 | 0.81 | 0.63 | 0.62 |
| Orthotropic | 0.49 | N/A | 0.49 | 0.53 | 0.53 |
| Hybrid isotropic | 0.84 | 0.57 | N/A | 0.83 | 0.85 |
| Hybrid orthotropic | 0.63 | 0.61 | 0.81 | N/A | 0.99 |
| Structural | 0.61 | 0.61 | 0.84 | 0.99 | N/A |
| Model | Isotropic | Orthotropic | Hybrid Isotropic | Hybrid Orthotropic | Structural |
|---|---|---|---|---|---|
| Isotropic | N/A | 1.49 | 0.59 | 0.36 | 0.36 |
| Orthotropic | 1.85 | N/A | 0.97 | 0.69 | 0.7 |
| Hybrid isotropic | 0.53 | 1.07 | N/A | 1.06 | 0.71 |
| Hybrid orthotropic | 0.33 | 0.74 | 1.1 | N/A | 0.98 |
| Structural | 0.33 | 0.74 | 0.71 | 0.98 | N/A |
| Model | Cortical Bone Volume (mm3) | Trabecular Bone Volume (mm3) | E < 2 GPa (mm3) | E >2 GPa (mm3) | Total Bone Volume (mm3) |
|---|---|---|---|---|---|
| CT scan | N/A | N/A | 23269.04 | 163487.15 | 186756.20 |
| Isotropic | N/A | N/A | 25041.63 | 30499.45 | 55541.09 |
| Orthotropic | N/A | N/A | 26810.03 | 34241.34 | 61051.37 |
| Hybrid isotropic | 14941.68 | 25750.14 | N/A | N/A | 40691.82 |
| Hybrid orthotropic | 16465.59 | 17396.64 | N/A | N/A | 33862.23 |
| Structural | 17969.76 | 42321.05 | N/A | N/A | 60290.81 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaharie, D.T.; Phillips, A.T.M. A Comparative Study of Continuum and Structural Modelling Approaches to Simulate Bone Adaptation in the Pelvic Construct. Appl. Sci. 2019, 9, 3320. https://doi.org/10.3390/app9163320
Zaharie DT, Phillips ATM. A Comparative Study of Continuum and Structural Modelling Approaches to Simulate Bone Adaptation in the Pelvic Construct. Applied Sciences. 2019; 9(16):3320. https://doi.org/10.3390/app9163320
Chicago/Turabian StyleZaharie, Dan T., and Andrew T.M. Phillips. 2019. "A Comparative Study of Continuum and Structural Modelling Approaches to Simulate Bone Adaptation in the Pelvic Construct" Applied Sciences 9, no. 16: 3320. https://doi.org/10.3390/app9163320
APA StyleZaharie, D. T., & Phillips, A. T. M. (2019). A Comparative Study of Continuum and Structural Modelling Approaches to Simulate Bone Adaptation in the Pelvic Construct. Applied Sciences, 9(16), 3320. https://doi.org/10.3390/app9163320





