FEM-Based Compression Fracture Risk Assessment in Osteoporotic Lumbar Vertebra L1
Abstract
1. Introduction
2. Methods and Materials
2.1. Problem Formulation
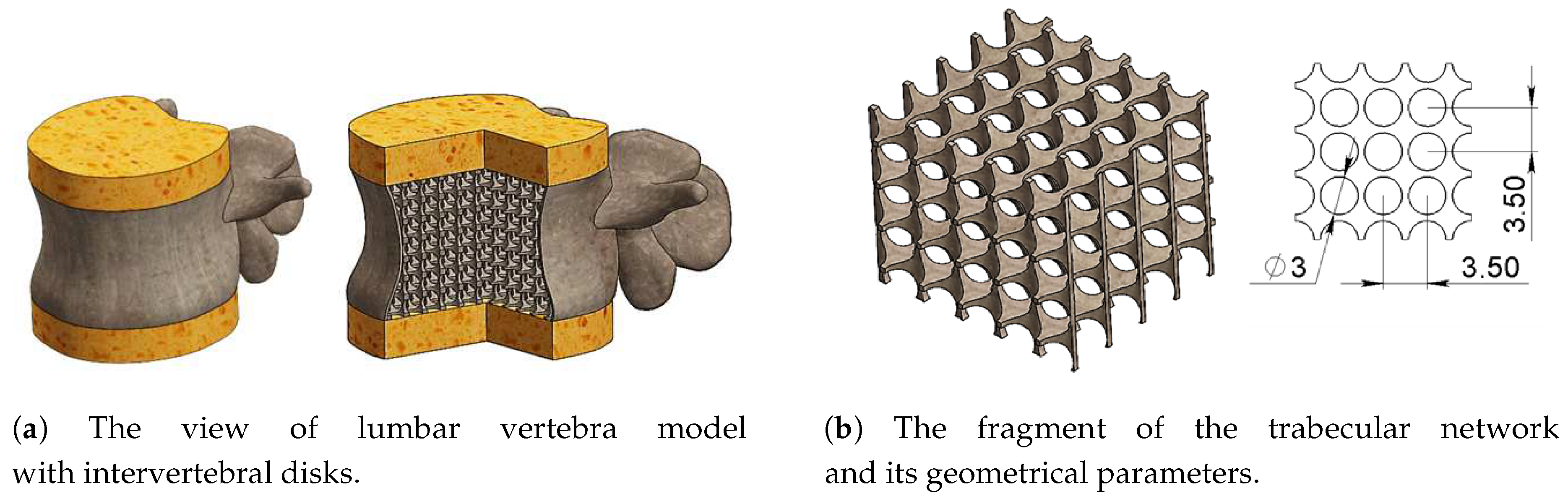
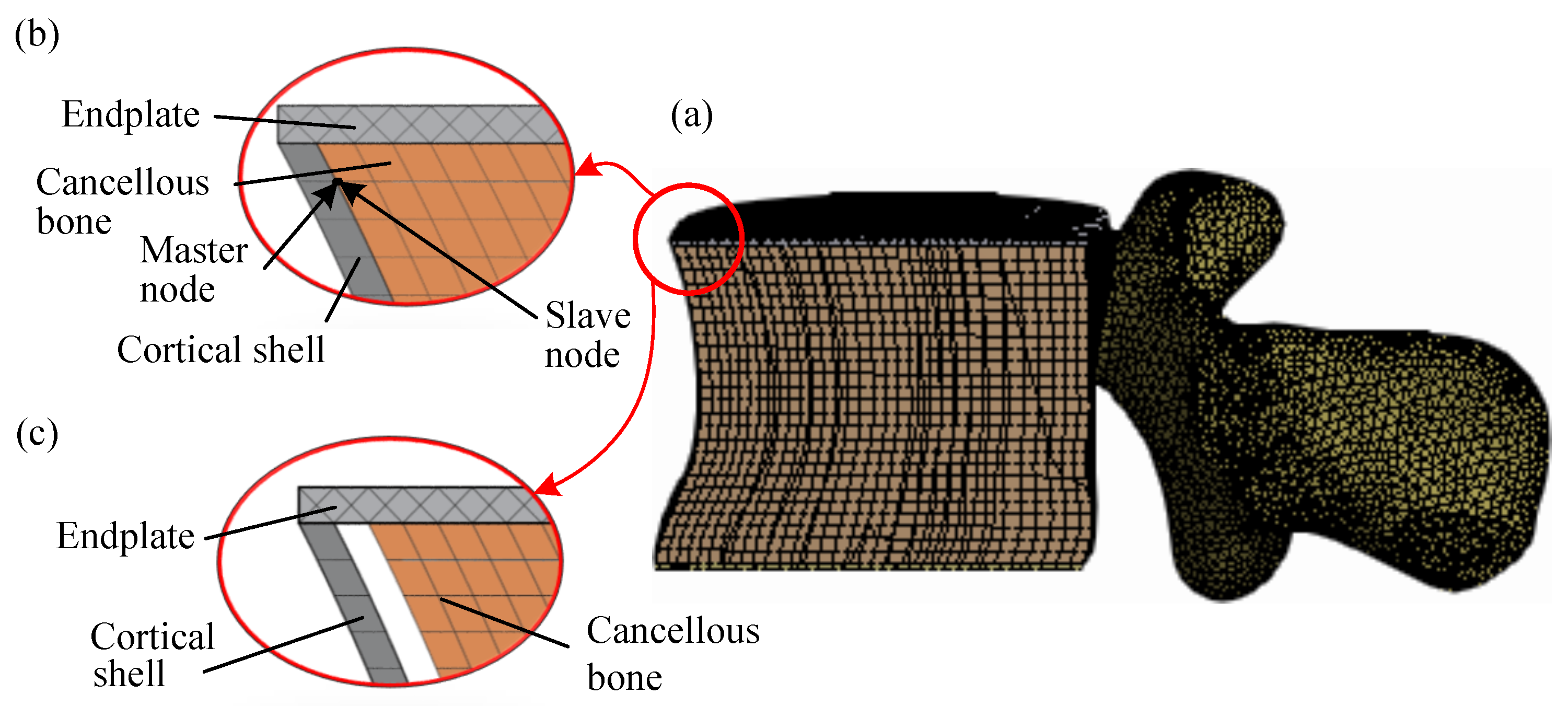
2.2. Structure and Geometrical Properties of the Model
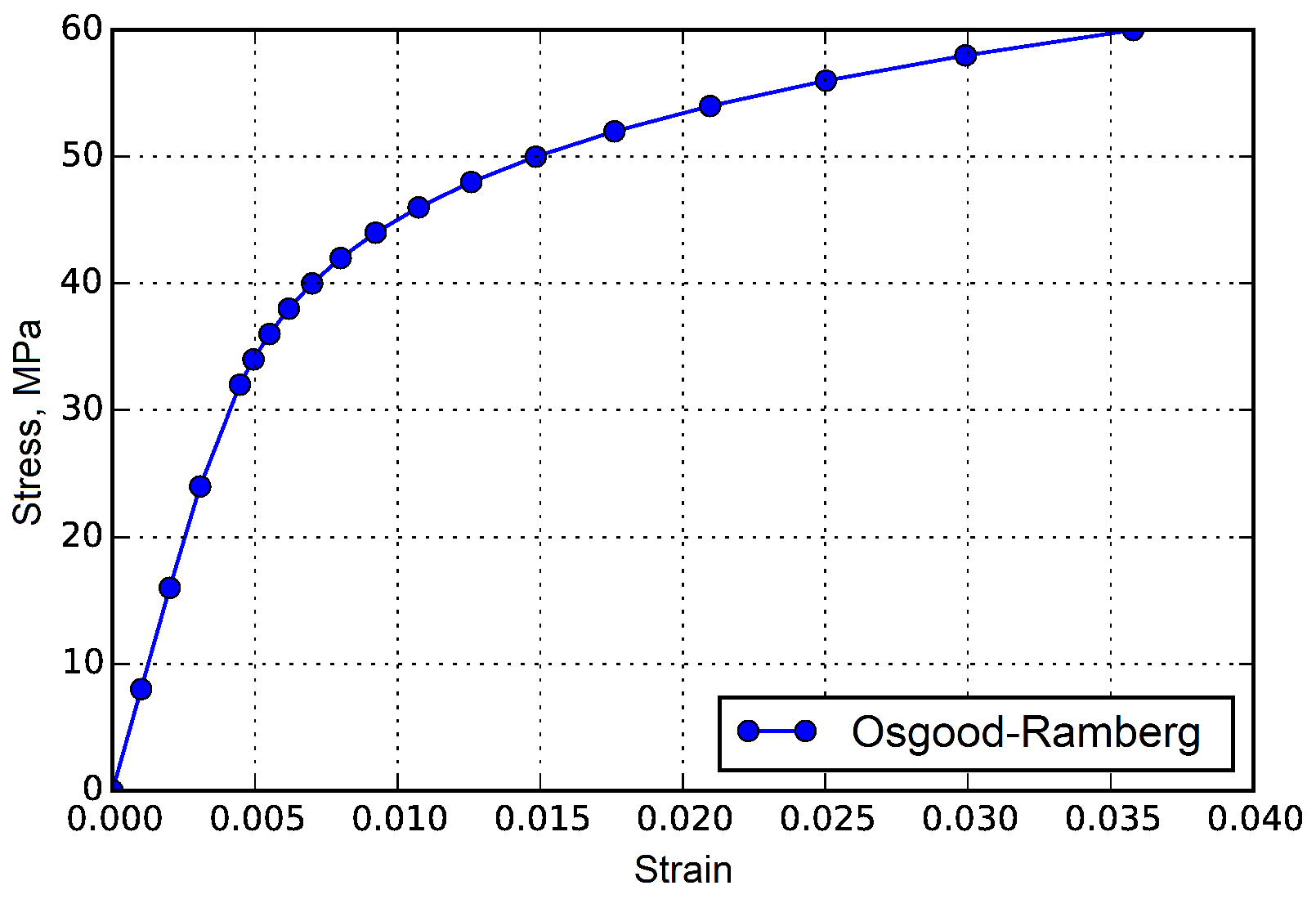
2.3. Mechanical Properties
2.4. The Parameters of Osteoporosis Impact
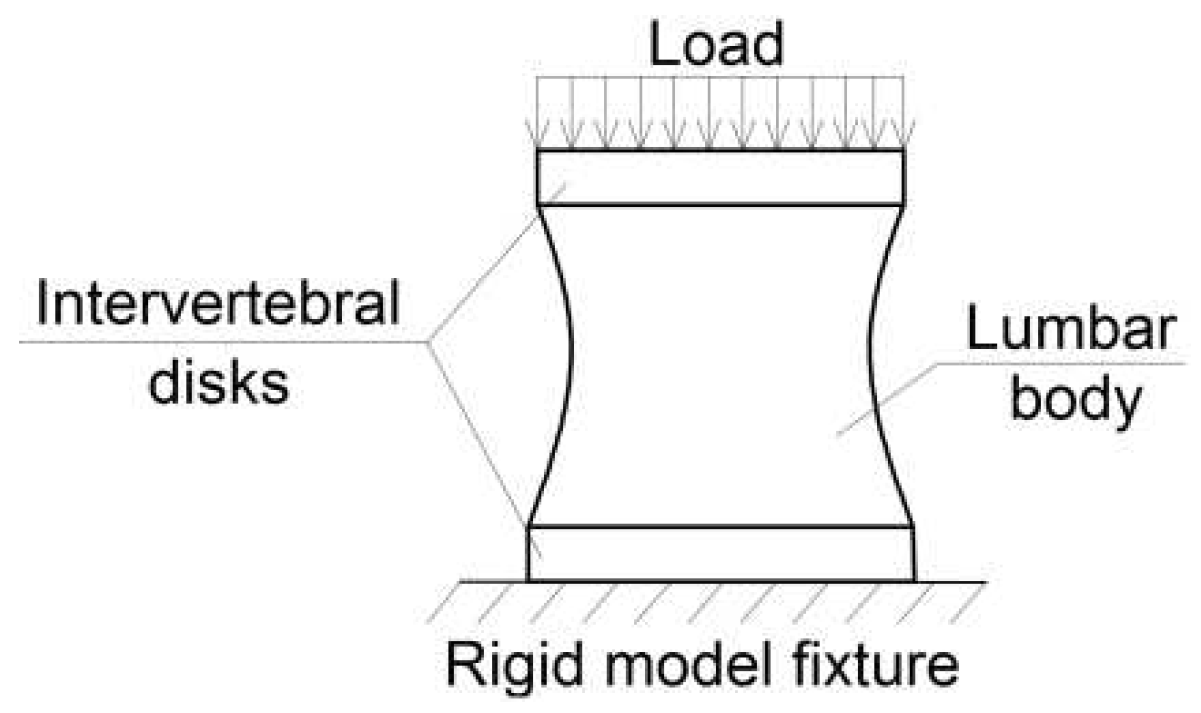
2.5. Boundary Conditions and Mesh
2.6. Risk Evaluation
3. Numerical Results and Discussion
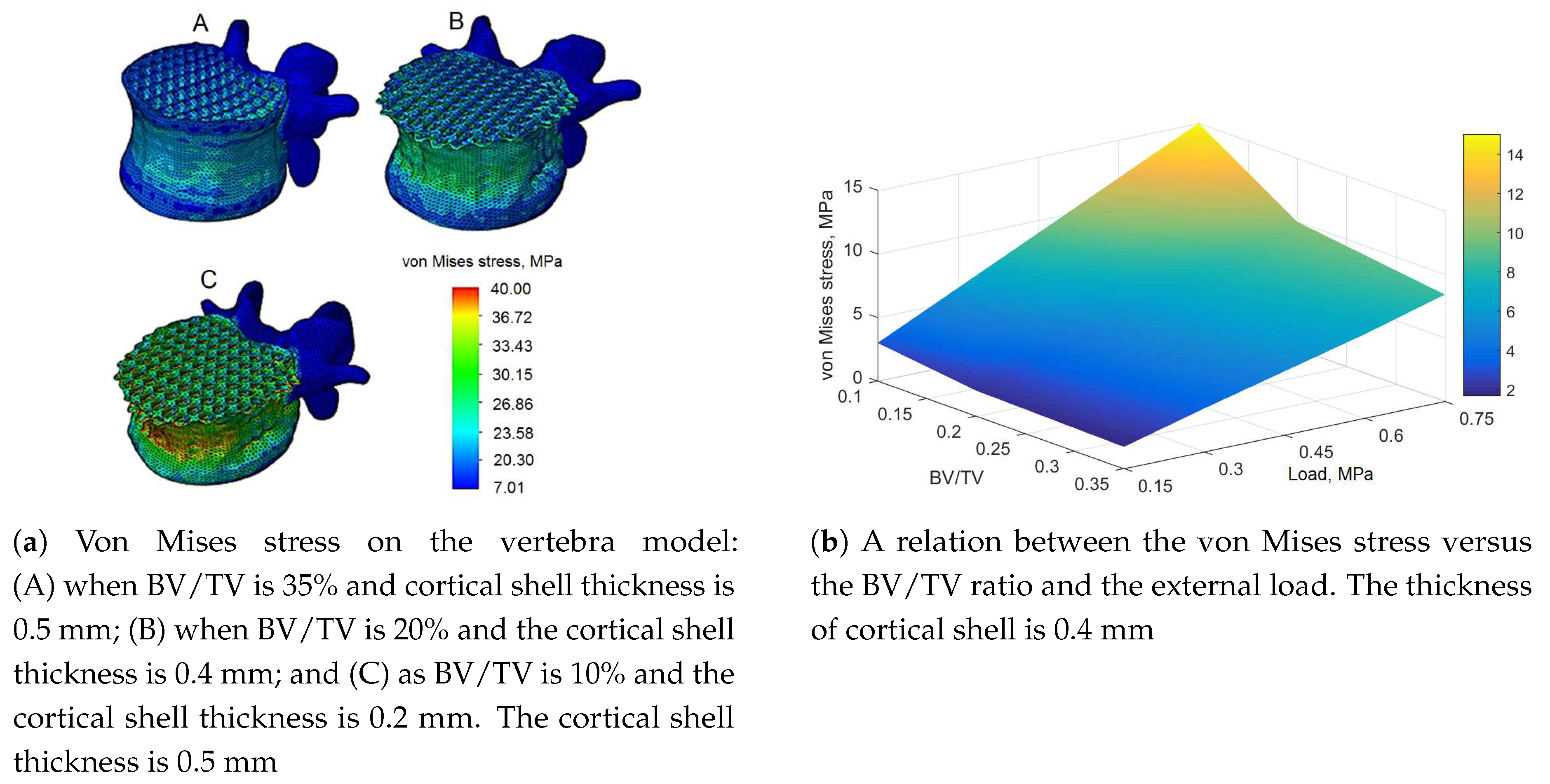
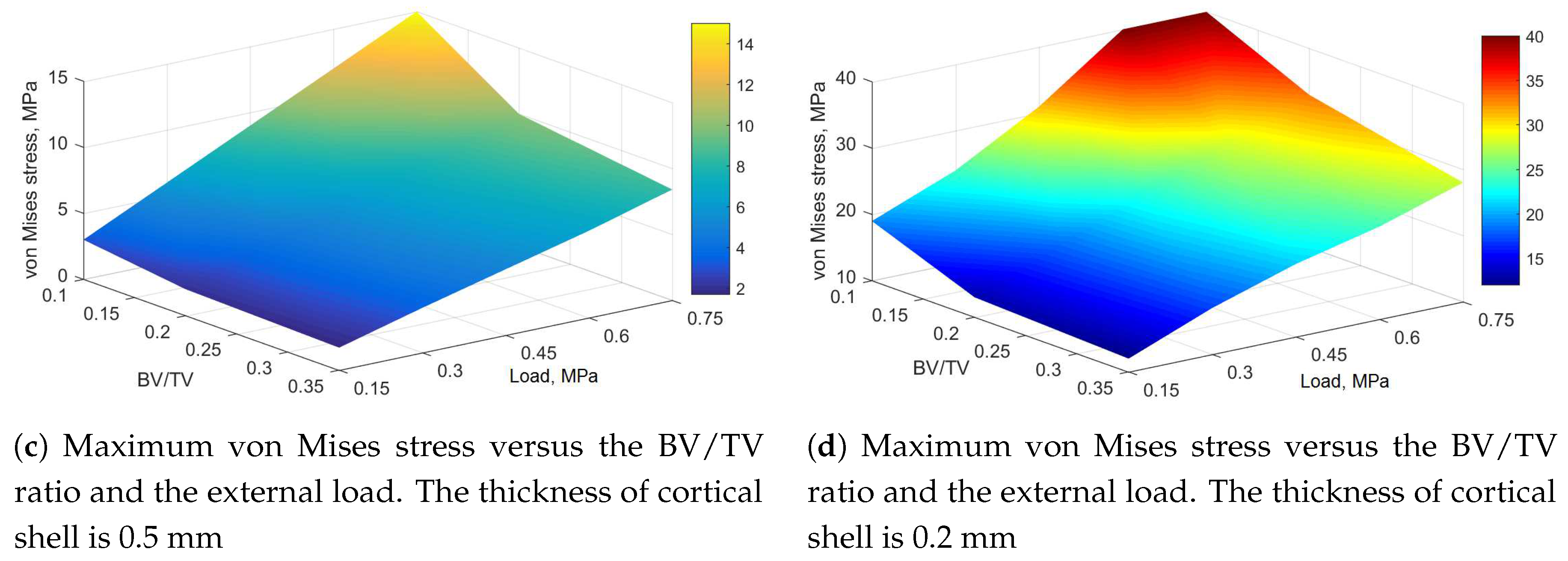
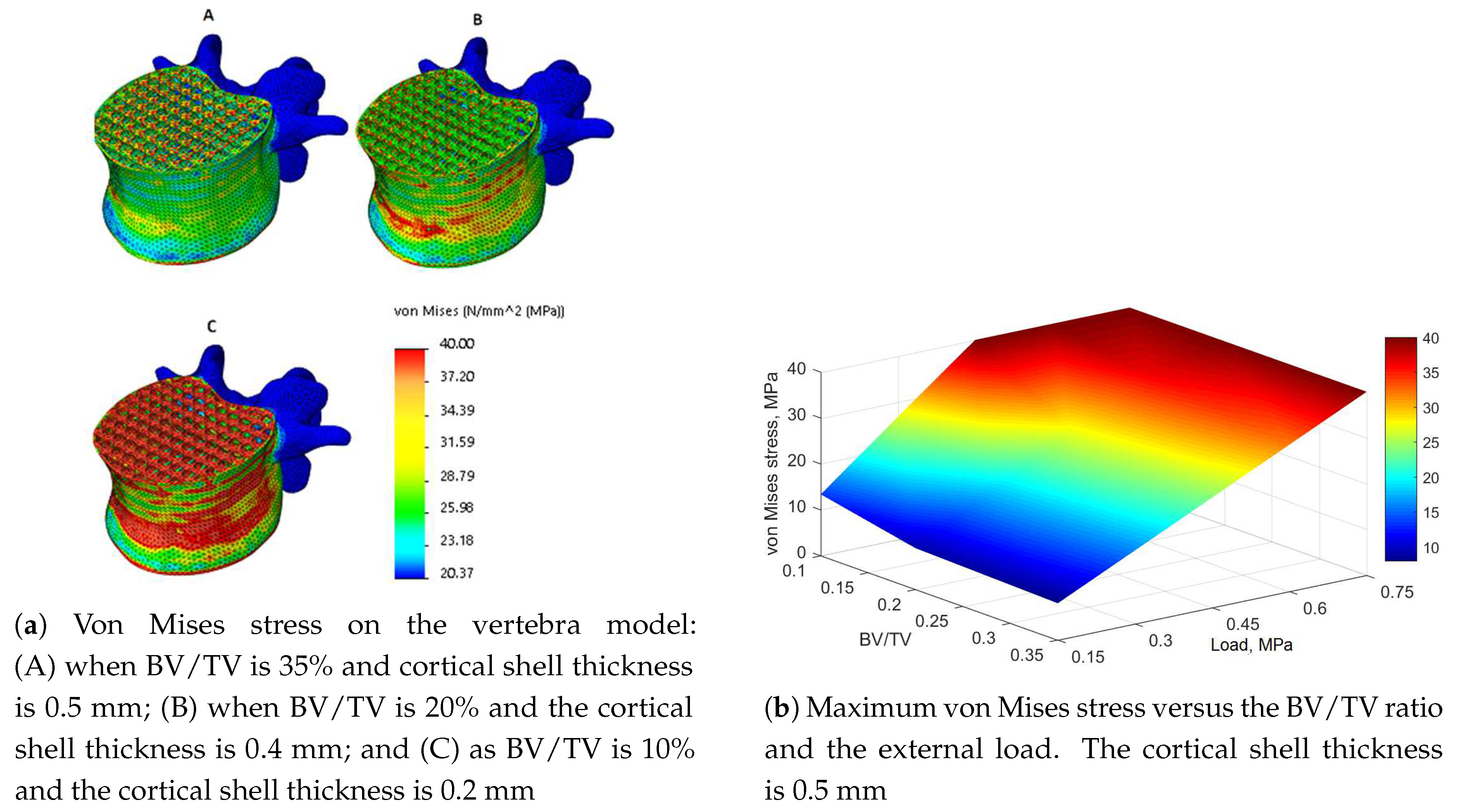
3.1. Static Analysis
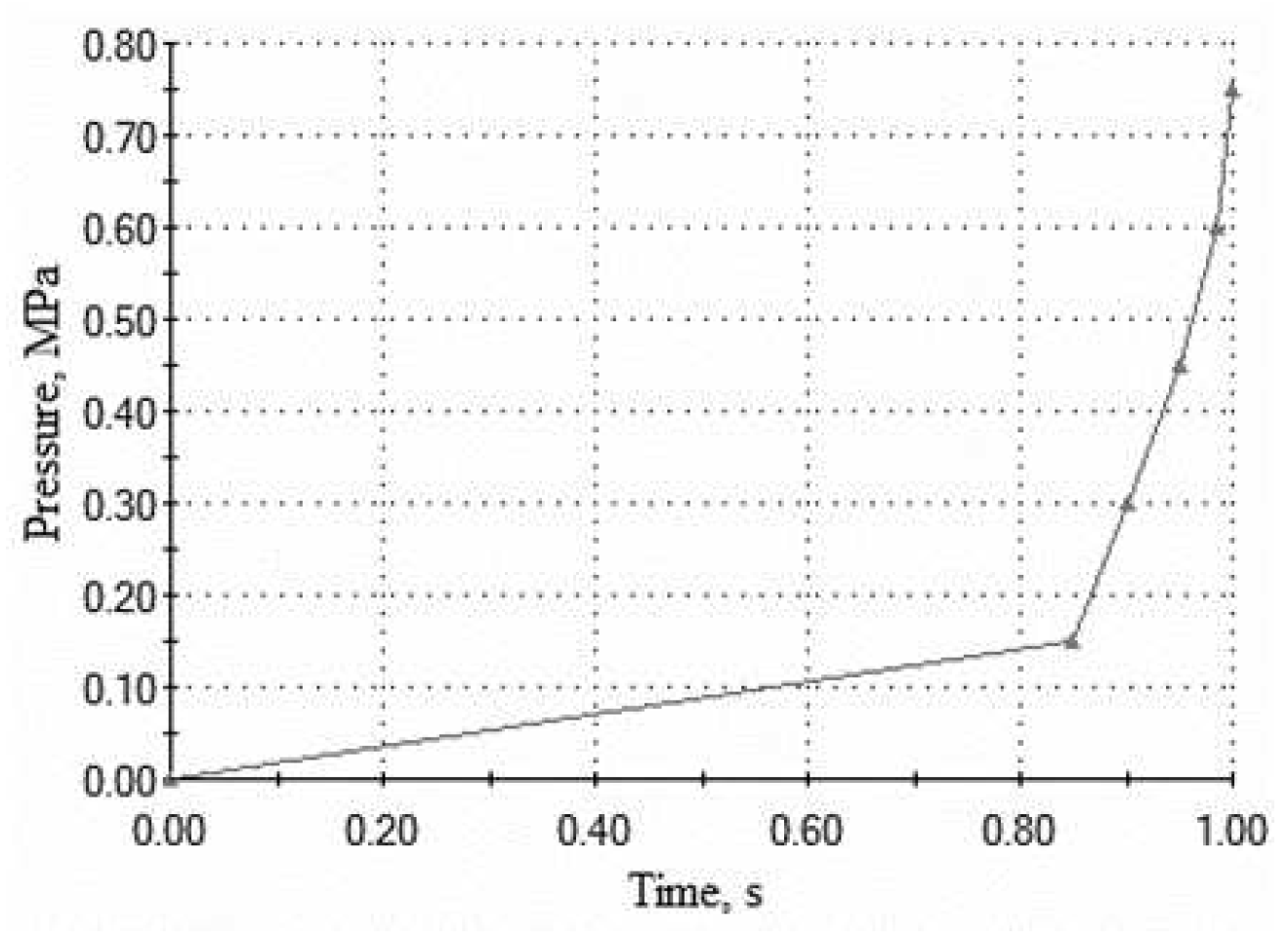
3.2. Dynamic Analysis
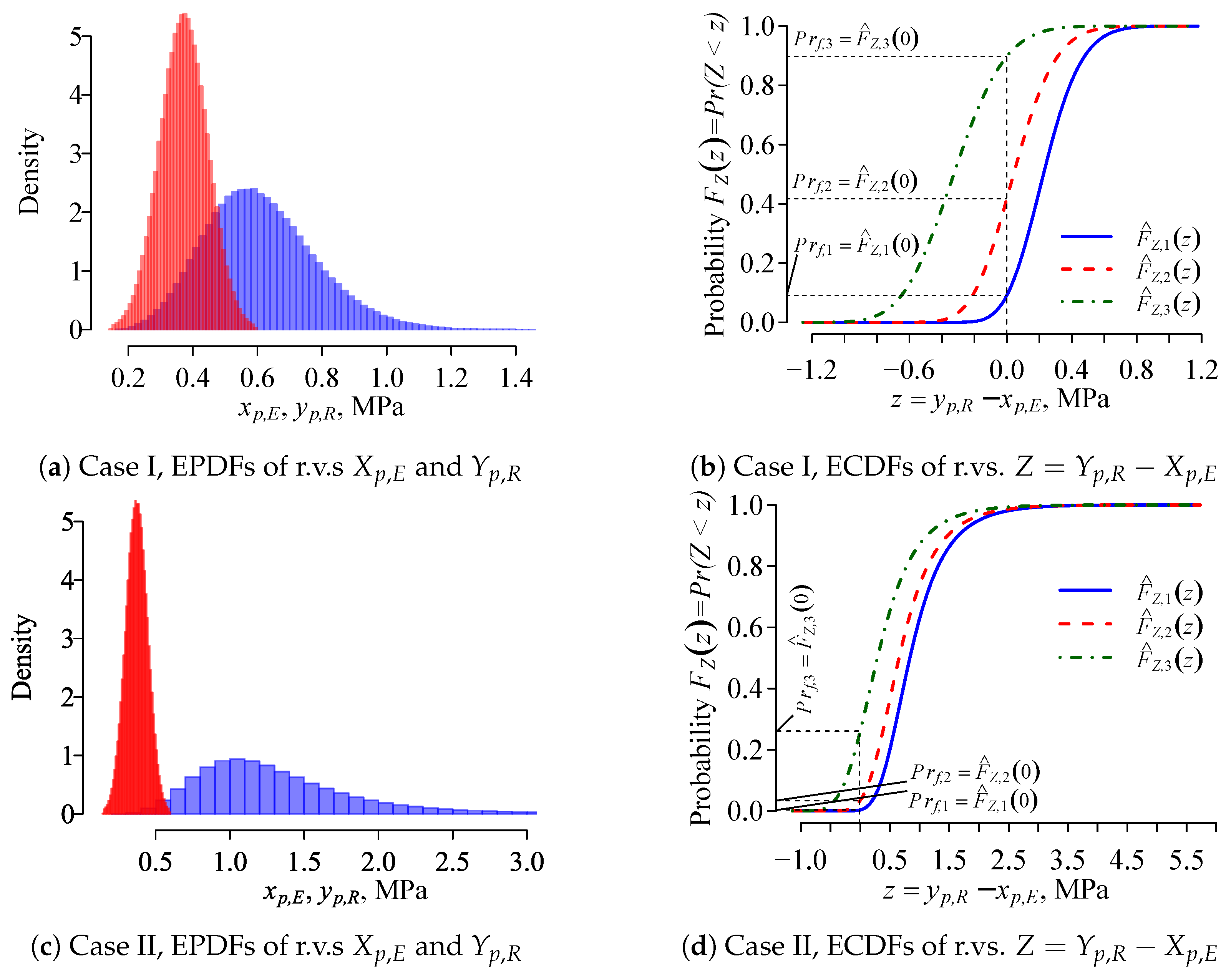
3.3. Estimation of the Fracture Risk
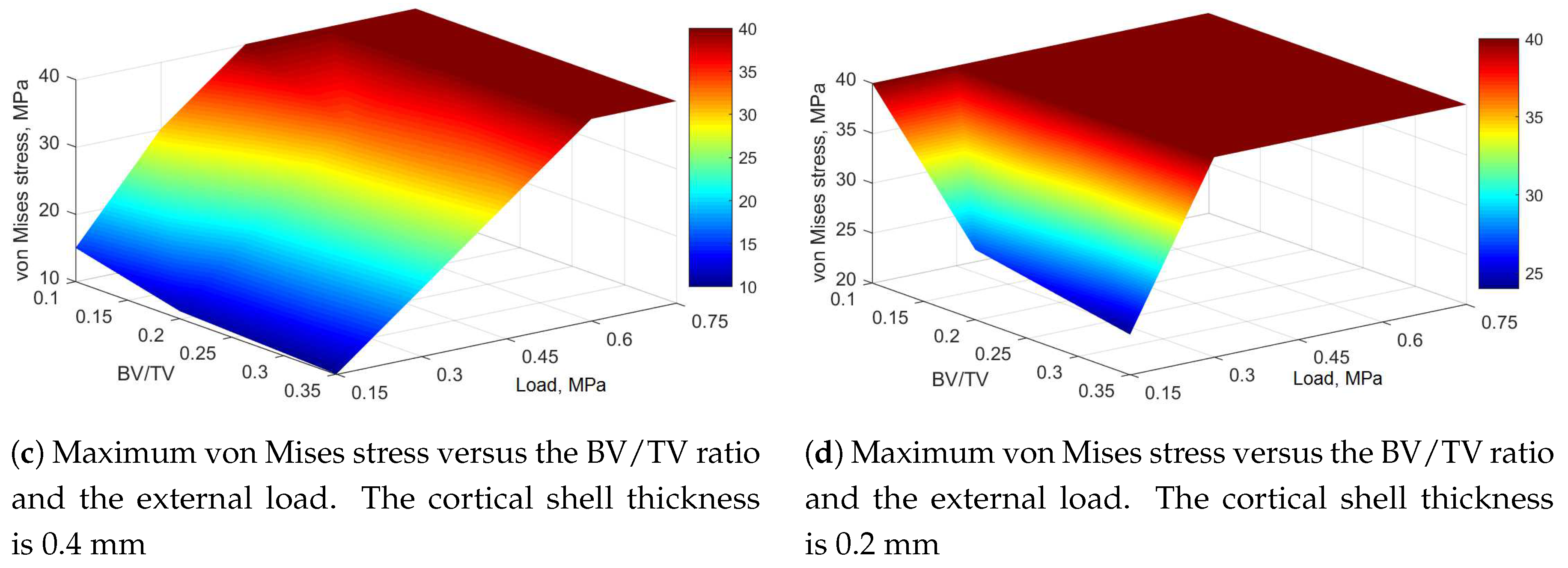
3.3.1. Approximation of the Maximum von Mises Stress
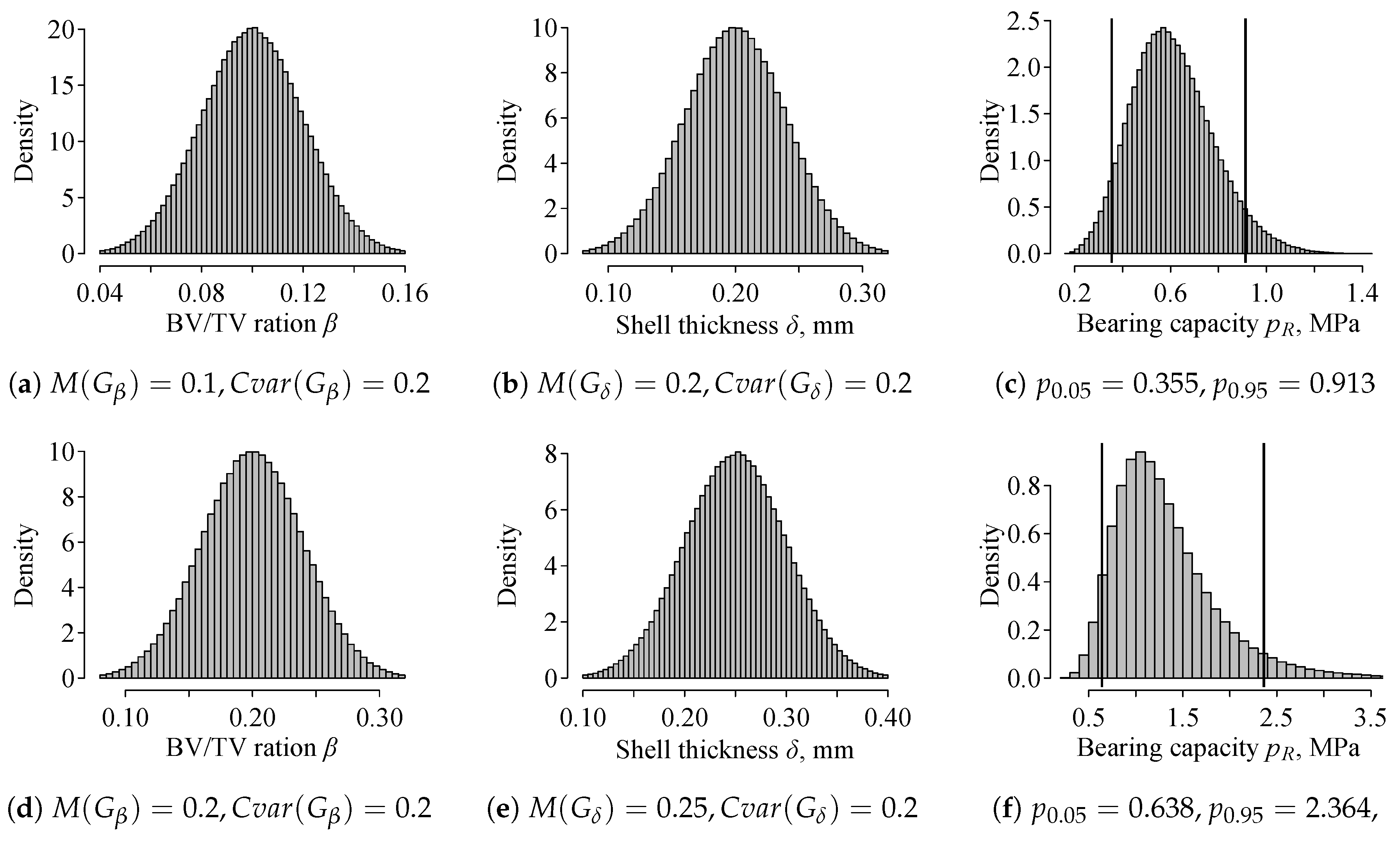
3.3.2. Stochastic Models and for the Risk Modelling
3.3.3. Fracture Risk Modelling Data, Results, and Discussion
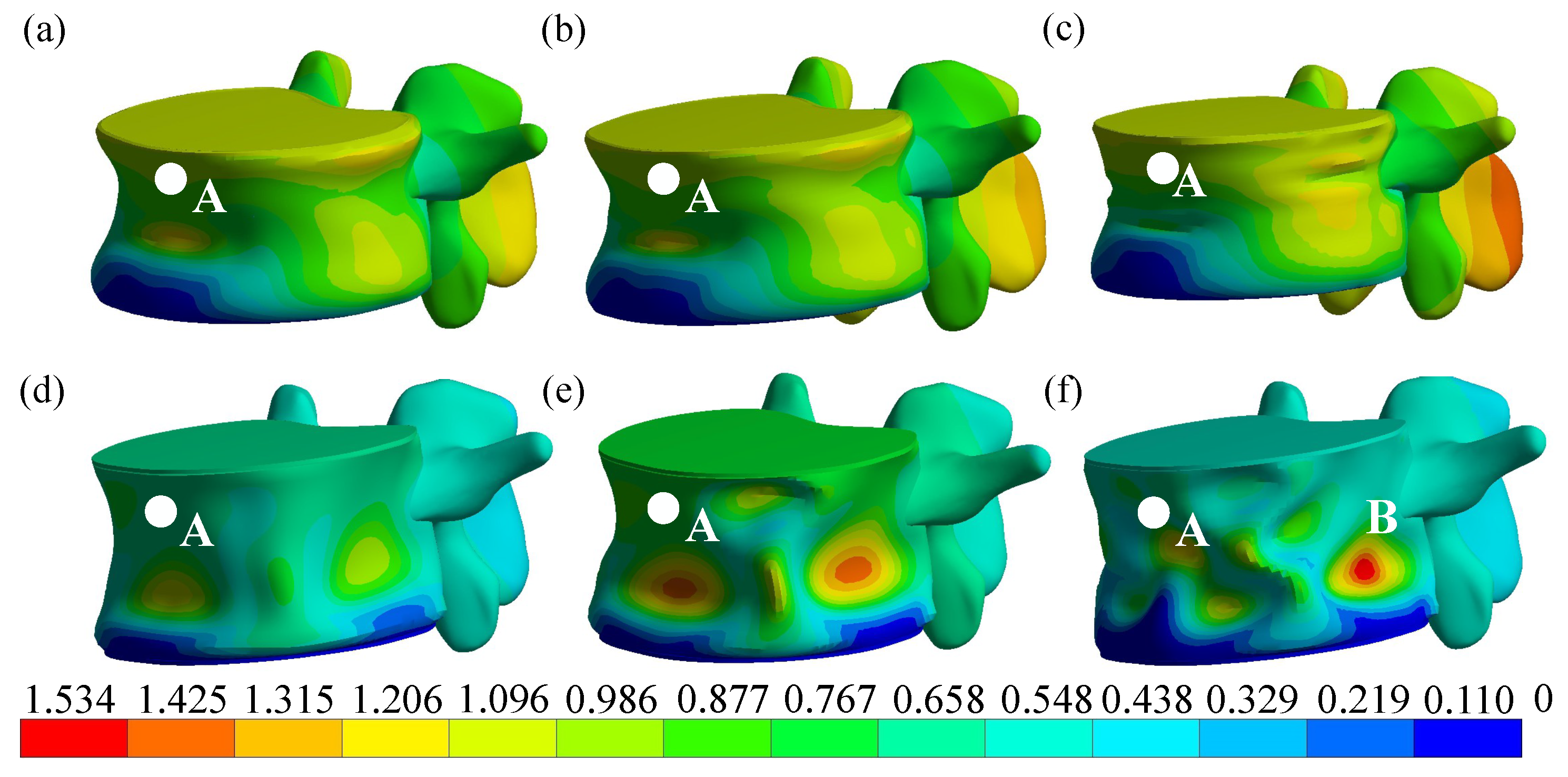
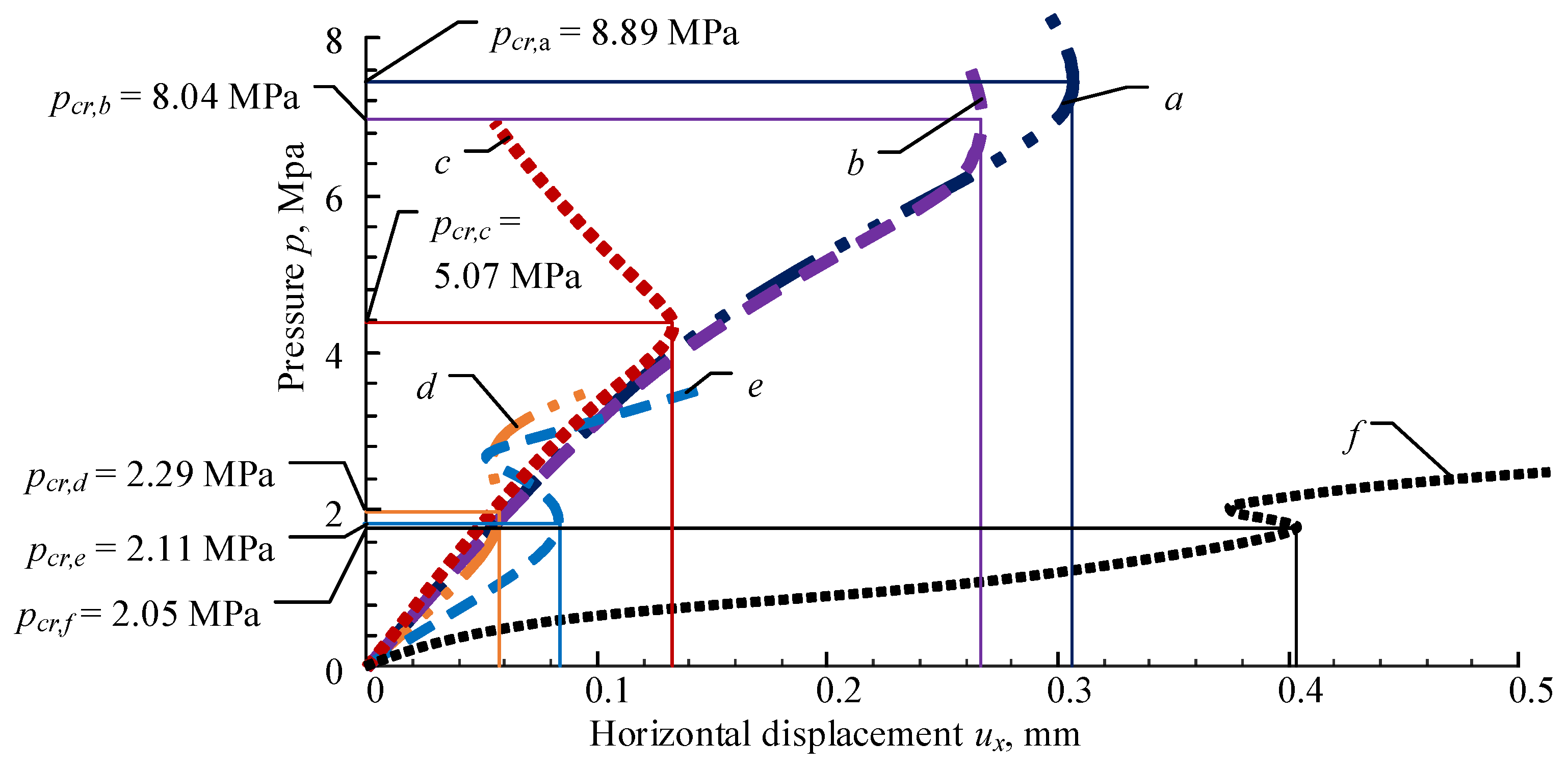
3.4. Influence of Vertebra Cortical Shell Buckling
3.5. Discussion on Model Limitations
3.6. Validation of Mechanical Model
- The printing of the vertebrae model;
- The printing of the cylindrical PLA sample for mechanical properties of PLA to define;
- The compression test of the printed PLA sample;
- The compression test of the printed PLA vertebrae;
- The determination of the mechanical properties of PLA by verifying the obtained load-displacement curve of the cylindrical sample;
- The implementation of the defined stress-strain curve of PLA onto the numerical calculation;
- The comparison of the results of the experimental and numerical studies.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| FEM | Finite element method |
| FE | Finite element |
| IVD | intervetebral disk |
| BV/TV | Bone volume vs total volume |
| QCT | Quantitative computational tomography |
| BMD | Bone mineral density |
| DXA | Dual-energy X-ray absorptiometry |
References
- Agrawal, A.; Kalia, R. Osteoporosis: Current Review. J. Orthop. Traumatol. Rehabil. 2014, 7, 101. [Google Scholar] [CrossRef]
- Lin, J.T.; Lane, J.M. Osteoporosis: A review. Clin. Orthop. Relat. Res. 2004, 425, 126–134. [Google Scholar] [CrossRef]
- Cooper, C.; Cole, Z.A.; Holroyd, C.R.; Earl, S.C.; Harvey, N.C.; Dennison, E.M.; Melton, L.J.; Cummings, S.R.; Kanis, J.A. The IOF CSA Working Group on Fracture Epidemiology. Secular trends in the incidence of hip and other osteoporotic fractures. Osteoporos. Int. 2011, 22, 1277–1288. [Google Scholar] [CrossRef]
- Cummings, S.R.; Melton, L.J., III. Epidemiology and outcomes of osteoporotic fractures. Lancet 2002, 359, 1761–1767. [Google Scholar] [CrossRef]
- Doblaré, M.; García, J.M.; Gómez, M.J. Modelling bone tissue fracture and healing: A review. Eng. Fract. Mech. 2004, 71, 1809–1840. [Google Scholar] [CrossRef]
- odygowski, T.; Kakol, W.; Wierszycki, M.; Ogurkowska, B.M. Three-dimensional nonlinear finite element model of the human lumbar spine segment. Acta Bioeng. Biomech. 2005, 7, 17–28. [Google Scholar]
- Su, J.; Cao, L.; Li, Z.; Yu, B.; Zhang, C.; Li, M. Three-dimensional finite element analysis of lumbar vertebra loaded by static stress and its biomechanical significance. Chin. J. Traumatol. 2009, 12, 153–156. [Google Scholar]
- Jones, A.C.; Wilcox, R.K. Finite element analysis of the spine: Towards a framework of verification, validation and sensitivity analysis. Med. Eng. Phys. 2008, 30, 1287–1304. [Google Scholar] [CrossRef]
- Crawford, R.P.; Cann, C.E.; Keaveny, T.M. Finite element models predict in vitro vertebral body compressive strength better than quantitative computed tomography. Bone 2003, 33, 744–750. [Google Scholar] [CrossRef]
- Maquer, G.; Schwiedrzik, J.; Huber, G.; Morlock, M.M.; Zysset, P.K. Compressive strength of elderly vertebrae is reduced by disc degeneration and additional flexion. J. Mech. Behav. Biomed. Mater. 2015, 42, 54–66. [Google Scholar] [CrossRef]
- Provatidis, C.; Vossou, C.; Koukoulis, I.; Balanika, A.; Baltas, C.; Lyritis, G. A pilot finite element study of an osteoporotic L1-vertebra compared to one with normal T-score. Comput. Methods Biomech. Biomed. Eng. 2010, 13, 185–195. [Google Scholar] [CrossRef]
- McDonald, K.; Little, J.; Pearcy, M.; Adam, C. Development of a multi-scale finite element model of the osteoporotic lumbar vertebral body for the investigation of apparent level vertebra mechanics and micro-level trabecular mechanics. Med. Eng. Phys. 2010, 32, 653–661. [Google Scholar] [CrossRef]
- Garo, A.; Arnoux, P.J.; Wagnac, E.; Aubin, C.E. Calibration of the mechanical properties in a finite element model of a lumbar vertebra under dynamic compression up to failure. Med. Biol. Eng. Comput. 2011, 49, 1371–1379. [Google Scholar] [CrossRef]
- Kim, Y.H.; Wu, M.; Kim, K. Stress Analysis of Osteoporotic Lumbar Vertebra Using Finite Element Model with Microscaled Beam-Shell Trabecular-Cortical Structure. J. Appl. Math. 2013, 2013, 285165. [Google Scholar] [CrossRef]
- Wierszycki, M.; Szajek, K.; Łodygowski, T.; Nowak, M. A two-scale approach for trabecular bone microstructure modeling based on computational homogenization procedure. Comput. Mech. 2014, 54, 287–298. [Google Scholar] [CrossRef]
- Wolfram, U.; Gross, T.; Pahr, D.H.; Schwiedrzik, J.; Wilke, H.J.; Zysset, P.K. Fabric-based Tsai-Wu yield criteria for vertebral trabecular bone in stress and strain space. J. Mech. Behav. Biomed. Mater. 2012, 15, 218–228. [Google Scholar] [CrossRef]
- El-Rich, M.; Arnoux, P.J.; Wagnac, E.; Brunet, C.; Aubin, C.E. Finite element investigation of the loading rate effect on the spinal load-sharing changes under impact conditions. J. Biomech. 2009, 42, 1252–1262. [Google Scholar] [CrossRef]
- Pothuaud, L.; Carceller, P.; Hans, D. Correlations between grey-level variations in 2D projection images (TBS) and 3D microarchitecture: Applications in the study of human trabecular bone microarchitecture. Bone 2008, 42, 775–778. [Google Scholar] [CrossRef]
- Hans, D.; Barthe, N.; Boutroy, S.; Pothuaud, L.; Winzenrieth, R.; Krieg, M.-A. Correlations Between Trabecular Bone Score, Measured Using Anteroposterior Dual-Energy X-Ray Absorptiometry Acquisition, and 3-Dimensional Parameters of Bone Microarchitecture: An Experimental Study on Human Cadaver Vertebrae. J. Clin. Densitom. 2011, 14, 302–312. [Google Scholar] [CrossRef]
- Kanis, J.A.; Oden, V.; Johnell, O.; Johansson, H.; De Laet, C.; Brown, J.; Burckhardt, P.; Cooper, C.; Christiansen, C.; Cummings, S.; et al. The use of clinical risk factors enhances the performance of BMD in the prediction of hip and osteoporotic fractures in men and women. Osteoporos. Int. 2007, 18, 1033–1046. [Google Scholar] [CrossRef]
- Marshall, D.; Johnell, O.; Wedel, H. Meta-analysis of how well measures of bone mineral density predict occurrence of osteoporotic fractures. BMJ 1996, 312, 1254–1259. [Google Scholar] [CrossRef]
- Taylor, B.C.; Schreiner, P.J.; Stone, K.L.; Fink, H.A.; Cummings, S.R.; Nevitt, M.C.; Bowman, P.J.; Ensrud, K.E. Long-term prediction of incident hip fracture risk in elderly white women: Study of osteoporotic fractures. J. Am. Geriatr. Soc. 2004, 52, 1479–1486. [Google Scholar] [CrossRef]
- Kanis, J.A.; Oden, A.; Johansson, H.; Borgstrom, F.; Strom, O.; McCloskey, E. FRAX and its applications to clinical practice. Bone 2009, 44, 734–743. [Google Scholar] [CrossRef]
- Kanis, J.A.; Johnell, O.; Oden, A.; Johansson, H.; McCloskey, E. FRAX and the assessment of fracture probability in men and women from the UK. Osteoporos. Int. 2008, 19, 385–397. [Google Scholar] [CrossRef]
- Timothy, H.K.; Brandeau, J.F. Mathematical modeling of the stress strain-strain rate behavior of bone using the Ramberg-Osgood equation. J. Biomech. 1983, 16, 445–450. [Google Scholar]
- Nazarian, A.; von Stechow, D.; Zurakowski, D.; Muller, R.; Snyder, B.D. Bone Volume Fraction Explains the Variation in Strength and Stiffness of Cancellous Bone Affected by Metastatic Cancer and Osteoporosis. Calcif. Tissue Int. 2008, 83, 368–379. [Google Scholar] [CrossRef]
- Abaqus FEA, SIMULIA Web Site. Dassault Systèmes, Retrieved 2017. Available online: https://www.3ds.com/ (accessed on 25 July 2019).
- Linthorne, N.P. Analysis of standing vertical jumps using a force platform. J. Sports Sci. Med. 2010, 9, 282–287. [Google Scholar] [CrossRef]
- Dodson, B.; Noland, D. Reliability Engineering Handbook; CRC Press LLC Main Office: Boca Raton, FL, USA, 1999; p. 592. [Google Scholar]
- Melton, L.J., III; Achenbach, S.J.; Atkinson, E.J.; Therneau, T.M.; Amin, S. Long-term mortality following fractures at different skeletai sites: A population-based cohort study. Osteoporos. Int. 2013, 24, 1689–1696. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.R-project.org/ (accessed on 25 July 2019).
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team (2017). Nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 3.1-131. 2017. Available online: https://CRAN.R-project.org/package=nlme (accessed on 25 July 2019).
- Fields, A.J.; Eswaran, S.K.; Jekir, M.G.; Keaveny, T.M. Role of trabecular microarchitecture in whole-vertebral body biomechanical behavior. J. Bone Miner. Res. 2009, 24, 1523–1530. [Google Scholar] [CrossRef]
- Roux, J.P.; Wegrzyn, J.; Arlot, M.E.; Guyen, O.; Delmas, P.D.; Chapurlat, R.; Bouxsein, M.L. Contribution of trabecular and cortical components to biomechanical behavior of human vertebrae: An ex vivo study. J. Bone Miner. Res. 2010, 25, 356–361. [Google Scholar] [CrossRef]
- Jaumard, N.V.; Bauman, J.A.; Weisshaar, C.L.; Guarino, B.B.; Welch, W.C.; Winkelstein, B.A. Contact pressure in the facet joint during sagittal bending of the cadaveric cervical spine. J. Biomech. Eng. 2011, 133, 071004. [Google Scholar] [CrossRef]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002; ISBN 0-387-95457-0. [Google Scholar]
- Mann, K.A.; Miller, M.A. Fluid-structure interactions in micro-interlocked regions of the cement-bone interface. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 1809–1820. [Google Scholar] [CrossRef][Green Version]
- Souzanchi, M.F.; Palacio-Mancheno, P.; Borisov, Y.A.; Cardoso, L.; Cowin, S.C. Microarchitecture and bone quality in the human calcaneus: Local variations of fabric anisotropy. J. Bone Min. Res. 2012, 27, 2562–2572. [Google Scholar] [CrossRef]
- Polikeit, A.; Nolte, L.P.; Ferguson, S.J. Simulated influence of osteoporosis and disc degeneration on the load transfer in a lumbar functional spinal unit. J. Biomech. 2004, 37, 1061–1069. [Google Scholar] [CrossRef]
- Helgason, B.; Perilli, E.; Schileo, E.; Taddei, F.; Brynjólfsson, S.S.; Viceconti, M. Mathematical relationships between bone density and mechanical properties: A literature review. Clin. Biomech. 2008, 23, 135–146. [Google Scholar] [CrossRef]
- Genant, H.K.; Wu, C.Y.; van Kuijk, C.; Nevitt, M.C. Vertebral fracture assessment using a semiquantitative technique. J. Bone Min. Res. 1993, 8, 1137–1148. [Google Scholar] [CrossRef]
- Lakes, R.S.; Katz, J.L.; Sternstein, S.S. Viscoelastic properties of wet cortical bone: Part I, torsional and biaxial studies. J. Biomech. 1979, 12, 657–678. [Google Scholar] [CrossRef]
- Lakes, R.S.; Katz, J.L. Viscoelastic properties of wet cortical bone: Part II, relaxation mechanisms. J. Biomech. 1979, 12, 679–687. [Google Scholar] [CrossRef]
- Lakes, R.S.; Katz, J.L. Viscoelastic properties of wet cortical bone: Part III, A non-linear constitutive equation. J. Biomech. 1979, 12, 689–698. [Google Scholar] [CrossRef]
- Burczinski, T. Multiscale Modelling of Osseous Tissues. J. Theor. Appl. Mech. 2010, 48, 855–870. [Google Scholar]
- Wolf, J. Das Gesetz der Transformation der Knochen; Hirschwald: Berlin, Germany, 1892. [Google Scholar]
- Goldenblar, I.I.; Kopnov, A. Strength of Glass Reinforced Plastics in the Complex Stress State. Polym. Mech. 1966, 1, 54–60. [Google Scholar] [CrossRef]
- von Mises, R. Mechanik der festen Körper im plastisch deformablen Zustand Göttin. Nachr. Math. Phys. 1913, 1, 582–592. [Google Scholar]
- Hill, R. The Mathematical Theory of Plasticity; Oxford, U.P.: Oxford, UK, 1950. [Google Scholar]
- Tsai, S.W. Strength Theories of Filamentary Structures. In Fundamental Aspects of Fibre Reinforced Plastic Composites; Schwartz, R.T., Schwartz, H.S., Eds.; Interscience: New York, NY, USA, Chapter 1; 1968. [Google Scholar]
- Korenczuk, C.E.; Votava, L.E.; Dhume, R.Y.; Kizilski, S.B.; Brown, G.E.; Narain, R.; Barocas, V.H. Isotropic Failure Criteria Are Not Appropriate for Anisotropic Fibrous Biological Tissues. J. Biomech. Eng. 2017, 139, 071008. [Google Scholar] [CrossRef]
- Wilcox, B.; Mobbs, R.J.; Wu, A.M.; Phan, K. Systematic review of 3D printing in spinal surgery: The current state of play. J. Spine Surg. 2017, 3, 433–443. [Google Scholar] [CrossRef]




| Property | Lumbar Body | Intervertebra Disc |
|---|---|---|
| Young modulus, MPa | 8000 | 10 |
| Ulimate strength, MPa | 60 | - |
| Yield strength, MPa | 40 | - |
| Poisson’s ratio | 0.30 | 0.40 |
| Model | Thickness, mm | BV/TV | TBS |
|---|---|---|---|
| Healthy | 0.5 | 0.35 | 1.45 |
| Ostseopenea | 0.4 | 0.20 | 1.33 |
| Osteoporosis | 0.2 | 0.10 | 1.20 |
| Cortical Shell Thickness, mm | BV/TV | TBS |
|---|---|---|
| 0.20 | 0.10 | 1.28 |
| 0.40 | 0.10 | 1.28 |
| 0.50 | 0.10 | 1.28 |
| 0.20 | 0.20 | 1.33 |
| 0.40 | 0.20 | 1.33 |
| 0.50 | 0.20 | 1.33 |
| 0.20 | 0.35 | 1.45 |
| 0.40 | 0.35 | 1.45 |
| 0.50 | 0.35 | 1.45 |
| Analysis | Thickness, mm, | BV/TV, | External Load, MPa, p | ||||
|---|---|---|---|---|---|---|---|
| 0.15 | 0.30 | 0.45 | 0.60 | 0.75 | |||
| Static | 0.5 | 0.10 | 2.9 | 6.1 | 9.3 | 12.3 | 15.2 |
| 0.20 | 2.0 | 4.1 | 6.1 | 8.2 | 8.5 | ||
| 0.35 | 1.6 | 3.4 | 5.0 | 6.7 | 8.5 | ||
| 0.4 | 0.10 | 3.4 | 6.7 | 10.2 | 14.1 | 17.0 | |
| 0.20 | 2.1 | 4.2 | 6.3 | 8.4 | 10.5 | ||
| 0.35 | 1.8 | 3.5 | 5.4 | 7.3 | 9.1 | ||
| 0.2 | 0.10 | 18.9 | 24.1 | 31.3 | 40.8 | 49.4 | |
| 0.20 | 13.3 | 18.4 | 23.2 | 28.1 | 33.5 | ||
| 0.35 | 12.1 | 17.4 | 21.0 | 24.5 | 28.0 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maknickas, A.; Alekna, V.; Ardatov, O.; Chabarova, O.; Zabulionis, D.; Tamulaitienė, M.; Kačianauskas, R. FEM-Based Compression Fracture Risk Assessment in Osteoporotic Lumbar Vertebra L1. Appl. Sci. 2019, 9, 3013. https://doi.org/10.3390/app9153013
Maknickas A, Alekna V, Ardatov O, Chabarova O, Zabulionis D, Tamulaitienė M, Kačianauskas R. FEM-Based Compression Fracture Risk Assessment in Osteoporotic Lumbar Vertebra L1. Applied Sciences. 2019; 9(15):3013. https://doi.org/10.3390/app9153013
Chicago/Turabian StyleMaknickas, Algirdas, Vidmantas Alekna, Oleg Ardatov, Olga Chabarova, Darius Zabulionis, Marija Tamulaitienė, and Rimantas Kačianauskas. 2019. "FEM-Based Compression Fracture Risk Assessment in Osteoporotic Lumbar Vertebra L1" Applied Sciences 9, no. 15: 3013. https://doi.org/10.3390/app9153013
APA StyleMaknickas, A., Alekna, V., Ardatov, O., Chabarova, O., Zabulionis, D., Tamulaitienė, M., & Kačianauskas, R. (2019). FEM-Based Compression Fracture Risk Assessment in Osteoporotic Lumbar Vertebra L1. Applied Sciences, 9(15), 3013. https://doi.org/10.3390/app9153013