Dynamical Manipulation of Surface Plasmon Polaritons
Abstract
1. Introduction
2. Directional Excitation of Surface Plasmon Polaritons (SPP)
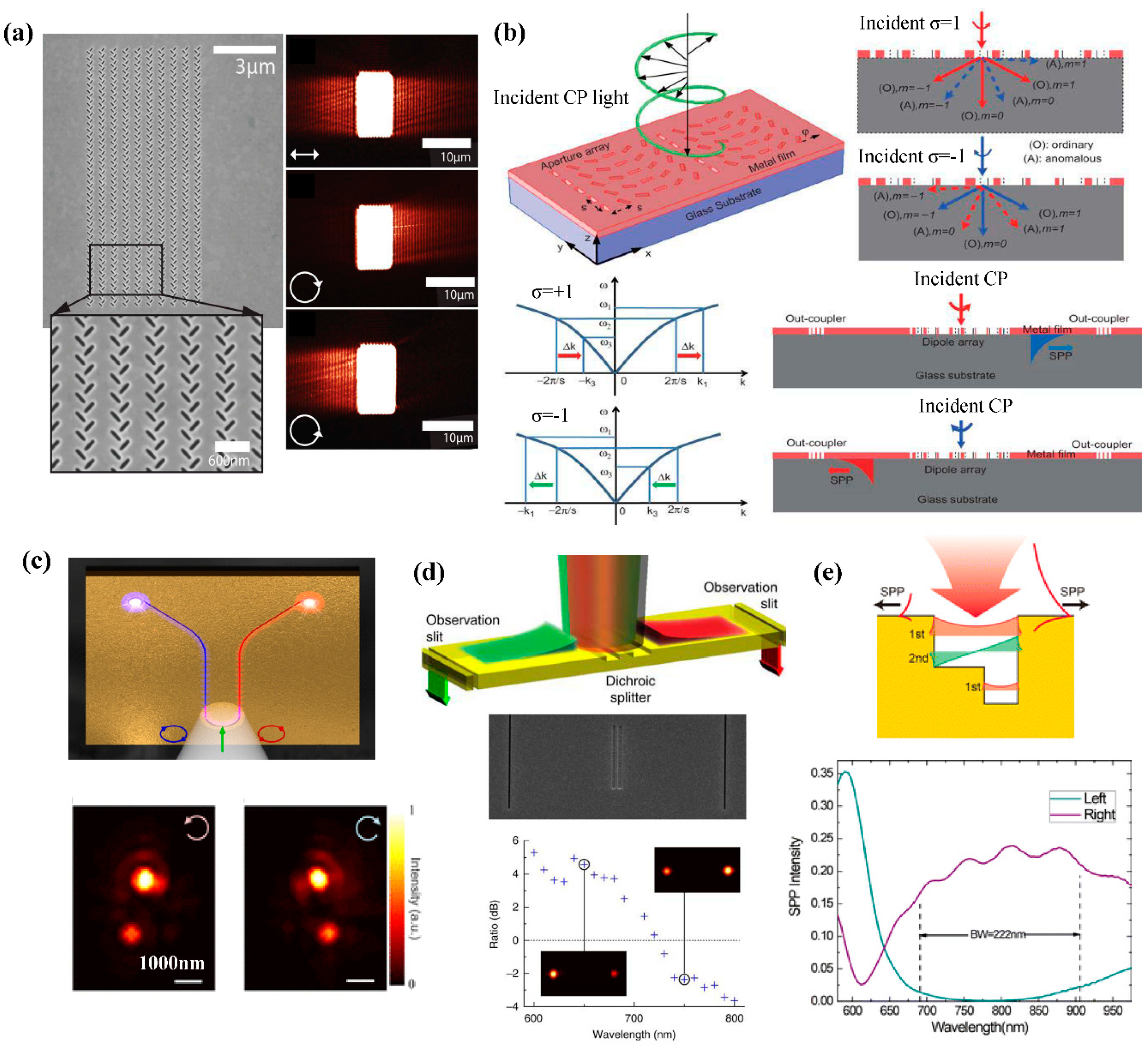
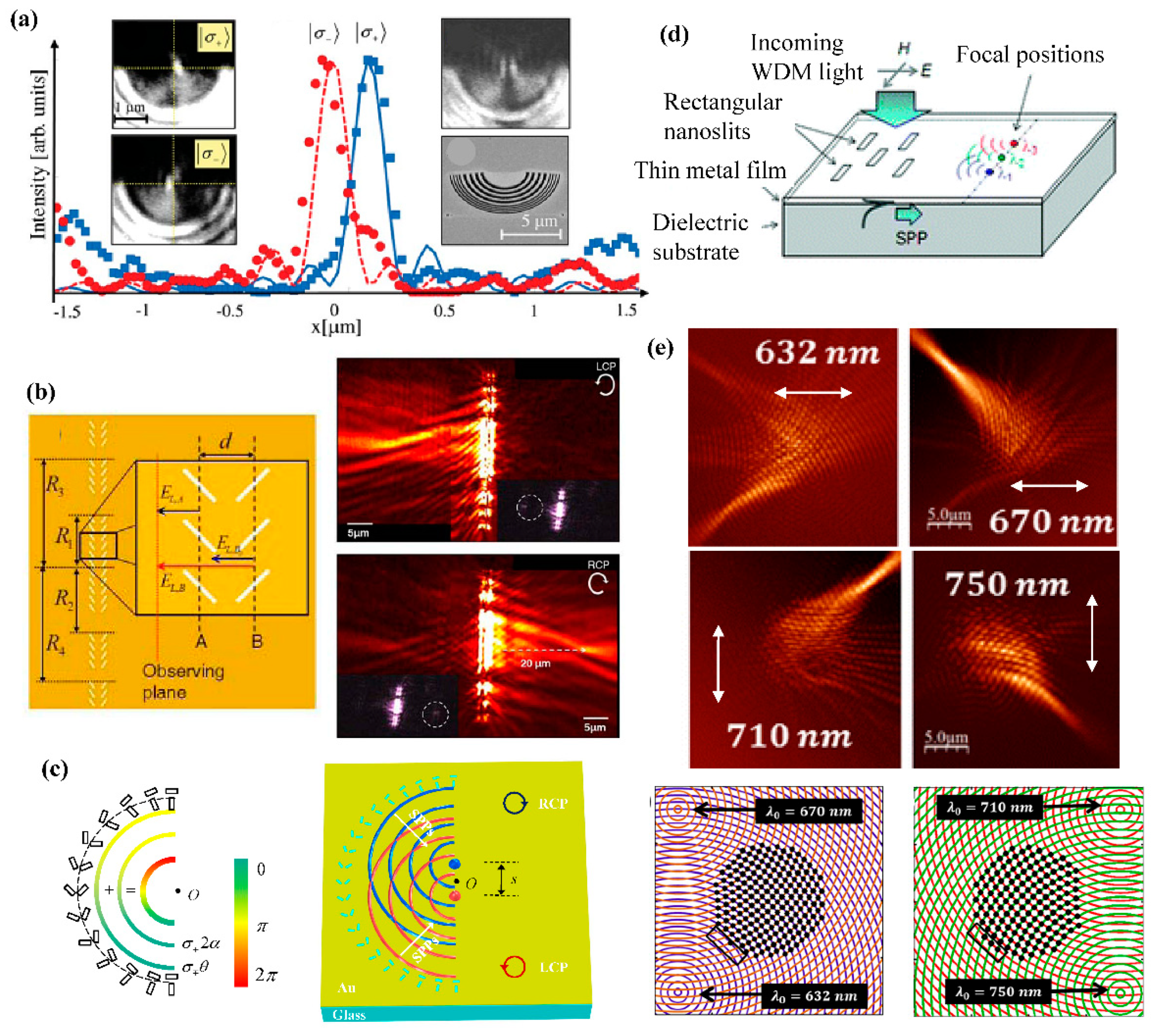
2.1. Polarization Controlled Excitation of SPP
2.2. Wavelength Dependent Directional SPP Excitation
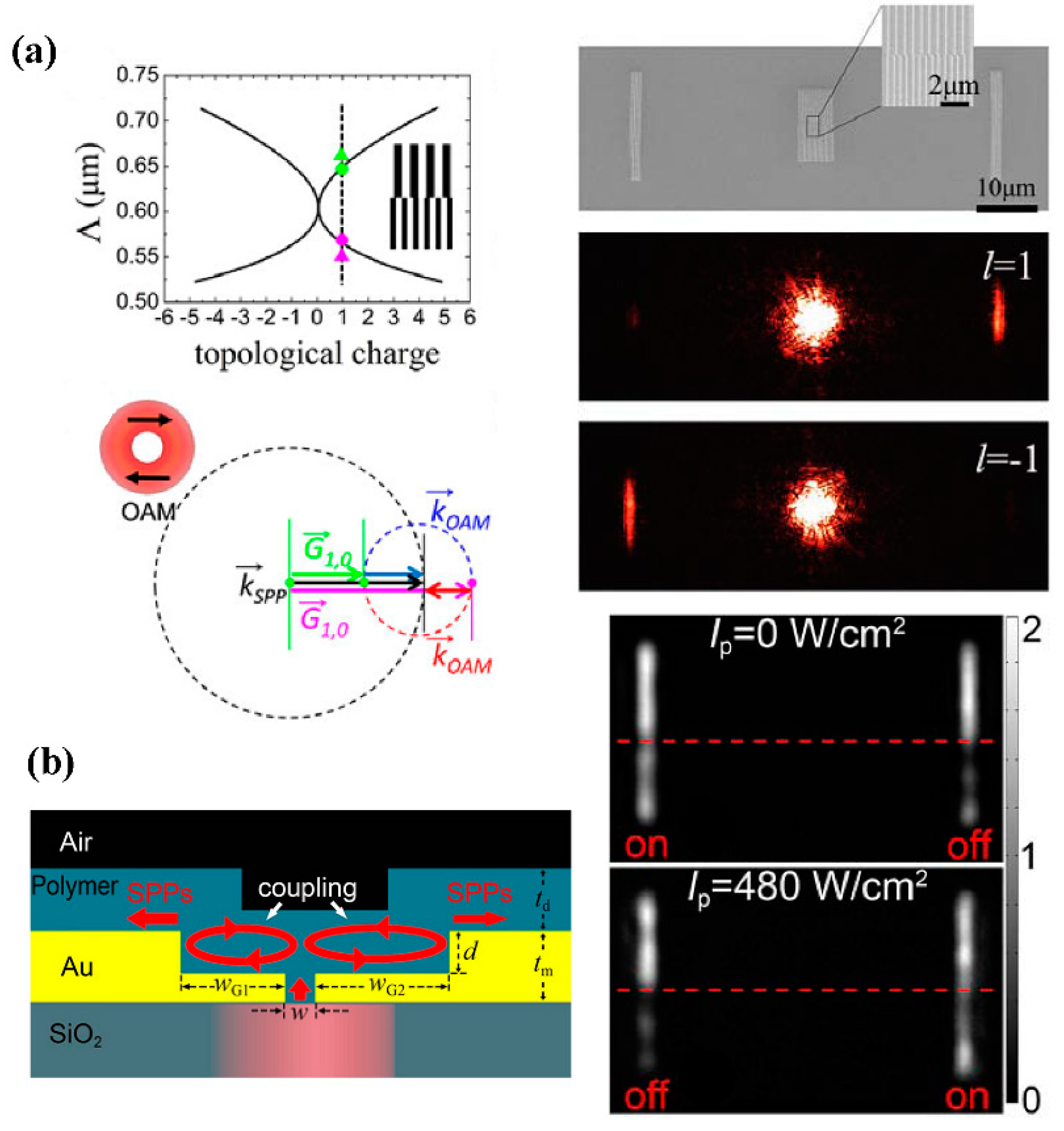
2.3. Directional SPP Excitation Determined by the Topological Charge of Vortex Beam
2.4. Directional SPP Propagation Based on Nonlinear Optical Materials
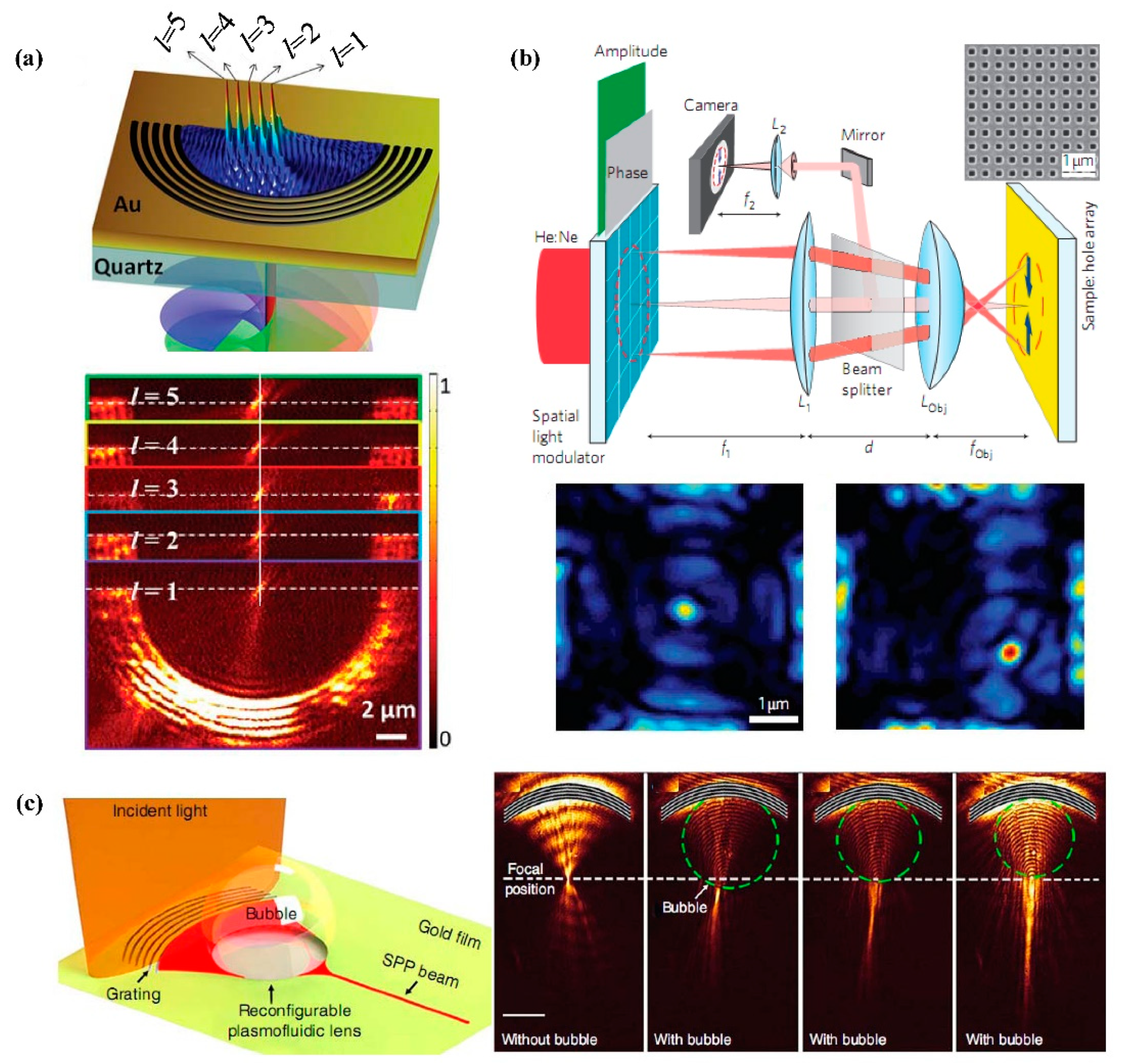
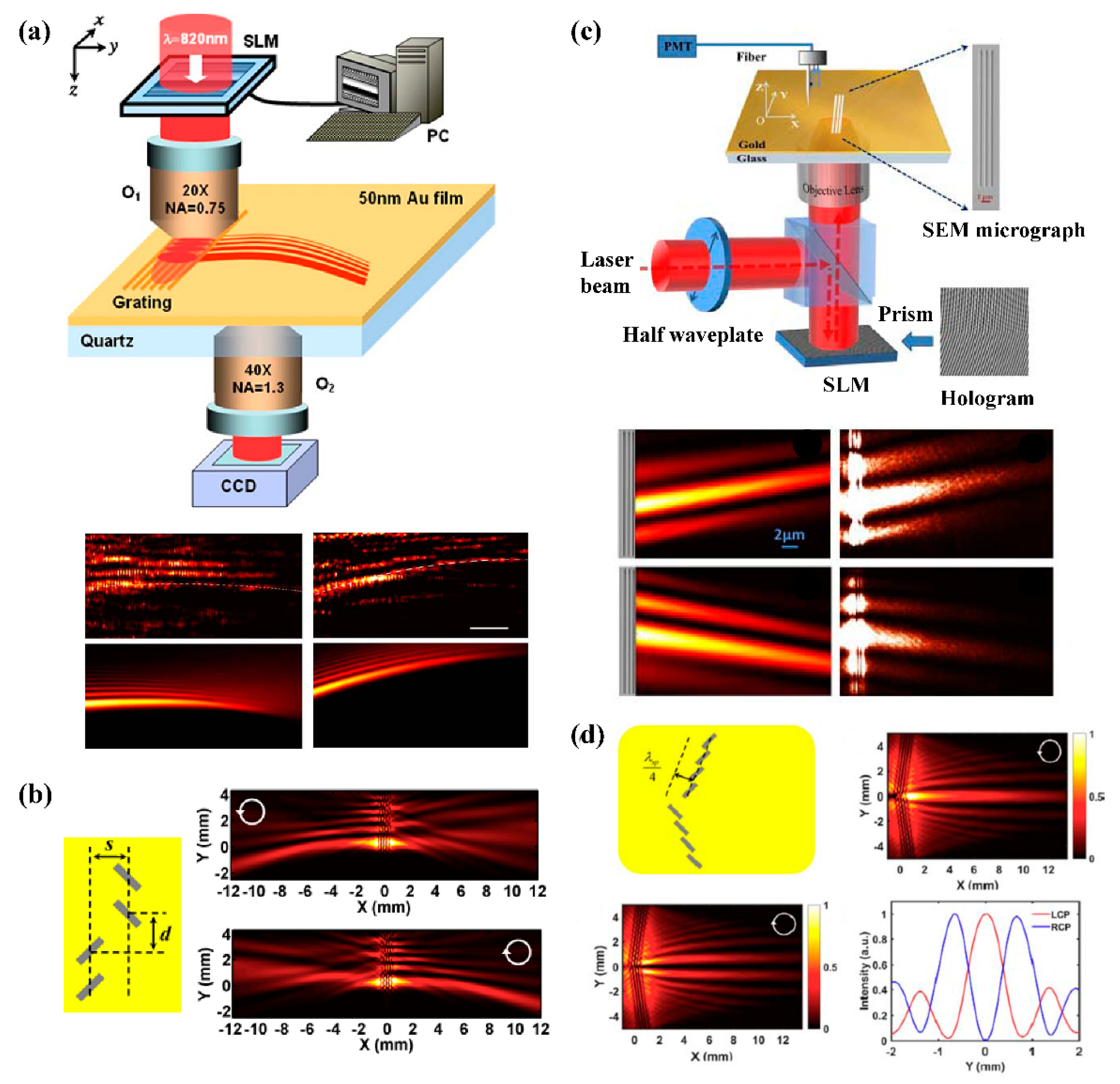
3. Dynamical Focusing of SPP
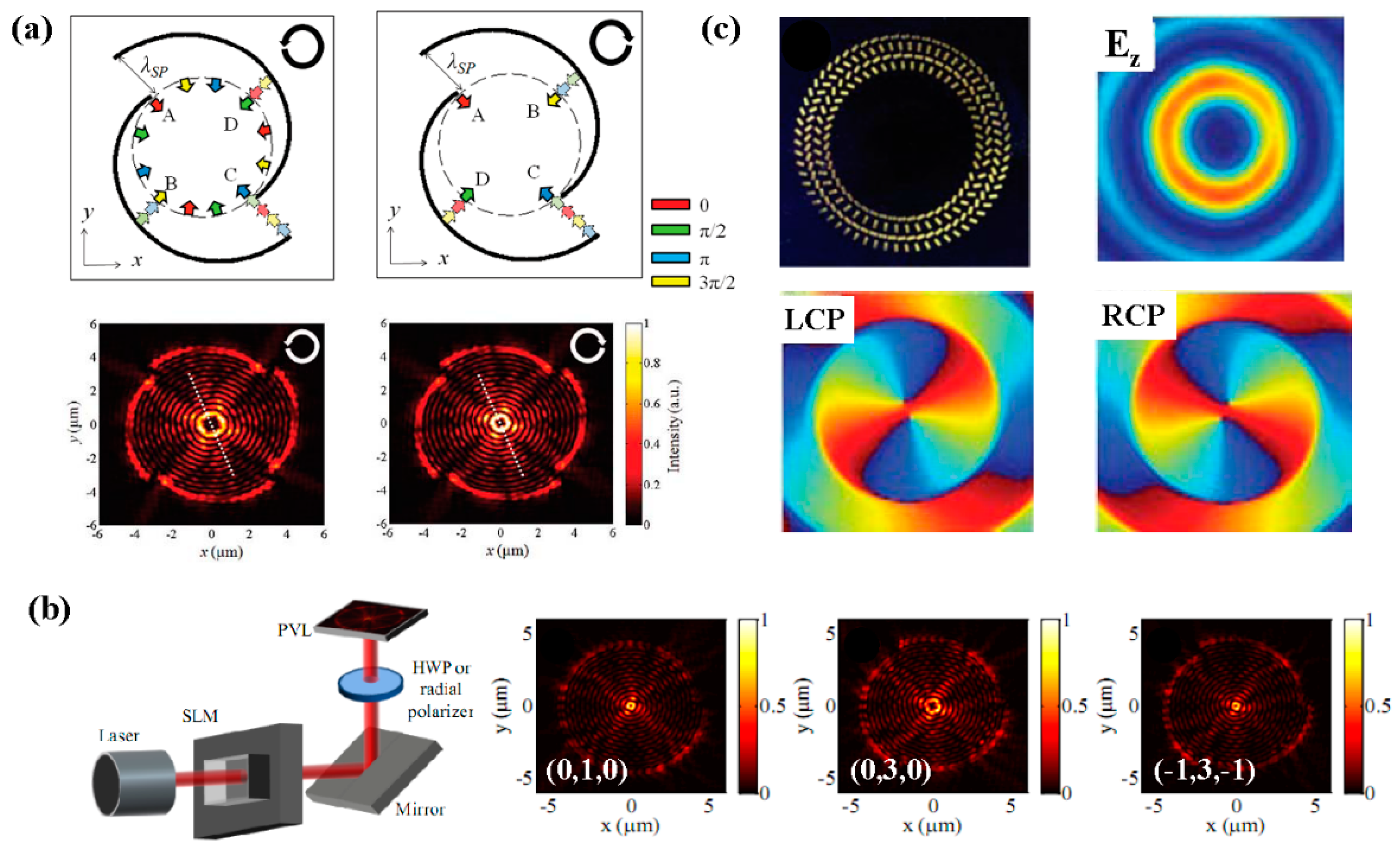
4. SPP Vortex Generation
5. Nondiffracting SPP Beams
6. Discussion and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Barnes, W.L.; Dereux, A.; Ebbesen, T.W. Surface plasmon subwavelength optics. Nature 2003, 424, 824–830. [Google Scholar] [CrossRef] [PubMed]
- Zayats, A.V.; Smolyaninov, I.I.; Maradudin, A.A. Nano-optics of surface plasmon polaritons. Phys. Rep. 2005, 408, 131–314. [Google Scholar] [CrossRef]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef] [PubMed]
- Pillai, S.; Catchpole, K.R.; Trupke, T.; Green, M.A. Surface plasmon enhanced silicon solar cells. J. Appl. Phys. 2007, 101, 093105. [Google Scholar] [CrossRef]
- Schuller, J.A.; Barnard, E.S.; Cai, W.; Jun, Y.C.; White, J.S.; Brongersma, M.L. Plasmonics for extreme light concentration and manipulation. Nat. Mater. 2010, 9, 193–204. [Google Scholar] [CrossRef] [PubMed]
- Fang, N.; Lee, H.; Sun, C.; Zhang, X. Sub-diffraction-limited optical imaging with a silver superlens. Science 2005, 308, 534–537. [Google Scholar] [CrossRef] [PubMed]
- Gramotnev, D.K.; Bozhevolnyi, S.I. Plasmonics beyond the diffraction limit. Nat. Photonics 2010, 4, 83–91. [Google Scholar] [CrossRef]
- Sorger, V.J.; Oulton, R.F.; Ma, R.-M.; Zhang, X. Toward integrated plasmonic circuits. MRS Bull. 2012, 37, 728–738. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, J.; Liu, H.; Wang, S.; Peng, L.M. Electrically driven monolithic subwavelength plasmonic interconnect circuits. Sci. Adv. 2017, 3, e1701456. [Google Scholar] [CrossRef]
- Fukuda, M.; Tonooka, Y.; Inoue, T.; Ota, M. Feasibility of plasmonic circuits for on-chip interconnects. Solid State Electron. 2019, 156, 33–40. [Google Scholar] [CrossRef]
- Zentgraf, T.; Liu, Y.; Mikkelsen, M.H.; Valentine, J.; Zhang, X. Plasmonic Luneburg and Eaton lenses. Nat. Nanotechnol. 2011, 6, 151–155. [Google Scholar] [CrossRef]
- Yin, L.; Vlasko-Vlasov, V.K.; Pearson, J.; Hiller, J.M.; Hua, J.; Welp, U.; Brown, D.E.; Kimball, C.W. Subwavelength focusing and guiding of surface plasmons. Nano Lett. 2005, 5, 1399–1402. [Google Scholar] [CrossRef]
- Lerman, G.M.; Yanai, A.; Levy, U. Demonstration of Nanofocusing by the use of Plasmonic Lens Illuminated with Radially Polarized Light. Nano Lett. 2009, 9, 2139–2143. [Google Scholar] [CrossRef]
- Fang, Z.; Peng, Q.; Song, W.; Hao, F.; Wang, J.; Nordlander, P.; Zhu, X. Plasmonic focusing in symmetry broken nanocorrals. Nano Lett. 2011, 11, 893–897. [Google Scholar] [CrossRef]
- Li, G.; Sun, Y.; Wang, S. Spin-Independent Plasmonic Lens. Nanoscale Res. Lett. 2019, 14, 156. [Google Scholar] [CrossRef]
- Li, L.; Li, T.; Wang, S.; Zhu, S.; Zhang, X. Broadband focusing and demultiplexing of in-plane propagating surface plasmons. Nano Lett. 2011, 11, 4357–4361. [Google Scholar] [CrossRef]
- Ditlbacher, H.; Krenn, J.R.; Schider, G.; Leitner, A.; Aussenegg, F.R. Two-dimensional optics with surface plasmon polaritons. Appl. Phys. Lett. 2002, 81, 1762–1764. [Google Scholar] [CrossRef]
- Randhawa, S.; Gonzalez, M.U.; Renger, J.; Enoch, S.; Quidant, R. Design and properties of dielectric surface plasmon Bragg mirrors. Opt. Express 2010, 18, 14496–14510. [Google Scholar] [CrossRef]
- Gonzalez, M.U.; Weeber, J.C.; Baudrion, A.L.; Dereux, A.; Stepanov, A.L.; Krenn, J.R.; Devaux, E.; Ebbesen, T.W. Design, near-field characterization, and modeling of 45 circle surface-plasmon Bragg mirrors. Phys. Rev. B 2006, 73, 155416. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Cho, S.W.; Lee, S.Y.; Kang, M.; Lee, B. Synthesis and dynamic switching of surface plasmon vortices with plasmonic vortex lens. Nano Lett. 2010, 10, 529–536. [Google Scholar] [CrossRef]
- Li, X.; Gao, Y.; Jiang, S.; Ma, L.; Liu, C.; Cheng, C. Experimental solution for scattered imaging of the interference of plasmonic and photonic mode waves launched by metal nano-slits. Opt. Express 2015, 23, 3507–3522. [Google Scholar] [CrossRef]
- Wang, H.; Liu, L.; Liu, C.; Li, X.; Wang, S.; Xu, Q.; Teng, S. Plasmonic vortex generator without polarization dependence. New J. Phys. 2018, 20, 033024. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, R.; Li, X.; Ma, L.; Liu, C.; He, C.; Cheng, C. Radially polarized plasmonic vector vortex generated by a metasurface spiral in gold film. Opt. Express 2017, 25, 32150–32160. [Google Scholar] [CrossRef]
- Minovich, A.; Klein, A.E.; Janunts, N.; Pertsch, T.; Neshev, D.N.; Kivshar, Y.S. Generation and near-field imaging of Airy surface plasmons. Phys. Rev. Lett. 2011, 107, 116802. [Google Scholar] [CrossRef]
- Li, L.; Li, T.; Wang, S.M.; Zhang, C.; Zhu, S.N. Plasmonic Airy beam generated by in-plane diffraction. Phys. Rev. Lett. 2011, 107, 126804. [Google Scholar] [CrossRef]
- Kou, S.S.; Yuan, G.; Wang, Q.; Du, L.; Balaur, E.; Zhang, D.; Tang, D.; Abbey, B.; Yuan, X.-C.; Lin, J. On-chip photonic Fourier transform with surface plasmon polaritons. Light Sci. Appl. 2016, 5, e16034. [Google Scholar] [CrossRef]
- Lin, J.; Dellinger, J.; Genevet, P.; Cluzel, B.; de Fornel, F.; Capasso, F. Cosine-Gauss plasmon beam: A localized long-range nondiffracting surface wave. Phys. Rev. Lett. 2012, 109, 093904. [Google Scholar] [CrossRef]
- Li, L.; Li, T.; Wang, S.M.; Zhu, S.N. Collimated plasmon beam: Nondiffracting versus linearly focused. Phys. Rev. Lett. 2013, 110, 046807. [Google Scholar] [CrossRef]
- Garcia-Ortiz, C.E.; Coello, V.; Han, Z.; Bozhevolnyi, S.I. Generation of diffraction-free plasmonic beams with one-dimensional Bessel profiles. Opt. Lett. 2013, 38, 905–907. [Google Scholar] [CrossRef]
- Fu, Y.; Hu, X.; Lu, C.; Yue, S.; Yang, H.; Gong, Q. All-optical logic gates based on nanoscale plasmonic slot waveguides. Nano Lett. 2012, 12, 5784–5790. [Google Scholar] [CrossRef]
- Lu, C.C.; Hu, X.Y.; Yang, H.; Gong, Q.H. Integrated all-optical logic discriminators based on plasmonic bandgap engineering. Sci. Rep. 2013, 3, 2778. [Google Scholar] [CrossRef]
- Baron, A.; Devaux, E.; Rodier, J.C.; Hugonin, J.P.; Rousseau, E.; Genet, C.; Ebbesen, T.W.; Lalanne, P. Compact Antenna for Efficient and Unidirectional Launching and Decoupling of Surface Plasmons. Nano Lett. 2011, 11, 4207–4212. [Google Scholar] [CrossRef]
- Lopez-Tejeira, F.; Rodrigo, S.G.; Martin-Moreno, L.; Garcia-Vidal, F.J.; Devaux, E.; Ebbesen, T.W.; Krenn, J.R.; Radko, I.P.; Bozhevolnyi, S.I.; Gonzalez, M.U.; et al. Efficient unidirectional nanoslit couplers for surface plasmons. Nat. Phys. 2007, 3, 324–328. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Yue, S.; Gong, Q. Efficient unidirectional generation of surface plasmon polaritons with asymmetric single-nanoslit. Appl. Phys. Lett. 2010, 97, 041113. [Google Scholar] [CrossRef]
- Gjonaj, B.; Aulbach, J.; Johnson, P.M.; Mosk, A.P.; Kuipers, L.; Lagendijk, A. Active spatial control of plasmonic fields. Nat. Photonics 2011, 5, 360–363. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, J. Flexible wavefront manipulation of surface plasmon polaritons without mechanical motion components. Appl. Phys. Lett. 2011, 98, 211108. [Google Scholar] [CrossRef]
- Gjonaj, B.; Aulbach, J.; Johnson, P.M.; Mosk, A.P.; Kuipers, L.; Lagendijk, A. Focusing and scanning microscopy with propagating surface plasmons. Phys. Rev. Lett. 2013, 110, 266804. [Google Scholar] [CrossRef]
- Yuan, G.H.; Wang, Q.; Tan, P.S.; Lin, J.; Yuan, X.C. A dynamic plasmonic manipulation technique assisted by phase modulation of an incident optical vortex beam. Nanotechnology 2012, 23, 385204. [Google Scholar] [CrossRef]
- Yuan, G.H.; Yuan, X.C.; Bu, J.; Tan, P.S.; Wang, Q. Manipulation of surface plasmon polaritons by phase modulation of incident light. Opt. Express 2011, 19, 224–229. [Google Scholar] [CrossRef]
- Xiao, K.; Wei, S.; Min, C.; Yuan, G.; Zhu, S.W.; Lei, T.; Yuan, X.C. Dynamic cosine-Gauss plasmonic beam through phase control. Opt. Express 2014, 22, 13541–13546. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, S.; Liu, Y.; Yin, X.; Lu, C.; Chen, Z.; Zhang, X. Plasmonic Airy beams with dynamically controlled trajectories. Opt. Lett. 2011, 36, 3191–3193. [Google Scholar] [CrossRef]
- Wei, S.; Si, G.; Malek, M.; Earl, S.K.; Du, L.; Kou, S.S.; Yuan, X.; Lin, J. Toward broadband, dynamic structuring of a complex plasmonic field. Sci. Adv. 2018, 4, eaao0533. [Google Scholar] [CrossRef]
- Cho, S.W.; Park, J.; Lee, S.Y.; Kim, H.; Lee, B. Coupling of spin and angular momentum of light in plasmonic vortex. Opt. Express 2012, 20, 10083–10094. [Google Scholar] [CrossRef]
- Gjonaj, B.; Aulbach, J.; Johnson, P.M.; Mosk, A.P.; Kuipers, L.; Lagendijk, A. Optical control of plasmonic Bloch modes on periodic nanostructures. Nano Lett. 2012, 12, 546–550. [Google Scholar] [CrossRef]
- Lee, S.; Kim, K.; Kim, S.; Park, H.; Kim, K.; Lee, B. Plasmonic meta-slit: Shaping and controlling near-field focus. Optica 2015, 2, 6–13. [Google Scholar] [CrossRef]
- Genevet, P.; Wintz, D.; Ambrosio, A.; She, A.; Blanchard, R.; Capasso, F. Controlled steering of Cherenkov surface plasmon wakes with a one-dimensional metamaterial. Nat. Nanotechnol. 2015, 10, 804–809. [Google Scholar] [CrossRef]
- Lin, J.; Mueller, J.P.; Wang, Q.; Yuan, G.; Antoniou, N.; Yuan, X.C.; Capasso, F. Polarization-controlled tunable directional coupling of surface plasmon polaritons. Science 2013, 340, 331–334. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Bai, B.; Tan, Q.; Jin, G.; Zentgraf, T.; Zhang, S. Helicity dependent directional surface plasmon polariton excitation using a metasurface with interfacial phase discontinuity. Light Sci. Appl. 2013, 2, e70. [Google Scholar] [CrossRef]
- Lefier, Y.; Salut, R.; Suarez, M.A.; Grosjean, T. Directing Nanoscale Optical Flows by Coupling Photon Spin to Plasmon Extrinsic Angular Momentum. Nano Lett. 2018, 18, 38–42. [Google Scholar] [CrossRef]
- Jin, J.; Li, X.; Guo, Y.; Pu, M.; Gao, P.; Ma, X.; Luo, X. Polarization-controlled unidirectional excitation of surface plasmon polaritons utilizing catenary apertures. Nanoscale 2019, 11, 3952–3957. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, X.; Yang, Q.; Tian, C.; Xu, Y.; Zhang, J.; Zhao, H.; Li, Y.; Ouyang, C.; Tian, Z.; et al. Polarization-controlled asymmetric excitation of surface plasmons. Optica 2017, 4, 1044–1051. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, Y.; Yue, W.; Tian, Z.; Gu, J.; Li, Y.; Singh, R.; Zhang, S.; Han, J.; Zhang, W. Anomalous Surface Wave Launching by Handedness Phase Control. Adv. Mater. 2015, 27, 7123–7129. [Google Scholar] [CrossRef]
- Pan, D.; Wei, H.; Gao, L.; Xu, H. Strong Spin-Orbit Interaction of Light in Plasmonic Nanostructures and Nanocircuits. Phys. Rev. Lett. 2016, 117, 166803. [Google Scholar] [CrossRef]
- Mueller, J.P.; Leosson, K.; Capasso, F. Polarization-selective coupling to long-range surface plasmon polariton waveguides. Nano Lett. 2014, 14, 5524–5527. [Google Scholar] [CrossRef]
- Pors, A.; Nielsen, M.G.; Bernardin, T.; Weeber, J.-C.; Bozhevolnyi, S.I. Efficient unidirectional polarization-controlled excitation of surface plasmon polaritons. Light Sci. Appl. 2014, 3, e197. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Gorodetski, Y.; Kleiner, V.; Hasman, E. Coriolis effect in optics: Unified geometric phase and spin-Hall effect. Phys. Rev. Lett. 2008, 101, 030404. [Google Scholar] [CrossRef]
- Gorodetski, Y.; Niv, A.; Kleiner, V.; Hasman, E. Observation of the spin-based plasmonic effect in nanoscale structures. Phys. Rev. Lett. 2008, 101, 043903. [Google Scholar] [CrossRef]
- Shitrit, N.; Nechayev, S.; Kleiner, V.; Hasman, E. Spin-dependent plasmonics based on interfering topological defects. Nano Lett. 2012, 12, 1620–1623. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.K.; Zhao, F.; Qu, S.L.; Zhang, Y. Observation and explanation of polarization-controlled focusing of terahertz surface plasmon polaritons. Phys. Rev. A 2015, 91, 053812. [Google Scholar] [CrossRef]
- Bao, Y.; Zu, S.; Liu, W.; Zhou, L.; Zhu, X.; Fang, Z. Revealing the spin optics in conic-shaped metasurfaces. Phys. Rev. B 2017, 95, 081406. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, C.; Li, G.; Li, X.; Wang, S. Enlarging spin-dependent transverse displacement of surface plasmon polaritons focus. Opt. Express 2019, 27, 11112–11121. [Google Scholar] [CrossRef]
- Lee, S.Y.; Kim, K.; Lee, G.Y.; Lee, B. Polarization-multiplexed plasmonic phase generation with distributed nanoslits. Opt. Express 2015, 23, 15598–15607. [Google Scholar] [CrossRef]
- Wintz, D.; Genevet, P.; Ambrosio, A.; Woolf, A.; Capasso, F. Holographic metalens for switchable focusing of surface plasmons. Nano Lett. 2015, 15, 3585–3589. [Google Scholar] [CrossRef]
- Man, Z.; Du, L.; Min, C.; Zhang, Y.; Zhang, C.; Zhu, S.; Paul Urbach, H.; Yuan, X.C. Dynamic plasmonic beam shaping by vector beams with arbitrary locally linear polarization states. Appl. Phys. Lett. 2014, 105, 011110. [Google Scholar] [CrossRef]
- Li, X.; Zhang, R.; Zhang, Y.; Ma, L.; He, C.; Ren, X.; Liu, C.; Cheng, C. Slit width oriented polarized wavefields transition involving plasmonic and photonic modes. New J. Phys. 2018, 20, 063037. [Google Scholar] [CrossRef]
- Lee, S.-Y.; Kim, S.-J.; Kwon, H.; Lee, B. Spin-Direction Control of High-Order Plasmonic Vortex with Double-Ring Distributed Nanoslits. IEEE Photonics Technol. Lett. 2015, 27, 705–708. [Google Scholar] [CrossRef]
- Liu, A.; Rui, G.; Ren, X.; Zhan, Q.; Guo, G.; Guo, G. Encoding photonic angular momentum information onto surface plasmon polaritons with plasmonic lens. Opt. Express 2012, 20, 24151–24159. [Google Scholar] [CrossRef]
- Tsai, W.Y.; Huang, J.S.; Huang, C.B. Selective trapping or rotation of isotropic dielectric microparticles by optical near field in a plasmonic archimedes spiral. Nano Lett. 2014, 14, 547–552. [Google Scholar] [CrossRef]
- Chen, W.; Abeysinghe, D.C.; Nelson, R.L.; Zhan, Q. Experimental confirmation of miniature spiral plasmonic lens as a circular polarization analyzer. Nano Lett. 2010, 10, 2075–2079. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Zeng, X.Y.; Zhang, R.R.; Zhan, Z.J.; Li, X.; Ma, L.; Liu, C.X.; He, C.W.; Cheng, C.F. Generation of a plasmonic radially polarized vector beam with linearly polarized illumination. Opt. Lett. 2018, 43, 4208–4211. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, H.; Liu, L.; Teng, S. Generation of vector beams using spatial variation nanoslits with linearly polarized light illumination. Opt. Express 2018, 26, 24145–24153. [Google Scholar] [CrossRef]
- Zang, X.; Zhu, Y.; Mao, C.; Xu, W.; Ding, H.; Xie, J.; Cheng, Q.; Chen, L.; Peng, Y.; Hu, Q.; et al. Manipulating Terahertz Plasmonic Vortex Based on Geometric and Dynamic Phase. Adv. Opt. Mater. 2018, 7, 1801328. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Zhang, Y. Simultaneous Airy beam generation for both surface plasmon polaritons and transmitted wave based on metasurface. Opt. Express 2017, 25, 23589–23596. [Google Scholar] [CrossRef]
- Wang, S.; Wang, S.; Zhang, Y. Polarization-based dynamic manipulation of Bessel-like surface plasmon polaritons beam. Opt. Express 2018, 26, 5461–5468. [Google Scholar] [CrossRef]
- Avayu, O.; Epstein, I.; Eizner, E.; Ellenbogen, T. Polarization controlled coupling and shaping of surface plasmon polaritons by nanoantenna arrays. Opt. Lett. 2015, 40, 1520–1523. [Google Scholar] [CrossRef]
- Xiao, S.; Zhong, F.; Liu, H.; Zhu, S.; Li, J. Flexible coherent control of plasmonic spin-Hall effect. Nat. Commun. 2015, 6, 8360. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, X.; Xu, Y.; Ouyang, C.; Tian, Z.; Gu, J.; Li, J.; Zhang, S.; Han, J.; Zhang, W. Polarization-controlled surface plasmon holography. Laser Photonics Rev. 2017, 11, 1600212. [Google Scholar] [CrossRef]
- Liu, J.S.; Pala, R.A.; Afshinmanesh, F.; Cai, W.; Brongersma, M.L. A submicron plasmonic dichroic splitter. Nat. Commun. 2011, 2, 525. [Google Scholar] [CrossRef]
- Yao, W.; Liu, S.; Liao, H.; Li, Z.; Sun, C.; Chen, J.; Gong, Q. Efficient directional excitation of surface plasmons by a single-element nanoantenna. Nano Lett. 2015, 15, 3115–3121. [Google Scholar] [CrossRef]
- Tanemura, T.; Balram, K.C.; Ly-Gagnon, D.S.; Wahl, P.; White, J.S.; Brongersma, M.L.; Miller, D.A. Multiple-wavelength focusing of surface plasmons with a nonperiodic nanoslit coupler. Nano Lett. 2011, 11, 2693–2698. [Google Scholar] [CrossRef]
- Chen, J.; Chen, X.; Li, T.; Zhu, S. On-Chip Detection of Orbital Angular Momentum Beam by Plasmonic Nanogratings. Laser Photonics Rev. 2018, 12, 1700331. [Google Scholar] [CrossRef]
- Mei, S.; Huang, K.; Liu, H.; Qin, F.; Mehmood, M.Q.; Xu, Z.; Hong, M.; Zhang, D.; Teng, J.; Danner, A.; et al. On-chip discrimination of orbital angular momentum of light with plasmonic nanoslits. Nanoscale 2016, 8, 2227–2233. [Google Scholar] [CrossRef]
- Liu, Z.; Steele, J.M.; Lee, H.; Zhang, X. Tuning the focus of a plasmonic lens by the incident angle. Appl. Phys. Lett. 2006, 88, 171108. [Google Scholar] [CrossRef]
- Qiu, P.; Zhang, D.; Jing, M.; Lu, T.; Yu, B.; Zhan, Q.; Zhuang, S. Dynamic tailoring of surface plasmon polaritons through incident angle modulation. Opt. Express 2018, 26, 9772–9783. [Google Scholar] [CrossRef]
- Drezet, A.; Koller, D.; Hohenau, A.; Leitner, A.; Aussenegg, F.R.; Krenn, J.R. Plasmonic crystal demultiplexer and multiports. Nano Lett. 2007, 7, 1697–1700. [Google Scholar] [CrossRef]
- Muskens, O.L.; Del Fatti, N.; Vallee, F. Femtosecond response of a single metal nanoparticle. Nano Lett. 2006, 6, 552–556. [Google Scholar] [CrossRef]
- Pelton, M.; Liu, M.; Park, S.; Scherer, N.F.; Guyot-Sionnest, P. Ultrafast resonant optical scattering from single gold nanorods: Large nonlinearities and plasmon saturation. Phys. Rev. B 2006, 73, 155419. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Coerwinkel, R.P.C.; Kristensen, M.; Woerdman, J.P. Helical wavefront laser beams produced with a spiral phaseplate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Chen, J.; Li, Z.; Zhang, X.; Xiao, J.; Gong, Q. Submicron bidirectional all-optical plasmonic switches. Sci. Rep. 2013, 3, 1451. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, Y.; Zhao, Y.; Fang, N.; Huang, T.J. A reconfigurable plasmofluidic lens. Nat. Commun. 2013, 4, 2305. [Google Scholar] [CrossRef]
- Sain, B.; Kaner, R.; Prior, Y. Phase-controlled propagation of surface plasmons. Light Sci. Appl. 2017, 6, e17072. [Google Scholar] [CrossRef]
- Morrill, D.; Li, D.; Pacifici, D. Measuring subwavelength spatial coherence with plasmonic interferometry. Nat. Photonics 2016, 10, 681–687. [Google Scholar] [CrossRef]
- Divitt, S.; Frimmer, M.; Visser, T.D.; Novotny, L. Modulation of optical spatial coherence by surface plasmon polaritons. Opt. Lett. 2016, 41, 3094–3097. [Google Scholar] [CrossRef]
- Guebrou, S.A.; Laverdant, J.; Symonds, C.; Vignoli, S.; Bellessa, J. Spatial coherence properties of surface plasmon investigated by Young’s slit experiment. Opt. Lett. 2012, 37, 2139–2141. [Google Scholar] [CrossRef]
- Laverdant, J.; AberraGuebrou, S.; Bessueille, F.; Symonds, C.; Bellessa, J. Leakage interferences applied to surface plasmon analysis. J. Opt. Soc. Am. A 2014, 31, 1067–1073. [Google Scholar] [CrossRef]
- Norrman, A.; Ponomarenko, S.A.; Friberg, A.T. Partially coherent surface plasmon polaritons. Europhys. Lett. 2016, 116, 64001. [Google Scholar] [CrossRef]
- Chen, Y.; Norrman, A.; Ponomarenko, S.A.; Friberg, A.T. Plasmon coherence determination by nanoscattering. Opt. Lett. 2017, 42, 3279–3282. [Google Scholar] [CrossRef]
- Chen, Y.; Norrman, A.; Ponomarenko, S.A.; Friberg, A.T. Partially coherent axiconic surface plasmon polariton fields. Phys. Rev. A 2018, 97, 041801. [Google Scholar] [CrossRef]
- Chen, Y.; Norrman, A.; Ponomarenko, S.A.; Friberg, A.T. Coherence lattices in surface plasmon polariton fields. Opt. Lett. 2018, 43, 3429–3432. [Google Scholar] [CrossRef]
- Mao, H.; Chen, Y.; Ponomarenko, S.A.; Friberg, A.T. Coherent pseudo-mode representation of partially coherent surface plasmon polaritons. Opt. Lett. 2018, 43, 1395–1398. [Google Scholar] [CrossRef]
- Daniel, S.; Saastamoinen, K.; Ponomarenko, S.A.; Friberg, A.T. Scattering of partially coherent surface plasmon polariton fields by metallic nanostripe. J. Eur. Opt. Soc. 2019, 15, 4. [Google Scholar] [CrossRef]
- He, X.; Liu, F.; Lin, F.; Xiao, G.; Shi, W. Tunable MoS2 modified hybrid surface plasmon waveguides. Nanotechnology 2019, 30, 125201. [Google Scholar] [CrossRef]
- Li, R.; Imran, M.; Lin, X.; Wang, H.; Xu, Z.; Chen, H. Hybrid Airy plasmons with dynamically steerable trajectories. Nanoscale 2017, 9, 1449–1456. [Google Scholar] [CrossRef]
- Gao, W.; Shi, G.; Jin, Z.; Shu, J.; Zhang, Q.; Vajtai, R.; Ajayan, P.M.; Kono, J.; Xu, Q. Excitation and active control of propagating surface plasmon polaritons in graphene. Nano Lett. 2013, 13, 3698–3702. [Google Scholar] [CrossRef]
- Yang, Y.; Dai, H.T.; Zhu, B.F.; Sun, X.W. Dynamic Control of the Airy Plasmons in a Graphene Platform. IEEE Photonics J. 2014, 6, 1–7. [Google Scholar] [CrossRef]
- Dintinger, J.; Klein, S.; Bustos, F.; Barnes, W.L.; Ebbesen, T.W. Strong coupling between surface plasmon-polaritons and organic molecules in subwavelength hole arrays. Phys. Rev. B 2005, 71, 035424. [Google Scholar] [CrossRef]
- Christ, A.; Tikhodeev, S.G.; Gippius, N.A.; Kuhl, J.; Giessen, H. Waveguide-plasmon polaritons: Strong coupling of photonic and electronic resonances in a metallic photonic crystal slab. Phys. Rev. Lett. 2003, 91, 183901. [Google Scholar] [CrossRef]
- Itoh, T.; Yamamoto, Y.S. Reproduction of surface-enhanced resonant Raman scattering and fluorescence spectra of a strong coupling system composed of a single silver nanoparticle dimer and a few dye molecules. J. Chem. Phys. 2018, 149, 244701. [Google Scholar] [CrossRef]
- Genevet, P.; Lin, J.; Kats, M.A.; Capasso, F. Holographic detection of the orbital angular momentum of light with plasmonic photodiodes. Nat. Commun. 2012, 3, 1278. [Google Scholar] [CrossRef]
- Lerman, G.M.; Levy, U. Pin cushion plasmonic device for polarization beam splitting, focusing, and beam position estimation. Nano Lett. 2013, 13, 1100–1105. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Kan, Q.; Qu, S.; Zhang, Y. Circular polarization analyzer with polarization tunable focusing of surface plasmon polaritons. Appl. Phys. Lett. 2015, 107, 243504. [Google Scholar] [CrossRef]
- Spektor, G.; Kilbane, D.; Mahro, A.K.; Frank, B.; Ristok, S.; Gal, L.; Kahl, P.; Podbiel, D.; Mathias, S.; Giessen, H.; et al. Revealing the subfemtosecond dynamics of orbital angular momentum in nanoplasmonic vortices. Science 2017, 355, 1187–1191. [Google Scholar] [CrossRef]
- Shen, Z.; Hu, Z.J.; Yuan, G.H.; Min, C.J.; Fang, H.; Yuan, X.C. Visualizing orbital angular momentum of plasmonic vortices. Opt. Lett. 2012, 37, 4627–4629. [Google Scholar] [CrossRef]
- Ertsgaard, C.T.; McKoskey, R.M.; Rich, I.S.; Lindquist, N.C. Dynamic placement of plasmonic hotspots for super-resolution surface-enhanced Raman scattering. ACS Nano 2014, 8, 10941–10946. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhao, C.; Li, X. Dynamical Manipulation of Surface Plasmon Polaritons. Appl. Sci. 2019, 9, 3297. https://doi.org/10.3390/app9163297
Wang S, Zhao C, Li X. Dynamical Manipulation of Surface Plasmon Polaritons. Applied Sciences. 2019; 9(16):3297. https://doi.org/10.3390/app9163297
Chicago/Turabian StyleWang, Sen, Chunying Zhao, and Xing Li. 2019. "Dynamical Manipulation of Surface Plasmon Polaritons" Applied Sciences 9, no. 16: 3297. https://doi.org/10.3390/app9163297
APA StyleWang, S., Zhao, C., & Li, X. (2019). Dynamical Manipulation of Surface Plasmon Polaritons. Applied Sciences, 9(16), 3297. https://doi.org/10.3390/app9163297



