Detection of a Semi-Rough Target in Turbulent Atmosphere by an Electromagnetic Gaussian Schell-Model Beam
Abstract
1. Introduction
2. Theoretical Analysis
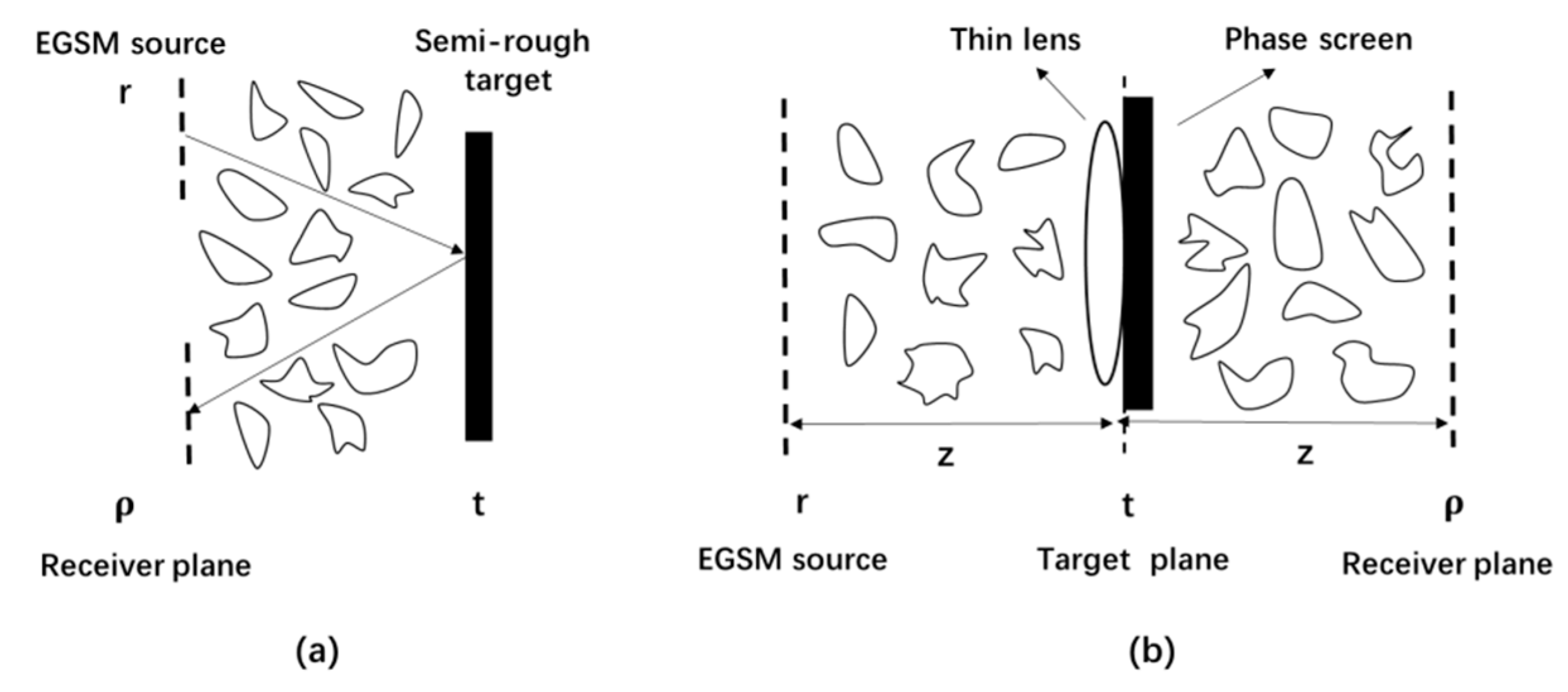
2.1. Transmission from the Source to the Target Plane
2.2. Transmission from the Target to the Receiver Plane
2.3. Degree of the Polarization
3. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Beran, M. Propagation of a Finite Beam in a Random Medium. J. Opt. Soc. Am. 1970, 60, 518–521. [Google Scholar] [CrossRef]
- Fante, R.L. Mutual coherence function and frequency spectrum of a laser beam propagating through atmospheric turbulence. J. Opt. Soc. Am. 1974, 64, 592–598. [Google Scholar] [CrossRef]
- Lutomirski, R.F.; Yura, H.T. Propagation of a Finite Optical Beam in an Inhomogeneous Medium. Appl. Opt. 1971, 10, 1652–1658. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, F.; Wei, C.; Cai, Y. Experimental study of turbulence-induced beam wander and deformation of a partially coherent beam. Opt. Lett. 2014, 39, 3336. [Google Scholar] [CrossRef] [PubMed]
- Dogariu, A.; Amarande, S. Propagation of partially coherent beams:turbulence-induced degradation. Opt. Lett. 2003, 28, 10–12. [Google Scholar] [CrossRef] [PubMed]
- Korotkova, O.; Andrews, L.C.; Phillips, R.L. Model for a Partially Coherent Gaussian Beam in Atmospheric Turbulence with Application in Lasercom. Opt. Eng. 2004, 43, 341. [Google Scholar] [CrossRef]
- Ricklin, J.C.; Davidson, F.M. Atmospheric turbulence effects on a partially coherent Gaussian beam: Implications for free-space laser communication. J. Opt. Soc. Am. A 2002, 19, 1794–1802. [Google Scholar] [CrossRef]
- Collett, E.; Wolf, E. Is complete spatial coherence necessary for the generation of highly directional light beams. Opt. Lett. 1978, 2, 27. [Google Scholar] [CrossRef]
- Foley, J.T.; Zubairy, M.S. The directionality of gaussian Schell-model beams. Opt. Commun. 1978, 26, 297–300. [Google Scholar] [CrossRef]
- Wang, F.; Wu, G.; Liu, X.; Zhu, S.; Cai, Y. Experimental measurement of the beam parameters of an electromagnetic Gaussian Schell-model source. Opt. Lett. 2011, 36, 2722–2724. [Google Scholar] [CrossRef]
- Voelz, D.; Xiao, X.; Korotkova, O. Numerical modeling of Schell-model beams with arbitrary far-field patterns. Opt. Lett. 2015, 40, 352–355. [Google Scholar] [CrossRef] [PubMed]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation through Random Media; SPIE Press: New York, NY, USA, 2005. [Google Scholar] [CrossRef]
- Gbur, G.; Wolf, E. Spreading of partially coherent beams in random media. J. Opt. Soc. Am. A 2002, 19, 1592. [Google Scholar] [CrossRef]
- Shirai, T.; Dogariu, A.; Wolf, E. Mode analysis of spreading of partially coherent beams propagating through atmospheric turbulence. J. Opt. Soc. Am. A 2003, 20, 1094–1102. [Google Scholar] [CrossRef]
- Cai, Y.; He, S. Propagation of a partially coherent twisted anisotropic Gaussian Schell-model beam in a turbulent atmosphere. Appl. Phys. Lett. 2006, 89, 2419. [Google Scholar] [CrossRef]
- Xu, Y.; Dan, Y.; Yu, J.; Cai, Y. Propagation properties of partially coherent dark hollow beam in inhomogeneous atmospheric turbulence. J. Mod. Opt. 2016, 63, 2186–2197. [Google Scholar] [CrossRef]
- Wei, W.; Ying, J.; Hu, M.; Liu, X.; Cai, Y.; Zou, C.; Luo, M.; Zhou, L.; Chu, X. Beam wander of coherent and partially coherent Airy beam arrays in a turbulent atmosphere. Opt. Commun. 2018, 415, 48–55. [Google Scholar] [CrossRef]
- Korotkova, O.; Wolf, E. Changes in the state of polarization of a random electromagnetic beam on propagation. Opt. Commun. 2005, 246, 35–43. [Google Scholar] [CrossRef]
- Cai, Y.; Chen, Y.; Yu, J.; Liu, X.; Liu, L. Generation of Partially Coherent Beams. Prog. Opt. 2016, 62, 157–223. [Google Scholar] [CrossRef]
- Cai, Y.; Lin, Q.; Eyyuboğlu, H.T.; Baykal, Y. Average irradiance and polarization properties of a radially or azimuthally polarized beam in a turbulent atmosphere. Opt. Express 2008, 16, 7665–7673. [Google Scholar] [CrossRef] [PubMed]
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge U. Press: Cambridge, UK, 2007. [Google Scholar] [CrossRef]
- Chen, X.; Chang, C.; Chen, Z.; Lin, Z.; Pu, J. Generation of stochastic electromagnetic beams with complete controllable coherence. Opt. Express 2016, 24, 21587–21596. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Visser, T.D. Hanbury Brown-Twiss effect with partially coherent electromagnetic beams. Opt. Lett. 2014, 39, 2561. [Google Scholar] [CrossRef] [PubMed]
- Davis, B.; Kim, E.; Piepmeier, J.R. Stochastic modeling and generation of partially polarized or partially coherent electromagnetic waves. Radio Sci. 2004, 39, 1–8. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M.; Borghi, R.; Ramírez-Sánchez, J. Realizability condition for electromagnetic Schell-model sources. J. Opt. Soc. Am. A 2008, 25, 1016–1021. [Google Scholar] [CrossRef]
- Roychowdhury, H.; Korotkova, O. Realizability conditions for electromagnetic Gaussian Schell-model sources. Opt. Commun. 2005, 249, 379–385. [Google Scholar] [CrossRef]
- Basu, S.; Hyde, M.W.; Xiao, X.; Voelz, D.G.; Korotkova, O. Computational approaches for generating electromagnetic Gaussian Schell-model sources. Opt. Express 2014, 22, 31691–31707. [Google Scholar] [CrossRef] [PubMed]
- Ostrovsky, A.S.; Rodríguezzurita, G.; Menesesfabián, C.; Olvera-Santamaría, M.Á.; Rickenstorff-Parrao, C. Experimental generating the partially coherent and partially polarized electromagnetic source. Opt. Express 2010, 18, 12864. [Google Scholar] [CrossRef]
- Korotkova, O.; Ahad, L.; Setälä, T. Three-dimensional electromagnetic Gaussian Schell-model sources. Opt. Lett. 2017, 42, 1792. [Google Scholar] [CrossRef]
- Hyde, M.W.; Bose-Pillai, S.R.; Korotkova, O. Monte Carlo simulations of three-dimensional electromagnetic Gaussian Schell-model sources. Opt. Express 2018, 26, 2303–2313. [Google Scholar] [CrossRef]
- Korotkova, O.; Salem, M.; Wolf, E. Beam conditions for radiation generated by an electromagnetic Gaussian Schell-model source. Opt. Lett. 2004, 29, 1173. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Electromagnetic Schell-model sources generating far fields with stable and flexible concentric rings profiles. Opt. Express 2016, 24, 5572. [Google Scholar] [CrossRef]
- Du, X.; Zhao, D. Propagation of random electromagnetic beams through axially nonsymmetrical optical systems. Opt. Commun. 2008, 281, 2711–2715. [Google Scholar] [CrossRef]
- Wang, J.; Zhu, S.; Wang, H.; Cai, Y.; Li, Z. Second-order statistics of a radially polarized cosine-Gaussian correlated Schell-model beam in anisotropic turbulence. Opt. Express 2016, 24, 11626–11639. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Cai, Y.; Korotkova, O. Propagation factor of a stochastic electromagnetic Gaussian Schell-model beam. Opt. Express 2010, 18, 12587–12598. [Google Scholar] [CrossRef] [PubMed]
- Cao, P.; Fu, W.; Sun, Q. The second–order moment statistics of a twisted electromagnetic Gaussian Schell-Model propagating in a uniaxial crystal. Optik 2018, 162, 19–26. [Google Scholar] [CrossRef]
- Zhuang, F.; Du, X.; Zhao, D. Polarization modulation for a stochastic electromagnetic beam passing through a chiral medium. Opt. Lett. 2011, 36, 2683–2685. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Huang, Y.; Chen, Y.; Guo, L.; Cai, Y. Orbital angular moment of an electromagnetic Gaussian Schell-model beam with a twist phase. Opt. Express 2015, 23, 30283. [Google Scholar] [CrossRef] [PubMed]
- Sahin, S.; Tong, Z.; Korotkova, O. Sensing of semi-rough targets embedded in atmospheric turbulence by means of stochastic electromagnetic beams. Opt. Commun. 2010, 283, 4512–4518. [Google Scholar] [CrossRef]
- Korotkova, O.; Salem, M.; Wolf, E. The far-zone behavior of the degree of polarization of electromagnetic beams propagating through atmospheric turbulence. Opt. Commun. 2004, 233, 225–230. [Google Scholar] [CrossRef]
- Salem, M. Changes in the polarization ellipse of random electromagnetic beams propagating through the turbulent atmosphere. Waves Random Complex 2005, 15, 353–364. [Google Scholar] [CrossRef]
- Salem, M.; Korotkova, O.; Dogariu, A.; Wolf, E. Polarization changes in partially coherent electromagnetic beams propagating through turbulent atmosphere. Waves Random Media 2004, 14, 513–523. [Google Scholar] [CrossRef]
- Li, J. Polarization singularities of random partially coherent electromagnetic beams in atmospheric turbulence. Opt. Laser Technol. 2018, 107, 67–71. [Google Scholar] [CrossRef]
- Cai, Y.; Korotkova, O.; Eyyuboğlu, H.T.; Baykal, Y. Active laser radar systems with stochastic electromagnetic beams in turbulent atmosphere. Opt. Express 2008, 16, 15834–15846. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Zhao, D.; Du, X. Propagation of stochastic Gaussian-Schell model array beams in turbulent atmosphere. Opt. Express 2008, 16, 18437–18442. [Google Scholar] [CrossRef] [PubMed]
- Roychowdhury, H.; Ponomarenko, S.A.; Wolf, E. Change in the polarization of partially coherent electromagnetic beams propagating through the turbulent atmosphere. J. Mod. Opt. 2005, 52, 1611–1618. [Google Scholar] [CrossRef]
- Wang, Y.; Li, C.; Wang, T.; Zhang, H.; Xie, J.; Liu, L.; Guo, J. The effects of polarization changes of stochastic electromagnetic beams on heterodyne detection in turbulence. Laser Phys. Lett. 2016, 13, 116006. [Google Scholar] [CrossRef]
- De Sande, J.C.G.; Piquero, G.; Santarsiero, M.; Gori, F. Partially coherent electromagnetic beams propagating through double-wedge depolarizers. J. Opt. 2014, 16, 035708. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M.; Piquero, G.; Borghi, R.; Mondello, A.; Simon, R. Partially polarized Gaussian Schell-model beams. J. Opt. A Pure Appl. Opt. 2001, 3, 1. [Google Scholar] [CrossRef]
- Hao, Q.; Cheng, Y.; Cao, J.; Zhang, F.; Zhang, X.; Yu, H. Analytical and numerical approaches to study echo laser pulse profile affected by target and atmospheric turbulence. Opt. Express 2016, 24, 25026. [Google Scholar] [CrossRef]
- Vorontsov, M.A.; Lachinova, S.L.; Majumdar, A.K. Target-in-the-loop remote sensing of laser beam and atmospheric turbulence characteristics. Appl. Opt. 2016, 55, 5172–5179. [Google Scholar] [CrossRef]
- Korotkova, O.; Cai, Y.; Watson, E. Stochastic electromagnetic beams for LIDAR systems operating through turbulent atmosphere. Appl. Phys. B 2009, 94, 681–690. [Google Scholar] [CrossRef]
- Zhao, Y.; He, T.; Shan, C.; Sun, H. Influence of atmosphere turbulence and laser coherence on the identification method based on interference multiple-beam scanning of optical targets. Ukr. J. Phys. Opt. 2017, 18, 213. [Google Scholar] [CrossRef][Green Version]
- Wu, G.; Cai, Y. Detection of a semirough target in turbulent atmosphere by a partially coherent beam. Opt. Lett. 2011, 36, 1939–1941. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhu, S.; Li, Z. Vector properties of a tunable random electromagnetic beam in non-Kolmogrov turbulence. Chin. Opt. Lett. 2016, 14. [Google Scholar] [CrossRef]
- Korotkova, O.; Andrews, L.C. Speckle propagation through atmospheric turbulence: Effects of partial coherence of the target[C]//Laser Radar Technology and Applications VII. Int. Soc. Opt. Photonics 2002, 4723, 73–84. [Google Scholar] [CrossRef]
- Korotkova, O.; Andrews, L.C.; Phillips, R.L. Laser radar in turbulent atmosphere: Effect of target with arbitrary roughness on second-and fourth-order statistics of Gaussian beam. Proc. Spie 2003, 5086, 173–183. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical properties of laser speckle patterns. In Laser Speckle & Related Phenomena; Dainty, J.C., Ed.; Springer: New York, NY, USA, 1975. [Google Scholar] [CrossRef]
- Lin, Q.; Cai, Y. Tensor ABCD law for partially coherent twisted anisotropic Gaussian-Schell model beams. Opt. Lett. 2002, 27, 216–218. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Wolf, E. Light beams whose degree of polarization does not change on propagation. Opt. Commun. 2008, 281, 3067–3070. [Google Scholar] [CrossRef]
- Meemon, P.; Salem, M.; Lee, K.S.; Chopra, M.; Rolland, J.P. Determination of the coherency matrix of a broadband stochastic electromagnetic light beam. J. Mod. Opt. 2008, 55, 2765–2776. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Zhao, Y.; Liu, X.; Cai, Y. Detection of a Semi-Rough Target in Turbulent Atmosphere by an Electromagnetic Gaussian Schell-Model Beam. Appl. Sci. 2019, 9, 2790. https://doi.org/10.3390/app9142790
Li X, Zhao Y, Liu X, Cai Y. Detection of a Semi-Rough Target in Turbulent Atmosphere by an Electromagnetic Gaussian Schell-Model Beam. Applied Sciences. 2019; 9(14):2790. https://doi.org/10.3390/app9142790
Chicago/Turabian StyleLi, Xiaofei, Yuefeng Zhao, Xianlong Liu, and Yangjian Cai. 2019. "Detection of a Semi-Rough Target in Turbulent Atmosphere by an Electromagnetic Gaussian Schell-Model Beam" Applied Sciences 9, no. 14: 2790. https://doi.org/10.3390/app9142790
APA StyleLi, X., Zhao, Y., Liu, X., & Cai, Y. (2019). Detection of a Semi-Rough Target in Turbulent Atmosphere by an Electromagnetic Gaussian Schell-Model Beam. Applied Sciences, 9(14), 2790. https://doi.org/10.3390/app9142790




