THz Superradiance from a GaAs: ErAs Quantum Dot Array at Room Temperature
Abstract
1. Introduction
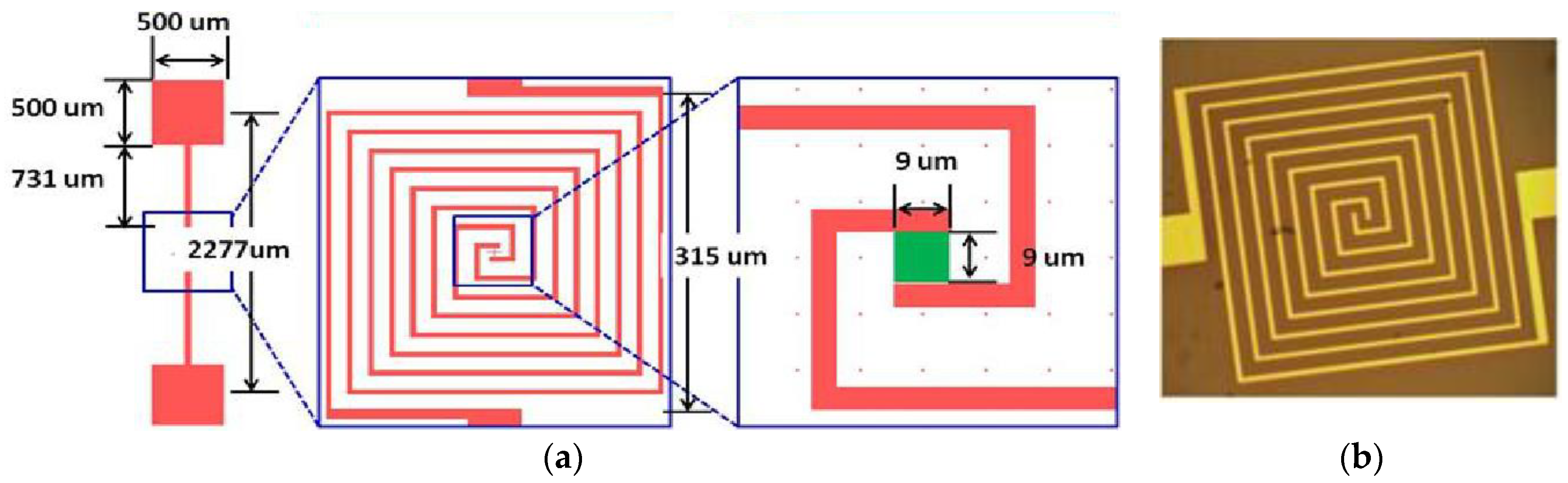
2. Materials and Methods
3. Results
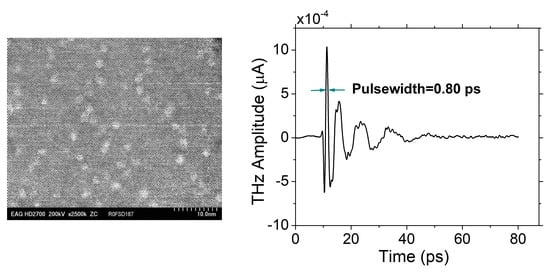
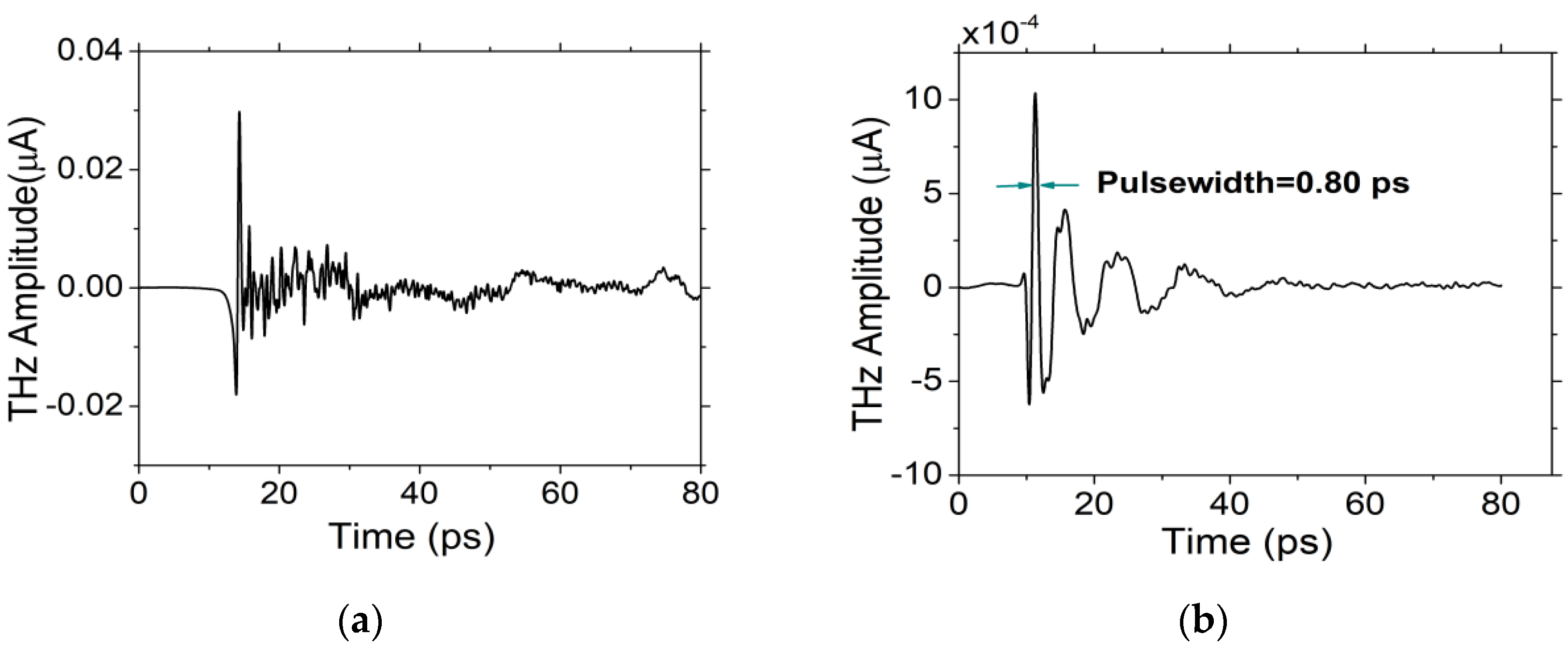
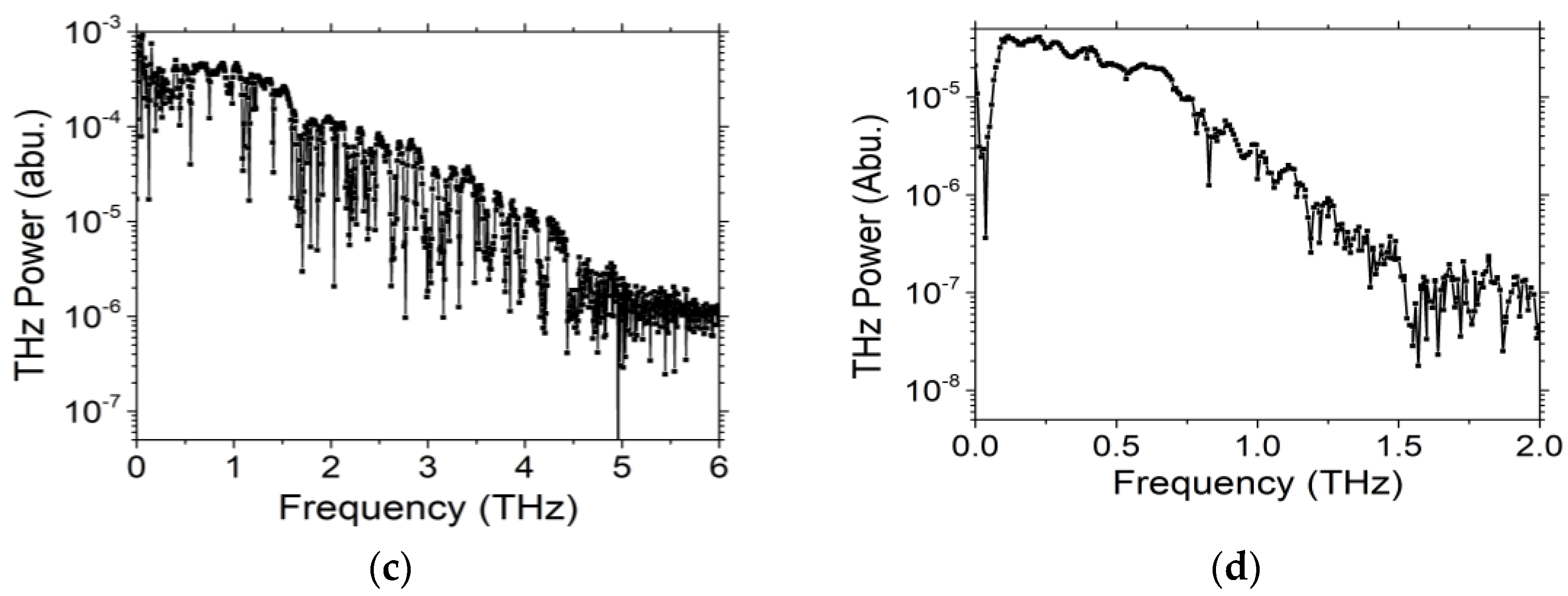
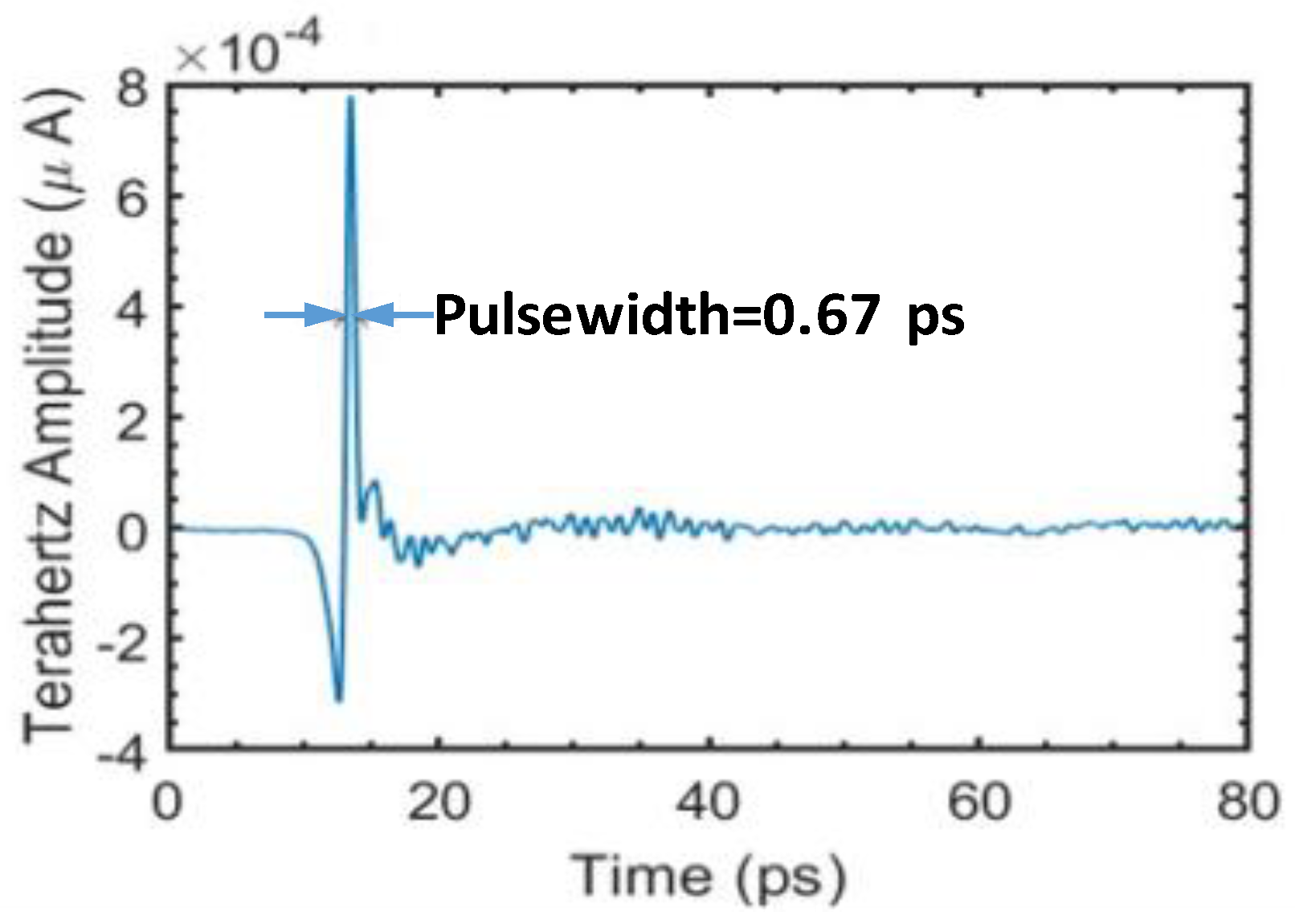
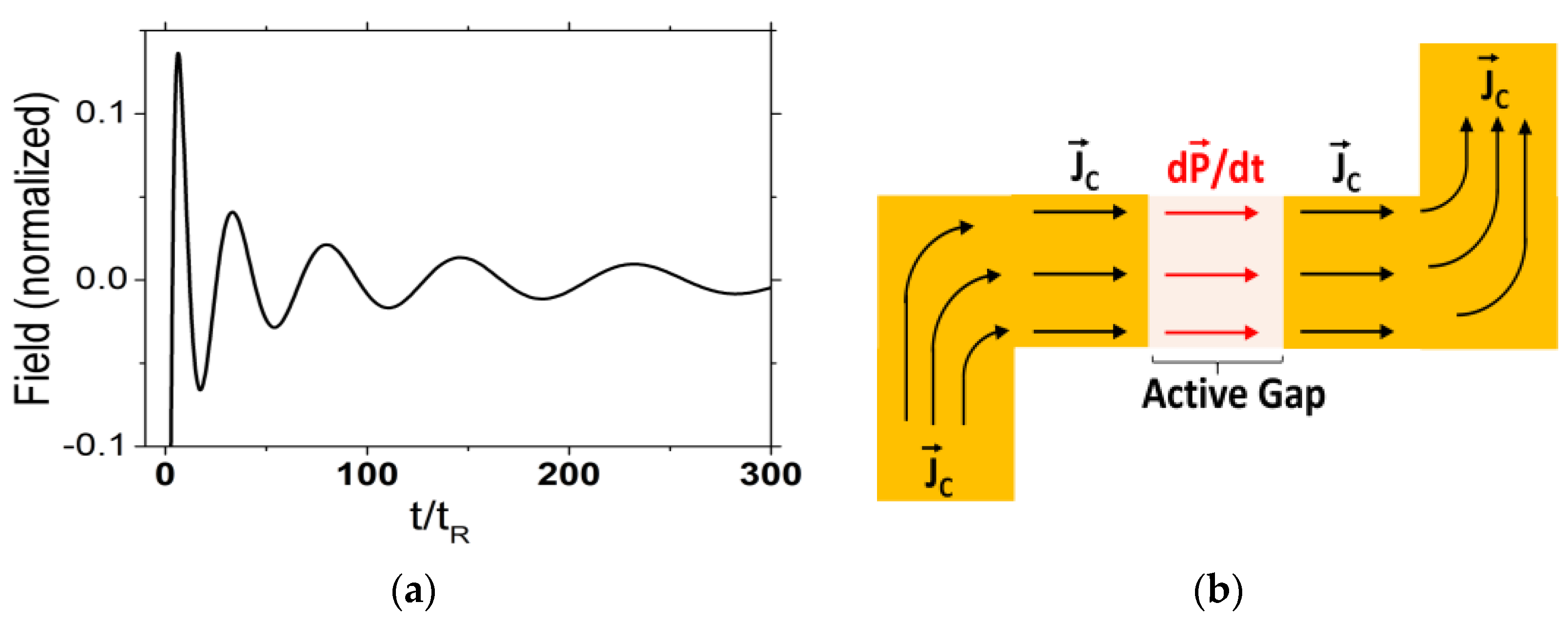
3.1. Pulsed Terahertz (THz) Emission
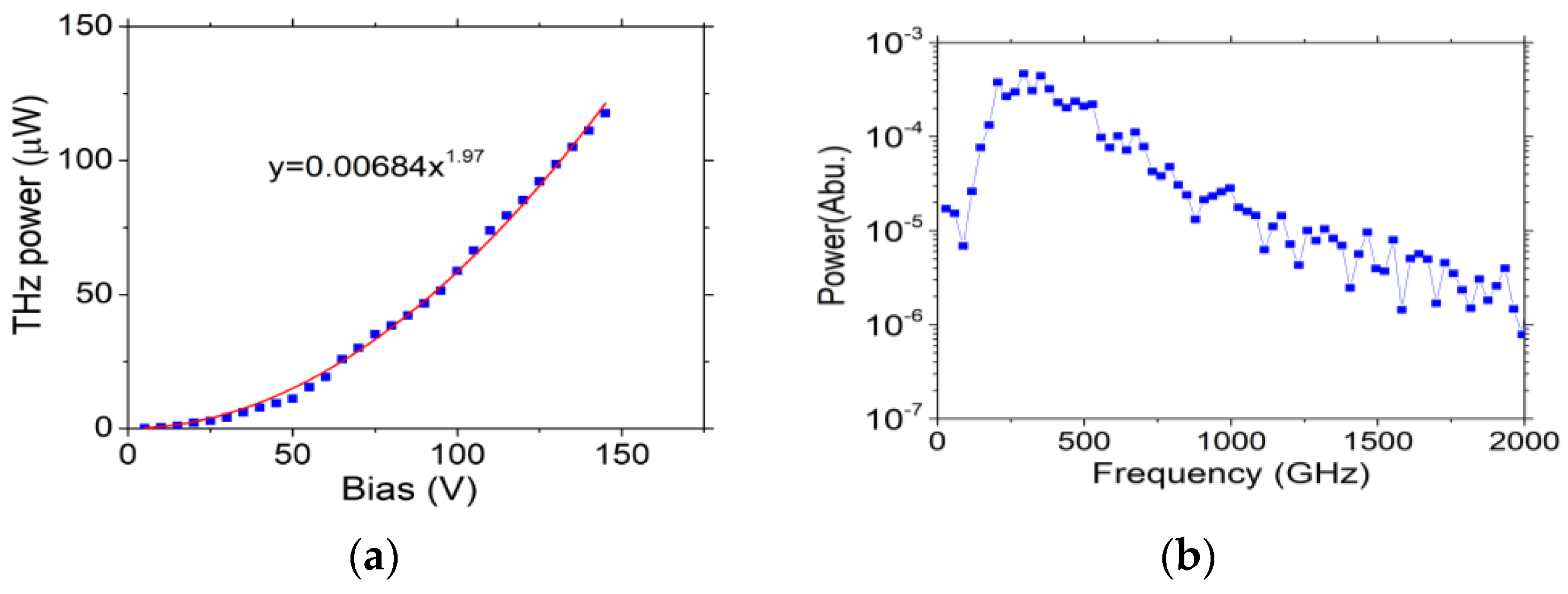
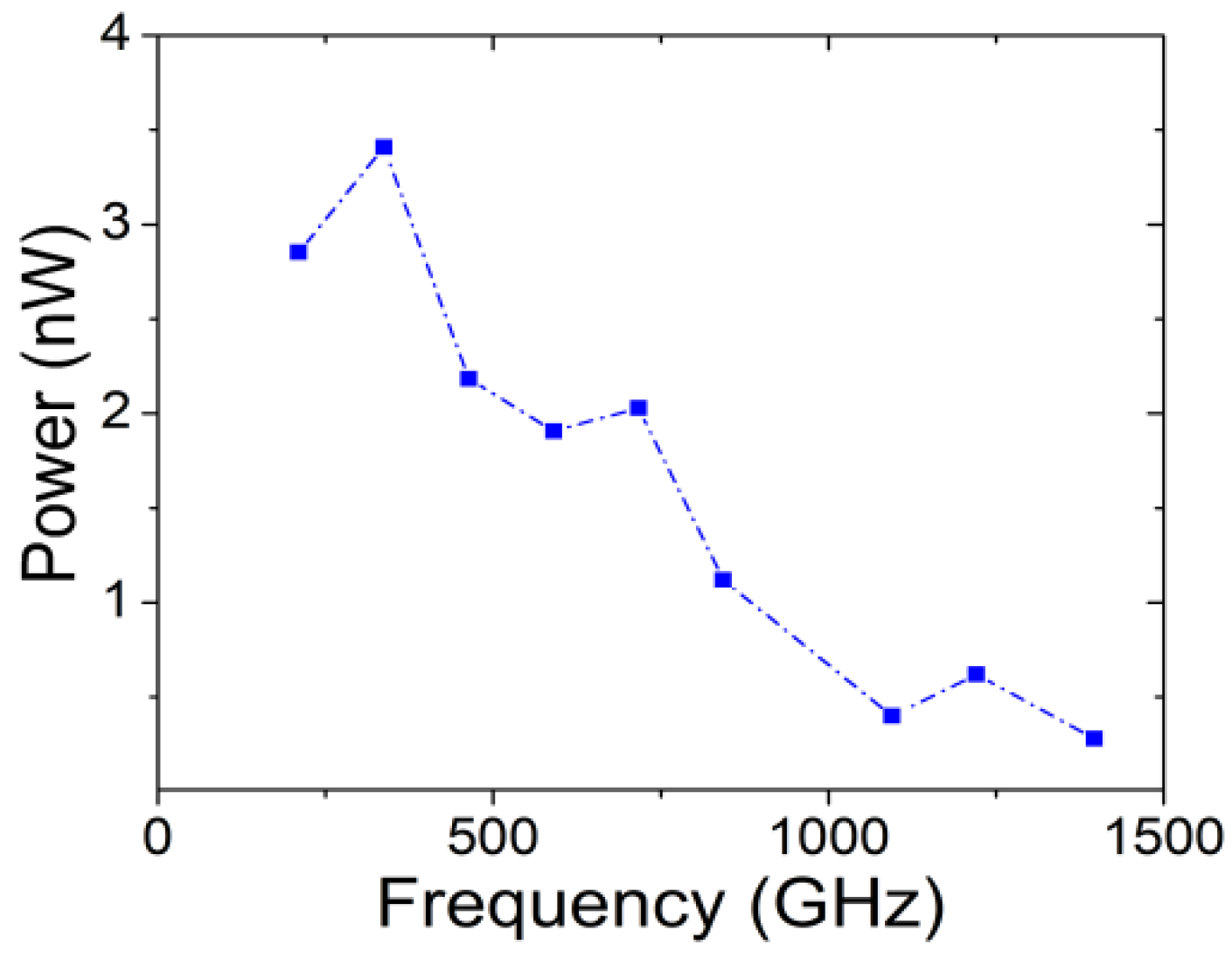
3.2. Efficiency and Photomixing Results
4. Discussion
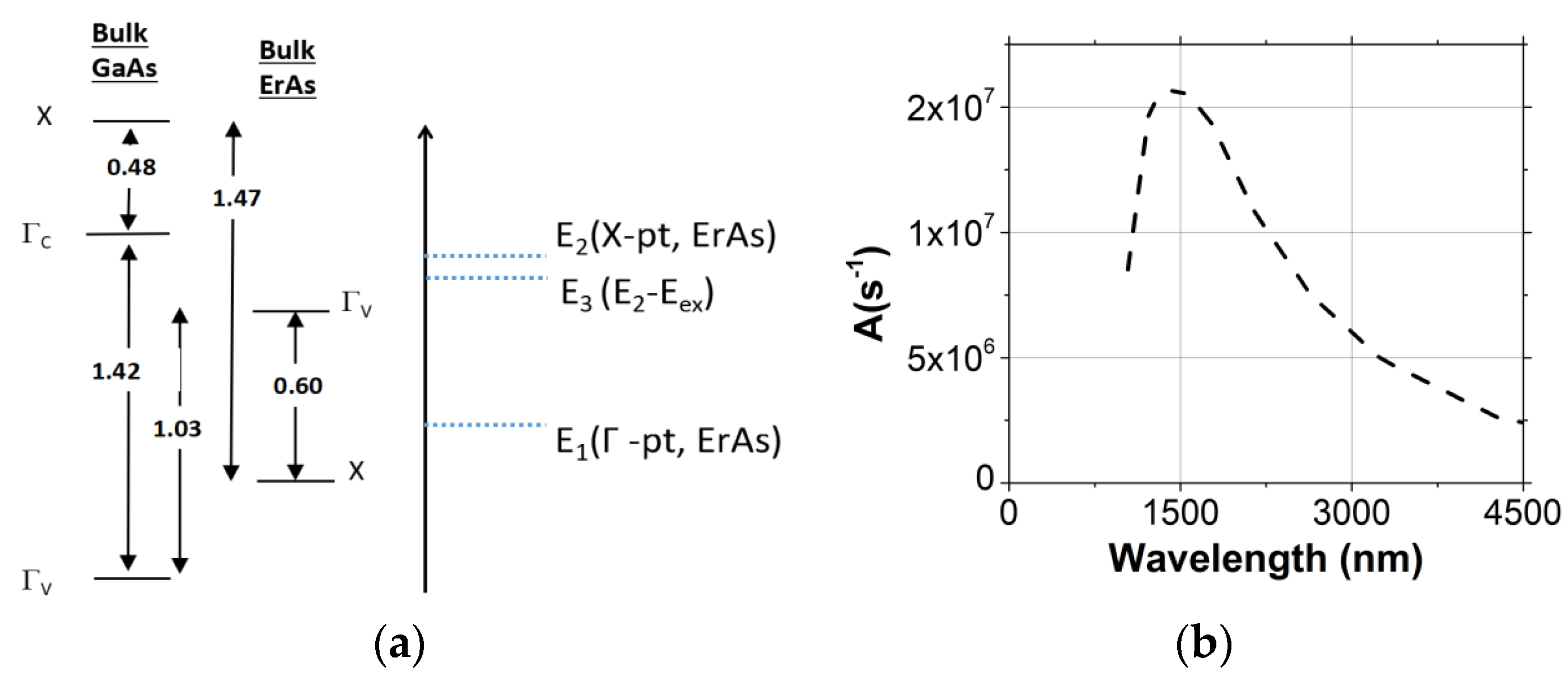
4.1. Quantum Dot (QD) Modeling
4.2. Comparison of THz Data with Superradiant Theory
4.3. Comparison of This Research with Previous Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dicke, R.H. Coherence in spontaneous radiation process. Phys. Rev. 1954, 93, 99–110. [Google Scholar] [CrossRef]
- MacGillivray, J.C.; Feld, M.S. Theory of superradiance in an extended, optically thick medium. Phys. Rev. A 1976, 14, 1169–1189. [Google Scholar] [CrossRef]
- Benedict, M.G.; Ermolaev, A.M.; Malyshev, V.A.; Sokolov, I.V.; Trifonov, E.D. Super-Radiance: Multiatomic Coherent Emission; Institute of Physics Publishing: Bristol, UK, 1996; pp. 31–37. [Google Scholar]
- Parascandolo, G.; Savona, V. Long-range radiative interaction between semiconductor quantum dots. Phys. Rev. B 2005, 71, 045335. [Google Scholar] [CrossRef]
- Temnov, V.V.; Woggon, U. Superrandiance and subradiance in an inhomogeneously broadened ensemble of two-level systems coupled to a low-Q cavity. Phys. Rev. Lett. 2005, 95, 243603. [Google Scholar] [CrossRef] [PubMed]
- Yukalov, V.I.; Yukalova, E.P. Dynamics of quantum dot superradiance. Phys. Rev. B 2010, 81, 075308. [Google Scholar] [CrossRef]
- Scheibner, M.; Schmidt, T.; Worschech, L.; Forchel, A.; Bacher, G.; Passow, T.; Hommel, D. Superradiance of quantum dots. Nat. Phys. 2007, 3, 106–110. [Google Scholar] [CrossRef]
- Mingardi, A.; Zhang, W.-D.; Brown, E.R.; Feldman, A.D.; Harvey, T.E.; Mirin, R.P. High power generation of THz from 1550-nm photoconductive emitters. Opt. Express 2018, 26, 14472–14478. [Google Scholar] [CrossRef]
- Dietz, R.J.B.; Gerhard, M.; Stanze, D.; Koch, M.; Sartorius, B.; Schell, M. THz Generation at 1.55 m excitation: Six-fold increase in THz conversion efficiency by separated photoconductive and trapping regions. Opt. Express 2011, 19, 25911–25917. [Google Scholar] [CrossRef] [PubMed]
- Kawasaki, J.K.; Timm, R.; Delaney, K.T.; Lundgren, E.; Mikkelsen, A.; Palmstrøm, C.J. Local Density of States and Interface Effects in Semimetallic ErAs Nanoparticles Embedded in GaAs. Phys. Rev. Lett. 2011, 107, 036806. [Google Scholar] [CrossRef] [PubMed]
- Kayanuma, Y. Quantum-size effects of interacting electrons and holes in semiconductor microcrystals with spherical shape. Phys. Rev. B 1988, 38, 9797–9805. [Google Scholar] [CrossRef] [PubMed]
- Burnham, D.C.; Chao, R.Y. Coherent resonance fluorescence excited by short light pulses. Phys. Rev. 1969, 188, 667–675. [Google Scholar] [CrossRef]
- Bonifacio, R.; Lugiato, L.A. Cooperative radiation processes in two-level systems: Superfluorescence. Phys. Rev. A 1975, 11, 1507–1521. [Google Scholar] [CrossRef]
- Leyman, R.R.; Gorodetsky, A.; Bazieva, N.; Molis, G.; Krotkus, A.; Clarke, E.; Rafailov, E.U. Quantum dot materials for terahertz generation applications. Laser Photon. Rev. 2016, 10, 772–779. [Google Scholar] [CrossRef]
- Kruczek, T.; Leyman, R.; Carnegie, N.; Baziev, N.; Erbert, G.; Schulz, S.; Reardon, C.; Reynolds, S.; Rafailov, E.U. Continuous wave terahertz radiation from an InAs/GaAs quantum-dot photomixer device. Appl. Phys. Lett. 2012, 101, 0811141. [Google Scholar] [CrossRef][Green Version]
- Fedorova, K.A.; Gorodetsky, A.; Rafailov, E.U. Compact all-quantum-fot based tunable THz laser source. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1900305. [Google Scholar] [CrossRef]
- Gorodetsky, A.; Yadav, A.; Avrutin, E.; Fedorova, K.A.; Rafaulov, E.U. Photoelectric properties of InAs/GaAs quantum dot photoconductive antenna wafers. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1900105. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Brown, E.R.; Mingardi, A.; Mirin, R.P.; Jahed, N.; Saeedkia, D. THz Superradiance from a GaAs: ErAs Quantum Dot Array at Room Temperature. Appl. Sci. 2019, 9, 3014. https://doi.org/10.3390/app9153014
Zhang W, Brown ER, Mingardi A, Mirin RP, Jahed N, Saeedkia D. THz Superradiance from a GaAs: ErAs Quantum Dot Array at Room Temperature. Applied Sciences. 2019; 9(15):3014. https://doi.org/10.3390/app9153014
Chicago/Turabian StyleZhang, Weidong, Elliott R. Brown, Andrea Mingardi, Richard P. Mirin, Navid Jahed, and Daryoosh Saeedkia. 2019. "THz Superradiance from a GaAs: ErAs Quantum Dot Array at Room Temperature" Applied Sciences 9, no. 15: 3014. https://doi.org/10.3390/app9153014
APA StyleZhang, W., Brown, E. R., Mingardi, A., Mirin, R. P., Jahed, N., & Saeedkia, D. (2019). THz Superradiance from a GaAs: ErAs Quantum Dot Array at Room Temperature. Applied Sciences, 9(15), 3014. https://doi.org/10.3390/app9153014