1. Introduction
The increasing environmental issues, such as air pollution and global climate change, force the airline industry and aircraft designers to seek more economical airplane designs with the maximum lift-to-drag ratio and minimum structural weight as well as favorable stability. The success of such an aircraft design can provide opportunities to consider the welfare and comfort of passengers in its design phase and lead to a decrease in fuel consumption. To achieve this aim, faster and more efficient approaches to design optimization of lightweight but strong aircraft have been well studied by many researchers [
1,
2,
3].
Aircraft design is an inherently multidisciplinary, iterative effort. However, conventional design methods weaken the collaborative effect of various disciplines so that aerodynamic, structural, and stability analyses have to be performed in a specific sequence to achieve an optimum of a system. The major limitation of this method relates to an iterative design process and will lead to less efficiency of computations, so it can hardly adapt to the design of a modern aircraft, especially the conceptual design with great potential for innovation in the early stage. Instead, multidisciplinary analysis and optimization (MAO) could take disciplines containing aerodynamics, structure, aircraft flight dynamics, etc. into consideration simultaneously and has been employed in large modern aircraft designs [
4,
5,
6,
7,
8,
9]. In light of its capability to overcome the limitations of the conventional method, the MAO technique with the integration of novel algorithms has been applied to solve complex problems in other industry sectors, such as automobile [
10,
11], energy [
12], mechatronic systems [
13], etc. Obviously, a crucial challenge of MAO is its massive computation burden, especially for computational fluid dynamics (CFD) simulations based on Reynolds-averaged Naiver-Stokes (RANS) equations. Though RANS method can simulate intricate turbulence and shedding vortex, the steady flight conditions make up most of the flight time of a large aircraft, hence some viscous-inviscid iteration methods are more suitable for cruise conditions with moderate flow separation [
14]. As the disturbance in the cruise condition is weak compared with the steady-state, the small-disturbance theory is valid for the stability analysis.
Although a gradient-based algorithm has the advantages of rapidity and effectiveness for solving an optimization problem, it is apt to converge to a local optimal solution and sometimes, it fails in special cases where calculating the partial derivatives is hard or the derivatives are not continuous. Considering these facts, the evolutionary algorithms are suitable to seek the globally optimal solution. Genetic algorithm (GA) is based on Darwin’s theory and is used most widely as a global algorithm for this purpose [
15,
16]. However, function evaluations in GA are the most time-consuming part as they are usually executed by finite element analysis (FEA) or CFD with high computational demands, for example, a single function evaluation could be of the order of hours or days. Hence, the computational burden of FEA or CFD for design evaluations is the main limitation of GA for solving multidisciplinary optimization problems.
To reduce the computational burden and benefit to a great extent of better exploration and exploitation in the design space, metamodel-based optimization has recently found widespread use owing to its promising potential [
17,
18,
19,
20,
21,
22,
23]. As a response surface method, genetic programming (GP) is a systematic way of selecting a structure of high-quality global approximations [
24]. The program can represent an empirical model to be used for approximation of a response function, and the explicit expression [
25], or even algorithms [
26], can be entirely attained for optimization. With the high accuracy, approximation models generated by GP have already been used for solving various design optimization problems [
18,
21,
27,
28,
29].
In light of the exploitation of the immense potential from a large aircraft conceptual design process and the advantages of GP methodology in support of MAO, an integrated GP metamodel-based optimization method to design a full-scale aircraft subject to aerodynamic, structural and stability constraints is proposed in this paper. Static aeroelasticity and flutter analyses are performed with the MSC/Nastran doublet-lattice method. The stability of flight dynamics is evaluated by the linear small-disturbance method. The lift-to-drag ratio is estimated by a viscous-inviscid iteration technique implemented in the CFD solver MGAERO. To address this MAO problem, a two-step procedure for designing a conceptual aircraft is proposed. First, GP methodology was applied to generate metamodels based on optimal Latin hypercube design of experiments (DoE). With these metamodels, multidisciplinary analysis can be efficiently executed due to the explicit mathematical approximations of the predictive models. Subsequently, parametric optimization was performed for the minimum stiffness of the wing structure subject to aerodynamic, aeroelastic and stability constraints. To demonstrate the strength and accuracy of GP methodology for solving complex design problems, both GA and GP methods were employed to find the optimal solutions for a representative beam-frame wing structure. Finally, sensitivity analysis was conducted to identify the critical input parameters that affect aircraft performance in the conceptual design phase.
2. Brief Review of Aircraft Multidisciplinary Analysis
In this research, the wing jig shape was optimized using the proposed MAO method. Its aerodynamic shape, elastic axis positions, and stiffnesses were considered in the process of parameterized modeling. Then, the structural deformation was obtained by the static aeroelastic analysis and the deflections of structural nodes were transformed into the deformations of aerodynamic grids using the infinite plate spline (IPS) interpolation. Once the aerodynamic model of the wing cruise shape was constructed, the flow field was estimated and the stability was analyzed using small-disturbance theory. A brief review of aerodynamics, flight stability and aeroelasticity in the multidisciplinary analysis is introduced in this section.
2.1. Aerodynamics
Aerodynamics analysis of a typical aircraft is usually performed using high-fidelity CFD tools based on the Reynolds-averaged Naiver-Stokes (RANS) equations. Solving RANS equations is a tedious process due to the massive computational burden involved, especially when the aerodynamic and structural coupling analysis is required to determine a preliminary aircraft design. In our research, the governing Euler equations for inviscid compressible flow were discretized by equally spatial Cartesian meshes, which greatly facilitated the grid generation. A viscous-inviscid iteration technique provided by the commercial CFD solver MGAERO was used to calculate the lift-to-drag ratio. The integral form of Euler equations for the general control volume can be written as:
where
means the general control volume,
is the vector of dependent variables, whose transpose is
,
is the air density,
,
and
are the velocity components in the Cartesian coordinate system,
is the internal energy of the unit volume,
is the outward normal vector, and
is the flux vector. By employing the far-field drag extraction theory [
30], the shock wave and the induced drag were determined by the decomposition of the total inviscid drag.
2.2. Flight Stability
It is quite common to consider momentary disturbances from non-stationary airflow, wakes, movements of passengers, or release of stores, on the aerodynamics of aircraft and stability during the steady flight mode. Such interference can be viewed as a small disturbance, thus the aircraft equations of motion can be decoupled according to the linear small-disturbance theory [
31]. In the cruise condition, the normal state-space equation of longitudinal/lateral stability is written as:
where
is the system matrix,
is the control matrix,
is the state vector, and
is the control vector.
and
are constructed by the aerodynamic derivatives, the mass property and the aerodynamic coefficients,
is composed by the disturbed flight parameters, and
is composed by the deflections of control surfaces.
2.3. Aeroelasticity
The basic equation of static aeroelasticity can be described as:
where the subscript
denotes the degree of freedom of the equation,
is the structural stiffness matrix,
is the matrix of aerodynamic influence coefficients,
is the structural mass matrix,
is the matrix of unit aerodynamic loads,
is the structural deformation vector,
is the acceleration vector of rigid body motion,
is the vector of aerodynamic trim parameters (e.g., angle of attack, elevator deflection), which is used to define the deflection of the aerodynamic control surface and the overall rigid motion of the aircraft,
is the vector of applied loads, and
is the dynamic pressure.
To perform flutter analysis, the equation of the p-k method is used as follows [
32]:
where
denotes the coordinate of the normal modes,
is the modal mass matrix,
is the modal damping matrix,
is the modal stiffness matrix,
is the flow speed,
is the reference chord length,
is the air density,
k is the reduced frequency,
is the modal amplitude vector,
is the generalized aerodynamic force matrix, which is the function of
k, and the superscripts
R and
I represent the real and imaginary parts, respectively. Equation (3) can also be rewritten as:
, where
denotes the vector containing modal displacements and velocities,
means the complex eigenvalue.
In terms of displacement interpolation between the structural nodes and the aerodynamic surface grid points, it is determined by the surface spline method [
33].
3. Genetic Algorithm (GA) Based Optimization Strategy
GA is considered a popular tool for locating the global optimum solution [
16,
34,
35,
36]. GA is a population-based evolutionary algorithm and inspired by genetic evolutions. It employs genetic operators of selection, mutation, and crossover to generate the populations for improving the fitness function to achieve its evolutionary strategy. Thus, the mechanism of GA can be described as a combination of an artificial survival of the fittest and genetic operators from nature to iteratively improve the fitness of the population.
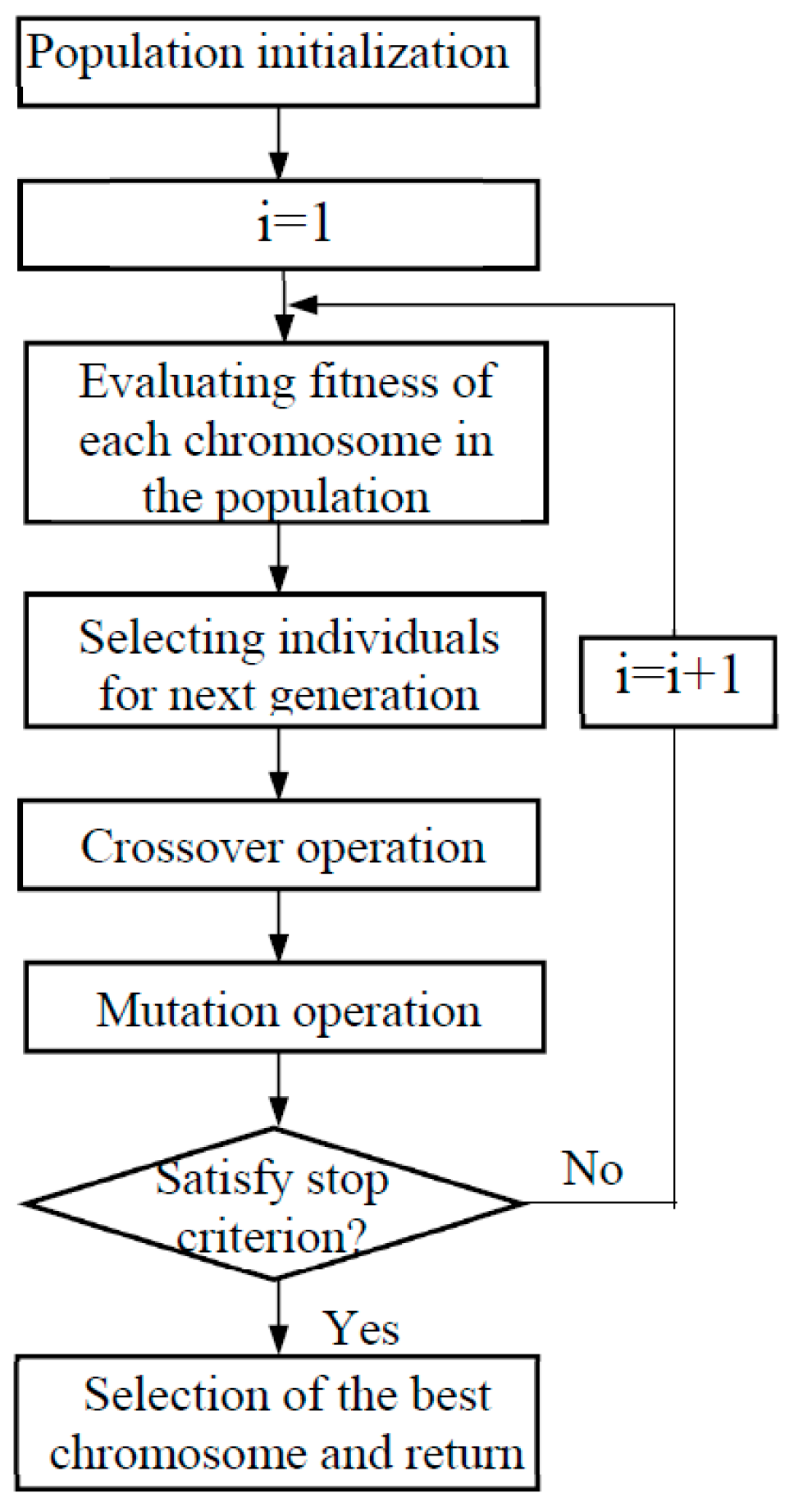
The flowchart of GA is shown in
Figure 1. The implementation of the GA procedure for solving the multidisciplinary analysis and optimization problem in this paper can be explained as consisting of three steps:
Step 1: Generate the initial population using genetic parameters and each individual represents a specific aircraft model.
Step 2: Perform the aforementioned multidisciplinary analysis to evaluate the responses of the interests for the current population.
Step 3: Apply genetic operators to create the next generation of population and repeat Step 2 until the number of generations is met.
To apply GA-based strategy for the aircraft design, a parameterized model of the representative aircraft configuration was developed and then was used to perform the simulations required by GA. The developed model included 19 design parameters depicted in
Table 1 in
Section 4.3 and
Section 4.4.
4. Genetic Programming Aided Optimization of Conceptual Aircraft Design
Based on the multidisciplinary analysis described in
Section 2, a preliminary aircraft design can be conducted using conventional methods. To overcome the low computational efficiency of traditional sequence approaches, multidisciplinary analysis and optimization (MAO) was used to apply the above theoretical principles in a multidisciplinary context across the disciplines of aerodynamics, structure, aircraft flight dynamics, etc. for efficient aircraft designs in this paper. However, the aircraft multidisciplinary design is actually a multi-parameter optimization problem, it is very difficult to predict and evaluate the influence of design variables on aircraft performance because there are many parameters. Based on this discussion, genetic programming, as a new artificial intelligence technique, is proposed to build mathematical expressions representing the relationship between the input parameters and output responses of the interests. Once this metamodeling process is completed, the optimal solution describing the aircraft configurations will be obtained with less computational cost by replacing the full model with a GP metamodel. The process of this metamodel-based MAO for the optimal design consisted of four steps and they were:
Design of experiments
Metamodel building by genetic programming (GP)
Parameterized finite element model
Optimization formulation, design variables and constraints
These four steps were integrated to perform the multi-parameter, multidisciplinary optimization of the conceptual aircraft design and explained in the following sub-sections.
4.1. Design of Experiments
Design of experiments (DoE) is a statistical technique to simultaneously study the effect of multiple variables with high efficiency and it can successfully deal with design optimization projects of various engineering applications [
37]. A survey of different kinds of DoE is given by Simpson et al. [
38]. However, the quality of the metamodel strongly depends on an appropriate choice of DoE type and sampling size. To improve the quality of the conventional random Latin hypercube DoE, a uniform Latin hypercube DoE based on the use of the Audze-Eglais optimality criterion [
39], was employed in this paper. The main principles in this approach are as follows:
The number of levels of factors (same for each factor) is equal to the number of experiments and for each level, there is only one experiment.
The points corresponding to the experiments are distributed as uniformly as possible in the domain of factors, which is controlled by Equation (5):
where
P is the number of points,
is the Euclidean distance between the points
p and
q (
p ≠ q) in the system.
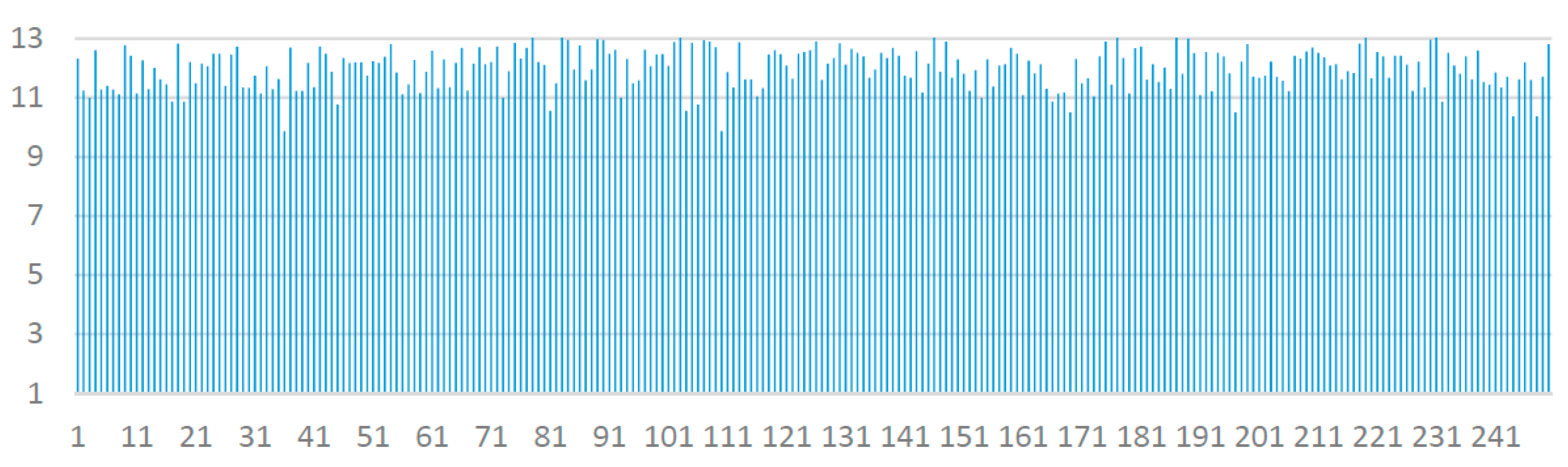
According to this extended optimal Latin hypercube design of numerical experiments (DoE), a 1997-point DoE has been developed for the FE simulation to be performed at each point. As an example, the bar chart of the minimum distances between the sampling points is shown in
Figure 2 indicating a good uniformity of 250-point DoE.
4.2. Metamodel Building by Genetic Programming (GP)
GP methodology is a systematic way of selecting a structure of high-quality global approximations, which can reflect the relationship between input parameters and output responses of the interests [
24]. As other nature-inspired methods, a population is generated in GP by three most important genetic operators: reproduction, mutation and crossover. The initial population is constructed by a blind random search of the space defined by the problem. The formula obtained by each individual in a population is composed of a random combination of functions (mathematical operators, such as square and addition) and terminals (variables and constants [
40,
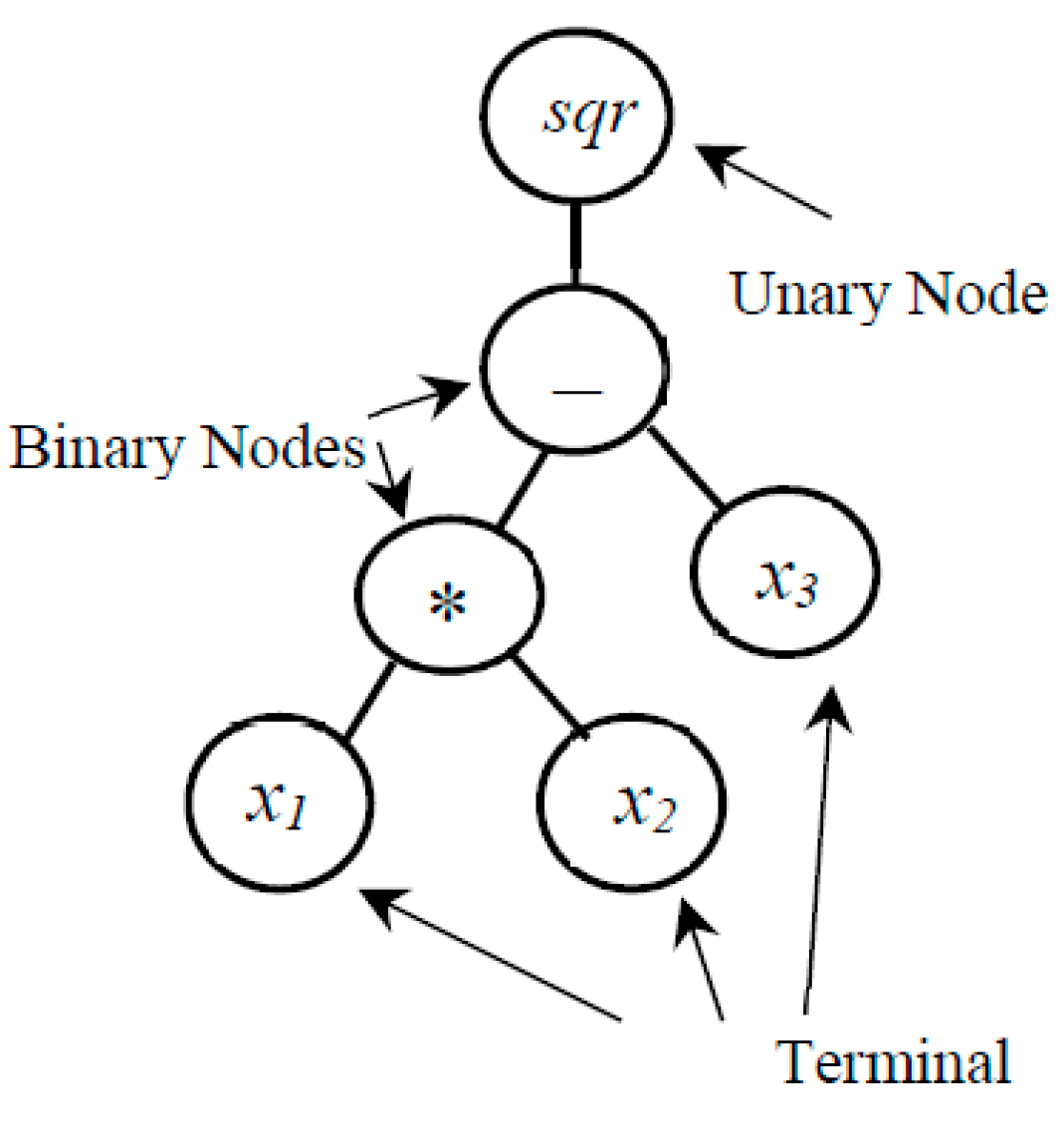
41]) and these mathematical approximations are actually computer programs with a tree structure. Selection of the structure of an analytical expression is a problem of empirical model building. A tree structure-based typical program, representing the expression (
x1 ×
x2 −
x3)
1/2, is shown in
Figure 3.
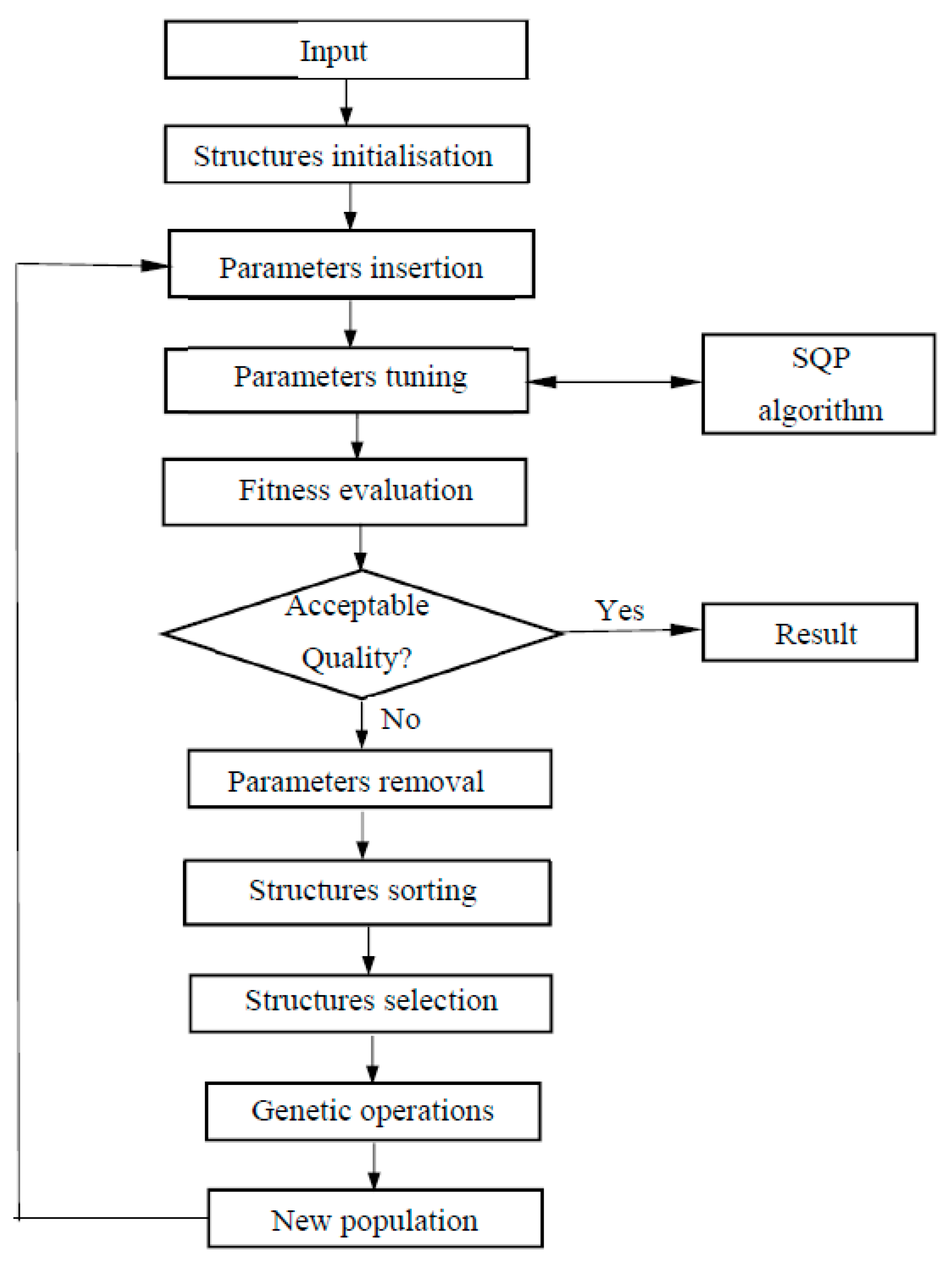
These randomly generated approximations are general and hierarchical, varying in size and shape. The main goal of GP is to solve a problem by searching a highly fit individual computer program in the space of all possible programs. GP methodology tries to find near-global solutions by keeping many solutions that may potentially be close to minima (local or global). A schematic description of the GP technique is sketched in
Figure 4 to demonstrate the process of metamodel building. First, initializing the population was performed to create various tree structures. Followed by parameter insertion to generate a family of mathematical expressions with coefficients, optimization by sequential quadratic programming (SQP) algorithm was conducted to determine the optimal locations and numbers of coefficients (or numerical terminals). After tuning, the individual that had the lowest error was chosen to represent the original individual. Finally, the fitness function was evaluated to assess the quality of each individual until the termination criterion was satisfied throughout the iterations of the whole process. More details about the procedure of GP methodology have been introduced in References [
24,
25,
42].
To encourage the evolution of smooth mathematical expressions, the fitness values
of individual i at generation t have been defined as a weighted sum of different terms or objectives, following an approach used for multi-objective optimization in evolution-based algorithms:
where
is the root mean square error (RMSE) of the
i-th individual in the
t-th generation evaluated on the given data set, divided by the average RMSE of the archive individuals at the previous generation, N is the total number of training data,
is the actual value,
is the estimated value;
is the square of the number of numerical coefficients (parameters) present in the individual;
is the number of operations not defined (i.e., division by zero) in the individual at any of the sample points;
is the number of nodes that the individual is made of and
,
,
and
are weighting factors (that add up to 1) determined by the exhaustive testing and tuning of the GP algorithm. To robustly solve multi-criterion optimization problems, a Pareto set method can be applied to select optimal weighting factors [
43]. In this paper, the weighting factors were
= 0.1, and
.
Two fit indices were computed to evaluate the accuracy of predictive models constructed by GP: one was the aforementioned RSME, and the coefficient of determination (R
2) was the other fit criterion used to control the predictive performance of the metamodels:
where
N is the total number of training data,
is the actual value,
is the estimated value, and
is the mean of the values
. Obviously, the predicted model will be quite perfect if
is equal to one and RMSE is zero. It is noted that there are 17 mathematical operators developed for GP-based metamodel building. They are {+, −, *, /, square, cube, constant, sine, cosine, sinh, cosh, tanh, exponential, negative exponential, natural logarithm, absolute, reciprocal}.
4.3. Parameterized Finite Element Model
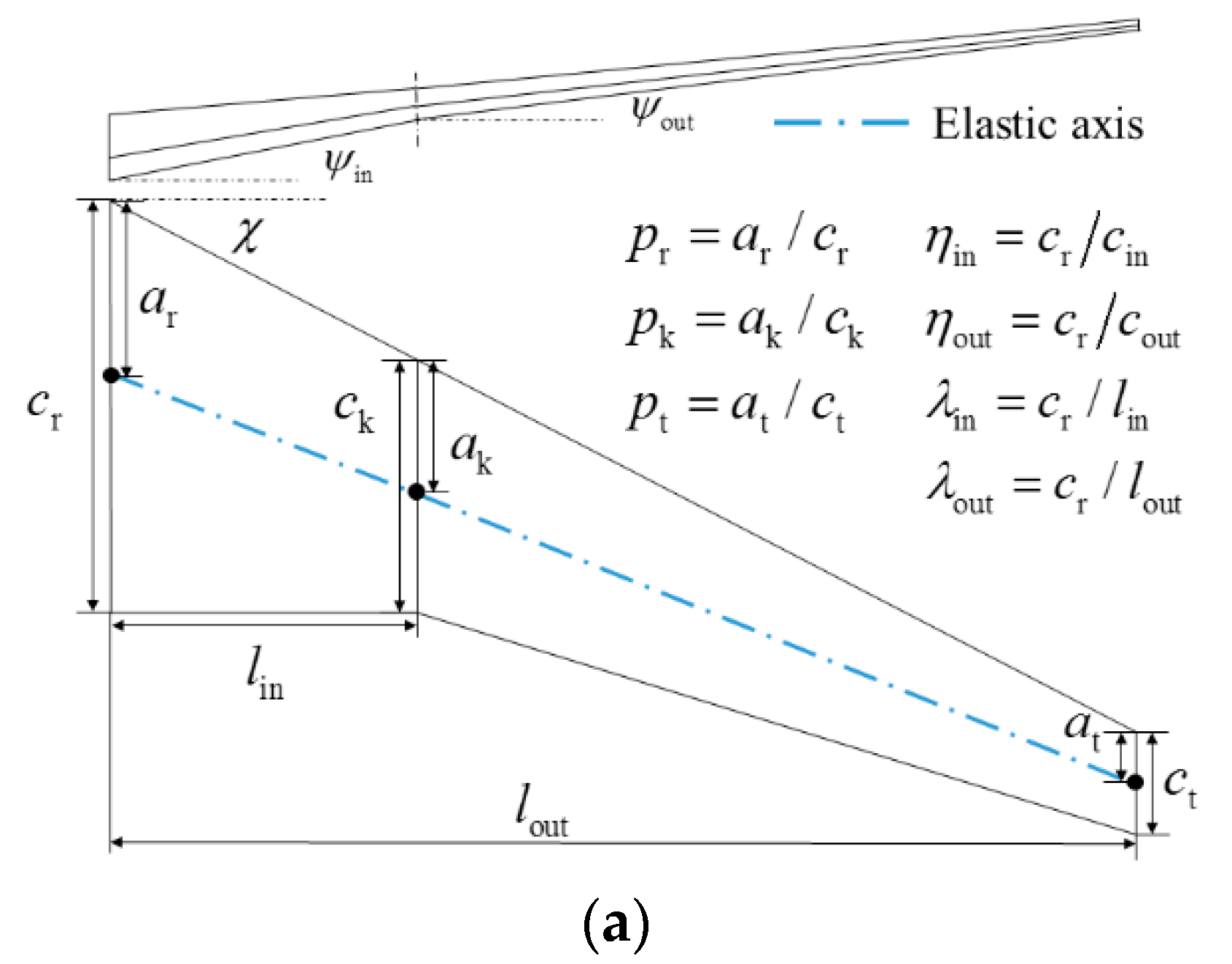
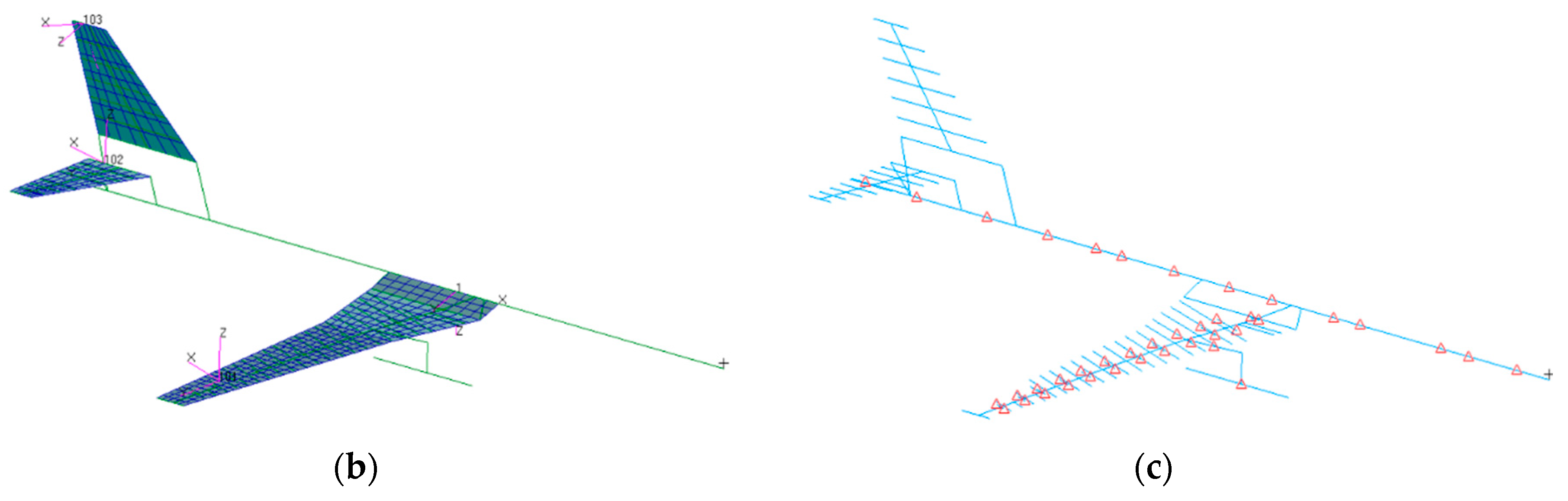
A representative beam-frame wing structure and its finite element model for static aeroelasticity and flutter analyses are shown in
Figure 5. The geometric configuration of this high-aspect-ratio wing model was decided by seven parameters in
Figure 5a, which are the inboard/outboard taper ratios (
), the inboard/outboard aspect ratios (
), the sweep angle of the leading edge (
), the inboard/outboard dihedral angles (
)). There are three more parameters (
,
) for determining the elastic axis positions at the root, the kink and the tip, respectively. The wing root length (
) was kept constant. The wing structural stiffness properties were modelled by a variable cross-section beam from the root to the tip and the structural mass was represented by lumped mass elements. Material properties of aluminum were assigned to the primary beam of the wing, and the components such as the body, tail and fin, were modelled using rigid elements. The wing lifting surface was modelled with 282 aerodynamic elements. A fixed maximum take-off weight of 84.5 tons and cruise Mach of 0.785 at a height of 11,200 m were applied to perform the analysis. The Reynolds number was 5.71 million based on the mean aerodynamic chord. The root chord remains a constant length with 6.17 m, and the reference area was varied with the geometric design variables.
4.4. Optimization Formulation, Design Variables and Constraints
Designing aircraft structures is a challenging procedure because the weight as an objective should be minimized and the stiffness provided should supply the required structural rigidity. The structural stiffnesses are expressed as
(flexural rigidity in the
x-direction),
(flexural rigidity in the y-direction),
GJ (torsional rigidity), and the mass is denoted by
, where
is the density of the air and
represents a fixed cross-section. For the constants
(Young’s modulus) and
(polar second moment of area), the stiffness is proportional to the mass:
where
is the reference length of the wing.
Thus, in the aircraft conceptual design phase, the optimization formation can be defined as:
Design Constraints: Four aeroelastic constraints and one aerodynamic constraint:
The maximum z-direction displacement at the wingtip was less than 7% of the magnitude at the semi-span. The wing deformation of the large aircraft will still obey the linear theory of elasticity in the cruise flight condition;
The maximum torsion at the wingtip was less than 2.14°. The elastic torsional deformation that might lead to a decrease of the local angle of attack;
The aileron efficiency was greater than 60%;
The flutter speed at sea level was greater than 320 m/s;
The total drag was less than the drag obtained by the baseline design.
Design Variables: The lower and upper bounds of design variables were determined by 90% and 110% of the baseline values [
44], respectively, which are shown in
Table 1.
The optimization flowchart shown in
Figure 6 demonstrates GP metamodel-assisted multidisciplinary optimization process for an aircraft conceptual design. Firstly, the Latin optimal hypercube design of experiments was used to determine the best distribution of sampling points for metamodel building. According to these design points, various jig shape models of the representative wing were generated for aeroelastic and stability analyses. Thus, the training data for GP metamodel building was obtained. By comparison of the predicted values from metamodels with the true results, more sampling points will be used to improve the accuracy of metamodels in the next iteration if the accuracy quality is not satisfactory. Finally, parametric optimization on the metamodels using SQP was performed to seek the optimal aircraft design.
5. Case Study
Both GA and GP techniques were applied to solve the above MAO problem for an aircraft conceptual design. Six responses related to stiffness, wingtip displacement, wingtip torsion, aileron efficiency, flutter and drag were built using GP. A cross-validation check of GP and GA approaches was carried out by comparison of the obtained optimal designs.
To construct the metamodels using GP, 1997 sampling points were selected as training data by the optimal Latin hypercube DoE to maximally represent information in the whole design space. Two fit indices were computed to evaluate the accuracy of predictive models constructed by GP, namely root mean square error (RSME) and coefficient of determination (R2) in Equations (6) and (9), respectively. In this paper, main parameters used in GP metamodel building are shown in
Table 2. As an example, the mathematical expression for the wingtip torsion is given as below:
where
to
are design variables detailed in
Table 1. It should be noted that results of two fit indices, for example, RSME = 1.27 × 10
−2 and R
2 = 0.995 for the predicted wingtip torsion response, indicate the metamodels by GP are quite accurate to estimate the nonlinear responses of the interests. Furthermore, design variables regarding horizontal bending stiffness and torsional stiffness have slight effects on the wingtip torsion, and this can be proved by sensitivity analysis performed in
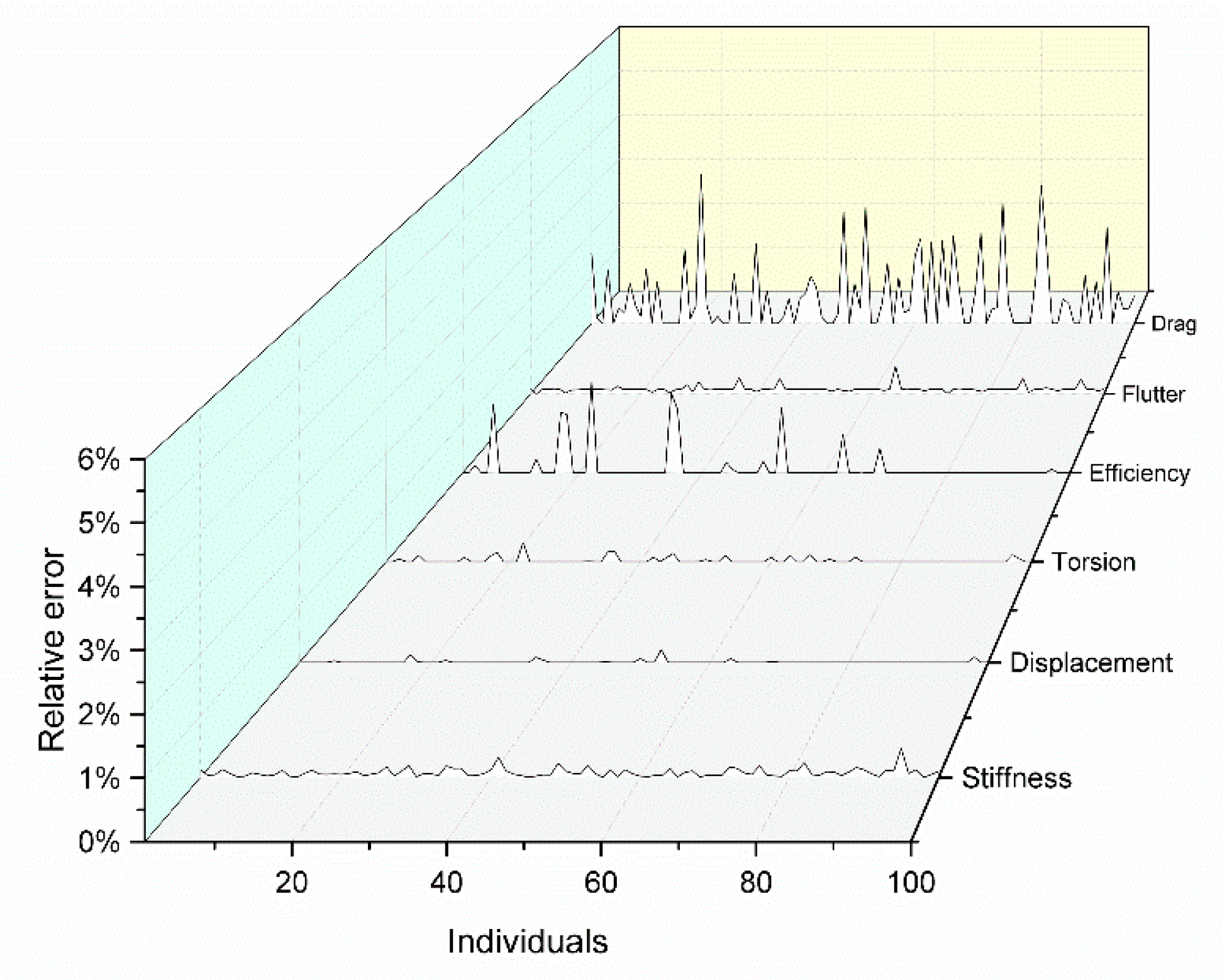
Section 5.2. To validate the accuracy of generated metamodels, a validation data set of 100 sampling points was also used to check the overall performance capacity of the metamodels. In this paper, the relative error was used to measure the discrepancy between the actual response and the predicted model,
where
is the actual response value and
is the prediction value. The relative errors of 100 validation points are given in
Figure 7 and their relative mean errors for all six responses were 0.083%, 0.008%, 0.024%, 0.119%, 0.106%, and 0.598%.
On average, the predictions of all the responses by GP technique were quite accurate. However, the most limitation of GP methodology was its complexity, discontinuity, and consumption of the model construction. The higher the dimension of the design space was, the more complicated the constructed GP expression was, the higher the number of step discontinuities of the response functions occurred, and more RAM was required. For the design space composed of 19 variables, it took more than three days for the GP methodology to construct the six responses on a personal computer with eight cores (E5-2670, 2.6 GHz) and 24 G RAM.
5.1. Optimal Designs by GP and GA
Metamodels were used to compute the responses of the interests during the MAO process for the representative aircraft conceptual design. The comparison of the optimal result by GP-based and GA-based optimizations and finite element validations is given in
Table 3 and the corresponding design variables are shown in
Table 4. The genetic parameters used by GA include Population 100, Generation 16, Tournament Selection, Crossover 0.7, and Mutation 0.4.
Since the optima obtained by GP metamodel-based and GA-based optimizations satisfy the design constraints, both results are feasible solutions. It is noted that the superiority of the GP method over GA for MAO was demonstrated by the overall performance of the optimal design except for the drag response shown in
Table 3. The stiffness by GP based optimization reduced from 0.806 to 0.535 by 33.6%, while the drag just deteriorated by 0.77% and no constraints were violated. In addition, it is observed that the predictions of responses agree well with finite element validation due to the high-accuracy models.
The most remarkable differences among the two cruise shapes shown in
Figure 8 are that the optimum by GA-based method had the largest sweep angle of the leading edge, while the optimal design using GP-based method had a largest outboard spanwise length. The increase of the sweep angle contributed to the decrease of the local shock wave drag and the higher aspect ratio led to the induced drag in reduction. The induced drag and the local shock wave drag are two significant types of a large aircraft flight drag under the cruise Mach of 0.785. The increase of the sweep angle also results in the increase of the vertical bending-torsional coupling effect as well as the structural weight. It is the reason why the optimum by GA method had a heavier structural weight and a larger wingtip torsional deformation than the optimal design by GP method.
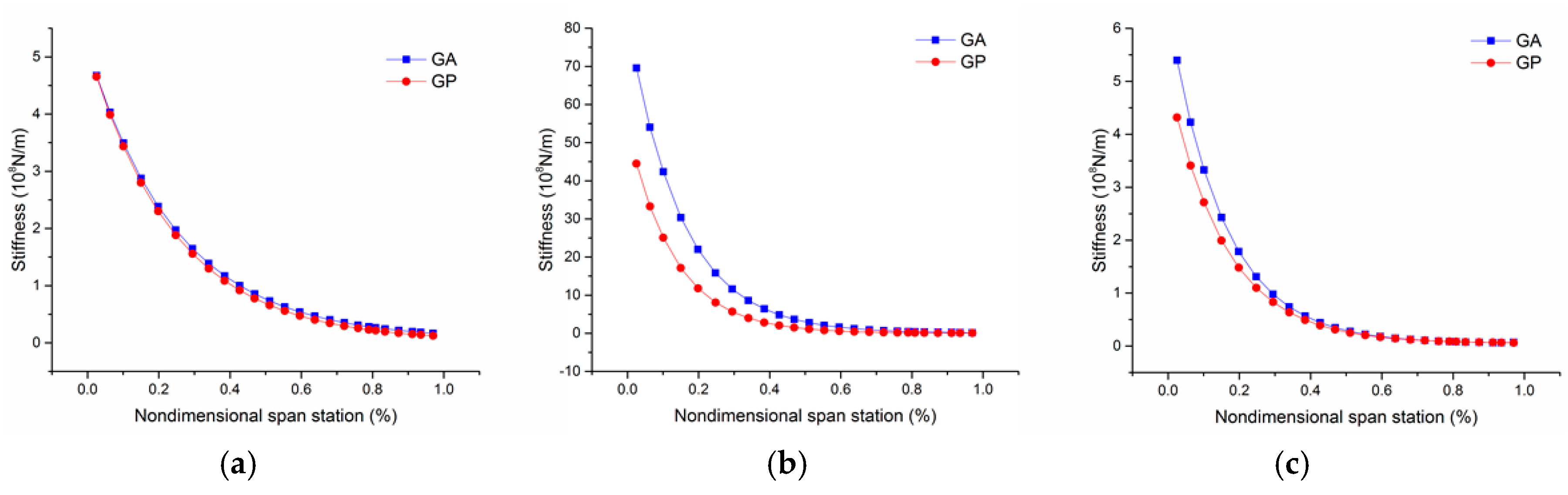
Figure 9 shows the variations of vertical, horizontal and torsional stiffnesses along the wingspan. Since the vertical stiffness is the most important parameter to reflect the aeroelastic character, it is reasonable to identify the slight variation of the vertical bending performance by these two methods. The GP method helped to remarkably reduce the horizontal stiffness in the region near the wing root and decrease the torsional stiffness shown in
Figure 9b,c, respectively.
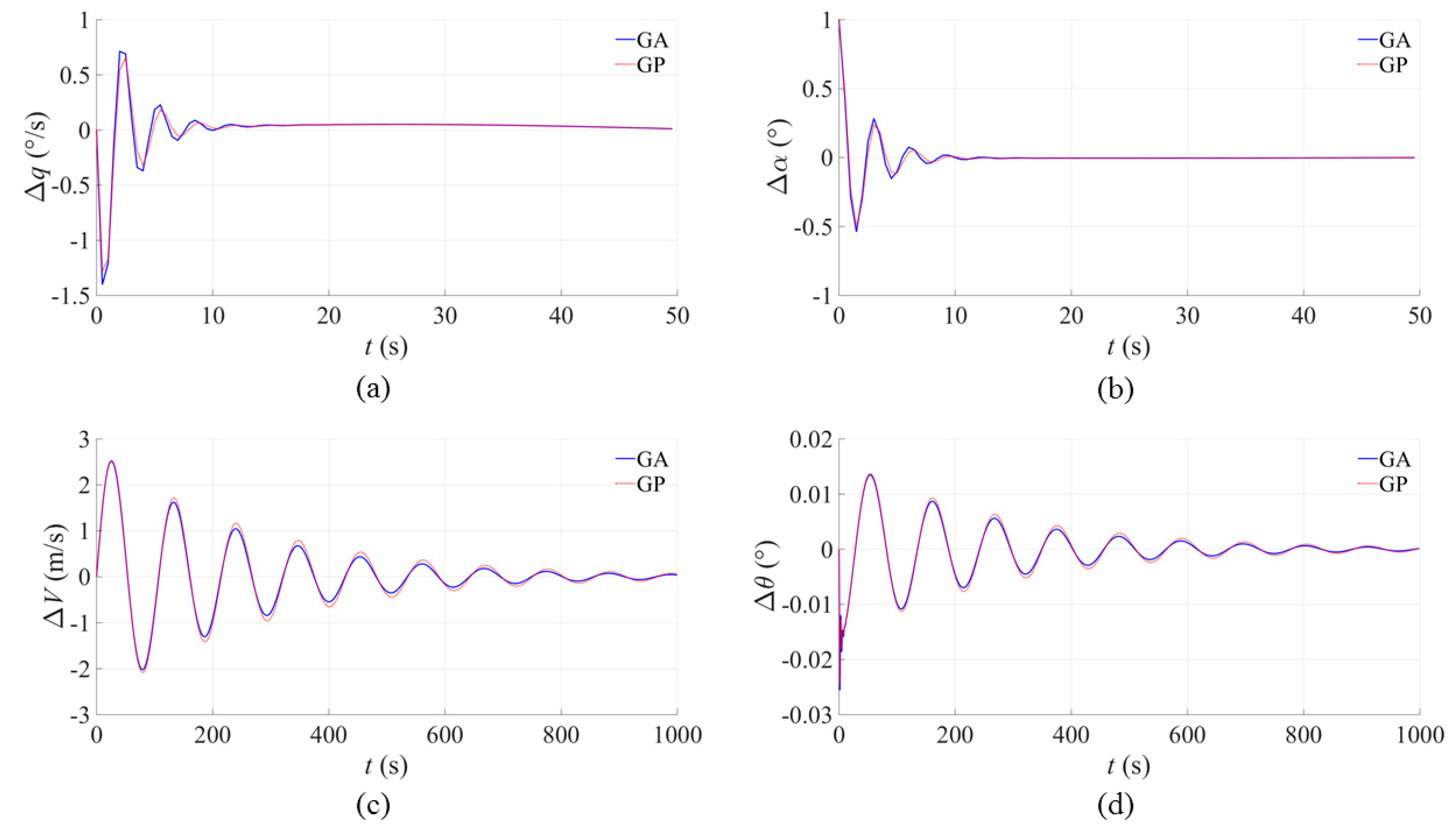
The transient behavior of the state variables in Equation (2) for the fourth-order model is shown in
Figure 10. It can be found that the disturbance quantities ultimately vanish and the responses converge towards a stable steady state. The natural response to perturbations consists of two damped modes: the short period and heavily damped mode (a and b) and the long period and lightly damped mode (phugoid mode: c and d). The results are quite typical for a large aircraft, and the stability of uncontrolled motion considered as a design constraint can be guaranteed during the optimization process.
5.2. Sensitivity Analysis
Finite difference method was used to determine the derivatives of the responses with respect to each design variable. The variation of each design variable was set at 5% of its design interval indicated in
Table 1. The occurrence of flutter was determined by the additional damping at a set of speeds, so the sensitivity of the flutter speed was not taken into consideration. In
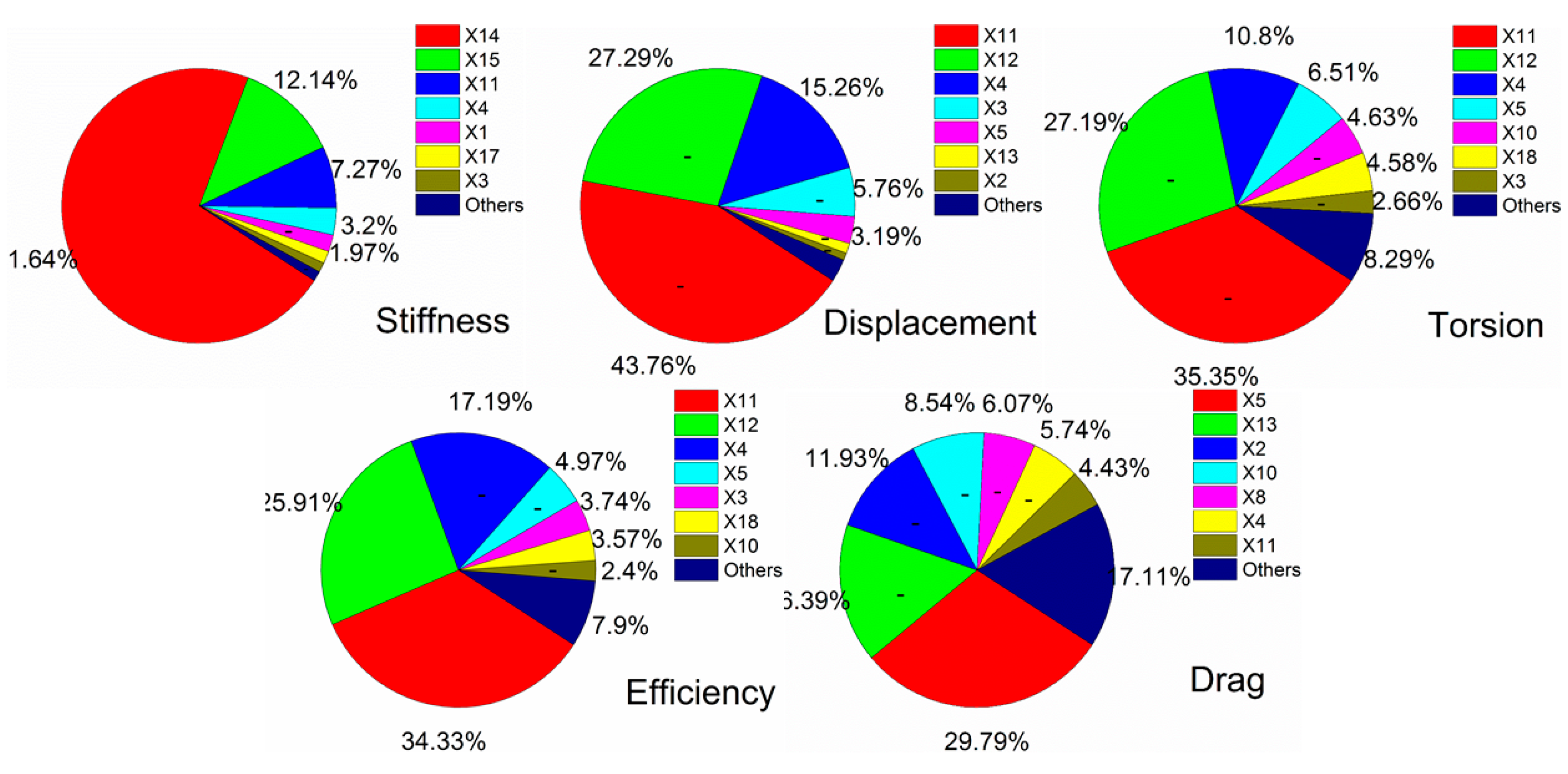
Figure 11, the results show that sensitivity analysis is used to explore how the variations of design variables have an impact on the response such as the weight, wingtip displacement, wingtip torsion, aileron efficiency, and drag. It can be also found that the more important the design variable was to the response, the larger the size of the slice displayed in the pie chart. X depicts the design variable, which is detailed in
Table 1. The symbol “-” means a negative correlation. Obviously, the horizontal bending stiffness (X14) had a great influence on the weight. The vertical bending stiffness (X11), the sweep angle of the leading edge (X5), and the outboard aspect ratio (X4) were the top three key parameters to have important impacts on the other responses. Hence, aircraft designers should pay more attention to these parameters in the conceptual phase of designing a large aircraft.
6. Summary
6.1. Research Significance
Research on the conceptual design of a large aircraft has revealed the immense benefits of improving overall performance, e.g., safety, comfort, and mitigation on environmental impacts. However, conventional sequence approaches can hardly adapt to the design of a modern aircraft, due to their iterative design methodology and low computational efficiency. To address this issue, the metaheuristic algorithm assisted aerostructural optimization method has been proposed in this paper and its superiority over the sequential design methods was examined by a representative beam-frame wing structure. The results give useful insights to tailoring parameters for the effective design of a large aircraft in the conceptual phase and also provide aircraft designers with a wealth of information for design practice.
6.2. Conclusions
Taking into account the interest in the integration of various disciplines for solving complex engineering design problems being rapidly growing within industries, GP metamodel-based multidisciplinary analysis and optimization (MAO) strategy has been proposed in this paper to improve the efficiency of an aircraft conceptual design. The correctness of this approach was examined by MAO of a representative beam-frame wing structure and its better strength and level of accuracy for seeking the optimum were demonstrated by comparison with the result obtained using the genetic algorithm technique. The results of the sensitivity analysis indicate that the horizontal bending stiffness had a great impact on the weight and three critical parameters significantly affecting the other responses of interest are determined: the vertical bending stiffness, the sweep angle of the leading edge, and the outboard aspect ratio. It is concluded that GP metamodel-based strategy for solving MAO problems is more efficient and accurate as compared with GA and has demonstrated the capability of becoming a systematic and robust approach to the aircraft design in the conceptual phase.
Author Contributions
Writing—original draft preparation and Genetic Programming method, G.D.; funding acquisition, G.D.; example and Genetic Algorithm method, X.W.; supervision, D.L.; writing—review and editing, D.L., G.D. and X.W.
Funding
This research received no external funding.
Acknowledgments
This study was supported by the first author’s research funding, which is used to pay the APC. The authors would like to thank the reviewers for their instructive comments on the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Elsayed, M.S.A.; Sedaghati, R.; Abdo, M. Accurate Stick Model Development for Static Analysis of Complex Aircraft Wing-Box Structures. AIAA J. 2009, 47, 2063–2075. [Google Scholar] [CrossRef]
- Wang, C. Insights from Developing a Multidisciplinary Design and Analysis Environment. Comput. Ind. 2014, 65, 786–795. [Google Scholar] [CrossRef]
- Kenway, G.K.W.; Martins, J.R.R.A. Multipoint Aerodynamic Shape Optimization Investigations of the Common Research Model Wing. AIAA J. 2016, 54, 113–128. [Google Scholar] [CrossRef]
- Zhang, K.S.; Han, Z.H.; Li, W.J.; Song, W.P. Coupled Aerodynamic/ Structural Optimization of a Subsonic Transport Wing Using a Surrogate Model. J. Aircr. 2008, 45, 2167–2170. [Google Scholar] [CrossRef]
- Yang, G.W.; Chen, D.W.; Cui, K. Response Surface Technique for Static Aeroelastic Optimization on a High-Aspect-Ratio Wing. J. Aircr. 2009, 46, 1444–1450. [Google Scholar] [CrossRef]
- Mastroddi, F.; Gemma, S. Analysis of Pareto Frontiers for Multidisciplinary Design Optimization of Aircraft. Aerosp. Sci. Technol. 2013, 28, 40–55. [Google Scholar] [CrossRef]
- Travaglini, L.; Ricci, S.; Bindolino, G. PyPAD: A Multidisciplinary Framework for Preliminary Airframe Design. Aircr. Eng. Aerosp. Technol. 2016, 88, 649–664. [Google Scholar] [CrossRef]
- Brooks, T.R.; Kenway, G.K.W.; Martins, J.R.R.A. Benchmark Aerostructural Models for the Study of Transonic Aircraft Wings. AIAA J. 2018, 56, 2840–2855. [Google Scholar] [CrossRef]
- Gray, J.S.; Hwang, J.T.; Martins, J.R.R.A.; Moore, K.T.; Naylor, B.A. Open MDAO: An Open-source Framework for Multidisciplinary Design, Analysis, and Optimization. Struct. Multidisc. Optim. 2019, 59, 1075–1104. [Google Scholar] [CrossRef]
- McAllister, C.D.; Simpson, T.W. Multidisciplinary Robust Design Optimization of an Internal Combustion Engine. J. Mech. Des. 2003, 125, 124–130. [Google Scholar] [CrossRef]
- Wang, K.; Zheng, Y. A New Particle Swarm Optimization Algorithm for Fuzzy Optimization of Armored Vehicle Scheme Design. Appl. Intell. 2012, 37, 520–526. [Google Scholar] [CrossRef]
- Van Dijk, M.T.; van Wingerden, J.W.; Ashuri, T.; Li, Y.Y. Wind Farm Multi-Objective Wake Redirection for Optimizing Power Production and Loads. Energy 2017, 121, 561–569. [Google Scholar] [CrossRef]
- Tabatabaei, S.K.; Behbahani, S.; de Silva, C.W. Self-Adjusting Multidisciplinary Design of Hydraulic Engine Mount Using Bond Graphs and Inductive Genetic Programming. Eng. Appl. Artif. Intel. 2016, 48, 32–39. [Google Scholar] [CrossRef]
- Sekar, W.K.; Laschka, B. Calculation of the Transonic Dip of Airfoils Using Viscous-Inviscid Aerodynamic interaction method. Aerosp. Sci. Technol. 2005, 9, 661–671. [Google Scholar] [CrossRef]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs; Springer: Berlin, Germany, 2013. [Google Scholar]
- Manan, A.; Vio, G.A.; Harmin, M.Y.; Cooper, J.E. Optimization of Aeroelastic Composite Structures Using Evolutionary Algorithms. Eng. Optim. 2010, 42, 171–184. [Google Scholar] [CrossRef]
- Wang, G.G.; Shan, S. Review of Metamodeling Techniques in Support of Engineering Design Optimization. J. Mech. Des. 2006, 129, 370–380. [Google Scholar] [CrossRef]
- Forrester, A.I.J.; Sobester, A.; Keane, A.J. Engineering Design via Surrogate Modelling: A Practical Guide; John Wiley & Sons: New York, NY, USA, 2008. [Google Scholar]
- Timme, S.; Marques, S.; Badcock, K.J. Transonic Aeroelastic Stability Analysis Using a Kriging-Based Schur Complement Formulation. AIAA J. 2011, 49, 1202–1213. [Google Scholar] [CrossRef]
- Raghavan, B.; Hamdaoui, M.; Xiao, M.; Breitkopf, P.; Villon, P. A Bi-level Meta-Modeling Approach for Structural Optimization Using Modified POD Bases and Diffuse Approximation. Comput. Struct. 2013, 127, 19–28. [Google Scholar] [CrossRef]
- Liu, D.; Lohse-Busch, H.; Toropov, V.; Huhne, C.; Armani, U. Detailed Design of a Lattice Composite Fuselage Structure by a Mixed Optimization Method. Eng. Optim. 2016, 48, 1707–1720. [Google Scholar] [CrossRef]
- Portelette, L.; Roux, J.; Robin, V.; Feulvarch, E. A Gaussian surrogate model for residual stresses induced by orbital multi-pass TIG welding. Comput. Struct. 2017, 183, 27–37. [Google Scholar] [CrossRef]
- Amouzgar, K.; Bandaru, S.; Ng, A.H.C. Radial Basis Functions with a Priori Bias as Surrogate Models: A Comparative Study. Eng. Appl. Artif. Intell. 2018, 71, 28–44. [Google Scholar] [CrossRef]
- Koza, J.R. Genetic Programming: On the Programming of Computers by Means of Natural Selection; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Armani, U. Development of a Hybrid Genetic Programming Technique for Computationally Expensive Optimisation Problems. Ph.D. Thesis, University of Leeds, Leeds, UK, 2014. [Google Scholar]
- Fajfar, I.; Bűrmen, Ä.; Puhan, J. Grammatical evolution as a hyper-heuristic to evolve deterministic real-valued optimization algorithms. In Genetic Programming and Evolvable Machines; Spector, L., Ed.; Springer: Berlin, Germany, 2018; Volume 19. [Google Scholar]
- Faradonbeh, R.S.; Monjezi, M.; Armaghani, D.J. Genetic Programing and Non-linear Multiple Regression Techniques to Predict Backbreak in Blasting Operation. Eng. Comput. 2016, 32, 123–133. [Google Scholar] [CrossRef]
- Pawiński, G.; Sapiecha, K. Speeding up Global Optimization with the Help of Intelligent Supervisors. Appl. Intell. 2016, 45, 777–792. [Google Scholar] [CrossRef]
- Rostami, M.F.; Sadrossadat, E.; Ghorbani, B.; Kazemi, S.M. New Empirical Formulations for Indirect Estimation of Peak-confined Compressive Strength and Strain of Circular RC Columns Using LGP Method. Eng. Comput. 2018, 34, 865–880. [Google Scholar] [CrossRef]
- Van Dam, C.P.; Nikfetrat, K.; Wong, K.; Vijgen, P.M.H.W. Drag Prediction at Subsonic and Transonic Speeds Using Euler Methods. J. Aircr. 1995, 32, 839–845. [Google Scholar] [CrossRef]
- Fang, Z.P.; Chen, W.C.; Zhang, S.G. Flight Dynamics of Aircraft; Beihang University Press: Beijing, China, 2005. [Google Scholar]
- MSC Software. 2014. MSC Nastran Version 68: Aeroelastic Analysis User’s Guide; MSC Software: Newport Beach, CA, USA, 1992. [Google Scholar]
- Harder, R.L.; Desmarais, R.N. Interpolation Using Surface Splines. J. Aircr. 1972, 9, 189–191. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems, 2nd ed.; MIT Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Carr, J. An Introduction to Genetic Algorithms. Senior Project 2014, 40, 7. [Google Scholar]
- Lin, H.; Lin, C. Optimization of Printed Circuit Board Component Placement Using an Efficient Hybrid Genetic Algorithm. Appl. Intell. 2016, 45, 622–637. [Google Scholar] [CrossRef]
- Box, J.F.; Fisher, R.A. Design of Experiments. Am. Stat. 1980, 34, 1–7. [Google Scholar]
- Simpson, T.; Peplinski, J.; Koch, P.; Allen, J. On the Use of Statistics in Design and the Implications for Deterministic Computer Experiments. Des. Theory Method. DTM 1997, 97, 14–17. [Google Scholar]
- Audze, P.; Eglais, V. New Approach for Planning out of Experiments. Probl. Dyn. Strengths 1977, 35, 104–107. [Google Scholar]
- Zhong, J.; Feng, L.; Ong, Y.-S. Gene Expression Programming: A Survey. IEEE Comput. Intell. Mag. 2017, 12, 54–72. [Google Scholar] [CrossRef]
- Fajfar, I.; Tuma, T. Creation of Numerical Constants in Robust Gene Expression Programming. Entropy 2018, 20, 756. [Google Scholar] [CrossRef]
- Sette, S.; Boullart, L. Genetic Programming: Principles and Applications. Eng. Appl. Artif. Intell. 2001, 14, 727–736. [Google Scholar] [CrossRef]
- Wang, H.; Yao, X. Corner Sort for Pareto-Based Many-Objective Optimization. IEEE Trans. Cybern. 2014, 44, 90–102. [Google Scholar]
- Wan, Z.Q.; Wang, X.; Yang, C. Integrated Aerodynamics/Structure/StabilitOptimization of Large Aaircraft in Conceptual Design. Proc. IMechE Part G J. Aerosp. Eng. 2018, 232, 745–756. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).