Particle Swarm Optimization Algorithm-Extreme Learning Machine (PSO-ELM) Model for Predicting Resilient Modulus of Stabilized Aggregate Bases
Abstract
1. Introduction
2. Research Data and Methods
2.1. Description of Used Data and Variables
2.2. Theoretical Backgrounds and Model Development
2.2.1. PSO
| Algorithm 1: The PSO algorithm for optimization problem of d-dimensional decision variables. |
|
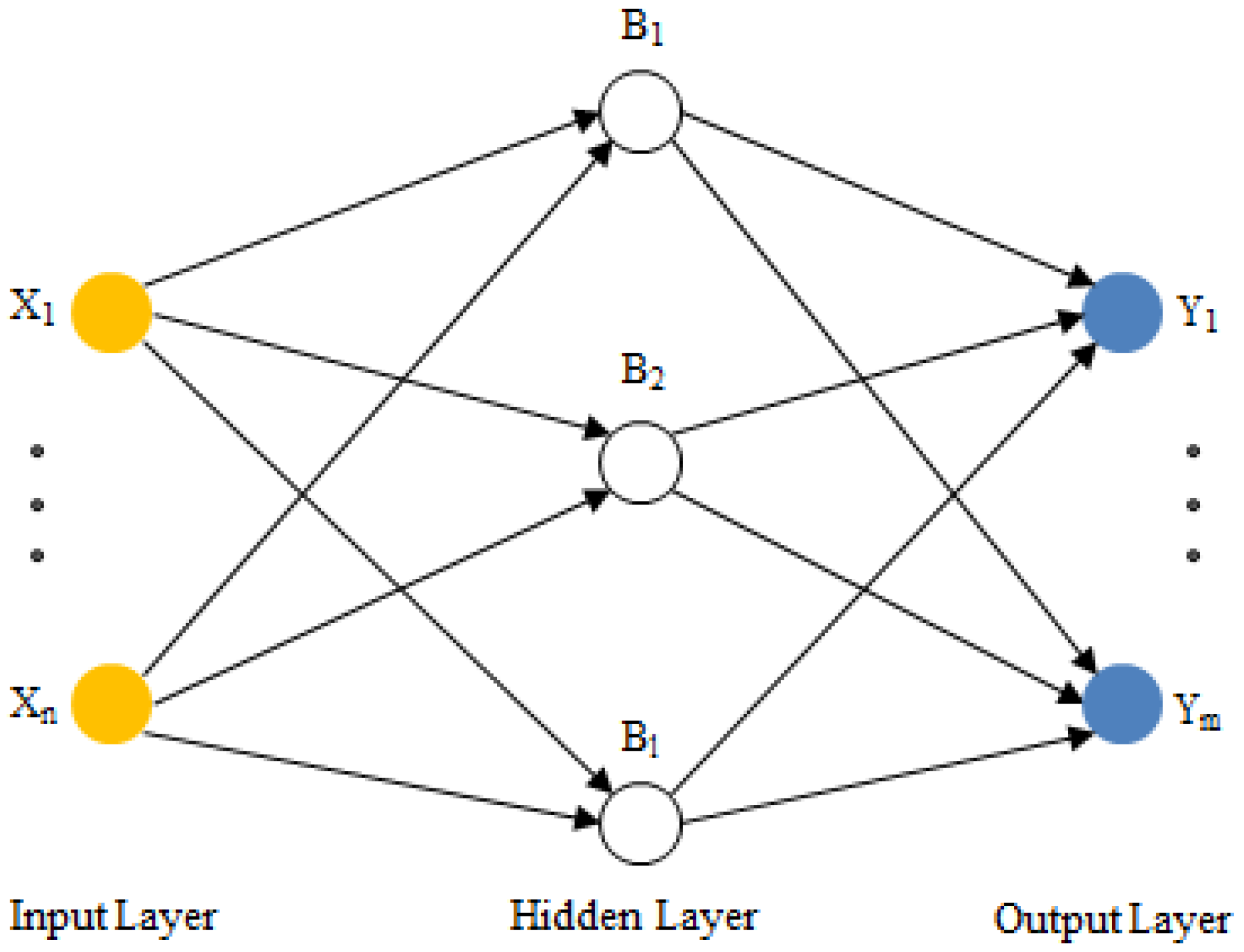
2.2.2. ANN
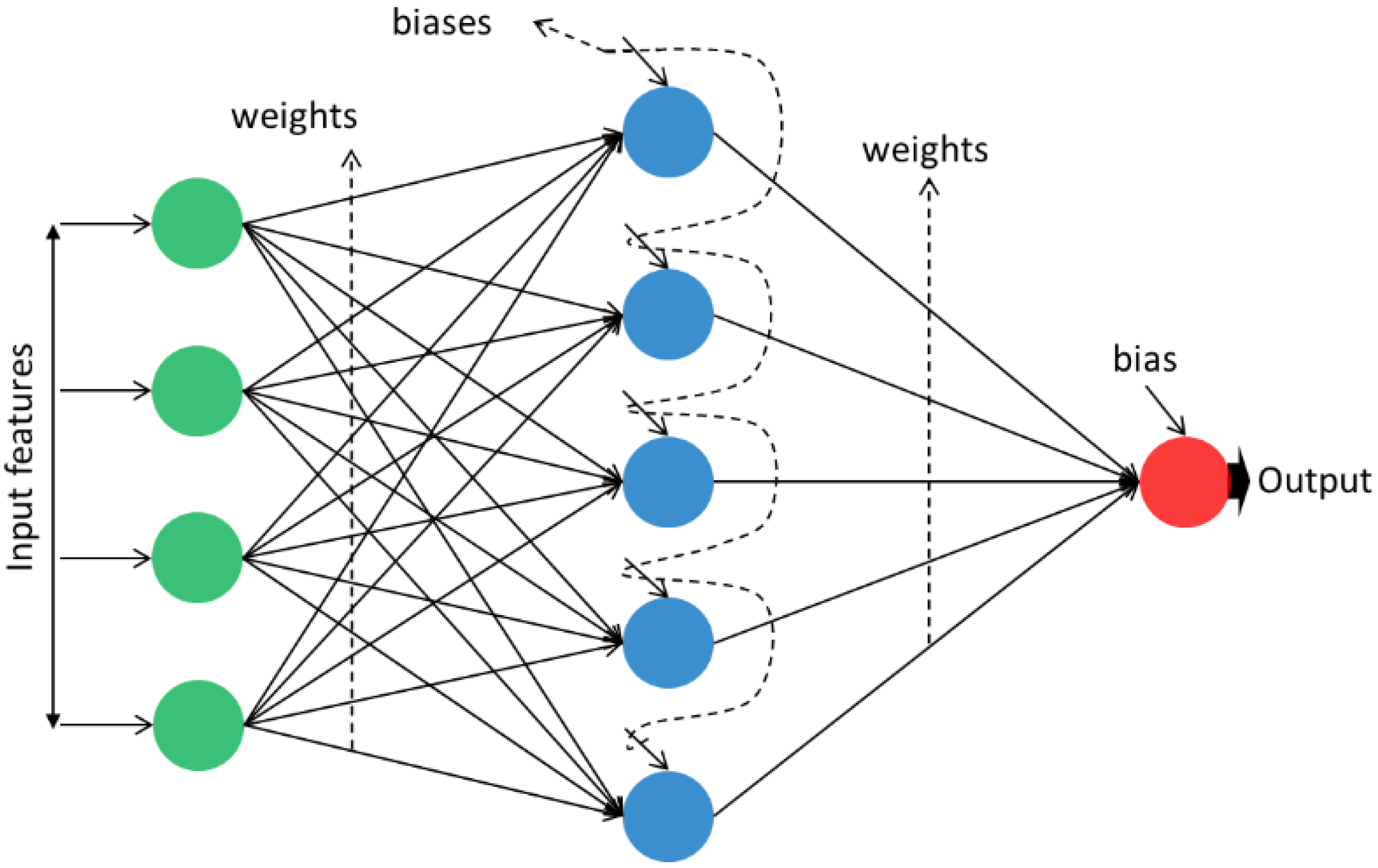
2.2.3. ELM
2.2.4. Hybridization (PSO-ANN, PSO-ELM)
| Algorithm 2: The algorithmic flow of PSO-ELM. |
|
2.2.5. Model Development and Performance Assessment
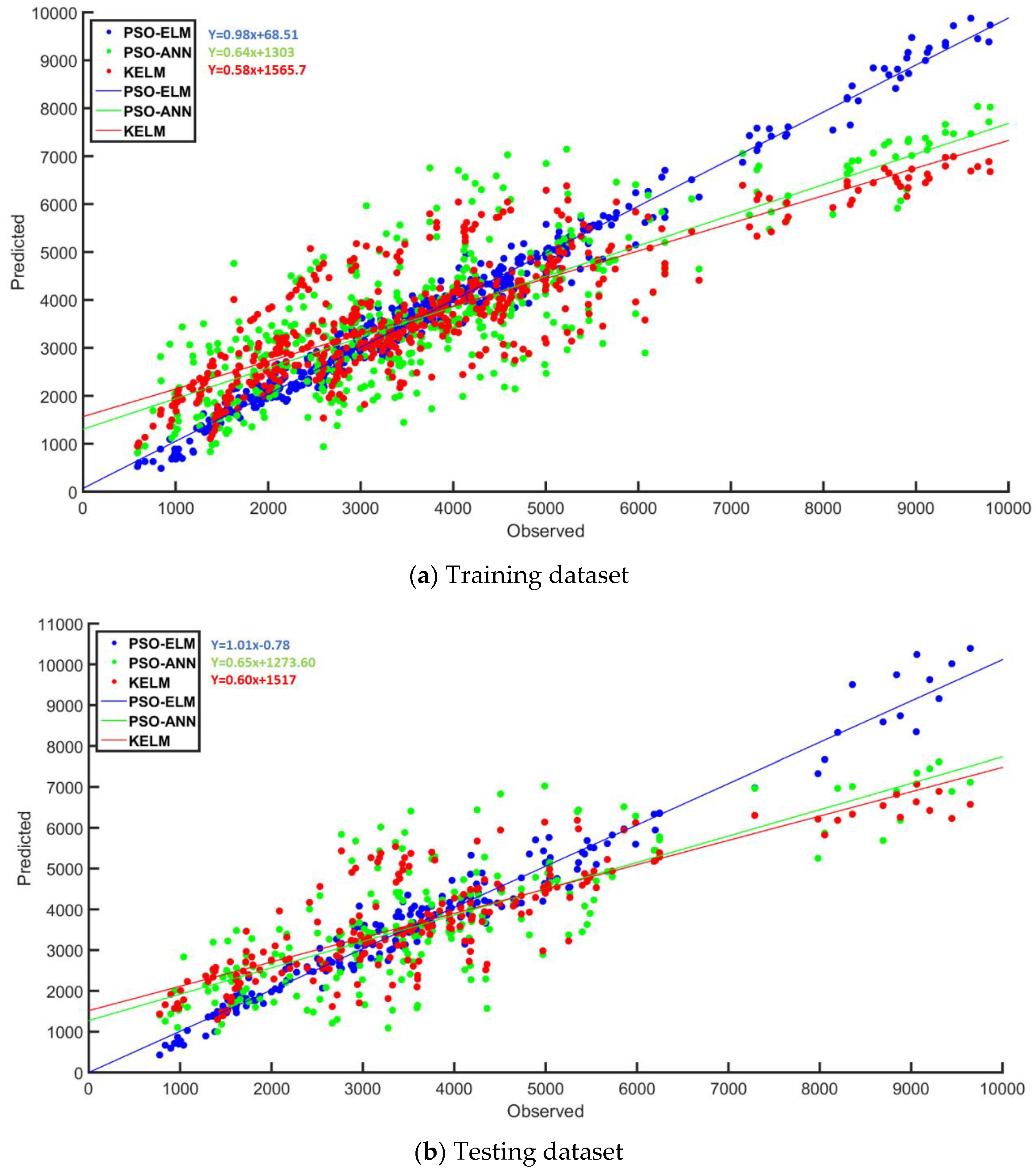
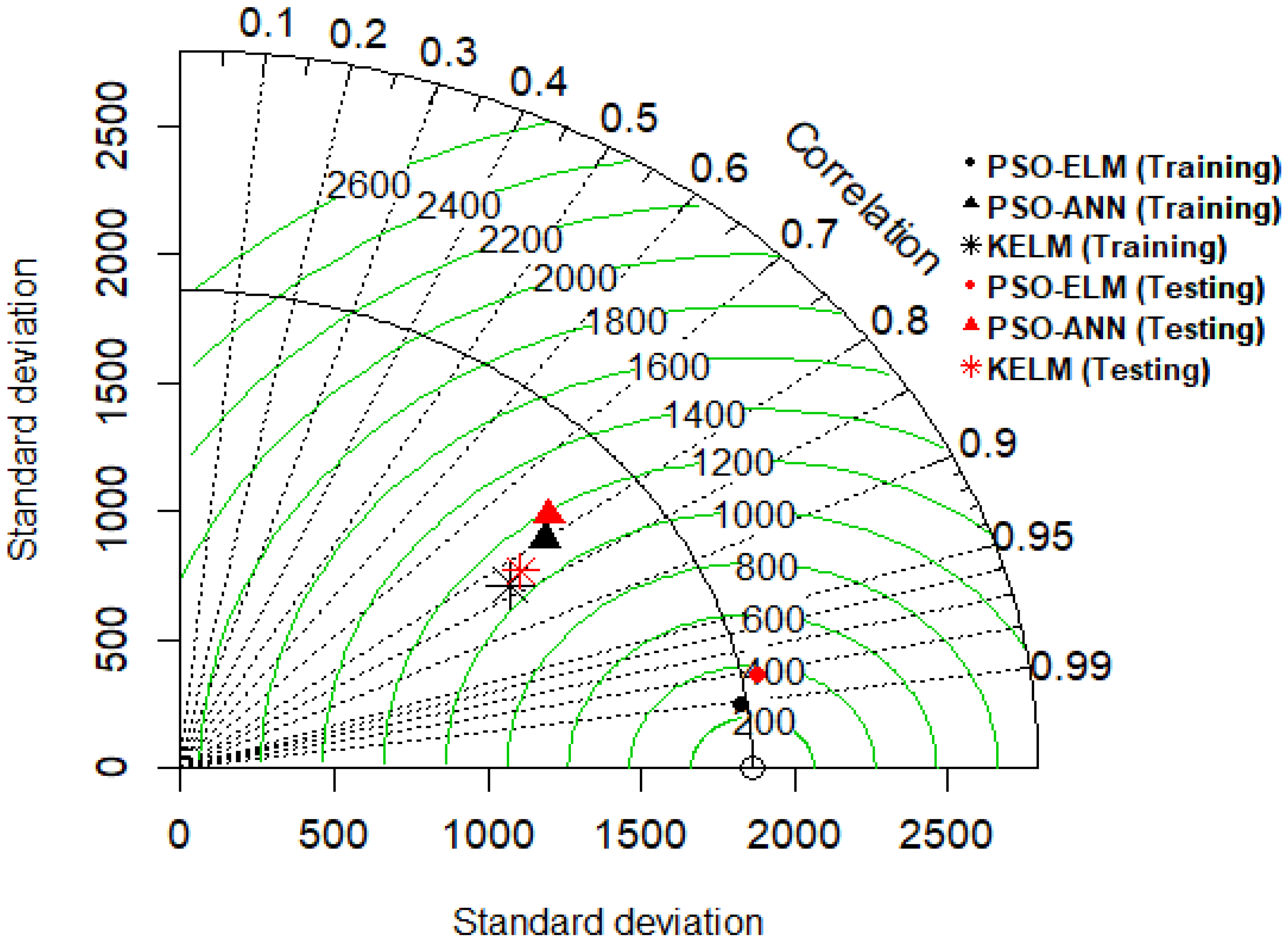
3. Results and Discussion
4. Concluding Remarks
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Khoury, N.N. Durability of Cementitiously Stabilized Aggregate Bases for Pavement Application. Ph.D. Thesis, University of Oklahoma, Norman, OK, USA, 2005. [Google Scholar]
- Halsted, G.E. Minimizing reflective cracking in cement-stabilized pavement bases. In Proceedings of the 2010 Annual Conference of the Transportation Association of Canada, Halifax, NS, Canada, 26–29 September 2010. [Google Scholar]
- AASHTO. Mechanistic-Empirical Pavement Design Guide: A Manual of Practice; American Association of Highways and Transportation Officials: Washington, DC, USA, 2008. [Google Scholar]
- Maalouf, M.; Khoury, N.; Laguros, J.G.; Kumin, H. Support vector regression to predict the performance of stabilized aggregate bases subject to wet–dry cycles. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 675–696. [Google Scholar] [CrossRef]
- Naji, K. Resilient modulus–moisture content relationships for pavement engineering applications. Int. J. Pavement Eng. 2018, 19, 651–660. [Google Scholar] [CrossRef]
- Mousa, R.; Gabr, A.; Arab, M.; Azam, A.; El-Badawy, S. Resilient modulus for unbound granular materials and subgrade soils in Egypt. In Proceedings of the International Conference on Advances in Sustainable Construction Materials & Civil. Engineering Systems, Sharjah, UAE, 18–20 April 2017; p. 06009. [Google Scholar] [CrossRef]
- Solanki, P.; Zaman, M. Effect of wet-dry cycling on the mechanical properties of stabilized subgrade soils. In Proceedings of the Geo-Congress 2014, Atlanta, GA, USA, 23–26 February 2014; pp. 3625–3634. [Google Scholar]
- AASHTO T-307. Standard Method of Test for Determining the Resilient Modulus of Soil and Aggregate Materials; AASHTO: Washington, DC, USA, 2017. [Google Scholar]
- Arisha, A.; Gabr, A.; El-badawy, S.; Shwally, S. Performance evaluation of construction and demolition waste materials for pavement construction in Egypt. J. Mater. Civ. Eng. 2018, 30, 04017270. [Google Scholar] [CrossRef]
- Khoury, N.; Zaman, M.; Laguros, J. Behavior of stabilized aggregate bases subjected to cyclic loading and wet-dry cycles. In Proceedings of the Geo-Frontiers Congress 2005, Austin, TX, USA, 24–26 January 2005. [Google Scholar] [CrossRef]
- Khoury, N.; Zaman, M.M. Durability of stabilized base courses subjected to wet-dry cycles. Int. J. Pavement Eng. 2007, 8, 265–276. [Google Scholar] [CrossRef]
- Reza, A.; Rahrovan, M. Application of artifitial neural network to predict the resilient modulus of stabilized base subjected to wet dry cycles. Comput. Mater. Civ. Eng. 2016, 1, 37–47. [Google Scholar]
- Arisha, A. Evaluation of Recycled Clay Masonry Blends in Pavement Construction. Master’s Thesis, Public Works Engineering Department, Mansoura University, Mansoura, Egypt, 2017. [Google Scholar]
- Zaman, M.; Solanki, P.; Ebrahimi, A.; White, L. Neural network modeling of resilient modulus using routine subgrade soil properties. Int. J. Geomech. 2010, 10, 1–12. [Google Scholar] [CrossRef]
- Kim, S.; Yang, J.; Jeong, J. Prediction of subgrade resilient modulus using artificial neural network. KSCE J. Civ. Eng. 2014, 18, 1372–1379. [Google Scholar] [CrossRef]
- Nazzal, M.D.; Tatari, O. Evaluating the use of neural networks and genetic algorithms for prediction of subgrade resilient modulus. Int. J. Pavement Eng. 2013, 14, 364–373. [Google Scholar] [CrossRef]
- Hanittinan, W. Resilient modulus prediction using neural network algorithms. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2007. [Google Scholar]
- Kaloop, M.; Gabr, A.; El-Badawy, S.; Arisha, A.; Shwally, S.; Hu, J. Predicting resilient modulus of recycled concrete and clay masonry blends for pavement applications using soft computing techniques. Front. Struct. Civ. Eng. 2019, in press. [Google Scholar] [CrossRef]
- Asteris, P.G.; Roussis, P.C.; Douvika, M.G. Feed-forward neural network prediction of the mechanical properties of sandcrete materials. Sensors 2017, 17, 1344. [Google Scholar] [CrossRef]
- Asteris, P.G.; Kolovos, K.G. Self-compacting concrete strength prediction using surrogate models. Neural Comput. Appl. 2019, 31, 409–424. [Google Scholar] [CrossRef]
- Chau, K. A review on the integration of artificial intelligence into coastal modeling. J. Environ. Manag. 2006, 80, 47–57. [Google Scholar] [CrossRef]
- Mohammadi, K.; Shamshirband, S.; Yee, P.L.; Petković, D.; Zamani, M.; Ch, S. Predicting the wind power density based upon extreme learning machine. Energy 2015, 86, 232–239. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Pulkkinen, J.; Gabbouj, M. Multi-dimensional particle swarm optimization in dynamic environments. Expert Syst. Appl. 2011, 38, 2212–2223. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. Extreme learning machine based modeling of resilient modulus of subgrade soils. Geotech. Geol. Eng. 2014, 32, 287–296. [Google Scholar] [CrossRef]
- Ghanizadeh, A.R.; Amlashi, A.T. Prediction of fine-grained soils resilient modulus using hybrid ANN-PSO, SVM-PSO and ANFIS-PSO methods. J. Transp. Eng. 2018, 9, 159–182. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Wilson, P.; Mantooth, H.A. Model-based optimization techniques. In Model-Based Engineering for Complex Electronic Systems; Elsevier: Waltham, MA, USA, 2013; Chapter 10; pp. 347–367. [Google Scholar] [CrossRef]
- Sharaf, A.M.; El-Gammal, A.A.A. Novel AI-Based Soft Computing Applications in Motor Drives, 4th ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Han, F.; Yao, H.F.; Ling, Q.H. An improved evolutionary extreme learning machine based on particle swarm optimization. Neurocomputing 2013, 116, 87–93. [Google Scholar] [CrossRef]
- Guo, H.; Li, B.; Li, W.; Qiao, F.; Rong, X.; Li, Y. Local coupled extreme learning machine based on particle swarm optimization. Algorithms 2018, 11, 174. [Google Scholar] [CrossRef]
- Shafabakhsh, G.H.; Talebsafa, M. Artificial neural network modeling (ANN) for predicting rutting performance of nano-modified hot-mix asphalt mixtures containing steel slag aggregates. Constr. Build. Mater. 2015, 85, 136–143. [Google Scholar] [CrossRef]
- Yan, K.; You, L. Investigation of complex modulus of asphalt mastic by artificial neural networks. Indian J. Eng. Mater. Sci. 2014, 21, 445–450. [Google Scholar]
- Adeli, H. Neural networks in civil engineering: 1989–2000. Comput. Aided Civ. Infrastruct. Eng. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Asteris, P.G.; Kolovos, K.G.; Douvika, M.G.; Roinos, K. Prediction of self-compacting concrete strength using artificial neural networks. Eur. J. Environ. Civ. Eng. 2016, 20 (Suppl. 1), s102–s122. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man. Cybern. Part B 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Cao, J.; Lin, Z.; Huang, G.B. Self-adaptive evolutionary extreme learning machine. Neural Process. Lett. 2012, 36, 285–305. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, L.; Siew, C.K. Universal approximation using incremental constructive feedforward networks with random hidden nodes. IEEE Trans. Neural Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef]
- Cui, D.; Bin Huang, G.; Liu, T. ELM based smile detection using Distance Vector. Pattern Recognit. 2018, 79, 356–369. [Google Scholar] [CrossRef]
- Karami, H.; Karimi, S.; Bonakdari, H.; Shamshirband, S. Predicting discharge coefficient of triangular labyrinth weir using extreme learning machine, artificial neural network and genetic programming. Neural Comput. Appl. 2018, 29, 983–989. [Google Scholar] [CrossRef]
- Khosravi, V.; Ardejani, F.D.; Yousefi, S.; Aryafar, A. Monitoring soil lead and zinc contents via combination of spectroscopy with extreme learning machine and other data mining methods. Geoderma 2018, 123, 694–705. [Google Scholar] [CrossRef]
- Liu, H.; Mi, X.; Li, Y. An experimental investigation of three new hybrid wind speed forecasting models using multi-decomposing strategy and ELM algorithm. Renew. Energy 2018, 123, 694–705. [Google Scholar] [CrossRef]
- Zhu, H.; Tsang, E.C.C.; Zhu, J. Training an extreme learning machine by localized generalization error model. Soft Comput. 2018, 22, 3477–3485. [Google Scholar] [CrossRef]
- Mohapatra, P.; Chakravarty, S.; Dash, P.K. An improved cuckoo search based extreme learning machine for medical data classification. Swarm Evol. Comput. 2015, 24, 25–49. [Google Scholar] [CrossRef]
- Satapathy, P.; Dhar, S.; Dash, P.K. An evolutionary online sequential extreme learning machine for maximum power point tracking and control in multi-photovoltaic microgrid system. Renew. Energy Focus 2017, 21, 33–53. [Google Scholar] [CrossRef]
- Li, L.L.; Sun, J.; Tseng, M.L.; Li, Z.G. Extreme learning machine optimized by whale optimization algorithm using insulated gate bipolar transistor module aging degree evaluation. Expert Syst. Appl. 2019, 127, 58–67. [Google Scholar] [CrossRef]
- Liu, D.; Li, G.; Fu, Q.; Li, M.; Liu, C.; Faiz, M.A.; Khan, M.I.; Li, T.; Cui, S. Application of particle swarm optimization and extreme learning machine forecasting models for regional groundwater depth using nonlinear prediction models as preprocessor. J. Hydrol. Eng. 2018, 23, 04018052. [Google Scholar] [CrossRef]
- Chen, S.; Shang, Y.; Wu, M. Application of PSO-ELM in electronic system fault diagnosis. In Proceedings of the 2016 IEEE International Conference on Prognostics and Health Management (ICPHM), Ottawa, ON, Canada, 20–22 June 2016. [Google Scholar] [CrossRef]
- Sun, W.; Duan, M. Analysis and forecasting of the carbon price in China’s regional carbon markets based on fast ensemble empirical mode decomposition, phase space reconstruction, and an improved extreme learning machine. Energies 2019, 12, 277. [Google Scholar] [CrossRef]
- Huang, G.B.; Wang, D.H.; Lan, Y. Extreme learning machines: A survey. Int. J. Mach. Learn. Cybern. 2011, 2, 107–122. [Google Scholar] [CrossRef]
- Lemon, J.; Bolker, B.; Oom, S.; Klein, E.; Rowlingson, B.; Wickham, H.; Tyagi, A.; Eterradossi, O.; Grothendieck, G.; Toews, M.; et al. Package Plotrix: Various Plotting Functions. R Package Version 3.7–6. 2019. Available online: https://rdrr.io/cran/plotrix/ (accessed on 21 June 2019).
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]

| Dataset | Variable | Mean | Median | Min. | Max. | SD | SK | KU |
|---|---|---|---|---|---|---|---|---|
| Training | W-D | 12.57 | 8.00 | 0.00 | 30.00 | 11.19 | −1.13 | 0.49 |
| CSAFR | 0.25 | 0.13 | 0.11 | 0.51 | 0.18 | −1.47 | 0.73 | |
| DMR | 3.26 | 3.37 | 2.34 | 4.63 | 0.71 | −0.94 | 0.39 | |
| σ3 | 69.35 | 69.00 | 0.00 | 138.00 | 49.60 | −1.34 | −0.02 | |
| σd | 173.50 | 208.00 | 69.00 | 277.00 | 78.73 | −1.40 | −0.02 | |
| Mr | 3690.88 | 3422.00 | 585.00 | 9803.00 | 1862.06 | 1.42 | 1.12 | |
| Testing | W-D | 13.32 | 16.00 | 0.00 | 30.00 | 11.10 | −1.19 | 0.35 |
| CSAFR | 0.26 | 0.13 | 0.11 | 0.51 | 0.19 | −1.67 | 0.58 | |
| DMR | 3.28 | 3.37 | 2.34 | 4.63 | 0.73 | −1.07 | 0.34 | |
| σ3 | 71.94 | 69.00 | 0.00 | 138.00 | 47.16 | −1.22 | −0.04 | |
| σd | 167.89 | 138.00 | 69.00 | 277.00 | 75.06 | −1.26 | 0.11 | |
| Mr | 3668.12 | 3443.00 | 773.00 | 9644.00 | 1861.16 | 1.65 | 1.15 |
| Model | r2 | RMSE | MAE |
|---|---|---|---|
| PSO-ANN (Train) | 0.640 | 1117.367 | 881.90 |
| PSO-ANN (Test) | 0.597 | 1184.155 | 929.18 |
| KELM (Train) | 0.692 | 1064.782 | 804.90 |
| KELM (Test) | 0.674 | 1075.378 | 815.94 |
| PSO-ELM (Train) | 0.981 | 253.439 | 191.66 |
| PSO-ELM (Test) | 0.963 | 369.592 | 280.00 |
| Model | Input Variables | r2 | RMSE | MAE |
|---|---|---|---|---|
| 1 | W-D, CSAFR, DMR, and | 0.981 | 253.439 | 191.66 |
| 2 | W-D, CSAFR, DMR and | 0.948 | 415.554 | 299.43 |
| 3 | W-D, CSAFR, DMR and | 0.973 | 304.451 | 204.98 |
| 4 | W-D, CSAFR and DMR | 0.921 | 521.08 | 378.71 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaloop, M.R.; Kumar, D.; Samui, P.; Gabr, A.R.; Hu, J.W.; Jin, X.; Roy, B. Particle Swarm Optimization Algorithm-Extreme Learning Machine (PSO-ELM) Model for Predicting Resilient Modulus of Stabilized Aggregate Bases. Appl. Sci. 2019, 9, 3221. https://doi.org/10.3390/app9163221
Kaloop MR, Kumar D, Samui P, Gabr AR, Hu JW, Jin X, Roy B. Particle Swarm Optimization Algorithm-Extreme Learning Machine (PSO-ELM) Model for Predicting Resilient Modulus of Stabilized Aggregate Bases. Applied Sciences. 2019; 9(16):3221. https://doi.org/10.3390/app9163221
Chicago/Turabian StyleKaloop, Mosbeh R., Deepak Kumar, Pijush Samui, Alaa R. Gabr, Jong Wan Hu, Xinghan Jin, and Bishwajit Roy. 2019. "Particle Swarm Optimization Algorithm-Extreme Learning Machine (PSO-ELM) Model for Predicting Resilient Modulus of Stabilized Aggregate Bases" Applied Sciences 9, no. 16: 3221. https://doi.org/10.3390/app9163221
APA StyleKaloop, M. R., Kumar, D., Samui, P., Gabr, A. R., Hu, J. W., Jin, X., & Roy, B. (2019). Particle Swarm Optimization Algorithm-Extreme Learning Machine (PSO-ELM) Model for Predicting Resilient Modulus of Stabilized Aggregate Bases. Applied Sciences, 9(16), 3221. https://doi.org/10.3390/app9163221








