Abstract
Psychoacoustic models of human auditory perception have found an important application in the realm of perceptual audio coding, where exploiting the limitations of perception and removal of irrelevance is key to achieving a significant reduction in bitrate while preserving subjective audio quality. To this end, psychoacoustic models do not need to be perfect to satisfy their purpose, and in fact the commonly employed models only represent a small subset of the known properties and abilities of the human auditory system. This paper provides a tutorial introduction of the most commonly used psychoacoustic models for low bitrate perceptual audio coding.
1. Introduction
Psychoacoustic models of human auditory perception have found an important application in the realm of perceptual audio coding, where exploiting limitations of perception and reduction of irrelevance are key to achieving a significant reduction in bitrate while preserving subjective audio quality, even at very high data compression factors. Popular audio codecs, such as Moving Picture Experts Group (MPEG) Advanced Audio Coding (AAC) “MPEG-2/4 AAC” [1,2], deliver high quality stereo at bitrates of 96 kbit/s, which corresponds to a data reduction factor of about 15 as compared to a Compact Disc (CD) audio originally sampled at 44.1 kHz and 16 bits. Newer codecs (e.g., High Efficiency AAC v2 [3], Unified Speech and Audio Coding (USAC) [4], or Enhanced Voice Services (EVS) [5]) deliver even higher compression at comparable audio quality. It is intriguing to acknowledge that audio coding exclusively based on reduction of redundancy (i.e., lossless audio coding) would lead to an average data reduction of just about 2:1 for a wide range of CD quality audio material [6]. Thus, the major part of data reduction provided by perceptual audio codecs can be attributed to the extensive exploitation of the properties of perception (irrelevance reduction), for which psychoacoustic models of human auditory perception are key.
In general, the most popular approach to perceptual audio encoding can be described as follows (see Figure 1):
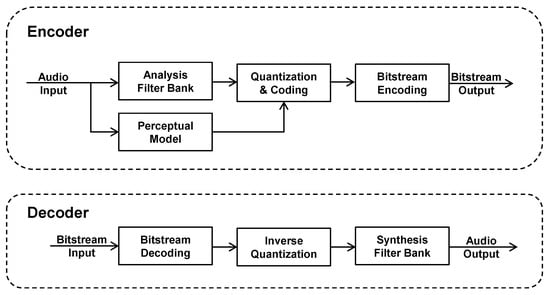
Figure 1.
Schematic principle of perceptual audio encoding and decoding.
- The time domain audio signal is transformed into a subsampled spectral representation using an analysis filterbank (or equivalently, a transform). This filterbank is usually critically sampled (i.e., the number of output samples is equal to the number of input samples) and (at least nearly) perfectly reconstructed.
- A psychoacoustic (perceptual) model is used to analyze the input audio signal and determine relevant perceptual signal aspects, most notably the signal’s masking ability (e.g., masking threshold) as a function of frequency and time. The result is passed to the quantization and encoding stage to control the injected coding distortion in a way that aims at rendering it inaudible, or at least produce minimal audible distortion and annoyance. This concept of perceptually controlled quantization makes the encoder a perceptual audio encoder;
- The spectral samples are subsequently quantized and possibly entropy coded to reduce the information to a compact representation [7], and packed into a bitstream as binary values;
- In the decoder, the bitstream is unpacked, entropy coding is undone, and the quantized spectral values are mapped back to their original dynamic range and transferred back to a time domain output signal by the synthesis filterbank, i.e., a filterbank that behaves complementarily to the analysis filterbank that has been used by the encoder.
The central idea of a perceptual audio codec is to use psychoacoustic criteria, such as masking thresholds, for the quantization of the spectral coefficients in order to maximize audio quality as perceived by human listeners rather than other simple least-mean-square type error metrics metrics such as Signal-to-Noise-Ratio (SNR), Root-Mean-Square (RMS) error, and the like. Specifically, the approach of perceptual audio coding may in fact even imply generating a perceptually shaped spectral distortion profile that provides improved subjective audio quality at the expense of the signal’s global SNR, as compared to a coder that does not employ psychoacoustic knowledge. More about subjective quality assessment and possible degradation of subjective audio quality can be found in BS.1116 [8], Multi-Stimulus Test with Hidden Reference and Anchor (MUSHRA) [9], and “What to listen for” [10].
In order to serve as a part of a perceptual audio coding system, psychoacoustic models do not need to be perfect to satisfy their purpose, and in fact the commonly employed models only represent a small subset of the known properties and abilities of the human auditory system (HAS). On one hand, it appears that the more completely and accurately a perceptual model is built compared to its natural counterpart (HAS), the better the performance that can be achieved for perceptual audio coding. On the other hand, such models are frequently designed to work together with a perceptual audio coder framework in a way that the performance of the overall coding system (“encoder” + “decoder” = “codec”) is optimized rather than that the accuracy of the model itself. Also, encoding at high bitrates (low compression factors) can make the accuracy of the model less relevant because plenty of bits are available to represent all perceptually relevant components in an accurate enough fashion.
In general, perceptual models for audio coding model the HAS responses to the input audio signal in a behavioral style (i.e., as a “black box”) rather than a detailed simulation of the physiological processes inside the HAS, due to the prohibitive computational complexity of such physiological models [11].
This paper provides a tutorial introduction of the most commonly used psychoacoustic models for low bitrate perceptual audio coding, starting with basic models that have been defined with the first audio coding standards, with a special focus on popular MPEG codec technology. It will discuss the relevant psychoacoustic properties of the HAS and the extent to which these are represented in the models. In many cases, the relevant technologies are too complex to be discussed in appropriate depth within the scope of this paper. More tutorial information on perceptual audio coding can be found in previous studies [12,13,14,15]. Well-known audio coding standards can also be found in the references [1,2,16,17,18,19,20,21,22,23].
2. Monaural Perceptual Effects and Models
As a first (and most important) step in perceptual audio coding, perceptual effects for monaural auditory perception have to be modeled. This section discusses the basic relevant monaural perceptual effects.
2.1. Properties of Monaural Human Hearing
The principles of the human auditory system and the underlying physiological properties of the ear have been studied by researchers in the field of medicine, biology, and engineering. Comprehensive psychoacoustic studies have been performed and described by Fastl and Zwicker [24] and Moore [25], among others.
Many psychoacoustic effects can be explained by the physiological properties of the hearing process itself. The outer ear and ear canal collect arriving air pressure waves, which are transmitted as mechanical vibration via the ear drum and inner ear to the liquid-filled cochlea. The cochlea’s shape resembles a tapered spiral similar to a coiled snail (the name is derived from the Ancient Greek word for “snail shell”). The inner surface of the cochlea is lined by sensory cells consisting of small hairs connected to nerve endings—so-called hair-cells. Depending on the frequency of the incoming sound, different areas of the cochlea resonate, causing the hair-cells at the respective region to vibrate (“tonotopic organization”). In turn, the stimulated nerve endings send impulses to the brain, allowing it to perceive and distinguish sounds of different frequency, level, and timbre.
Due to these physiological properties of the hearing process, the perception and resolution of frequency is not linear and becomes coarser at higher frequencies. The bandwidth of the auditory filters in the HAS—the so-called “critical bandwidth”—describes the bandwidth within which the signal components interact perceptually with each other rather than being perceived as independent from each other. Based on modeling this auditory filter bandwidth, perceptually motivated frequency scales can be derived, such as the Bark-Scale proposed by Zwicker [25,26] or the Equivalent Rectangular Bandwidth (ERB)-scale by Moore and Glasberg [27,28] (see Figure 2).
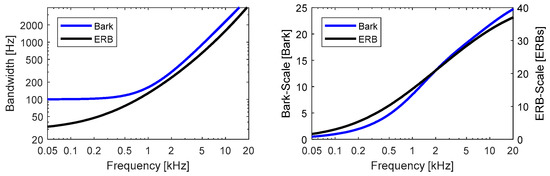
Figure 2.
Critical Bandwidth and resulting perceptual scales, as modeled by the Bark-Scale and Equivalent Rectangular Bandwidth (ERB)-Scale.
An important aspect for perceptual audio coding is the consideration of masking effects in the human auditory system, i.e., the effect that louder sounds (“masker”) tend to suppress the perception of other, weaker sounds (“probe”) in the masker’s spectral or temporal vicinity. A common example for masking is how the sound of a bird (probe) can be drowned by the sound of a car passing by (masker) in human auditory perception. One category of such masking effects is known as “spectral masking effects” or “simultaneous masking” [25] (see Figure 3), for which the following aspects were observed:
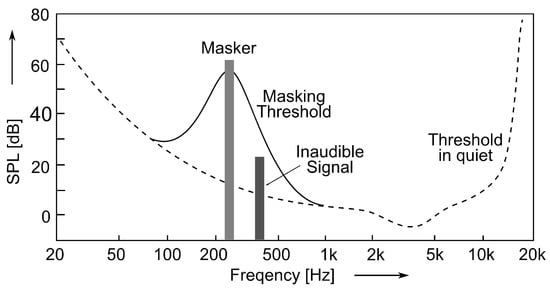
Figure 3.
Illustration of spectral masking effects. Dashed line represents threshold of hearing in quiet, solid line illustrates the masking threshold due to the presence of a masker signal (e.g., narrow-band noise), due to which weaker signals at neighboring frequencies become inaudible.
- A frequency dependent threshold of hearing in quiet describes the minimum sound pressure level (SPL) of a sound to be perceivable in isolation and under extremely quite conditions.
- In the presence of a masker, the threshold in quiet curve changes into a masking threshold, which shows a bell-shaped increase in frequencies in the vicinity of the masker, depending on its frequency, level, and signal type. Any sound beneath this threshold is masked by the louder signal, and thus inaudible for the average listener. In perceptual audio coding, the coding error (i.e., the introduced quantization noise) corresponds to the probe signal in this experimental scenario.
- Masking effects are strongest for signals that are within the critical bandwidth of the masker. Within the critical bandwidth, the masking threshold remains constant. Furthermore, the masking effects spread to frequencies beyond the critical bandwidth (so-called inter-band masking). The upper slope of the masking threshold depends on multiple factors, such as absolute frequency and sound pressure level of the masker, whereas the lower slope hardly shows a level dependency.
- Depending on the type of masker, i.e., tone or (narrow-band) noise, the strength of the masking effect varies. While noise-like maskers can mask tone-like signals very well (up to a masker-to-probe level ratio of about 6 dB), tone-like maskers can mask noise only to a much weaker extent [29] (about 20 dB).
The second category of masking effects can be described as “temporal masking effects” and describe masking behavior when the masker and probe signals are not present at the same point in time (see Figure 4). For “post-masking”, quiet sounds that occur after a loud stimulus are masked due to the reduced sensitivity of the ear for approximately 100–200 ms. Additionally, there is also “pre-masking” in a short time window of approximately 20 ms before the masker, where the perception of soft (probe) sounds is masked by subsequent louder (masker) signals. This seemingly non-causal behavior is assumed to be caused by the fact that softer sounds have a longer build-up time for cognitive processing in the brain than louder signals.
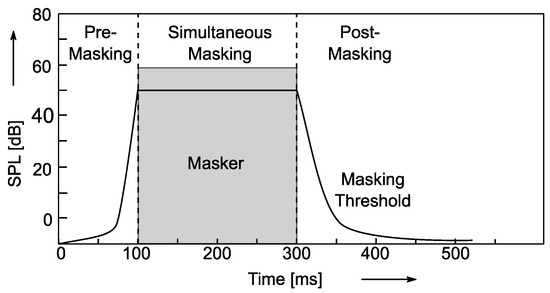
Figure 4.
Illustration of temporal masking effects.
These effects regarding masking of energy describe the core behavior of the HAS that has to be modeled for perceptual audio coding.
2.2. Classic Models for Perceptual Audio Coding
The first audio coding standards for generic signals (i.e., for all types of audio material) were MPEG-1 [16,30], MPEG-2 [1], and MPEG-2 Advanced Audio Coding (AAC) [2,31]. As is customary for MPEG, the standards normatively specify bitstream format and decoder operation, which leaves room for encoder optimization, and thus improved codec performance, while retaining full compatibility, even after the publication of the standard. Consequently, these standards only provide suggestions for perceptual models that are published as informative annexes and may be implemented and modified as deemed appropriate by the implementer.
The MPEG-1 Audio standard specifies two psychoacoustic models:
- Perceptual model 1 is intended mainly for use with the Layer I and II codecs that employ a 32-band pseudo Quadrature Mirror Filter (pQMF) filterbank (also known as “polyphase filterbank”). It uses a windowed Discrete Fourier Transform (DFT) to perform a high-resolution spectral analysis of the input audio signals (512 samples Hann window length for Layer I, 1024 samples Hann window for Layer II). Then, the signal energy is computed in frequency bands that are designed to resemble the Bark perceptual frequency scale [26] by appropriate grouping of the DFT coefficients. A minimum level for maskers in each band is required to be considered as relevant, thus modeling the psychoacoustic Threshold in Quiet. The model distinguishes between tonal and non-tonal masker components by examining whether a spectral contribution belongs to a spectral peak according to certain specified rules and uses specific masking index functions for tonal and non-tonal components. Separate partial masking thresholds are then calculated for tonal and non-tonal components, with each one considering inter-band masking by spreading the energy contributions to the adjacent lower or higher bands with appropriate definitions for the lower and higher slopes of the masking function. Finally, the individually computed masking thresholds are combined together with the threshold in quiet into a single global masking threshold, mapped to the 32 sub-bands of the codec pQMF filterbank and output to the codec’s bit allocation procedure as sub-band Signal-To-Mask Ratios.
- Perceptual model 2 is intended mainly for use with the Layer III codec (aka “mp3”) and appears in similar form as the MPEG-2 AAC psychoacoustic model. A 1024-samples Hann-windowed DFT is used and its output is grouped into frequency bands inspired by the Bark scale. A major difference in Perceptual Model 1 lies in the fact that the computation of the tonality is based on a so-called unpredictability measure, i.e., a figure which measures how well the complex DFT coefficients within a frequency band can be predicted (in radius and angle, i.e., in polar coordinates) from their counterparts from the preceding block. Both quantities—the single coefficient energies and the coefficient-by-coefficient unpredictability measure—are grouped into perceptual spectral bands and convolved with a spreading function that models inter-band masking. From this, a tonality value for each spectral band is calculated and the required tonality-dependent Signal-To-Mask Ratio is determined. Finally, the model considers the threshold in quiet and adjusts the result for the avoidance of pre-echoes [10,32] to generate the final Signal-To-Mask Ratio output for each spectral band of the codec.
The basic psychoacoustic features included in both psychoacoustic models can be summarized as follows:
- Use of a perceptual (here, Bark-type) frequency scale for masking computations;
- Modeling of intra-band and inter-band masking;
- Use of tonality metrics to distinguish the stronger masking ability of noise-like maskers from the weaker masking ability of tone-like signal components. Both tonality metrics are based on signal processing rather than actually being rooted in HAS perception. In fact, for the purpose of audio coding it seems far from trivial to come up with a computationally inexpensive measure that is able to correctly quantify a signals’ masking ability with respect to its tone- and noise-likeness (“tonality”), not only for pure tones or noise but for all types of audio signals. As a remark from the authors, a tonality detection based on modulation spectra [33] would, most likely, be closest to modeling the underlying physiological processes as an algorithm.
- Modeling of the HAS threshold in quiet
- Adaptation of the masking threshold values computed inside the perceptual model (which is inherently agnostic to the rest of the codec) to the analysis and synthesis framework (mostly filterbank, an associated time/frequency resolution) of the codec.
In addition to representing a number of fundamental perceptual effects that are well known from psychoacoustic literature, the described perceptual models also address a number of general practical aspects that are important for use as part of a perceptual audio coder:
- Both models employ a separate filterbank (Discrete Fourier Transform DFT) for the calculation of the masking effects. Compared to using the critically sampled codec filterbanks, the DFT offers at least two advantages: Firstly, the DFT representation preserves the full energy present in the original signal (rather than that of a subsampled or time-aliased signal version). This is important for an accurate estimation of masking components inside the signal. Secondly, the availability of a magnitude-phase representation plus energy preservation opens the door for computing a plethora of tonality metrics, such as spectral flatness [34] or chaos measure [35]. As a practical consequence of using a DFT for threshold calculation, the calculated masking threshold needs to be adapted (scaled) to the domain of the codecs analysis/synthesis filterbank pair.
- In contrast to psychoacoustic experiments, where playback level environment can be controlled very precisely, an audio codec is entirely agnostic of the playback setup and environment following the decoder. As an example, the listener can use the volume adjustment of the playback amplifier at will, and thus play back the same encoded/decoded signal both very softly and extremely loud. Thus, the effect of the codec’s threshold in quiet model curve is effectively shifted with the playback volume, and is thus applied far from psychoacoustic reality. Similarly, the audio reproduction system following the decoder may be very imperfect and in practice exhibit significant linear or even non-linear distortions (e.g., small loudspeakers used in mobile devices can have a very uneven frequency response and considerable non-linear distortion). This effectively post-processes the coding noise introduced into the audio signal and may strongly distort the masking situation assumed by the codec. In order to account for this, practical psychoacoustic models for audio coding frequently refrain from attempting to fully model or exploit the effects of known masking phenomena (threshold in quiet, inter-band masking) and are instead conservative in their modeling assumptions in the interest of robustness of audio quality to unknown playback conditions.
- While basic psychoacoustic masking effects only depend on the involved audio signals, the perceptual model inside an audio coder needs to adapt its output to the basic properties of the codec system in order to achieve high coding performance. In other words, beyond purely psychoacoustic calculations, properties that interact with the codec algorithms need to be considered, including aspects such as:
- ○
- Time/frequency resolution of analysis/synthesis systemDue to the involved analysis/synthesis filterbanks and the coder’s block processing structure, the codec system has a certain time/frequency resolution. Ideally, the time/frequency resolution is matched to the stationarity properties of the input audio signal to guarantee optimum coding performance, such that the precision requirements calculated inside the perceptual model for quantization of spectral coefficients correspond to nearly stationary segments of the input signal. Generally, the quantization error of the spectral coefficients causes a time-domain error signal which is spread out over the entire length of the synthesis filterbank window length. If the input signal has a very distinct temporal fine structure (e.g., transient signals, such as percussive instrument signals or applause), the error signal may occur at the codec’s output as preceding the signal onset, and thus may cause so-called pre-echo artifacts [15,32]. Thus, pre-echoes are a consequence of the codec’s limited time resolution, which is connected to the codec’s analysis/synthesis system and block structure. In practice, the raw calculated masking threshold values determined by the perceptual model may be adjusted to account for the effects of limited codec time resolution. This technique is called pre-echo control [1] and limits the permissible increase in calculated threshold between subsequent frames [32]. Furthermore, modern audio codecs usually offer the possibility of dynamically adjusting the time/frequency resolution of the codec to the input signal by means of block switching or window switching [15,36,37]. The control of the window switching algorithm is usually also considered as a part of a practical perceptual model for audio codecs [1,2] and plays an important role for their performance.
- ○
- Threshold adjustment for target bitrateWhile coding at a constant target quality leads to a (potentially strongly) varying bitrate, most audio codecs operate with a specified constant target bitrate. Consequently, the codec tries to achieve optimum subjective audio quality under the constraint of the given target bitrate. If the target bitrate clearly exceeds the perceptual masking requirements, there are no special measures to be taken during the encoding process. For very low bitrates, however, there are not enough bits available to satisfy the masking requirements, as they are calculated as masking thresholds by the perceptual model. Thus, the target thresholds for the quantization precision have to be adjusted (increased) to reduce the bitrate demand in a way that causes minimum loss in subjective quality. Such threshold adaptation strategies have been developed under the name Bit Allocation and Noise Allocation [38] to accommodate constant rate coding. They can be considered as bridges between the codec’s psychoacoustic model and its quantization or coding stage.
- ○
- Bit reservoir usageThe properties of the input audio signal—and thus the bitrate demand—may change rapidly over time. However, it is desirable to keep the subjective quality constant also for a constant bitrate scenario. This can be achieved by allowing a local variation of bitrate over time, within the limits of the decoder’s bitstream buffer size. The control over the bit budget usage for each block is usually considered an integral part of the perceptual model of modern audio codecs. To this end, the perceptual model can calculate an estimate of the required bitrate for the current frame from its knowledge of the signal spectrum and associated computed masking threshold. This knowledge allows implementation of a so-called bit reservoir [15,38]. Thereby, the codec has the ability to consume more bits for frames that are hard-to-encode (e.g., sudden signal onsets) and to use fewer bits for easy-to-encode frames (e.g., periods of silence). Proper control of the bit reservoir usage is of utmost importance for good codec performance.
2.3. High Efficiency Models for Perceptual Audio Coding
The previous sections described the classic codec implementation structure with separate modules for perceptual (psychoacoustic) model and quantization or coding. In practice, there are successful codec implementations that grossly depart from the concept of a distinct perceptual model attempting to match psychoacoustic phenomena as accurately as possible. A prominent example is the so-called FastEnc implementation of the High Efficiency v2 (HE-AAC v2) codec, as it has become ubiquitous through its standardization within 3rd Generation Partnership Project 3GPP [39] and its widespread deployment on virtually all existing mobile phones. Compared to the classic implementations (which historically computed the final codec output from a computationally complex nested two-loop iterative algorithm [38]), the FastEnc implementation is faster in execution by a factor of up to 15 (e.g., for MP3 at 128 kbit/s), while providing at least the same subjective quality at each given bitrate.
A closer look at the implementation reveals some interesting aspects:
- The psychoacoustic model is calculated directly in the critically sampled codec filterbank (i.e., a Modified Discrete Cosine Transform—MDCT [40]) domain. This omits the additional computational complexity of calculating a dedicated DFT-based filterbank for the psychoacoustic model.
- The threshold calculation is based on few very basic assumptions that represent a simple worst-case masking threshold. Initially, a (very conservative) Signal-to-Mask Ratio (SMR) of 29 dB is assumed, i.e., a minimum masking ability that is satisfied by all types of signals, be they of tonal or noise-like nature. Consequently, no tonality is computed or taken into consideration. Modeling of inter-band masking uses fixed slopes of +30 dB/Bark (lower slope) and −15 dB/Bark (upper slope). Furthermore, the raw thresholds are adjusted by a pre-echo control stage.
- Subsequent to the initial threshold calculation, a threshold adaption stage adjusts the overly conservative thresholds to fit into the available bit budget. The amount of threshold reduction needed is estimated from a simplified estimate of the required bitrate, based on the signal spectrum and associated computed masking threshold—the so-called Perceptual Entropy, or PE [35]. The final quantizer setting (scale factors) are computed directly from the threshold values rather than determined by an iterative procedure. For improved perceptual performance, the introduction of holes into the signal spectrum by too coarse quantization (“birdies” [10]) is avoided by guaranteeing a minimum spectral precision in each relevant frequency band.
In summary, the described model represents a state-of-the-art way of implementing a perceptual model as part of a codec that is designed to be highly attractive in both computational complexity and subjective audio quality. To this end, the original reference coder design using a complex iterative encoding procedure has been replaced essentially by a one-shot estimation process that includes many aspects of numerical optimization, which are beyond the scope of this article.
3. Coding of Stereo Signals
3.1. Binaural Hearing
Spatial or binaural hearing describes the ability of the human auditory system to analyze the spatial aspects of sound, including localization of sound sources and perception of room (environment) acoustics [41]. Sound waves are shadowed and diffracted by the listener’s head and pinnae, depending on frequency and direction of arrival. This corresponds to a direction dependent filtering of the signals that are perceived at the two ears. The human brain interprets the resulting monaural and binaural cues to localize sound. Specifically, binaural cues describe the relationship between the two ear signals. The frequency resolution in which these cues can be distinguished corresponds to the critical bandwidth. The most important binaural cues are:
- Interaural Level Differences (ILD),caused by shadowing of sound waves by the head (see Figure 5a);
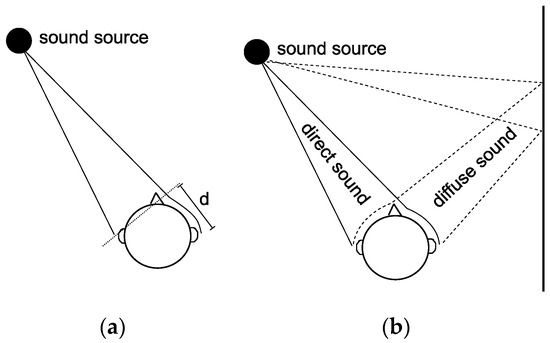 Figure 5. Illustration of different binaural sound propagation to the ears. (a) Propagation path length difference; (b) direct and diffuse sound due to wall reflection.
Figure 5. Illustration of different binaural sound propagation to the ears. (a) Propagation path length difference; (b) direct and diffuse sound due to wall reflection. - Interaural Time Differences (ITD) and Interaural Phase Differences (IPD),caused by the different distances that sound has to travel to both ears (d in Figure 5a);
- Interaural Cross-Correlation (ICC),influenced by diffuse or reverberant sounds (e.g., different path lengths and head shadowing of direct sound and diffuse sound from wall reflection; see Figure 5b)
The ILD and ITD cues are commonly associated with the perceived localization and lateralization of sound, whereas the ICC relates to the perceived sound source width and the acoustic properties of the surrounding room.
Spatial hearing can also improve the perception of single sound sources in the presence of spatially distributed masking sources. This is commonly known as the “cocktail-party effect”, where binaural hearing provides the ability to focus on the voice of one particular talker in the presence of many concurrent talkers [42]. Consequently, binaural hearing can reduce masking; this effect is described by the binaural masking level difference (BMLD) [41]. The BMLD can lead to a reduction of masking threshold of up to 15 dB, as compared to the classic masker/probe experiments, in which both stimuli are presented monaurally. Those “unmasking effects” are most prominent for stereo headphone playback (where each tested signal is identically fed into one ear), but also occur for stereo or multi-channel loudspeakers to a lesser extent (where cross-talk between the signals appears before they arrive at the ears). More details about the properties of spatial hearing can be found in previous studies [24,41,43].
3.2. Models for Coding of Stereo Signals
When coding a stereo pair of audio channels, audio coders attempt to take advantage of possible redundancy or irrelevance between the two channel signals. To this end, techniques for joint stereo coding are employed [15,44], which jointly process the two channel signals in their spectral representations. While there are different approaches for joint processing, in many cases the use of joint stereo processing leads to further extensions of the coder’s psychoacoustic model for:
- adaptation of the coding thresholds (i.e., thresholds used for controlling the codec’s quantization noise) to fit to the joint stereo processing, if used;
- on/off control of the joint stereo processing.
Therefore, in an encoder with joint stereo processing (see Figure 6), the joint stereo encoding is controlled by the perceptual model and the coding thresholds are adapted according to the joint stereo coding. The control information for the joint stereo processing is multiplexed as side information into the bitstream. This side information is used in the decoder (see Figure 7) to control the joint stereo decoder processing.
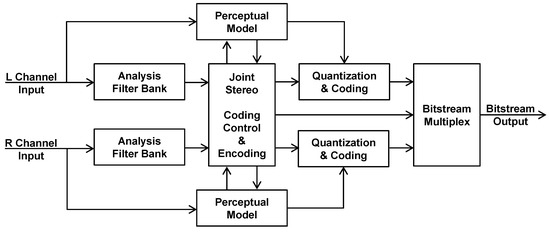
Figure 6.
Encoder with Joint Stereo Processing.
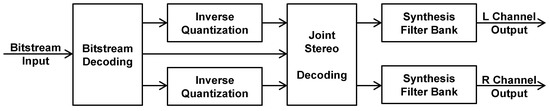
Figure 7.
Decoder with Joint Stereo Processing.
The most widely known and simple scheme for joint stereo coding is Mid/Side (M/S) stereo coding, which encodes the sum and the difference between left and right channel signal rather than the original signals [45,46]. The primary benefits of M/S stereo coding can be described by two factors:
- Spatial unmasking prevention: Since independent coding of channel signals introduces uncorrelated quantization noise signals into both channels, masking of this noise by the music signal may be significantly reduced due to spatial unmasking by the BMLD effect. This is especially severe for near-monophonic signals where the spatial image of the signal is perceived in the center of the sound stage, whereas the noise is spread out to the far left and right [44]. In such cases, the activation of M/S stereo helps to put the coding noise “behind” the masker signal into the center of the sound stage, and thus prevent BMLD-induced unmasking.
- Bitrate saving: For near-monophonic signals, significant savings in bitrate can be achieved as compared to independent coding of the channel signals.
Thus, for using M/S stereo, the psychoacoustic model of the codec has to be extended in two ways:
- Adaptation of coding thresholds: When M/S stereo coding is activated in a codec, the quantization noise signals of the two coding channels pass through a sum-difference matrix before being presented to the listener as left and right channel output signals. As a consequence, the same amount of noise contribution is present in both output channels (independent control over noise levels is no longer possible) and the noise contributions appear at the output as correlated (M channel) and anti-correlated (S channel) rather than uncorrelated from each other, leading to different BMLD conditions. Thus, the coding thresholds have to be modified for M/S processing to ensure that all monaural and spatial masking conditions are met properly at the codec’s output. One approach is to calculate suitable thresholds using explicit models for BMLD effects, as has been described in previous studies [2,17,46]. A second, more simplistic approach to threshold calculation has been described in another study [44], where the consideration of meeting individual target thresholds that ensure proper monophonic masking at the channel outputs leads to a common coding threshold for M and S channels as the minimum of the monophonic L and R channel thresholds in each frequency band to consider the worst-case for each individual output channel. Even though this approach does not employ any explicit model of BMLD effects, it has become common implementation practice due to its simplicity and the fact that resulting codec quality does not suffer from the simplicity of the model.
- Coding mode control: When M/S stereo is activated, the bitrate consumption for quantization or coding changes due to altered spectra and coding thresholds, as compared to individual (L/R) coding. For stereo signals that are far off from the stereo image’s center, employing M/S coding may, therefore, be even more expensive than separate coding. In order to enable proper use of M/S stereo coding, an extension of the psychoacoustic model (“M/S decision”) usually controls the use of M/S vs. L/R (individual) coding by estimating the bitrate demand (via Perceptual Entropy) for each alternative and then deciding on the more bitrate-efficient alternative. Depending on the coding scheme, this decision can be made for individual frequency bands [2] or broadband [44].
While M/S stereo coding provides the highest (approximately 50%) bitrate saving for center-dominant, near-monophonic signals, it does not enable efficient coding of near-monophonic signals that are panned to either side of the stereo image (even though this is possible, in principle, due to the high correlation between the channel signals).
Generalizations to the basic M/S coding scheme also allow efficient coding of such signals. As an example, the “Unified Stereo” handling in MPEG-D Unified Speech and Audio Coding” (USAC) [4,18,47] adds a (complex-valued) prediction stage from M to S (or from S to M for out-of-phase signals) after the encoder sum/difference matrix in order to remove the redundancy between M and S channels for near-monophonic signals that are panned off-center.
While M/S stereo coding was the most widely used early technique for joint stereo coding, the intensity stereo coding approach emerged concurrently. It will be discussed in the section on models for parametric audio coding (see Section 4.1).
3.3. Generalization to Coding of Multi-Channel Audio
The next evolutionary steps after coding of two-channel stereo signals are coding of multi-channel (surround) audio (e.g., 5.1 or 7.1) [48] and coding of 3D audio (e.g., 5.1 + 2 height (H), 7.1 + 4 H or 22.2) [49,50]. While the number of loudspeakers grows tremendously along this path, the relevant psychoacoustic considerations still remain the same, since human auditory perception is based on reception of two ear signals, where the ears are positioned on the left and right side of the head. For these reasons, the perception of surround and 3D sound is based on a set of cues with different dominance:
- Left/right perception: The most important (and thus most sensitive) aspect of spatial sound relates to the perception of the left/right distribution of auditory events relative to the listener’s head, since this is directly represented by inter-aural (binaural) cues, i.e., ILD, ITD, and ICC, as they originate from the HAS’s differential analysis of the two ear signals. Thus, in order to deliver excellent audio quality, these aspects of surround and 3D sound have to be represented most carefully by audio codecs.
- Front/back perception: Compared to left/right perception, front/back perception is much less dominant, since it cannot rely on inter-aural difference cues but has to exclusively evaluate spectral colorization in the ear signals, as described in Blauert’s concept of directional bands [51]. The effect of directional filtering of the incoming signals (i.e., spectral coloration according to the angle of coincidence) is a comparably weak auditory cue as compared to inter-aural difference based cues, and consequently psychoacoustic studies indicate a high tendency for front/back confusion in 2D and 3D localization experiments. More generally, locations with identical left/right cues form so-called cones of confusion [51], within which differentiation between candidate locations on the same cone of confusion has to rely solely on the (weak) directional filtering cues. Thus, for audio coding this means that front/back localization aspects of surround and 3D signals have to be preserved less accurately than left/right aspects, since distortions are less likely to be perceivable.
- Elevation perception: Very much like front/back perception, elevation perception on the same cone of confusion is exclusively based on (weak) directional filtering cues, and thus the related signal aspects have to be handled less accurately than left/right aspects.
Considering this psychoacoustic background, a number of approaches for joint coding of surround and 3D sound have been proposed. The simplest strategy is to apply traditional M/S stereo coding to multiple left/right pairs of the audio input. As an example, for coding of 5.1 audio, the left and right front channel form an M/S channel pair and the corresponding surround channels form a second one. For coding of 5.1 + 4H, the corresponding height channels form pairs as well. The center channel is not included into any joint stereo processing. This approach is implemented in multichannel AAC [17,31] and later generations of multichannel-enabled MPEG-4 audio codecs. It addresses the above-mentioned aspects of left/right perception and successfully prevents ICC distortions (and thus BMLD-type artifacts) in the spatial sound image.
Other strategies for coding of surround and 3D sound employ generalizations of intensity stereo coding, which are addressed in the section on parametric audio coding. In the context of 3D audio coding, a hybrid approach between M/S channel pairs and parametric coding of associated height channels can be found in previous studies [19,52] under the name Quad-Channel-Element (QCE).
A further extension of the M/S coding approach conceived for use in 3D audio coding is called the Multichannel Coding Tool (MCT) [53]. It allows the extraction of redundancy and avoidance of BMLD unmasking artifacts in channel pairs that contain off-center panned signals, and can be applied sequentially to arbitrary pairs of channels of surround and 3D sound material. The discussion of these (and many other) approaches is beyond the scope of this article.
4. Models for Parametric Audio Coding
Beyond the classic codec architecture shown in the introduction of this article, major advances in audio coding have been achieved since the year 2000 by introducing so-called parametric audio coding techniques, i.e., techniques that represent the audio waveform by a sparse set of parameters rather than temporal or spectral samples. Due to the sparseness of such parametric representation, such techniques are usually not waveform-preserving in the sense that they can produce a decent perceptual replication of the original signal, but will not converge to the original waveform (i.e., a significantly different signal between reconstructed and original waveforms will remain even at high subjective quality). Such extensions, also called “coding tools”, can provide good-quality audio representations at extremely low bitrates [54].
There exist parametric tools for coding of one particular audio waveform, as well as tools for joint coding of several spatial audio signals (called spatial audio coding). In the following, two successful flavors of parametric coding tools will be reviewed, together with the corresponding psychoacoustic model features.
4.1. Parametric (monophonic) Waveform Coding
An early example of the integration of a parametric coding tool into the classic filterbank-based perceptual audio coder is Perceptual Noise Substitution (PNS) [17,55]. A similar concept is found under the name Noise Filling [18]. The underlying idea of the tool is based on the psychoacoustic observation that individual realizations and observations of noise-like signals cannot be distinguished perceptually from each other if their spectral or temporal envelopes are similar enough, i.e., that the actual signal waveform does not play a relevant role within the HAS. Consequently, spectral parts of the input signal that were identified as being noise-like are omitted from regular transmission of spectral coefficients. Instead, the energy levels present in the noisy frequency bands are transmitted as parametric side information to the decoder and a pseudo-random noise generator re-inserts spectral coefficients with appropriate scaling into the respective frequency bands.
A perceptual model for controlling PNS processing within a codec may include the following aspects:
- First, the model has to detect which frequency bands solely contain noise-like signal components (signals without a distinct spectral fine structure). This task is related to a tonality calculation, as it is needed for masking calculations, but may employ different tonality or noisiness measures. This ensures that no signal parts containing tonal components are substituted erroneously by noise in the decoder.
- Furthermore, the model should also detect if the noise signal in a particular detected coder frequency band has any relevant or distinct temporal fine structure that could not be reproduced appropriately by pseudo-random noise. As one example, the temporally modulated noise of applause signals also includes transients, and thus cannot be substituted by PNS without causing significant artifacts.
While PNS allows for parametric coding of noise-like components in the high-frequency (HF) region, the much more successful bandwidth extension (BWE) techniques allow for parametric substitution of the entire high-frequency range of an audio signal without severe restrictions. The first widely deployed BWE technique is called Spectral Bandwidth Replication (SBR) [17,56]. The basic idea is that above a certain border frequency (e.g., 6 kHz), the HF part of the signal spectrum is entirely reconstructed from the transmitted low-frequency (LF) part. The LF part is transposed (i.e., linearly shifted in frequency) to higher frequencies and adapted in its time/frequency properties to match the perceptual properties of the original HF part as closely as possible using a compact set of perceptually motivated parameters. Strictly speaking, SBR and related techniques are hybrid approaches between parametric and waveform coding, since the waveform transmitted for the LF part is subsequently transformed into the HF part by parametric means. This is sometimes denoted as being a semi-parametric processing.
The perceptual control of SBR in the decoder typically performs the following steps:
- The spectral envelope of the original HF part is captured with appropriate time/frequency resolution and sent as compact parameters to the decoder as side information.
- The properties of the transposed LF frequency content are compared to the properties of the original HF part. When significant differences arise, additional post-processing of the transposed part has to be enabled:
- ○
- When the target timbre characteristic is much more tonal than the one of the transposed LF part, additional sine tones can be generated for each band [57].
- ○
- When the target timbre characteristic is noise-like, whereas the transposed source LF region is tonal (which is common for music signals), the transposed signal spectrum can be flattened or whitened to a selectable extent.
Similar to most parametric coding techniques, SBR generally does not produce perfect (“transparent”) audio quality but excels through its ability to provide good quality even at extremely low bitrates. Most importantly, it allowed for the first time audio coding with full-bandwidth audio output even at extremely low bitrates, such as 24 kbit/s stereo, where only very limited audio bandwidth could be provided before.
While classic SBR generates the HF part simply by scaled copy-up of the LF parts, enhanced versions (eSBR [58]) allow a better preservation of the frequency structure of harmonic signals. Other more recent approaches, such as the Intelligent Gap Filling (IGF) tool [19,59], which can perform audio bandwidth, enable a mixture of waveform coded components and parametrically reconstructed components. Such schemes benefit from sophisticated perceptual control mechanisms (as described in Section 5) for proper operation [11].
4.2. Parametric Spatial Audio Coding
The second important class of (hybrid) parametric coding techniques is the family of spatial audio coding algorithms that will be described in this subsection.
The forerunner of parametric spatial audio coding algorithms is the intensity stereo (IS) coding approach that was mentioned before under the heading “coding for stereo signals” and adheres to the basic framework shown in Figure 6. In the encoder, the spectral values of the left and right channel are downmixed into a single mono channel, plus some directional information that indicates the energy ratio between the two channel signals in each codec frequency band. In the decoder, the transmitted mono signal is scaled differently to calculate left and right output spectral values. This is done using the directional information, such that the original energy (intensity) of both channel signals is preserved (whereas the waveforms come out quite differently due to the downmix/upmix process). As a consequence, intensity stereo is a lossy joint stereo technique independent of any possible quantization-related errors. Both output signals are scaled copies of each other that only differ in their intensity (thus the name of the technique) in each frequency band, just as if they had been created on a mixing console with frequency band-wise dynamic left-right panning controls. This basic technique has been published under different names, including “intensity stereo” [60,61] and “channel coupling” [62], and generalizes to multi-channel (i.e., down/upmixing) of several audio channels.
Due to the lossy nature and simplicity of the approach, intensity stereo can be applied only to high frequencies (typically above 4 kHz) without unduly degrading the stereo image. Nonetheless, for certain classes of stereo signals with high temporal complexity (e.g., applause), artifacts are introduced due to the limited temporal resolution of the scheme (owing the codec’s filterbank and temporal framing design). Consequently, also the use of sophisticated perceptual control mechanisms has been proposed to be advantageous for controlling the technique with a special focus on the signal’s fine temporal structure [60,63].
The next generation of spatial audio coding is the Parametric Stereo (PS) scheme, as described in previous studies [17,64]. Similar to intensity stereo, it is a 2-1-2 scheme, i.e., two input channels are mixed into one downmix channel, transmitted, and upmixed in the decoder into two output channels. In contrast to intensity stereo, PS has numerous enhancements that allow its use throughout the entire frequency range (at the expense of increased computational complexity):
- Whereas intensity stereo works on the codec’s native spectral representation (with all its constraints regarding time/frequency resolution and aliasing due to critical sampling), PS employs a dedicated additional complex-valued filterbank with high time resolution and reduced aliasing due to oversampling by factor two.
- For each of the binaural inter-aural cues (ILD, ITD, ICC) described previously, corresponding inter-channel cues (IID, IPD and OPD, ICC) are extracted from the original channels by perceptual cue extractors, transmitted as compact side information, and re-synthesized in the PS decoder.
- While Inter-channel Intensity Difference (IID) corresponds to the well-known ILD cue and is conceptually similar to the function of the intensity stereo algorithm, two new cue types were introduced in this scheme. As a more practical implementation of ITDs, Inter-channel Phase Difference (IPD) cues plus overall (broadband) phase information (OPD) are provided to model time differences of arrival for laterally placed sound sources. The major innovation, however, lies in the introduction of Inter-channel Cross Correlation (ICC) cues that are vital for representing ambient (decorrelated) sound components, as they are required for proper spatial reproduction of spatially distributed sound sources, e.g., orchestral music or reverberant spaces. As a novel algorithmic ingredient, a decorrelator filter was introduced to synthesize decorrelation between the output channels, as specified by the transmitted ICC value in each band [65].
The inter-channel cues can be determined using the following formulae, from the energies , of the first and second audio channels and their complex-valued spectral coefficients , for samples within a given frequency band and time-slot:
Generalizations of the PS concept to multi-channel and surround sound can be found in the Binaural Cue Coding (BCC) scheme [66,67] (which was even published before PS) and MPEG Surround [68,69,70], both utilizing very similar spatial cues. In all cases, the perceptual model of the coding scheme is represented by the extraction of the inter-channel cues.
A further extrapolation of these concepts for coding of several audio channels to parametric coding of several object signals can be found in [71] and MPEG-D Spatial Audio Object Coding (SAOC) [72]. Instead or inter-channel cues, inter-object cues (such as Inter-Object Level Difference (IOLD) or Inter-Object Correlation (IOC)) are employed.
Both joint parametric coding of multi-channel sound and multiple objects can be extended with so-called residual signals that offer an option for approaching waveform preservation in selected frequency regions [71,72]. This allows the saturation of the perceptual quality obtainable (as it is typical for parametric coding schemes) at the expense of considerable additional bitrate to be overcome. Similar concepts of mixed parametric and waveform coding with a focus on lower computational complexity can be found in a previous study [73].
5. Some Recent Developments
So far, this tutorial has focused exclusively on perceptual models that have been used for coding applications. These were subject to severe constraints regarding permissible computational and memory complexity, as well as processing delay (i.e., algorithmic delay until the model output is available for the coding process, which usually has to be in the same processing block). Beyond these specific codec models, a plethora of psychoacoustic models has been developed since the beginning to calculate psychoacoustic attributes such as loudness [25,74], pitch [25], sharpness [25,75], roughness [25], listener envelopment (LEV) [76], etc. Many models are (at least partially) based on the physiology of the HAS, including the auditory pathway, the cochlea, and the hair cells. Some focus on more exact prediction of the masking behavior [77]. Others form a perceptual measurement system that attempts to objectively predict the audio quality as assessed in subjective listening tests [9,78,79]. While none of these models was suitable as part of a first-generation perceptual audio codec, some of them are on their way to being adapted to audio coding, given the increased availability of computational resources nowadays. Specifically, such sophisticated and computationally complex models can be used for offline encoding, i.e., for non-real-time encoding of audio material with file-level access (allowing unlimited look ahead into the signal’s “future” and multi-pass encoding). This section briefly reviews one example of an advanced model that has been utilized to investigate what benefit it can bring to audio coding.
The publication [11] describes a sophisticated psychoacoustic model for the perceptually optimal control of a particular coding tool. The psychoacoustic model part is based on an excitation model by Dau [33], which has a strong focus on correct modeling of temporal masking behavior. The model comprises the following processing steps:
- The audio signal is mapped to the cochlea domain by a fourth order gamma-tone filterbank, which produces 42 bandpass filter outputs that are equally spaced on the ERB scale.
- The behavior of the inner hair cells is modeled by half-wave rectification and subsequent low-pass processing of the filter outputs. This can be seen as a demodulation process of each of the individual bandpass signals.
- As a next step, the temporal adaptation of the auditory system (that accounts for phenomena like post masking) is represented by a set of adaptation loops.
- A modulation filterbank then spectrally analyzes, for each bandpass output, the signal’s temporal amplitude modulation for modulation center frequencies between 0 and 243 Hz.
- Finally, some internal noise is added to represent the threshold of sensitivity for detection of changes to the signal, as they can occur due to various processing or coding options.
This processing derives a so-called Internal Representation (IR) of an audio signal that can be calculated for both an original (reference) signal and the encoded or decoded (processed) signal. The accumulated squared difference of the IRs between original and processed signal forms a metric for the audibility of the differences between both signals. Further relevant perceptual effects are considered by appropriate weighting of the difference of the two internal representations:
- In order to account for the phenomenon of Comodulation Masking Release (CMR) [80,81], the degree of comodulate-ion between the analyzed band and its surrounding bands is estimated and the IR difference is scaled up correspondingly. CMR describes the phenomenon that thresholds for masking at one frequency band can drop dramatically due to the presence of other (adjacent or non-adjacent) frequency bands that have the same temporal modulation pattern. This effect may play a significant role in the perception of speech signals. An earlier model for consideration of CMR in audio coding was proposed in a previous study [82].
- The internal representations are smoothed over a period of approximately 100 ms to put more emphasis on the modulation characteristics of the signals rather than specific temporal details.
- Following the hypothesis that added sound components are usually perceived as more noticeable than missing components, the difference is scaled as a function of its sign, i.e., compared to the original IR, positive differences (increase in IR) are weighted more heavily than negative ones (decrease in IR).
Compared to previous models used for audio coding, the model includes a number of advanced aspects, such as using internal representations rather than difference or noise signals (which has become a common concept in perceptual measurement before), modulation perception (which implies observation of the signal over extended periods of time), CMR, and asymmetry of perception, as it is motivated by auditory scene analysis [83]. In a previous publication [11], this elaborated psychoacoustic model was used to control parameters for an advanced tool within MPEG-H 3DAudio for enhanced noise filling (“IGF”) that includes bandwidth extension functionality. To this end, the model estimates the perceived degradation caused by the bandwidth extension process for different settings of its control parameters and then selects the encoding option that leads to a minimum of predicted perceptual distortion. Also, conditions for a timely change of parameters are taken into account, ensuring signal continuity where perceptually beneficial.
Listening tests demonstrate an average increase in subjective quality of 5 points on the 100-point MUSHRA test scale, thus confirming the benefit of the model, even in a difficult scenario (i.e., non-waveform-preserving processing) where traditional models based on difference signals would have failed.
The authors hope that similar advances are possible in the near future for enhanced models for coding of spatial (e.g., 3D) audio content.
6. Summary and Conclusions
The art of perceptual audio coding allows substantial bitrate savings in the representation of high quality audio material. A major part of the bitrate reduction can be attributed to the elaborated exploitation of psychoacoustic effects and appropriate signal processing methods, including:
- noise shaping of the quantization error in frequency and time dimension to achieve best possible masking of the error signal, and thus optimal subjective quality;
- controlling the use of optional coding tools for improved codec performance.
Within an audio codec, the psychoacoustic model is of central importance in implementing these functions. This article provides a tutorial overview of common psychoacoustic models for use in perceptual audio coding. The core functionality of a basic psychoacoustic model consists of a masking threshold calculation, including aspects such as the non-uniform layout of the frequency perceptual scale, masking within and between frequency bands, the impact of tonality on masking, and masking over time. In addition to modeling these effects, practical models often have to adapt the masking model output to the rest of the codec architecture, such that the overall system achieves optimum coding performance (i.e., highest possible subjective quality at a given bitrate) at moderate computational complexity.
Beyond simple monophonic masking, spatial masking and BMLD-related effects are typically considered in psychoacoustic models for coding of stereo, surround, or 3D signals.
Over time, optimized psychoacoustic models have been developed that are not meant to operate as stand-alone modules but are tightly integrated into the codec structure to provide excellent system quality with very high computational efficiency.
Beyond calculation of masking effects, the proper control of coding tools also frequently requires a perceptual model. This includes tools for joint stereo processing, tools for parametric coding options (bandwidth extension and parametric multi-channel or 3D coding), and may include on/off switching decisions, as well as the choice of optimal coding parameters.
Historically, there have been numerous advancements over the years in both audio coding and its perceptual models. With the availability of more computational resources, next generations of perceptual models have been evolving, including novel aspects such as modulation perception, and are on their way to proving their usefulness.
Future generations of perceptual models may face new challenges in the context of compressed audio for virtual reality (VR) applications with 6 Degrees of Freedom (6DoF) [84,85], where beyond spatial audio, also visual representation and user movement become very relevant and need to be understood and integrated as part of a multi-modal experience. The authors look forward to the further evolution in the understanding of the relevant perceptual aspects of audio coding, rendering, and processing in such highly immersive and holistic perceptual scenarios.
Author Contributions
Conceptualization, J.H. and S.D.; methodology, J.H. and S.D.; software, S.D.; validation, J.H. and S.D.; formal analysis, J.H. and S.D.; investigation, J.H. and S.D.; resources, J.H.; data curation, S.D.; writing—original draft preparation, J.H. and S.D.; writing—review and editing, J.H. and S.D.; visualization, J.H. and S.D.; supervision, J.H.; project administration, J.H.; funding acquisition, J.H.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| 3D | Three Dimensional |
| 3GPP | 3rd Generation Partnership Project |
| 6DoF | Six Degrees of Freedom |
| AAC | Advanced Audio Coding |
| BCC | Binaural Cue Coding |
| BMLD | Binaural Masking Level Difference |
| CD | Compact Disc |
| CMR | Comodulation Masking Release |
| DFT | Discrete Fourier Transform |
| ERB | Equivalent Rectangular Bandwidth |
| HAS | Human Auditory System |
| HF | High Frequency |
| ICC | Interaural/Inter-channel Cross-Correlation |
| IGF | Intelligent gap filling |
| IID | Inter-Channel Intensity Difference |
| ILD | Inter-aural/Inter-channel Level Differences |
| IOC | Inter-Object Correlation |
| IOLD | Inter-Object Level Difference |
| IPD | Interaural/Inter-channel Phase Differences |
| IR | Internal Representation |
| ITD | Inter-aural/Inter-channel Time Differences |
| L/R | Left/Right |
| LEV | Listener Envelopment |
| LF | Low Frequency |
| M/S | Mid/Side |
| MCT | Multichannel Coding Tool |
| MPEG | Moving Picture Experts Group |
| MUSHRA | Multiple Stimulus with Hidden Reference and Anchor |
| OPD | Overall Phase Difference |
| PE | Perceptual Entropy |
| PNS | Perceptual Noise Substitution |
| PS | Parametric Stereo |
| (p)QMF | (pseudo) Quadrature Mirror Filter |
| QCE | Quad-Channel-Element |
| RMS | Root Mean Square |
| SAOC | Spatial Audio Object Coding |
| SBR | Spectral Band Replication |
| SMR | Signal-to-Mask Ratio |
| SNR | Signal-to-Noise Ratio |
| SPL | Sound Pressure Level |
| TNS | Temporal Noise Shaping |
| USAC | Unified Speech and Audio Coding |
| VR | Virtual Reality |
References
- ISO/IEC. Information Technology—Generic Coding of Moving Pictures and Associated Audio Information—Part 3: Audio; International Standard 13818-3; ISO/IEC: Geneva, Switzerland, 1998. [Google Scholar]
- ISO/IEC. Information Technology—Generic Coding of Moving Pictures and Associated Audio Information—Part 7: Advanced Audio Coding (AAC); International Standard 13818-7; ISO/IEC: Geneva, Switzerland, 1997. [Google Scholar]
- Herre, J.; Dietz, M. Standards in a Nutshell: MPEG-4 High-Efficiency AAC. IEEE Signal Process. Mag. 2008, 25, 137–142. [Google Scholar] [CrossRef]
- Neuendorf, M.; Multrus, M.; Rettelbach, N.; Fuchs, G.; Robilliard, J.; Lecomte, J.; Wilde, S.; Bayer, S.; Disch, S.; Helmrich, C.; et al. The ISO/MPEG Unified Speech and Audio Coding Standard—Consistent High Quality for all Content Types and at all Bit Rates. J. Audio Eng. Soc. 2013, 61, 956–977. [Google Scholar]
- 3GPP. TS 26.441 (V15.0.0): Codec for Enhanced Voice Services (EVS); 3GPP: Sophia Antipolis Cedex, France, 2018. [Google Scholar]
- Geiger, R.; Yu, R.; Herre, J.; Rahardja, S.; Kim, S.-W.; Lin, X.; Schmidt, M. ISO/IEC MPEG-4 High-Definition Scalable Advanced Audio Coding. J. Audio Eng. Soc. 2007, 55, 27–43. [Google Scholar]
- Sayood, K. Introduction to Data Compression; Morgan Kaufmann: Burlington, MA, USA, 2017. [Google Scholar]
- International Telecommunication Union, Radiocommunication Sector. Recommendation ITU-R BS.1116-3: Methods for the Subjective Assessment of Small Impairments in Audio Systems; International Telecommunication Union: Geneva, Switzerland, 2015. [Google Scholar]
- International Telecommunication Union, Radiocommunication Sector. Recommendation ITU-R BS.1534-3: Method for the Subjective Assessment of Intermediate Quality Level of Audio Systems; International Telecommunication Union: Geneva, Switzerland, 2015. [Google Scholar]
- Erne, M. Perceptual Audio Coders “What to listen for”. In Proceedings of the Audio Engineering Society 111th Convention, New York, NY, USA, 30 November–3 December 2001; Audio Engineering Society: New York, NY, USA, 2001. [Google Scholar]
- Disch, S.; Par, S.; Niedermeier, A.; Pérez, E.B.; Ceberio, A.B.; Edler, B. Improved Psychoacoustic Model for Efficient Perceptual Audio Codecs. In Proceedings of the Audio Engineering Society145th Convention, New York, NY, USA, 17–20 October 2018; Audio Engineering Society: New York, NY, USA, 2018. [Google Scholar]
- Bosi, M.; Goldberg, R.E. Introduction to Digial Audio Coding and Standards, 2nd ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003. [Google Scholar]
- Brandenburg, K. MP3 and AAC Explained. In Proceedings of the Audio Engineering Society Conference: 17th International Conference: High-Quality Audio Coding, Villa Castelletti, Signa, Italy, 2–5 September 1999. [Google Scholar]
- Dueñas, A.; Perez, R.; Rivas, B.; Alexandre, E.; Pena, A. A robust and efficient implementation of MPEG-2/4 AAC Natural Audio Coders. In Proceedings of the Audio Engineering Society 112th Convention, München, Germany, 10–13 May 2002; Audio Engineering Society: New York, NY, USA, 2002. [Google Scholar]
- Herre, J.; Disch, S. Chapter 28—Perceptual Audio Coding. In Academic Press Library in Signal Processing; Elsevier: Amsterdam, The Netherlands, 2014; Volume 4, pp. 757–800. [Google Scholar]
- ISO/IEC. Information technology – Coding of moving pictures and associated audio for digital storage media at up to about 1,5 Mbit/s—Part 3: Audio; International Standard ISO/IEC 11172-3; ISO/IEC: Geneva, Switzerland, 1993. [Google Scholar]
- ISO/IEC. Information Technology—Coding of Audio-Visual Objects—Part 3: Audio; International Standard 14496-3; ISO/IEC: Geneva, Switzerland, 2009. [Google Scholar]
- ISO/IEC. Information Technology—MPEG Audio Technologies—Part 3: Unified Speech and Audio Coding; International Standard 23003-3; ISO/IEC: Geneva, Switzerland, 2012. [Google Scholar]
- ISO/IEC. Information Technology—High Efficiency Coding and Media Delivery in Heterogeneous Environments—Part 3: 3D Audio; International Standard 23008-3; ISO/IEC: Geneva, Switzerland, 2015. [Google Scholar]
- ATSC. A/52:2018: Digital Audio Compression (AC-3) (E-AC-3) Standard; ATSC: Washington, DC, USA, 2018. [Google Scholar]
- ETSI. TS 103 190 V1.1.1: Digital Audio Compression (AC-4) Standard; ETSI: Sophia Antipolis, France, 2014. [Google Scholar]
- IETF. RFC 5215: RTP Payload Format for Vorbis Encoded Audio; IETF: Fremont, CA, USA, 2008. [Google Scholar]
- IETF. RFC 6716: Definition of the Opus Audio Codec; IETF: Fremont, CA, USA, 2012. [Google Scholar]
- Moore, B.C.J. An Introduction to the Psychology of Hearing, 5th ed.; Academic Press: San, Diego, CA, USA, 2003. [Google Scholar]
- Fastl, H.; Zwicker, E. Psychoacoustics: Facts and Models, 3rd ed.; Springer: Heidelberg/Berlin, Germany, 2007. [Google Scholar]
- Zwicker, E.; Terhardt, E. Analytical expressions for critical-band rate and critical bandwidth as a function of frequency. J. Acoust. Soc. Am. 1980, 68, 1523–1525. [Google Scholar] [CrossRef]
- Moore, B.; Glasberg, B. A Revision of Zwicker’s Loudness Model. Acta Acust. 1996, 82, 335–345. [Google Scholar]
- Moore, B.C.J.; Glasberg, B.R. Suggested formulae for calculating auditory-filter bandwidths and excitation. J. Acoust. Soc. Am. 1983, 74, 750–753. [Google Scholar] [CrossRef] [PubMed]
- Hellman, R.P. Asymmetry of Masking between Noise and Tone. Percept. Psychophys. 1972, 11, 241–246. [Google Scholar] [CrossRef]
- Brandenburg, K.; Stoll, G. ISO/MPEG-1 Audio: A Generic Standard for Coding of High-Quality Digital Audio. J. Audio Eng. Soc. 1994, 42, 780–792. [Google Scholar]
- Bosi, M.; Brandenburg, K.; Quackenbush, S.; Fielder, L.; Akagiri, K.; Fuchs, H.; Dietz, M.; Herre, J.; Davidson, G.; Oikawa, Y. ISO/IEC MPEG-2 Advanced Audio Coding. J. AES 1997, 45, 789–814. [Google Scholar]
- Herre, J.; Johnston, J.D. Enhancing the Performance of Perceptual Audio Coders by Using Temporal Noise Shaping (TNS). In Audio Engineering Society 101st Convention; Audio Engineering Society: New York, NY, USA, 1996. [Google Scholar]
- Dau, T.; Kollmeier, B.; Kohlrausch, A. Modeling auditory processing of amplitude modulation. I. Detection and masking with narrow-band carriers. J. Acoust. Soc. Am. 1997, 102, 2892–2905. [Google Scholar] [CrossRef]
- Jayant, N.; Noll, P. Digital Coding of Waveforms—Principles and Applications to Speech and Video; Prentice-Hall: Englwood Cliffs, NJ, USA, 1984. [Google Scholar]
- Johnston, J.D. Estimation of perceptual entropy using noise masking criteria. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), New York, NY, USA, 11–14 April 1988. [Google Scholar]
- Edler, B. Codierung von audiosignalen mit überlappender transformation und adaptiven fensterfunktionen (Coding of Audio Signals with Overlapping Block Transform and Adaptive Window Functions). Frequenz 1989, 43, 252–256. [Google Scholar] [CrossRef]
- Bosi, M. Filter Banks in Perceptual Audio Coding. In Proceedings of the AES 17th International Conference: High-Quality Audio Coding, Audio Engineering Society, New York, NY, USA, September 1999. [Google Scholar]
- Herre, J. Temporal Noise Shaping, Quantization and Coding Methods in Perceptual Audio Coding—A Tutorial Introduction. In Proceedings of the 17th International AES Conference on High Quality Audio Coding, Audio Engineering Society, New York, NY, USA, September 1999. [Google Scholar]
- 3GPP TS 26.403 V10.0.0 General Audio Codec Audio Processing Functions; Enhanced aacPlus General Audio Codec; Encoder Specification; Advanced Audio Coding (AAC) Part; 3GPP: Sophia Antipolis Cedex, France, 2011.
- Princen, J.; Johnson, A.; Bradley, A. Subband/Transform coding using filter bank designs based on time domain aliasing cancellation. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Dallas, TX, USA, 6–9 April 1987. [Google Scholar]
- Blauert, J. Spatial Hearing: The Psychophysics of Human Sound Localization; MIT Press: Cambridge, MA, USA, 1997. [Google Scholar]
- Bronkhorst, A.W. The cocktail party phenomenon: A review of research on speech intelligibility in multiple-talker conditions. Acta Acust. United Acust. 2000, 86, 117–128. [Google Scholar]
- Gelfand, S.A. Hearing: An Introduction to Psychological and Physiological Acoustics; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Herre, J.; Eberlein, E.; Brandenburg, K. Combined Stereo Coding. In Audio Engineering Society 93rd Convention; Audio Engineering Society: New York, NY, USA, 1992. [Google Scholar]
- Johnston, J.D. Perceptual Transform Coding of Wideband Stereo Signals. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Glasgow, UK, 23–26 May 1989. [Google Scholar]
- Johnston, J.; Ferreira, A. Sum-difference stereo transform coding. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), San Francisco, CA, USA, 23–26 March 1992. [Google Scholar]
- Helmrich, C.R.; Carlsson, P.; Disch, S.; Edler, B.; Hilpert, J.; Kjörling, K.; Neusinger, M.; Purnhagen, H.; Rettelbach, N.; Robilliard, J.; et al. Efficient Transform Coding of Two-Channel Audio Signals by Means of Complex-Valued Stereo Prediction. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- ITU-R. BS.775-3: Multichannel Stereophonic Sound System with and Without Accompanying Picture; ITU-R: Geneva, Switzerland, 2012. [Google Scholar]
- ITU-R. BS.2159-4: Multichannel Sound Technology in Home; ITU-R: Geneva, Switzerland, 2012. [Google Scholar]
- Hamasaki, K.; Hiyama, K.; Okumura, R. The 22.2 Multichannel Sound System and Its Application. In Audio Engineering Society 118th Convention; Audio Engineering Society: New York, NY, USA, 2005. [Google Scholar]
- Blauert, J. Sound localization in the median plane. Acta Acust. United Acust. 1969, 22, 205–213. [Google Scholar]
- Herre, J.; Hilpert, J.; Kuntz, A.; Plogsties, J. MPEG-H 3D audio—The new standard for coding of immersive spatial audio. IEEE J. Sele. Top. Signal Process. 2015, 9, 770–779. [Google Scholar] [CrossRef]
- Schuh, F.; Dick, S.; Füg, R.; Helmrich, C.R.; Rettelbach, N.; Schwegler, T. Efficient Multichannel Audio Transform Coding with Low Delay and Complexity. In Audio Engineering Society 141st Convention; Audio Engineering Society: New York, NY, USA, 2016. [Google Scholar]
- ISO/IEC JTC 1/SC 29/WG 11. N7137—Listening Test Report on MPEG-4 High Efficiency AAC v2; ISO/IEC: Geneva, Switzerland, 2005. [Google Scholar]
- Herre, J.; Schultz, D. Extending the MPEG-4 AAC Codec by Perceptual Noise Substitution. In Audio Engineering Society 104th Convention; Audio Engineering Society: New York, NY, USA, 1998. [Google Scholar]
- Dietz, M.; Liljeryd, L.; Kjorling, K.; Kunz, O. Spectral Band Replication, a Novel Approach in Audio Coding. In Audio Engineering Society 112th Convention; Audio Engineering Society: New York, NY, USA, 2002. [Google Scholar]
- Den Brinker, A.C.; Breebaart, J.; Ekstrand, P.; Engdegård, J.; Henn, F.; Kjörling, K.; Oomen, W.; Purnhagen, H. An overview of the coding standard MPEG-4 audio amendments 1 and 2: HE-AAC, SSC, and HE-AAC v2. EURASIP J. Audio Speech Music Process. 2009, 2009, 3. [Google Scholar] [CrossRef][Green Version]
- Nagel, F.; Disch, S. A harmonic bandwidth extension method for audio codecs. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009. [Google Scholar]
- Disch, S.; Niedermeier, A.; Helmrich, C.R.; Neukam, C.; Schmidt, K.; Geiger, R.; Lecomte, J.; Ghido, F.; Nagel, F.; Edler, B. Intelligent Gap Filling in Perceptual Transform Coding of Audio. In Audio Engineering Society 141st Convention; Audio Engineering Society: New York, NY, USA, 2016. [Google Scholar]
- Herre, J.; Brandenburg, K.; Lederer, D. Intensity Stereo Coding. In Audio Engineering Society 96th Convention; Audio Engineering Society: New York, NY, USA, 1994. [Google Scholar]
- Johnston, J.D.; Herre, J.; Davis, M.; Gbur, U. MPEG-2 NBC Audio-Stereo and Multichannel Coding Methods. In Audio Engineering Society 101st Convention; Audio Engineering Society: New York, NY, USA, 1996. [Google Scholar]
- Todd, C.C.; Davidson, G.A.; Davis, M.F.; Fielder, L.D.; Link, B.D.; Vernon, S. AC-3: Flexible perceptual coding for audio transmission and storage. In Audio Engineering Society 96th Convention; Audio Engineering Society: New York, NY, USA, 1994. [Google Scholar]
- Silzle, A.; Stoll, G.; Theile, G.; Link, M. Method of Transmitting or Storing Digitalized, Multi-Channel Audio Signals. U.S. Patent US5,682,461, 28 October 1997. [Google Scholar]
- Breebaart, J.; Par, S.V.D.; Kohlrausch, A.; Schuijers, E. Parametric Coding of Stereo Audio. EURASIP J. Adv. Signal Process. 2005, 9, 561917. [Google Scholar] [CrossRef]
- Purnhagen, H.; Engdegard, J.; Roden, J.; Liljeryd, L. Synthetic Ambience in Parametric Stereo Coding. In Audio Engineering Society 116th Convention; Audio Engineering Society: New York, NY, USA, 2004. [Google Scholar]
- Baumgarte, F.; Faller, C. Binaural cue coding-Part I: Psychoacoustic fundamentals and design principles. IEEE Trans. Speech Audio Process. 2003, 11, 509–519. [Google Scholar] [CrossRef]
- Faller, C.; Baumgarte, F. Binaural cue coding-Part II: Schemes and applications. IEEE Trans. Speech Audio Process. 2003, 11, 520–531. [Google Scholar] [CrossRef]
- Herre, J.; Kjörling, K.; Breebaart, J.; Faller, C.; Disch, S.; Purnhagen, H.; Koppens, J.; Hilpert, J.; Rödén, J.; Oomen, W.; et al. MPEG Surround—The ISO/MPEG Standard for Efficient and Compatible Multichannel Audio Coding. J. Audio Eng. Soc. 2008, 56, 932–955. [Google Scholar]
- Breebaart, J.; Faller, C. Spatial Audio Processing: MPEG Surround and Other Applications; John Wiley and Sons Ltd.: Chichester, UK, 2007. [Google Scholar]
- ISO/IEC. Information Technology—MPEG Audio Technologies—Part 1: MPEG Surround; International Standard 23003-1; ISO/IEC: Geneva, Switzerland, 2007. [Google Scholar]
- Faller, C.; Baumgarte, F. Efficient representation of spatial audio using perceptual parametrization. In Proceedings of the 2001 IEEE Workshop on the Applications of Signal Processing to Audio and Acoustics (Cat. No. 01TH8575), New Platz, NY, USA, 24 October 2001. [Google Scholar]
- Herre, J.; Purnhagen, H.; Koppens, J.; Hellmuth, O.; Engdegård, J.; Hilper, J.; Villemoes, L.; Terentiv, L.; Falch, C.; Hölzer, A.; et al. MPEG Spatial Audio Object Coding—The ISO/MPEG Standard for Efficient Coding of Interactive Audio Scenes. J. Audio Eng. Soc. 2012, 60, 655–673. [Google Scholar]
- Helmrich, C.R.; Niedermeier, A.; Bayer, S.; Edler, B. Low-complexity semi-parametric joint-stereo audio transform coding. In Proceedings of the 23rd European Signal Processing Conference (EUSIPCO), Nice, France, 31 August–4 Septmber 2015. [Google Scholar]
- ITU-R. Recommendation BS.1770: Algorithms to Measure Audio Programme Loudness and True-Peak Audio Level; ITU-R: Geneva, Switzerland, 2015. [Google Scholar]
- DIN. DIN 45692: Measurement Technique for the Simulation of the Auditory Sensation of Sharpness; DIN: Berlin, Germany, 2009. [Google Scholar]
- George, S.; Zielinski, S.; Rumsey, F.; Jackson, P.; Conetta, R.; Dewhirst, M.; Meares, D.; Bech, S. Development and Validation of an Unintrusive Model for Predicting the Sensation of Envelopment Arising from Surround Sound Recordings. J. Audio Eng. Soc. 2011, 58, 1013–1031. [Google Scholar]
- Dau, T. Modeling Auditory Processing of Amplitude Modulation; BIS Verlag: Oldenburg, Germany, 1999. [Google Scholar]
- ITU-T. Recommendation P.862 PESQ (Perceptual Evaluation of Speech Quality); ITU-T: Geneva, Switzerland, 2001. [Google Scholar]
- ITU-T. Recommendation P.863—POLQA (Perceptual Objective Listening Quality Prediction); ITU-T: Geneva, Switzerland, 2018. [Google Scholar]
- Verhey, J.L.; Pressnitzer, D.; Winter, I.M. The psychophysics and physiology of comodulation masking release. Exp. Brain Res. 2003, 153, 405–417. [Google Scholar] [CrossRef] [PubMed]
- Hall, J.W.; Grose, J.H. Comodulation masking release and auditory grouping. J. Acoust. Soc. Am. 1990, 88, 119–125. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, A.J.S.; Sinha, D. A New Broadcast Quality Low Bit Rate Audio Coding Scheme Utilizing Novel Bandwidth Extension Tools. In Audio Engineering Society 119th Convention; Audio Engineering Society: New York, NY, USA, 2005. [Google Scholar]
- Bregman, A.S. Auditory Scene Analysis: The Perceptual Organization of Sound; MIT Press: Cambridge, MA, USA, 1994. [Google Scholar]
- Rumsey, F. Virtual Reality, Will It Be a Game-Changer. J. Audio Eng. Soc. 2018, 66, 399–402. [Google Scholar]
- Domański, M.; Stankiewicz, O.; Wegner, K.; Grajek, T. Immersive visual media—MPEG-I: 360 video, virtual navigation and beyond. In Proceedings of the IEEE International Conference on Systems, Signals and Image Processing (IWSSIP), Poznan, Poland, 22–24 May 2017. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).