Heuristic Approaches to Attribute Reduction for Generalized Decision Preservation
Abstract
:1. Introduction
2. Preliminaries
2.1. Rough Approximations in a Decision System
2.2. Discernibility Matrix-Based Attribute Reduction for Generalized Decision Preservation
- (1)
- ;
- (2)
- .
| Algorithm 1 A discernibility matrix-based reduction algorithm for generalized decision preservation (DMRAG) |
|
3. Heuristic Attribute Reduction for Generalized Decision Preservation
3.1. The Similarity Degree for Generalized Decision Preservation
- (1)
- ;
- (2)
- , .
- (1)
- ;
- (2)
- , .
- (1)
- If Q is a reduct for generalized decision preservation in , then Q can leave the positive region unchanged in a ; and
- (2)
- if Q is a reduct for distribution preservation in , then Q can leave the generalized decision unchanged in a .
- (1)
- As Q is a reduct for generalized decision preservation, we have for any . Then, for , it is clear that , . Therefore, , i.e., . Then, we have holds, i.e., . Therefore, Q can keep the positive region unchanged in a .
- (2)
- For , , if , then we have . Therefore, we can easily obtain . As Q is a reduct for distribution preservation in , we have . Then, . Therefore, . Then, . According to the hypothesis , we have . From Theorem 1, we can find . Then, holds. Therefore, Q can keep the generalized decision unchanged in a .
3.2. Heuristic Attribute Reduction Algorithms for Generalized Decision Preservation
| Algorithm 2 A forward greedy reduction algorithm for generalized decision preservation (FGRAG) |
|
| Algorithm 3 A backward greedy reduction algorithm for generalized decision preservation (BGRAG) |
|
4. Experimental Analyses
4.1. Monotonicity of the Similarity Degree for Generalized Decision Preservation
4.2. Correctness of Proposed Attribute Reduction Algorithms
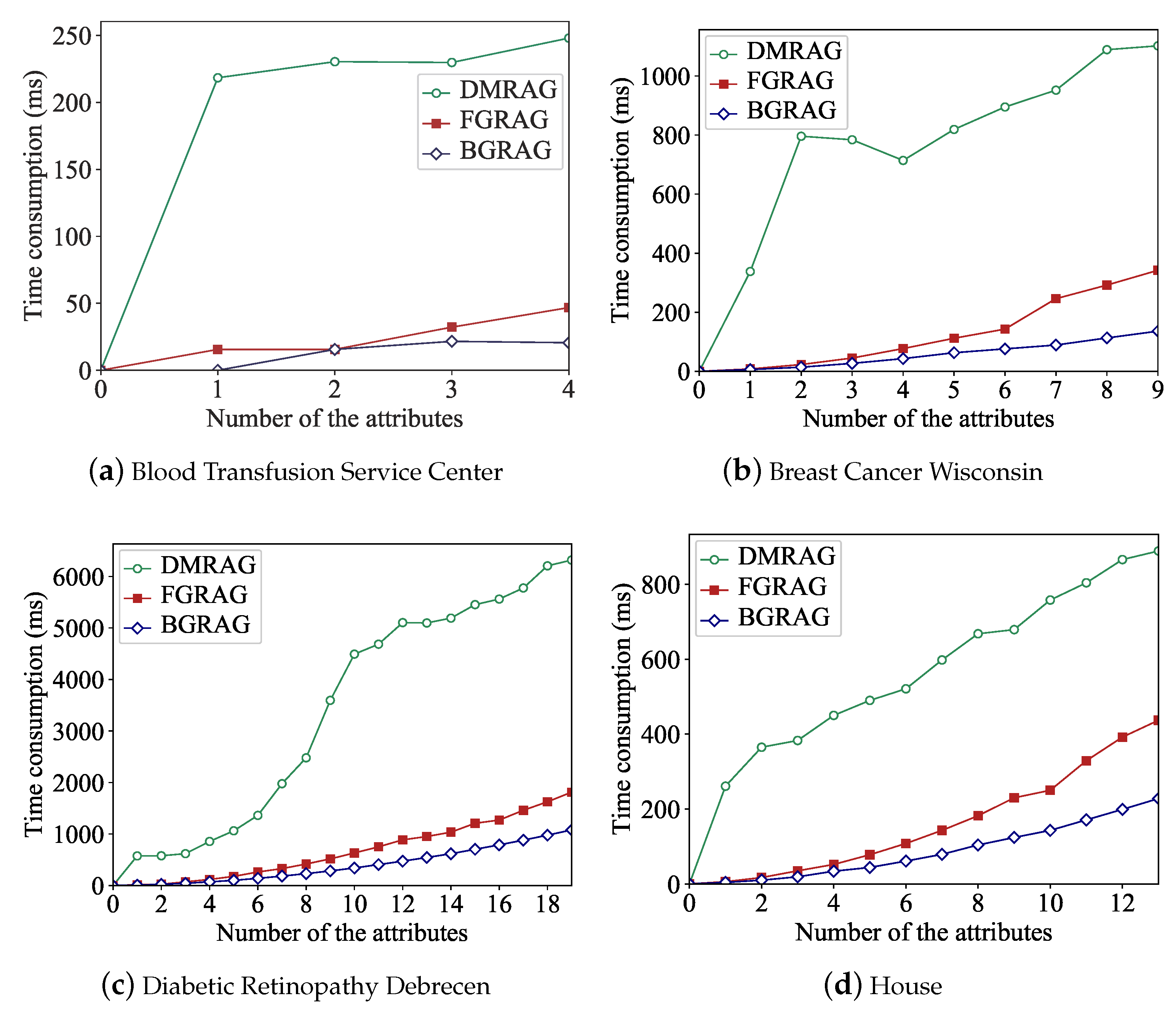
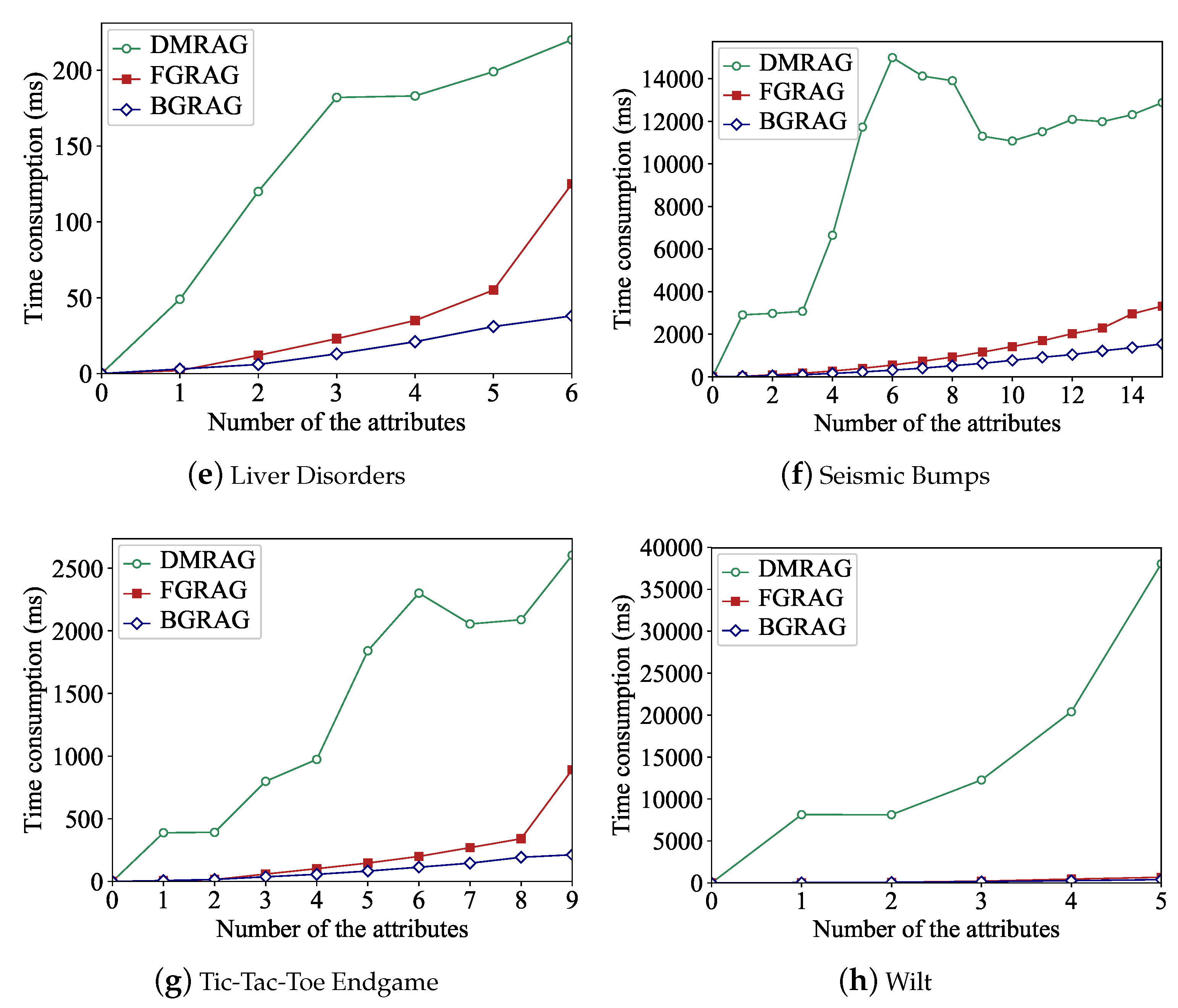
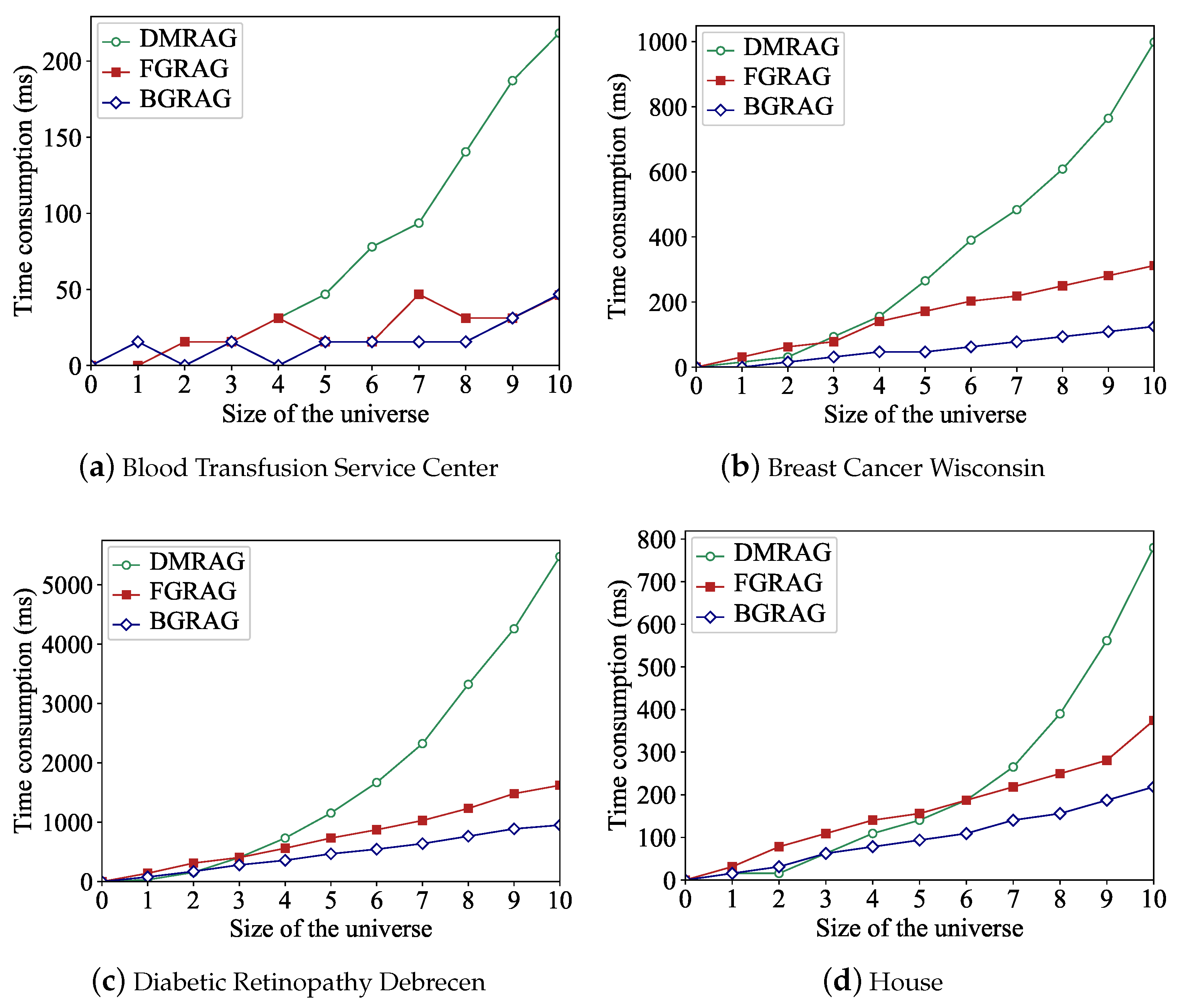
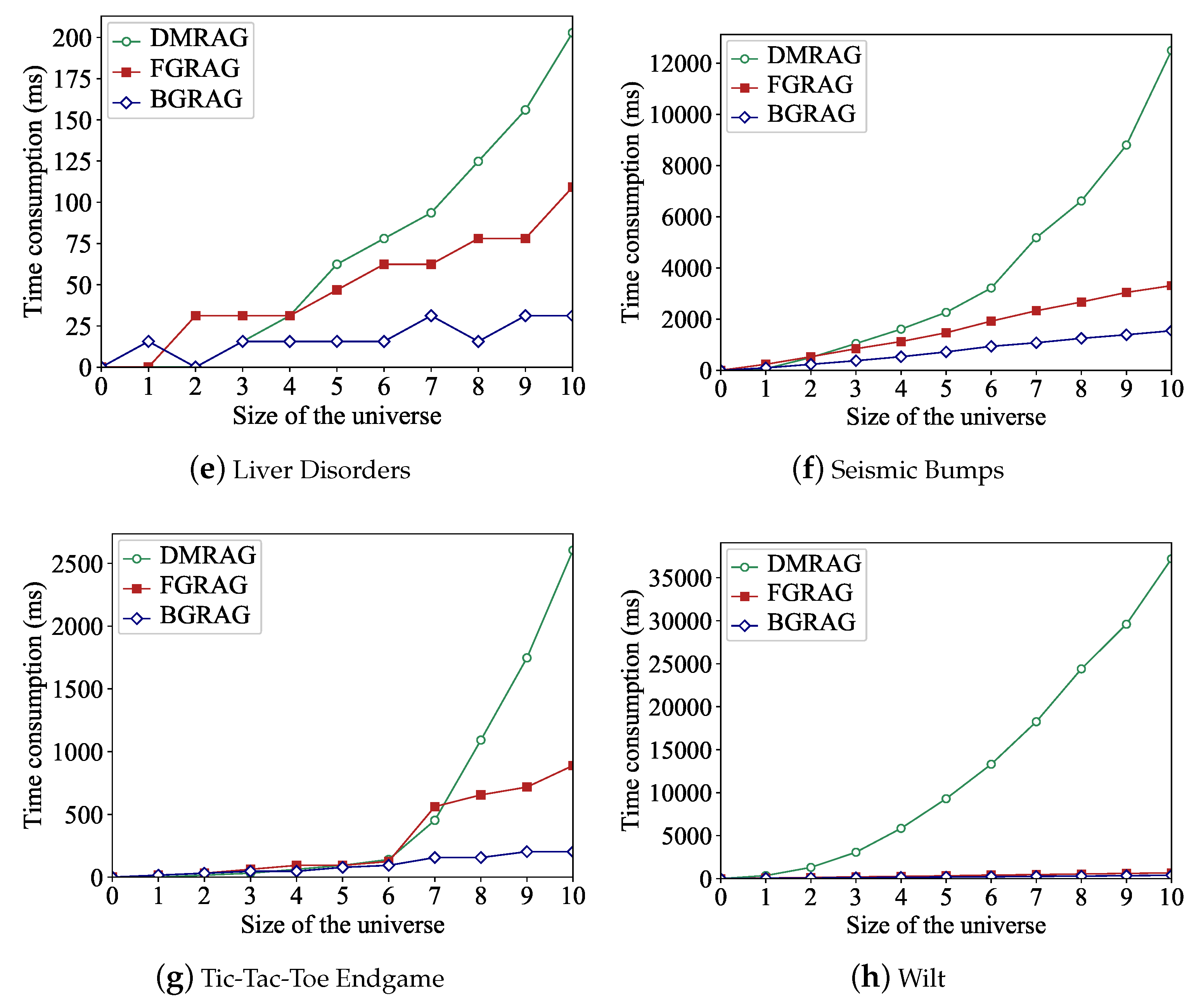
4.3. Efficiency of Proposed Attribute Reduction Algorithms
5. Conclusions and Future Researches
Author Contributions
Funding
Conflicts of Interest
References
- Pawlak, Z. Rough sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Yao, Y.Y. Three-way decisions and cognitive computing. Cogn. Comput. 2016, 8, 543–554. [Google Scholar] [CrossRef]
- Yao, Y.Y.; Zhou, B. Two Bayesian approaches to rough sets. Eur. J. Oper. Res. 2016, 251, 904–917. [Google Scholar] [CrossRef]
- Qian, Y.H.; Liang, J.Y.; Yao, Y.Y.; Dang, C.Y. MGRS: A multi-granulation rough set. Inf. Sci. 2010, 180, 949–970. [Google Scholar] [CrossRef]
- Zhang, N.; Li, B.Z.; Zhang, Z.X.; Guo, Y.Y. A quick algorithm for binary discernibility matrix simplification using deterministic finite automata. Information 2018, 9, 314. [Google Scholar] [CrossRef]
- Wang, C.Z.; Qi, Y.L.; Shao, M.W.; Hu, Q.H.; Chen, D.G.; Qian, Y.H.; Lin, Y.J. A fitting model for feature selection with fuzzy rough sets. IEEE Trans. Fuzzy Syst. 2017, 25, 741–752. [Google Scholar] [CrossRef]
- Lin, Y.J.; Hu, Q.H.; Liu, J.H.; Chen, J.K.; Duan, J. Multi-label feature selection based on neighborhood mutual information. Appl. Soft Comput. 2016, 38, 244–256. [Google Scholar] [CrossRef]
- Skowron, A.; Rauszer, C. The discernibility matrices and functions in information systems. In Intelligent Decision Support: Handbook of Applications and Advances of the Rough Sets Theory; Słowiński, R., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1992; pp. 331–362. [Google Scholar]
- Chebrolu, S.; Sanjeevi, S.G. Forward tentative selection with backward propagation of selection decision algorithm for attribute reduction in rough set theory. Int. J. -Reason.-Based Intell. Syst. 2015, 7, 221–243. [Google Scholar] [CrossRef]
- Zhang, X.; Mei, C.L.; Chen, D.G.; Li, J.H. Feature selection in mixed data: a method using a novel fuzzy rough set-based information entropy. Pattern Recognit. 2016, 56, 1–15. [Google Scholar] [CrossRef]
- Hu, X.H.; Cercone, N. Learning in relational databases: a rough set approach. Int. J. Comput. Intell. 1995, 11, 323–338. [Google Scholar] [CrossRef]
- Miao, D.Q.; Zhao, Y.; Yao, Y.Y.; Li, H.; Xu, F. Relative reducts in consistent and inconsistent decision tables of the Pawlak rough set model. Inf. Sci. 2009, 179, 4140–4150. [Google Scholar] [CrossRef]
- Kryszkiewicz, M. Rough set approach to incomplete information systems. Inf. Sci. 1998, 112, 39–49. [Google Scholar] [CrossRef]
- Miao, D.Q.; Hu, G.R. A heuristic algorithm for reduction of knowledge. J. Comput. Res. Dev. 1999, 36, 681–684. [Google Scholar]
- Zhang, W.X.; Mi, J.S. Knowledge reductions in inconsistent information systems. Chin. J. Comput. 2003, 261, 12–18. [Google Scholar]
- Guan, Y.Y.; Wang, H.K.; Wang, Y.; Yang, F. Attribute reduction and optimal decision rules acquisition for continuous valued information systems. Inf. Sci. 2009, 179, 2974–2984. [Google Scholar] [CrossRef]
- Xu, W.H.; Li, Y.; Liao, X.W. Approaches to attribute reductions based on rough set and matrix computation in consistent order information systems. Knowl.-Based Syst. 2012, 27, 78–91. [Google Scholar] [CrossRef]
- Yang, X.B.; Qi, Y.; Yu, D.J.; Yu, H.L.; Yang, J.Y. α-Dominance relation and rough sets in interval-valued information systems. Inf. Sci. 2015, 294, 334–347. [Google Scholar] [CrossRef]
- Du, W.S.; Hu, B.Q. Dominance-based rough fuzzy set approach and its application to rule induction. Eur. J. Oper. Res. 2017, 261, 690–703. [Google Scholar] [CrossRef]
- Zhou, J.; Miao, D.Q.; Pedrycz, W.; Zhang, H.Y. Analysis of alternative objective functions for attribute reduction in complete decision tables. Soft Comput. 2011, 15, 1601–1616. [Google Scholar] [CrossRef]
- Li, H.; Li, D.Y.; Zhai, Y.H.; Wang, S.G.; Zhang, J. A novel attribute reduction approach for multi-label data based on rough set theory. Inf. Sci. 2016, 367–368, 827–847. [Google Scholar] [CrossRef]
- Du, W.S.; Hu, B.Q. A fast heuristic attribute reduction approach to ordered decision systems. Eur. J. Oper. Res. 2018, 264, 440–452. [Google Scholar] [CrossRef]
- Wang, F.; Liang, J.Y.; Dang, C.Y. Attribute reduction for dynamic data sets. Appl. Soft Comput. 2013, 13, 676–689. [Google Scholar] [CrossRef]
- Jensen, R. Combining Rough and Fuzzy Sets for Feature Selection. Ph.D. Thesis, University Of Edinburgh, Edinburgh, UK, 2005. [Google Scholar]
- Chebrolu, S.; Sanjeevi, S.G. Attribute reduction on real-valued data in rough set theory using hybrid artificial bee colony: Extended FTSBPSD algorithm. Soft Comput. 2017, 21, 7543–7569. [Google Scholar] [CrossRef]
- Chebrolu, S.; Sanjeevi, S.G. Attribute reduction in decision-theoretic rough set models using genetic algorithm. In Proceedings of the International Conference on Swarm, Evolutionary, and Memetic Computing (LNCS 7076), Visakhapatnam, India, 19–21 December 2011; pp. 307–314. [Google Scholar]
- Chebrolu, S.; Sanjeevi, S.G. Attribute reduction on continuous data in rough set theory using ant colony optimization metaheuristic. In Proceedings of the Third International Symposiumon Women in Computing and Informatics, Kochi, India, 10–13 August 2015; pp. 17–24. [Google Scholar]
- Chebrolu, S.; Sanjeevi, S.G. Attribute reduction in decision-theoretic rough set model using particle swarm optimization with the threshold parameters determined using LMS training rule. Procedia Comput. Sci. 2015, 57, 527–536. [Google Scholar] [CrossRef]
- Chen, Y.M.; Miao, D.Q.; Wang, R.Z. A rough set approach to feature selection based on ant colony optimization. Pattern Recognit. Lett. 2010, 31, 226–233. [Google Scholar] [CrossRef]
- Min, F.; Zhang, Z.H.; Dong, J. Ant colony optimization with partial-complete searching for attribute reduction. J. Comput. Sci. 2018, 25, 170–182. [Google Scholar] [CrossRef]
- Leung, Y.; Li, D.Y. Maximal consistent block technique for rule acquisition in incomplete information systems. Inf. Sci. 2003, 153, 85–106. [Google Scholar] [CrossRef]
- Miao, D.Q.; Zhang, N.; Yue, X.D. Knowledge reduction in interval-valued information systems. In Proceedings of the 8th International Conference on Cognitive Informatics, Hongkong, China, 15–17 June 2009; pp. 320–327. [Google Scholar]
- Liu, G.L.; Hua, Z.; Zou, J.Y. Local attribute reductions for decision tables. Inf. Sci. 2018, 179, 204–217. [Google Scholar] [CrossRef]
- Qian, Y.H.; Liang, J.Y.; Pedrycz, W.; Dang, C.Y. Positive approximation: an accelarator for attribute reduction in rough set thoery. Artifical Intell. 2010, 174, 595–618. [Google Scholar] [CrossRef]
- Dai, J.H.; Hu, H.; Zheng, G.J.; Hu, Q.H.; Han, H.F.; Shi, H. Attribute reduction in interval-valued information systems based on information entropies. Front. Inf. Technol. Electron. Eng. 2016, 17, 919–928. [Google Scholar] [CrossRef]
- Jia, X.Y.; Liao, W.H.; Tang, Z.M.; Shang, L. Minimum cost attribute reduction in decision-theoretic rough set models. Inf. Sci. 2013, 219, 151–167. [Google Scholar] [CrossRef]
- Cheng, Y.; Zheng, Z.R.; Wang, J.; Yang, L.; Wan, S.H. Attribute reduction based on genetic algorithm for the coevolution of meteorological data in the industrial internet of things. Wirel. Commun. Mob. Comput. 2019, 2019, 3525347. [Google Scholar] [CrossRef]
- Li, M.; Shang, C.X.; Feng, S.Z.; Fan, J.P. Quick attribute reduction in inconsistent decision tables. Inf. Sci. 2014, 254, 155–180. [Google Scholar] [CrossRef]
- Wang, C.Z.; Shao, M.W.; Sun, B.Z.; Hu, Q.H. An improved attribute reduction scheme with covering based rough sets. Appl. Soft Comput. 2015, 26, 235–243. [Google Scholar] [CrossRef]
- Wang, G.Y.; Yu, H.; Yang, D.C. Decision table reduction based on conditional information entropy. Chin. J. Comput. 2002, 25, 759–766. [Google Scholar]
- Gao, C.; Lai, Z.H.; Zhou, J.; Zhao, C.R.; Miao, D.Q. Maximum decision entropy-based attribute reduction in decision-theoretic rough set model. Knowl.-Based Syst. 2018, 143, 179–191. [Google Scholar] [CrossRef]

| U | d | ||||
|---|---|---|---|---|---|
| 1 | 1 | 2 | 4 | 2 | |
| 1 | 1 | 2 | 4 | 1 | |
| 1 | 1 | 2 | 4 | 1 | |
| 1 | 1 | 3 | 4 | 1 | |
| 1 | 1 | 3 | 4 | 3 | |
| 2 | 2 | 3 | 4 | 2 | |
| 2 | 2 | 3 | 4 | 1 | |
| 2 | 2 | 3 | 4 | 2 |
| Data Sets | Objects | Attributes | Data Types | Classes | |
|---|---|---|---|---|---|
| 1 | Blood Transfusion Service Center | 748 | 4 | Numerical | 2 |
| 2 | Breast Cancer Wisconsin | 699 | 9 | Numerical | 2 |
| 3 | Diabetic Retinopathy Debrecen | 1151 | 19 | Numerical | 2 |
| 4 | House | 506 | 13 | Numerical | 4 |
| 5 | Liver Disorders | 345 | 6 | Numerical, Nominal | 2 |
| 6 | Seismic Bumps | 2584 | 15 | Numerical, Nominal | 2 |
| 7 | Tic-Tac-Toe Endgame | 958 | 9 | Nominal | 2 |
| 8 | Wilt | 4339 | 5 | Numerical | 2 |
| Data Sets | DMARG | FGARG | BGARG |
|---|---|---|---|
| 1 | {1, 4} | {1, 4} | {1, 4} |
| 2 | { {1, 3, 5, 6}, {1, 3, 6, 8}, {1, 2, 6, 7}, {1, 5, 6, 8}, {1, 4, 6, 7}, {1, 3, 4, 6, 9}, {1, 2, 3, 4, 6}, {1, 2, 4, 6, 9}, {1, 2, 4, 6, 8}, {1, 2, 5, 6, 9}, {2, 3, 4, 6, 7}, {2, 4, 5, 6, 7}, {2, 5, 6, 7, 9}, {2, 5, 6, 7, 8}, {2, 3, 5, 6, 8, 9}, {3, 5, 6, 7}, {3, 4, 6, 8}, {3, 4, 6, 7, 9}, {5, 6, 7, 8, 9}} | {1, 3, 5, 6} | {1, 3, 6, 8} |
| 3 | {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 16, 17, 18, 19} | {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 16, 17, 18, 19} | {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 16, 17, 18, 19} |
| 4 | {1, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13}, {1, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13} | {1, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13} | {1, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13} |
| 5 | {1, 2, 3, 4, 5}, {1, 2, 3, 5, 6}, {1, 2, 4, 5, 6}, {1, 2, 3, 4, 6}, {2, 3, 4, 5, 6} | {1, 2, 3, 4, 5} | {2, 3, 4, 5, 6} |
| 6 | {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14, 15}, {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15}, {1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 14, 15} | {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 14, 15} | {1, 2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 14, 15} |
| 7 | {{1, 2, 3, 4, 5, 6, 7, 9}, {1, 2, 3, 4, 5, 7, 8, 9}, {1, 2, 3, 5, 6, 7, 8, 9}, {1, 2, 3, 4, 5, 6, 8, 9}, {1, 2, 3, 4, 6, 7, 8, 9}, {1, 3, 4, 5, 6, 7, 8, 9}, {1, 2, 4, 5, 6, 7, 8, 9}, {1, 2, 3, 4, 5, 6, 7, 8}, {2, 3, 4, 5, 6, 7, 8, 9} } | {1, 2, 3, 4, 5, 7, 8, 9} | {2, 3, 4, 5, 6, 7, 8, 9} |
| 8 | {1, 2, 3, 4, 5} | {1, 2, 3, 4, 5} | {1, 2, 3, 4, 5} |
| Data Sets | Objects | Attributes | FGARG | BGARG | DMARG | |||
|---|---|---|---|---|---|---|---|---|
| t/ms | t/ms | t/ms | ||||||
| 1 | 748 | 4 | 2 | 46 | 2 | 46 | 2 | 234 |
| 2 | 699 | 9 | 4 | 312 | 4 | 140 | 4.6 | 1029 |
| 3 | 1151 | 19 | 16 | 1687 | 16 | 1029 | 16 | 5678 |
| 4 | 506 | 13 | 11 | 405 | 11 | 202 | 11 | 920 |
| 5 | 345 | 6 | 5 | 109 | 5 | 46 | 5 | 218 |
| 6 | 2584 | 15 | 13 | 3123 | 13 | 1484 | 13 | 11,140 |
| 7 | 958 | 9 | 8 | 795 | 8 | 187 | 8 | 2888 |
| 8 | 4339 | 5 | 5 | 592 | 5 | 353 | 5 | 34,264 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Gao, X.; Yu, T. Heuristic Approaches to Attribute Reduction for Generalized Decision Preservation. Appl. Sci. 2019, 9, 2841. https://doi.org/10.3390/app9142841
Zhang N, Gao X, Yu T. Heuristic Approaches to Attribute Reduction for Generalized Decision Preservation. Applied Sciences. 2019; 9(14):2841. https://doi.org/10.3390/app9142841
Chicago/Turabian StyleZhang, Nan, Xueyi Gao, and Tianyou Yu. 2019. "Heuristic Approaches to Attribute Reduction for Generalized Decision Preservation" Applied Sciences 9, no. 14: 2841. https://doi.org/10.3390/app9142841
APA StyleZhang, N., Gao, X., & Yu, T. (2019). Heuristic Approaches to Attribute Reduction for Generalized Decision Preservation. Applied Sciences, 9(14), 2841. https://doi.org/10.3390/app9142841





