Abstract
Buckling Restrained Bracings (BRBs) are widely used to improve the seismic behavior of buildings. They are employed for bridges as well, but their application in this respect is limited. BRBs can also be used as a function of the individual damper rather than the structural component or the bracing, in which case the device may be called a Buckling Restrained Damper (BRD). Yet, such application has not been explored much. There are quite a few bridges designed according to the old design codes in Japan. Their seismic resistance may not be satisfactory for the current seismic design codes. Against this background, the behavior of a steel truss bridge under a large seismic load was investigated by nonlinear dynamic finite element analysis. Some members were indeed found to be damaged in the earthquake. Retrofitting is needed. To this end, the application of BRD was tried in the present study: a parametric study on the seismic behavior of the truss bridge with BRD was conducted by changing the length, the cross-sectional area, the location and the inclination of BRD. The effectiveness of BRD was then discussed based on the numerical results thus obtained. In all the analyses, ABAQUS was used.
1. Introduction
Earthquakes are the biggest threat to bridge structures, and design codes have been revised after each natural disaster. For example, in Japan, the design specifications for highway bridges was revised several times right after Hyogoken-Nanbu (1995) and Tohoku (2011) incidents which include the capacity loss of bridges [1,2]. Currently, many existing bridges which were designed by old design codes exist. The seismic performance of those bridges needs to be assessed by the new seismic design code criteria. If the seismic performance is not satisfactory, existing bridges should be retrofitted [1]. To that end, many dampers are being developed such as fluid viscous dampers, solid viscoelastic dampers, friction dampers, added damping and stiffness dampers (ADAS), and buckling restrained braces (BRBs). In these, the design process of BRBs is the most familiar to design engineers due to its material behavior [3]. It is also important to note that BRBs have been proved to be superior in durability and long-term reliability.
BRBs have only been focused on seismic-resistant building designs, and have been gradually developed for bridge application since first being reported in 1988. BRBs are new for bridge structures [4], and their application in the domain is discussed in the literature [5,6]. Usami et al. [6] conducted an analytical study on a steel arch truss bridge in which diagonal members and lateral brace members were replaced by BRBs. Based on the result, the authors highlighted that the employed approach could be an efficient solution not only for earthquake-resistant new designs but also for retrofitting existing steel truss bridges. As can be seen in previous studies, BRBs are usually used in such a way that they replace members of truss bridges.
Generally, buckling restrained braces (BRBs) have been considered as part of a bracing system, rather than as part of a damping system in seismic-resistant designs [3]. Therefore, we propose the idea of using BRB as an additional individual member or an external damper, not as the structural component or bracings. In this case, the device may be called a buckling restrained damper (BRD). The damper ‘BRD’ and the bracing ‘BRB’ are identical in terms of behavior and the design. They belong to the metallic damper that works based on the inelastic behavior of steel, and typically consist of a steel core and buckling restrainer case (i.e., concrete filled tube; Figure 1). During seismic load, the steel core or the yielding member of the damper undergo plastic deformation and dissipate the seismic energy by hysteretic behavior [3,4,5,6,7,8,9,10,11].
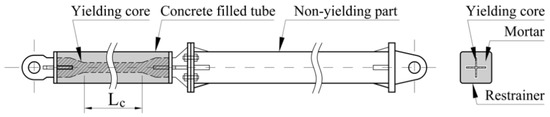
Figure 1.
Buckling restrained damper (BRD) with a non-yielding part.
In order to enhance the seismic behavior of bridges using BRD, design parameters such as the length, the cross-sectional area, the location, and the inclination of BRD shall be taken into account. Regarding the length of BRDs, some studies are available in the literature, for example, [7,8,9,10,11]. Razavi et al. [10] have conducted analytical and experimental studies on the entire model of the BRD with a yielding part and a rigid part. The ratio between the length of the yielding core and the total length (Lc/Ltotal) of the BRD was taken to be 0.2 to 0.4, and the axial strain was shown to be higher than 3%. For common BRBs, the length ratio typically varies from 0.6 to 0.8, and the axial strain is 1% to 2%. Therefore, they investigated the buckling load of the BRD in two cases: (i) the yielding core was placed in the middle of the BRD, and (ii) the yielding core was placed at the one end of the BRD. The authors also compared the energy dissipated by the BRD with a reduced length of the yielding part and the energy dissipated by a conventional BRD. The study showed that higher buckling capacity is achieved when the short yielding core is placed at the one end of the BRD; therefore, the BRD with the short core has a higher energy absorption capacity of 1.3 times than that of the conventional BRD.
Other reports [7,8,9] highlighted that as the core length decreases, the plastic strain demand on the BRD increases, and consequently, its energy absorption becomes greater. Therefore, the BRD could efficiently sustain the seismic performance of the structure. Although the effectiveness of the core length of the BRD has been studied previously, its influence on the seismic performance of the actual or the existing bridge under real earthquake conditions has not been assessed. Moreover, the effectiveness of other parameters such as the inclination and the cross-sectional area of the BRD yielding core has not been evaluated yet. Thus, this study will consider the effectiveness of the BRD design parameters such as the length, the cross-sectional area, the location, and the inclination of BRD on the seismic performance of an existing steel truss bridge.
In summary, the aim of the present study is to propose an option to enhance the seismic behavior of an existing truss bridge under a large earthquake using BRDs, and to investigate the influence of the aforementioned design parameters of the BRD on the seismic performance of the bridge.
2. Analysis Model
2.1. Model of the Existing Bridge
The existing truss bridge is a single-span simply supported bridge with a span length of 74.40 m. It has a reinforced concrete upper deck with a width of 10.60 m and a thickness of 200 mm. The schematic of the bridge is given in Figure 2, and the member details, including the steel grades, are shown in Table 1. Steel grades, employed for the truss bridge, are SM490Y (yield stress, σy = 355 N/mm2) and SM400 (yield stress, σy = 235 N/mm2). The mass density, Young’s modulus, and Poison’s ratio of each steel are taken to be ρ = 7.851 × 10−9 t/mm3, E = 2.0 × 105 N/mm2, and ν = 0.3, respectively. Moreover, beyond the yield stress, the material stiffness is assumed to be E/100, and the elastic-plastic behavior of von Mises type with kinematic hardening rule is assumed.
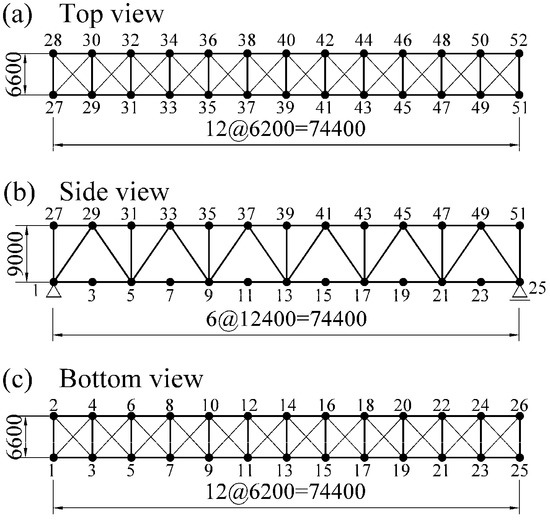
Figure 2.
Truss bridge model.

Table 1.
Member details of the truss bridge.
For the concrete deck, the mass density, Young’s modulus, and Poison’s ratio are taken to be ρ = 2.35 × 10−9 t/mm3, E = 2.1 × 104 N/mm2, and ν = 0.2, respectively. The damage in the concrete deck slab is not taken into account in this study; therefore, the simplified elastic model is employed to consider its spatial stiffness and inertia in the dynamic analysis.
ABAQUS [12] is used for all the analyses in the present study. A three-dimensional beam-element of type B33 is employed. Ten finite elements are used in the modeling of each member of all the lateral bracings (27–30, 2–3, 1–28, 5–32, etc. in Figure 2), and five finite elements are used for other members of the truss. The joints of each truss member are modeled to be the fully rigid connections since the difference in any types of joints has little effect on the dynamic response of the stress [13]. The concrete deck is modeled by the shell element of type S4R. Floor beams are rigidly connected to the concrete deck; 1180 beam-elements and 168 shell-elements are used in total.
The dynamic implicit method is employed in which the maximum time increment used in the numerical integration of the equation motion in the dynamic analysis is taken to be Δt = 0.03 s. Rayleigh damping is employed in which coefficients α and β are determined assuming damping ratio ζ (damping ratio: ζ = 0.03 for concrete deck; ζ = 0.02 for steel members) for the first two dominant vibration modes of the bridge model [14].
The live and traffic loads are not considered in this study, and the distributed dead load is taken into account in accordance with the Japanese Code, in which load factors 1.7 and 1.5 are applied to consider the mass of non-structural components of the bridge and the mass of bolts and other details, respectively [15]. Therefore, the defined mass density is employed for the material properties of the model.
The Niigata Chuetsu (2004) earthquake acceleration wave with a maximum acceleration of 1.164 g (Figure 3) is employed to evaluate the seismic resistance because it is much stronger compared to the recommended accelerogram for Level 2 (Type II) earthquake ground motion [16]. It is also important to note that in Level 2 (Type II) ground motion specified in [16], there are three earthquake ground motions that have been commonly utilized for seismic design of highway bridges (the maximum acceleration is 0.828 g).
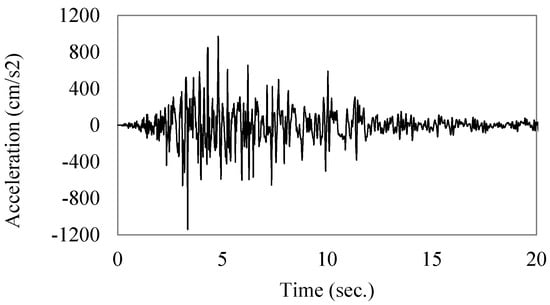
Figure 3.
Niigata Chuetsu earthquake wave.
2.2. Safety Evaluation of the Truss Bridge Members
The existing bridge was initially designed according to the old design codes considering the moderate earthquake before the 1995 Hyogoken-Nanbu earthquake, and has not been seismically retrofitted so far. The seismic behavior of the bridge is evaluated by the acceleration wave of the Niigata Chuetsu earthquake mentioned above and the criteria of the current Japanese design codes [15,17]. To this end, a nonlinear time history analysis is carried out. It is important to note that the nonlinear time history analysis has the potential to provide much better information for predicting the amount of damage, and hence for evaluating any risk due to earthquake, and the nonlinear time history analysis is also recommended in evaluating the dynamic response of structures to Level 2 earthquakes [17].
The seismic behavior only in the longitudinal direction of the bridge is considered herein, and the analysis is therefore arranged with two steps, considering the material and geometrical non-linearity of the bridge members. The safety of the bridge members is examined by the following two conditions [15]:
- when the normal stress of the member is positive (in tension):
- when the normal stress of the member is negative (compression):
where and are the demand-capacity ratio, and is the axial stress value of the i-th member, obtained from the dynamic time history response (i.e., Figure 4). and are the design local buckling stress of the member and the material yield stress of the member, respectively.
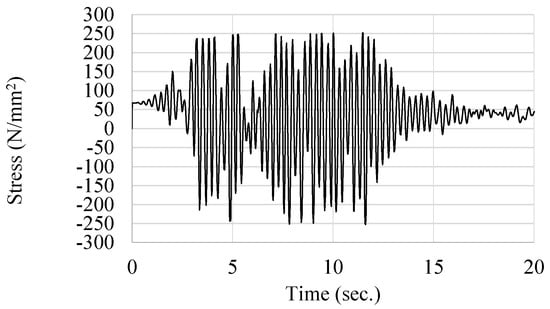
Figure 4.
Time-history response of the normal stress of the damaged member, during the earthquake.
The member that satisfies the above two equations is safe; otherwise, the member is considered damaged.
The numerical results are shown in Table 2. The maximum and minimum stress values, shown in Table 2 are determined based on the comparison among the stress time history responses in each damaged member.

Table 2.
The axial stress results.
Figure 5 shows the deformed shapes of the truss bridge during the large earthquake. As can be seen in Figure 5b,c, the damaged members are also highlighted in black (see also the node numbers in Figure 2).
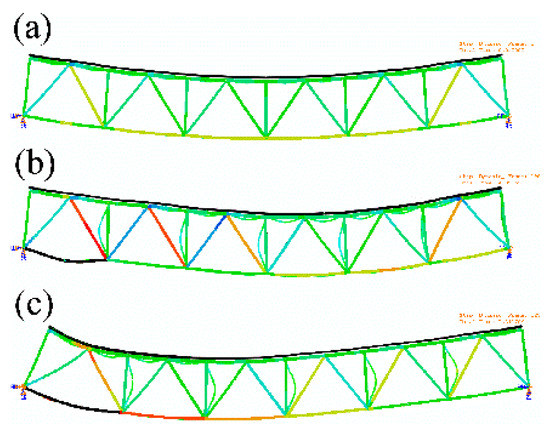
Figure 5.
Deformation patterns of the truss bridge due to (a) dead-load; (b) the large earthquake in compressive direction; (c) the large earthquake in tensile direction.
3. Seismic Upgrading Model with BRDs
The seismic performance in the longitudinal direction of the steel truss bridge is not sufficient under the large earthquake as shown in the previous section. Retrofitting the bridge is required. For this purpose, two pairs of BRDs are individually attached between the bridge abutment and the bottom ends of vertical links that are rigidly connected to joints at the lower chord of the truss bridge. The two pairs of vertical links are modeled to be absolute rigid bodies, and their properties are not taken into account in this study. BRDs are modeled to have pinned end connections and supposed to consist of two parts: the yielding part and the non-yielding part. Moreover, the condition that the yielding core is placed at the one end of the BRD [10] is adopted (Figure 1). The steel LY225 is employed for the BRD yielding core, which is commonly used for hysteretic damping device in Japan [4]. The yield stress σy of the BRD yielding core is 225 N/mm2. Young’s modulus of steel and Poison’s ratio are taken to be E = 2.0 × 105 N/mm2 and ν = 0.3, respectively, and the elastic-plastic behavior of von Mises type with kinematic hardening rule and the uniaxial stress-strain relationship with hardening slope 3E/100 are assumed. The yielding part of BRDs is modeled by 2-node truss-element T3D2. The non-yielding part of the BRD is considered to be absolute rigid, and 2 beam-elements and 2 truss-elements are used in modeling of two pairs of BRDs. The damping properties of each model with BRD are assumed to be the same as the damping properties defined for the model without BRD.
The non-linear dynamic finite element analyses are performed based on the assumption that BRDs do not reduce the initial stress state of the bridge members due to the gravity load. Notably, the calculations were arranged within two steps: (1) Static analysis of the truss bridge without BRDs, under the gravity load; (2) Nonlinear dynamic analysis of the bridge with two pairs of BRDs based on the initial stress state obtained in the first step.
4. Parametric Evaluation of the BRD
The non-linear dynamic finite element analyses are conducted to observe the effectiveness of the BRD parameters, including the influence of the three sources of nonlinearity in mechanics (material, boundary, and geometrical). Within the scope of this study, the properties of the rigid part of the BRD are not considered as mentioned earlier, and the following four different parameters are investigated in this part, namely:
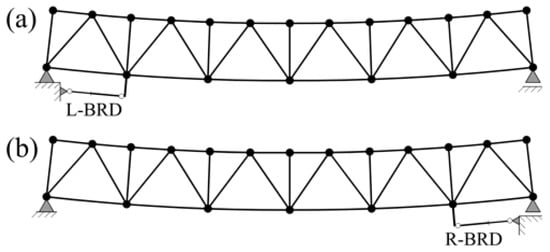 Figure 6. Installation scheme of BRDs: (a) Left-sided BRD; (b) Right-sided BRD.
Figure 6. Installation scheme of BRDs: (a) Left-sided BRD; (b) Right-sided BRD.- Length of the yielding core, Lc: 10.5, 7, 3.5 and 1.75 m
- Cross-sectional area of the yielding core of the BRD, Ac: 5, 10, 20, 30 and 40 cm2
- Inclination of the BRD, αd: 0°, 5°, 10°, and 15°.
The numerical investigations were carried out under the control of the safety condition (Equations (1) and (2)) of the damaged members of the bridge. Figure 7 shows the name description of models used in the numerical analyses.

Figure 7.
The name description of models.
4.1. Influence of the BRD Location on the Axial Stress of the Damaged Members
This section examines the influence of the BRD location on the axial stress of the damaged members of the truss bridge. For this purpose, a series of normal stress responses were determined from each model with various BRD attached. Although the location is limited, the parametric analyses were done based on two possible locations for the design of the BRDs: close to the fixed support (L-BRD; Figure 6a); near the roller support of the bridge (R-BRD; Figure 6b).
Table 3 and Table 4 compare the resulting stress responses that correspond to each location of BRD. Figure 8a–d show the hysteretic responses of L-BRDs with different characteristics, and Figure 8e–h show the hysteretic responses of R-BRDs with different characteristics.

Table 3.
Axial stress reduction by L-BRDs.

Table 4.
Axial stress reduction by R-BRDs.
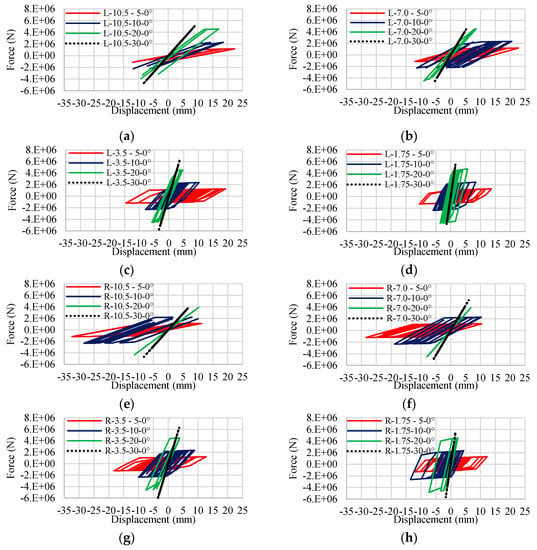
Figure 8.
The behavior of each BRD with different characteristics.
As observed, the influence of the BRD on the axial stress of the damaged member is clear in Table 3: with L-BRDs, the compressive and the tensile stresses are decreased by 17.9–78.4% and 5.1–41.9%, respectively, and for the R-BRDs (Table 4), those values are 5.4–60.2% and 4.3–6.3%, respectively. Therefore, the safety condition is satisfied by L-BRDs whereas the R-BRDs cannot satisfy the safety condition. It indicates that the right side location for the design of BRDs (Figure 6b) is not effective, or the R-BRDs cannot sustain the seismic performance of the bridge.
The damage may be caused by the axial deformation of the member. So, the horizontal displacements at the moveable end of the damaged members are determined for BRDs, “L-1.75-20-0°” and “R-1.75-20-0°” to prove the above observation. The results are shown in Table 5.

Table 5.
Effect of the BRD location on the horizontal displacement due to the earthquake.
The comparison can be seen in Table 5 that the R-BRD does not sufficiently reduce the horizontal displacement at the moveable end of the damaged members. It should be noted that the L-BRDs reduced the horizontal displacement in compressive direction by 59.3% while the R-BRDs reduces 16.4%. Also, L-BRDs and R-BRDs reduce the horizontal displacement in tensile direction by 91.6% and 83.0%, respectively.
It can be clearly seen in these comparisons that R-BRD has a minor effect in reducing the axial displacement of the damaged members compared to the L-BRD and that the L-BRD satisfies both safety conditions. This is the evidence to suppose that the design of the BRD near the right end or the roller support is not efficient for this truss bridge.
4.2. Influence of the Length of the BRD Yielding Core on the Axial Stress of the Damaged Members
The influence of the length of the BRD yielding core (Lc) on the axial stress of the damaged members is discussed in this section based on the model with the L-BRD. For this purpose, the ratio between the length of the yielding core and the total length of the BRD (Lc/Ltotal) is chosen approximately to be 0.85, 0.6, 0.3, and 0.15, and depending on these values, the variable lengths of Lc are given by 10.5, 7.0, 3.5 and 1.75 m, respectively.
The numerical results are shown in Table 3. The hysteretic loops which correspond to each BRD parameters are shown in Figure 8a–d. For Lc is given by 10.5, 7.0, 3.5 and 1.75 m, the axial compressive stress is reduced by 17.9–68.0%, 23.3–72.1%, 24.5–76.6%, and 52.0–78.4%, respectively, and the axial tensile stress is also reduced by 5.1–13.8%, 5.2–21.3%, 5.6–33.7%, and 6.1–41.9%, respectively. It can be observed that the axial stress reduces as the length of the yielding core decreases. The damage may be occurred due to the length change of the members, and thus, the horizontal displacements at the moveable end of the damaged members are determined from each BRD model to verify the above observation. The horizontal displacement results are shown in Table 6.

Table 6.
Influence of the length of the BRD yielding core on the horizontal displacement due to the earthquake.
Table 6 compares the horizontal displacement results. For the initial model, the joint displacement in compressive direction and tensile direction due to the earthquake was determined by −8.468 and 67.525 mm, respectively. When the BRD core length, Lc is given by 10.5 to 1.75 m, the horizontal displacement in compressive direction is reduced by −7.4–59.3% while in the tensile direction it is reduced by 74.9–91.6%. It indicates that as the core length Lc reduces, the horizontal displacement at the moveable end of the damaged members is reduced. As a result, the axial stress can be significantly reduced, providing evidence that shortening the yielding part of the BRD is effective not only in reducing the horizontal displacement change at that joint but also in reducing the axial stress on the damaged members.
4.3. Influence of the Cross-Sectional Area of the BRD Yielding Core on the Axial Stress of the Damaged Members
This section discusses the influence of the cross-sectional area of the BRD yielding core on the axial stress of the damaged members. The observation on the influence of the cross-sectional area of the yielding core of the BRD, Ac, is made that as can be seen from the results that when Lc = 3.5 m and when its cross-sectional area, Ac is given by 5, 10, 20, 30 and 40 cm2, the axial compressive stress is reduced by 24.5%, 44.5%, 72.2%, 74.7%, and 76.6%, respectively, and the axial tensile stress is decreased by 5.6%, 6.3%, 22.5%, 27.2%, and 33.7%, respectively as shown in Table 3. It indicates that as the cross-sectional area of the yielding core increases, the axial stress can also be significantly reduced. Figure 8c shows the plastic behavior of each BRD.
The observation can also be verified by comparing the horizontal displacements at the moveable end of the damaged members.
As shown in Table 7, the horizontal displacement is reduced as the cross-sectional area becomes bigger. Notably, when the cross-sectional area, Ac increases from 5 to 40 cm2, the horizontal displacement in compressive direction is reduced by 7.1% to 69.4%, while it is in tensile direction, which is 71.6% to 95.8%. The results prove that the horizontal displacement of the moveable end of the damaged members is reduced as the cross-sectional area of the yielding core increases, and, consequently, that of the axial stress has been reduced.

Table 7.
Influence of the cross-sectional area of the BRD yielding core on the horizontal displacement due to the earthquake.
4.4. Influence of the Inclination of the BRD on the Axial Stress of the Damaged Members
The effectiveness of the inclination of the BRD on the axial stress of the damaged member is evaluated in this section based on the model known as having an effective cross-sectional area and length. The R-BRDs are also considered so as to assess the inclination effect on the efficiency of R-BRDs. The analysis results are shown in Table 8.

Table 8.
Axial stress reduction by the BRDs with an inclination.
It can be observed that for the L-BRD, with the inclination of 0°, 5°, 10°, and 15°, the axial compressive stress of the damaged member is reduced by 72.2%, 73.6%, 45.0%, and 63.1%, respectively, whereas the axial tensile stress of the damaged member is decreased by 22.5%, 6.02%, 5.97%, and 6.46%, respectively, as shown in Table 8. For the R-BRD (attached near the roller support), the safety condition has not been satisfied even if the various inclination is introduced. The results indicate that the inclination is not effective on the axial stress of the damaged members for this truss bridge.
The observation can be verified similarly to the parameters as mentioned earlier. For this purpose, the horizontal displacements at the moveable end of the damaged members, corresponding to each inclined BRD, are determined. The numerical results are compared in Table 9.

Table 9.
Influence of the inclination on the horizontal displacement due to the earthquake.
As can be seen from this comparison, the horizontal displacement at the moveable end of the damaged member has not been significantly decreased as the angle of inclination increases. This proves that any inclination for the design of BRDs is not effective for the retrofitting of this truss bridge.
5. Conclusive Remarks
Analytical studies on the effectiveness of the buckling restrained damper (BRD) on the seismic behavior of an existing steel truss bridge were carried out. Four design parameters of the BRD, i.e., location, length, cross-sectional area of the yielding core, and inclination, were studied. To this end, the safety of the existing truss bridge under a large earthquake was assessed by nonlinear finite element analyses. The seismic behavior only in the longitudinal direction of the bridge was considered. Through the safety evaluation, some members were damaged due to the large earthquake. To improve the seismic resistance of the bridge, two pairs of BRDs are individually attached between the bridge abutment and each bottom-end of vertical links that are rigidly connected to joints at the lower chord of the truss bridge. The vertical links were modeled to be absolute rigid bodies, and their properties are not taken into account in the scope of this study.
Based on the safety condition of the model with BRD, the effectiveness of the four parameters for the design of the BRD was evaluated: (1) Location: near the roller support of the current truss bridge is not effective; (2) Length: shortening the yielding part of the BRD is more efficient; (3) Cross-sectional area: increasing the cross-section of the BRD yielding core is also effective; (4) Inclination: the inclination for the design of BRD is not effective.
The performance-based verification proves that the BRD is applicable for the existing truss bridge to sustain its resistance against large earthquakes. Figure 9 indicates that the axial compressive and tensile stresses of damaged members could be reduced by BRDs with different design parameters that are shown to be effective.
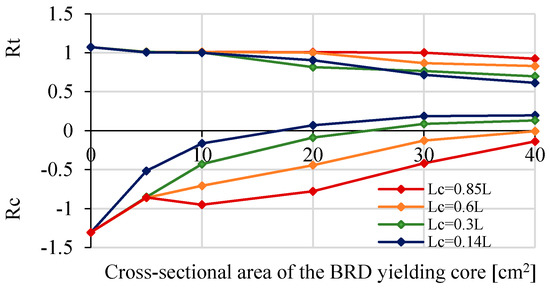
Figure 9.
Effectiveness of the design parameters of the BRD.
The results open a path for the use of BRD to provide high levels of seismic resistance to existing bridges.
Author Contributions
Analysis, investigation, and writing–original draft, P.S.; supervision and software, E.Y.
Funding
This research received no external funding.
Acknowledgments
P.S. thanks to Mongolia-Japan higher Engineering Education Development project (MJEED), the Government of Mongolia for the financial support.
Conflicts of Interest
The authors declare that there is no conflict of interests.
References
- Jun-ichi, H.; Guangfeng, Z. Performance of seismic retrofitted highway bridges based on observation of damage due to the 2011 Great East Japan Earthquake. J. JSCE 2013, 1, 343–352. [Google Scholar] [CrossRef]
- Kawashima, K.; Unjoh, S. Seismic design of highway bridges. J. Japan Assoc. Earthq. Eng. 2004, 4, 283–297. [Google Scholar] [CrossRef][Green Version]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; McNamara, R.J. Energy dissipation systems for seismic applications: current practice and recent developments. J. Struct. Eng. 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Takeuchi, T.; Wada, A. Buckling Restrained Braces and Applications, 1st ed.; in English; The Japan Society of Seismic Isolation: Tokyo, Japan, 2017; pp. 3–5. [Google Scholar]
- Usami, T. A new seismic performance upgrading method for existing steel bridges using BRBs. In Proceedings of the SECED Earthquake Risk and Engineering towards a Resilient World, Cambridge, UK, 9–10 July 2015. [Google Scholar]
- Usami, T.; Lu, Z.; Ge, H. A seismic upgrading method for steel arch bridges using buckling-restrained braces. Earthquake Engng Struct. Dyn. 2005, 34, 471–496. [Google Scholar] [CrossRef]
- Hoveidae, N.; Tremblay, R.; Rafezy, B.; Davaran, A. Numerical investigation of seismic behavior of short-core all-steel buckling restrained braces. J. Constr. Steel Res. 2015, 114, 89–99. [Google Scholar] [CrossRef]
- Mirtaheri, M.; Gheidi, A.; Zandi, A.P.; Alanjari, P.; Samani, H.R. Experimental optimization studies on steel core lengths in buckling restrained braces. J. Constr. Steel Res. 2011, 67, 1244–1253. [Google Scholar] [CrossRef]
- Muhamed, P.; Sahoo, D.R. Cyclic testing of short-length buckling-restrained braces with detachable casings. Earthq. Struct. 2016, 10, 699–716. [Google Scholar] [CrossRef]
- Razavi Tabatabaei, S.A.; Mirghaderi, S.R.; Hosseini, A. Experimental and numerical developing of reduced length buckling-restrained braces. Eng. Struct. 2014, 77, 143–160. [Google Scholar] [CrossRef]
- Tsai, K.; Lai, J.; Hwang, Y.; Lin, S.; Weng, C. Research and application of double-core buckling restrained braces in Taiwan. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Abaqus/CAE Ver. 6.13. User’s Manual; Dassault Systems Simulia Corp.: Providence, RI, USA, 2013. [Google Scholar]
- Goto, Y.; Kawanishi, N.; Honda, I. On impacts caused by sudden failure of diagonal tension members in steel truss bridges. J. Struct. Eng. 2010, 56A, 792–805. [Google Scholar]
- Chopra, A.K. Dynamics of Structures: theory and applications to earthquake engineering, 4th ed.; Prentice Hall: London, UK, 2013. [Google Scholar]
- Japan Society of Civil Engineers. Standard Specifications for Steel and Composite Structures, First Edition, I General Provision, II Structural Planning, III Design, 2009. Available online: http://www.jsce-int.org/system/files/Standard.pdf (accessed on 21 October 2010).
- Japan Road Association, Technical data. Available online: https://www.road.or.jp/dl/tech.html (accessed on 2 March 2012).
- J.R. Association. Design Specifications for Highway Bridges, Part V Seismic Design. 2002. Available online: http://iisee.kenken.go.jp/worldlist/29_Japan/29_Japan_2_HighwayBridge_Code_2002_01.pdf (accessed on 1 September 2002).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).