Practical Design Method of Yielding Steel Dampers in Concrete Cable-Stayed Bridges
Abstract
Featured Application
Abstract
1. Introduction
2. The Analytical Model and Input Ground Motions
2.1. FE Modelling of the Cable-Stayed Bridge
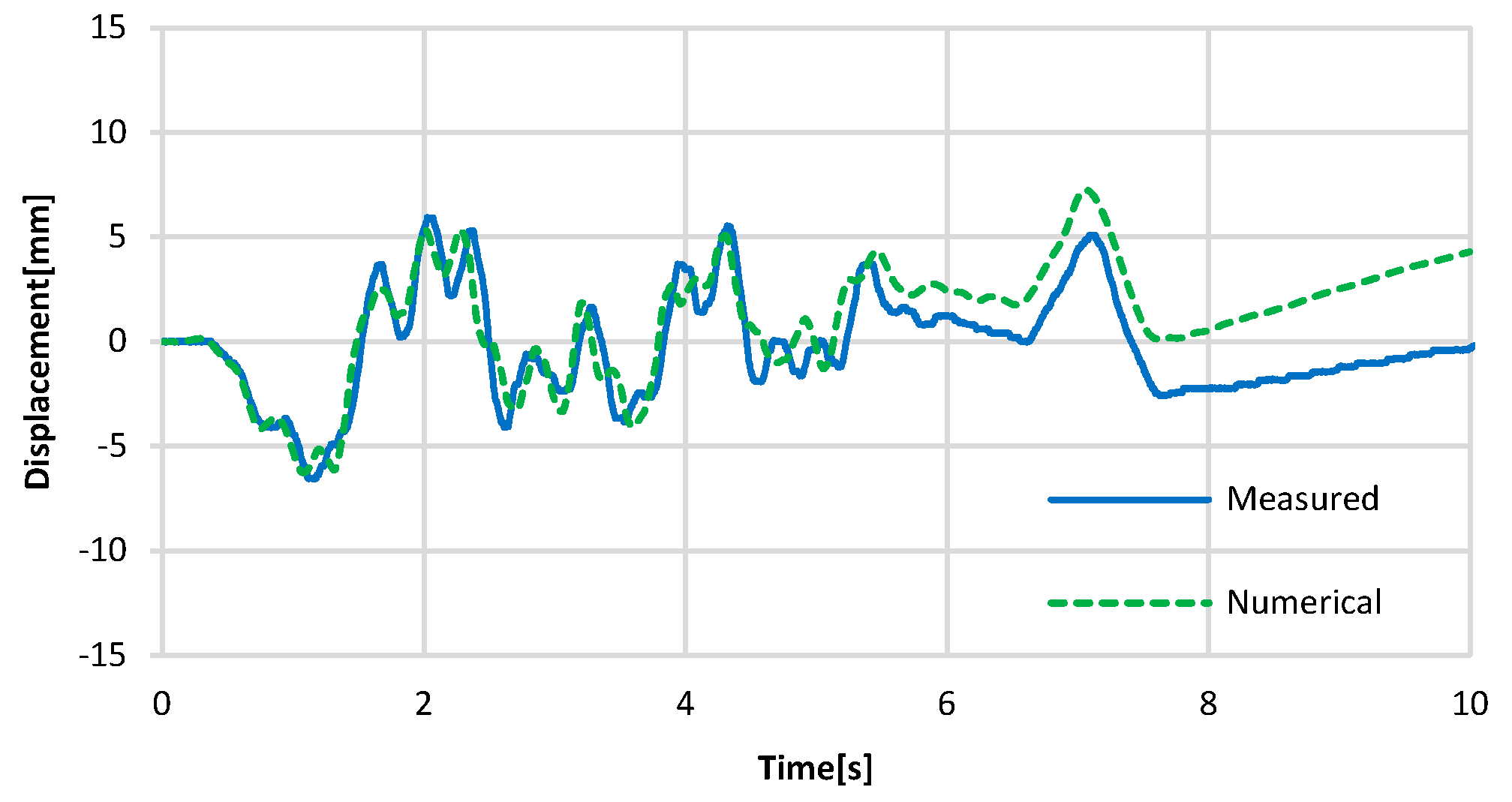
2.2. FE Model Validation
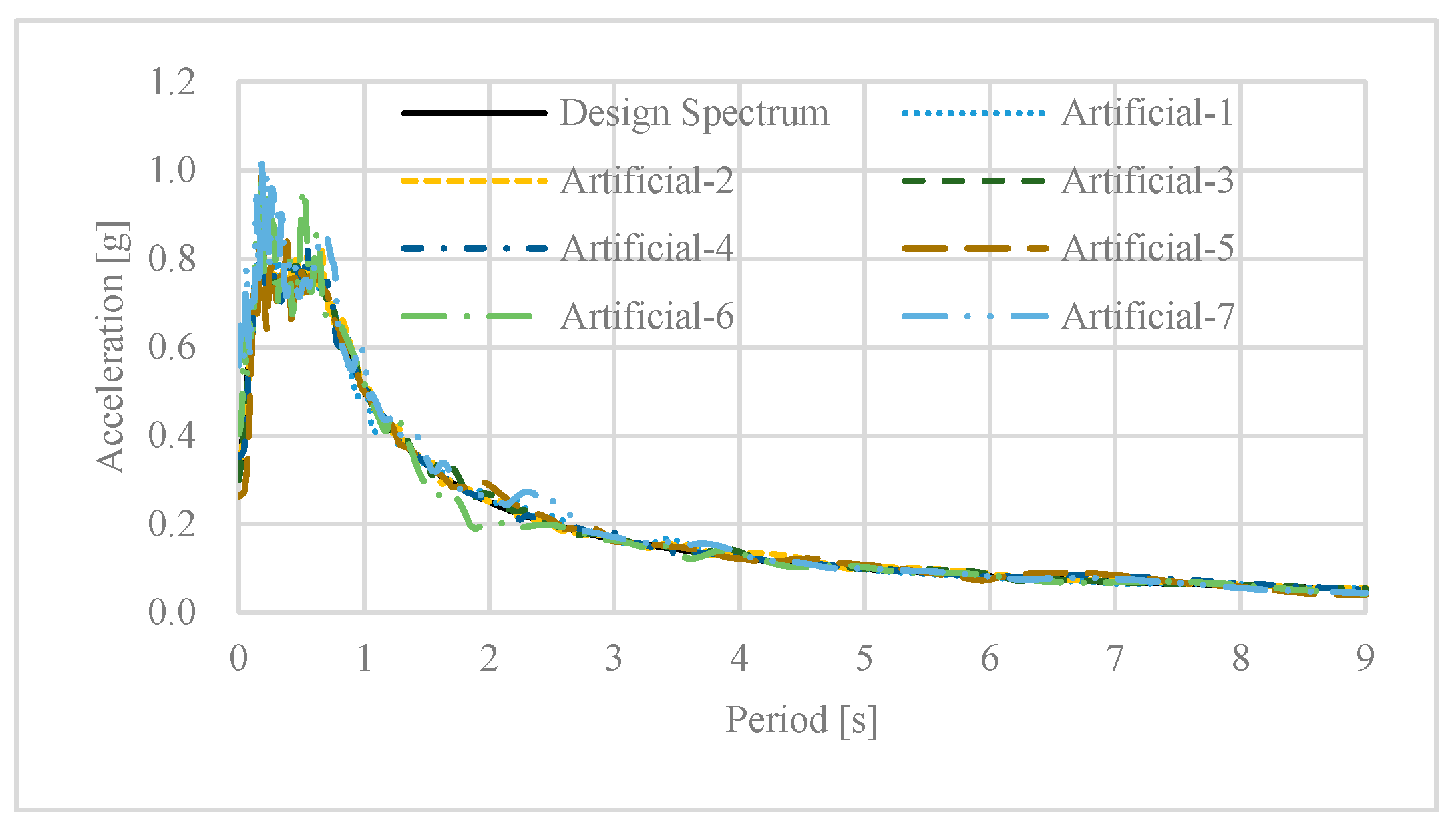
2.3. Input Ground Motions
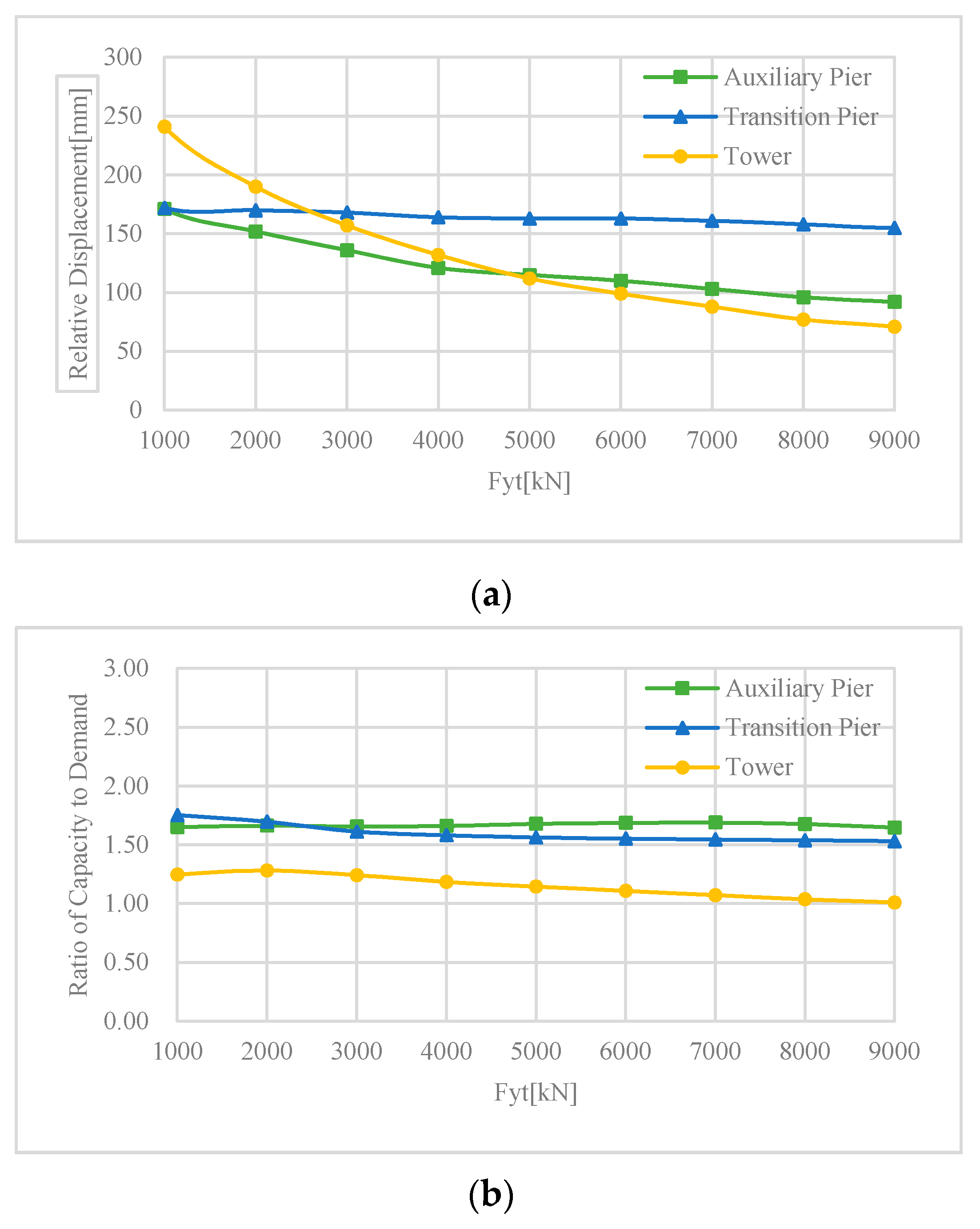
3. The Influence of the Fy of YSD
3.1. Determining the Scope of Analysis
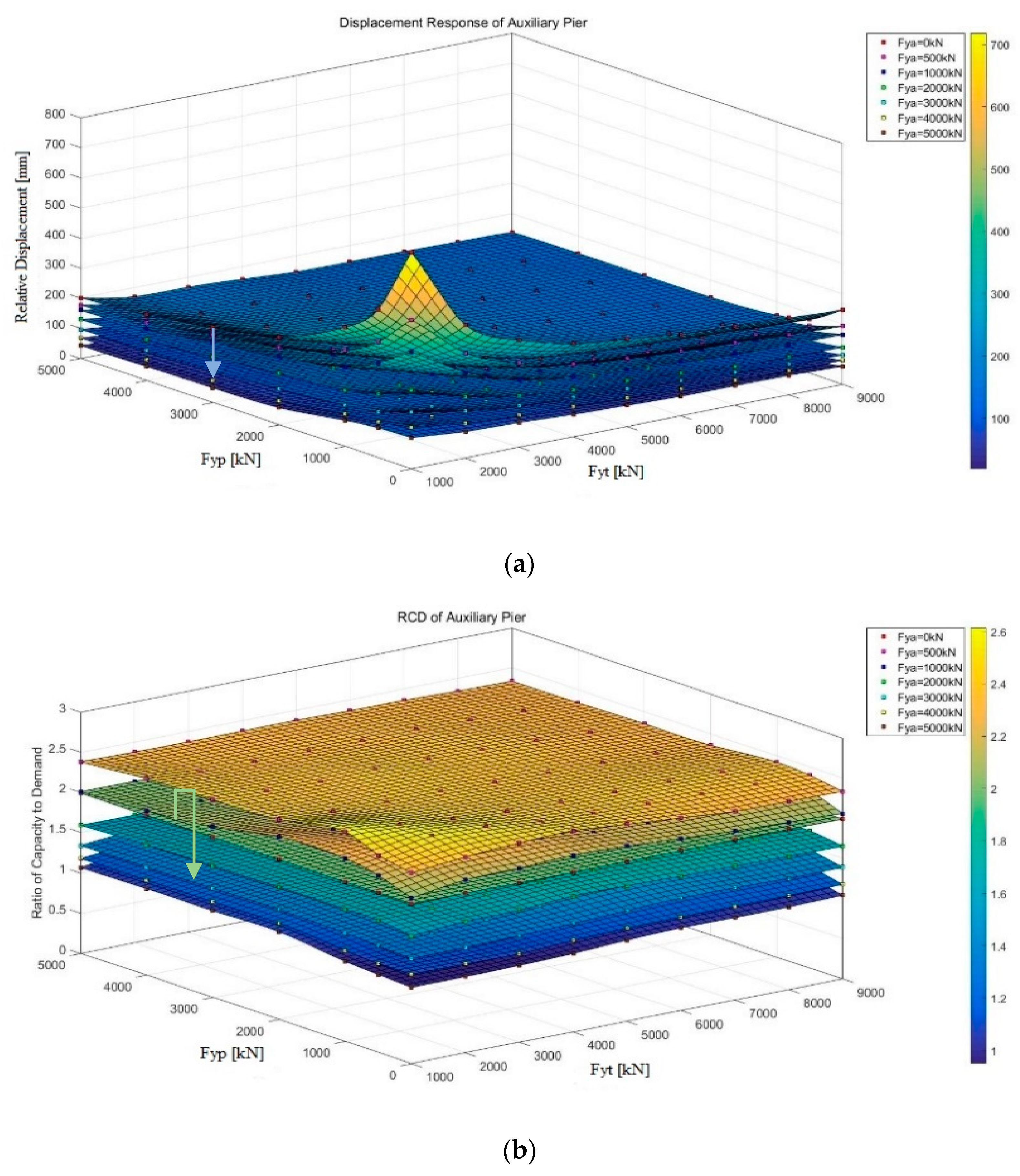
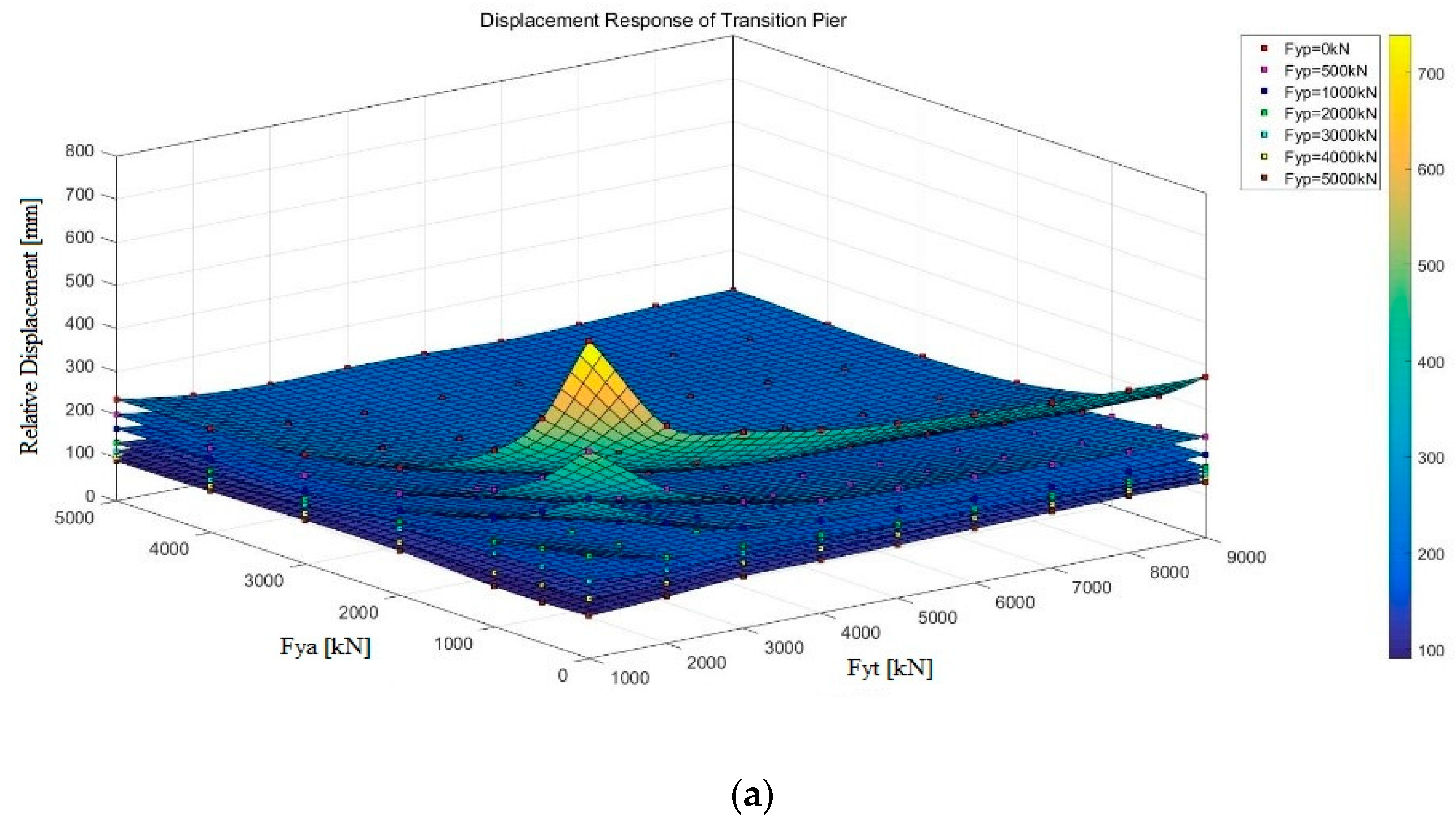
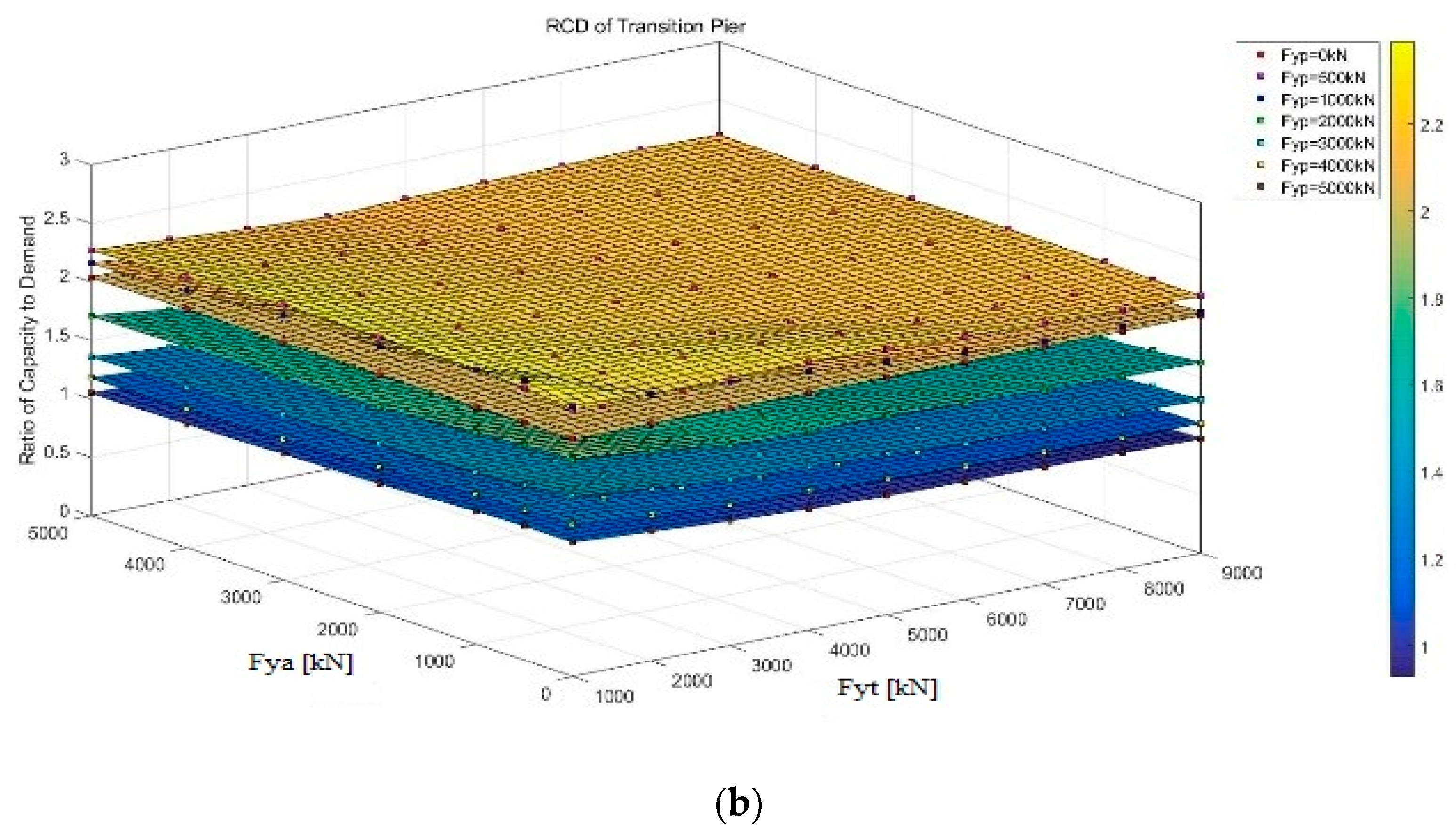
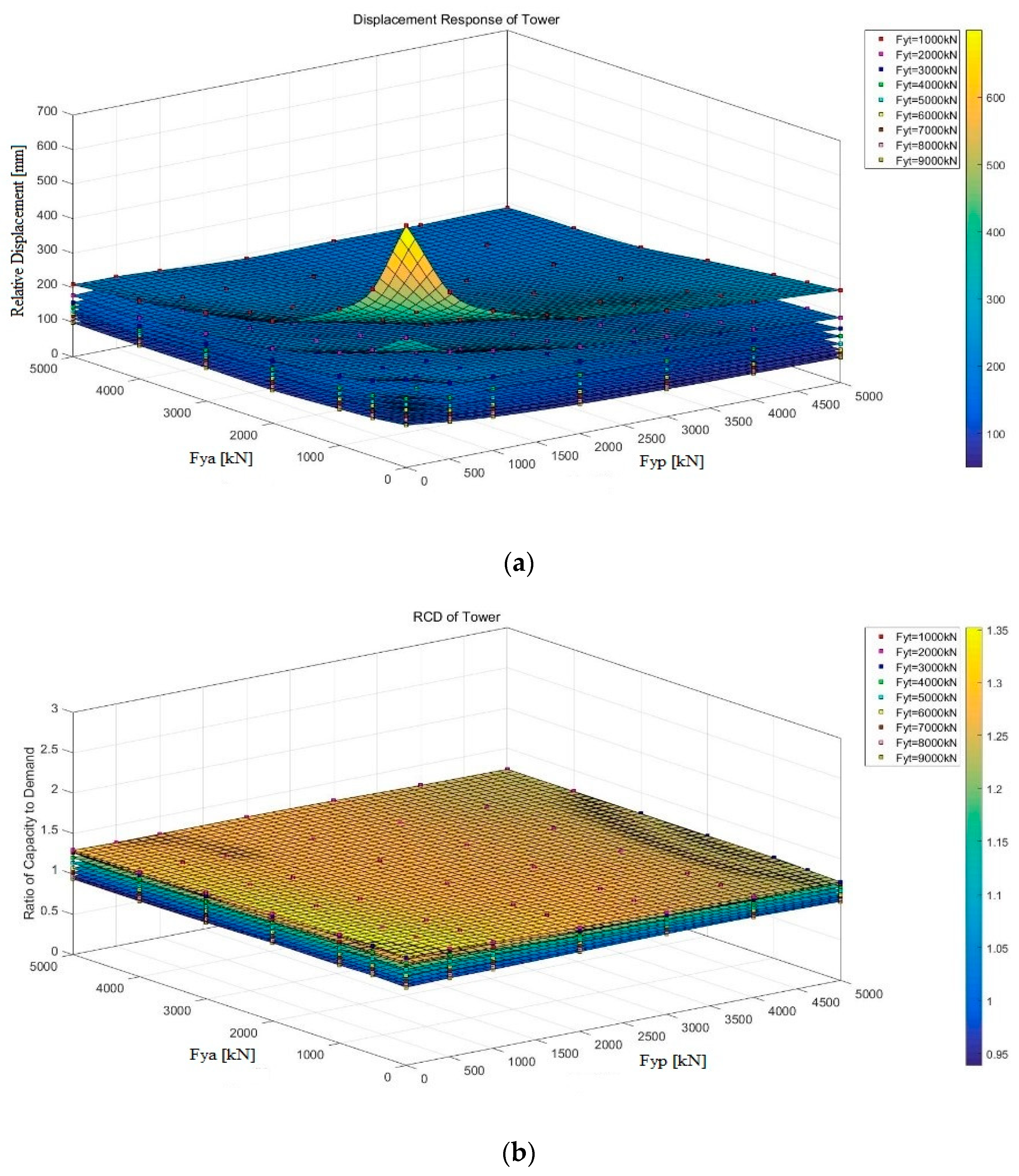
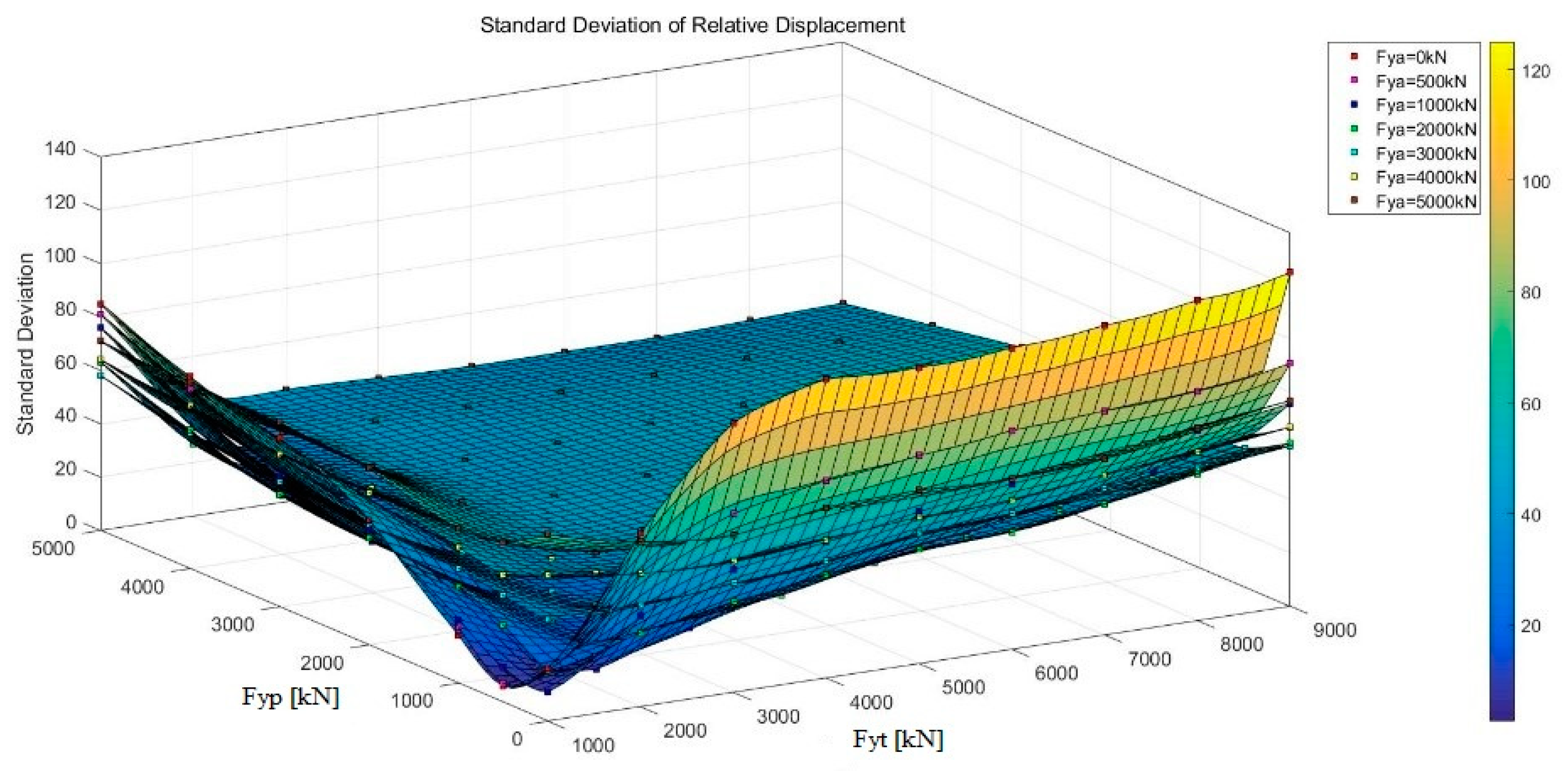
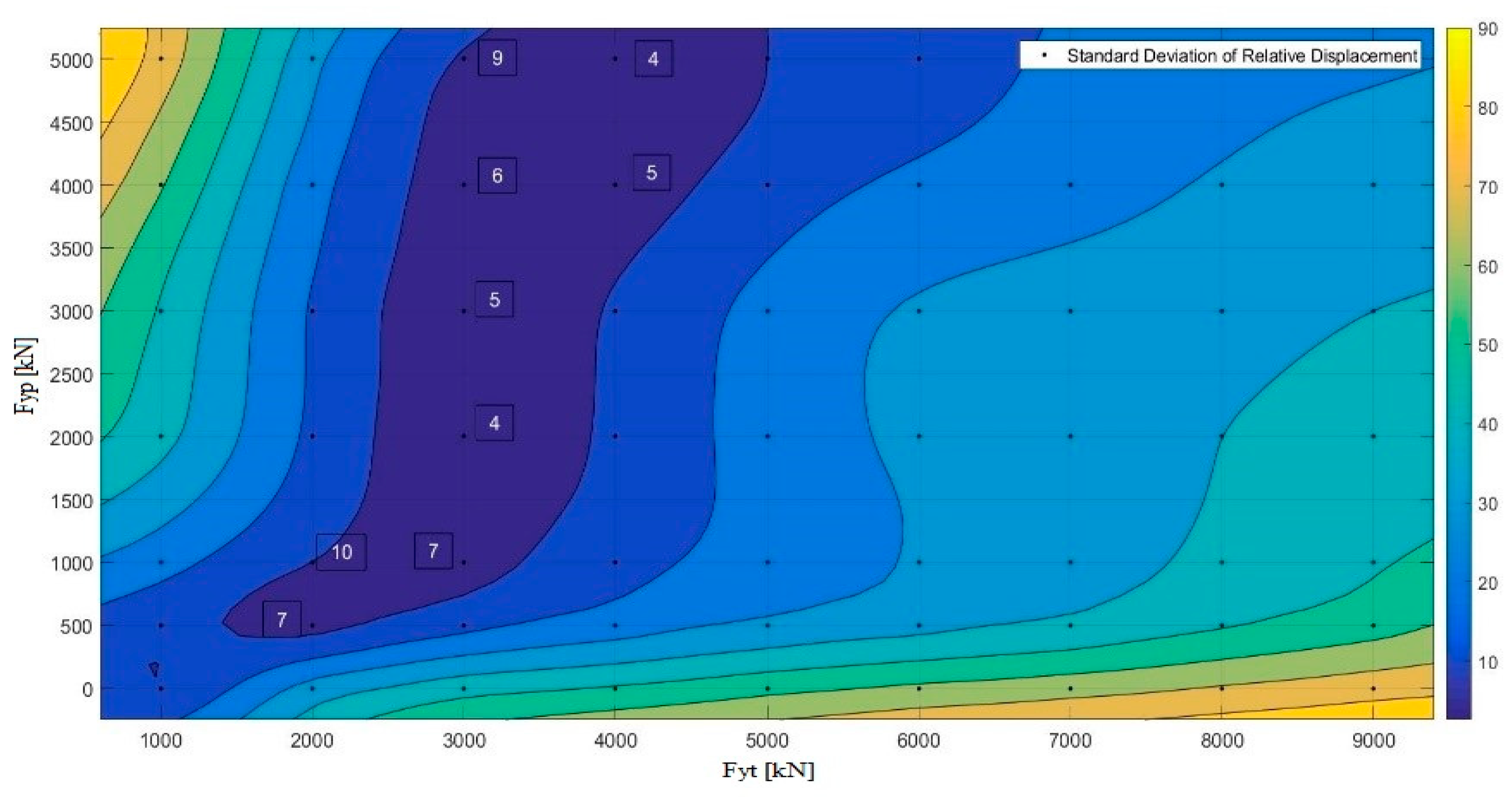
3.2. Multivariate Function Analysis
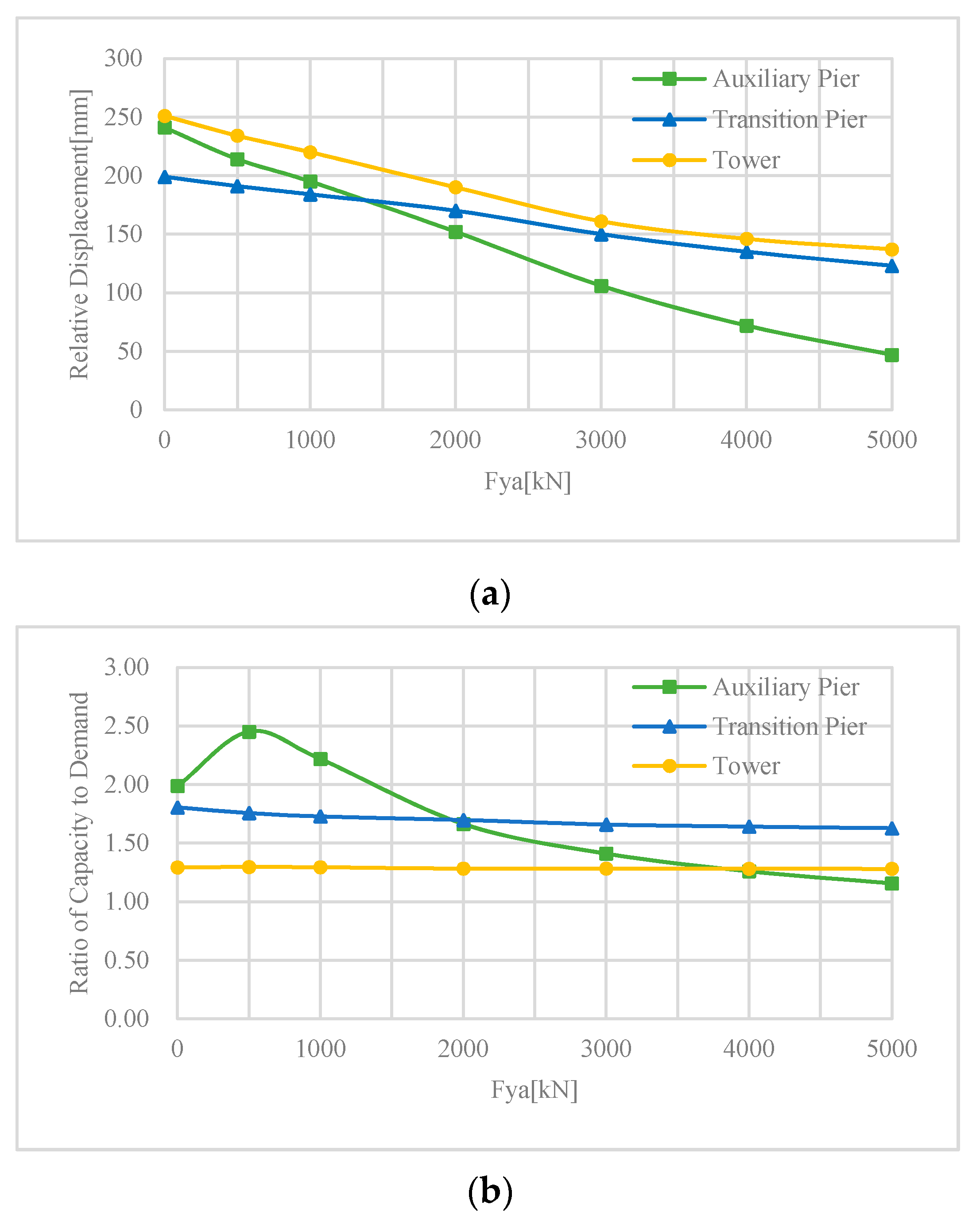
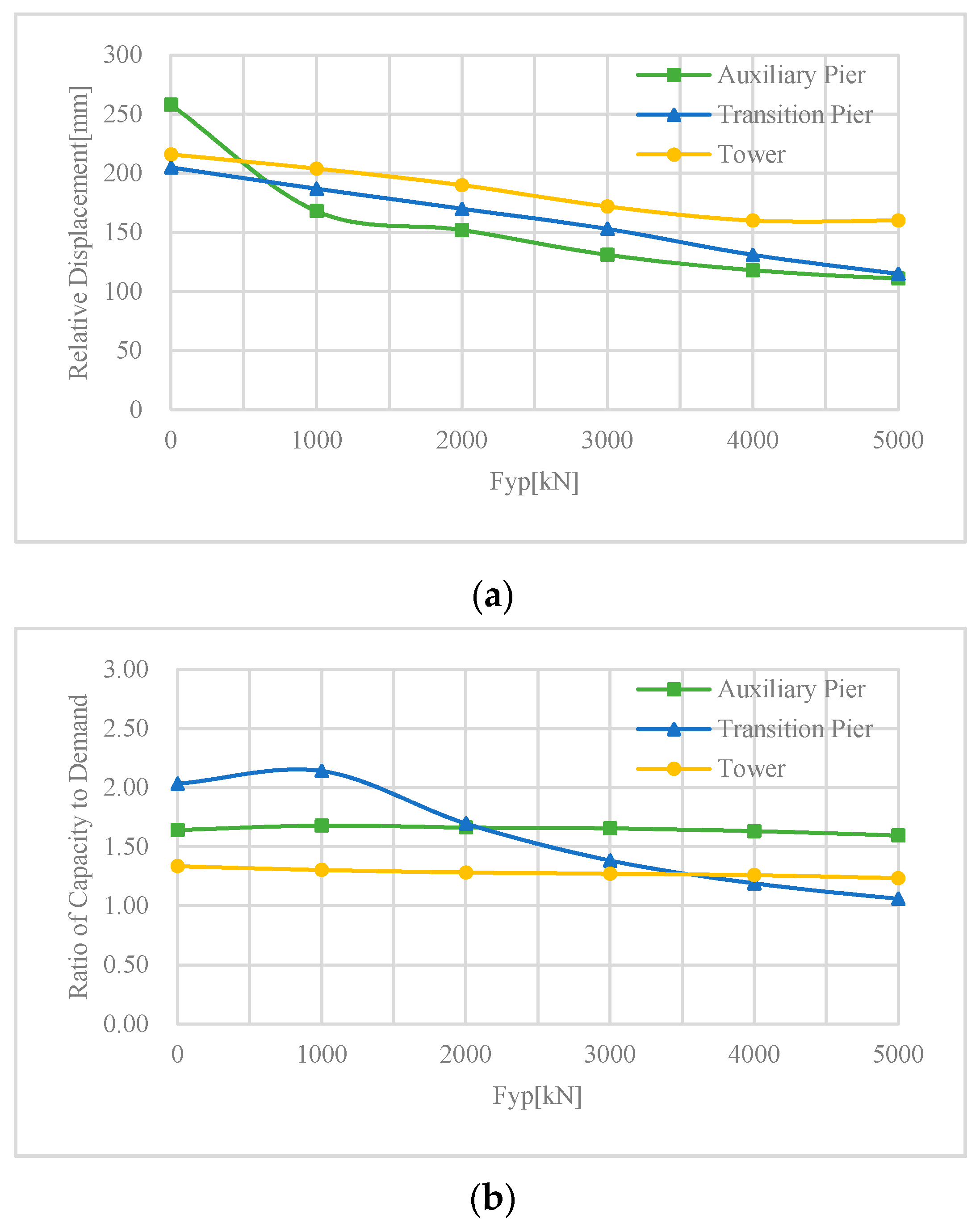
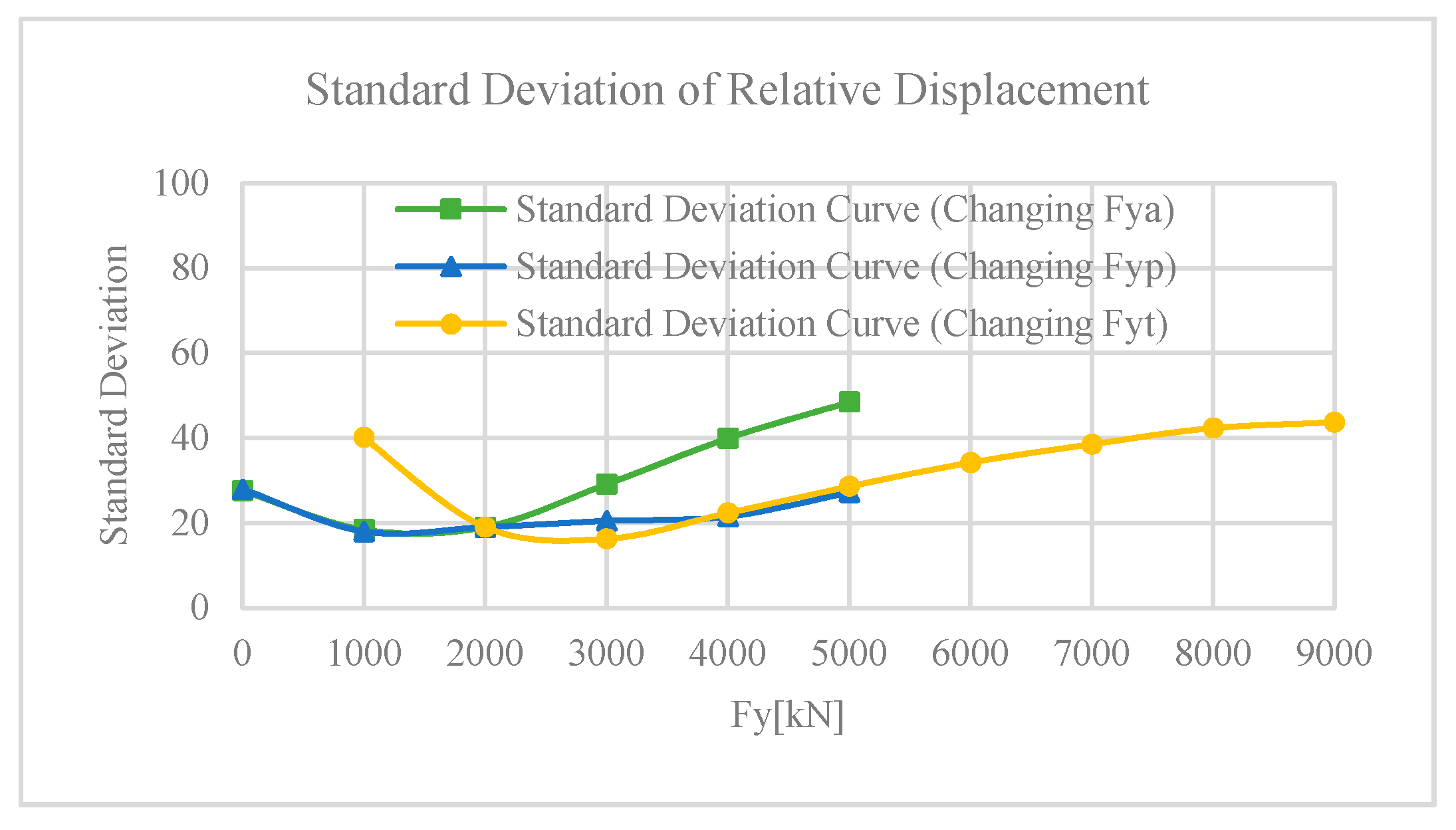
3.3. Single Variable Function Analysis
3.4. Comparison of the Designed Results
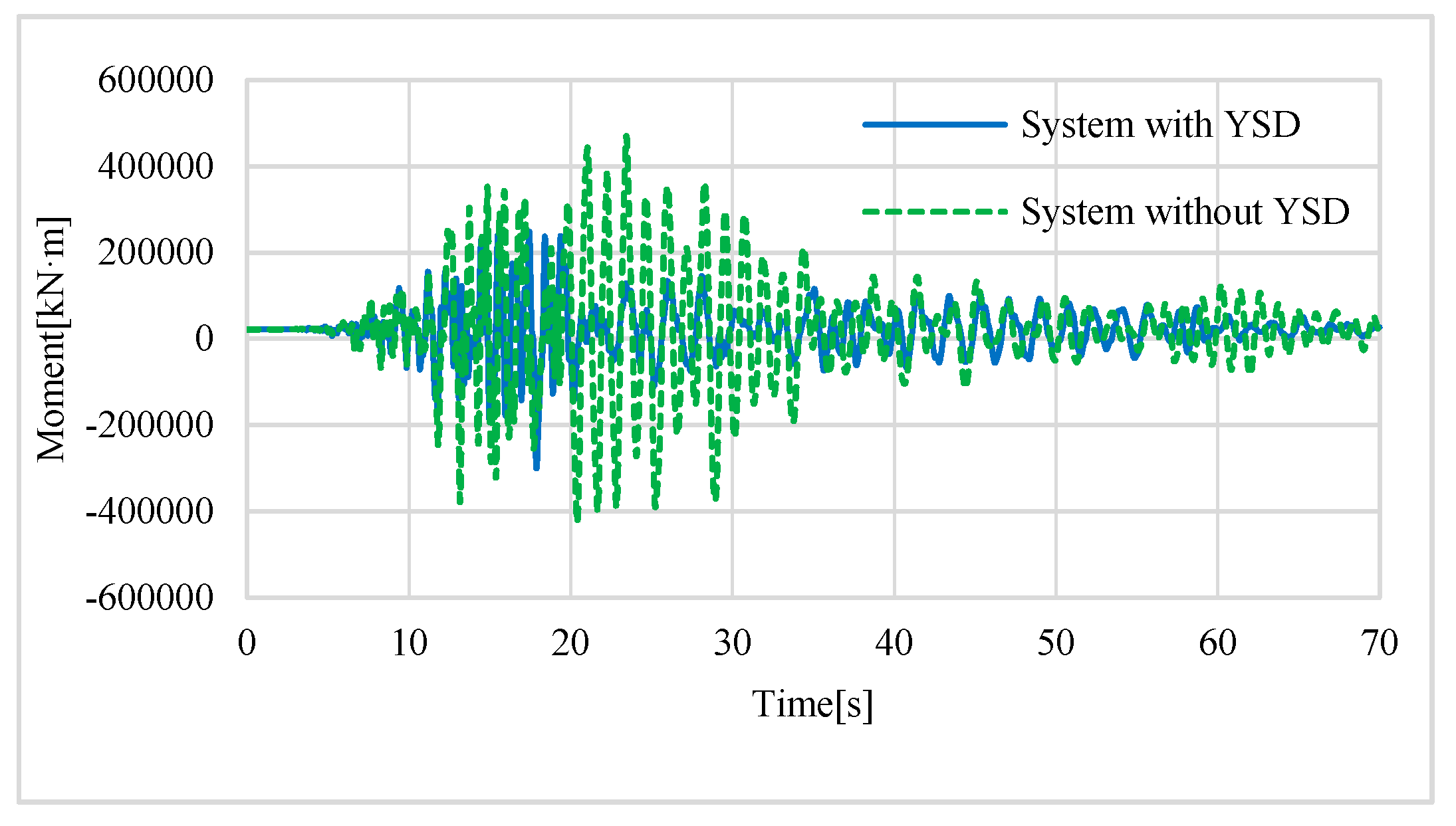
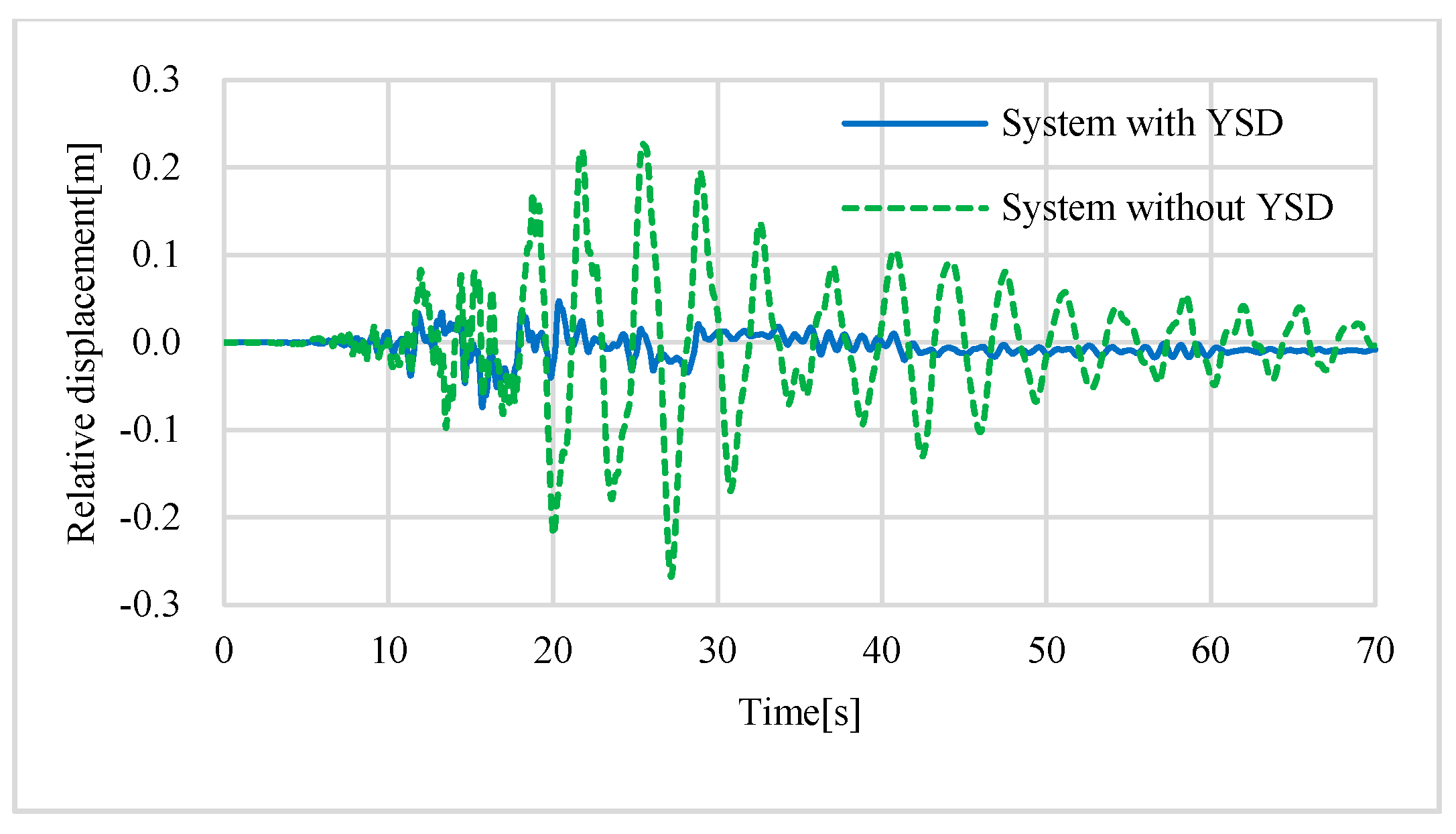
4. Dynamic Vibration of Bridge Systems with and without YSDs
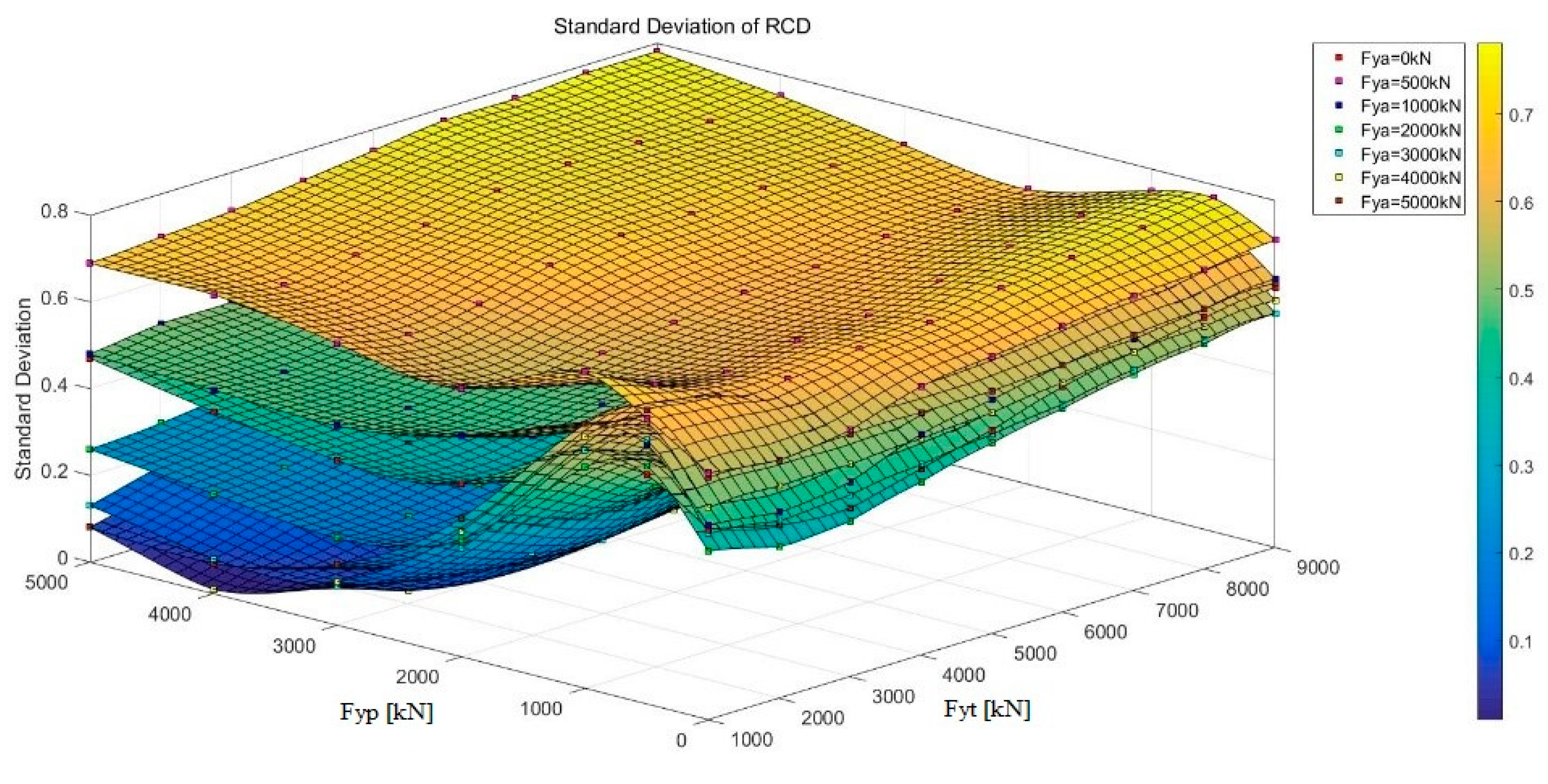
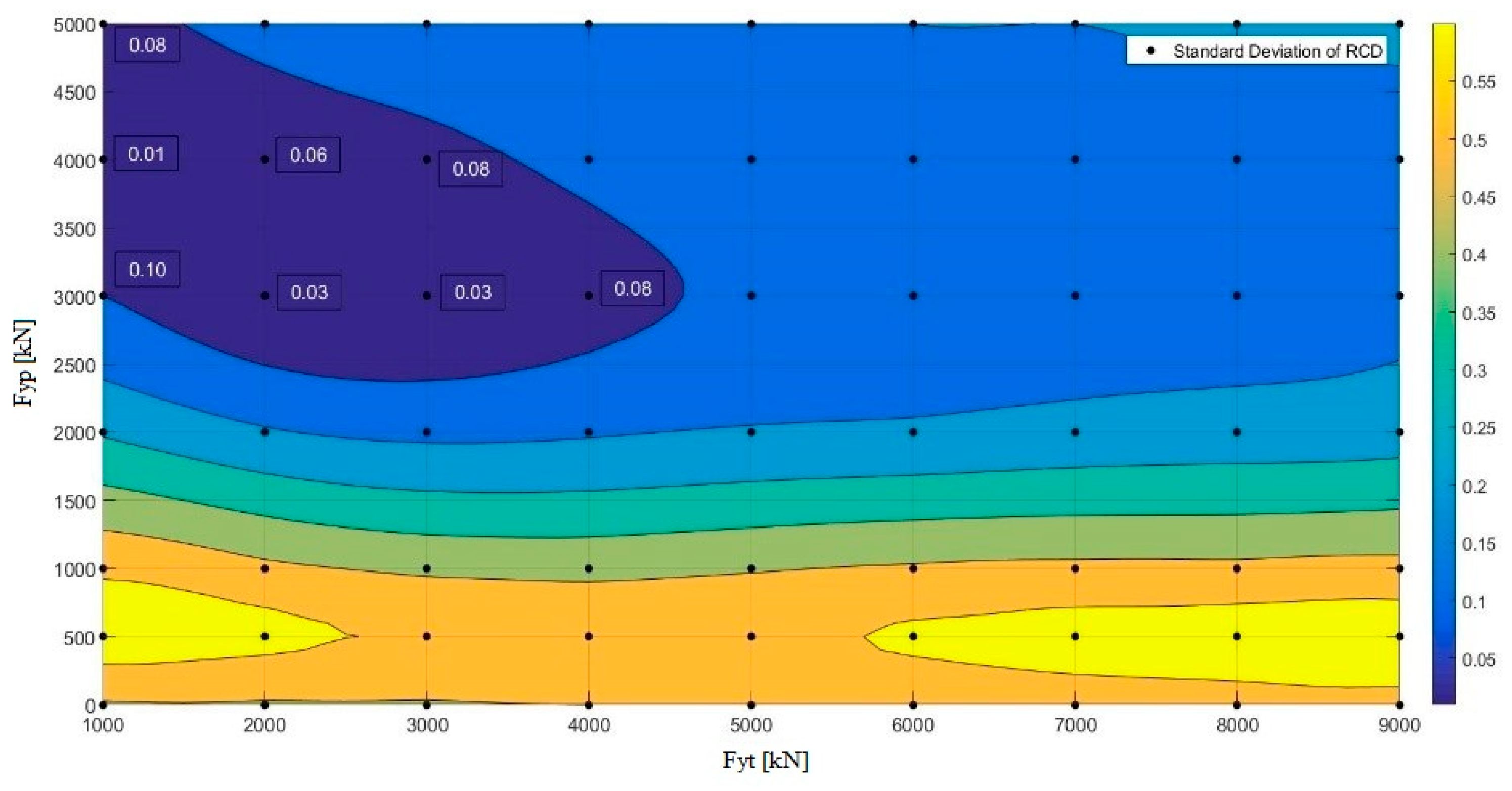
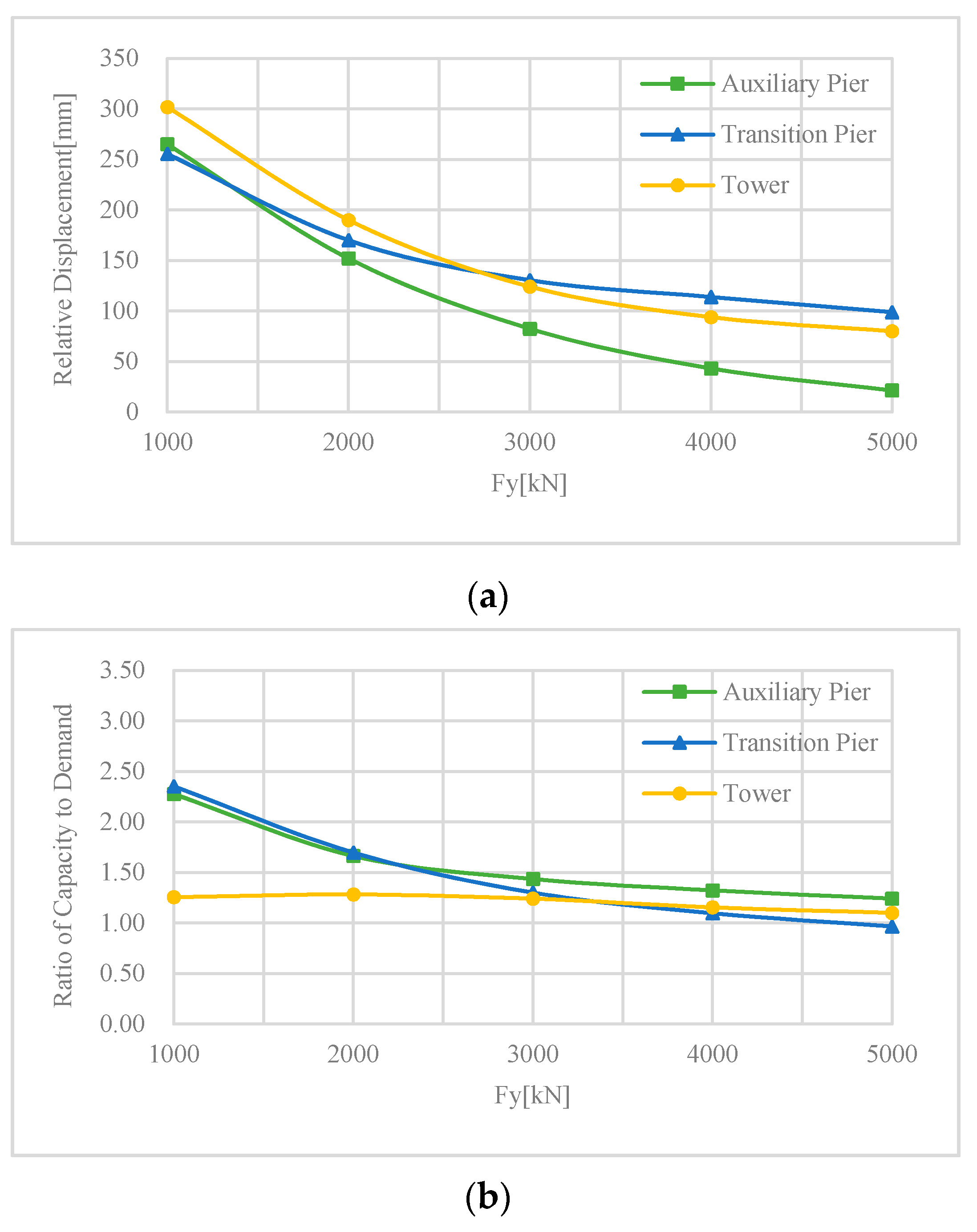
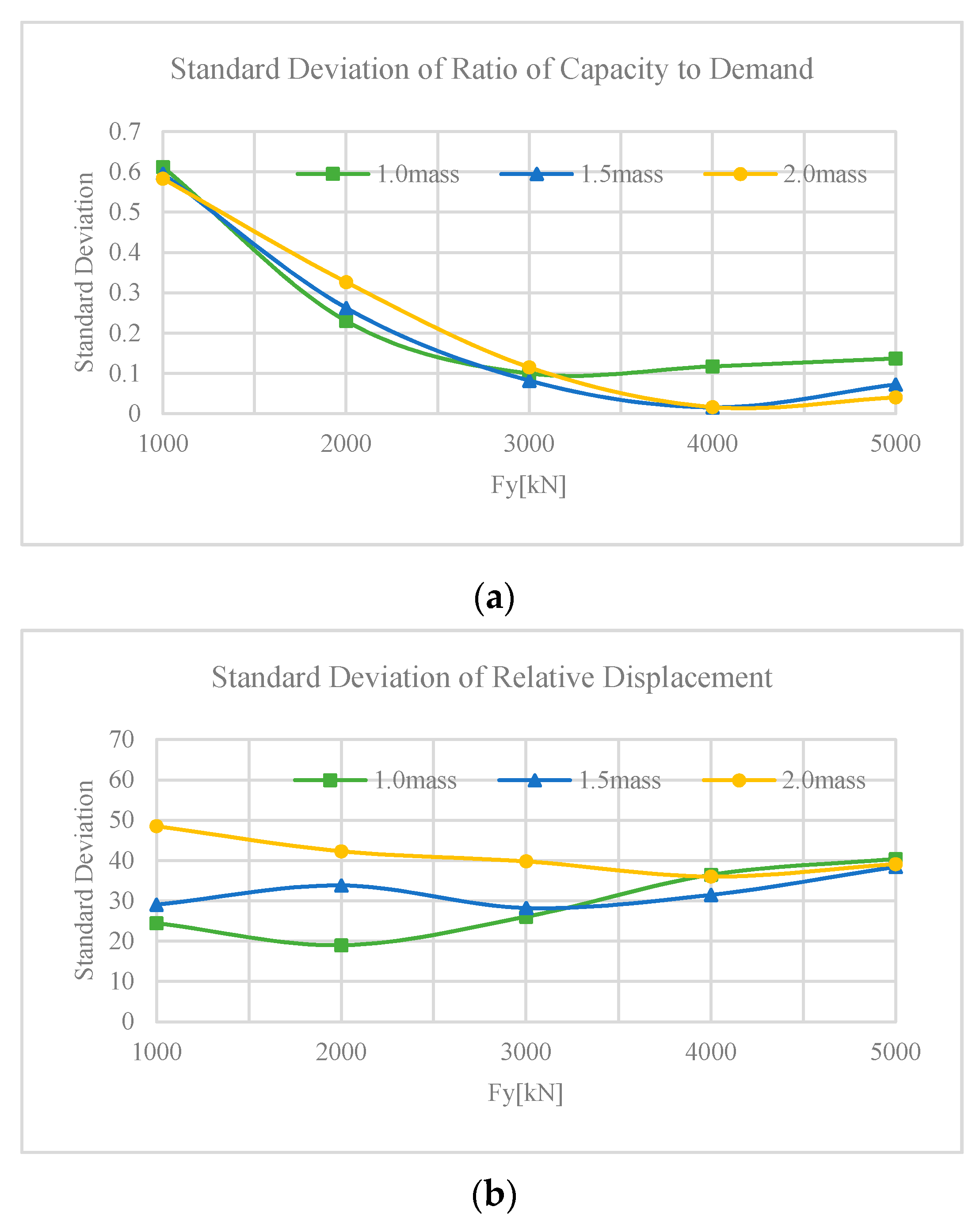
5. Equal Yielding Strength Analysis
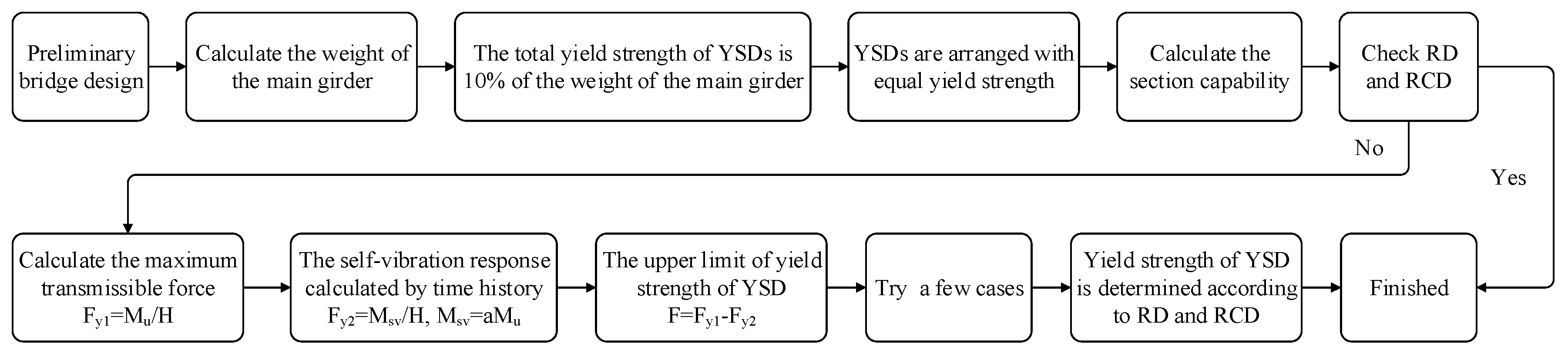
6. Practical Method of YSD Design
7. Conclusions
- 1
- The increase of the yielding strength can effectively reduce the RD at each location, but its efficiency decreases with the increase of the yielding strength. For current engineering practice, the seismic design capacity of the auxiliary pier can essentially be decreased for cost efficiency.
- 2
- Equal yielding strength analysis is much simpler than unequal yielding strength analysis; however, it may not be the most appropriate result theoretically, but it is effective enough for engineering practices.
- 3
- The practical design method using equal yielding strength analysis can greatly reduce the analysis cases and hence improve the efficiency of seismic analysis.
Author Contributions
Funding
Conflicts of Interest
References
- Guidelines for Seismic Design of Highway Bridges; China Communications Press: Beijing, China, 2008.
- Code for Seismic Design of Urban Bridges; China Architecture & Building Press: Beijing, China, 2011.
- Eurocode8: Design Provisions for Earthquake Resistance of Structures (Draft for Development); BSI Group: London, UK, 1998.
- Duan, X.; Xu, Y. Seismic Design Strategy of Cable Stayed Bridges Subjected to Strong Ground Motio. J. Comput. Theor. Nanosci. 2012, 9, 946–951. [Google Scholar] [CrossRef]
- Ali, H.E.M.; Abdel-Ghaffar, A.M. Seismic energy dissipation for cable-stayed bridges using passive devices. Earthq. Eng. Struct. Dyn. 1994, 23, 877–893. [Google Scholar] [CrossRef]
- Ali, H.M.; Abdel-Ghaffar, A.M. Modeling the nonlinear seismic behavior of cable-stayed bridges with passive control bearings. Comput. Struct. 1995, 54, 461–492. [Google Scholar] [CrossRef]
- Domaneschi, M.; Martinelli, L. Extending the benchmark cable-stayed bridge for transverse response under seismic loading. J. Bridge Eng. 2014, 19, 04013003. [Google Scholar] [CrossRef]
- Caicedo, J.M.; Dyke, S.J.; Moon, S.J.; Bergman, L.A.; Turan, G.; Hague, S. Phase ii benchmark control problem for seismic response of cable-stayed bridges. J. Struct. Control 2003, 10, 137–168. [Google Scholar] [CrossRef]
- Dyke, S.J.; Caicedo, J.M.; Turan, G.; Bergman, L.A.; Hague, S. Phase i benchmark control problem for seismic response of cable-stayed bridges. J. Struct. Eng. 2003, 129, 857–872. [Google Scholar] [CrossRef]
- Agrawal, A.K.; Yang, J.N.; He, W.L. Applications of some semiactive control systems to benchmark cable-stayed bridge. J. Struct. Eng. 2003, 129, 884–894. [Google Scholar] [CrossRef]
- Domaneschi, M.; Martinelli, L. Performance comparison of passive control schemes for the numerically improved asce cable-stayed bridge model. Earthq. Struct. 2012, 3, 181–201. [Google Scholar] [CrossRef]
- Soneji, B.B.; Jangid, R.S. Passive hybrid systems for earthquake protection of cable-stayed bridge. Eng. Struct. 2007, 29, 57–70. [Google Scholar] [CrossRef]
- Soneji, B.; Jangid, R. Response of an isolated cable-stayed bridge under bi-directional seismic actions. Struct. Infrastruct. Eng. 2010, 6, 347–363. [Google Scholar] [CrossRef]
- Casciati, F.; Cimellaro, G.P.; Domaneschi, M. Seismic reliability of a cable-stayed bridge retrofitted with hysteretic devices. Comput. Struct. 2008, 86, 1769–1781. [Google Scholar] [CrossRef]
- Saha, P.; Jangid, R. Seismic control of benchmark cable-stayed bridge using passive hybrid systems. IES J. Part A Civ. Struct. Eng. 2009, 2, 1–16. [Google Scholar] [CrossRef]
- Jung, H.-J.; Spencer Billie, F.; Lee, I.-W. Control of seismically excited cable-stayed bridge employing magnetorheological fluid dampers. J. Struct. Eng. 2003, 129, 873–883. [Google Scholar] [CrossRef]
- Iemura, H.; Pradono, M.H. Application of pseudo-negative stiffness control to the benchmark cable-stayed bridge. J. Struct. Control 2003, 10, 187–203. [Google Scholar] [CrossRef]
- Moon, S.-J.; A Bergman, L.; Asce, M.G.; Voulgaris, P. Sliding mode control of cable-stayed bridge subjected to seismic excitation. J. Eng. Mech. 2003, 129. [Google Scholar] [CrossRef]
- Zhou, L.; Wang, X.; Ye, A. Shake table test on transverse steel damper seismic system for long span cable-stayed bridges. Eng. Struct. 2019, 179, 106–119. [Google Scholar] [CrossRef]
- Shen, X.; Camara, A.; Ye, A. Effects of seismic devices on transverse responses of piers in the sutong bridge. Earthq. Eng. Eng. Vib. 2015, 14, 611–623. [Google Scholar] [CrossRef]
- Shen, X.; Wang, X.; Ye, Q.; Ye, A. Seismic performance of transverse steel damper seismic system for long span bridges. Eng. Struct. 2017, 141, 14–28. [Google Scholar] [CrossRef]
- Deng, K.; Pan, P.; Wang, C. Development of crawler steel damper for bridges. J. Constr. Steel Res. 2013, 85, 140–150. [Google Scholar] [CrossRef]
- Ismail, M.; Rodellar, J.; Ikhouane, F. An innovative isolation device for aseismic design. Eng. Struct. 2010, 32, 1168–1183. [Google Scholar] [CrossRef]
- Maleki, S.; Bagheri, S. Pipe damper, part i: Experimental and analytical study. J. Constr. Steel Res. 2010, 66, 1088–1095. [Google Scholar] [CrossRef]
- Maleki, S.; Bagheri, S. Pipe damper, part ii: Application to bridges. J. Constr. Steel Res. 2010, 66, 1096–1106. [Google Scholar] [CrossRef]
- Guan, Z.; Li, J.; Xu, Y. Performance test of energy dissipation bearing and its application in seismic control of a long-span bridge. J. Bridge Eng. 2010, 15, 622–630. [Google Scholar] [CrossRef]
- Parducci, A.M. Seismic isolation of bridges in italy. Bull. N. Z. Natl. Soc. Earthq. Eng. 1992, 25, 193–202. [Google Scholar]
- Xu, Y.; Wang, R.; Li, J. Experimental verification of a cable-stayed bridge model using passive energy dissipation devices. J. Bridge Eng. 2016, 21, 04016092. [Google Scholar] [CrossRef]
- Agostino, M. Development of a new type of hysteretic damper for the seismic protection of bridges. Spec. Publ. 1996, 164, 955–976. [Google Scholar]
- Zhu, B.; Wang, T.; Zhang, L. Quasi-static test of assembled steel shear panel dampers with optimized shapes. Eng. Struct. 2018, 172, 346–357. [Google Scholar] [CrossRef]
- Xiao-xian, L.I.U.; Jian-zhong, L.I.; Xu, C. Effects of x-shaped elastic-plastic steel shear keys on transverse seismic responses of a simply-supported girder bridge. J. Vib. Shock 2015, 34, 143–149. [Google Scholar]
- Pan, P.; Yan, H.; Wang, T.; Xu, P.; Xie, Q. Development of steel dampers for bridges to allow large displacement through a vertical free mechanism. Earthq. Eng. Eng. Vib. 2014, 13, 375–388. [Google Scholar] [CrossRef]
- Vasseghi, A. Energy dissipating shear key for precast concrete girder bridges. Sci. Iran. 2011, 18, 296–303. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, R.; Zong, Z.; Wang, C.; Li, A. Study on seismic response control of a single-tower self-anchored suspension bridge with elastic-plastic steel damper. Sci. China Technol. Sci. 2012, 55, 1496–1502. [Google Scholar] [CrossRef]
- Ismail, M.; Casas Joan, R. Novel isolation device for protection of cable-stayed bridges against near-fault earthquakes. J. Bridge Eng. 2014, 19, A4013002. [Google Scholar] [CrossRef]
- SAP2000; University of California: Berkeley, CA, USA, 1996.
- CSI Aanalysis Reference Manual; Computers & Structures, Inc.: Berkeley, CA, USA, 2016.
- Bathe, K.-J.; Wilson, E.L. Numerical Methods in Finite Element Analysis; Prentice Hall: Englewood Cliffs, NJ, USA, 1976. [Google Scholar]
- Ernst, H.J. Der e-modul von seilen unter beruecksichtigung des durchhanges. Der Bauing. 1965, 40, 52–55. [Google Scholar]
- Battaini, M.M. Base isolation of allied join force command headquarters naples. In Proceedings of the 10th World Conference on Seismic Isolation, Energy Dissipation and Active Vibrations Control of Structures, Istanbul, Turkey, 27–30 May 2007. [Google Scholar]
- Priestley, M.J.N.; Seible, F.; Calvi, G.M. Seismic Design and Retrofit of Bridge; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Oh, S.-H.; Song, S.-H.; Lee, S.-H.; Kim, H.-J. Seismic response of base isolating systems with u-shaped hysteretic dampers. Int. J. Steel Struct. 2012, 12, 285–298. [Google Scholar] [CrossRef]
- Martins, A.M.B.; Simões, L.M.C.; Negrão, J.H.J.O. Optimization of cable forces on concrete cable-stayed bridges including geometrical nonlinearities. Comput. Struct. 2015, 155, 18–27. [Google Scholar] [CrossRef]
- Anil, K.C. Dynamics of Structures: Theory and Applications to Earthquake Engineering; Pearson Education, Inc.: London, UK, 2012. [Google Scholar]
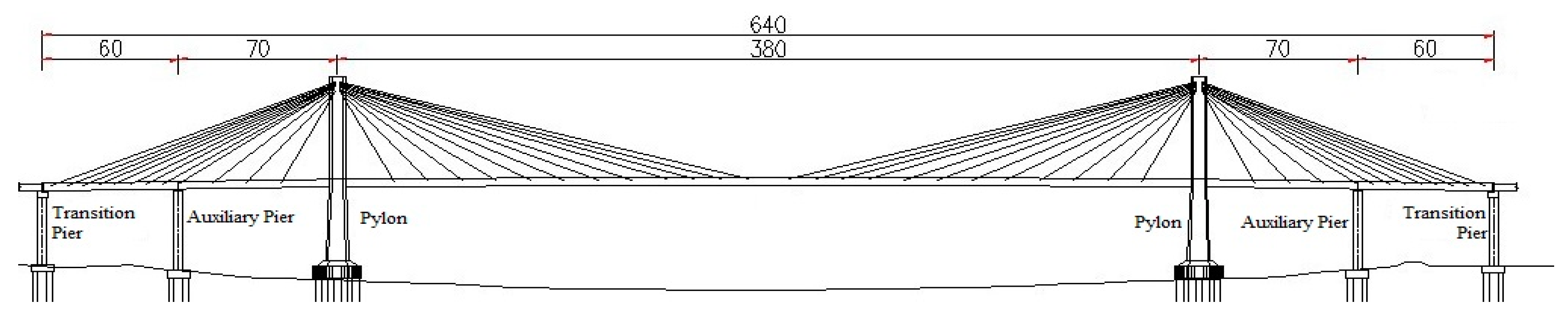
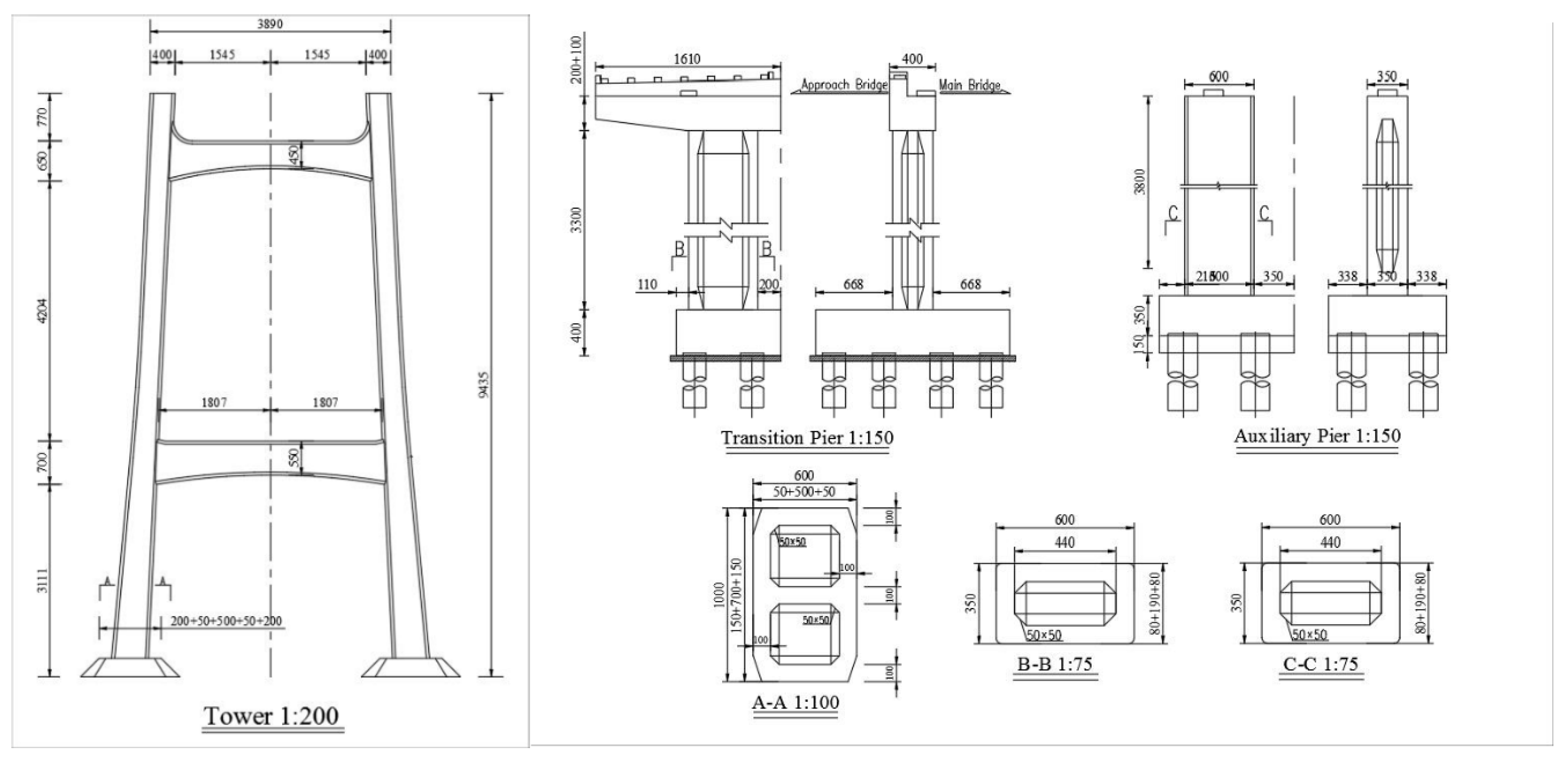
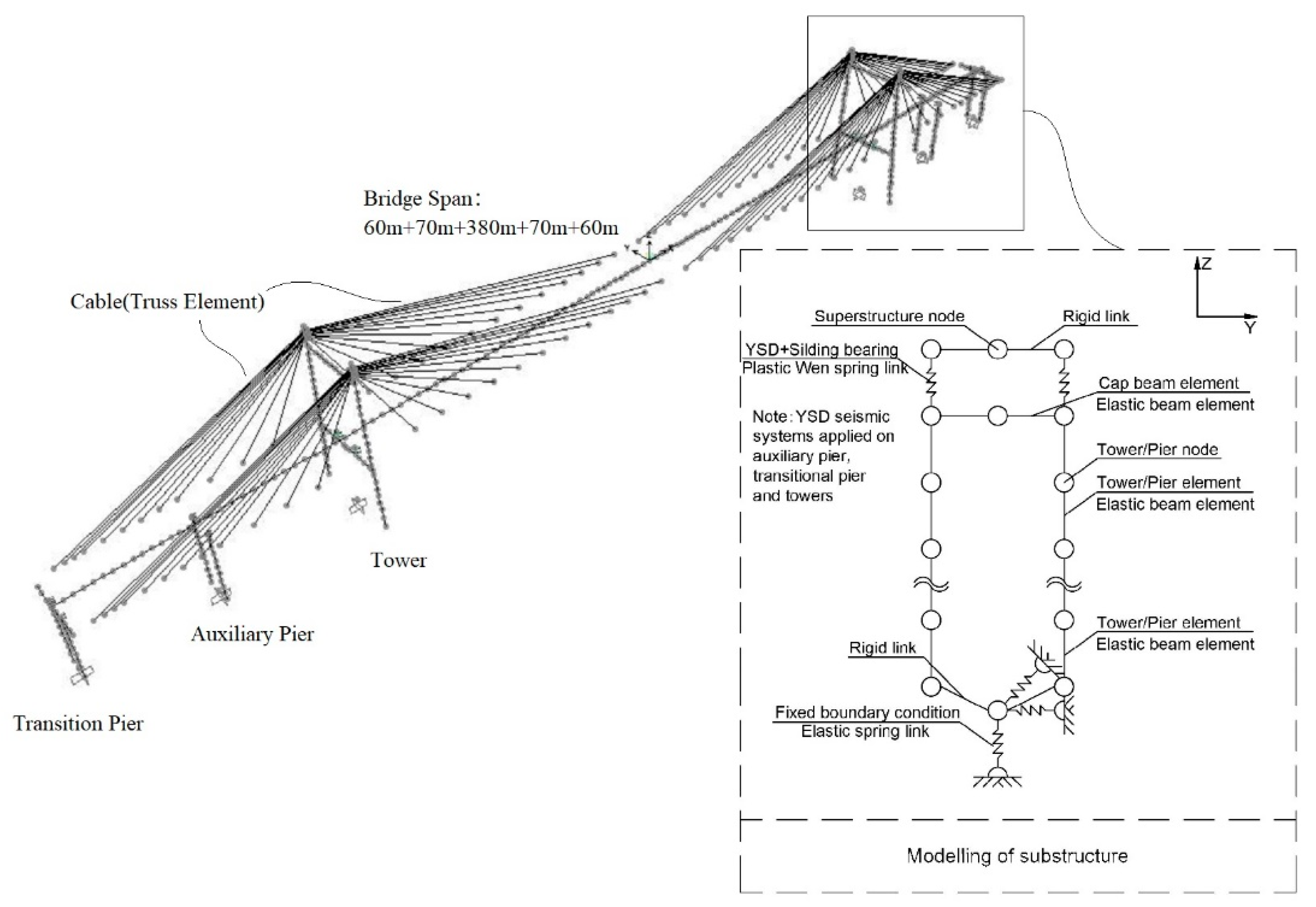
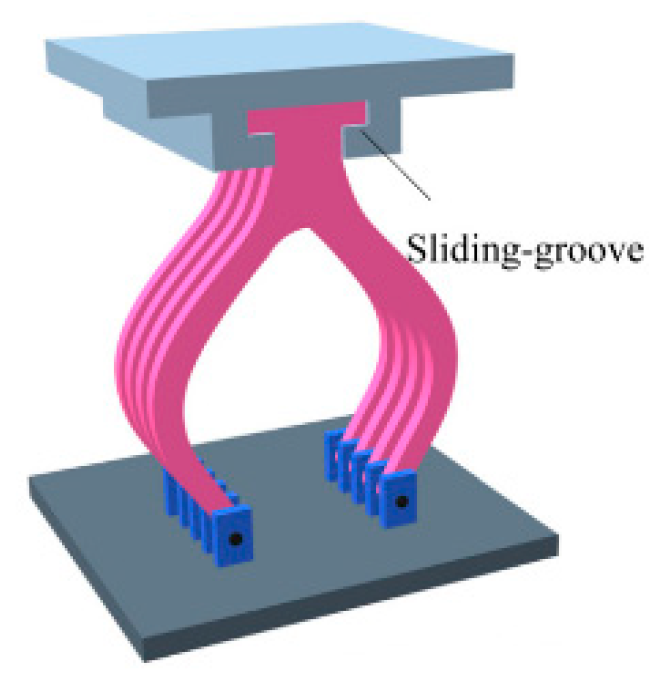

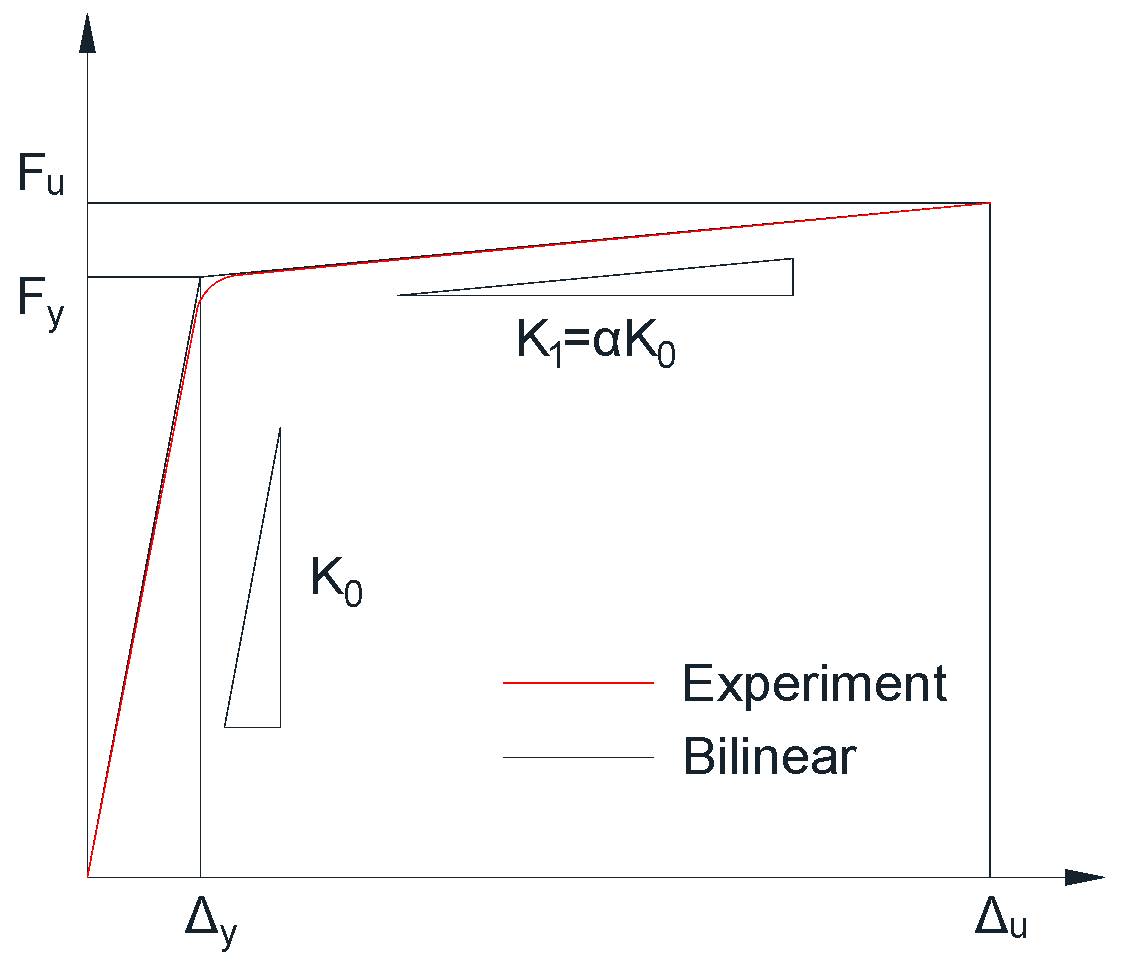
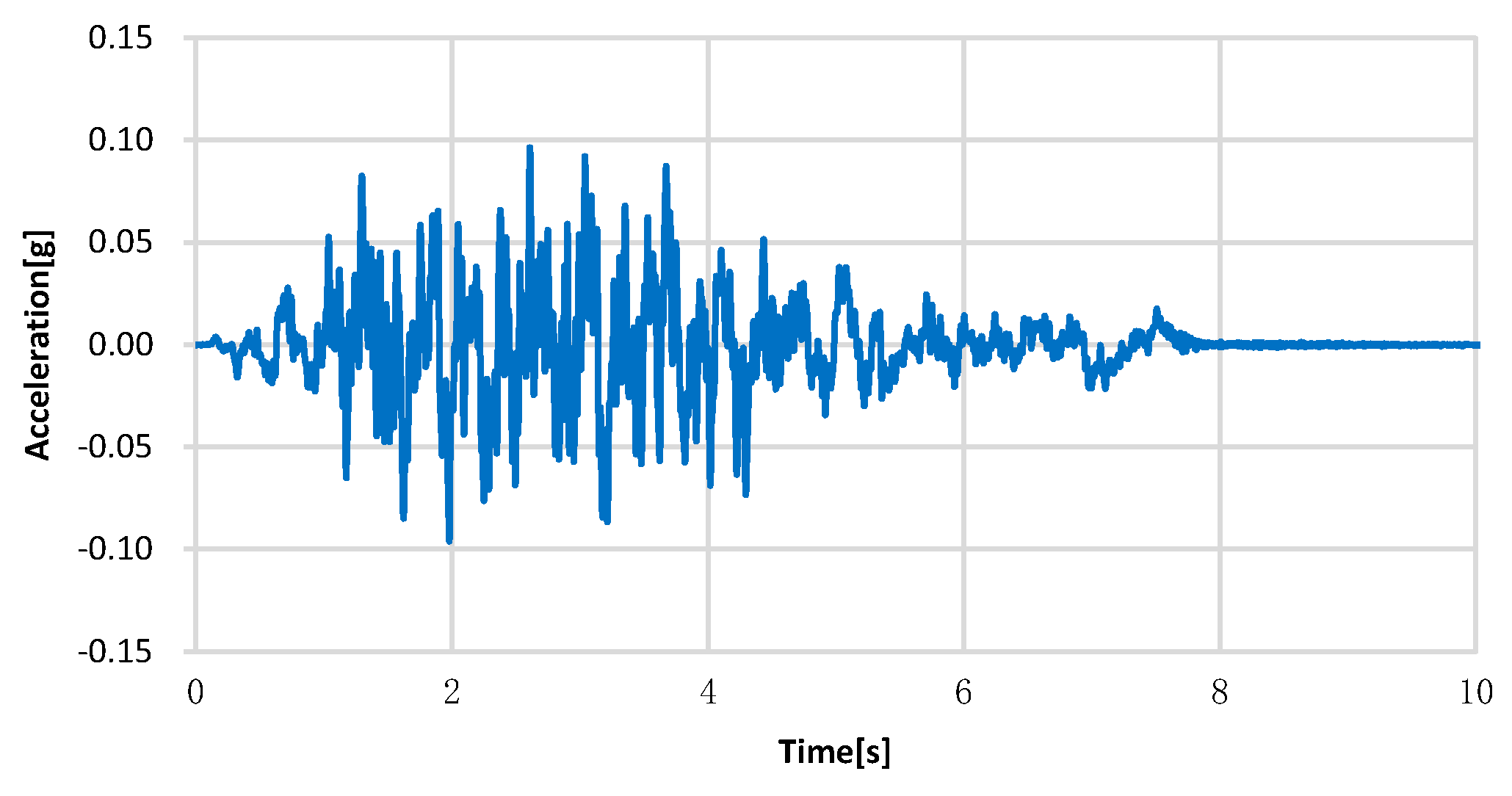
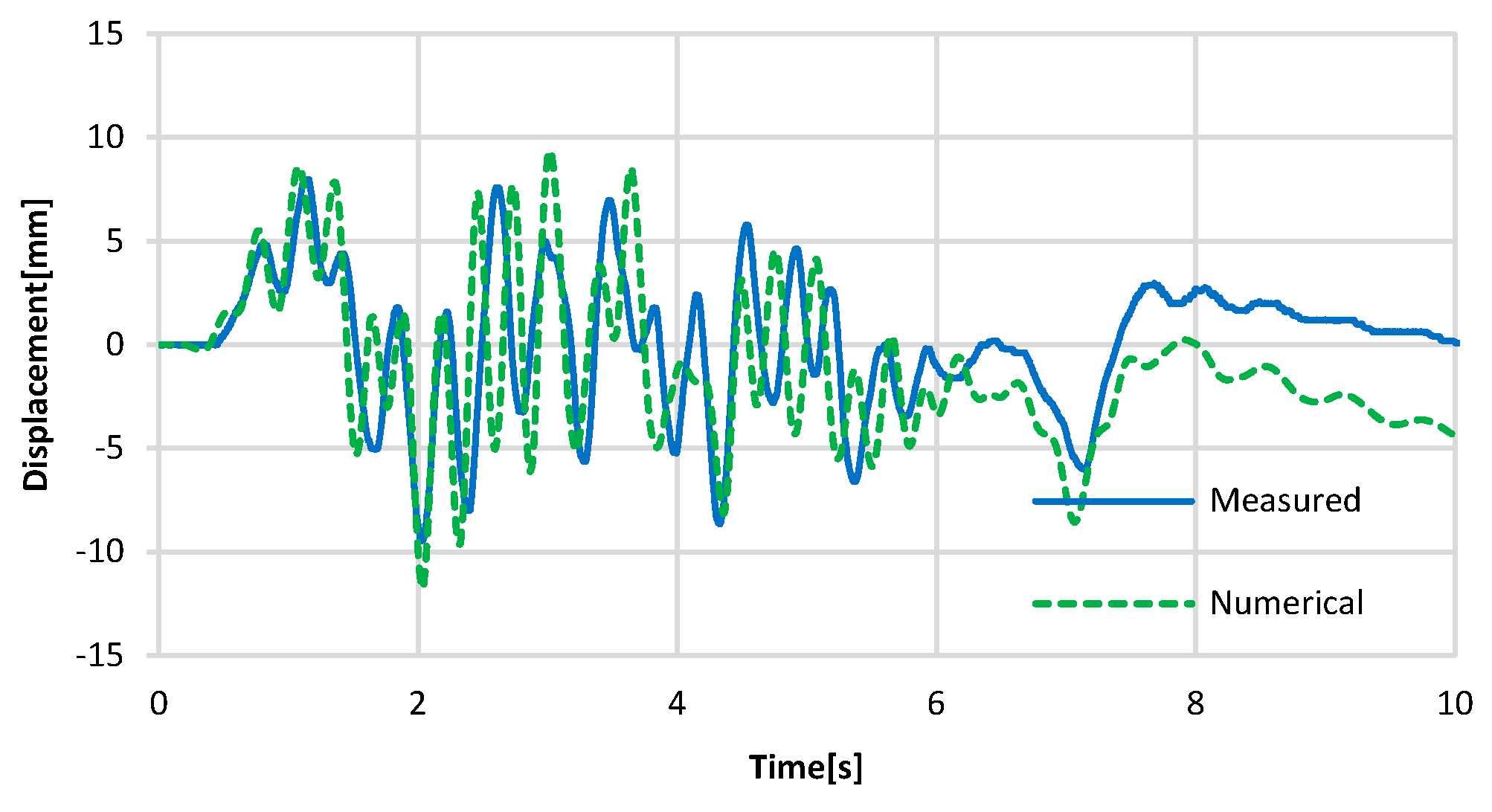
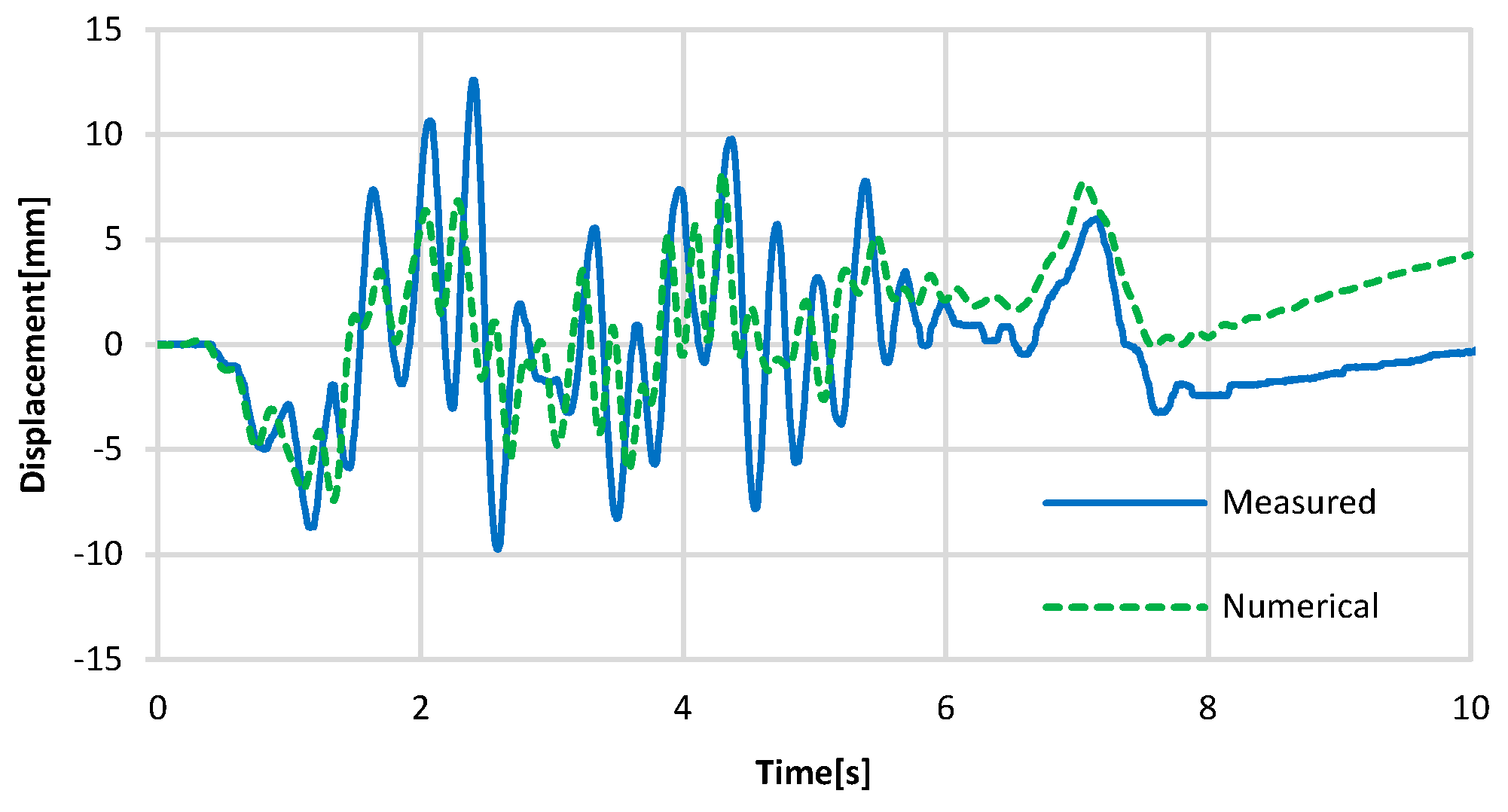

| Material and Component | Standard Strength (MPa) | Young’s Modulus (MPa) |
|---|---|---|
| Concrete (tower) | 32.4 | 3.45 × 104 |
| Concrete (transition pier) | 26.8 | 3.25 × 104 |
| Concrete (auxiliary pier) | 26.8 | 3.25 × 104 |
| Cable | 1770 | 2.05 × 105 |
| Rebar | 400 | 2.06 × 105 |
| Location | Degree of Freedom (without YSDs) | Degree of Freedom (with YSDs) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| UX | UY | UZ | RX | RY | RZ | UX | UY | UZ | RX | RY | RZ | |
| Tower | 0 | 1 | 1 | 0 | 0 | 0 | 0 | YSD (2) | 1 | 0 | 0 | 0 |
| Auxiliary pier | 0 | 0 | 1 | 0 | 0 | 0 | 0 | YSD (2) | 1 | 0 | 0 | 0 |
| Transition pier | 0 | 0 | 1 | 0 | 0 | 0 | 0 | YSD (2) | 1 | 0 | 0 | 0 |
| Bridge System | YSD Layout Plan | RCD at Tower | RCD at TP | RCD at AP | RD at Tower | RD at TP | RD at AP | Tower TD | Mid-Span Lateral Drift |
|---|---|---|---|---|---|---|---|---|---|
| A | Without YSDs | 0.59 | 2.04 | 1.99 | 0 | 417 | 235 | 173 | 515 |
| B | Designed layout 1 (M) | 1.21 | 1.19 | 1.19 | 189 | 108 | 69 | 174 | 312 |
| Designed layout 2 (M) | 1.17 | 1.02 | 1.99 | 118 | 125 | 125 | 168 | 227 | |
| Designed layout 3 (S) | 1.25 | 1.15 | 1.24 | 126 | 106 | 53 | 169 | 235 | |
| Designed layout 4 (S) | 1.18 | 1.14 | 2.02 | 125 | 135 | 131 | 164 | 209 |
| Fyt | M1 | M of Tower | Msv of Tower | α of Tower | Fyp/Fya | M2 | M of TP | M of AP | Msv of TP | Msv of AP | α of TP | α of AP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9000 | 360000 | 508542 | 148542 | 0.29 | 5000 | 200000 | 272719 | 256396 | 72719 | 56396 | 0.27 | 0.22 |
| Conventional System | YSD System (After Yielding) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Top View | Side View | layout 3 | layout 4 | ||||||
| Top View | Side View | MPMR | Period | MPMR | Period | MPMR | Period | ||
 |  | 10.8% | 3.42 s |  |  | 48.0% | 7.30 s | 48.4% | 7.52 s |
 |  | 53.5% | 1.18 s |  |  | 19.0% | 0.95 s | 19.0% | 0.95 s |
| Bridge System | YSD Layout Plan | RCD of Tower | RCD of TP | RCD of AP | RD of Tower | RD of TP | RD of AP | Tower TD | Mid-Span Lateral Drift |
|---|---|---|---|---|---|---|---|---|---|
| A | Without YSDs | 0.59 | 2.04 | 1.99 | 0 | 417 | 235 | 173 | 515 |
| B | Designed layout 5 | 1.24 | 1.30 | 1.44 | 124 | 130 | 80 | 164 | 198 |
| Designed layout 6 | 1.28 | 1.70 | 1.66 | 189 | 170 | 152 | 165 | 245 |
| For a Large and Uniform RCD | For a Small and Uniform RD | |||||
|---|---|---|---|---|---|---|
| Yield Strength | Weight | Ratio | Yield Strength | Weight | Ratio | |
| 1.0 mass | 12 × 3000 | 280,000 | 13% | 12 × 2000 | 280,000 | 9% |
| 1.5 mass | 12 × 4000 | 420,000 | 11% | 12 × 3000 | 420,000 | 9% |
| 2.0 mass | 12 × 4000 | 560,000 | 9% | 12 × 4000 | 560,000 | 9% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Y.; Zeng, Z.; Cui, C.; Zeng, S. Practical Design Method of Yielding Steel Dampers in Concrete Cable-Stayed Bridges. Appl. Sci. 2019, 9, 2857. https://doi.org/10.3390/app9142857
Xu Y, Zeng Z, Cui C, Zeng S. Practical Design Method of Yielding Steel Dampers in Concrete Cable-Stayed Bridges. Applied Sciences. 2019; 9(14):2857. https://doi.org/10.3390/app9142857
Chicago/Turabian StyleXu, Yan, Zeng Zeng, Cunyu Cui, and Shijie Zeng. 2019. "Practical Design Method of Yielding Steel Dampers in Concrete Cable-Stayed Bridges" Applied Sciences 9, no. 14: 2857. https://doi.org/10.3390/app9142857
APA StyleXu, Y., Zeng, Z., Cui, C., & Zeng, S. (2019). Practical Design Method of Yielding Steel Dampers in Concrete Cable-Stayed Bridges. Applied Sciences, 9(14), 2857. https://doi.org/10.3390/app9142857




