Geometry of the Vocal Tract and Properties of Phonation near Threshold: Calculations and Measurements
Abstract
Featured Application
Abstract
1. Introduction
2. Models and Methods
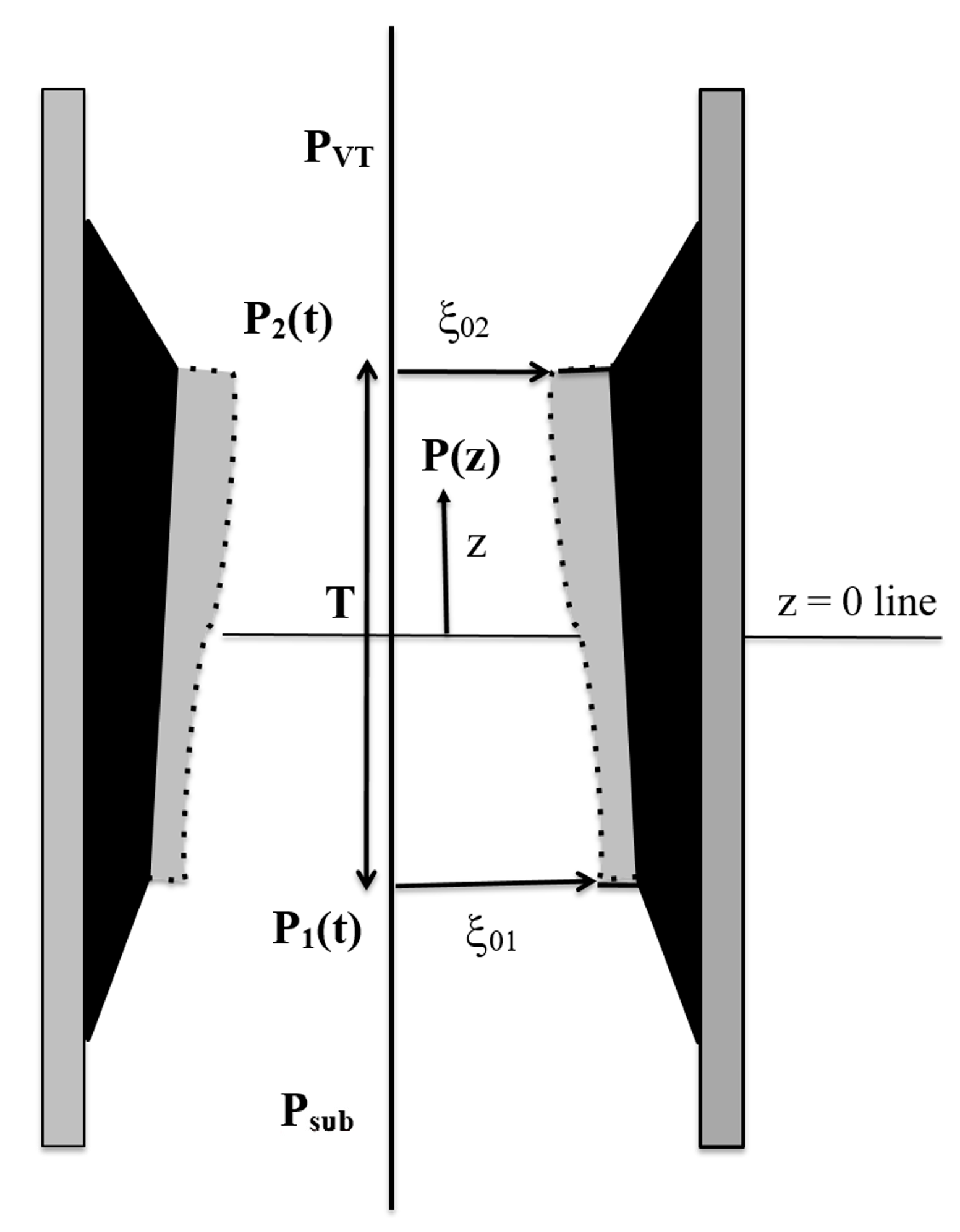
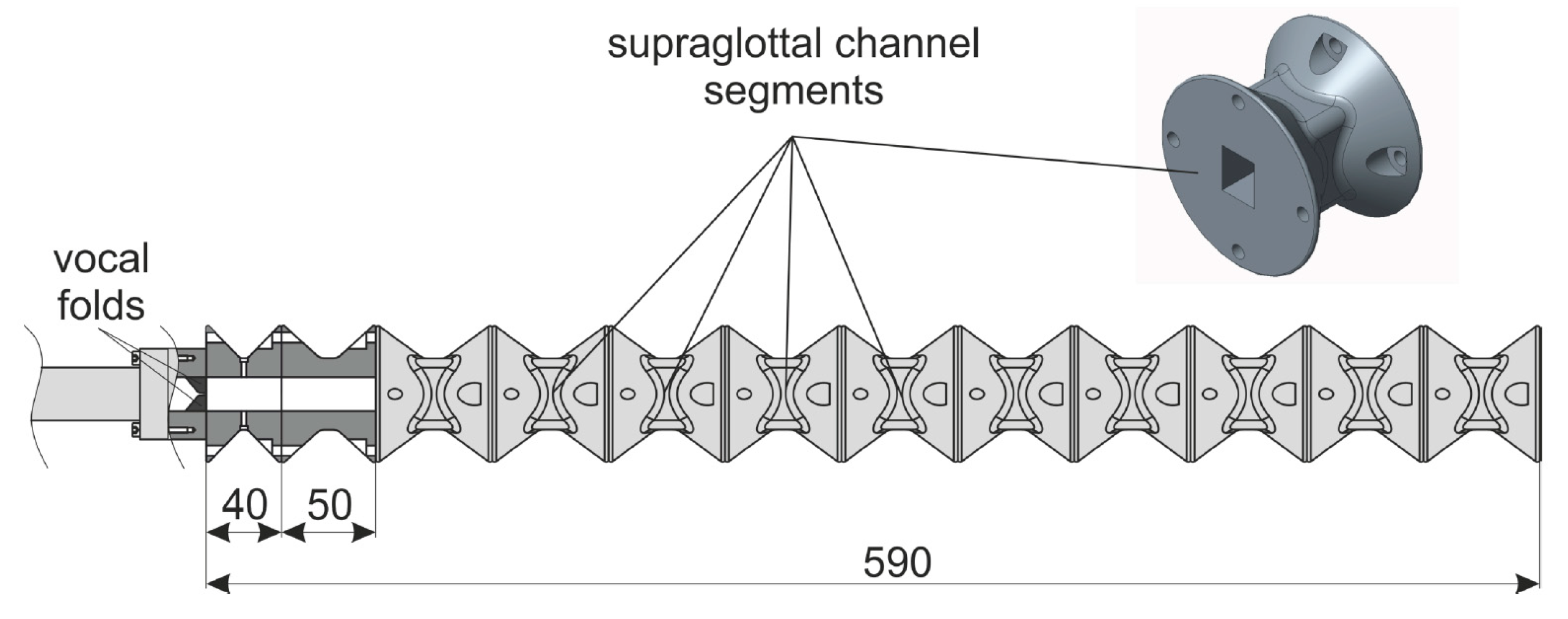
2.1. Surface Wave Model and the Vocal Tract
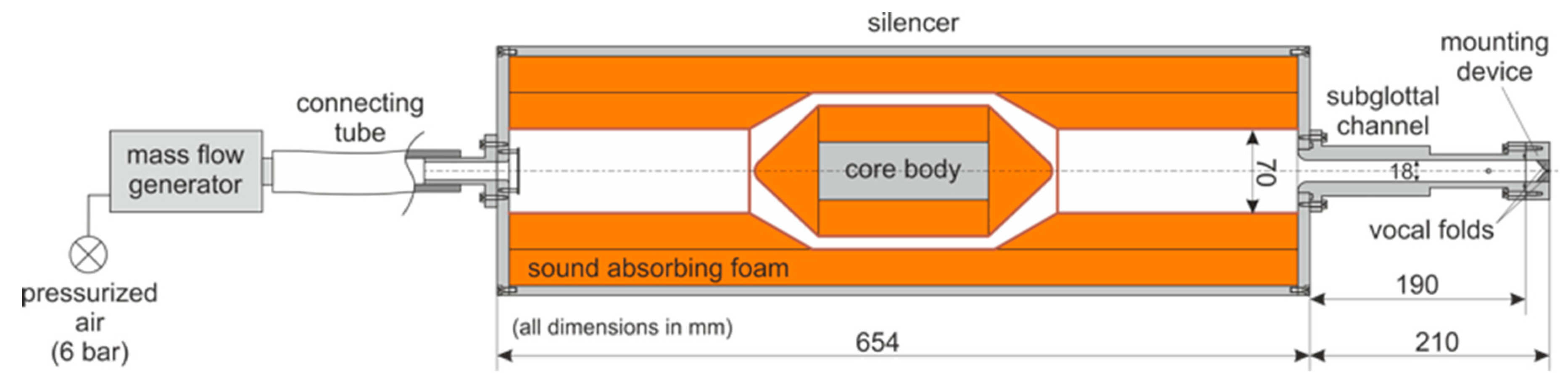
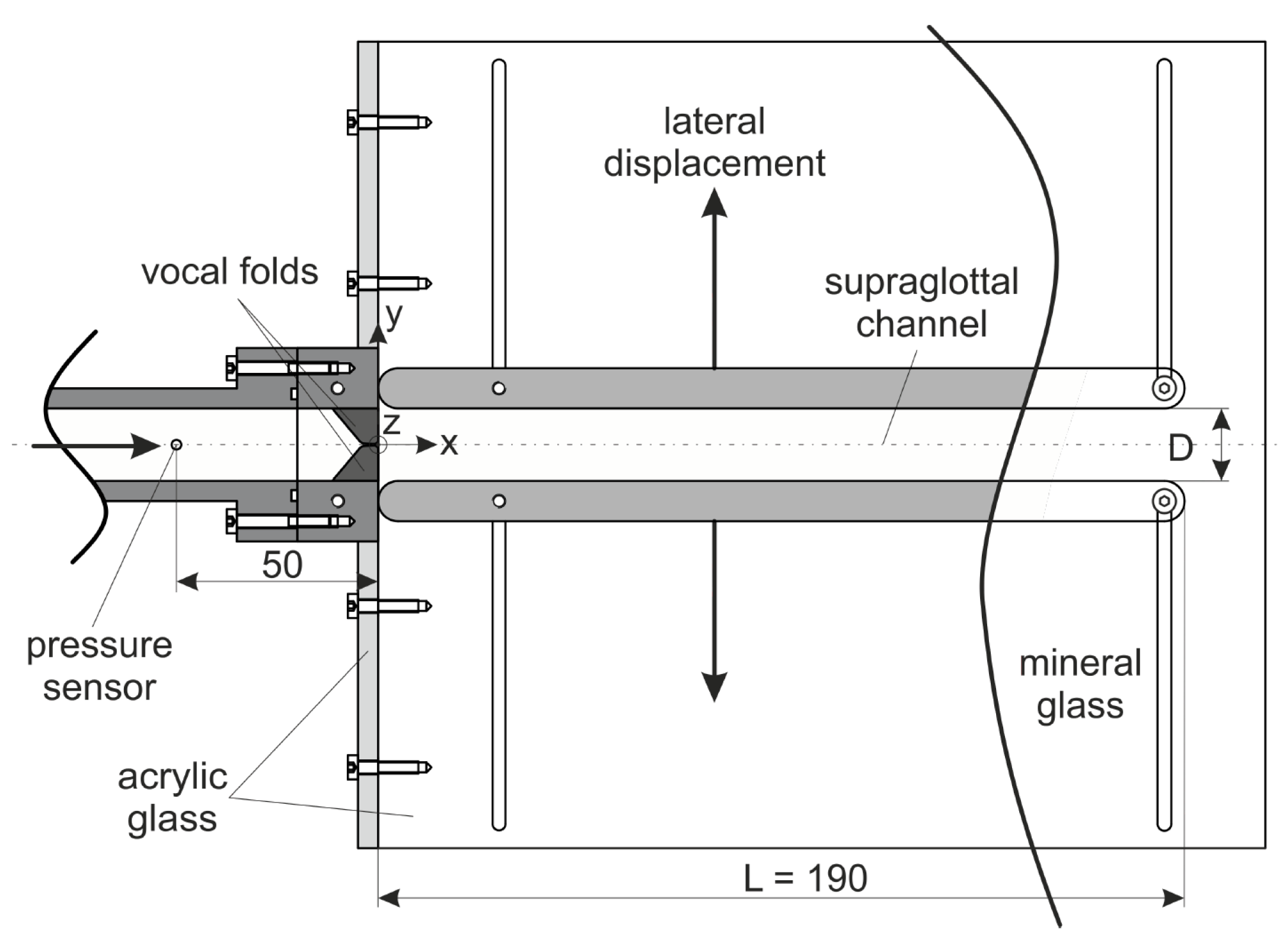
2.2. Larynx Model and Measuring Setup
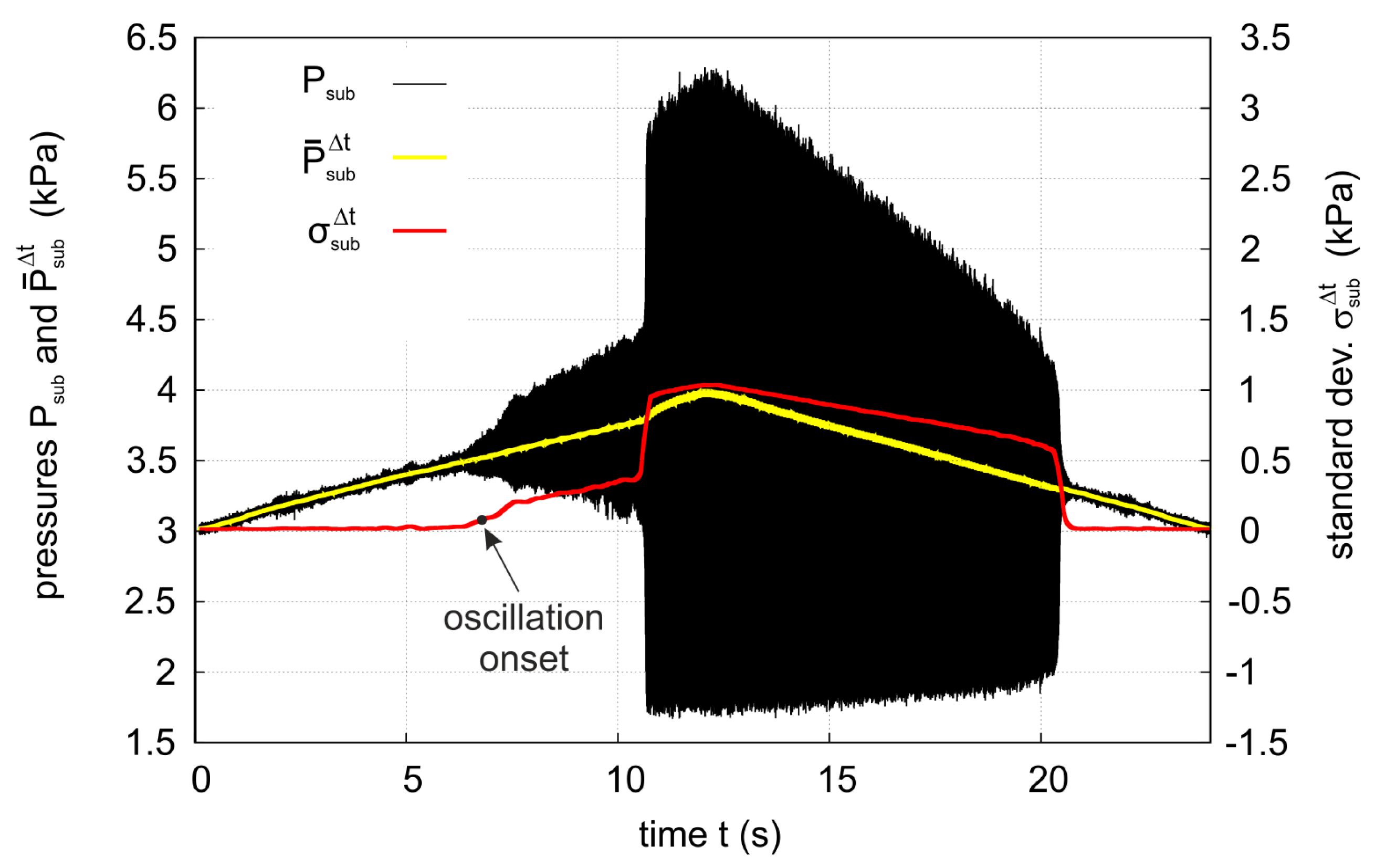
2.3. Onset Detection: Methodology
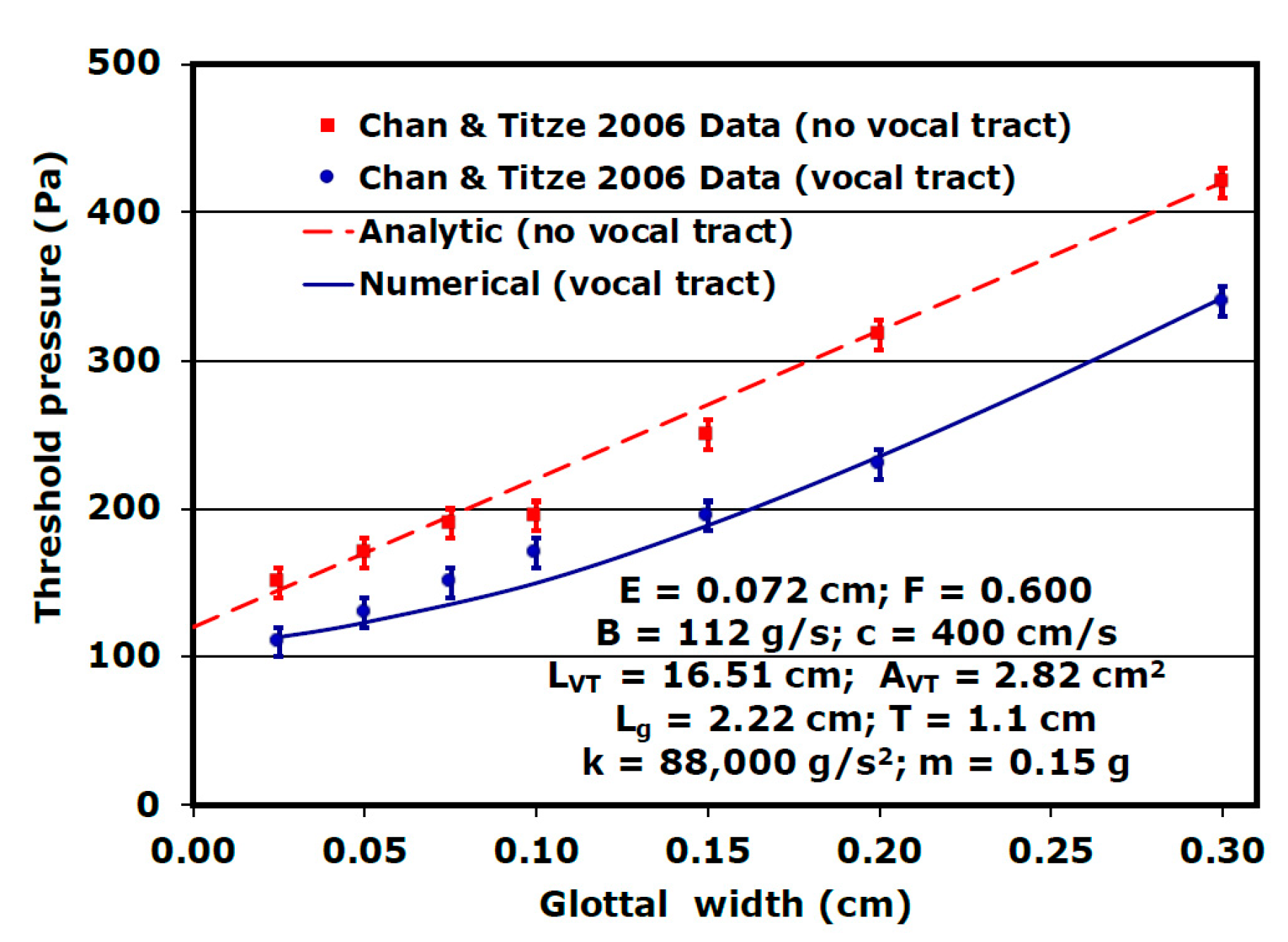
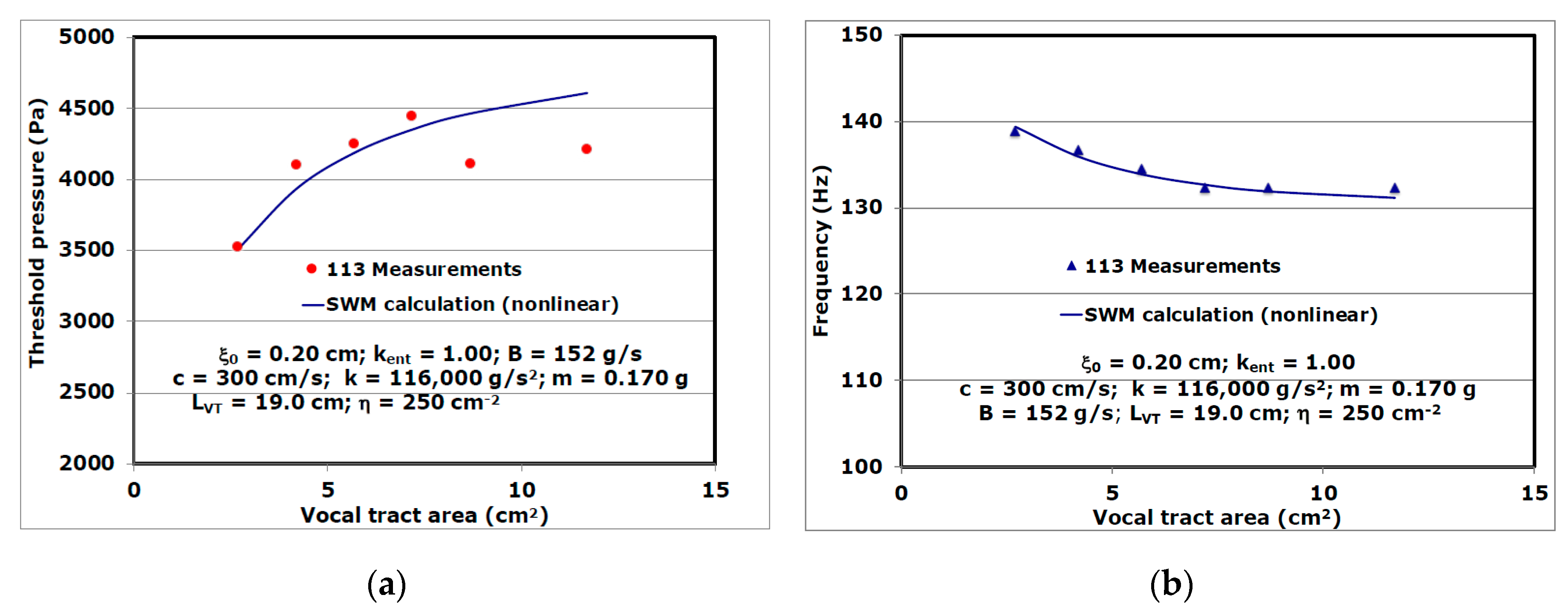
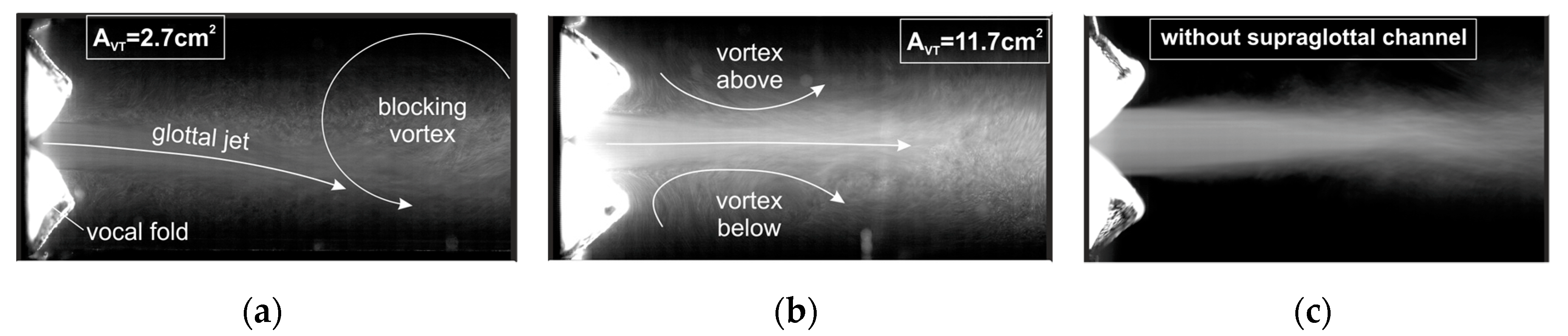
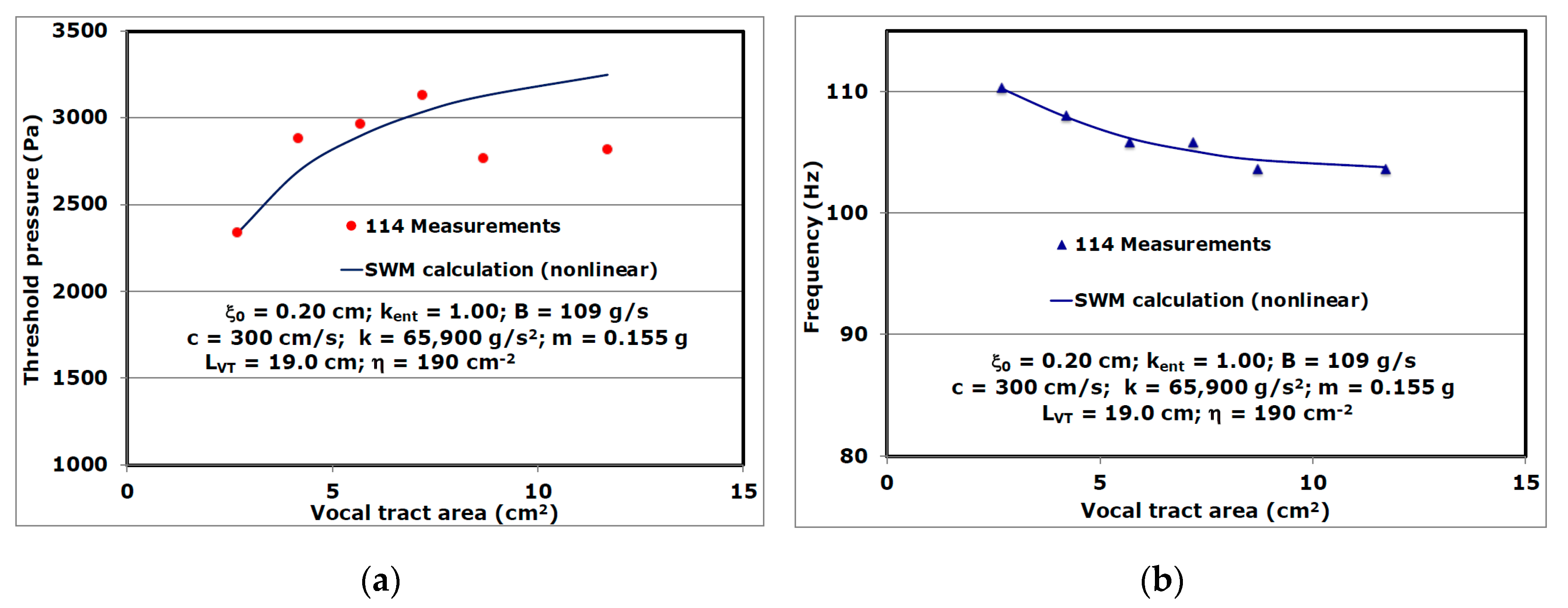
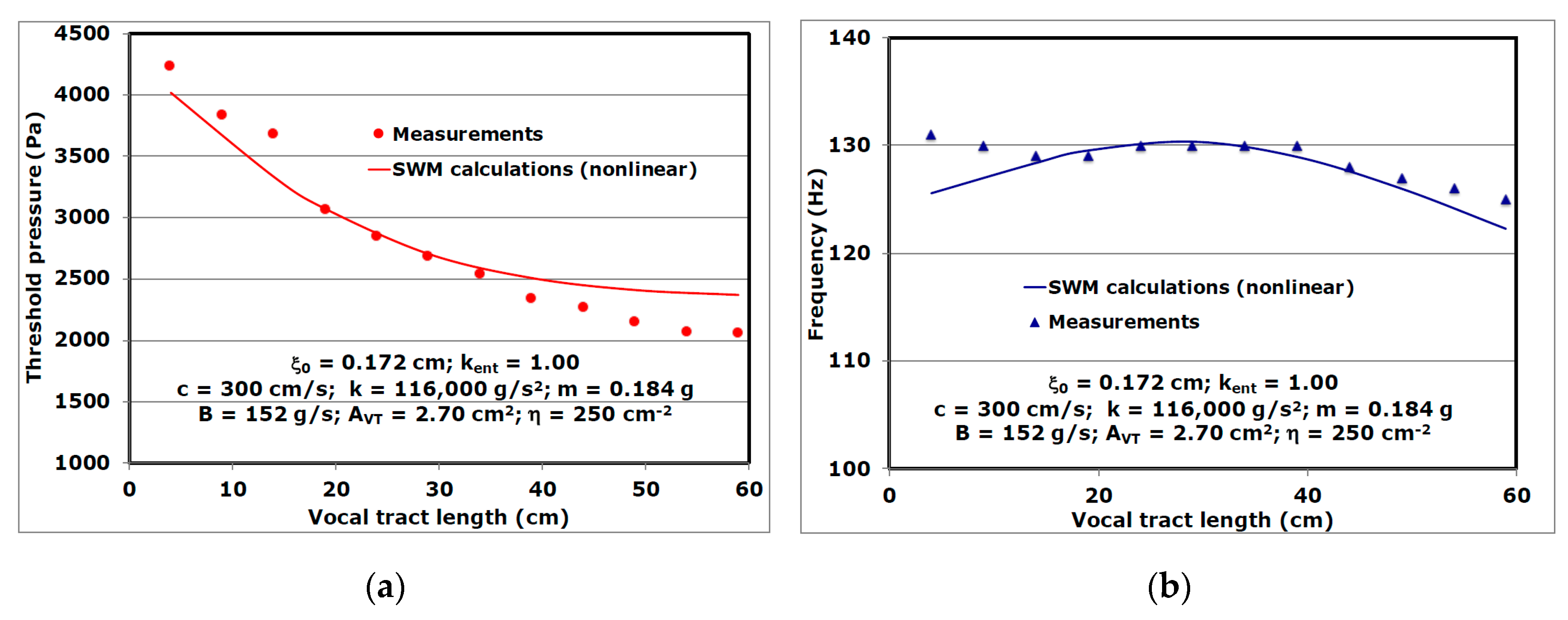
3. Results and Discussion
4. Limitations
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ishizaka, K.; Flanagan, J. Synthesis of voiced sounds from a two-mass model of the vocal cords. Bell Syst. Tech. J. 1972, 51, 1233–1268. [Google Scholar] [CrossRef]
- Titze, I. The physics of small amplitude oscillation of the vocal folds. J. Acoust. Soc. Am. 1988, 83, 1536–1552. [Google Scholar] [CrossRef]
- Titze, I.; Schmidt, S.; Titze, M. Phonation threshold pressure in a physical model of the vocal fold mucosa. J. Acoust. Soc. Am. 1995, 97, 3080–3084. [Google Scholar] [CrossRef]
- Chan, R.; Titze, I.; Titze, M. Further studies of phonation threshold pressure in a physical model of the vocal fold mucosa. J. Acoust. Soc. Am. 1997, 101, 3722–3727. [Google Scholar] [CrossRef]
- Chan, R.; Titze, I. Dependence of phonation threshold pressure on vocal tract acoustics and vocal fold tissue mechanics. J. Acoust. Soc. Am. 2006, 119, 2351–2362. [Google Scholar] [CrossRef]
- Fulcher, L.; Scherer, R. Phonation threshold pressure: Comparison of calculations and measurements taken with physical models of the vocal fold mucosa. J. Acoust. Soc. Am. 2011, 130, 1597–1605. [Google Scholar] [CrossRef]
- Flanagan, J.; Landgraf, L. Self-oscillating source for vocal-tract synthesizers. IEEE Trans. Audio Electroacoust. 1968, 16, 57–64. [Google Scholar] [CrossRef]
- Koizumi, T.; Taniguchi, S.; Hiromitsu, S. Two-mass models of the vocal cords for natural sounding voice synthesis. J. Acoust. Soc. Am. 1987, 82, 1179–1192. [Google Scholar] [CrossRef]
- Koizumi, T.; Taniguchi, S.; Hiromitsu, S. Reply to ‘Two-mass model of the vocal cords for natural sounding voice synthesis‘. J. Acoust. Soc. Am. 1989, 85, 2221–2223. [Google Scholar] [CrossRef]
- Pelorson, X.; Hirschberg, A.; van Hassel, R.; Wijnands, A.; Auregan, Y. Theoretical and experimental study of quasisteady-flow separation within the glottis during phonation. Application to a modified two-mass model. J. Acoust. Soc. Am. 1994, 96, 3416–3431. [Google Scholar] [CrossRef]
- De Mul, F.; George, N.; Qiu, Q.; Rakhorst, G.; Schutte, H. Depth kymography of vocal fold vibrations: Part II. Simulations and direct comparisons with 3 D profile measurements. Phys. Med. Biol. 2009, 54, 3955–3977. [Google Scholar] [CrossRef]
- Cisonni, J.; van Hirtum, A.; Pelorson, X.; Willems, J. Theoretical simulation and experimental validation of inverse quasi-one-dimensional steady and unsteady glottal flow models. J. Acoust. Soc. Am. 2008, 124, 535–545. [Google Scholar] [CrossRef]
- Zhang, Z.; Neubauer, J.; Berry, D. The influence of subglottal acoustics on laboratory models of phonation. J. Acoust. Soc. Am. 2006, 120, 1558–1569. [Google Scholar] [CrossRef]
- Gupta, V.; Wilson, T.; Beavers, G. A model for vocal cord excitation. J. Acoust. Soc. Am. 1973, 54, 1607–1617. [Google Scholar] [CrossRef]
- Zhang, Z.; Neubauer, J.; Berry, D. Influence of vocal fold stiffness and acoustic loading on flow-induced vibration of a single-layer vocal fold model. J. Sound Vib. 2009, 322, 299–313. [Google Scholar] [CrossRef]
- Lucero, J.; Lourenco, K.; Hermant, N.; Van Hirtum, A.; Pelorson, X. Effect of source-tract acoustical coupling on the oscillation onset of the vocal folds. J. Acoust. Soc. Am. 2012, 132, 403–411. [Google Scholar] [CrossRef]
- Kniesburges, S. Fluid-Structure-Acoustic Interaction during Phonation in a Synthetic Larynx Model. Ph.D. Thesis, Friedrich-Alexander Universitaet Erlangen-Nuernberg, Erlangen, Germany, 2014. [Google Scholar]
- Kähler, G. Acoustic Phonetic Study of Additive Manufactured Supra-Glottal Geometries. Master’s Thesis, Friedrich-Alexander University Erlangen-Nürnberg, Erlangen, Germany, 2016. [Google Scholar]
- Titze, I. Phonation threshold pressure measurement with a semi-occluded vocal tract. J. Speech Lang. Hear. Res. 2009, 52, 1062–1072. [Google Scholar] [CrossRef]
- Titze, I. Voice training and therapy with a semi-occluded vocal tract: Rationale and scientific underpinnings. J. Speech Lang. Hear. Res. 2006, 49, 448–459. [Google Scholar] [CrossRef]
- Agarwal, M.; Scherer, R.; Holien, H. The false vocal folds: Shape and size in frontal view during phonation based on laminagraphic tracings. J. Voice 2003, 17, 97–113. [Google Scholar] [CrossRef]
- Plexico, L.; Sandage, M.; Faver, K. Assessment of phonation threshold pressure: A critical review and clinical applications. Am. J. Speech Lang. Pathol. 2011, 20, 348–366. [Google Scholar] [CrossRef]
- Fulcher, L.; Scherer, R.; Powell, T. Pressure distributions in a static physical model of the uniform glottis: Entrance and exit coefficients. J. Acoust. Soc. Am. 2011, 129, 1548–1553. [Google Scholar] [CrossRef] [PubMed]
- Fulcher, L.; Scherer, R.; Anderson, N. Entrance loss coefficients and exit coefficients for a physical model of the glottis with convergent angles. J. Acoust. Soc. Am. 2014, 136, 1312–1319. [Google Scholar] [CrossRef] [PubMed]
- Steinecke, I.; Herzel, H. Bifurcations in an asymmetric vocal fold model. J. Acoust. Soc. Am. 1995, 97, 1874–1884. [Google Scholar] [CrossRef] [PubMed]
- Tokuda, I.; Horacek, J.; Svec, J.; Herzel, H. Comparison of biomechanical modeling of register transitions and voice instabilities with excised larynx experiments. J. Acoust. Soc. Am. 2007, 122, 519–531. [Google Scholar] [CrossRef] [PubMed]
- Lucero, J. Dynamics of the two-mass model of the vocal folds: Equilibria, bifurcations, and oscillation region. J. Acoust. Soc. Am. 1993, 94, 3104–3111. [Google Scholar] [CrossRef]
- Durst, F.; Heim, U.; Ünsal, B.; Kullik, G. Mass flow rate control system for time-dependent laminar and turbulent flow investigations. Meas. Sci. Technol. 2003, 14, 893–903. [Google Scholar] [CrossRef]
- Rupitsch, S.; Ilg, J.; Sutor, A.; Lerch, R.; Döllinger, M. Simulation based estimation of dynamic mechanical properties of viscoelastic materials used for vocal fold models. J. Sound Vib. 2011, 330, 4447–4459. [Google Scholar] [CrossRef]
- Ilg, J.; Rupitsch, S.; Sutor, A.; Lerch, R. Determination of dynamic material properties of silicone rubber using one-point measurements and finite element simulations. IEEE Trans. Instrum. Meas. 2012, 61, 3031–3038. [Google Scholar] [CrossRef]
- Thomson, S.; Mongeau, L.; Frankel, S. Physical and numerical flow-excited vocal fold model. In Proceedings of the Third International Workshop MAVEBA, Florence, Italy, 10–12 December 2003; pp. 147–150. [Google Scholar]
- Thomson, S.; Mongeau, L.; Frankel, S. Aerodyamic transfer of energy to the vocal folds. J. Acoust. Soc. Am. 2005, 118, 1689–1700. [Google Scholar] [CrossRef]
- Scherer, R.; Shinwari, D.; De Witt, K.; Zhang, C.; Kucinsch, B.; Afjeh, A. Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees. J. Acoust. Soc. Am. 2001, 109, 1616–1630. [Google Scholar] [CrossRef]
- Crump, S. Apparatus and Method for Creating Three-Dimensional Objects. US Patent US5121329 A, 10 October 1989. [Google Scholar]
- Kniesburges, S.; Birk, V.; Lodermeyer, A.; Schützenberger, A.; Bohr, C.; Becker, S. Effect of the ventricular folds in a synthetic larynx model. J. Biomech. 2017, 55, 128–133. [Google Scholar] [CrossRef]
- Roderer, H. Digitale Signalverarbeitung, 1st ed.; Vogel Buchverlag: Würzburg, Germany, 2010. [Google Scholar]
- Lodermeyer, A.; Becker, S.; Döllinger, M.; Kniesburges, S. Phase-locked flow field analysis in a synthetic human larynx model. Exp. Fluids 2015, 56, 1–13. [Google Scholar] [CrossRef]
- Lodermeyer, A.; Tautz, M.; Becker, S.; Döllinger, M.; Birk, V.; Kniesburges, S. Aeroacoustic analysis of the human phonation process based on a hybrid PIV approach. Exp. Fluids 2018, 59, 1–15. [Google Scholar] [CrossRef]
- Lucero, J. A theoretical study of the hysteresis phenomenon at vocal fold onset-offset. J. Acoust. Soc. Am. 1999, 105, 423–431. [Google Scholar] [CrossRef] [PubMed]
- Kniesburges, S.; Hesselmann, C.; Becker, S.; Schlücker, E.; Döllinger, M. Influence of vortical structures on the glottal jet location in the supraglottal, region. J. Voice 2013, 27, 531–544. [Google Scholar] [CrossRef] [PubMed]
- Giambattista, A.; Richardson, B.; Richardson, R. College Physics, 3rd ed.; McGraw Hill: Boston, MA, USA, 2010. [Google Scholar]
- Marion, J.; Thornton, S. Classical Dynamics of Particles and Systems, 4th ed.; Saunders College Publishing: Philadelphia, PA, USA, 1995. [Google Scholar]
- Fowles, G.; Cassidy, G. Analytical Mechanics, 7th ed.; Thomson Learning: Boston, MA, USA, 2005. [Google Scholar]
- Bailly, L.; Pelorson, X.; Henrich, N.; Ruty, N. Influence of a constriction in the near field of the vocal folds: Physical modeling and experimental validation. J. Acoust. Soc. Am. 2008, 124, 3296–3308. [Google Scholar] [CrossRef]
- Sadeghi, H.; Kniesburges, S.; Falk, S.; Kaltenbacher, M.; Schützenberger, A.; Döllinger, M. Towards a clinically applicable computational larynx model. Appl. Sci. 2019, 9, 2288. [Google Scholar] [CrossRef]
- Story, B.; Titze, I. Voice simulation with a body-cover model of the vocal folds. J. Acoust. Soc. Am. 1995, 97, 1249–1260. [Google Scholar] [CrossRef]
- Gómez, P.; Schützenberger, A.; Kniesburges, S.; Bohr, C.; Döllinger, M. Physical parameter estimation from porcine ex vivo vocal fold dynamics in an inverse problem framework. Biomech. Model. Mechanobiol. 2018, 17, 777–792. [Google Scholar] [CrossRef]
- Gómez, P.; Schützenberger, A.; Semmler, M.; Döllinger, M. Laryngeal pressure estimation with a recurrent neural network. IEEE J. Transl. Eng. Health Med. 2019, 7, 8590726. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fulcher, L.; Lodermeyer, A.; Kähler, G.; Becker, S.; Kniesburges, S. Geometry of the Vocal Tract and Properties of Phonation near Threshold: Calculations and Measurements. Appl. Sci. 2019, 9, 2755. https://doi.org/10.3390/app9132755
Fulcher L, Lodermeyer A, Kähler G, Becker S, Kniesburges S. Geometry of the Vocal Tract and Properties of Phonation near Threshold: Calculations and Measurements. Applied Sciences. 2019; 9(13):2755. https://doi.org/10.3390/app9132755
Chicago/Turabian StyleFulcher, Lewis, Alexander Lodermeyer, George Kähler, Stefan Becker, and Stefan Kniesburges. 2019. "Geometry of the Vocal Tract and Properties of Phonation near Threshold: Calculations and Measurements" Applied Sciences 9, no. 13: 2755. https://doi.org/10.3390/app9132755
APA StyleFulcher, L., Lodermeyer, A., Kähler, G., Becker, S., & Kniesburges, S. (2019). Geometry of the Vocal Tract and Properties of Phonation near Threshold: Calculations and Measurements. Applied Sciences, 9(13), 2755. https://doi.org/10.3390/app9132755




