On Sharing Spatial Data with Uncertainty Integration Amongst Multiple Robots Having Different Maps
Abstract
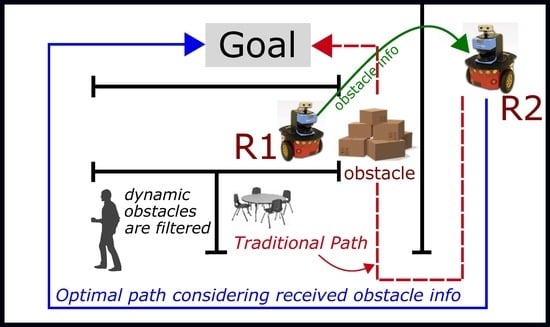
1. Introduction
Related Works
- Uncertainty Integration in the Improved Confidence Decay Mechanism: The previous work [12] did not consider the amount of estimated positional uncertainty of obstacles in the confidence decay. Both were decoupled entities. However, this was a serious drawback in the previous work because irrespective of the amount of positional uncertainty, confidence of all the obstacles decayed at the same rate. This caused several false map updates corresponding to dynamic obstacles which generally have large uncertainty associated. In the extended work, we have mathematically modeled the integration of positional uncertainty in the confidence decay mechanism. This is discussed in ‘Section 4.1 Integrating Uncertainty in Confidence Decay Mechanism’.
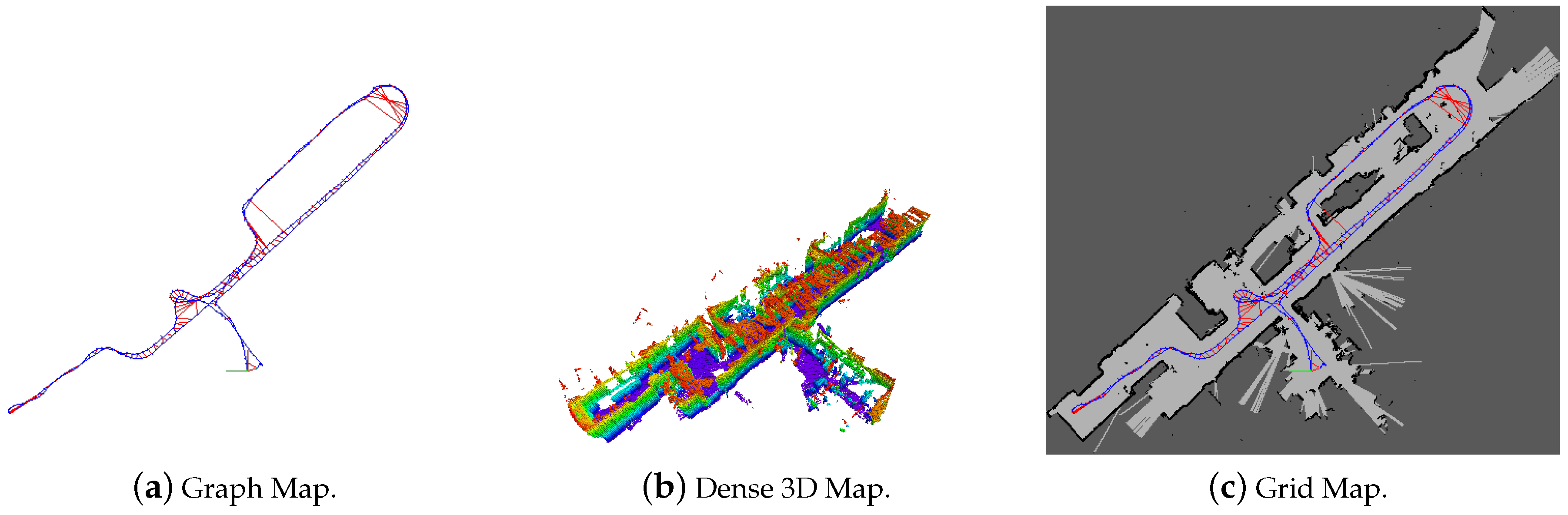
- New Experiments with Heterogeneous Maps with Different Sensors: Another shortcoming of the previous work was that it only worked with the same type of 2D grid-maps made with the same type of sensors. However, in the extended work, we include new experiments with heterogeneous maps (3 dimensional RGBD map and 2D grid-map) made from different sensors. In this regard, the merits of using the ‘node-map’ as a means of smoothly sharing information coherently between heterogeneous maps are also discussed. This is discussed in ‘Section 6.1 Experiments with Heterogeneous Maps’.
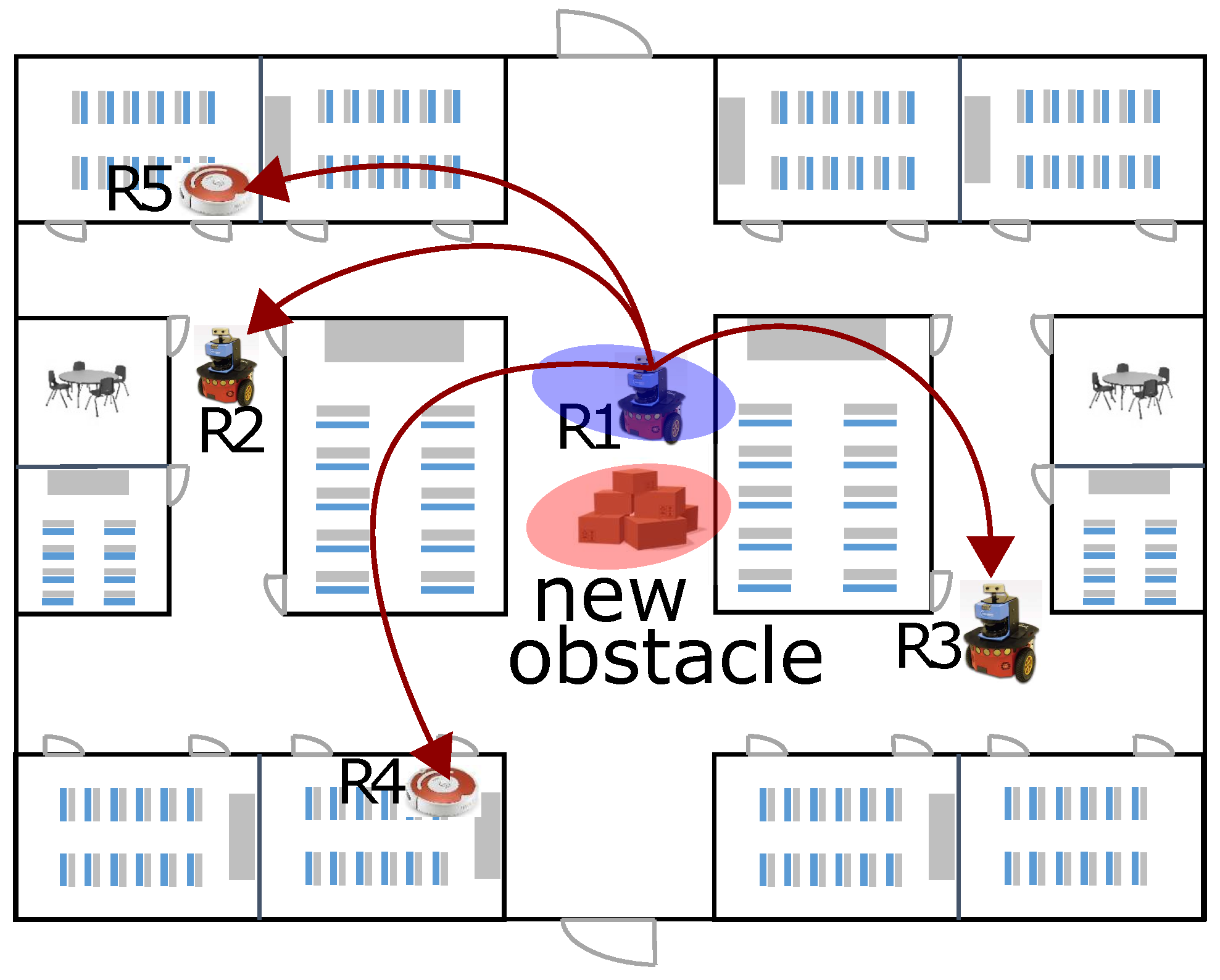
- New Experiments in Dynamic Environment with Moving People and Testing Under Pressure: The previous work only worked with static obstacles. In the extended work, new experiments have been performed to test the method when people are randomly moving in the vicinity of the robot and obstructing its navigation. In this regard, the tight coupling of new obstacle’s uncertainty in the confidence decay mechanism plays a vital role to avoid false map-updates corresponding to the dynamic obstacles. This is discussed in ‘Section 6.2. Results with Dynamic Entities (Moving Obstacle)’.
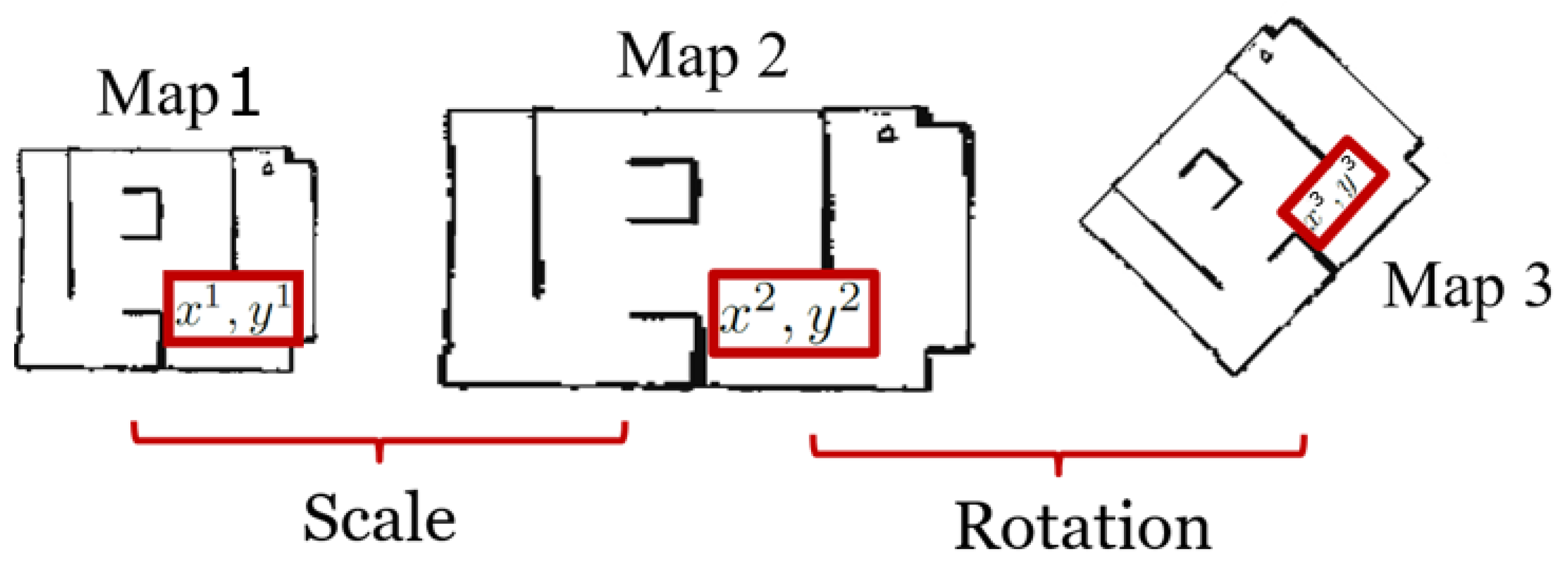
2. Correspondence Problem in Different Maps
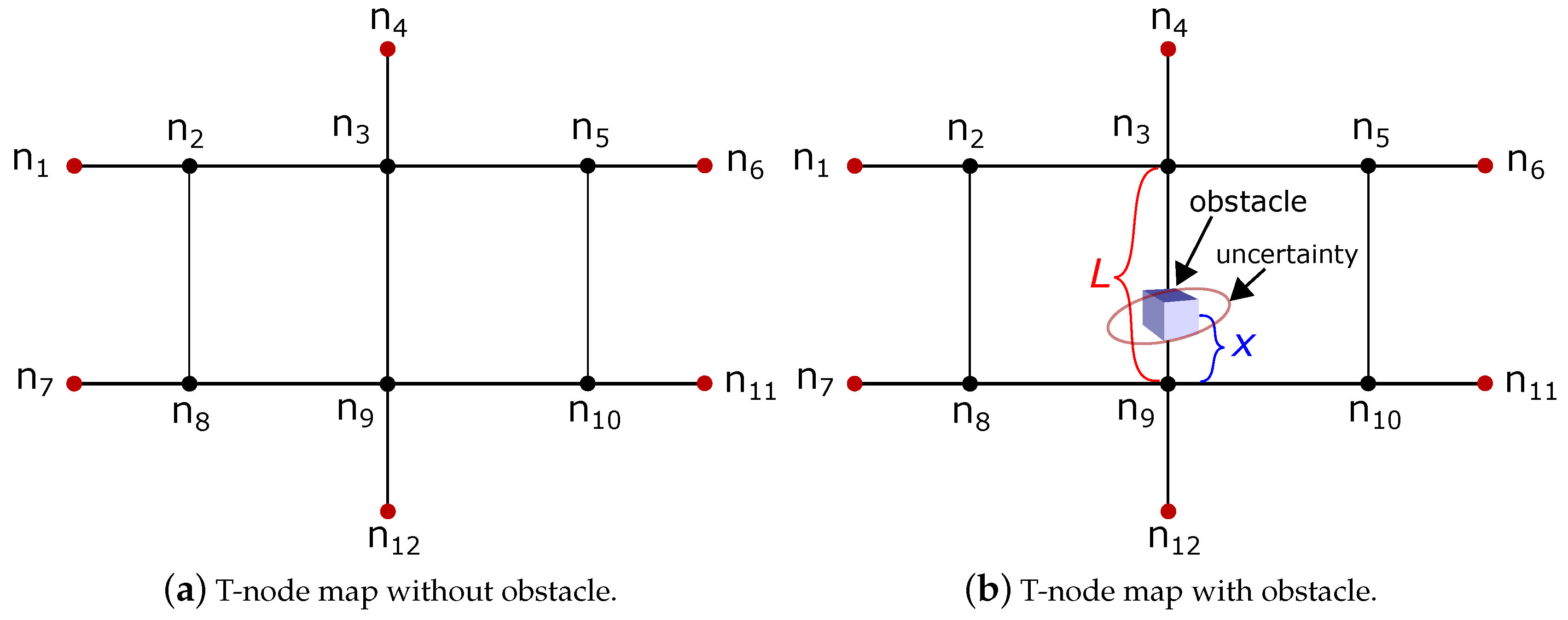
3. ‘T-Node’ Map Representation
| Algorithm 1: T-node-map Generation |
 |
4. Obstacle Removal and Update in T-Node Map
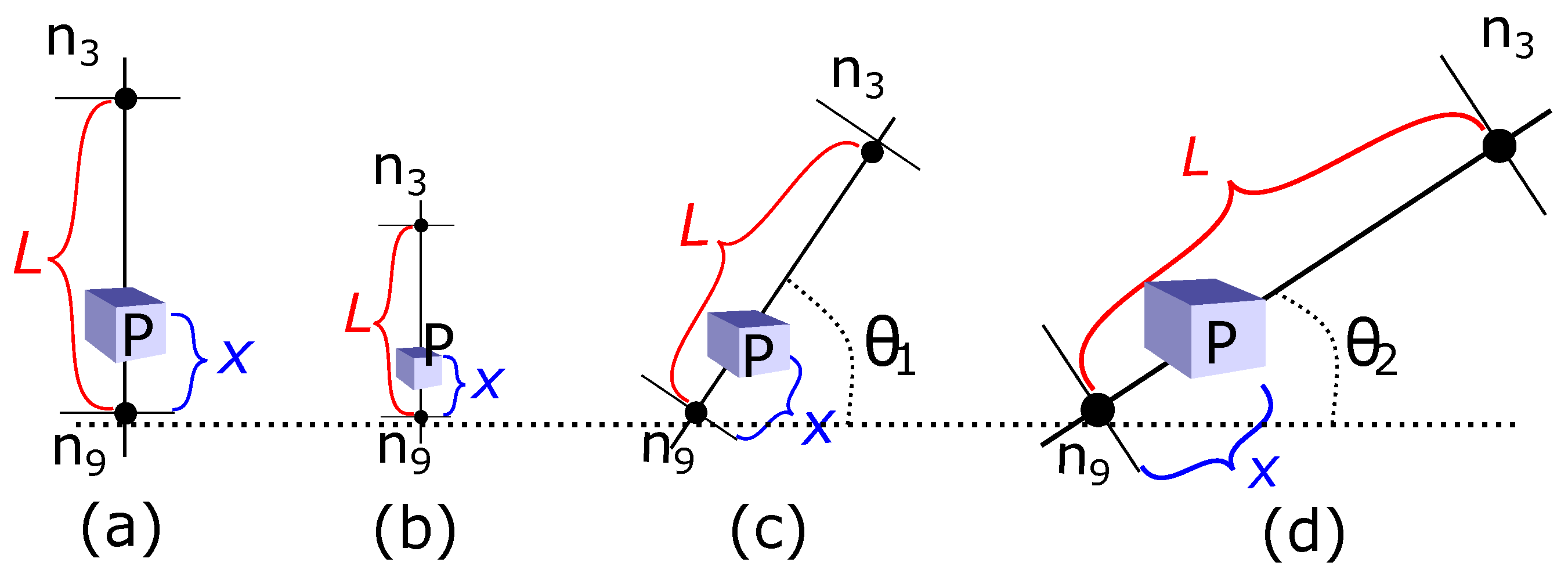
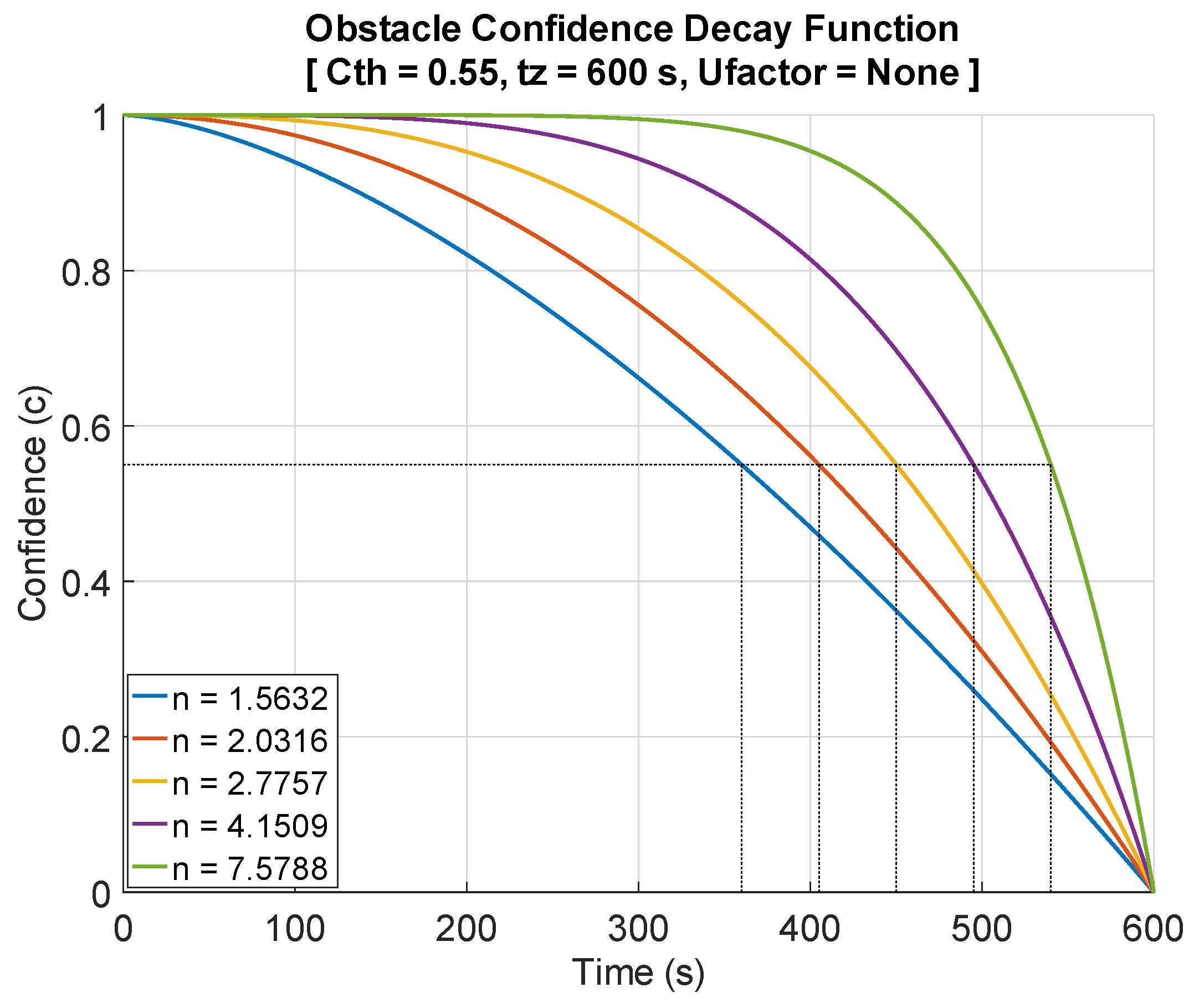
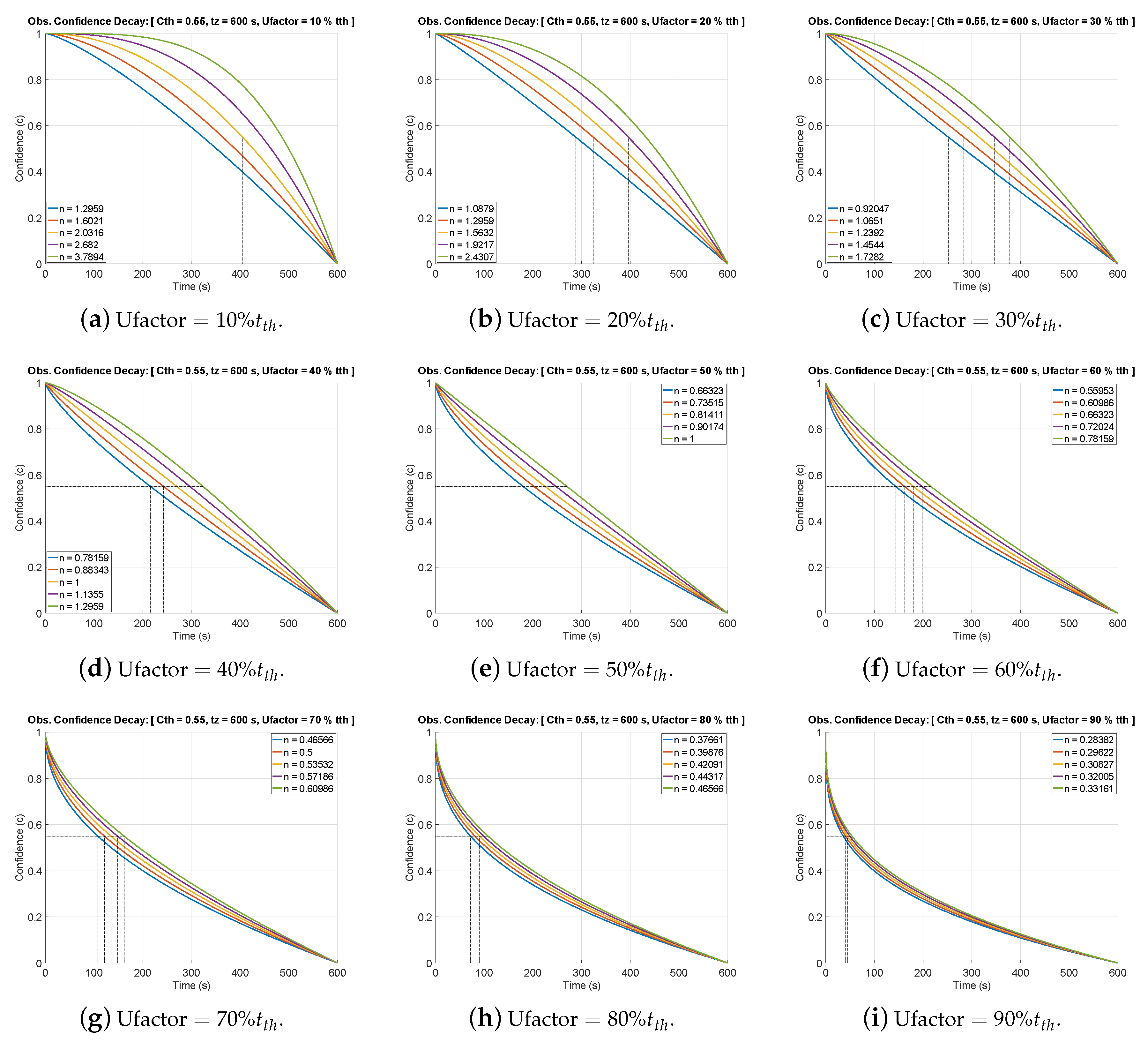
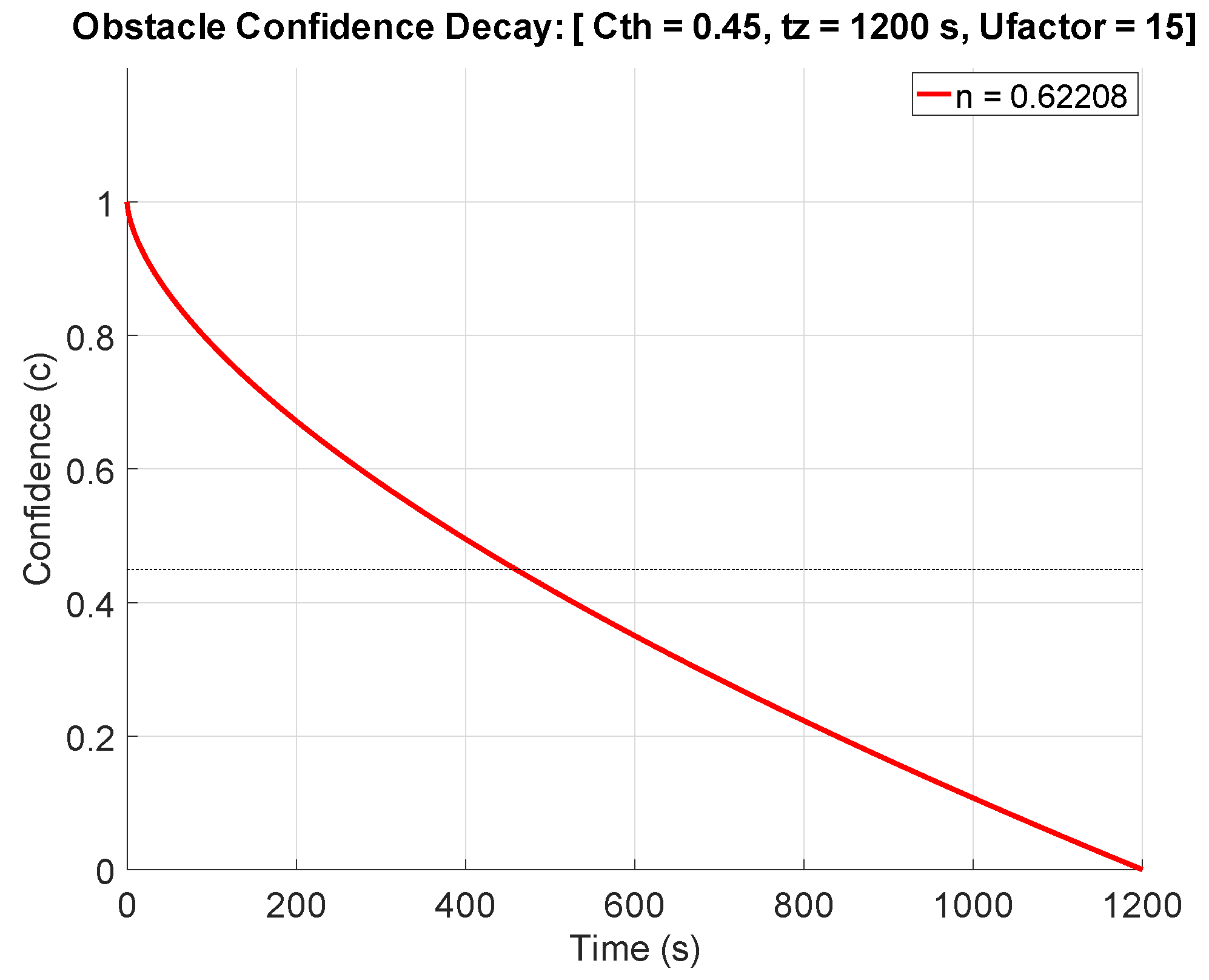
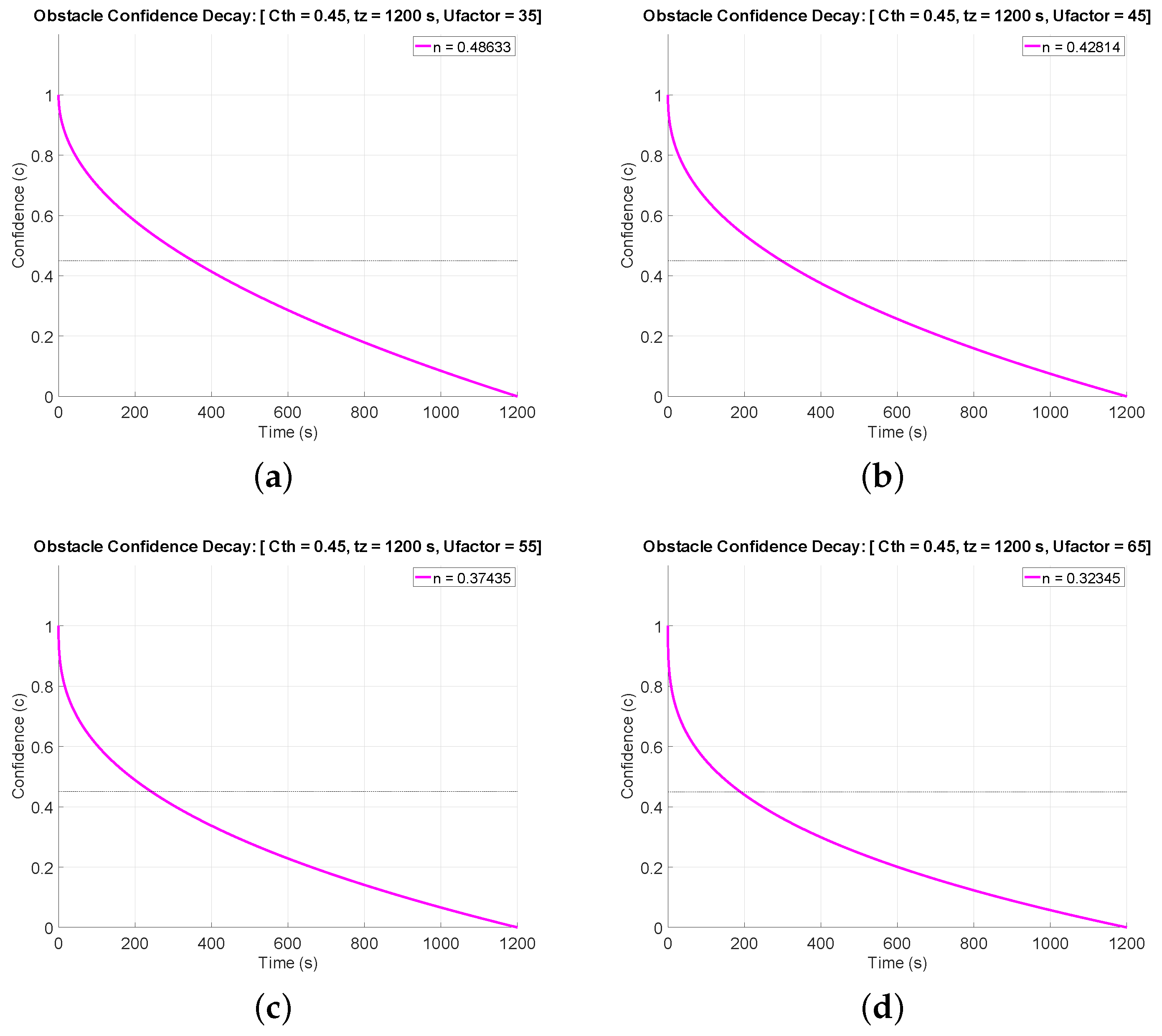
4.1. Integrating Uncertainty in Confidence Decay Mechanism
5. Uncertainty Integrated Confidence Decay Mechanism with Extended Kalman Filter
6. Experimental Results
| Algorithm 2: Uncertainty Integrated Confidence Decay with Extended Kalman Filter | |
| 1 | #: robot state,: translation and rotational velocity. |
| 2 | # EKF uses Jacobian to handle non-linearity.: Jacobian of motion function w.r.t state |
| 3 | #: Jacobian of motion w.r.t control |
| 4 | #: Covariance of noise in control space.: Error-specific parameters. |
| 5 | #: Prediction updates in state. |
| 6 | #: Prediction updates in covariance. |
| 7 | #: Covariance of the sensor noise. |
| 8 | #: coordinates of the ith landmark.: measurement. q: squared distance. |
| 9 | #: Jacobian of measurement with respect to state. |
| 10 | #: Measurement covariance matrix. |
| 11 | #: likely correspondence after applying maximum likelihood estimate. |
| 12 | #: Kalman gain,: state,: covariance. |
| 13 | # Apply Singular Value Decomposition and get Eigen-values: |
| 14 | #n: degree of decay curve,: threshold time,: threshold confidence,: time to decay to zero. |
| 15 | #: degree of decay curve with uncertainty integrated,: decay control factor. |
6.1. Experiments with Heterogeneous Maps
6.2. Results with Dynamic Entities (Moving Obstacle)
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Ravankar, A.; Ravankar, A.A.; Hoshino, Y.; Emaru, T.; Kobayashi, Y. On a Hopping-points SVD and Hough Transform Based Line Detection Algorithm for Robot Localization and Mapping. Int. J. Adv. Robot. Syst. 2016, 13, 98. [Google Scholar] [CrossRef]
- Wang, R.; Veloso, M.; Seshan, S. Multi-robot information sharing for complementing limited perception: A case study of moving ball interception. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 1884–1889. [Google Scholar] [CrossRef]
- Riddle, D.R.; Murphy, R.R.; Burke, J.L. Robot-assisted medical reachback: using shared visual information. In Proceedings of the ROMAN 2005, IEEE International Workshop on Robot and Human Interactive Communication, Nashville, TN, USA, 13–15 Augest 2005; pp. 635–642. [Google Scholar] [CrossRef]
- Cai, A.; Fukuda, T.; Arai, F. Cooperation of multiple robots in cellular robotic system based on information sharing. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Tokyo, Japan, 20–20 June 1997; p. 20. [Google Scholar] [CrossRef]
- Rokunuzzaman, M.; Umeda, T.; Sekiyama, K.; Fukuda, T. A Region of Interest (ROI) Sharing Protocol for Multirobot Cooperation With Distributed Sensing Based on Semantic Stability. IEEE Trans. Syst. Man Cybern. Syst. 2014, 44, 457–467. [Google Scholar] [CrossRef]
- Samejima, S.; Sekiyama, K. Multi-robot visual support system by adaptive ROI selection based on gestalt perception. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3471–3476. [Google Scholar] [CrossRef]
- Özkucur, N.E.; Kurt, B.; Akın, H.L. A Collaborative Multi-robot Localization Method without Robot Identification. In RoboCup 2008: Robot Soccer World Cup XII; Springer: Berlin/Heidelberg, Germany, 2009; pp. 189–199. [Google Scholar] [CrossRef]
- Sukop, M.; Hajduk, M.; Jánoš, R. Strategic behavior of the group of mobile robots for robosoccer (category Mirosot). In Proceedings of the 2014 23rd International Conference on Robotics in Alpe-Adria-Danube Region (RAAD), Smolenice, Slovakia, 3–5 September 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. Avoiding blind leading the blind. Int. J. Adv. Robot. Syst. 2016, 13. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. On a bio-inspired hybrid pheromone signalling for efficient map exploration of multiple mobile service robots. Artif. Life Robot. 2016, 221–231. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. Intelligent Robot Guidance in Fixed External Camera Network for Navigation in Crowded and Narrow Passages. Proceedings 2017, 1, 37. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Emaru, T. Symbiotic Navigation in Multi-Robot Systems with Remote Obstacle Knowledge Sharing. Sensors 2017, 17, 1581. [Google Scholar] [CrossRef] [PubMed]
- Hunziker, D.; Gajamohan, M.; Waibel, M.; D’Andrea, R. Rapyuta: The RoboEarth Cloud Engine. In Proceedings of the 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 6–10 May 2013; pp. 438–444. [Google Scholar] [CrossRef]
- Waibel, M.; Beetz, M.; Civera, J.; D’Andrea, R.; Elfring, J.; Gálvez-López, D.; Häussermann, K.; Janssen, R.; Montiel, J.M.M.; Perzylo, A.; et al. RoboEarth. IEEE Robot. Autom. Mag. 2011, 18, 69–82. [Google Scholar] [CrossRef]
- Tenorth, M.; Perzylo, A.C.; Lafrenz, R.; Beetz, M. Representation and Exchange of Knowledge About Actions, Objects, and Environments in the RoboEarth Framework. IEEE Trans. Autom. Sci. Eng. 2013, 10, 643–651. [Google Scholar] [CrossRef]
- Stenzel, J.; Luensch, D. Concept of decentralized cooperative path conflict resolution for heterogeneous mobile robots. In Proceedings of the 2016 IEEE International Conference on Automation Science and Engineering (CASE), Fort Worth, TX, USA, 21–25 Augest 2016; pp. 715–720. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Jixin, L.; Emaru, T.; Hoshino, Y. An intelligent docking station manager for multiple mobile service robots. In Proceedings of the Control, Automation and Systems (ICCAS), 2015 15th International Conference on, Busan, Korea, 13–16 October 2015; pp. 72–78. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Emaru, T. Hitchhiking Robots: A Collaborative Approach for Efficient Multi-Robot Navigation in Indoor Environments. Sensors 2017, 17, 1878. [Google Scholar] [CrossRef] [PubMed]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Hoshino, Y.; Peng, C.C.; Watanabe, M. Hitchhiking Based Symbiotic Multi-Robot Navigation in Sensor Networks. Robotics 2018, 7, 37. [Google Scholar] [CrossRef]
- Guo, Y.; Parker, L. A distributed and optimal motion planning approach for multiple mobile robots. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), Washington, DC, USA, 11–15 May 2002; Volume 3, pp. 2612–2619. [Google Scholar] [CrossRef]
- Svestka, P.; Overmars, M.H. Coordinated Path Planning for Multiple Robots; Technical Report UU-CS-1996-43; Department of Information and Computing Sciences, Utrecht University: Utrecht, The Netherlands, 1996. [Google Scholar]
- Clark, C.M.; Rock, S.M.; Latombe, J. Motion planning for multiple mobile robots using dynamic networks. In Proceedings of the 2003 IEEE International Conference on Robotics and Automation (Cat. No.03CH37422), Taipei, Taiwan, 14–19 September 2003; Volume 3, pp. 4222–4227. [Google Scholar] [CrossRef]
- Teng, R.; Yano, K.; Kumagai, T. Efficient Acquisition of Map Information Using Local Data Sharing over Hierarchical Wireless Network for Service Robots. In Proceedings of the 2018 Asia-Pacific Microwave Conference (APMC), Kyoto, Japan, 6–9 November 2018; pp. 896–898. [Google Scholar] [CrossRef]
- Ravankar, A.A.; Ravankar, A.; Peng, C.; Kobayashi, Y.; Emaru, T. Task coordination for multiple mobile robots considering semantic and topological information. In Proceedings of the 2018 IEEE International Conference on Applied System Invention (ICASI), Chiba, Japan, 13–17 April 2018; pp. 1088–1091. [Google Scholar] [CrossRef]
- Pinkam, N.; Bonnet, F.; Chong, N.Y. Robot collaboration in warehouse. In Proceedings of the 2016 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Korea, 16–19 October 2016; pp. 269–272. [Google Scholar] [CrossRef]
- Regev, T.; Indelman, V. Multi-robot decentralized belief space planning in unknown environments via efficient re-evaluation of impacted paths. In Proceedings of the 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Daejeon, Korea, 9–14 October 2016; pp. 5591–5598. [Google Scholar] [CrossRef]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Path Planning and Trajectory Planning Algorithms: A General Overview. In Motion and Operation Planning of Robotic Systems: Background and Practical Approaches; Springer International Publishing: Cham, Switzeland, 2015; pp. 3–27. [Google Scholar] [CrossRef]
- Tang, S.H.; Kamil, F.; Khaksar, W.; Zulkifli, N.; Ahmad, S.A. Robotic motion planning in unknown dynamic environments: Existing approaches and challenges. In Proceedings of the 2015 IEEE International Symposium on Robotics and Intelligent Sensors (IRIS), Langkawi, Malaysia, 18–20 October 2015; pp. 288–294. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.; Kobayashi, Y.; Hoshino, Y.; Peng, C.C. Path Smoothing Techniques in Robot Navigation: State-of-the-Art, Current and Future Challenges. Sensors 2018, 18, 3170. [Google Scholar] [CrossRef] [PubMed]
- Montijano, E.; Aragues, R.; Sagüés, C. Distributed Data Association in Robotic Networks With Cameras and Limited Communications. IEEE Trans. Robot. 2013, 29, 1408–1423. [Google Scholar] [CrossRef]
- Ravankar, A. Probabilistic Approaches and Algorithms for Indoor Robot Mapping in Structured Environments. Ph.D. Thesis, Hokkaido University, Sapporo, Japan, 2015. [Google Scholar]
- Ravankar, A.; Kobayashi, Y.; Ravankar, A.; Emaru, T. A connected component labeling algorithm for sparse Lidar data segmentation. In Proceedings of the 2015 6th International Conference on Automation, Robotics and Applications (ICARA), Queenstown, New Zealand, 17–19 Feburary 2015; pp. 437–442. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Jixin, L.; Emaru, T.; Hoshino, Y. A novel vision based adaptive transmission power control algorithm for energy efficiency in wireless sensor networks employing mobile robots. In Proceedings of the 2015 Seventh International Conference on Ubiquitous and Future Networks, Sapporo, Japan, 7–10 July 2015; pp. 300–305. [Google Scholar] [CrossRef]
- Zhang, T.Y.; Suen, C.Y. A Fast Parallel Algorithm for Thinning Digital Patterns. Commun. ACM 1984, 27, 236–239. [Google Scholar] [CrossRef]
- Yang, D.H.; Hong, S.K. A roadmap construction algorithm for mobile robot path planning using skeleton maps. Adv. Robot. 2007, 21, 51–63. [Google Scholar] [CrossRef]
- Bai, X.; Latecki, L.; Yu Liu, W. Skeleton Pruning by Contour Partitioning with Discrete Curve Evolution. Pattern Anal. Mach. Intell. IEEE Trans. 2007, 29, 449–462. [Google Scholar] [CrossRef] [PubMed]
- Ravankar, A.A.; Hoshino, Y.; Ravankar, A.; Jixin, L.; Emaru, T.; Kobayashi, Y. Algorithms and a framework for indoor robot mapping in a noisy environment using clustering in spatial and Hough domains. Int. J. Adv. Robot. Syst. 2015, 12. [Google Scholar] [CrossRef]
- MacQueen, J.B. Some Methods for Classification and Analysis of MultiVariate Observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability; Cam, L.M.L., Neyman, J., Eds.; University of California Press: Berkeley, CA, USA, 1967; Volume 1, pp. 281–297. [Google Scholar]
- Lloyd, S.P. Least squares quantization in pcm. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Ester, M.; Kriegel, H.P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise; AAAI Press: Menlo Park, CA, USA, 1996; pp. 226–231. [Google Scholar]
- Fox, D.; Ko, J.; Konolige, K.; Limketkai, B.; Schulz, D.; Stewart, B. Distributed Multirobot Exploration and Mapping. Proc. IEEE 2006, 94, 1325–1339. [Google Scholar] [CrossRef]
- Ravankar, A.A.; Ravankar, A.; Emaru, T.; Kobayashi, Y. A hybrid topological mapping and navigation method for large area robot mapping. In Proceedings of the 2017 56th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Kanazawa, Japan, 19–22 September 2017; pp. 1104–1107. [Google Scholar] [CrossRef]
- Pioneer P3-DX. Pioneer P3-DX Robot. 2018. Available online: https://www.robotshop.com/community/robots/show/pioneer-d3-px (accessed on 11 Janurary 2019).
- TurtleBot 2. TurtleBot 2 Robot. 2018. Available online: http://turtlebot.com/ (accessed on 11 Janurary 2019).
- Quigley, M.; Conley, K.; Gerkey, B.P.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An Open-Source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–15 May 2009. [Google Scholar]
- Hart, P.; Nilsson, N.; Raphael, B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. Syst. Sci. Cybern. IEEE Trans. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. Path smoothing extension for various robot path planners. In Proceedings of the 2016 16th International Conference on Control, Automation and Systems (ICCAS), Gyeongju, Korea, 16–19 October 2016; pp. 263–268. [Google Scholar] [CrossRef]
- Ravankar, A.; Ravankar, A.A.; Kobayashi, Y.; Emaru, T. SHP: Smooth Hypocycloidal Paths with Collision-Free and Decoupled Multi-Robot Path Planning. Int. J. Adv. Robot. Syst. 2016, 13, 133. [Google Scholar] [CrossRef]
- Xu, B.; Jiang, W.; Shan, J.; Zhang, J.; Li, L. Investigation on the Weighted RANSAC Approaches for Building Roof Plane Segmentation from LiDAR Point Clouds. Remote Sens. 2015, 8, 5. [Google Scholar] [CrossRef]
- Enzweiler, M.; Gavrila, D.M. Monocular Pedestrian Detection: Survey and Experiments. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 2179–2195. [Google Scholar] [CrossRef] [PubMed]
- Spinello, L.; Arras, K.O. People detection in RGB-D data. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, 25–30 September 2011; pp. 3838–3843. [Google Scholar] [CrossRef]
- Pantofaru, C. Leg Detector. 2019. Available online: http://wiki.ros.org/leg_detector (accessed on 3 May 2019).
- Moeslund, T.B.; Granum, E. A Survey of Computer Vision-Based Human Motion Capture. Comput. Vis. Image Understand. 2001, 81, 231–268. [Google Scholar] [CrossRef]

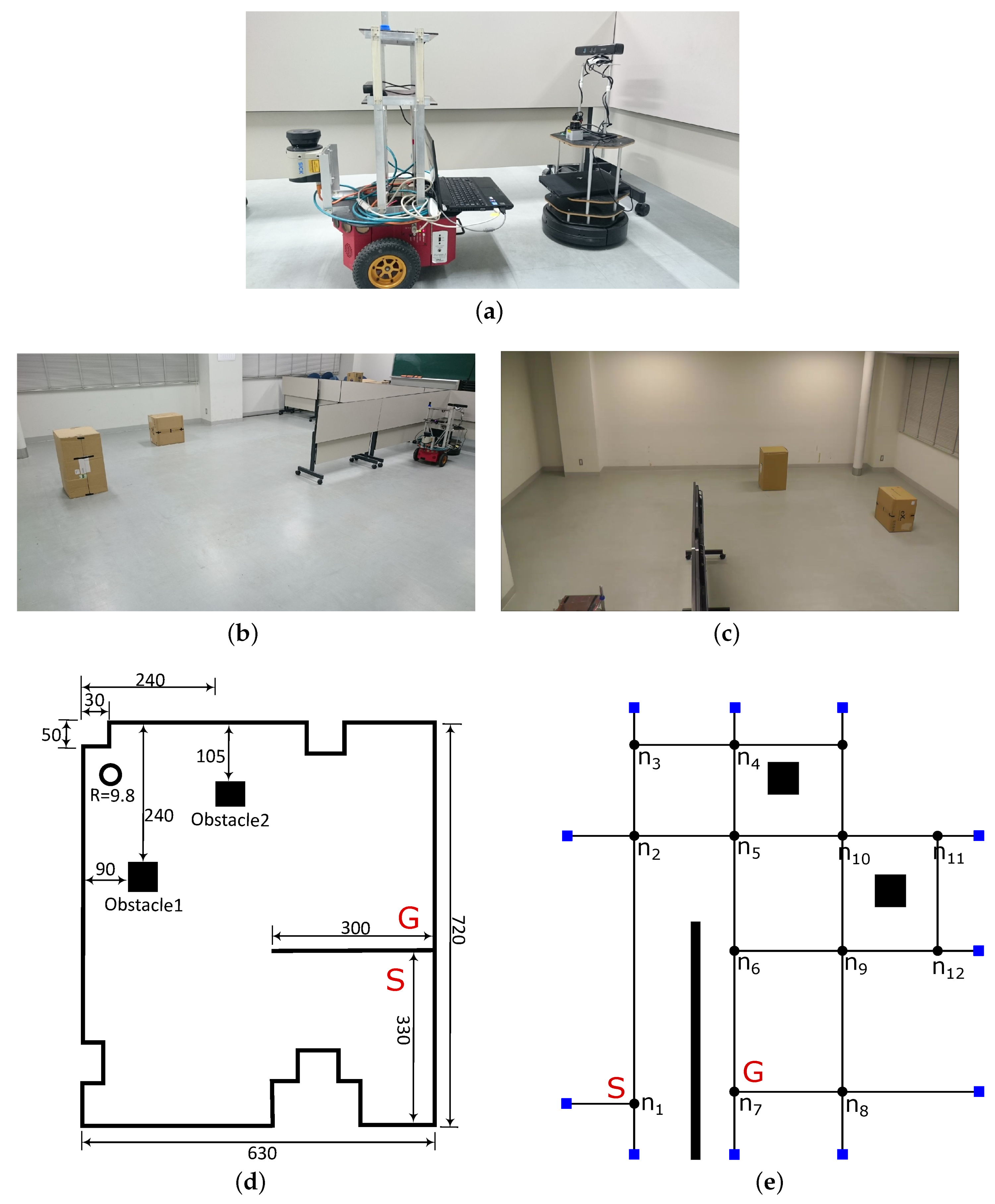






| Feature | Previous Work [12] | Extended Work |
|---|---|---|
| Sharing New Obstacle’s Position Information | Yes | Yes |
| Consideration of Positional Uncertainty of Obstacles | No | Yes |
| Confidence Decay Mechanism | Yes | Yes |
| Uncertainty Influence Over Confidence Decay | No | Yes |
| Experiments in Very Dynamic Environment (e.g., Moving People) | No | Yes |
| Robots have Different Types of Sensors | No | Yes |
| Tests with Heterogeneous Maps | No | Yes |
| Node Path | New Obstacle | Path Blocked | Meta-Data |
|---|---|---|---|
| 0 | 0 | - | |
| ⋯ | ⋯ | ⋯ | ⋯ |
| 1 | 1 | { d:,w:,h:,:(), } | |
| 0 | 0 | - |
| Obstacle | Length × Width × Height |
|---|---|
| Obstacle1 | 40 cm × 40 cm × 68 cm |
| Obstacle2 | 50 cm × 35 cm × 50 cm |
| Newly Added Obstacle | 300 cm × 5 cm × 100 cm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ravankar, A.; Ravankar, A.A.; Hoshino, Y.; Kobayashi, Y. On Sharing Spatial Data with Uncertainty Integration Amongst Multiple Robots Having Different Maps. Appl. Sci. 2019, 9, 2753. https://doi.org/10.3390/app9132753
Ravankar A, Ravankar AA, Hoshino Y, Kobayashi Y. On Sharing Spatial Data with Uncertainty Integration Amongst Multiple Robots Having Different Maps. Applied Sciences. 2019; 9(13):2753. https://doi.org/10.3390/app9132753
Chicago/Turabian StyleRavankar, Abhijeet, Ankit A. Ravankar, Yohei Hoshino, and Yukinori Kobayashi. 2019. "On Sharing Spatial Data with Uncertainty Integration Amongst Multiple Robots Having Different Maps" Applied Sciences 9, no. 13: 2753. https://doi.org/10.3390/app9132753
APA StyleRavankar, A., Ravankar, A. A., Hoshino, Y., & Kobayashi, Y. (2019). On Sharing Spatial Data with Uncertainty Integration Amongst Multiple Robots Having Different Maps. Applied Sciences, 9(13), 2753. https://doi.org/10.3390/app9132753