1. Introduction
Numerical models have long been employed to better understand the complex physics involved in human phonation. For example, reduced-order and finite element numerical models of the vocal folds (VFs) can self-oscillate in a manner representative of actual VF kinematics during sustained vowels [
1], pitch glides [
2], and, in a few cases, running speech [
3]. Such models have explored a wide range of phenomena relevant to normal and pathological phonation, including the impact of a posterior glottal gap [
4], the ventricular folds [
5], phonation onset pressure [
6], and the efficacy of various compensation mechanisms for vocal hyperfunction [
7,
8].
Whereas the majority of modeling efforts in speech, to date, have employed models with general population-based parameters to uncover the universal physical underpinnings of human phonation, a few research teams have begun to explore the development of subject-specific numerical models for phonation [
9,
10,
11,
12,
13]. The dynamics of the VFs are sensitive to a variety of factors, including subglottal pressure [
14], laryngeal muscle activation [
15], and a posterior glottal gap [
4], to name a few. These factors, which can play a role in vocal hyperfunction [
16] and other pathologies [
17,
18,
19,
20], can be a challenge to observe clinically. Subject-specific models, on the other hand, are constructed based on measurements of the subject through less challenging media, such as high speed videoendoscopy (HSV) [
9,
11,
21] and offer the potential to elucidate clinically opaque features and parameters, such as VF contact pressures.
In general, development of a subject-specific model entails estimation of numerical parameters such that the model behavior “matches” some observed data from the individual of interest, such as VF kinematics from HSV [
9,
11,
21]. Specifically, numerical model parameters are sought such that some model output(s) (e.g., the VF kinematics) best match the equivalent observation data from the subject. This problem is ill-posed, thus necessitating inverse analysis techniques to determine the model parameters [
22]. To date, optimization [
9,
22], machine learning [
23], and Bayesian [
10,
11,
21] frameworks have been developed to estimate VF model parameters.
Optimization-based approaches define a cost functional and employ optimization techniques to determine the parameter values that minimize the functional. Döllinger et al. [
22] was the first to successfully use this approach, employing the Nelder-Mead algorithm to determine the vibrating masses, spring stiffnesses, and subglottal pressure of a two mass VF model by minimizing the least-squares error between specific Fourier coefficients of the measured VF trajectories and the simulated trajectories. Genetic algorithms were subsequently employed to determine parameters of a two mass model that best reproduced the trajectories from patients suffering from unilateral VF paralysis [
16]. Inverse procedures have also been used to classify disordered versus healthy VF oscillations. Wurzbacher et al. [
24] employed simulated annealing to minimize the Euclidean distance between the model and experimental vocal fold trajectories to distinguish between normal and dysphonic subjects during sustained vowel phonation and a pitch glide. Very recently, deep learning tools have been employed for subject-specific modeling [
23]. A long short-term memory network, trained on simulated data, was used to estimate the subglottal pressure from ex vivo recordings of porcine vocal folds. They were able to produce accurate estimates of the subglottal pressure with very low online computational costs.
The vast majority of these subject-specific VF modeling efforts, and all of those mentioned above, have used lumped-element representations of the VFs and employed inverse methods to determine the reduced-order parameters. Of noted exception are the efforts by Xue et al. [
12] and Chang et al. [
13] that employ finite element model representations of the VFs. Xue et al. used computed tomography to reconstruct the larynx of a subject in a computational domain. The external geometry of the VFs was obtained from the scan, whereas the VF layers and material properties were assumed from population-based histological data. Chang et al. constructed a laryngeal model of a rabbit from magnetic resonance images. Two VF layers were observed in the scans, leading to a body-cover-type construction wherein the densities and Poisson ratios were assumed a priori. The elastic moduli of the layers were determined by an informal optimization that attempted to match the maximum glottal width and fundamental frequency of the model with HSV measurements.
In contrast to optimization-based and machine learning methods that treat estimated model parameters as deterministic, the Bayesian framework treats all parameters and measurements as random variables. Such a framework has the benefit of elucidating the propagation of measurement uncertainties to the model parameters and outputs. Uncertainty estimates are powerful as they provide additional information about the fidelity of the model outputs, which are expected to be of value for clinical decisions. Cataldo et al. [
10] introduced the Bayesian framework to estimate stationary (non-time-varying) parameters of a two mass VF model using an importance sampling approach. This work was extended to estimate non-stationary parameters of a three mass body-cover model using both a particle filter [
11] and an extended Kalman filter [
21]. The Bayesian framework has, thus far, been demonstrated using simulated observation data from a reduced-order VF model, wherein the ground truth was known a priori, to estimate the parameters of a different reduced-order VF fitting model. The similarity between the generation and fitting models enabled direct assessment of the performance of the Bayesian framework. Herein we build on the Bayesian inference framework for developing subject-specific VF models by: (i) considering real HSV recordings of self-oscillating silicone VFs as the observation data; and, for the first time, (ii) employing a two-dimensional (2D) finite element (FE) model of the VFs as the fitting model. These two considerations address several limitations in prior Bayesian estimation-based inference studies applied to voiced speech, while simultaneously extending the methodology to more complex VF representations. Specifically, actual experimental data, with its inherent uncertainties, are used as the observations. Furthermore, by employing a FE representation of the VFs, the estimated FE parameters have direct relation to the material properties of the silicone VF models, reducing the layer of abstraction associated with reduced-order models. By using silicone VFs to generate the observation data, however, the “ground truth” is still available to assess the performance (estimated properties and their uncertainties) of the estimation procedure. Lastly, the use of experimental data provides a more realistic test bed due to the dynamical differences between the data source and the fitting model.
We consider two different VF base configurations, with and without medial compression, as well as multiple subglottal pressures. Exploring medial compression offers insights into how FE models and Bayesian estimation can incorporate VF posturing for subject-specific models, while varying subglottal pressure affords a mechanism for evaluating how well Bayesian inference, when accounting for measurement uncertainty, can differentiate between phonation conditions.
The paper is structured as follows:
Section 2 discusses the silicone VFs and experimental conditions used during collection of the data sets and handling of the HSV. Respectively,
Section 3 and
Section 4 briefly discuss the mathematical model and estimation procedure used in the analysis.
Section 5 presents the results of the estimates and provides discussion of the findings. Additionally, this section examines how the numerical parameters, including the triangulation density and step size in time, effect the subject-specific estimates. The manuscripts concludes with
Section 6.
5. Results and Discussion
Considering the case without medial compression as an exemplar, the estimated material properties from the Bayesian inferences are presented in
Table 3. Overall, the estimated parameters show good agreement with the “ground truth” experimental values; the maximum discrepancy between the estimates and the experimental values occurs with the Young’s modulus of the ligament with a
difference. We note that the experimental values, while considered the “ground truth”, are themselves approximate values estimated from the silicone mixture fractions.
We observe that and are over-estimated while is under-estimated when compared with the experimental values. The under-estimation of subglottal pressure is likely due to the simplified fluids model being used resulting in high nodal pressures. Over-estimating Young’s modulus of the cover is likely due to the lack of an epithelium in the FE model. The epithelium in the silicone VFs is extremely thin, but has a high Young’s modulus (). As a result it is likely that the estimate for is slightly elevated to compensate. It is unclear why the estimate for the body is consistently higher than expected, but may be related with the under-estimation of . An important observation, however, is that all of the experimental values fall within two standard deviations of the estimated values. This indicates that the use of a FE model of the VFs is statistically capable of inferring accurate estimates of the material properties from a GAW. The relative uncertainty (standard deviation divided by the estimated value) shows that all estimates except for the Young’s modulus of the ligament have uncertainties of approximately ; the Young’s modulus of the ligament has an level of uncertainty.
The relatively large bias and uncertainty for the ligament stiffness in comparison with the other parameters potentially results from the comparative insensitivity of the FE kinematics to this parameter. The ligament is a small internal region of the geometry and as a result has less impact on the large scale kinematics compared with the body and cover layers. Since is the only parameter defined in this region, a range of values are likely to generate similar GAWs, and any error in the estimate of can be compensated for by slight adjustments to and/or . Despite the modest difficulty in estimating this parameter, overall Bayesian inference is able to accurately estimate the VF material properties from HSV data alone, presuming that the histology of the folds are known a priori.
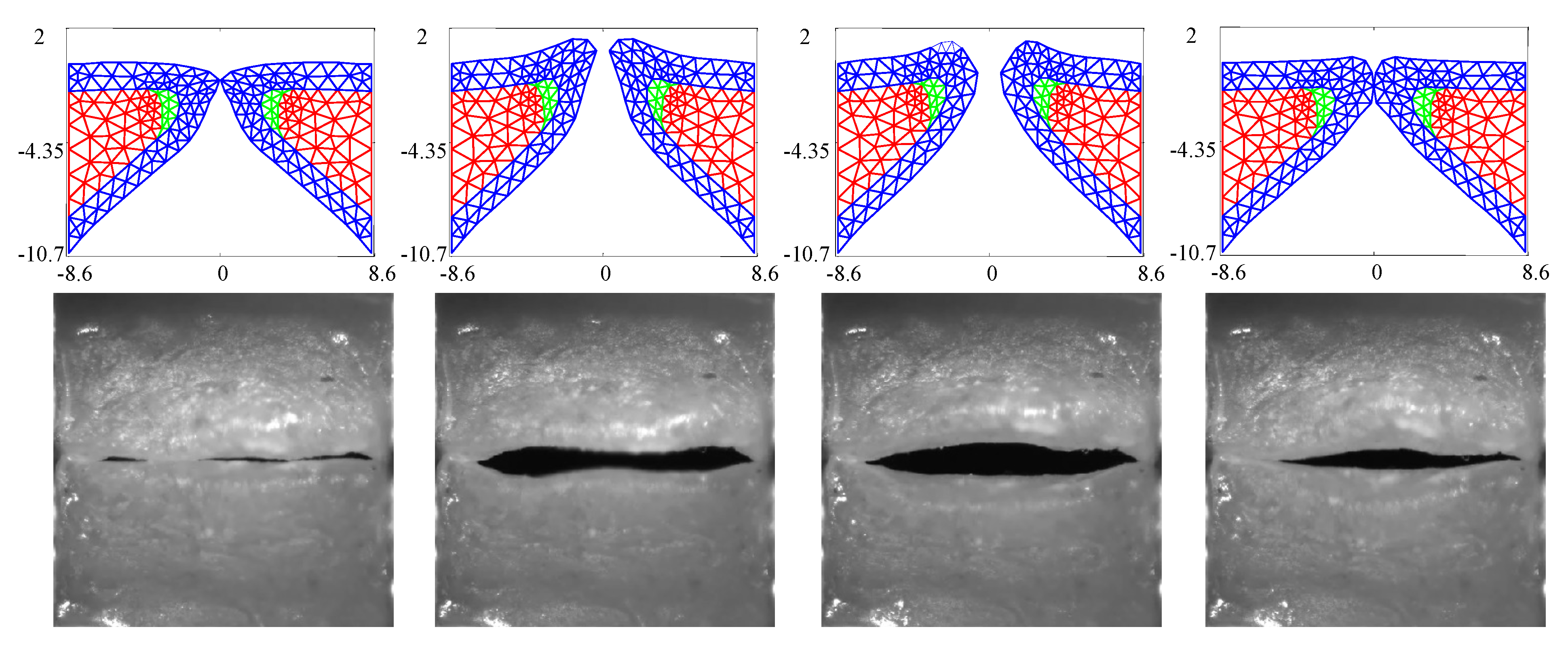
Figure 3 compares the kinematics of the FE model employing the estimated material properties from
Table 3 with the HSV over a single vibratory cycle. The FE model captures the silicone VF motion well, including the mucosal wave and the pronounced inferior-superior motion of the folds (see the third column in
Figure 3). The fourth column highlights that closure of the FE model does not necessarily always correspond with closure of the silicone VFs.
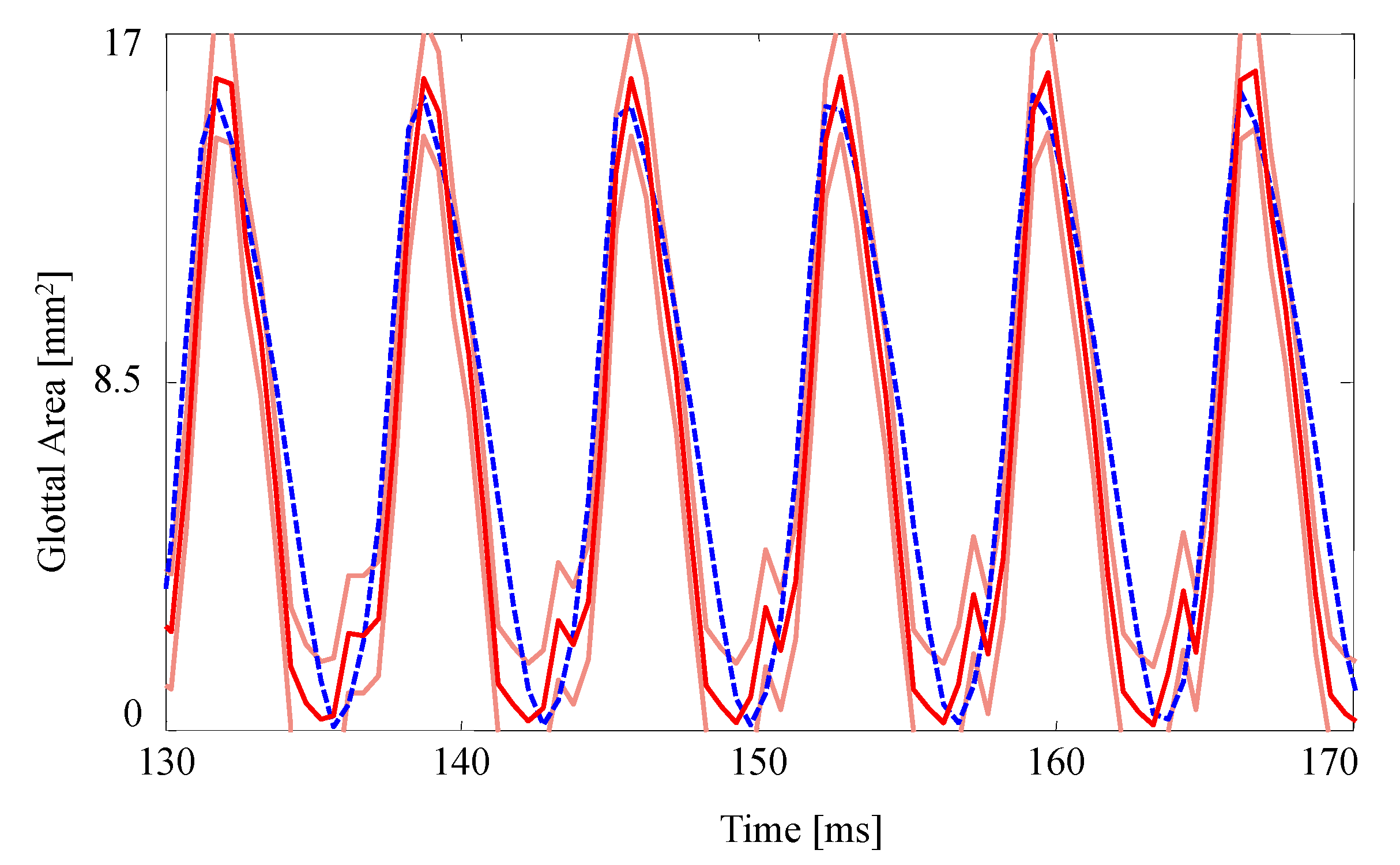
The GAW extracted from the FE model and the corresponding HSV for the no medial compression case is presented in
Figure 4. As suggested by the fourth column of
Figure 3, the FE model closes (GAW reaches zero) before the silicone VFs close. In fact, small openings along the span of the silicone VFs exist during the “closed” phase, as suggested by
Figure 2a. Overall, however, the simulated GAW fits the observed data well, with the measured GAW falling within the estimated uncertainty bounds the majority of the time. There are a few persistent mismatches, such as the small peak immediately after opening. Such errors are likely to be model errors induced by approximations, including the use of a simplified 2D approximation of the VFs.
5.1. Effect of Medial Compression
As discussed in
Section 2.1, HSV was captured with and without medial compression for
. Since it was difficult to measure the degree of medial compression experimentally, the actual pre-stress is highly uncertain. As such, the initial position parameter
in the FE model is included as an estimated parameter for both cases.
Table 4 presents the estimated material properties for both medial compression cases. The estimated properties (excepting
) agree well with each other and with the “ground truth” values. This is encouraging in two respects: the same silicone VFs were used in both cases, and the pre-stress in the medial compression case is captured in
and thus does not appreciably bias the stiffness estimates. However, the higher parameter uncertainties for the medial compression case is very likely due to the fact that the pre-stress associated with medial compression can be approximated by varying other stiffness parameters. This yields more overall uncertainty in the results, as other parameter combinations can explain the observed data.
The estimates for the initial position parameter,
, are statistically different between the two cases. When there is no medial compression the initial position is estimated to be
(
corresponds to zero compression, see
Figure 2a); with compression,
is estimated to be
. This
difference in the estimates is more than double the sum of the two estimated standard deviations, with a t-value of
, indicating that the FE model was capable of distinguishing between the experimental configurations. This does differ from the
shim placed experimentally to produce the medial compression, though again, the actual degree of experimental medial compression was very difficult to ascertain.
Comparing the case without medial compression with the results in
Table 3 shows that the uncertainties in the estimated parameters are larger in the present case despite using the same observation data. By including the extra fitting parameter,
, the estimated uncertainties increase due to the higher dimensionality (more parameters being fit given the same input data). That is, with the addition of
as a parameter, there is now an alternative pathway to influence the energy in the system. That said, the uncertainties in both estimates are large enough and the estimated values are similar enough that the two data sets cannot be distinguished statistically.
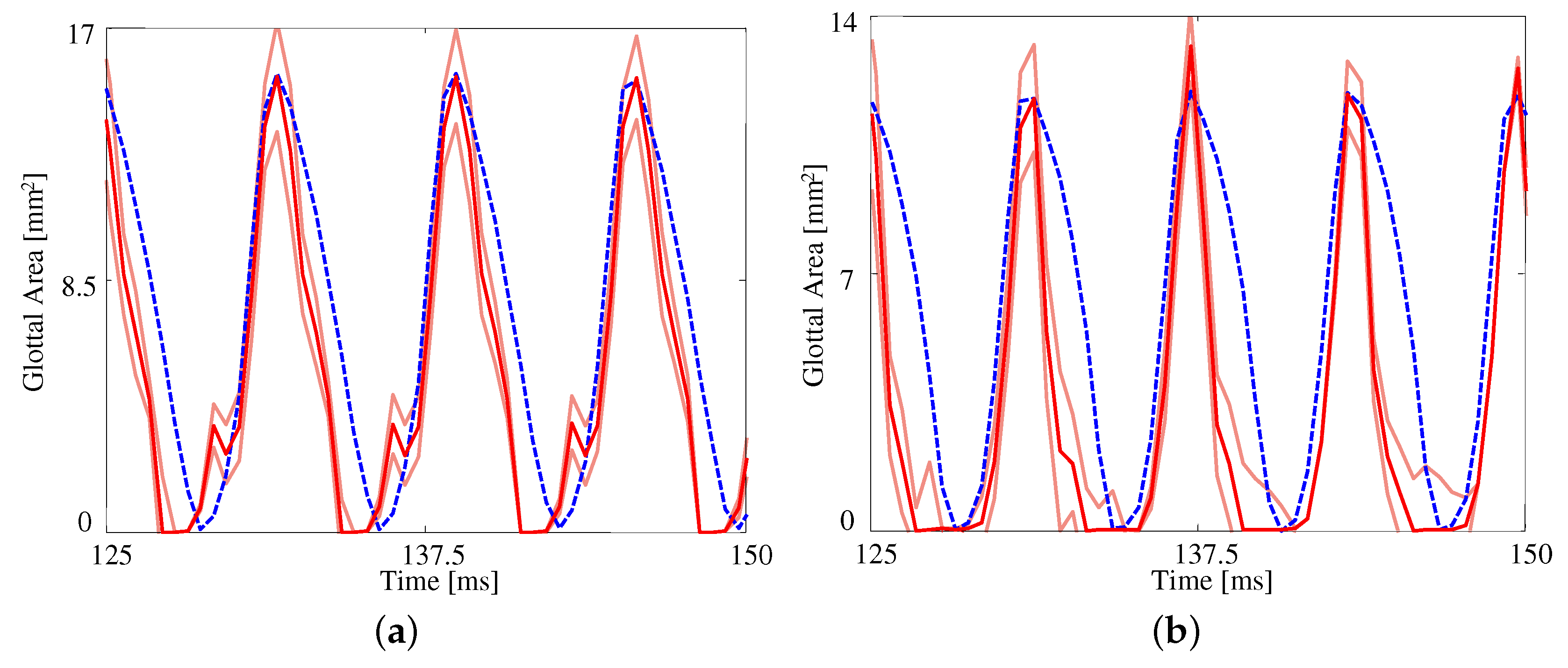
Figure 5 presents the measured and estimated GAWs for the two medial compression cases, wherein the FE models employ the material properties given in
Table 4. Both estimates fit the data reasonably well given the simplified FE model being used. The open quotient and speed quotients are both lower for the FE models, with the effect more pronounced for the case with medial compression. This results in a more peaked GAW in comparison with the HSV. The case without medial compression exhibits larger maximum glottal area, however the maximum contact pressure experienced during collision in the case with compression is
higher, on average, due to the pre-stress of the system (
versus
).
5.2. Distinguishing between Model Configurations
As the eventual goal of this research is patient-specific modeling, we wish to investigate whether the FE model is sufficiently sensitive and if HSV data provide enough information to distinguish between similar experimental configurations. As a first order exploration we consider varying subglottal pressures for silicone VFs with medial compression. As discussed in
Section 2.1, the pressures considered range from
to
.
The fits to each GAW are shown in
Figure 6 and the resulting estimates of the degree of medial compression, along with the other material properties, are shown in
Table 5. Similar to
Figure 5, the fits are again reasonable given the simplified model being used. As the subglottal pressure increases, so too does the maximum glottal area, as expected; this increase is captured by the FE model. As with the previous comparison, the open quotient and speed quotient are both lower for the FE model, though the difference decreases with increasing subglottal pressure.
As shown in
Table 5, all experimental values fall within two standard deviations of the estimated values; furthermore, the viscosity is estimated to be approximately
, which is consistent with the previous results. The estimated medial compression,
, varies somewhat from case to case, but all values are within two standard deviations of one another, indicating statistical consistency. Overall, comparing the estimates in
Table 3,
Table 4 and
Table 5, we find that the estimated material properties are quite consistent across all cases studied, engendering confidence in the method.
Considering the uncertainty in the estimates, we see that as the subglottal pressure increases its uncertainty decreases. As the variance of the measurement noise is treated as fixed at in all estimates, this decrease in uncertainty is not due to a decrease in measurement uncertainty. Furthermore, the same prior distributions are used in all cases. Hence, this decrease in uncertainty is due to an increase in sensitivity of the model, which could be due to the larger glottal width having fewer parameter combinations that are capable of matching the data. Alternatively, the change in uncertainty could be due to the pre-stress model. The estimates computed for and have , whereas the other two estimates have ; in addition, there is a marked decrease in the uncertainties in as increases. This could indicate that a higher level of VF compression results in a model with lower sensitivity to the parameters. That is, the dynamics may be more influenced by pre-stress at higher subglottal pressures.
Overall, the consistency in the material property estimates and the reasonably low relative uncertainty in indicates that the FE model is capable of distinguishing between operational conditions. In pairwise t-tests of the four estimates only two pairs fail to reject the hypothesis of unique data sets ( confidence); those pairs are versus and versus . In these two pairs there are small changes in the experimental subglottal pressures () and similar fundamental frequencies. Interestingly, there is significant difference between the two cases with the highest subglottal pressures, despite also only differing by in line with the decreased uncertainty in subglottal pressure at these conditions. We note there is a more marked difference between fundamental frequencies in these cases.
For further validation we compare the volumetric flow rate,
Q, estimated from the model with the experimentally measured values; volumetric flow rate was not included in the estimation process and thus provides an independent measure for method/model validation.
Table 6 compares the estimated and experimentally measured values. The estimated flow rate is derived directly from the Bernoulli flow model embedded in the FE model (see
Section 3) as
where
is the density of air. As can be seen in the table, the estimated values generally agree well with, but tend to slightly over-predict, the experimentally measured values. Excepting for the case of
, the estimated values are all within one standard deviation of the measurements.
With the FE models developed for the four cases and validated with an independent measure (
Q), an additional parameter is explored that is not available experimentally.
Table 7 presents the average mean and maximum contact pressures experienced during collisions for the four subglottal pressures. The contact pressures increase with increasing subglottal pressure, which qualitatively agrees with previous studies [
37]. Excepting for the
case, the contact pressures are all less than the subglottal pressure. The silicone VFs employed in this study qualitatively do not appear to have vigorous contact when self-oscillating, and as such, the contact pressures may indeed be less than the subglottal pressure. The outlier in the estimated pressure data is the highest subglottal pressure, which exhibits mean and maximum contact pressures well above the subglottal pressure. This is also the case that predicted a volumetric flow rate well above the measured value, suggesting that this model is less reliable. Interestingly, this is the case that had the lowest material property uncertainties. It is likely that the poor agreement in
Q, and the exceedingly high contact pressures for this case, are a result of more complex vibratory patterns for the silicone VFs at this higher subglottal pressure that are not captured well with the simplified 2D FE model. This suggests that additional measures may be required in the estimation process to generate an accurate model for this case.
5.3. Sensitivity Analysis
The estimates presented in
Section 5 were produced for fixed ensemble size for the importance sampling, and fixed time step size and mesh density for the FE model. These parameters influence the quality of the numerical model and the estimation procedure while also impacting the computational load. The estimates presented in the previous sections, for example, took 140 h for 16 parallel threads on a AMD Ryzen Threadripper 1950X with 16 cores at 3.4 GHz and 128 GB of RAM to run the importance sampling for all 50,000 samples. As such, there is motivation to use a coarser model (larger/fewer elements and larger time step) and fewer samples to decrease the computational load. To ensure that the estimates presented in this work are not conditional on the numerical parameters being used in the model we explore the sensitivity of the results to them in this section. We use the case without medial compression, again, as the exemplar.
5.3.1. Ensemble Size
Sensitivity of the results to the importance sampling ensemble size was checked by computing estimates with a progressively smaller number of samples from the priors.
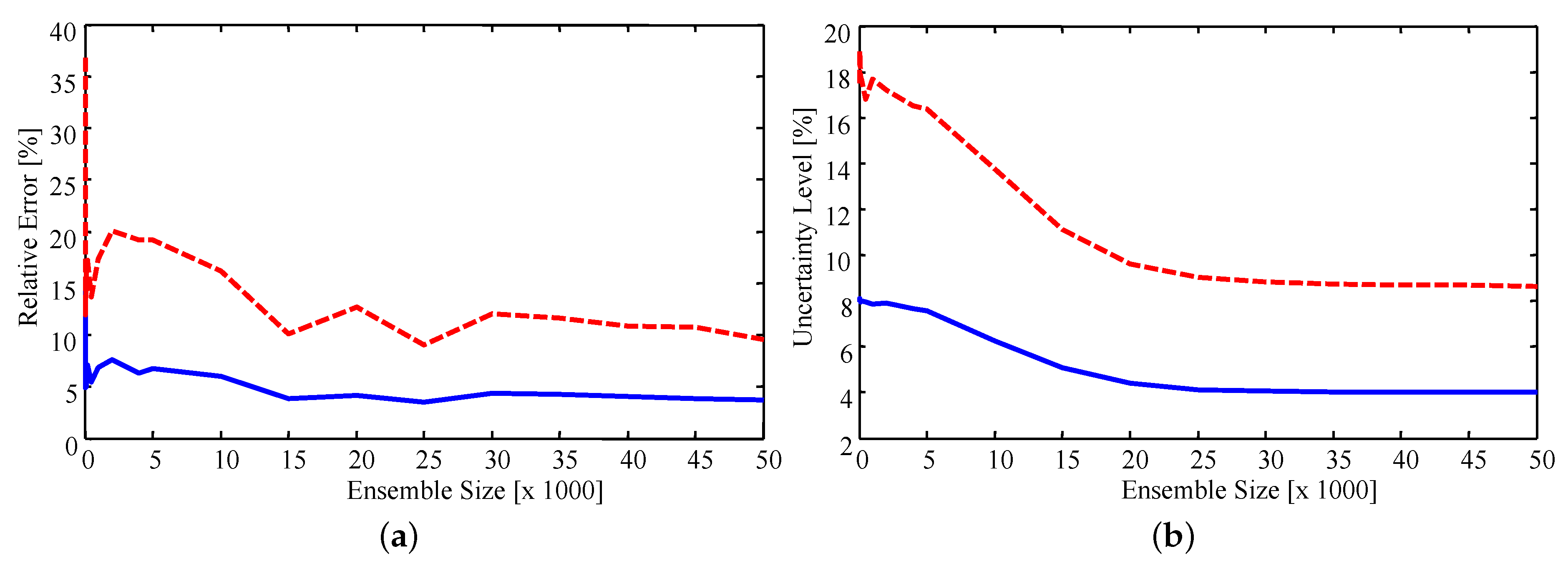
Figure 7 presents the relative error, defined as the percentage difference in the estimate and experimental value, and uncertainty level for ensemble sizes ranging from 100 to 50,000. It was found that, on average, the estimated values stabilize as the ensemble size increases. The peaks which occur at approximately 15,000 and 25,000 samples are due to the sample-based nature of the estimate. Since the estimates are the sample mean of the resampled ensemble the exact estimated value for each parameter changes as more samples are included in the ensemble. As such, it is encouraging to note that the estimates do appear to stabilize. Specifically, the average error of the estimates stabilizes when using an ensemble size of approximately 15,000, with the maximum error stabilizing with approximately 40,000 samples. The uncertainty smoothly decreases as the ensemble increases, stabilizing when approximately 25,000 samples are used. Error in the estimates converges faster than the uncertainty since an accurate estimate of the mean is easier to attain than a stable estimate of the variance.
5.3.2. FE Time Step and Triangulation
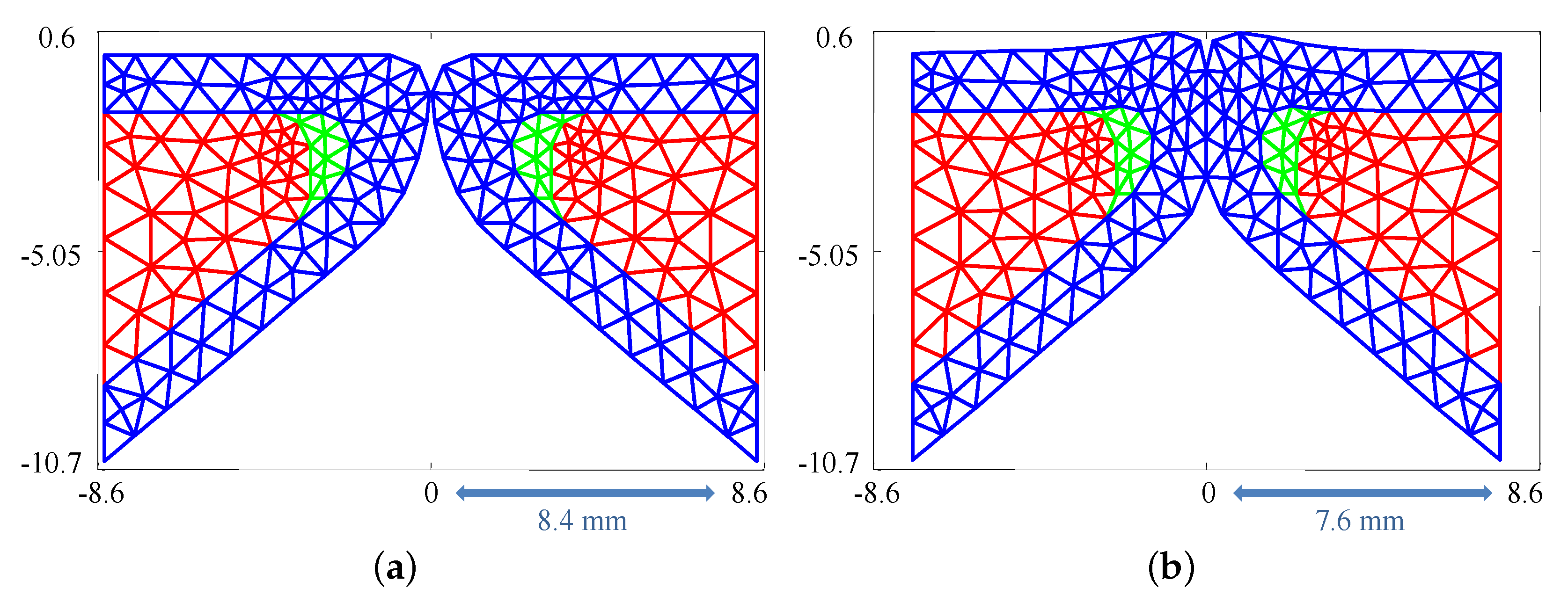
Estimates were produced using time step sizes of , , and and triangulations with 172, 205, and 263 elements over the same geometry. For direct comparison, the estimates were computed using an importance sampling ensemble size of 50,000.
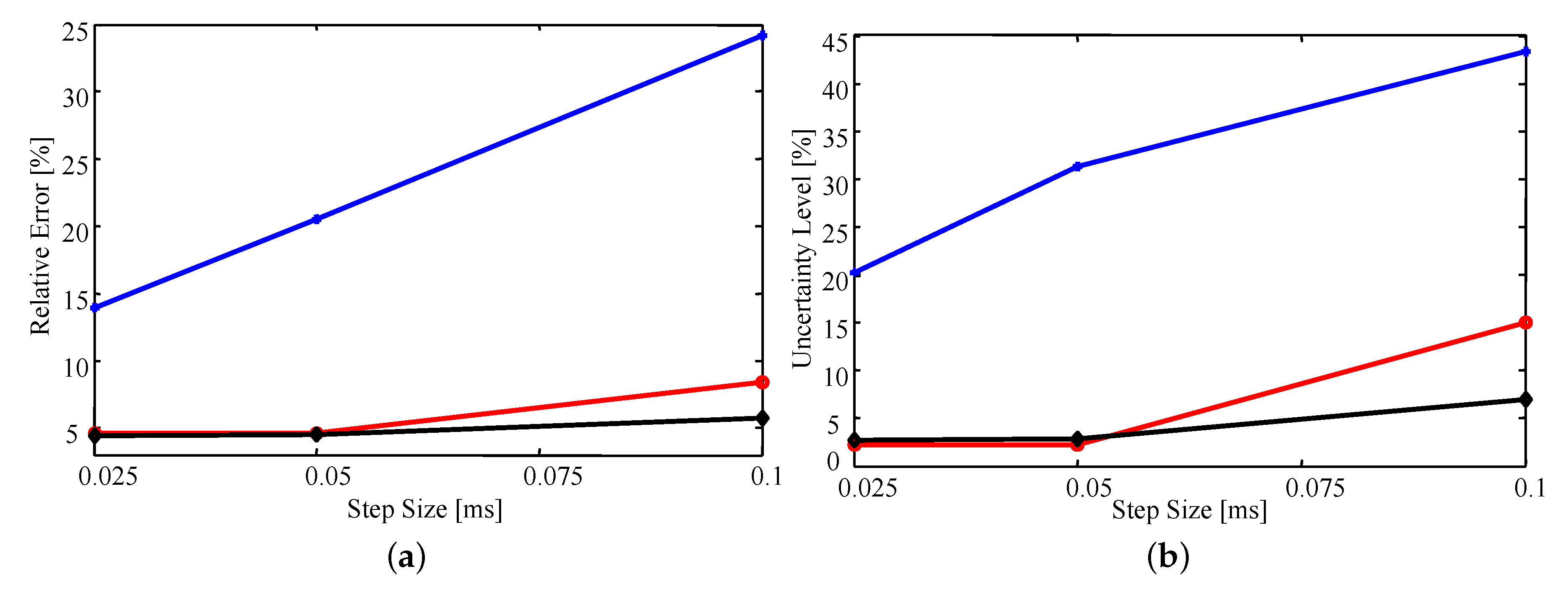
Figure 8a shows that, on average, the relative error (as defined above) in the estimates is very similar whether the triangulation involves 263 or 205 elements. In fact, all estimated parameter values differ by
or less for the two triangulations. This difference is likely due to numerical error resulting from the sample-based nature of importance sampling. In contrast, the lower density mesh introduces a larger error for all step sizes, but rapidly improves with decreasing step size.
Similar trends are observed in
Figure 8b where decreasing step size or increasing mesh density results in a decrease in uncertainty. The observed decrease in uncertainty with decreasing time step and increasing mesh density results from having a higher fidelity numerical model that is more sensitive to the parameter values; that is, small changes in the parameter values will have a larger impact on the simulated data [
33]. As a result, the uncertainty of the estimates will decrease as the fidelity of the model increases. However, as the time step decreases and mesh density increases the computational cost grows exponentially. Thus, examining how the estimated uncertainty behaves as the fidelity of the model increases becomes quickly infeasible.
6. Conclusions
To date, the approaches employed for developing subject-specific numerical VF models have focused on lumped-elements for the fitting model in the inverse analysis; as such, parameter estimates are often greatly abstracted from the physical tissue properties. To overcome these limitations, the present work proposes a FE model of the VFs for a fitting model. The FE model captures the geometry and layered structure of the VFs more accurately, treating them as a multi-layered viscoelastic body, thus better approximating their kinematics. Since the FE model directly employs the tissue properties, such as Young’s moduli, these properties are estimated directly. Estimation of material properties was demonstrated using HSV data of silicone VFs as the observation, showing good agreement between the estimated and “ground truth” material properties.
The robustness of the method was demonstrated by considering experimental data with different degrees of medial compression and differing subglottal pressures. The FE model faithfully recovered the material properties in all cases, including the degree of medial compression, which was embedded into the FE model in the form of base displacement. This suggests that the employed Bayesian framework using a FE fitting model is sufficiently sensitive to distinguish between different experimental conditions, even though the model was restricted to two dimensions.
The FE models were validated by comparing the volumetric flow rate predicted by the model with experimentally measured values. This observation was not included in the estimation process and, as such, was an independent measure. The volumetric flow rate was slightly over-predicted, but generally agreed well. The exception was the highest subglottal pressure case, which was considerably over-predicted. Additionally, the contact pressures extracted from the developed FE models were found to increase with increasing subglottal pressure and medial compression, which is a trend that qualitatively agrees with previous studies. The highest subglottal pressure case was again an outlier, suggesting that the FE model for that case does not accurately capture the kinematics of the silicone VFs, likely due to the 2D geometry. This could potentially be improved by incorporating additional observations in the estimation procedure or expanding to a three-dimensional model.
The stability of the results was examined with respect to numerical parameters, such as the importance sampling ensemble size, time step size, and mesh density. Estimated values converged at relatively modest ensemble sizes, though resolving the uncertainties required considerably more samples. Decreasing the time step size and increasing the mesh density lead to smaller uncertainties at the cost of significant computational time. One of the main drawbacks to our proposed model is the computational complexity; this cost will increase if more complex fluids models, a three-dimensional geometry, or acoustics are included.
One source of uncertainty that has not been considered in this work is the structure of the layers. All estimates in this work have been computed with a FE model that was formed treating the layers and dimensions of the silicone VFs as perfectly known. The use of imperfect layers will affect the estimates and uncertainties of the material properties, however, this is the subject of ongoing research and requires a further examination.
As an introductory effort, incorporating a FE fitting model into the Bayesian estimation framework has shown good promise. Future work includes validating the contact pressure estimates with experimental data, implementing a three-dimensional FE model, and employing clinical HSV.