The Impact of Node Location Imperfections on the Reliability of Single-Layer Steel Domes
Abstract
Featured Application
Abstract
1. Introduction
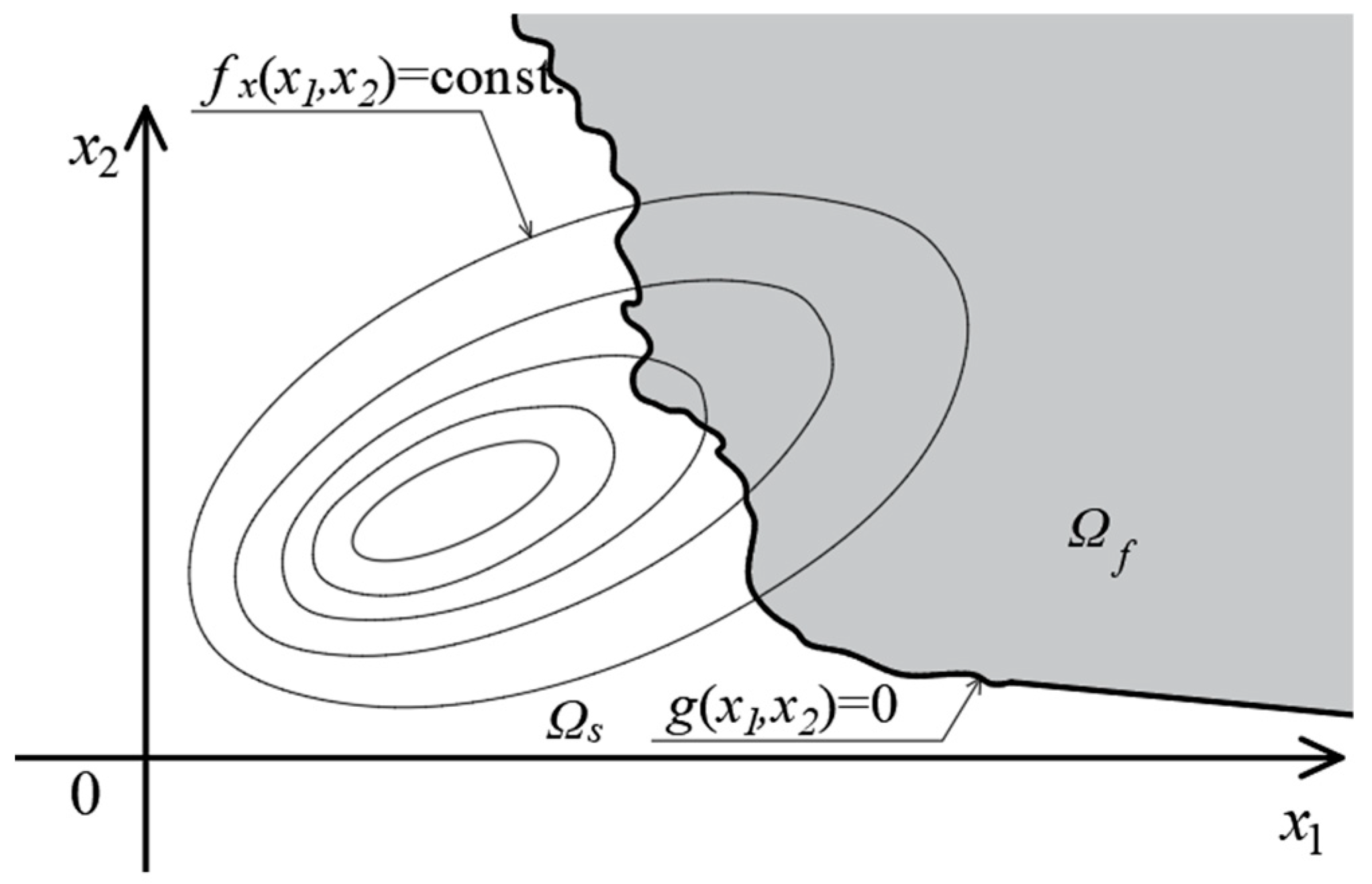
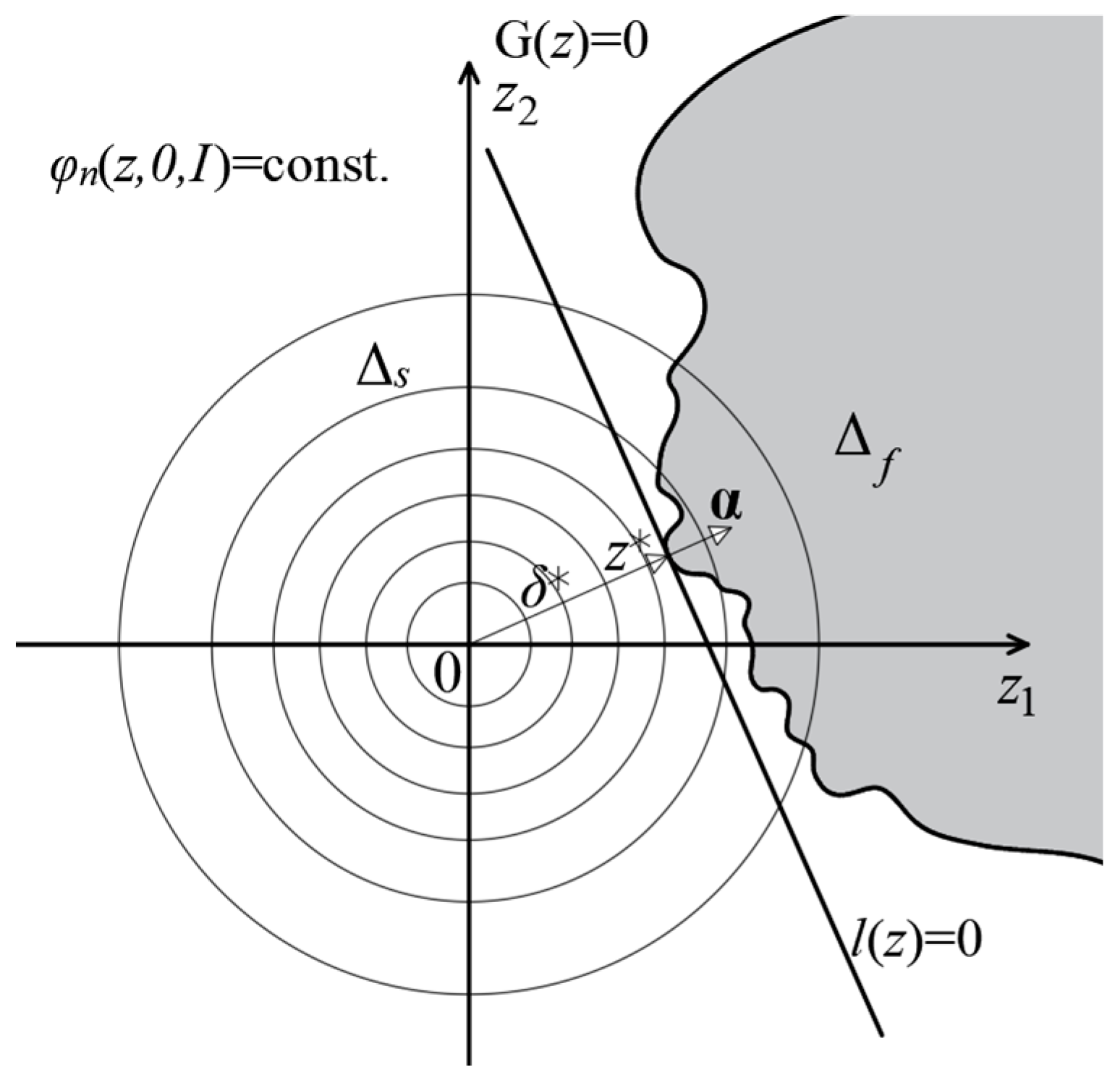
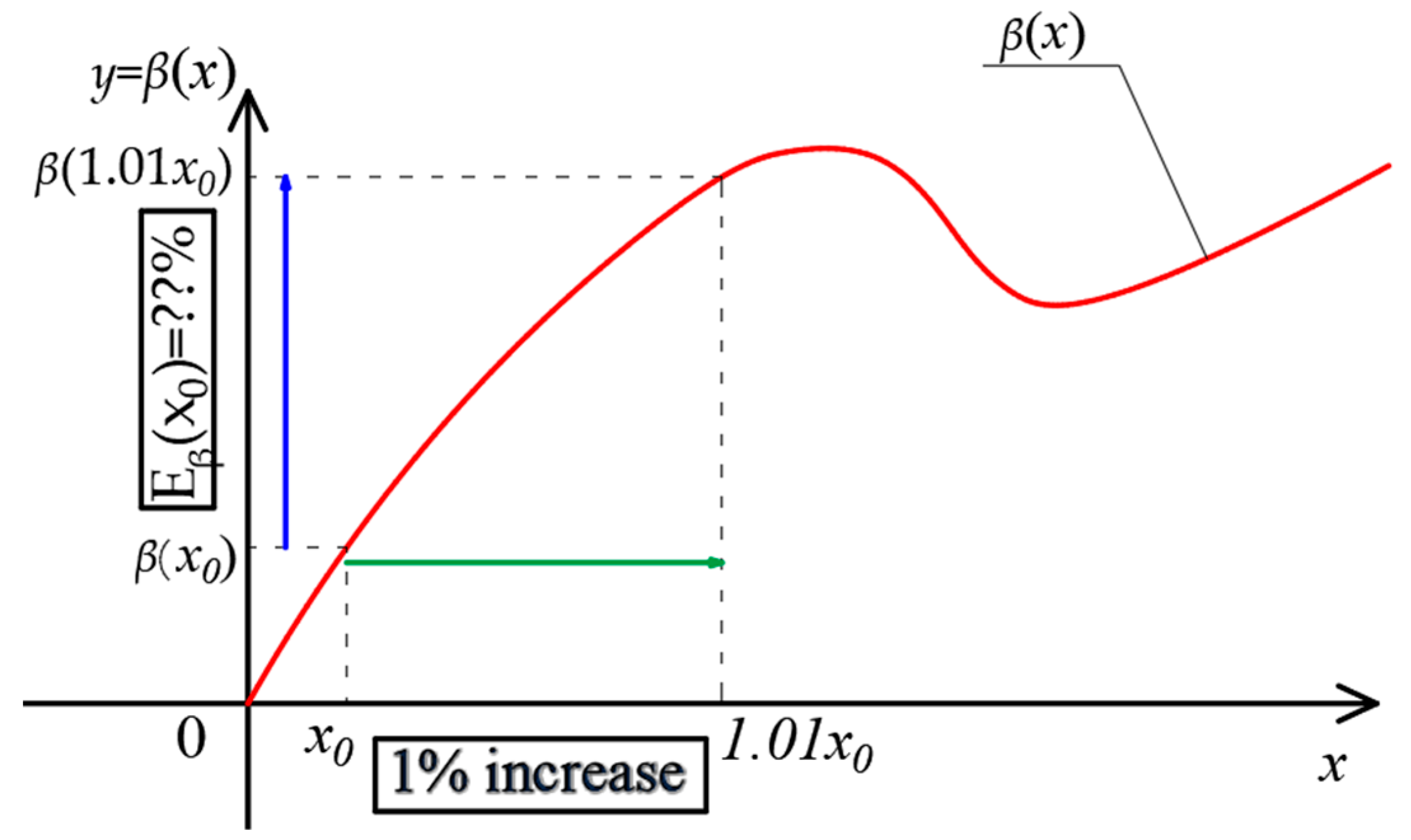
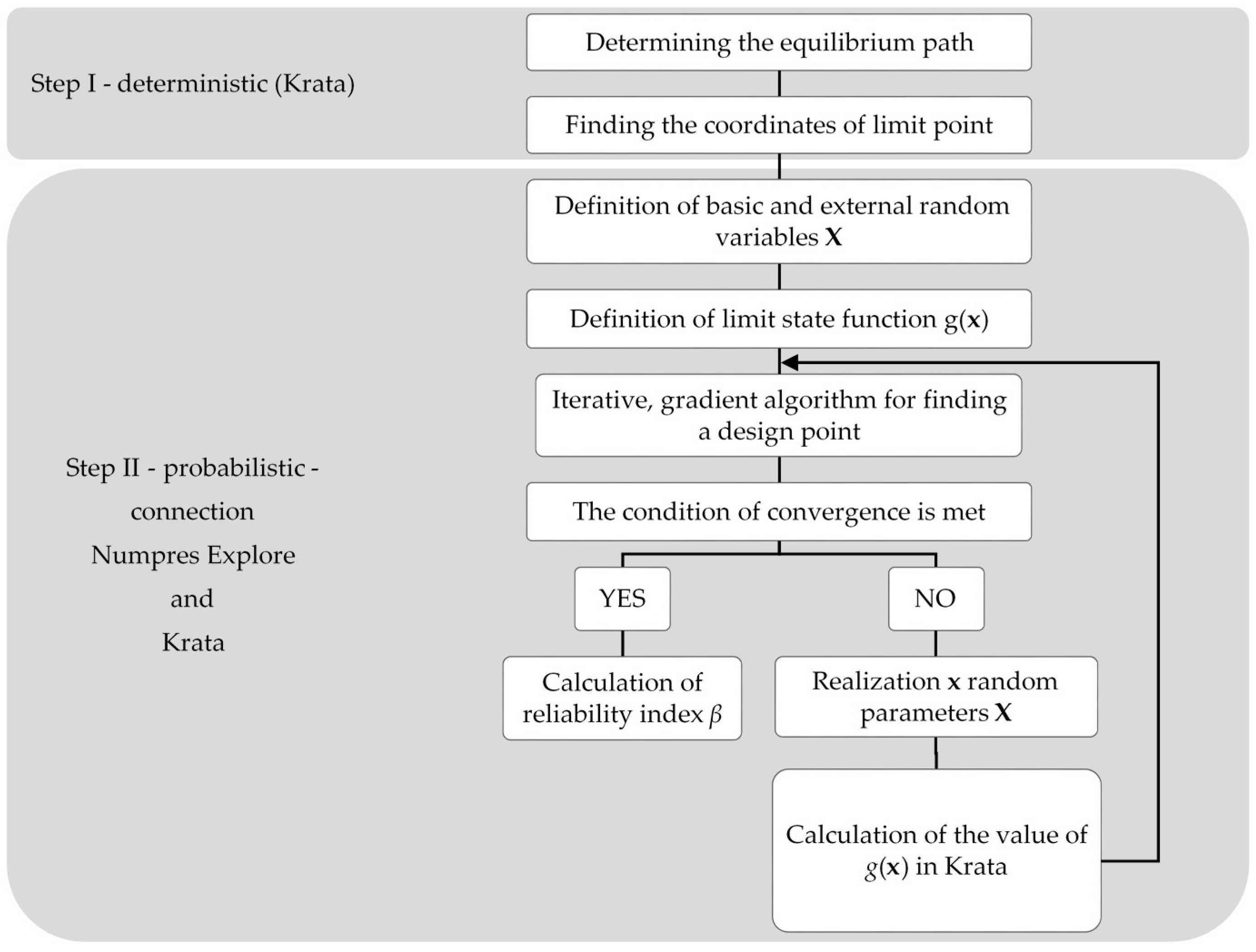
2. Reliability and Elasticity Indexes
g(x) > 0 − safe area ΩS
g(x) = 0 − limit area
Ωs = {x:g(x) > 0} → ∆s = {z : G(z) > 0}
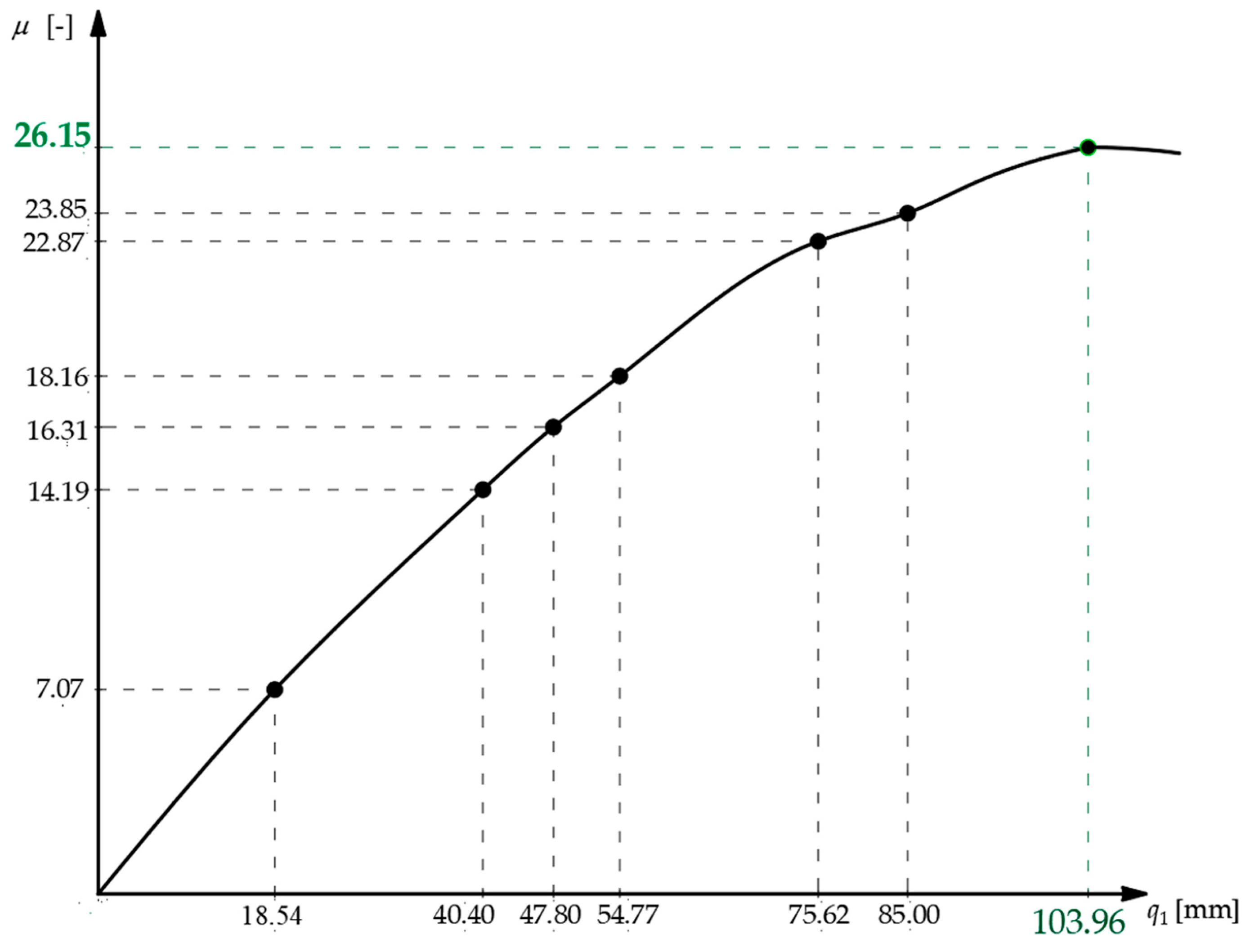
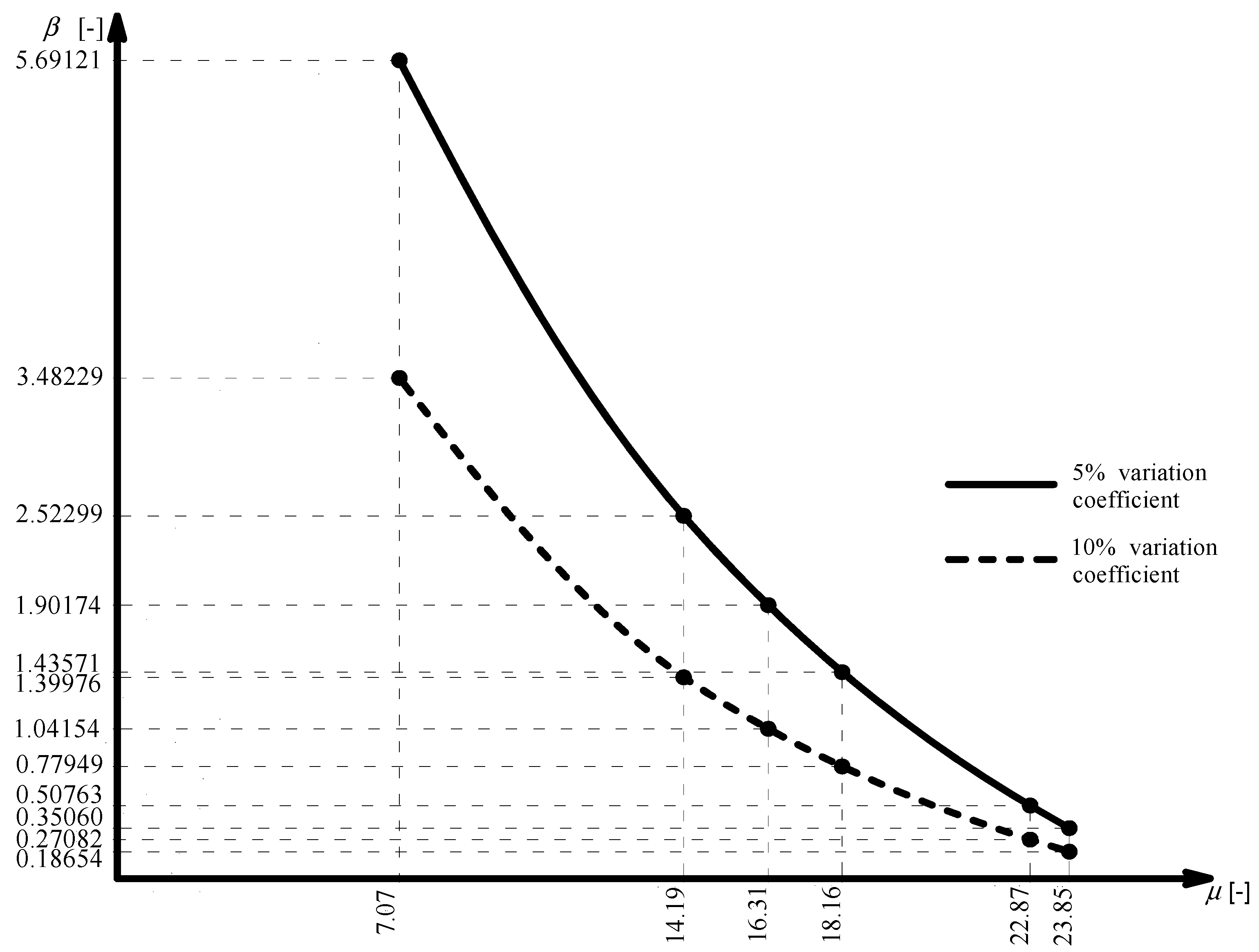
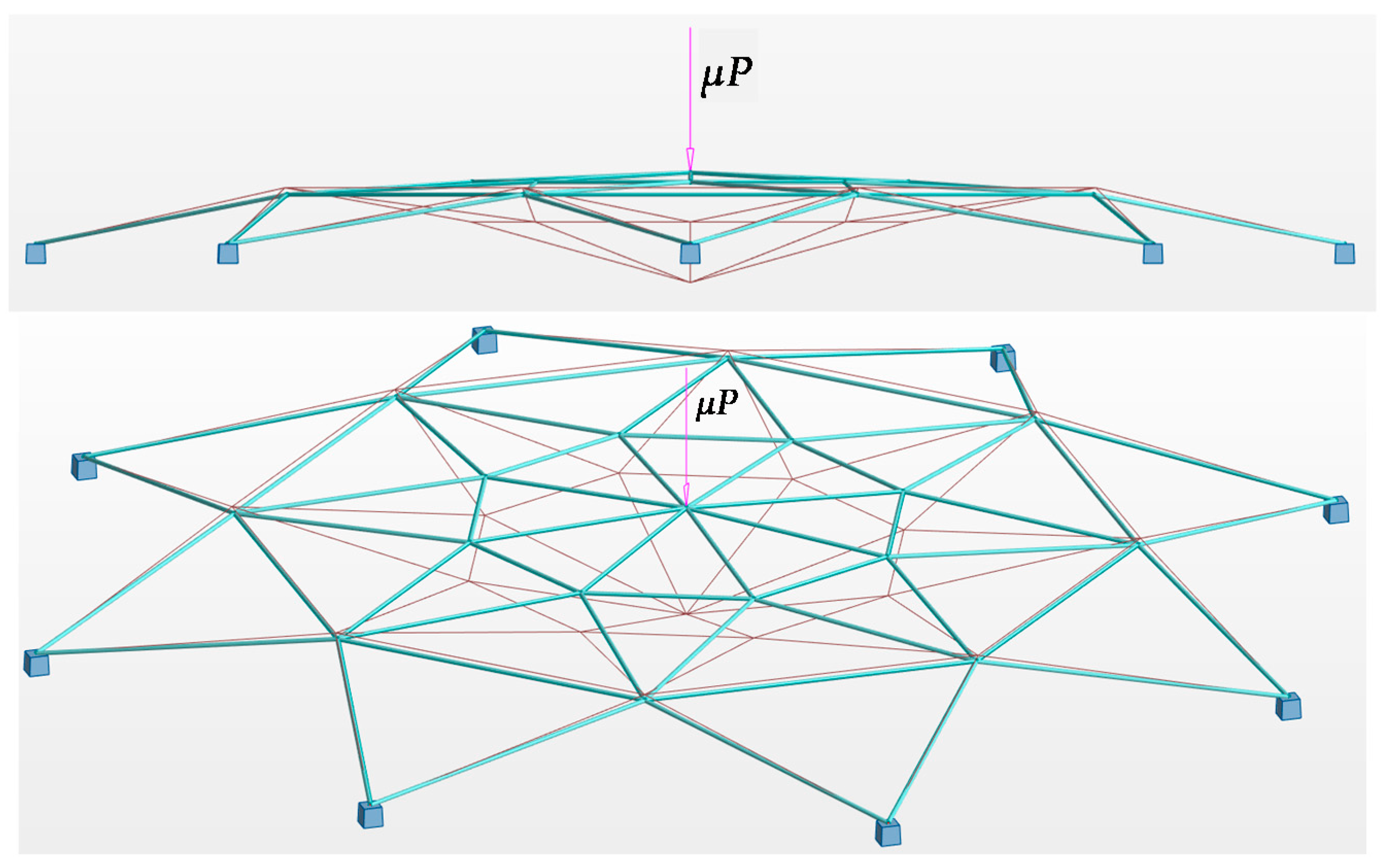
3. Numerical Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Madsen, H.O.; Krenk, S.; Lind, N.C. Methods of Structural Safety; Prentice-Hall: Upper Saddle River, NJ, USA, 1986. [Google Scholar]
- Melchers, R.E. Structural Reliability Analysis and Predictions, 2nd ed.; Wiley: Hoboken, NJ, USA, 1999. [Google Scholar]
- Ditlevsen, O.; Madsen, H.O. Structural Reliability Methods; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Thoft-Christensen, P.; Baker, M.J. Structural Reliability Theory and its Applications; Springer: Berlin, Germany, 1982. [Google Scholar]
- Augusti, G.; Baratta, A.; Casciati, F. Probabilistic Methods in Structural Engineering; Chapman and Hall: London, UK, 1984. [Google Scholar]
- Harr, M.E. Reliability-Based Design in Civil Engineering; McGraw-Hill: New York, NY, USA, 1987. [Google Scholar]
- Nowak, A.S.; Collins, K.R. Reliability of Structures; McGraw-Hill Higher Education: New York, NY, USA, 2000. [Google Scholar]
- Hasofer, A.M.; Lind, N.C. Exact and invariant second moment code format. J. Engin. Mech. Div. ASCE 1974, 100, 111–121. [Google Scholar]
- Cornell, C.A. A probability-based structural code. J. Am. Concr. Inst. 1969, 66, 974–985. [Google Scholar]
- Rackwitz, R.; Fiessler, B. Structural reliability under combined random load sequences. Comput. Struct. 1978, 9, 489–494. [Google Scholar] [CrossRef]
- Hohenbichler, M.; Rackwitz, R. Non-normal dependent vectors in structural safety. J. Engin. Mech. Div. ASCE 1981, 107, 1227–1238. [Google Scholar]
- Rosenblatt, M. Remarks on a Multivariate Transformation. Ann. Math. Stat. 1952, 23, 470–472. [Google Scholar] [CrossRef]
- Der Kiureghian, A.; Liu, P.L. Structural reliability under incomplete probability information. J. Eng. Mech. ASCE 1986, 112, 85–104. [Google Scholar] [CrossRef]
- Hisada, T.; Nakagiri, S. Role of the stochastic finite element method in structural safety and reliability. In Proceedings of the 4th International Conference on Structural Society Safety Reliability, Cobe, Japan, 27–29 May 1985; pp. 385–394. [Google Scholar]
- Liu, W.K.; Mani, A.; Belytschko, T. Finite elements methods in probabilistic mechanics. Probabilistics Eng. Mech. 1987, 2, 201–213. [Google Scholar] [CrossRef]
- Shinozuka, M. Basic issues in stochastic finite element analysis. In Proceedings of the Fifth International Conference on Applications of Statistics and Probability in Soil and Structural Engineering, University of British Columbia, Vancouver, BC, Canada, 25–29 May 1987; pp. 507–520. [Google Scholar]
- Li, C.C.; der Kiureghian, A. Optimal discretization of random fields. J. Engin. Mech. ASCE 1993, 119, 1136–1154. [Google Scholar] [CrossRef]
- Matthies, H.G.; Brenner, C.E.; Bucher, C.G.; Guedes Soares, C. Uncertainties in probabilistic numerical analysis of structures and solids—Stochastics finite elements. Struct. Saf. 1997, 19, 283–336. [Google Scholar] [CrossRef]
- Pellissetti, M.F.; Schuëller, G.I. On general purpose software in structural reliability—An overview. Struc. Saf. 2006, 28, 3–16. [Google Scholar] [CrossRef]
- Reh, S.; Beley, J.D.; Mukherjee, S.; Khor, E.H. Probabilistic finite element analysis using ANSYS. Struct. Saf. 2006, 28, 17–43. [Google Scholar] [CrossRef]
- Der Kiureghian, A.; Haukaas, T.; Fujimura, K. Structural reliability software at the University of California, Berkeley. Struct. Saf. 2006, 28, 44–67. [Google Scholar] [CrossRef]
- Schuëller, G.I.; Pradlwarter, H.J. Computational stochastic structural analysis (COSSAN)-software tool. Struct. Saf. 2006, 28, 68–82. [Google Scholar] [CrossRef]
- Thacker, B.H.; Riha, D.S.; Fitch, S.K.H.; Huyse, L.J.; Pleming, J.B. Probabilistic engineering analysis using the NESSUS software. Struct. Saf. 2006, 28, 83–107. [Google Scholar] [CrossRef]
- Gollwitzer, S.; Kirchgabner, B.; Fischer, R.; Rackwitz, R. PERMAS-RA/STRUREL system of programs for probabilistic reliability analysis. Struct. Saf. 2006, 28, 108–129. [Google Scholar] [CrossRef]
- Lemaire, M. Pendola phimeca-soft M. Struct. Saf. 2006, 28, 130–149. [Google Scholar] [CrossRef]
- Tvedt, L. Proban-probabilistic analysis. Struct. Saf. 2006, 28, 150–163. [Google Scholar] [CrossRef]
- Wu, Y.T.; Shin, Y.; Sues, R.H.; Cesare, M.A. Probabilistic function evaluation system (ProFES) for reliability-based design. Struct. Saf. 2006, 28, 164–195. [Google Scholar] [CrossRef]
- Lin, H.Z.; Khalessi, M.R. General outlook of UNIPASSV5.0: A general-purpose probabilistic software system. Struct. Saf. 2006, 28, 196–216. [Google Scholar] [CrossRef]
- Schuëller, G.I.; Stix, R. A critical appraisal of methods to determine failure probabilities. Struct. Saf. 1987, 4, 293–309. [Google Scholar] [CrossRef]
- Hohenbichler, M.; Rackwitz, R. Improvement of second-order reliability estimates by importance sampling. J. Engin. Mech. ASCE 1988, 114, 2195–2199. [Google Scholar] [CrossRef]
- Doliński, K. First-order second-moment approximation in reliability of structural systems: Critical review and alternative approach. Struct. Saf. 1983, 1, 211–231. [Google Scholar] [CrossRef]
- Rubinstein, R.Y. Simulation and the Monte Carlo Method; Wiley: Hoboken, NJ, USA, 1981. [Google Scholar]
- Obara, P.; Radoń, U.; Zabojszcza, P.; Mochocki, W. Effects of single-layer truss dome geometry on critical load capacity. Struct. Environ. 2017, 3, 152–164. [Google Scholar]
- Zabojszcza, P.; Radoń, U.; Obara, P. Impact of single-layer dome modelling on the critical load capacity. Matec. Web Conf. 2018, 219. [Google Scholar] [CrossRef][Green Version]
- Zabojszcza, P.; Radoń, U. Effect of increased density of nodes in geodesic dome on its critical load capacity. IOP Conf. Ser. Mater. Sci. Eng. 2019, 471. [Google Scholar] [CrossRef]
- Riks, E. The application of Newton’s method to the problem of elastic stability. J. Appl. Mech. 1972, 39, 1060–1065. [Google Scholar] [CrossRef]
- Riks, E. An incremental approach to the solution of snapping and buckling problems. Int. J. Solids Struct. 1979, 15, 529–551. [Google Scholar] [CrossRef]
- Zhao, C.; Zhao, Y.; Ma, J. The stability of new single-layer combined lattice shell based on aluminum alloy honeycomb panels. Appl. Sci. 2017, 7, 1150. [Google Scholar] [CrossRef]
- Galambos, T.V. Guide to Stability Design for Metal Structures; Wiley and Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Thompson, J.M.T.; Hunt, G.W. A General Theory of Elastic Stability; Wiley and Sons: Hobooken, NJ, USA, 1973. [Google Scholar]
- Pignatero, M.; Rizzi, N.; Luongo, A. Stability, Bifurcation and Postcritical Behavior of Elastic Structures; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Stocki, R.; Kolanek, K.; Knabel, J.; Tauzowski, P. FE based structural reliability analysis using STAND environment. Comput. Assist. Mech. Eng. Sci. 2009, 16, 35–58. [Google Scholar]
- Lasota, R.; Stocki, R.; Tauzowski, P.; Szolc, T. Polynomial chaos expansion method in estimating probability distribution of rotor-shaft dynamic responses. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 413–422. [Google Scholar] [CrossRef]
- Szolc, T.; Tauzowski, P.; Stocki, R.; Knabel, J. Damage identification in vibrating rotor-shaft systems by efficient sampling approach. Mech. Syst. Signal. Process. 2009, 23, 1615–1633. [Google Scholar] [CrossRef]
- Stocki, R.; Tauzowski, P.; Knabel, J. Reliability analysis of a crashed thin-walled s-rail accounting for random spot weld failures. Int. J. Crashworthiness 2008, 13, 693–706. [Google Scholar] [CrossRef]
- European Committee for Standardization. Basis of Structural Design; Technical Report PN-EN-1990:2002; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Schittkowski, K. The nonlinear programming method of Wilson, Han and Powell with an augmented Lagrangian type line search function, part 1: Convergence analysis. Numer. Math. 1982, 38, 83–114. [Google Scholar] [CrossRef]
- Schittkowski, K.; Zillober, C.; Zotemantel, R. Numerical comparison of nonlinear programming algorithms for structural optimization. Struct. Multidiscip. Optim. 1994, 7, 1–19. [Google Scholar] [CrossRef]
- Budnick, F.S. Finite Mathematics with Applications; McGraw-Hill: New York, NY, USA, 1985. [Google Scholar]
- Radoń, U. Reliability analysis of misses truss. Arch. Civ. Mech. Eng. 2011, 11, 723–738. [Google Scholar] [CrossRef]
- Radoń, U.; Dudzik, A. The evaluation of algorithms for determination of the reliability index. Arch. Civ. Eng. 2015, 3, 133–147. [Google Scholar]
- Radoń, U.; Dudzik, A. The Reliability Assessment of a Steel Industrial Hall, Advances in Mechanics: Theoretical, Computational and Interdisciplinary Issues; Taylor & Francis Group: London, UK, 2016; pp. 163–166. [Google Scholar]
- NUMPRESS. Available online: http://numpress.ippt.pan.pl/opis.html (accessed on 4 June 2019).
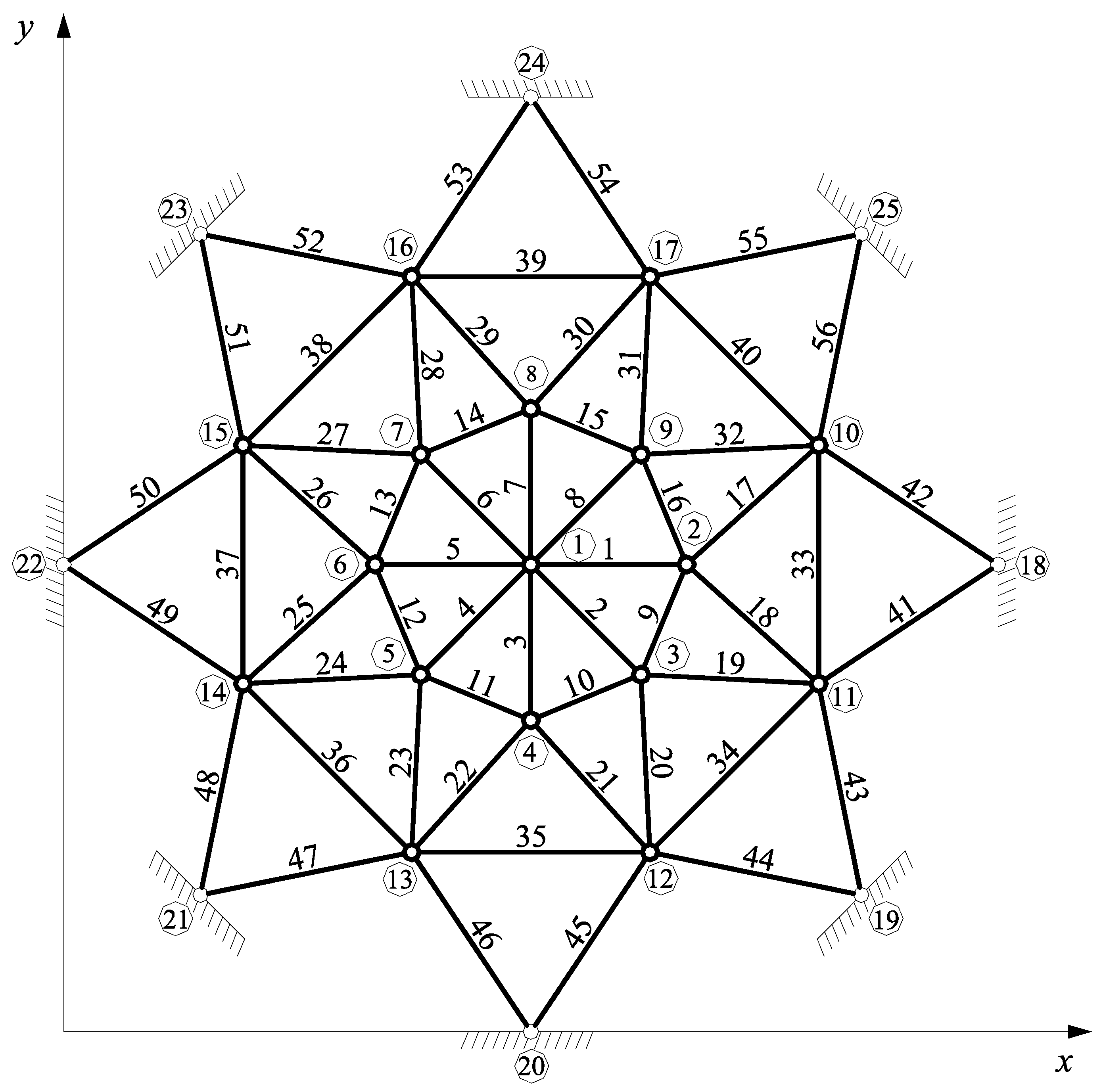
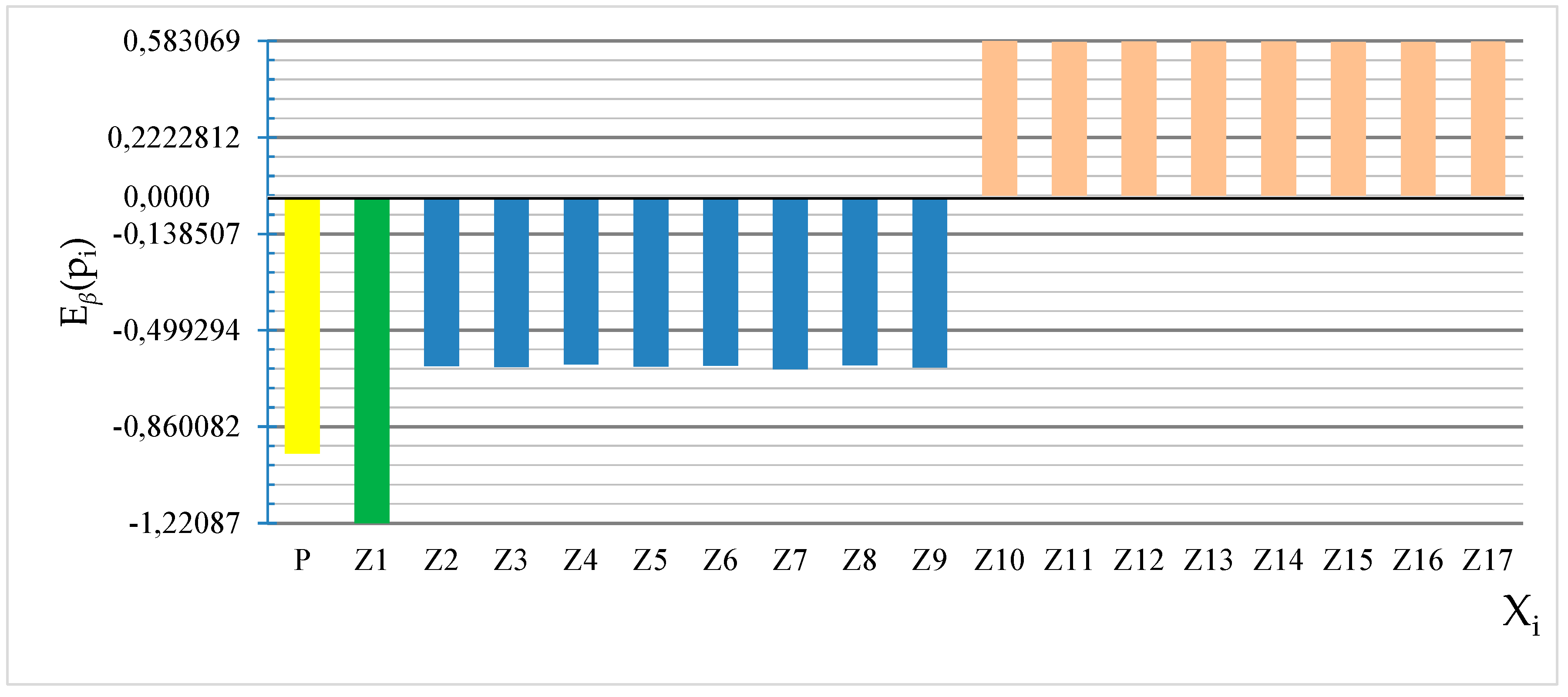

| No. of Node | x [m] | y [m] | z [m] | No. of Node | x [m] | y [m] | z [m] |
|---|---|---|---|---|---|---|---|
| 1 | 15.000 | 15.000 | 1.6465 | 14 | 5.761 | 11.173 | 1.14 |
| 2 | 20.000 | 15.000 | 1.432 | 15 | 5.761 | 18.827 | 1.14 |
| 3 | 18.536 | 11.464 | 1.432 | 16 | 11.173 | 24.239 | 1.14 |
| 4 | 15.000 | 10.000 | 1.432 | 17 | 18.827 | 24.239 | 1.14 |
| 5 | 11.464 | 11.464 | 1.432 | 18 | 30.000 | 15.000 | 0 |
| 6 | 10.000 | 15.000 | 1.432 | 19 | 25.607 | 4.393 | 0 |
| 7 | 11.464 | 18.536 | 1.432 | 20 | 15.000 | 0.000 | 0 |
| 8 | 15.000 | 20.000 | 1.432 | 21 | 4.393 | 4.393 | 0 |
| 9 | 18.536 | 18.536 | 1.432 | 22 | 0.000 | 15.000 | 0 |
| 10 | 24.239 | 18.827 | 1.14 | 23 | 4.393 | 25.607 | 0 |
| 11 | 24.239 | 11.173 | 1.14 | 24 | 15.000 | 30.000 | 0 |
| 12 | 18.827 | 5.761 | 1.14 | 25 | 25.607 | 25.607 | 0 |
| 13 | 11.173 | 5.761 | 1.14 | ||||
| Random Variable | Mean Value | Probability Distribution Type | Case 1 | Case 2 | ||
|---|---|---|---|---|---|---|
| Standard Deviation σ1,i | Variation Coefficient | Standard Deviation σ2,i | Variation Coefficient | |||
| Load P | 1 | Normal | 0.1 | 10% | 0.1 | 10% |
| Coordinate “z” of node 1–Z1 | 1.6465 | Normal | 0.16465 | 10% | 0.082325 | 5% |
| Coordinate “z” of node 2–Z2 | 1.432 | Normal | 0.1432 | 10% | 0.0716 | 5% |
| Coordinate “z” of node 3–Z3 | 1.432 | Normal | 0.1432 | 10% | 0.0716 | 5% |
| Coordinate “z” of node 4–Z4 | 1.432 | Normal | 0.1432 | 10% | 0.0716 | 5% |
| Coordinate “z” of node 5–Z5 | 1.432 | Normal | 0.1432 | 10% | 0.0716 | 5% |
| Coordinate “z” of node 6–Z6 | 1.432 | Normal | 0.1432 | 10% | 0.0716 | 5% |
| Coordinate “z” of node 7–Z7 | 1.432 | Normal | 0.1432 | 10% | 0.0716 | 5% |
| Coordinate “z” of node 8–Z8 | 1.432 | Normal | 0.1432 | 10% | 0.0716 | 5% |
| Coordinate “z” of node 9–Z9 | 1.432 | Normal | 0.1432 | 10% | 0.0716 | 5% |
| Coordinate “z” of node 10–Z10 | 1.14 | Normal | 0.114 | 10% | 0.057 | 5% |
| Coordinate “z” of node 11–Z11 | 1.14 | Normal | 0.114 | 10% | 0.057 | 5% |
| Coordinate “z” of node 12–Z12 | 1.14 | Normal | 0.114 | 10% | 0.057 | 5% |
| Coordinate “z” of node 13–Z13 | 1.14 | Normal | 0.114 | 10% | 0.057 | 5% |
| Coordinate “z” of node 14–Z14 | 1.14 | Normal | 0.114 | 10% | 0.057 | 5% |
| Coordinate “z” of node 15–Z15 | 1.14 | Normal | 0.114 | 10% | 0.057 | 5% |
| Coordinate “z” of node 16–Z16 | 1.14 | Normal | 0.114 | 10% | 0.057 | 5% |
| Coordinate “z” of node 17–Z17 | 1.14 | Normal | 0.114 | 10% | 0.057 | 5% |
| Load Multiplier µ | Displacement q1 [mm] | Case 1 | Case 2 | ||
|---|---|---|---|---|---|
| Failure Probability Pf | Reliability Index β | Failure Probability Pf | Reliability Index β | ||
| 7.07 | 18.54 | 0.000248568 | 3.48229 | 6.30709 × 10−9 | 5.69121 |
| 14.19 | 40.40 | 0.0807931 | 1.39976 | 0.0058181 | 2.52299 |
| 16.31 | 47.80 | 0.148813 | 1.04154 | 0.0286027 | 1.90174 |
| 18.16 | 54.77 | 0.217846 | 0.77949 | 0.0755421 | 1.43571 |
| 22.87 | 75.62 | 0.393263 | 0.270823 | 0.305856 | 0.507631 |
| 23.85 | 81.00 | 0.42604 | 0.186542 | 0.362944 | 0.3506 |
| Case 1 | Case 2 | |||
|---|---|---|---|---|
| µ = 7,07 | µ = 23,85 | µ = 7,07 | µ = 23,85 | |
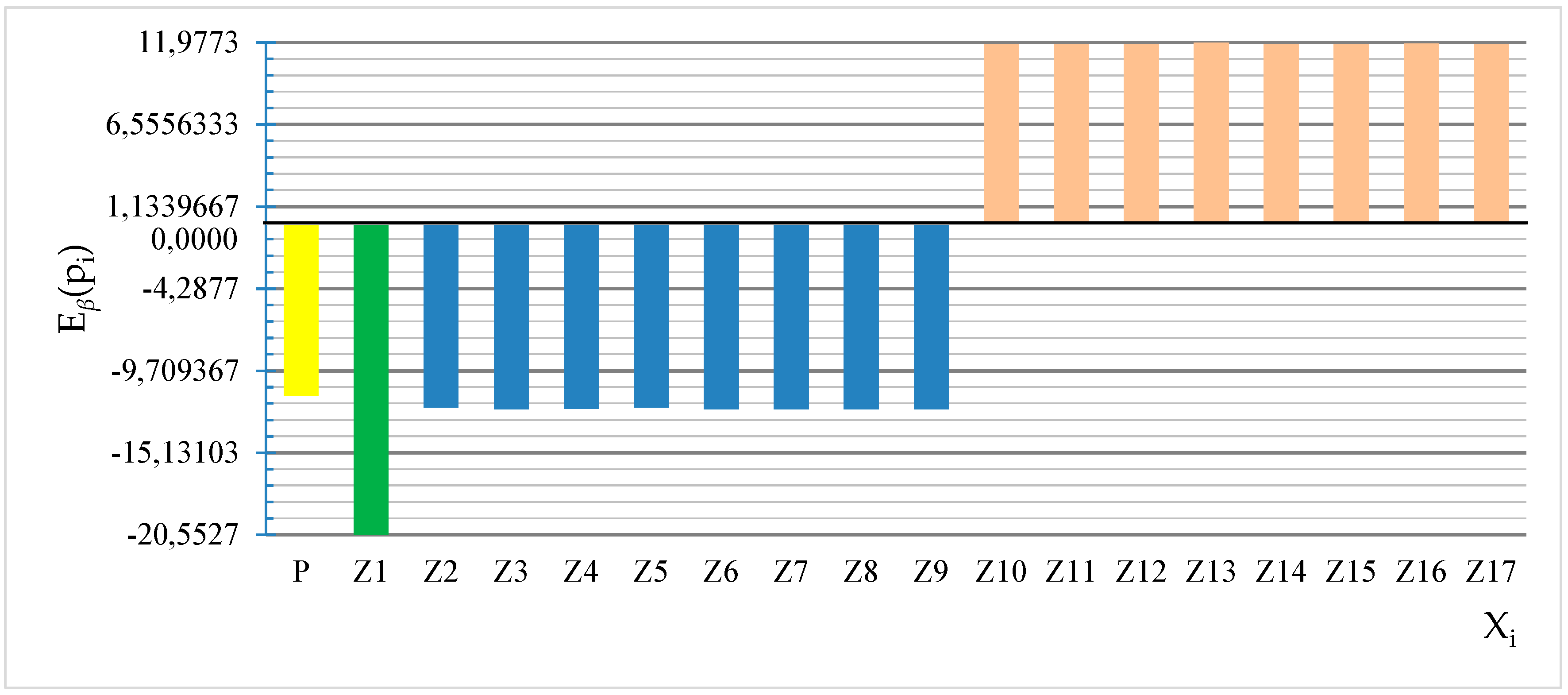
| P | −0,960682 | −11,3796 | −0,94165 | −11,295 |
| Z1 | −1,22087 | −20,5527 | −1,04297 | −20,428 |
| Z2 | −0,633033 | −12,1532 | −0,55432 | −12,1929 |
| Z3 | −0,636345 | −12,248 | −0,63249 | −12,2128 |
| Z4 | −0,627177 | −12,2261 | −0,57223 | −12,1834 |
| Z5 | −0,634882 | −12,1534 | −0,60514 | −12,2013 |
| Z6 | −0,63134 | −12,2363 | −0,59676 | −12,1821 |
| Z7 | −0,643971 | −12,2566 | −0,60399 | −12,2017 |
| Z8 | −0,630684 | −12,2457 | −0,57788 | −12,1823 |
| Z9 | −0,638158 | −12,2553 | −0,62899 | −12,1231 |
| Z10 | 0,583069 | 11,8805 | 0,546972 | 11,9319 |
| Z11 | 0,578446 | 11,8845 | 0,551486 | 11,8314 |
| Z12 | 0,580928 | 11,8773 | 0,552808 | 11,8252 |
| Z13 | 0,580211 | 11,9773 | 0,551094 | 11,9262 |
| Z14 | 0,58106 | 11,8772 | 0,548862 | 11,9283 |
| Z15 | 0,578546 | 11,8836 | 0,548516 | 11,9291 |
| Z16 | 0,578429 | 11,8875 | 0,55195 | 11,9279 |
| Z17 | 0,58093 | 11,8778 | 0,553645 | 11,8224 |
| Case 1 | Case 2 | |||
|---|---|---|---|---|
| µ = 7,07 | µ = 23,85 | µ = 7,07 | µ = 23,85 | |
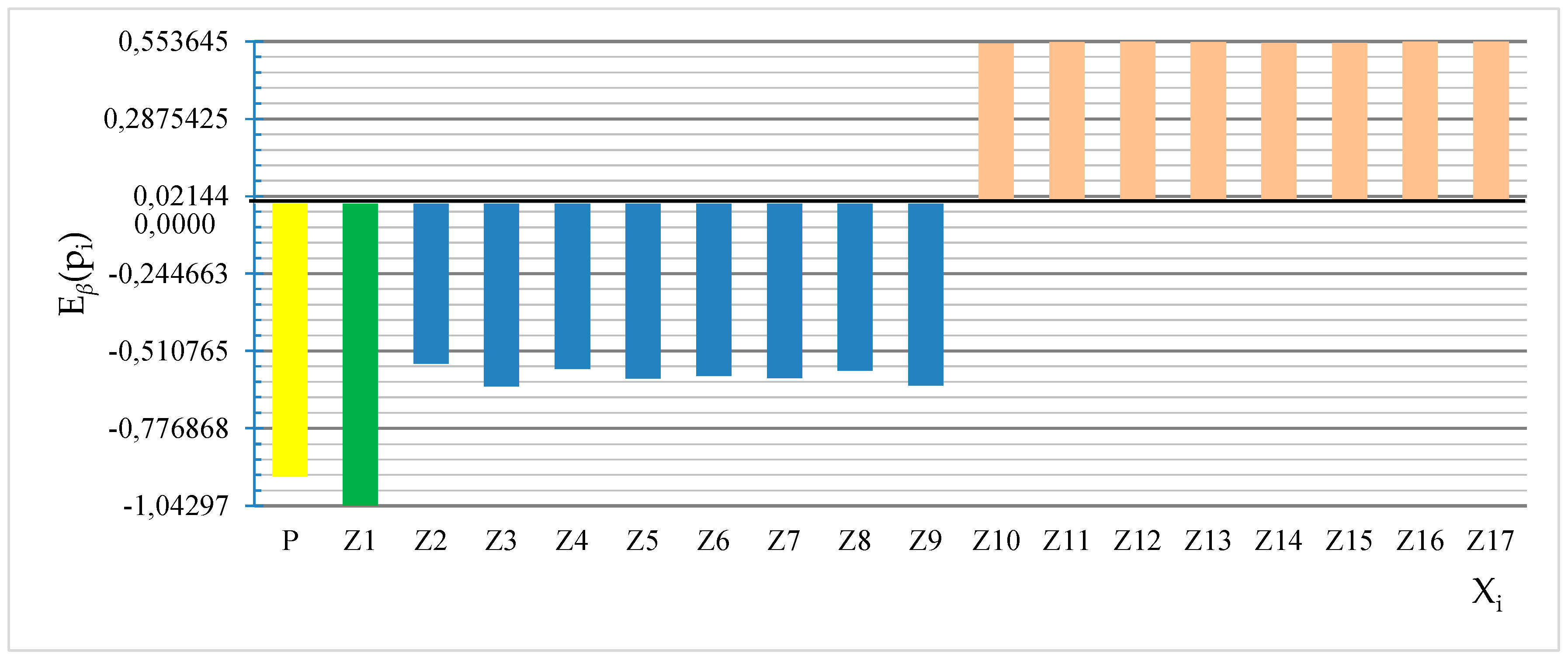
| P | 0,060838 | 0,00047 | 0,683858 | 0,00588722 |
| Z1 | 0,075018 | 0,003919 | 0,0575702 | 0,00598635 |
| Z2 | 0,010806 | 0,00056 | 0,00792583 | 0,00085315 |
| Z3 | 0,01099 | 0,000565 | 0,0107745 | 0,00085699 |
| Z4 | 0,010546 | 0,000567 | 0,0085271 | 0,000851656 |
| Z5 | 0,010921 | 0,000561 | 0,00969135 | 0,000852898 |
| Z6 | 0,010715 | 0,000568 | 0,00941762 | 0,000848981 |
| Z7 | 0,011342 | 0,000566 | 0,00963334 | 0,000856157 |
| Z8 | 0,010686 | 0,000568 | 0,00871643 | 0,000851986 |
| Z9 | 0,011073 | 0,00057 | 0,0106294 | 0,000841353 |
| Z10 | 0,011552 | 0,000533 | 0,00893249 | 0,000836612 |
| Z11 | 0,011284 | 0,000534 | 0,00910208 | 0,000821875 |
| Z12 | 0,011468 | 0,000533 | 0,00917403 | 0,000820686 |
| Z13 | 0,011429 | 0,000542 | 0,00910028 | 0,000835488 |
| Z14 | 0,01147 | 0,000528 | 0,0090027 | 0,000833421 |
| Z15 | 0,011286 | 0,000534 | 0,00901152 | 0,000836247 |
| Z16 | 0,011275 | 0,000534 | 0,00912094 | 0,000832002 |
| Z17 | 0,011464 | 0,000528 | 0,00919437 | 0,000820104 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabojszcza, P.; Radoń, U. The Impact of Node Location Imperfections on the Reliability of Single-Layer Steel Domes. Appl. Sci. 2019, 9, 2742. https://doi.org/10.3390/app9132742
Zabojszcza P, Radoń U. The Impact of Node Location Imperfections on the Reliability of Single-Layer Steel Domes. Applied Sciences. 2019; 9(13):2742. https://doi.org/10.3390/app9132742
Chicago/Turabian StyleZabojszcza, Paweł, and Urszula Radoń. 2019. "The Impact of Node Location Imperfections on the Reliability of Single-Layer Steel Domes" Applied Sciences 9, no. 13: 2742. https://doi.org/10.3390/app9132742
APA StyleZabojszcza, P., & Radoń, U. (2019). The Impact of Node Location Imperfections on the Reliability of Single-Layer Steel Domes. Applied Sciences, 9(13), 2742. https://doi.org/10.3390/app9132742





