Medical Augmented-Reality Visualizer for Surgical Training and Education in Medicine
Abstract
1. Introduction
- face validity (i.e., extent to which the examination resembles the situation in the real world),
- content validity (i.e., extent to which the intended content domain is being measured by the assessment exercise),
- construct validity (i.e., extent to which a test is able to differentiate between a good and bad performer),
- concurrent validity (i.e., extent to which the results of the test correlate with gold-standard tests known to measure the same domain),
- predictive validity (i.e., extent to which this assessment will predict future performance),
- acceptability (i.e., extent to which assessment procedure is accepted by subjects in assessment),
- educational impact (i.e., extent to which test results and feedback contribute to improve the learning strategy on behalf of the trainer and the trainee),
- cost effectiveness (i.e., technical and nontechnical requirements for implementation of test into clinical practice)
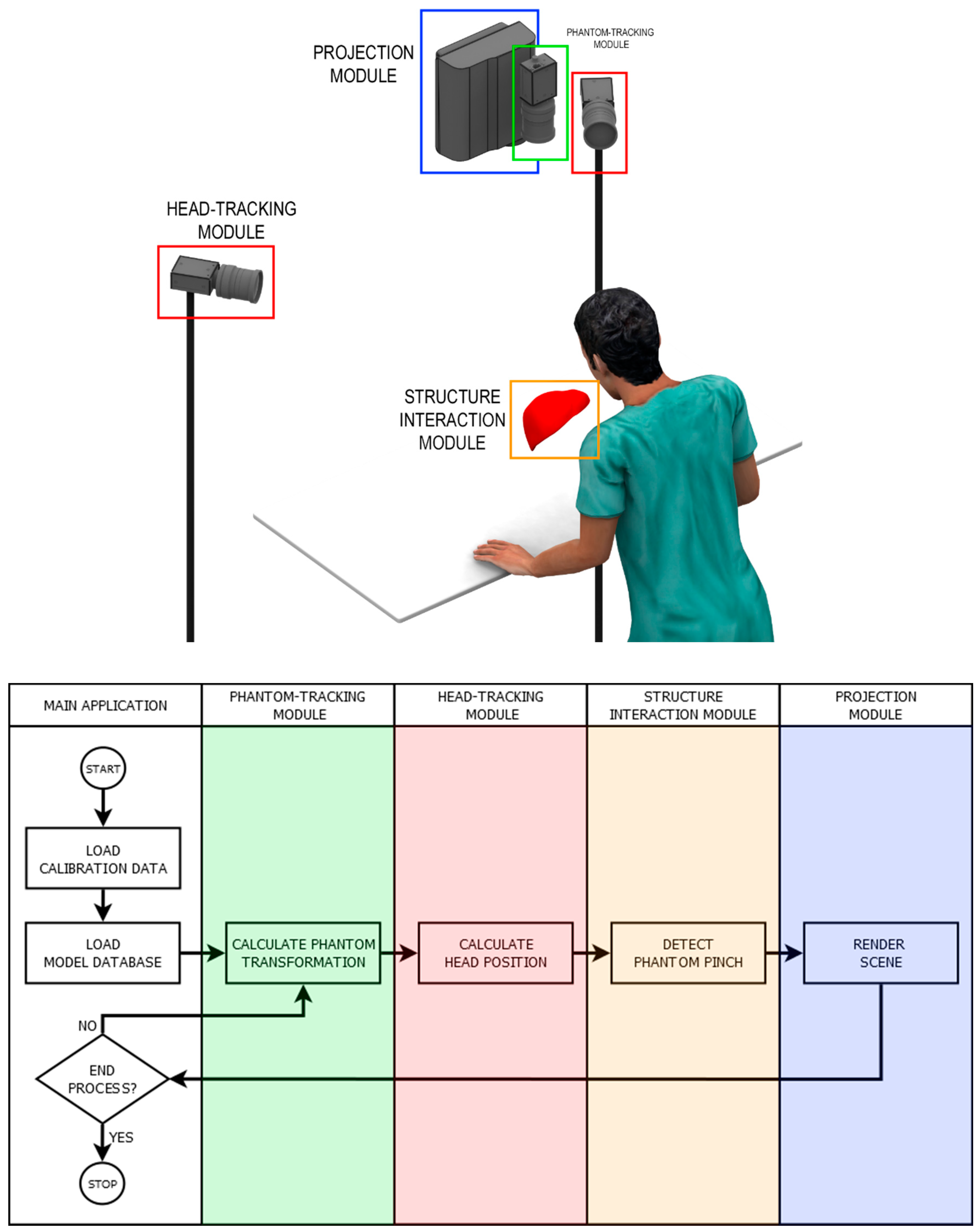
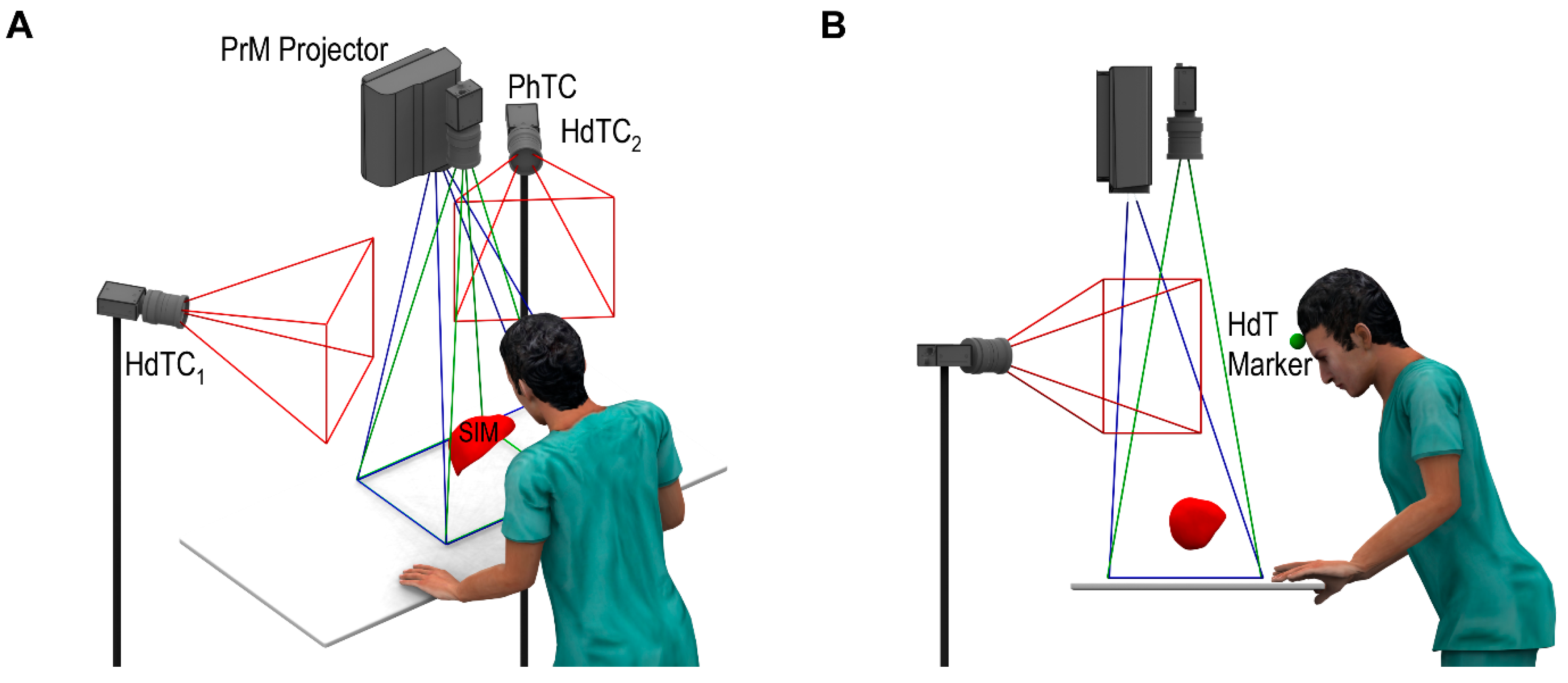
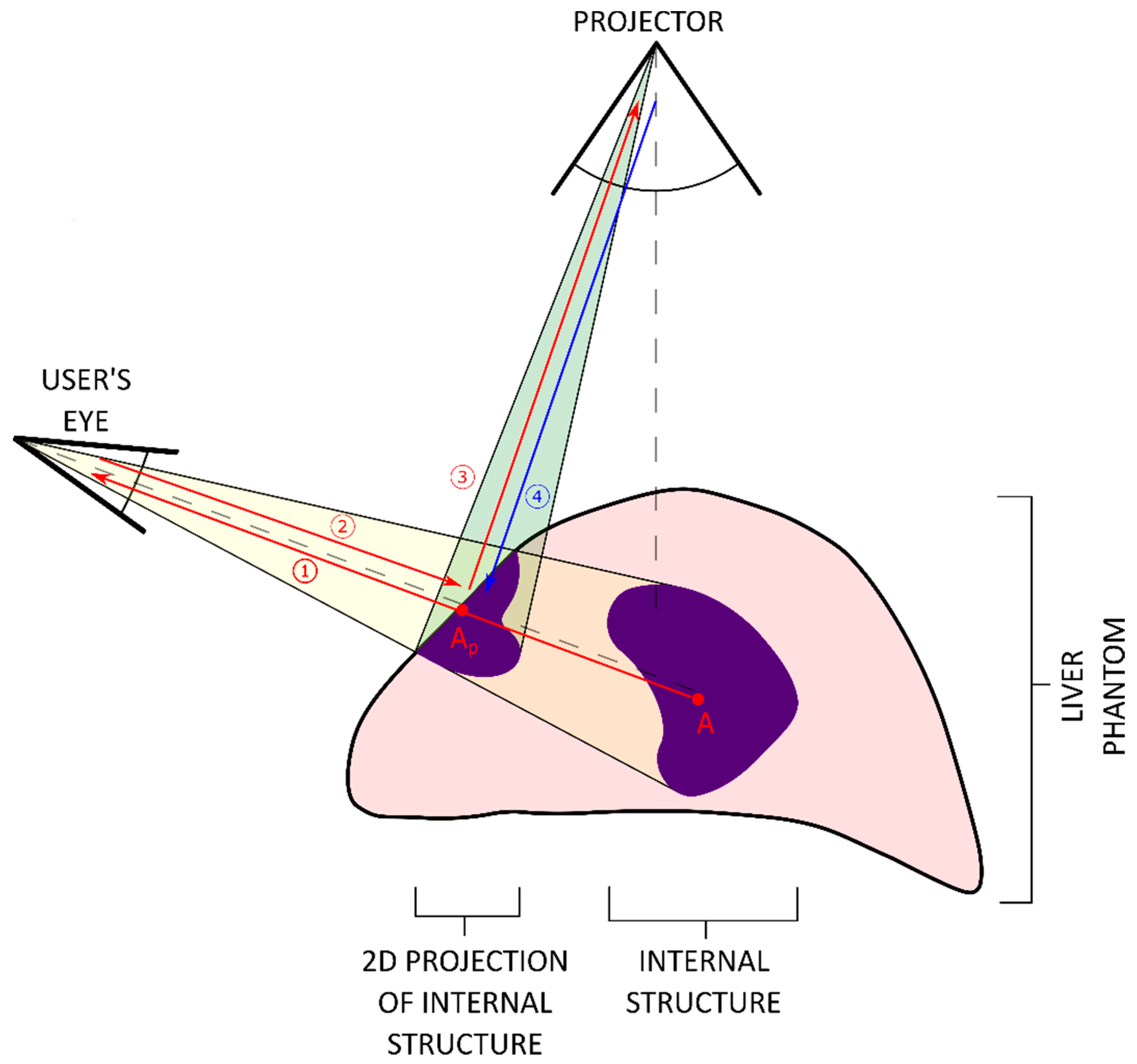
- Optical tracking of the user’s head while practicing on the organ phantom. Information related to the spatial relationship between the phantom and operator’s head is calculated in real time.
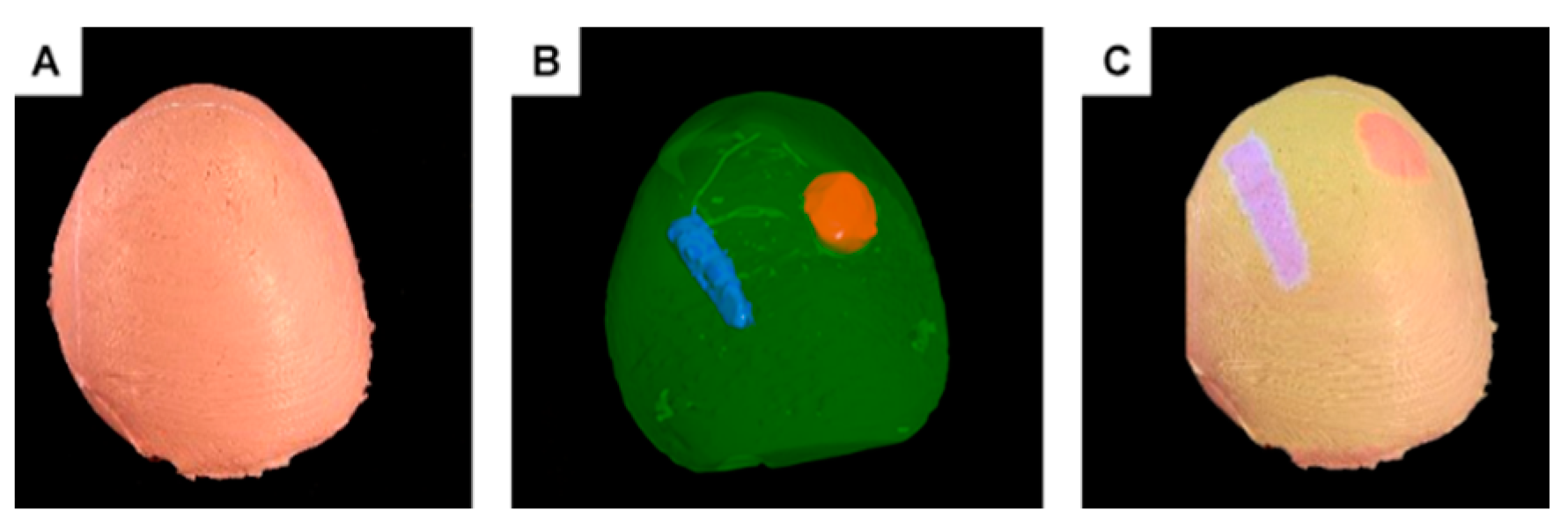
- Projection of internal structures onto the surface of the liver phantom in conjunction with naked-eye observation. This type of observation along with monoscopic motion parallax provides 3D perception through simple motions of either the operator’s head or the phantom. No additional goggles or headsets are required.
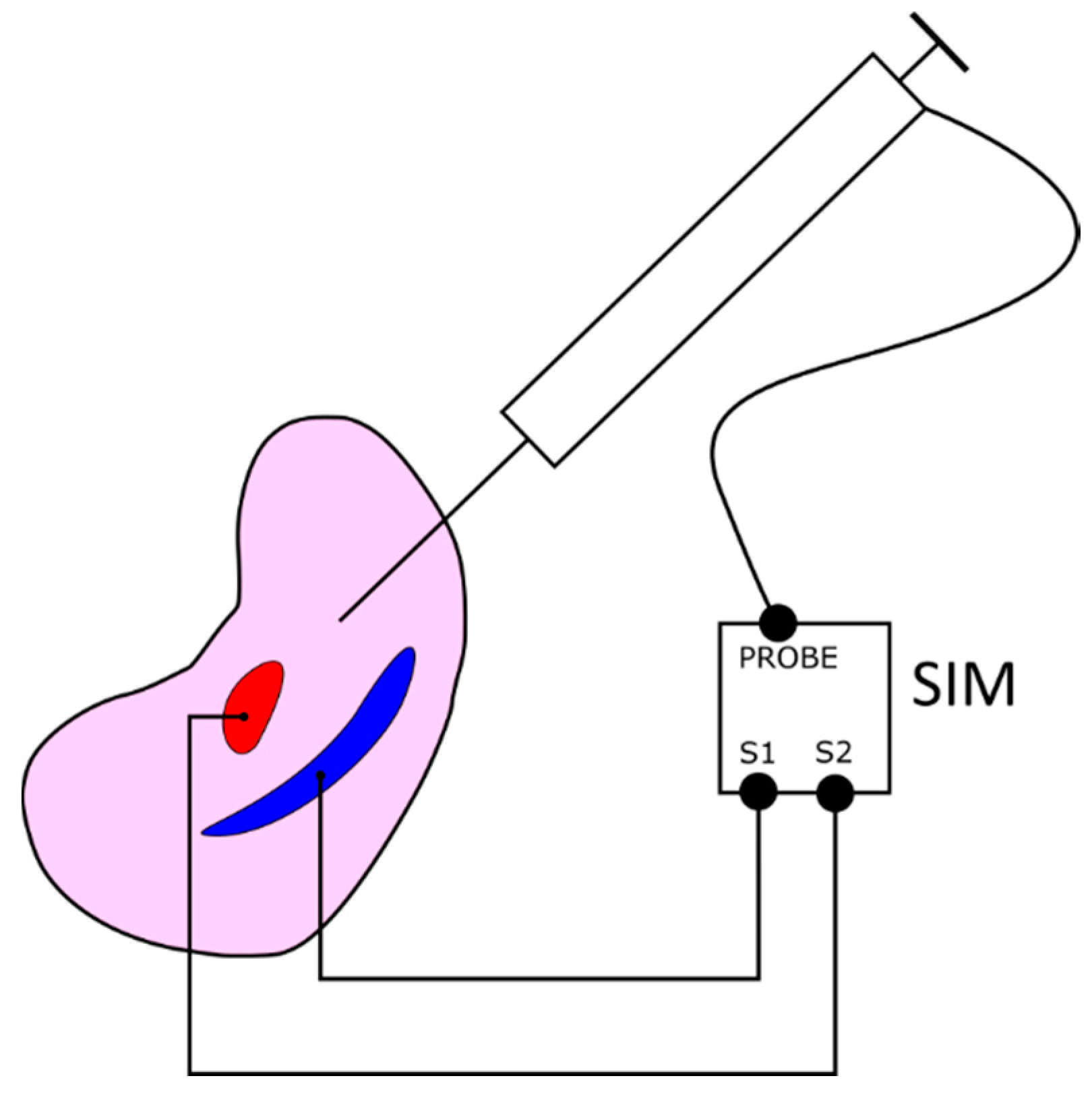
- A dedicated phantom composed of segments with different electric conductivities and an electronic module. This subsystem provides objective information about the procedure results in terms of the correct targeting rate of the internal structures.
2. Materials and Methods
2.1. Overview
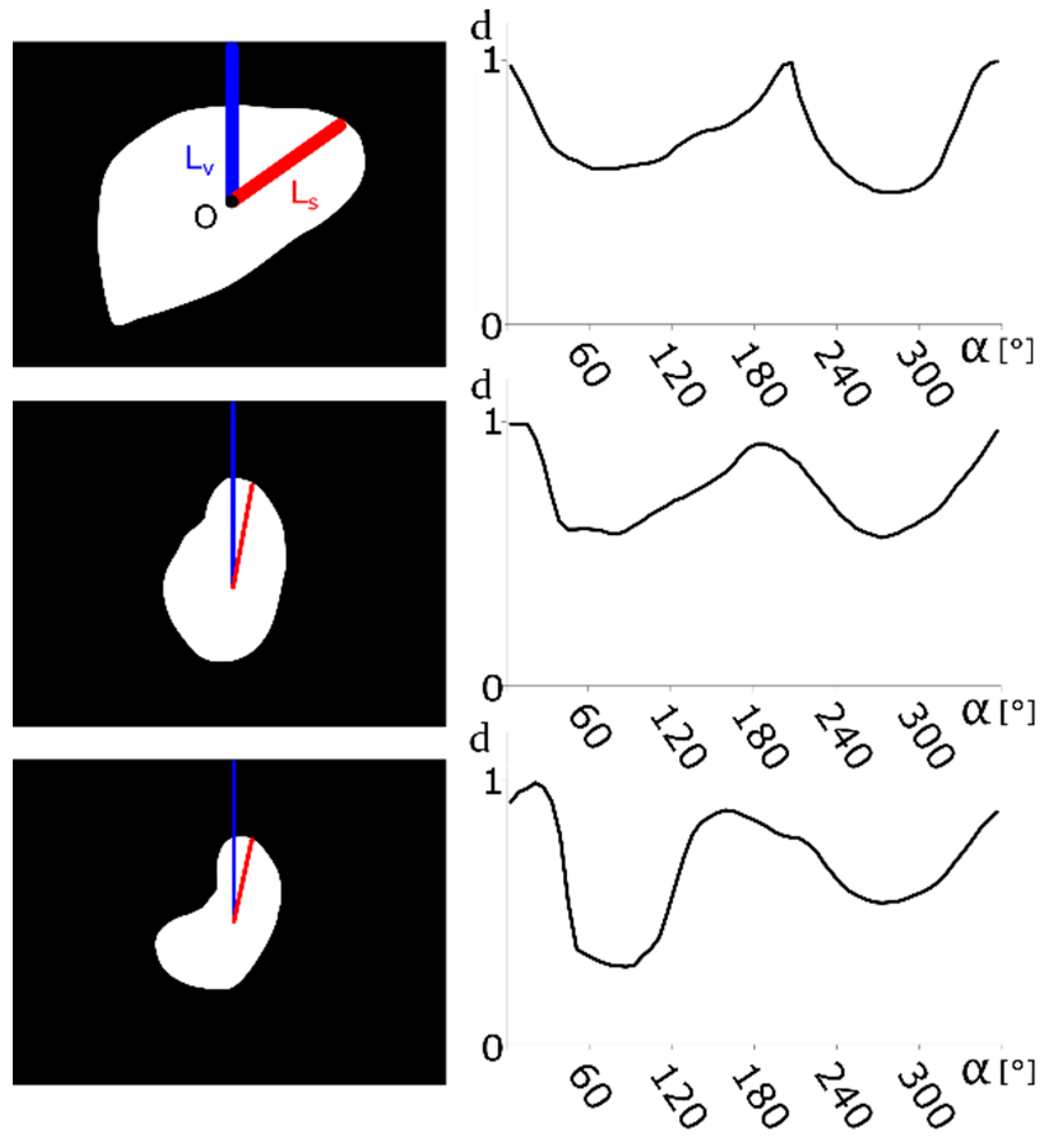
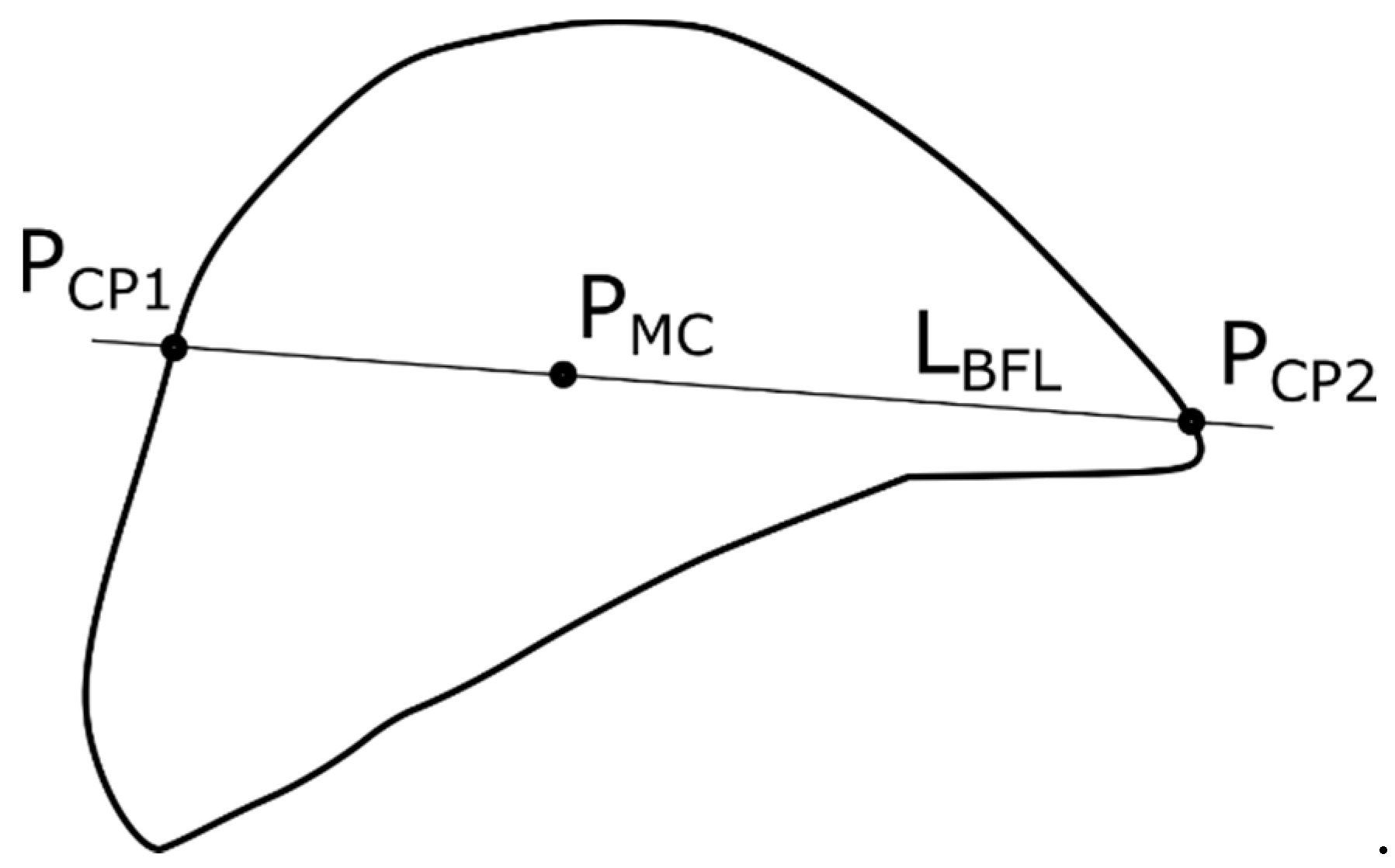
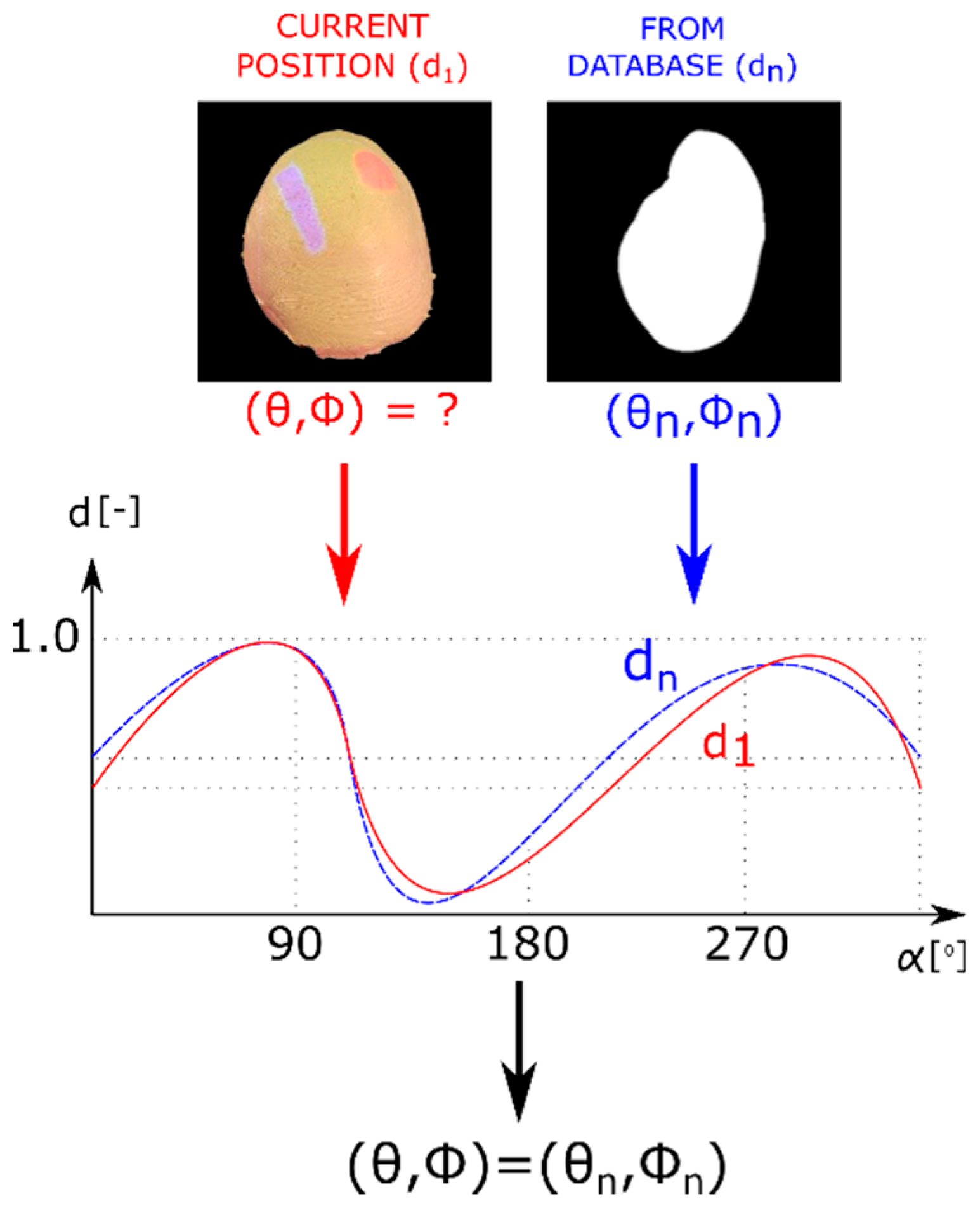
2.2. Contour-Based Shape Descriptor
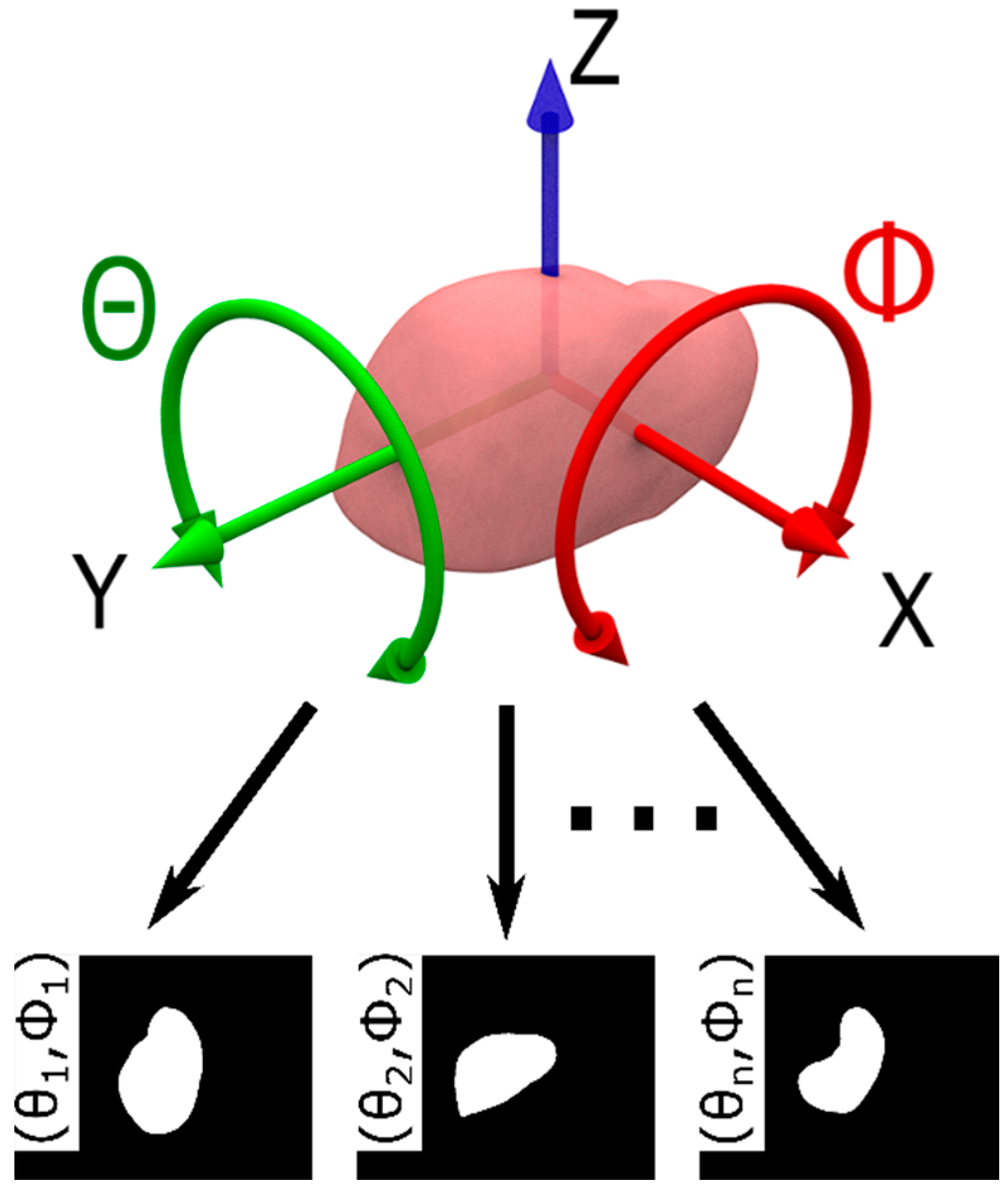
2.3. Model Database
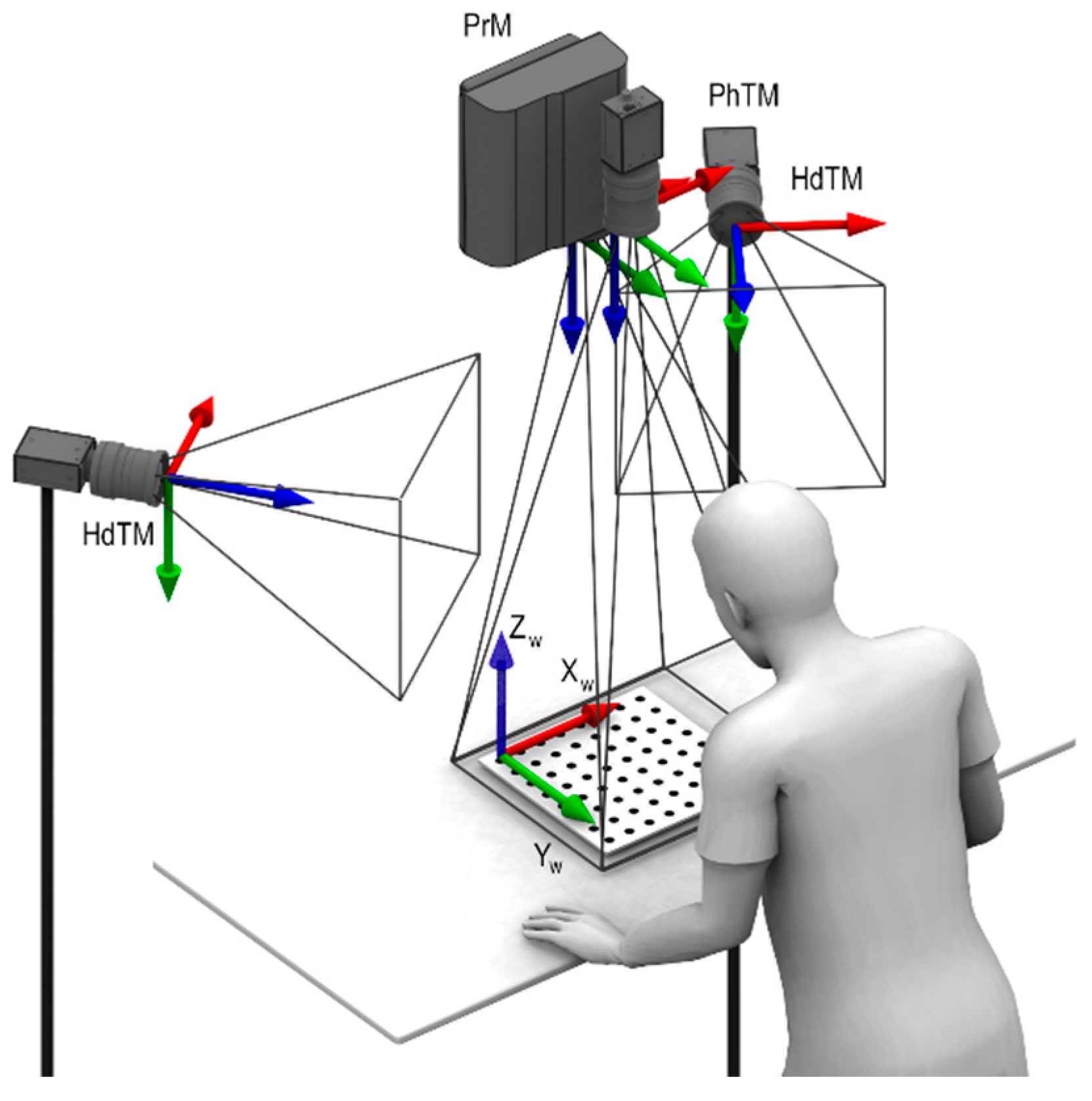
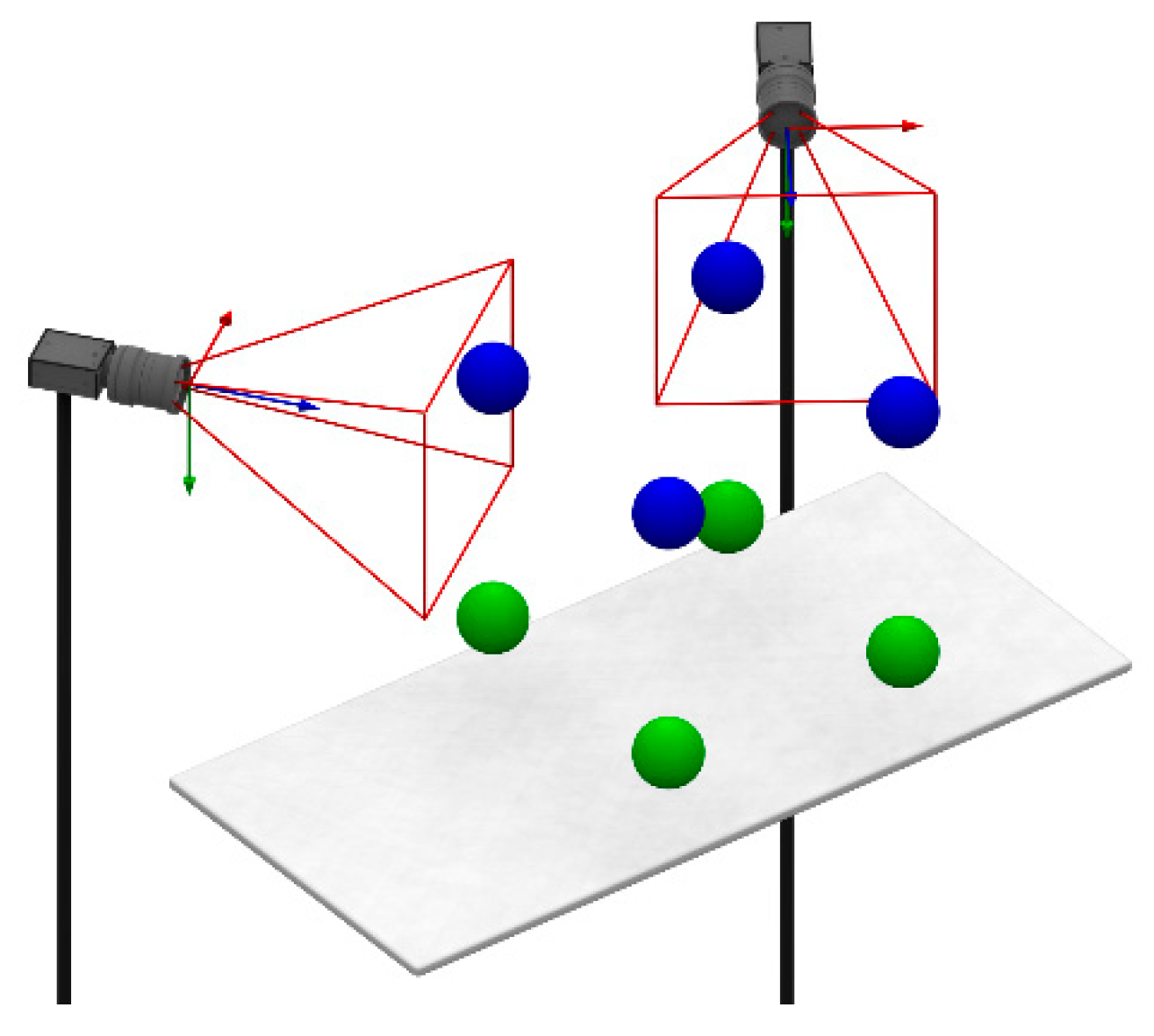
2.4. Phantom-Tracking Module
2.5. Head-Tracking Module
2.6. Projection Module
2.7. Structure Interaction Module
2.8. Global Calibration
2.9. Prototype Fabrication
3. Results
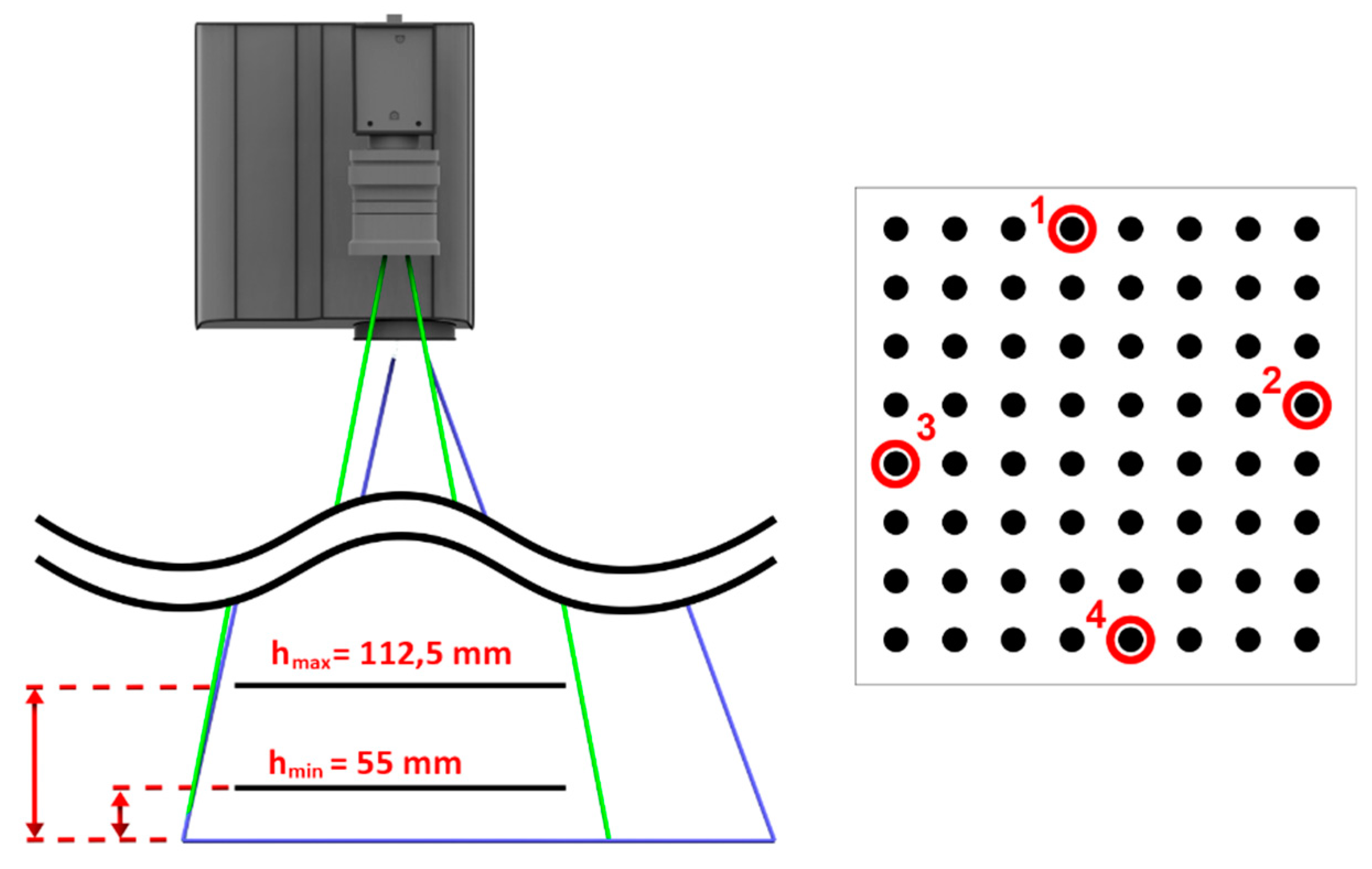
3.1. Angular Accuracy of Phantom Tracking
3.2. Mutual Calibration of Phantom-Tracking and Projection Modules
3.3. Head-Tracking Accuracy
3.4. System Validation
- Control experiment: Author R.G. selected an internal structure from the 3D model displayed on the external monitor. The 3D model was generated using CT data of the first phantom (two phantoms with different internal structure shapes were used for each participant of the experiment in order to avoid the influence of the user remembering the particular case). The participant was asked to prick the structure in the first liver phantom with a syringe probe by looking at the 3D model. The 3D model could be rotated accordingly using a computer keyboard. The time to complete the task was measured manually by the test supervisor until the participant informed task accomplishment.
- Test experiment: Author R.G. selected an internal structure projected by the MARVIS system onto the second phantom. The participant was asked to prick the structure with the syringe probe. Holding the phantom in his hand in a way that would not interfere with phantom contour detection, the participant inspected the internal structures as they were projected onto the phantom’s surface. Phantom position and participant’s head were tracked with PhTM and HdTM, respectively.
- When the participant decided to prick the structure, he had to put the phantom on the desk (for stability) and pause PhTM tracking by depressing a foot pedal. Otherwise, his hands or the syringe occluding the phantom contour would cause PhTM to provide false data about phantom position. Only then pricking could be performed. HdTM and PrM were working continuously so the projection parameters of the internal structures depended on the current position of the participant’s head. The duration time of the pricking procedure was measured as in the control experiment.
- The test experiment was performed with the first phantom.
- The control experiment was performed with the second phantom.
3.5. System Performance
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ma, M.; Jain, L.C.; Anderson, P. Virtual, Augmented Reality and Serious Games for Healthcare 1; Springer: Berlin/Heidelberg, Germany, 2014; Volume 68. [Google Scholar]
- Martín-Gutiérrez, J.; Fabiani, P.; Benesova, W.; Meneses, M.D.; Mora, C.E. Augmented reality to promote collaborative and autonomous learning in higher education. Comput. Human Behav. 2015, 51, 752–761. [Google Scholar] [CrossRef]
- Fonseca, D.; Martí, N.; Redondo, E.; Navarro, I.; Sánchez, A. Relationship between student profile, tool use, participation, and academic performance with the use of Augmented Reality technology for visualized architecture models. Comput. Human Behav. 2014, 31, 434–445. [Google Scholar] [CrossRef]
- Lee, K. Augmented Reality in Education and Training. TechTrends 2012, 56, 13–21. [Google Scholar] [CrossRef]
- Bacca, J.; Baldiris, S.; Fabregat, R.; Graf, S. Augmented Reality Trends in Education: A Systematic Review of Research and Applications. Educ. Technol. Soc. 2014, 17, 133–149. [Google Scholar]
- Pantelidis, P.; Chorti, A.; Papagiouvanni, I.; Paparoidamis, G.; Drosos, C.; Panagiotakopoulos, T.; Lales, G.; Sideris, M. Virtual and Augmented Reality in Medical Education. In Medical and Surgical Education—Past, Present and Future; InTechOpen: Rijeka, Croatia, 2018. [Google Scholar]
- Kluger, M.D.; Vigano, L.; Barroso, R.; Cherqui, D. The learning curve in laparoscopic major liver resection. J. Hepatobiliary Pancreat. Sci. 2013, 20, 131–136. [Google Scholar] [CrossRef] [PubMed]
- Hopper, A.N.; Jamison, M.H.; Lewis, W.G. Learning curves in surgical practice. Postgrad. Med. J. 2007, 83, 777–779. [Google Scholar] [CrossRef] [PubMed]
- Koehn, J.K.; Kuchenbecker, K.J. Surgeons and non-surgeons prefer haptic feedback of instrument vibrations during robotic surgery. Surg. Endosc. 2015, 29, 2970–2983. [Google Scholar] [CrossRef]
- Van der Meijden, O.A.J.; Schijven, M.P. The value of haptic feedback in conventional and robot-assisted minimal invasive surgery and virtual reality training: A current review. Surg. Endosc. 2009, 23, 1180–1190. [Google Scholar] [CrossRef]
- Lovegrove, C.E.; Abe, T.; Aydin, A.; Veneziano, D.; Sarica, K.; Khan, M.S.; Dasgupta, P.; Ahmed, K. Simulation training in upper tract endourology: Myth or reality? Minerva Urol. Nefrol. 2017, 69, 579–588. [Google Scholar] [CrossRef]
- Chen, H.; Lee, A.S.; Swift, M.; Tang, J.C. 3D Collaboration Method over HoloLensTM and SkypeTM End Points. In Proceedings of the 23rd ACM International Conference on Multimedia, Brisbane, Australia, 26–30 October 2015; pp. 27–30. [Google Scholar] [CrossRef]
- Hua, H.; Gao, C.; Brown, L.D.; Ahuja, N.; Rolland, J.P. Using a head-mounted projective display in interactive augmented environments. In Proceedings of the IEEE and ACM International Symposium on Augmented Reality, Washington, DC, USA, 29–30 October 2001; pp. 217–223. [Google Scholar] [CrossRef]
- Hanna, M.G.; Ahmed, I.; Nine, J.; Prajapati, S.; Pantanowitz, L. Augmented Reality Technology Using Microsoft HoloLens in Anatomic Pathology. Arch. Pathol. Lab. Med. 2018, 142, 638–644. [Google Scholar] [CrossRef]
- Jeroudi, O.M.; Christakopoulos, G.; Christopoulos, G.; Kotsia, A.; Kypreos, M.A.; Rangan, B.V.; Banerjee, S.; Brilakis, E.S. Accuracy of Remote Electrocardiogram Interpretation with the Use of Google Glass Technology. Am. J. Cardiol. 2015, 115, 374–377. [Google Scholar] [CrossRef] [PubMed]
- Mischkowski, R.A.; Zinser, M.J.; Kübler, A.C.; Krug, B.; Seifert, U.; Zöller, J.E. Application of an augmented reality tool for maxillary positioning in orthognathic surgery—A feasibility study. J. Cranio-Maxillofac. Surg. 2006, 34, 478–483. [Google Scholar] [CrossRef] [PubMed]
- Riecke, B.E.; Schulte-Pelkum, J.; Buelthoff, H.H. Perceiving Simulated Ego-Motions in Virtual Reality: Comparing Large Screen Displays with HMDs; Rogowitz, B.E., Pappas, T.N., Daly, S.J., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2005; p. 344. [Google Scholar]
- Lacoche, J.; Le Chenechal, M.; Chalme, S.; Royan, J.; Duval, T.; Gouranton, V.; Maisel, E.; Arnaldi, B. Dealing with frame cancellation for stereoscopic displays in 3D user interfaces. In Proceedings of the 2015 IEEE Symposium on 3D User Interfaces (3DUI), Arles, France, 23–24 March 2015; pp. 73–80. [Google Scholar]
- Kramida, G. Resolving the vergence-accommodation conflict in head-mounted displays. IEEE Trans. Vis. Comput. Graph. 2016, 22, 1912–1931. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, D.M.; Girshick, A.R.; Banks, M.S. Vergence—Accommodation conflicts hinder visual performance and cause visual fatigue. J. Vis. 2015, 8, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Mandalika, V.B.H.; Chernoglazov, A.I.; Billinghurst, M.; Bartneck, C.; Hurrell, M.A.; Ruiter, N.; Butler, A.P.H.; Butler, P.H. A Hybrid 2D/3D User Interface for Radiological Diagnosis. J. Digit. Imaging 2018, 31, 56–73. [Google Scholar] [CrossRef] [PubMed]
- Daher, S.; Hochreiter, J.; Norouzi, N.; Gonzalez, L.; Bruder, G.; Welch, G. Physical-Virtual Agents for Healthcare Simulation. In Proceedings of the 18th International Conference on Intelligent Virtual Agents—IVA ’18, Sydney, Australia, 5–8 November 2018; pp. 99–106. [Google Scholar]
- Magee, D.; Zhu, Y.; Ratnalingam, R.; Gardner, P.; Kessel, D. An augmented reality simulator for ultrasound guided needle placement training. Med. Biol. Eng. Comput. 2007, 45, 957–967. [Google Scholar] [CrossRef]
- Coles, T.R.; John, N.W.; Gould, D.; Caldwell, D.G. Integrating haptics with augmented reality in a femoral palpation and needle insertion training simulation. IEEE Trans. Haptics 2011. [Google Scholar] [CrossRef]
- Fleck, S.; Busch, F.; Biber, P.; Straber, W. 3D Surveillance A Distributed Network of Smart Cameras for Real-Time Tracking and its Visualization in 3D. In Proceedings of the 2006 Conference on Computer Vision and Pattern Recognition Workshop (CVPRW’06), Washington, DC, USA, 17–22 June 2006; p. 118. [Google Scholar]
- Cui, Y.; Schuon, S.; Chan, D.; Thrun, S.; Theobalt, C. 3D shape scanning with a time-of-flight camera. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010; pp. 1173–1180. [Google Scholar]
- Seitz, S.M.; Curless, B.; Diebel, J.; Scharstein, D.; Szeliski, R. A Comparison and Evaluation of Multi-View Stereo Reconstruction Algorithms. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition—Volume 1 (CVPR’06), Washington, DC, USA, 17–22 June 2006; Volume 1, pp. 519–528. [Google Scholar]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Szelag, K.; Maczkowski, G.; Gierwialo, R.; Gebarska, A.; Sitnik, R. Robust geometric, phase and colour structured light projection system calibration. Opto-Electron. Rev. 2017, 25, 326–336. [Google Scholar] [CrossRef]
- Mayol-Cuevas, W.W.; Juarez-Guerrero, J.; Munoz-Gutierrez, S. A first approach to tactile texture recognition. In Proceedings of the SMC’98 Conference IEEE International Conference on Systems, Man, and Cybernetics (Cat. No.98CH36218), San Diego, CA, USA, 14 October 1998; Volume 5, pp. 4246–4250. [Google Scholar]
- MM922 Silicone Moulding Rubbers. Available online: https://acc-silicones.com/products/moulding_rubbers/MM922 (accessed on 15 February 2019).
- Matsuhashi, T. ‘Agar’. In Food Gels; Springer: Dordrecht, The Netherlands, 1990; pp. 1–51. [Google Scholar]
- Borrego, A.; Latorre, J.; Alcañiz, M.; Llorens, R. Comparison of Oculus Rift and HTC Vive: Feasibility for Virtual Reality-Based Exploration, Navigation, Exergaming, and Rehabilitation. Games Health J. 2018, 7, 151–156. [Google Scholar] [CrossRef]
- Ribo, M.; Pinz, A.; Fuhrmann, A.L. A new optical tracking system for virtual and augmented reality applications. In Proceedings of the 18th IMTC 2001 IEEE Instrumentation and Measurement Technology Conference. Rediscovering Measurement in the Age of Informatics (Cat. No.01CH 37188), Budapest, Hungary, 21–23 May 2001; IEEE: Piscataway, NJ, USA; Volume 3, pp. 1932–1936. [Google Scholar]
- Charman, W.N.; Whitefoot, H. Pupil Diameter and the Depth-of-field of the Human Eye as Measured by Laser Speckle. Opt. Acta Int. J. Opt. 1977, 24, 1211–1216. [Google Scholar] [CrossRef]
- Schor, C.; Wood, I.; Ogawa, J. Binocular sensory fusion is limited by spatial resolution. Vision Res. 1984, 24, 661–665. [Google Scholar] [CrossRef]
- Julesz, B. Foundations of Cyclopean Perception; Chicago University Press: Chicago, IL, USA, 1971. [Google Scholar]
- Blakemore, C. The range and scope of binocular depth discrimination in man. J. Physiol. 1970, 211, 599–622. [Google Scholar] [CrossRef] [PubMed]
- Emoto, M.; Niida, T.; Okano, F. Repeated Vergence Adaptation Causes the Decline of Visual Functions in Watching Stereoscopic Television. J. Disp. Technol. 2005, 1, 328–340. [Google Scholar] [CrossRef]
- Takada, H. The progress of high presence and 3D display technology the depth-fused 3-D display for the eye sweetly. Opt. Electro. Opt. Eng. Contact 2006, 44, 316–323. [Google Scholar]
- Takaki, Y. Novel 3D Display Using an Array of LCD Panels; Chien, L.-C., Ed.; International Society for Optics and Photonics: Bellingham, WA, USA, 2003; p. 1. [Google Scholar]



| (a) | (b) | (c) | ||||||
|---|---|---|---|---|---|---|---|---|
| φref | φmeas | ∆|φ| | θref | θmeas | ∆|θ| | ψref | ψmeas | ∆|ψ| |
| 30.0 | 28.0 | 2.0 | 30.0 | 31.0 | 10 | 0.0 | 0.01 | 0.01 |
| 25.0 | 24.0 | 1.0 | 25.0 | 23.0 | 2.0 | 22.5 | 22.89 | 0.39 |
| 20.0 | 18.0 | 2.0 | 20.0 | 17.0 | 3.0 | 45.0 | 45.70 | 0.70 |
| 15.0 | 16.0 | 1.0 | 15.0 | 11.0 | 4.0 | 67.5 | 68.60 | 1.10 |
| 10.0 | 10.0 | 0.0 | 10.0 | 9.0 | 1.0 | 90.0 | 89.47 | 0.53 |
| 5.0 | 6.0 | 1.0 | 5.0 | 5.0 | 0.0 | 112.5 | 111.35 | 0.15 |
| 0.0 | 0.0 | 0.0 | 0.0 | –1.0 | 1.0 | 135.0 | 135.42 | 0.42 |
| −5.0 | –4.0 | 1.0 | –5.0 | –7.0 | 2.0 | 157.5 | 156.87 | 0.62 |
| –10.0 | –10.0 | 0.0 | –10.0 | –13.0 | 3.0 | 180.0 | 179.27 | 0.73 |
| –15.0 | –12.0 | 3.0 | –15.0 | –17.0 | 2.0 | |||
| –20.0 | –18.0 | 2.0 | –20.0 | –21.0 | 1.0 | |||
| –25.0 | –22.0 | 3.0 | –25.0 | –25.0 | 0.0 | |||
| –30.0 | –28.0 | 2.0 | –30.0 | –33.0 | 3.0 | |||
| Marker 1 | Marker 2 | Marker 3 | Marker 4 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| On Camera | On Projector | On Camera | On Projector | On Camera | On Projector | On Camera | On Projector | |||||||||
| Z | X | Y | X | Y | X | Y | X | Y | X | Y | X | Y | X | Y | X | Y |
| [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] |
| 55.5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| 65.5 | −0.02 | 0.01 | −0.04 | 0.02 | 0.011 | 0.00 | 0.03 | 0.02 | −0.02 | 0.01 | 0.07 | 0.00 | 0.014 | −0.00 | 0.02 | 0.00 |
| 75.5 | −0.01 | 0.02 | 0.00 | 0.03 | −0.01 | −0.02 | −0.02 | 0.02 | 0.01 | 0.02 | 0.17 | 0.00 | 0.00 | −0.01 | 0.00 | 0.00 |
| 85.5 | −0.01 | 0.04 | 0.00 | −0.08 | 0.01 | 0.01 | 0.11 | 0.03 | −0.01 | −0.01 | 0.05 | −0.03 | −0.02 | −0.02 | −0.02 | 0.00 |
| 95.5 | −0.02 | 0.05 | −0.01 | 0.03 | −0.02 | 0.01 | 0.03 | 0.04 | 0.01 | 0.01 | 0.12 | −0.01 | −0.01 | −0.02 | −0.01 | −0.05 |
| 105.5 | −0.02 | 0.06 | −0.01 | −0.01 | −0.04 | 0.01 | −0.04 | 0.05 | 0.02 | −0.00 | 0.17 | −0.02 | 0.02 | −0.04 | 0.02 | −0.18 |
| 112.8 | 0.01 | 0.05 | 0.00 | −0.05 | −0.01 | 0.00 | −0.02 | 0.03 | 0.00 | 0.00 | 0.11 | −0.01 | 0.00 | −0.02 | −0.02 | −0.16 |
| X0 | Y0 | Z0 | X1 | Y1 | Z1 | ∆X | ∆Y | ∆Z |
|---|---|---|---|---|---|---|---|---|
| [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] | [mm] |
| −504.35 | 338.53 | 1367.02 | −505.87 | 338.90 | 1370.98 | 1.52 | 0.37 | 3.96 |
| −517.29 | −348.87 | 1350.01 | −517.96 | −348.57 | 1351.60 | 0.67 | 0.31 | 1.59 |
| 329.76 | 112.35 | 964.45 | 330.37 | 111.57 | 966.91 | 0.61 | 0.78 | 2.46 |
| 339.01 | −135.37 | 968.48 | 339.60 | −135.44 | 970.28 | 0.59 | 0.08 | 1.80 |
| 46.13 | 174.12 | 588.10 | 46.24 | 174.62 | 592.71 | 0.11 | 0.50 | 4.61 |
| 28.39 | −128.10 | 578.11 | 28.41 | −128.06 | 582.33 | 0.01 | 0.04 | 4.22 |
| 204.44 | 137.02 | 632.78 | 205.57 | 137.01 | 637.43 | 1.14 | 0.01 | 4.65 |
| 206.63 | −148.44 | 629.07 | 207.64 | −148.42 | 633.28 | 1.01 | 0.02 | 4.21 |
| 236.37 | 19.10 | 682.92 | 237.92 | 18.94 | 687.45 | 1.55 | 0.15 | 4.53 |
| 45.74 | 21.10 | 877.70 | 45.91 | 20.99 | 881.10 | 0.17 | 0.11 | 3.39 |
| −118.27 | 63.50 | 1069.90 | −118.63 | 63.38 | 1072.95 | 0.35 | 0.12 | 3.05 |
| −270.32 | 69.22 | 1234.31 | −270.96 | 69.11 | 1237.19 | 0.64 | 0.10 | 2.88 |
| −186.02 | −257.16 | 1080.75 | −186.49 | −257.02 | 1082.93 | 0.46 | 0.14 | 2.18 |
| −195.27 | 228.51 | 1040.83 | −196.05 | 228.67 | 1044.49 | 0.78 | 0.17 | 3.66 |
| Average error | 0.69 | 0.21 | 3.37 | |||||
| Median error | 0.63 | 0.13 | 3.53 | |||||
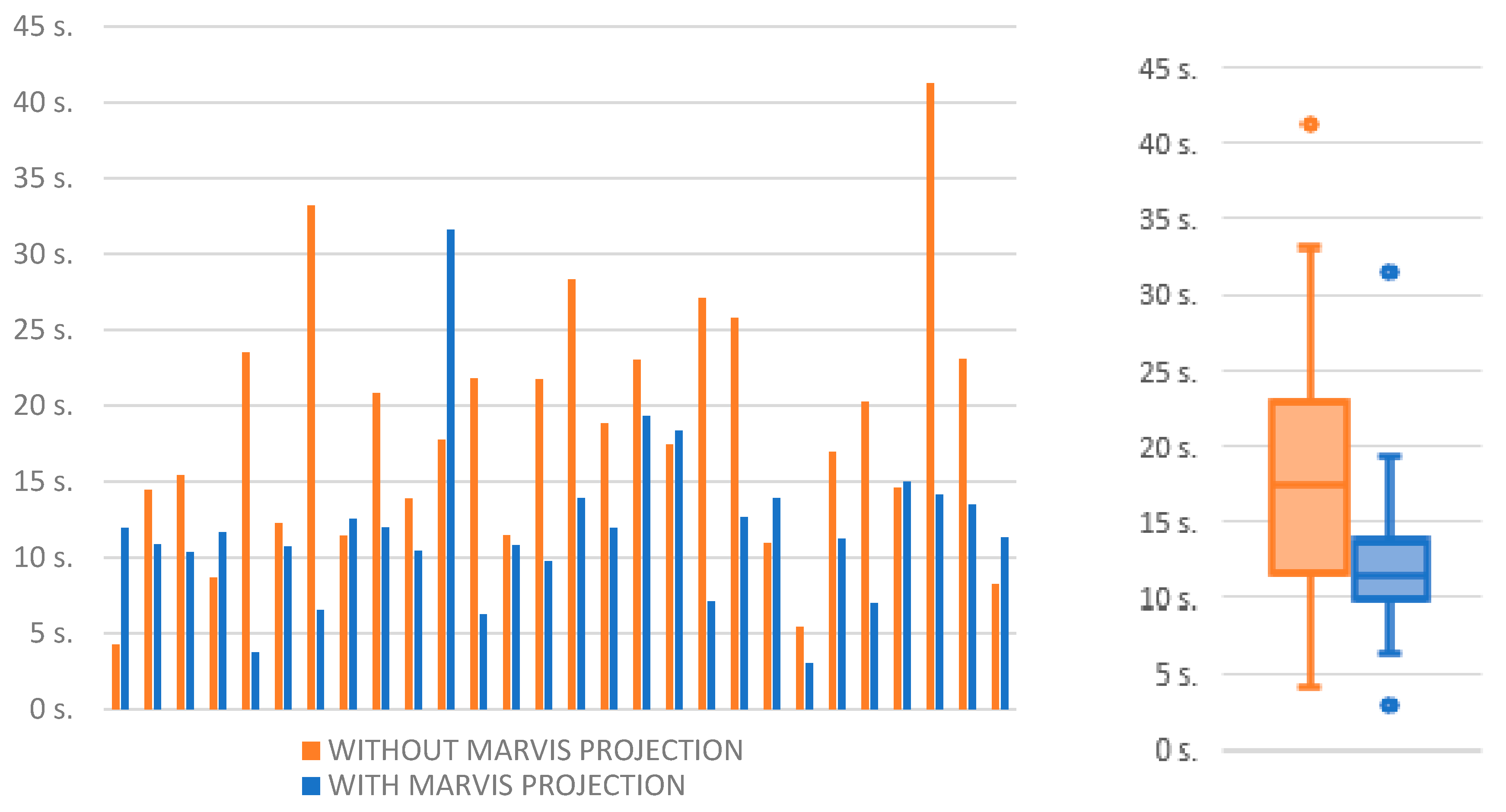
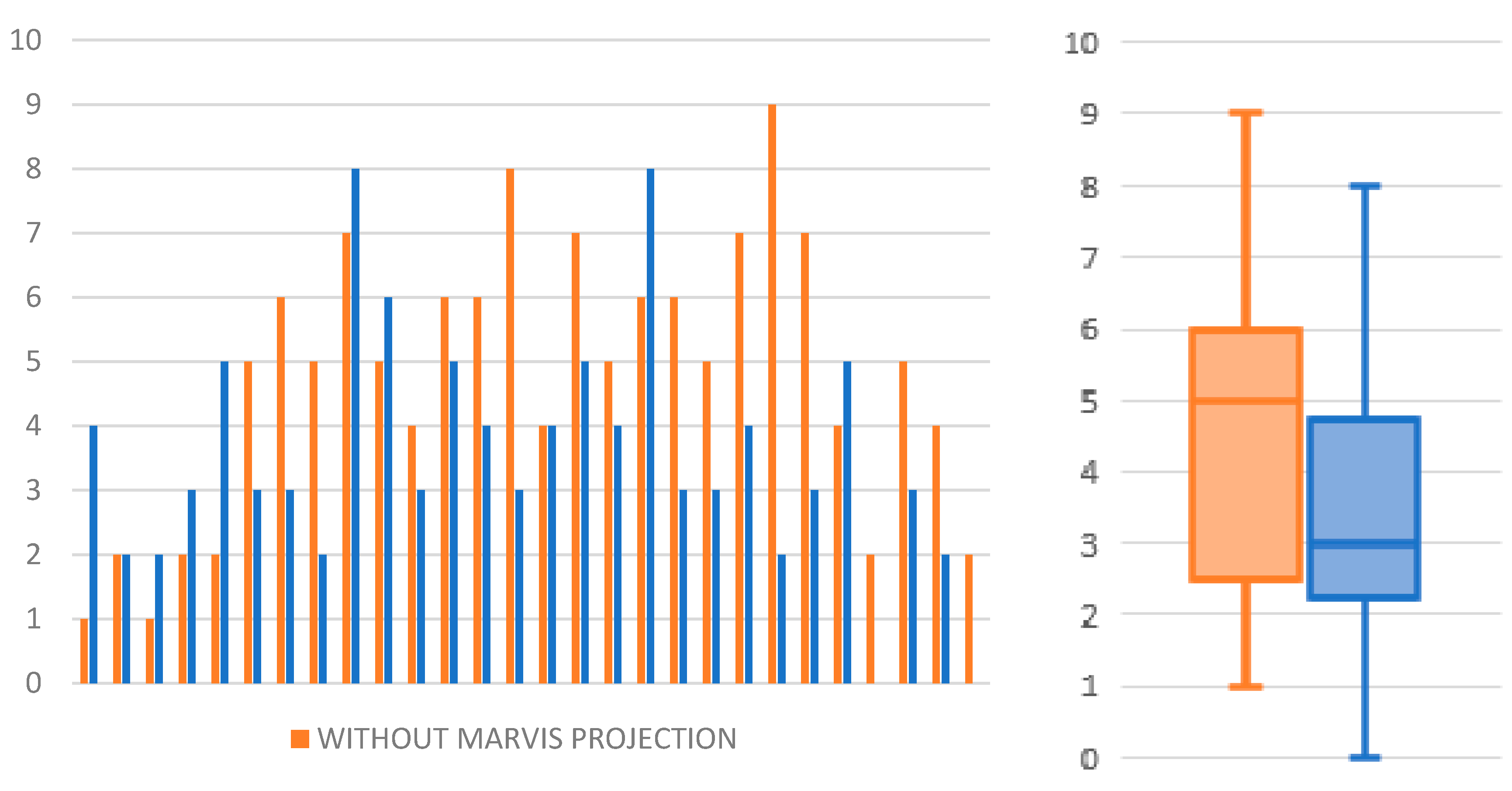
| Without Projection | With Projection | Comparison | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Participant | Number of Correct Attempts | Number of Incorrect Attempts | Average Time to Correctly Prick Needle | SD | Median Time to Correctly Prick Needle | Failure Rate | Number of Correct Attempts | Number of Incorrect Attempts | Average Time to Correctly Prick Needle | SD | Median time to Correctly Prick Needle | Failure Rate | Median Time Difference | Failure Rate Difference |
| - | - | - | [s] | [s] | [s] | [%] | - | - | [s] | [s] | [s] | [%] | [s] | [%] |
| 1 | 9 | 1 | 26.25 | 49.05 | 4.26 | 10.0 | 6 | 4 | 11.97 | 1.59 | 11.97 | 40.0 | 7.7 | 30.0 |
| 2 | 8 | 2 | 14.19 | 8.15 | 14.47 | 20.0 | 8 | 2 | 16.58 | 13.38 | 10.88 | 20.0 | −3.6 | 0.0 |
| 3 | 9 | 1 | 14.04 | 9.18 | 15.42 | 10.0 | 8 | 2 | 11.29 | 10.99 | 10.35 | 20.0 | −5.1 | 10.0 |
| 4 | 8 | 2 | 8.11 | 2.63 | 8.67 | 20.0 | 7 | 3 | 10.42 | 3.71 | 11.67 | 30.0 | 3.0 | 10.0 |
| 5 | 8 | 2 | 27.75 | 16.24 | 23.51 | 20.0 | 5 | 5 | 4.05 | 1.99 | 3.74 | 50.0 | −19.8 | 30.0 |
| 6 | 5 | 5 | 18.21 | 11.71 | 12.26 | 50.0 | 7 | 3 | 15.97 | 13.8 | 10.73 | 30.0 | −1.5 | −20.0 |
| 7 | 4 | 6 | 26.95 | 10.92 | 33.21 | 60.0 | 7 | 3 | 10.89 | 10.4 | 6.55 | 30.0 | −26.7 | −30.0 |
| 8 | 5 | 5 | 12.48 | 3.1 | 11.45 | 50.0 | 8 | 2 | 12.04 | 2.61 | 12.55 | 20.0 | 1.1 | −30.0 |
| 9 | 3 | 7 | 18.77 | 3.39 | 20.84 | 70.0 | 2 | 8 | 13.16 | 2.67 | 11.98 | 80.0 | −8.9 | 10.0 |
| 10 | 5 | 5 | 19.67 | 16.56 | 13.89 | 50.0 | 4 | 6 | 9.39 | 3.97 | 10.44 | 60.0 | −3.5 | 10.0 |
| 11 | 6 | 4 | 17.56 | 6.37 | 17.75 | 40.0 | 7 | 3 | 31.88 | 15.85 | 31.6 | 30.0 | 13.9 | −10.0 |
| 12 | 4 | 6 | 22.14 | 9.41 | 21.8 | 60.0 | 5 | 5 | 11.58 | 10.33 | 6.27 | 50.0 | −15.5 | −10.0 |
| 13 | 4 | 6 | 20.66 | 14.71 | 11.46 | 60.0 | 6 | 4 | 12.92 | 5.37 | 10.83 | 40.0 | −0.6 | −20.0 |
| 14 | 2 | 8 | 21.74 | 5.32 | 21.74 | 80.0 | 7 | 3 | 11.17 | 4.19 | 9.75 | 30.0 | −12.0 | −50.0 |
| 15 | 6 | 4 | 35.19 | 24.93 | 28.34 | 40.0 | 6 | 4 | 14.9 | 9.26 | 13.91 | 40.0 | −14.4 | 0.0 |
| 16 | 3 | 7 | 38.22 | 41.95 | 18.85 | 70.0 | 5 | 5 | 11.01 | 8.38 | 11.95 | 50.0 | −6.9 | −20.0 |
| 17 | 5 | 5 | 28.22 | 16.59 | 23.02 | 50.0 | 6 | 4 | 21.33 | 8.17 | 19.32 | 40.0 | −3.7 | −10.0 |
| 18 | 4 | 6 | 16.31 | 8.75 | 17.45 | 60.0 | 2 | 8 | 21.6 | 11.45 | 18.35 | 80.0 | 0.9 | 20.0 |
| 19 | 4 | 6 | 28.1 | 8.02 | 27.12 | 60.0 | 7 | 3 | 8.59 | 6.72 | 7.12 | 30.0 | −20.0 | −30.0 |
| 20 | 5 | 5 | 27.42 | 10.12 | 25.8 | 50.0 | 7 | 3 | 12.7 | 8.58 | 12.68 | 30.0 | −13.1 | −20.0 |
| 21 | 3 | 7 | 15.06 | 8.99 | 10.96 | 70.0 | 6 | 4 | 14.37 | 4.01 | 13.93 | 40.0 | 3.0 | −30.0 |
| 22 | 1 | 9 | 5.27 | 0.0 | 5.43 | 90.0 | 8 | 2 | 6.21 | 5.3 | 3.04 | 20.0 | −2.4 | −70.0 |
| 23 | 3 | 7 | 23.72 | 9.66 | 16.96 | 70.0 | 7 | 3 | 13.62 | 13.34 | 11.24 | 30.0 | −5.7 | −40.0 |
| 24 | 6 | 4 | 21.25 | 7.94 | 20.27 | 40.0 | 5 | 5 | 8.32 | 6.57 | 7.01 | 50.0 | −13.3 | 10.0 |
| 25 | 8 | 2 | 25.92 | 25.77 | 14.61 | 20.0 | 10 | 0 | 15.18 | 6.21 | 15 | 0.0 | 0.4 | −20.0 |
| 26 | 5 | 5 | 62.35 | 35.96 | 41.28 | 50.0 | 7 | 3 | 21.9 | 13.5 | 14.16 | 30.0 | −27.1 | −20.0 |
| 27 | 6 | 4 | 24.13 | 7.14 | 23.1 | 40.0 | 8 | 2 | 12.46 | 6.26 | 13.49 | 20.0 | −9.6 | −20.0 |
| 28 | 8 | 2 | 11.93 | 8.05 | 8.26 | 20.0 | 10 | 0 | 24.77 | 34.45 | 11.32 | 0.0 | 3.1 | −20.0 |
| Avarage | 22.56 | 13.59 | 18.29 | 47.50 | 13.94 | 8.68 | 11.32 | 35.36 | ||||||
| Median | 21.50 | 9.30 | 17.60 | 50.0 | 12.58 | 7.45 | 11.32 | 30.0 | ||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gierwiało, R.; Witkowski, M.; Kosieradzki, M.; Lisik, W.; Groszkowski, Ł.; Sitnik, R. Medical Augmented-Reality Visualizer for Surgical Training and Education in Medicine. Appl. Sci. 2019, 9, 2732. https://doi.org/10.3390/app9132732
Gierwiało R, Witkowski M, Kosieradzki M, Lisik W, Groszkowski Ł, Sitnik R. Medical Augmented-Reality Visualizer for Surgical Training and Education in Medicine. Applied Sciences. 2019; 9(13):2732. https://doi.org/10.3390/app9132732
Chicago/Turabian StyleGierwiało, Radosław, Marcin Witkowski, Maciej Kosieradzki, Wojciech Lisik, Łukasz Groszkowski, and Robert Sitnik. 2019. "Medical Augmented-Reality Visualizer for Surgical Training and Education in Medicine" Applied Sciences 9, no. 13: 2732. https://doi.org/10.3390/app9132732
APA StyleGierwiało, R., Witkowski, M., Kosieradzki, M., Lisik, W., Groszkowski, Ł., & Sitnik, R. (2019). Medical Augmented-Reality Visualizer for Surgical Training and Education in Medicine. Applied Sciences, 9(13), 2732. https://doi.org/10.3390/app9132732







