Compensating Uncertainties in Force Sensing for Robotic-Assisted Palpation
Abstract
1. Introduction
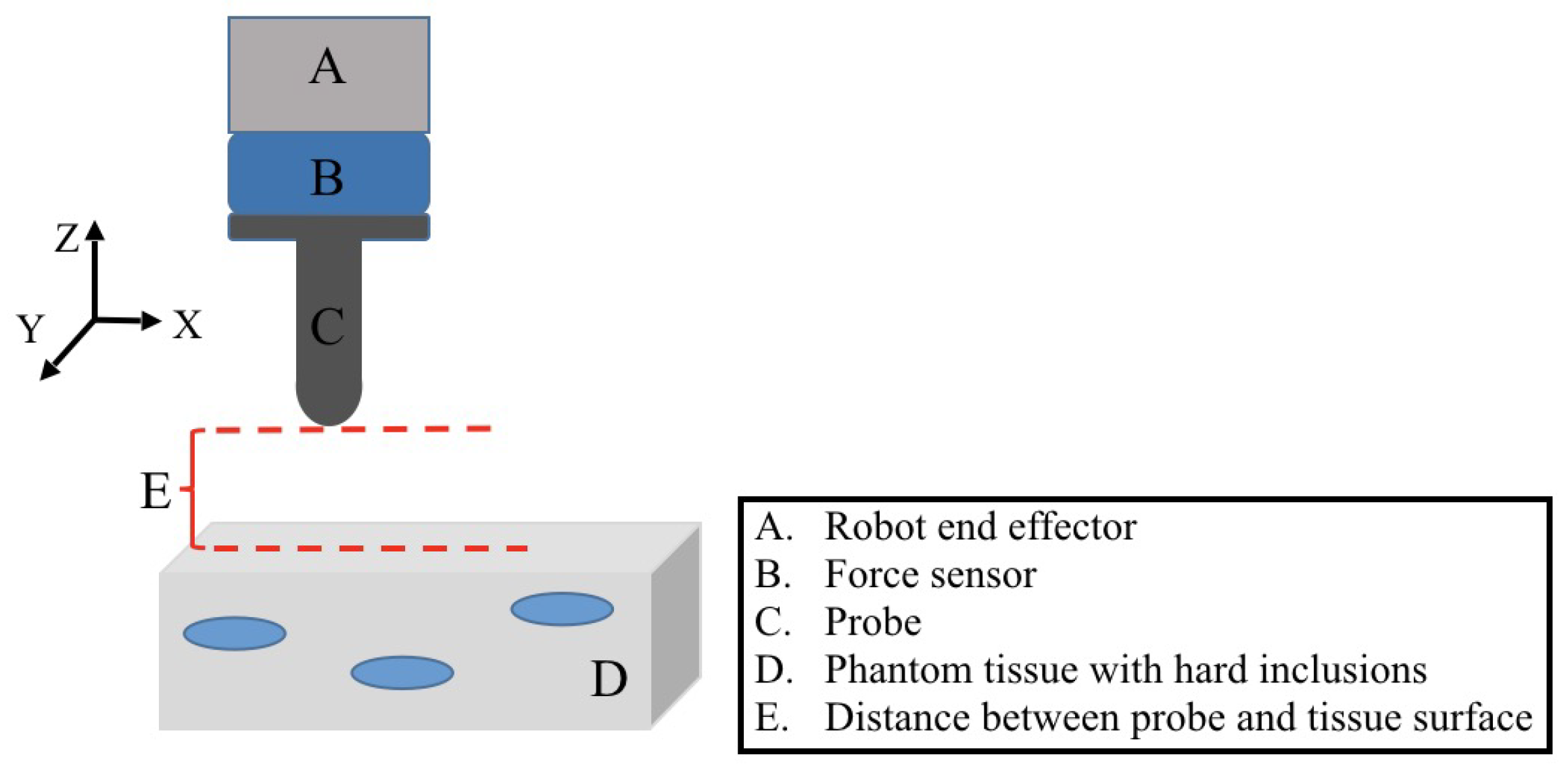
2. Robotic Palpation with Force Based Approach
2.1. Force Based Robotic Palpation
2.2. Stiffness Analysis Through Young’s Modulus
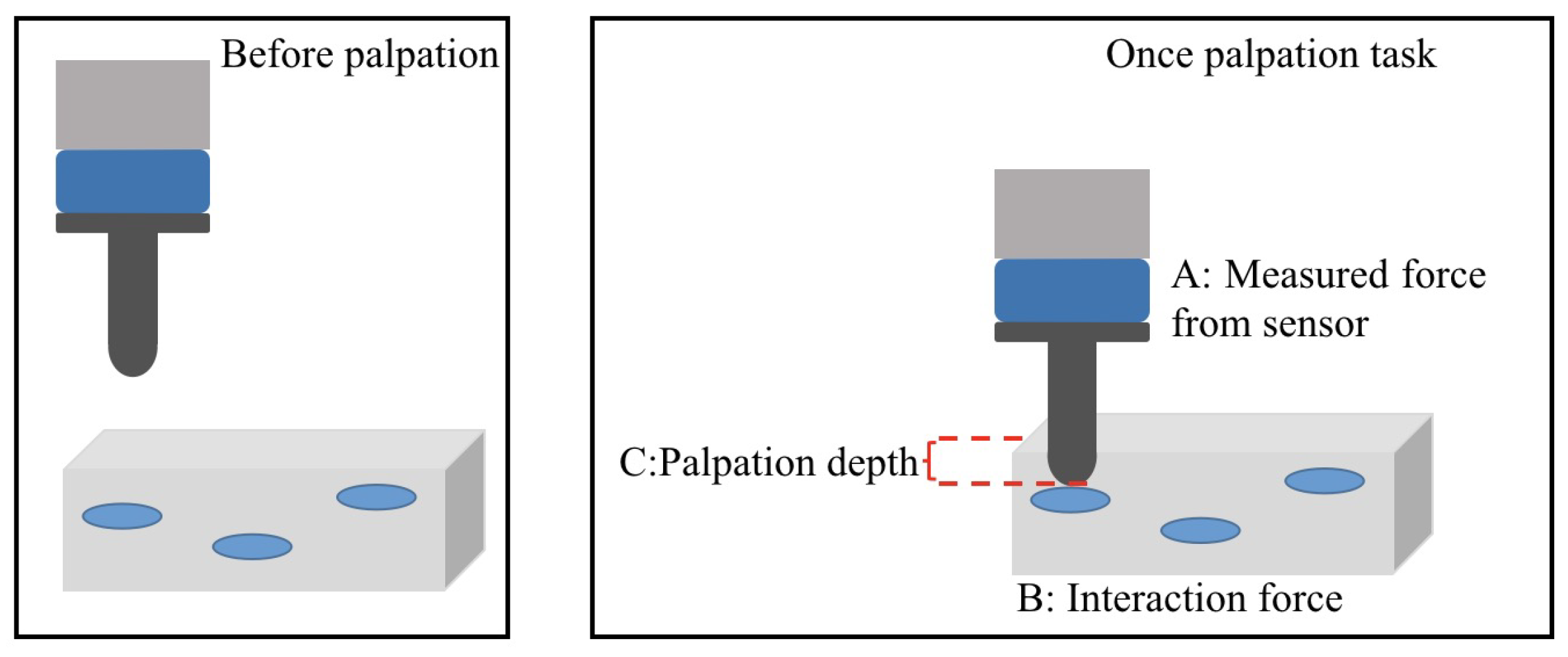
2.3. Uncertainty Analysis of Force Measurement
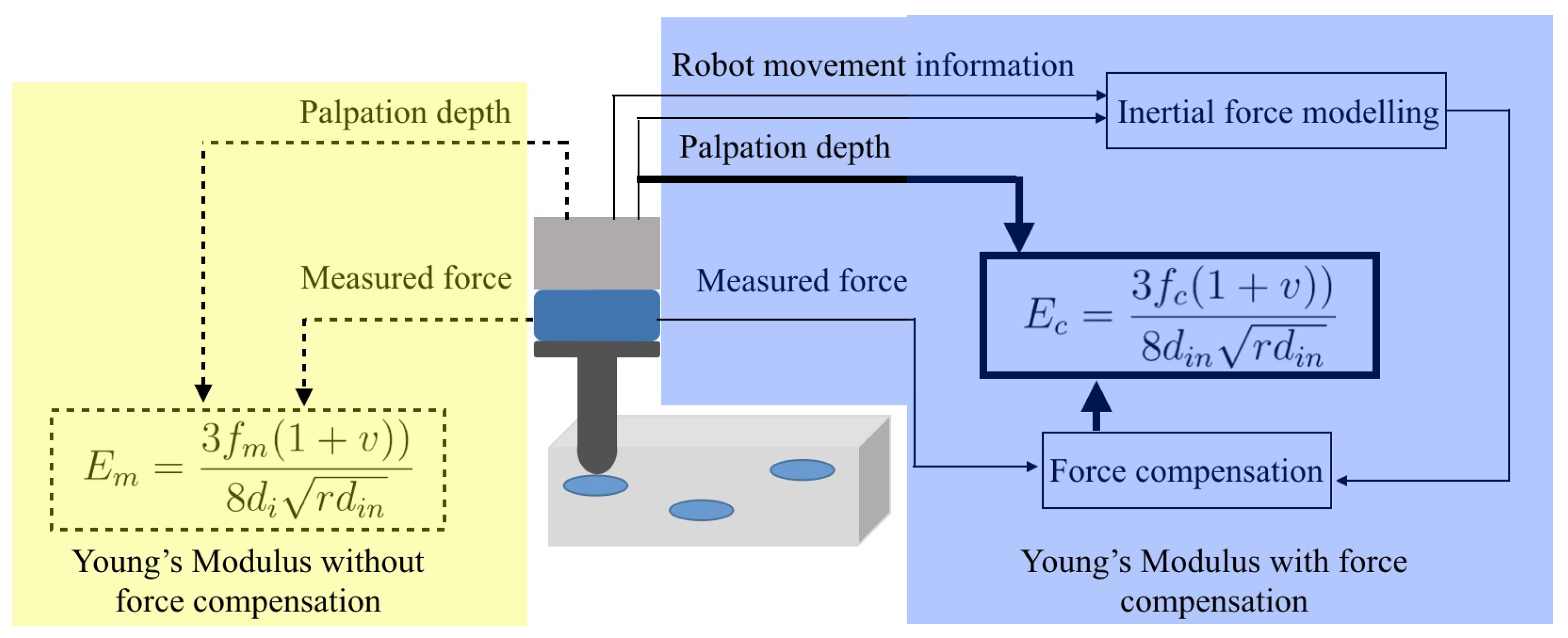
2.4. Robotic Palpation with Force Compensation
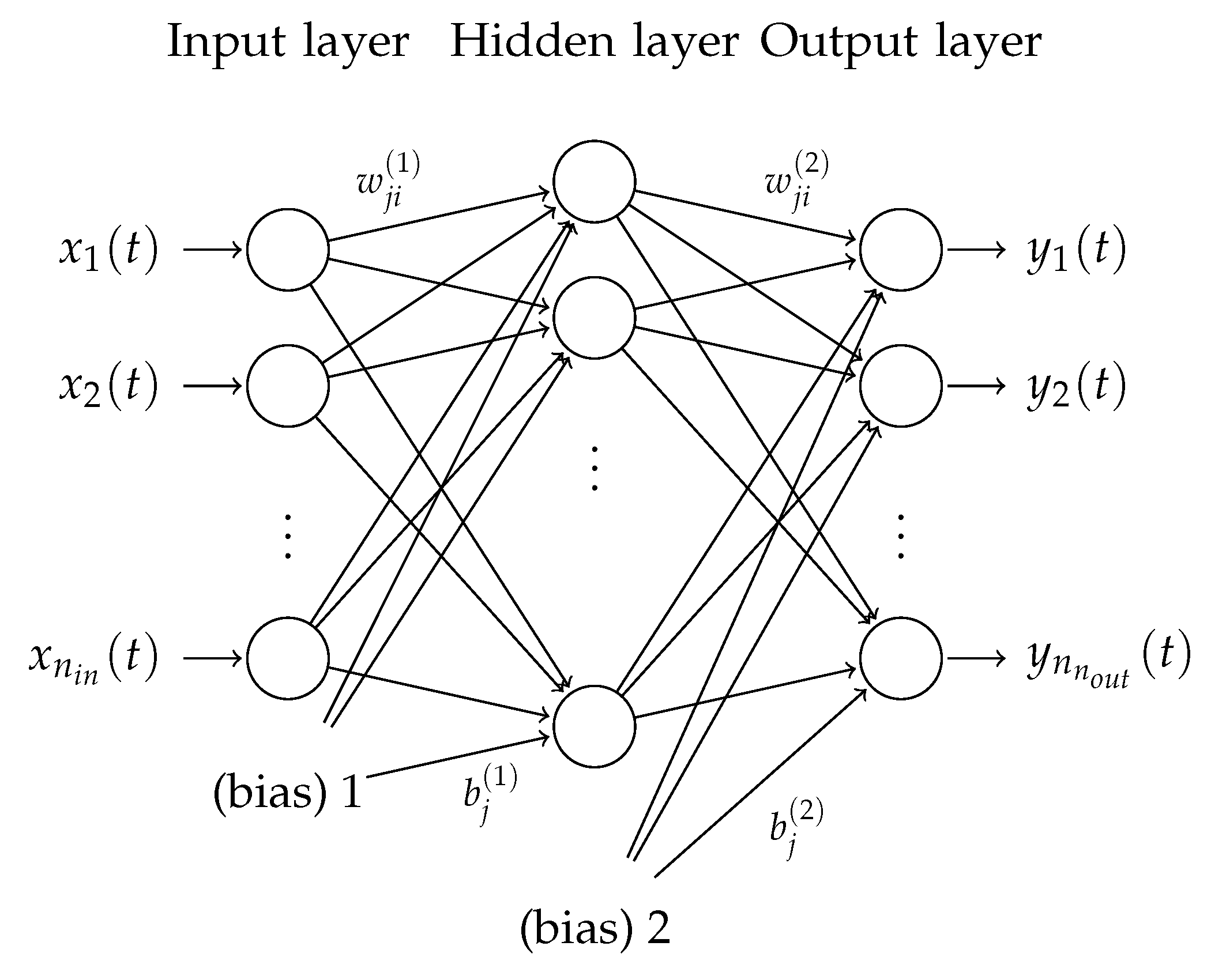
3. Neural-Network-Based Modelling of Inertial Force and Compensation
4. Experiment Studies and Result Analysis
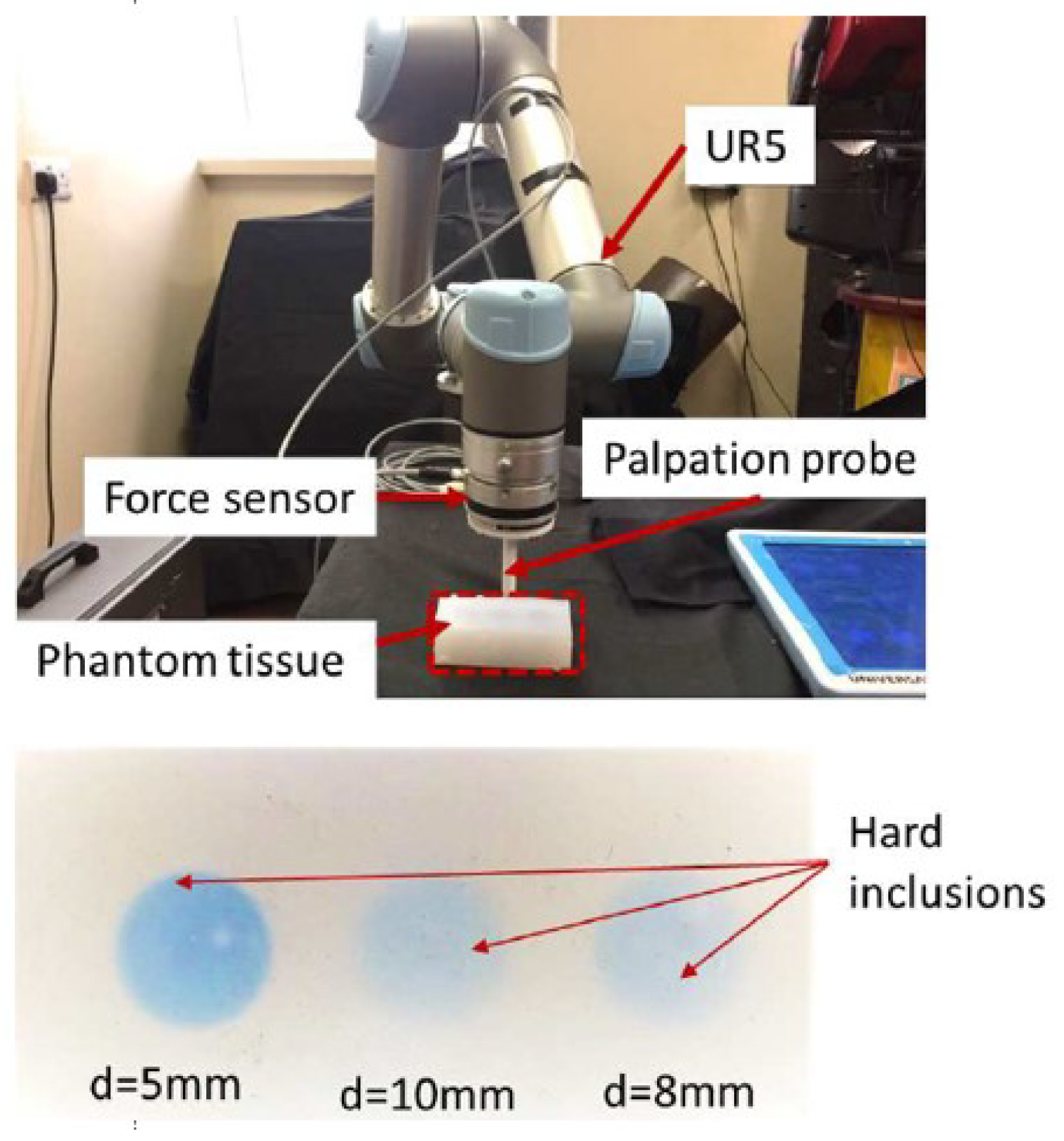
4.1. Experiment Setup
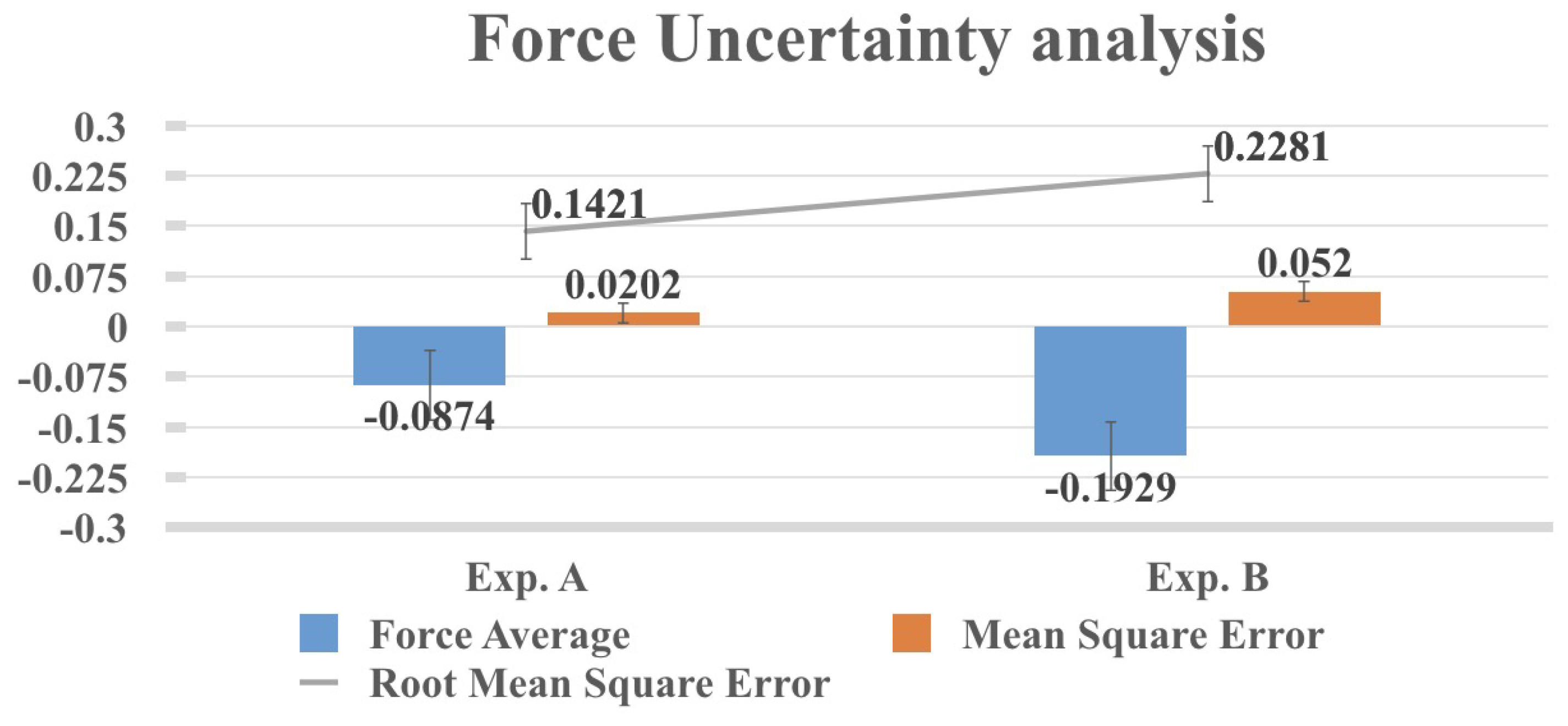
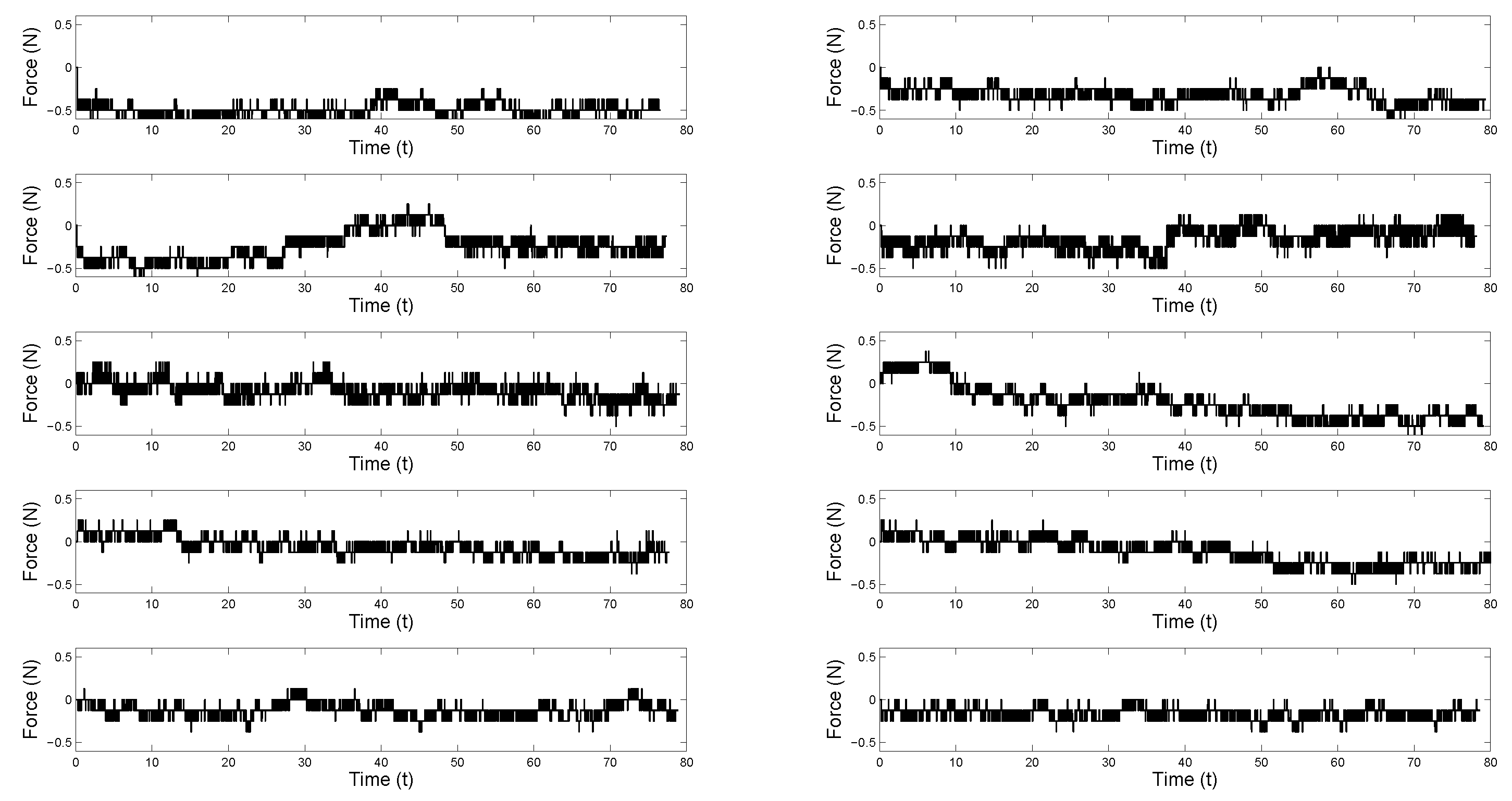
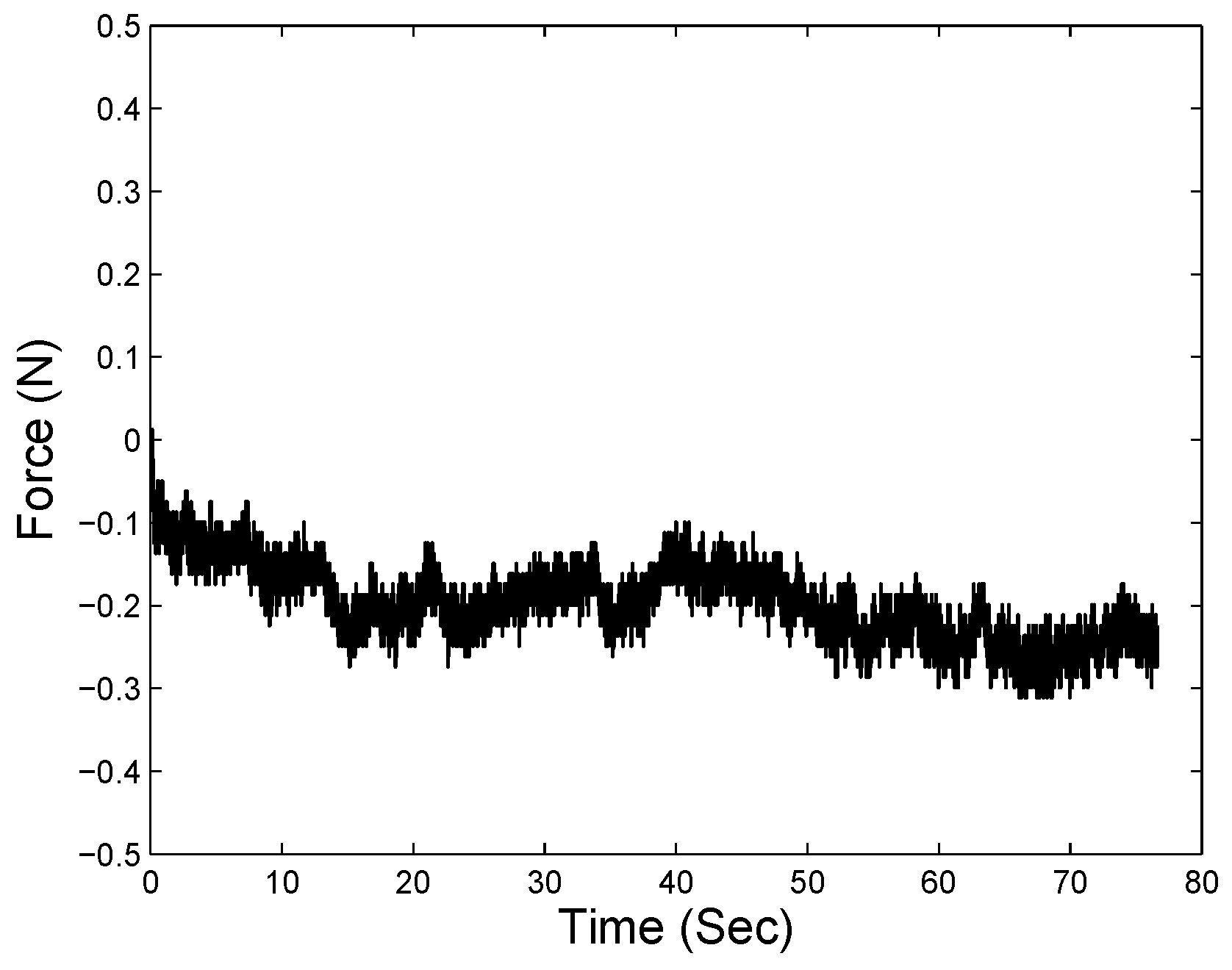
4.2. Uncertainties of Force Measurement
4.3. Static Palpation Experiments
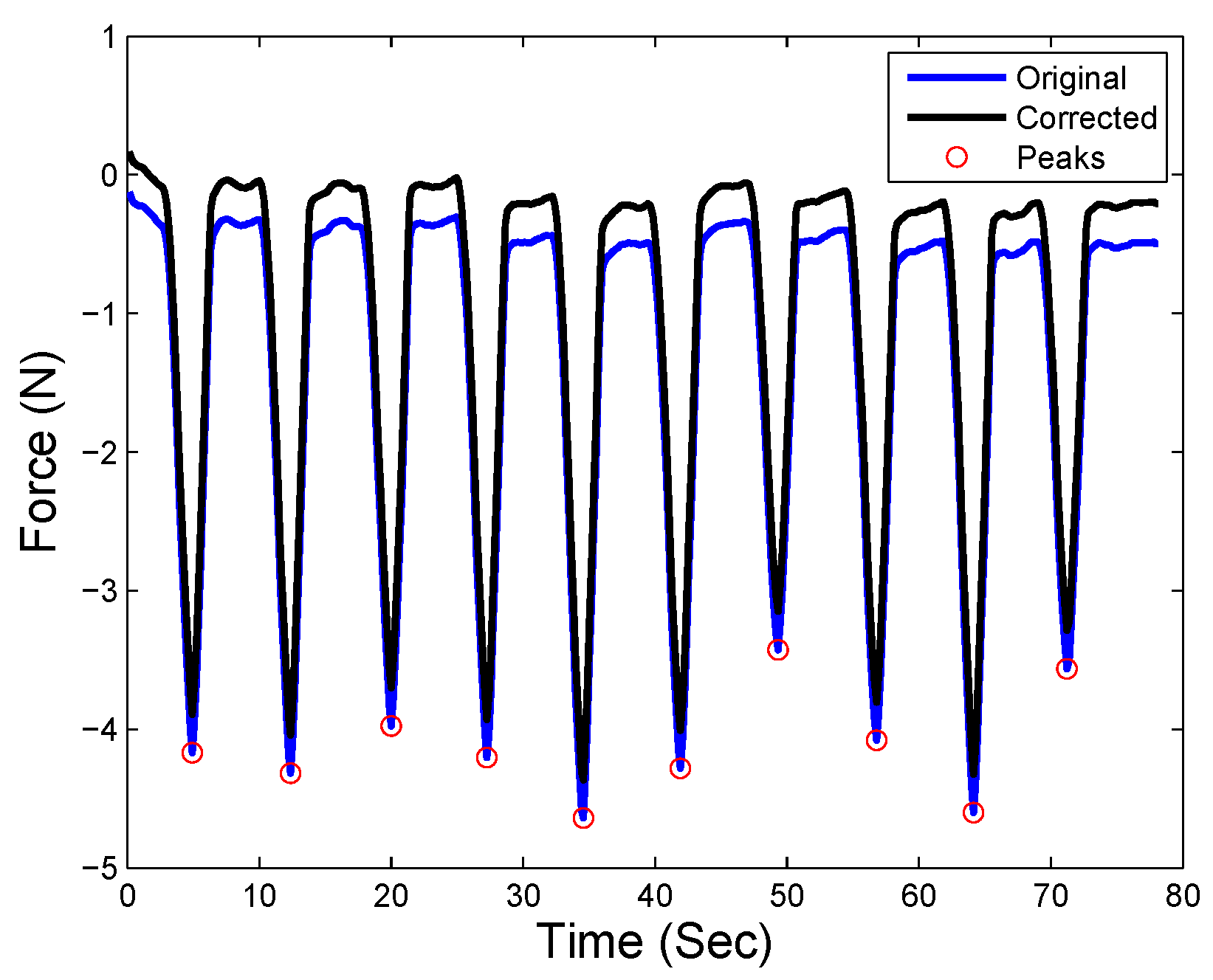
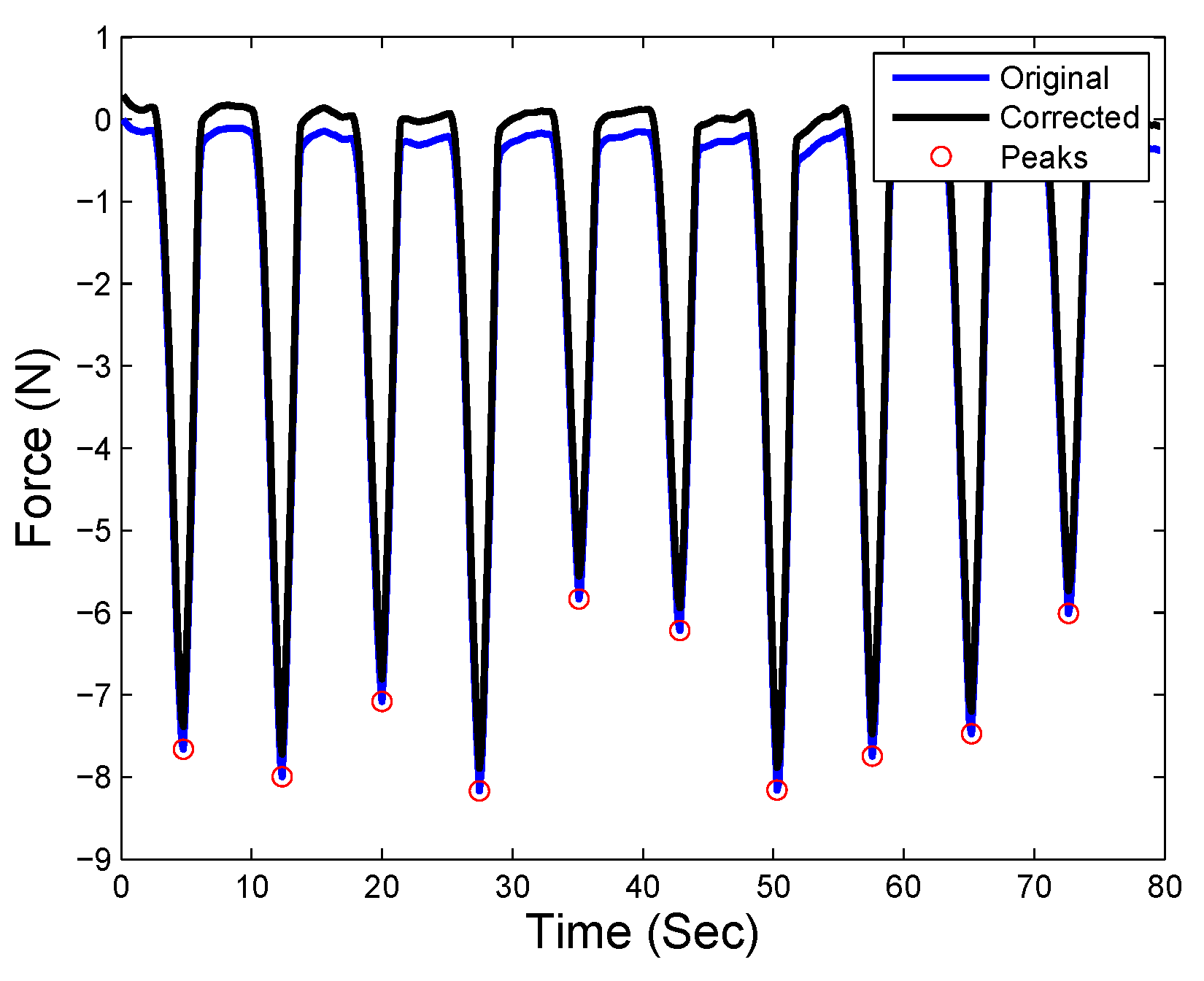
4.4. Neural-Network-Based Force Compensation of Robotic Palpation
5. Discussion
Future Work
- In vivo experiments with robotic palpation setup will be performed to present a real clinical environment.
- Various modeling approaches with different features (force, mass, position, velocity acceleration etc.) will be conducted to evaluate the performance of inertial force modeling.
- To extract more information from the dynamic palpation process, advanced modeling approaches that favor the time-series data like recurrent neural network (RNN) will be investigated to further improve the compensation performance.
- Heterogeneity of the tissue will be considered and various sample of tissues will be used to verify the proposed approach.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fisher, T.; Hamed, A.; Vartholomeos, P.; Masamune, K.; Tang, G.; Ren, H.; Tse, Z.T.H. Intraoperative magnetic resonance imaging conditional robotic devices for therapy and diagnosis. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2014, 228, 303–318. [Google Scholar] [CrossRef] [PubMed]
- Ren, H.; Lim, C.M.; Wang, J.; Liu, W.; Song, S.; Li, Z.; Herbert, G.; Tse, Z.T.H.; Tan, Z. Computer assisted transoral surgery with flexible robotics and navigation technologies: A review of recent progress and research challenges. Crit. Rev. Biomed. Eng. 2013, 41, 365–391. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Ren, H.; Meng, M.Q.-H.; Tse, Z.T.H.; Yu, H. Robotics in natural orifice transluminal endoscopic surgery. J. Mech. Med. Biol. 2013, 13, 1350044. [Google Scholar] [CrossRef]
- Osa, T.; Sugita, N.; Mitsuishi, M. Online Trajectory Planning and Force Control for Automation of Surgical Tasks. IEEE Trans. Autom. Sci. Eng. 2018, 15, 675–691. [Google Scholar] [CrossRef]
- Lederman, S.J.; Klatzky, R.L. Sensing and displaying spatially distributed fingertip forces in haptic interfaces for teleoperator and virtual environment systems. Presence Teleoperators Virtual Environ. 1999, 8, 86–103. [Google Scholar] [CrossRef]
- Girão, P.S.; Ramos, P.M.; Postolache, O.; Pereira, J.M. Tactile sensors for robotic applications. Measurement 2013, 46, 1257–1271. [Google Scholar] [CrossRef]
- Tiwana, M.I.; Redmond, S.J.; Lovell, N.H. A review of tactile sensing technologies with applications in biomedical engineering. Sens. Actuators A Phys. 2012, 179, 17–31. [Google Scholar] [CrossRef]
- Konstantinova, J.; Jiang, A.; Althoefer, K.; Dasgupta, P.; Nanayakkara, T. Implementation of tactile sensing for palpation in robot-assisted minimally invasive surgery: A review. IEEE Sens. J. 2014, 14, 490–501. [Google Scholar] [CrossRef]
- McKay, D.; Blake, G. Optimum incision length for port insertion in laparoscopic surgery. Ann. R. Coll. Surg. Engl. 2006, 88, 78. [Google Scholar] [CrossRef]
- ANSI/AAMI ST79. Comprehensive Guide to Steam Sterilization and Sterility Assurance in Health Care Facilities; Association for the Advancement of Medical Instrumentation: Arlington, VA, USA, 2010. [Google Scholar]
- Beccani, M.; Di Natali, C.; Sliker, L.J.; Schoen, J.A.; Rentschler, M.E.; Valdastri, P. Wireless tissue palpation for intraoperative detection of lumps in the soft tissue. IEEE Trans. Biomed. Eng. 2014, 61, 53–61. [Google Scholar] [CrossRef]
- Escoto, A.; Bhattad, S.; Shamsil, A.; Sanches, A.; Trejos, A.L.; Naish, M.D.; Malthaner, R.A.; Patel, R.V. A multi-sensory mechatronic device for localizing tumors in minimally invasive interventions. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 4742–4747. [Google Scholar]
- Gafford, J.B.; Kesner, S.B.; Degirmenci, A.; Wood, R.J.; Howe, R.D.; Walsh, C.J. A monolithic approach to fabricating low-cost, millimeter-scale multi-axis force sensors for minimally-invasive surgery. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 1419–1425. [Google Scholar]
- Liu, H.; Li, J.; Song, X.; Seneviratne, L.D.; Althoefer, K. Rolling indentation probe for tissue abnormality identification during minimally invasive surgery. IEEE Trans. Robot. 2011, 27, 50–60. [Google Scholar] [CrossRef]
- Murayama, Y.; Haruta, M.; Hatakeyama, Y.; Shiina, T.; Sakuma, H.; Takenoshita, S.; Omata, S.; Constantinou, C.E. Development of a new instrument for examination of stiffness in the breast using haptic sensor technology. Sens. Actuators A Phys. 2008, 143, 430–438. [Google Scholar] [CrossRef]
- Peng, P.; Rajamani, R. Handheld microtactile sensor for elasticity measurement. IEEE Sens. J. 2011, 11, 35–42. [Google Scholar] [CrossRef]
- McKinley, S.; Garg, A.; Sen, S.; Kapadia, R.; Murali, A.; Nichols, K.; Lim, S.; Patil, S.; Abbeel, P.; Okamura, A.M.; et al. A single-use haptic palpation probe for locating subcutaneous blood vessels in robot-assisted minimally invasive surgery. In Proceedings of the IEEE International Conference on Automation Science and Engineering (CASE), Gothenburg, Sweden, 24–28 August 2015; pp. 1151–1158. [Google Scholar]
- Ahn, B.; Kim, Y.; Oh, C.K.; Kim, J. Robotic palpation and mechanical property characterization for abnormal tissue localization. Med. Biol. Eng. Comput. 2012, 50, 61–71. [Google Scholar] [CrossRef] [PubMed]
- Yen, P.L.; Chen, D.R.; Yeh, K.T.; Chu, P.Y. Lateral exploration strategy for differentiating the stiffness ratio of an inclusion in soft tissue. Med. Eng. Phys. 2008, 30, 1013–1019. [Google Scholar] [CrossRef] [PubMed]
- Trejos, A.L.; Jayender, J.; Perri, M.T.; Naish, M.D.; Patel, R.V.; Malthaner, R.A. Experimental evaluation of robot-assisted tactile sensing for minimally invasive surgery. In Proceedings of the 2nd IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), Scottsdale, AZ, USA, 19–22 October 2008; pp. 971–976. [Google Scholar]
- Trejos, A.L.; Jayender, J.; Perri, M.T.; Naish, M.D.; Patel, R.V.; Malthaner, R.A. Robot-assisted tactile sensing for minimally invasive tumor localization. Int. J. Robot. Res. 2009, 28, 18–33. [Google Scholar] [CrossRef]
- Konstantinova, J.; Cotugno, G.; Dasgupta, P.; Althoefer, K.; Nanayakkara, T. Palpation force modulation strategies to identify hard regions in soft tissue organs. PLoS ONE 2017, 12, e0171706. [Google Scholar] [CrossRef] [PubMed]
- Nichols, K.A.; Okamura, A.M. Autonomous robotic palpation: Machine learning techniques to identify hard inclusions in soft tissues. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Karlsruhe, Germany, 6–10 May 2013; pp. 4384–4389. [Google Scholar]
- Romano, J.M.; Kuchenbecker, K.J. Methods for robotic tool-mediated haptic surface recognition. In Proceedings of the IEEE Haptics Symposium (HAPTICS), Houston, TX, USA, 23–26 February 2014; pp. 49–56. [Google Scholar]
- Sangpradit, K.; Liu, H.; Seneviratne, L.D.; Althoefer, K. Tissue identification using inverse finite element analysis of rolling indentation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Kobe, Japan, 12–17 May 2009; pp. 1250–1255. [Google Scholar]
- Sangpradit, K.; Liu, H.; Dasgupta, P.; Althoefer, K.; Seneviratne, L.D. Finite-element modeling of soft tissue rolling indentation. IEEE Trans. Biomed. Eng. 2011, 58, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Konstantinova, J.; Xu, G.; He, B.; Aminzadeh, V.; Xie, J.; Wurdemann, H.; Althoefer, K. Evaluation of stiffness feedback for hard nodule identification on a phantom silicone model. PLoS ONE 2017, 12, e0172703. [Google Scholar] [CrossRef]
- Mahvash, M.; Gwilliam, J.; Agarwal, R.; Vagvolgyi, B.; Su, L.M.; Yuh, D.D.; Okamura, A.M. Force-feedback surgical teleoperator: Controller design and palpation experiments. In Proceedings of the IEEE Haptics Symposium Haptic Interfaces for Virtual Environment and Teleoperator Systems, Reno, NE, USA, 13–14 March 2008; pp. 465–471. [Google Scholar]
- Kubus, D.; Kroger, T.; Wahl, F.M. Improving force control performance by computational elimination of non-contact forces/torques. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Pasadena, CA, USA, 19–23 May 2008; pp. 2617–2622. [Google Scholar]
- Kubus, D.; Wahl, F.M. Scaling and eliminating non-contact forces and torques to improve bilateral teleoperation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), St. Louis, MO, USA, 10–15 October 2009; pp. 5133–5139. [Google Scholar]
- Bätz, G.; Weber, B.; Scheint, M.; Wollherr, D.; Buss, M. Dynamic contact force/torque observer: Sensor fusion for improved interaction control. Int. J. Robot. Res. 2013, 32, 46–57. [Google Scholar] [CrossRef]
- Farsoni, S.; Landi, C.T.; Ferraguti, F.; Secchi, C.; Bonfè, M. Compensation of Load Dynamics for Admittance Controlled Interactive Industrial Robots Using a Quaternion-Based Kalman Filter. IEEE Robot. Autom. Lett. 2017, 2, 672–679. [Google Scholar] [CrossRef]
- Carter, F.J.; Frank, T.G.; Davies, P.J.; McLean, D.; Cuschieri, A. Measurements and modeling of the compliance of human and porcine organs. Med. Image Anal. 2001, 5, 231–236. [Google Scholar] [CrossRef]
- Nesme, M.; Marchal, M.; Promayon, E.; Chabanas, M.; Payan, Y.; Faure, F. Physically realistic interactive simulation for biological soft tissues. Recent Res. Dev. Biomech. 2005, 2, 1–22. [Google Scholar]
- Jordan, P.; Socrate, S.; Zickler, T.E.; Howe, R.D. Constitutive modeling of porcine liver in indentation using 3D ultrasound imaging. J. Mech. Behav. Biomed. Mater. 2009, 2, 192–201. [Google Scholar] [CrossRef]
- Lee, E.H.; Radok, J.R. The contact problem for viscoelastic bodies. J. Appl. Mech. 1960, 27, 438–444. [Google Scholar] [CrossRef]
- Lam, H.-K.; Ekong, U.; Xiao, B.; Ouyang, G.; Liu, H.; Chan, K.Y.; Ling, S.H. Variable weight neural networks and their applications on material surface and epilepsy seizure phase classifications. Neurocomputing 2015, 149, 1177–1187. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Zaharakis, I.; Pintelas, P. Supervised machine learning: A review of classification techniques. In Proceedings of the 2007 Conference on Emerging Artificial Intelligence Applications in Computer Engineering: Real Word AI Systems with Applications in eHealth, HCI, Information Retrieval and Pervasive Technologies; IOS Press: Amsterdam, The Netherlands, 2007; pp. 3–24. [Google Scholar]
- Lam, H.-K.; Ekong, U.; Liu, H.; Xiao, B.; Araujo, H.; Ling, S.H.; Chan, K.Y. A study of neural-network-based classifiers for material classification. Neurocomputing 2014, 144, 367–377. [Google Scholar] [CrossRef]
- Andersen, T.T. Optimizing the Universal Robots ROS Driver; Department of Electrical Engineering, Technical University of Denmark: Kongens Lyngby, Denmark, 2015. [Google Scholar]

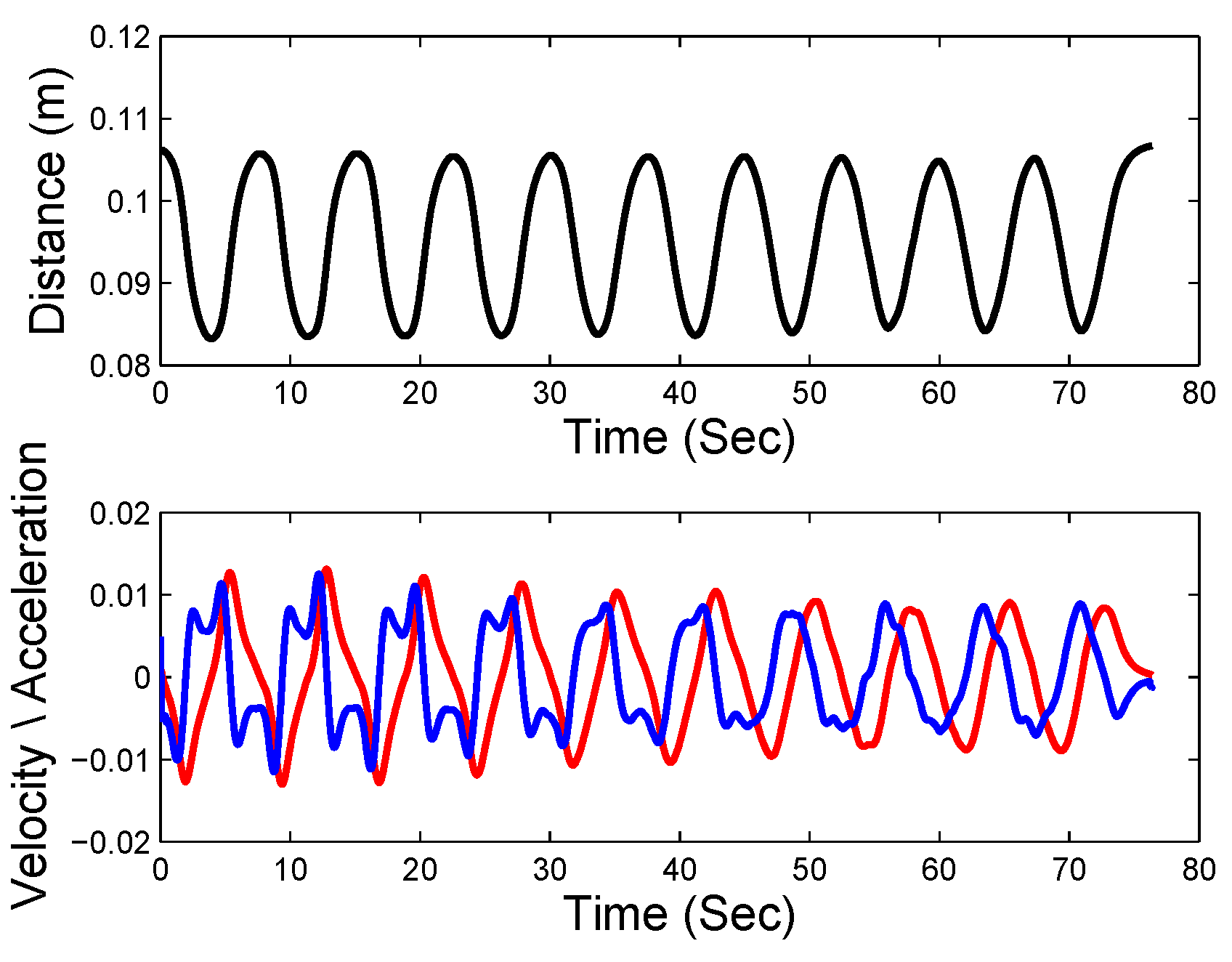
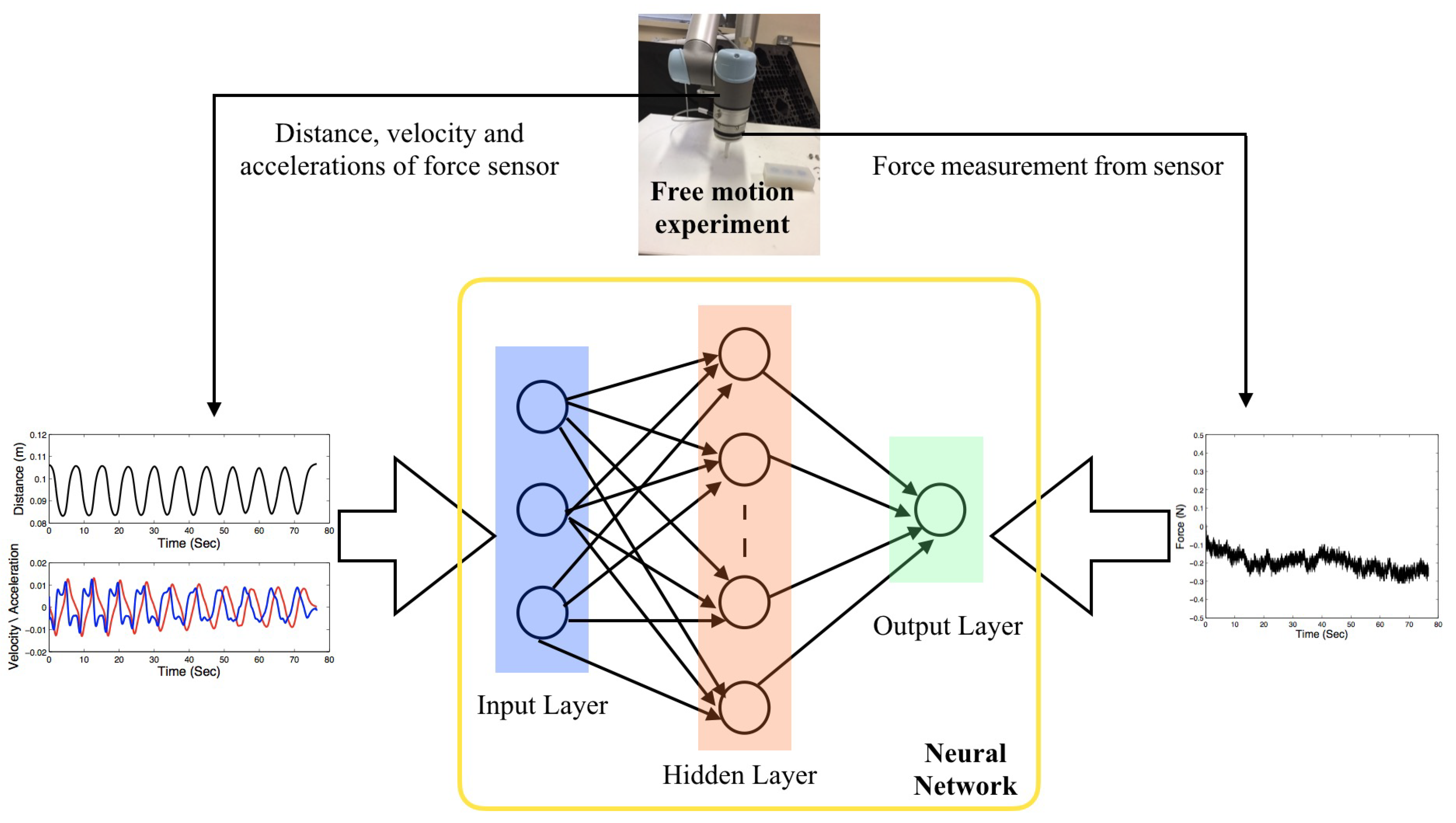
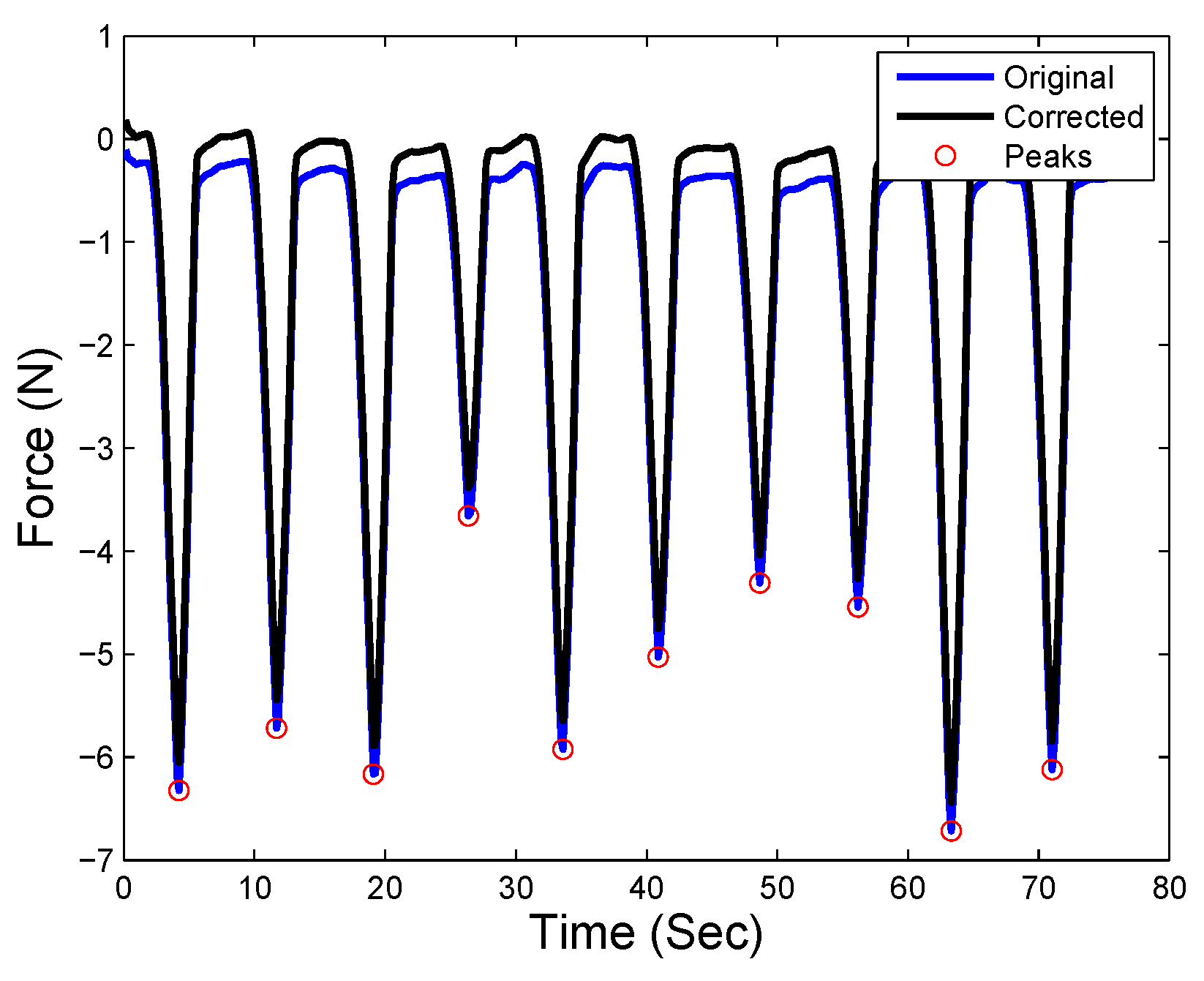
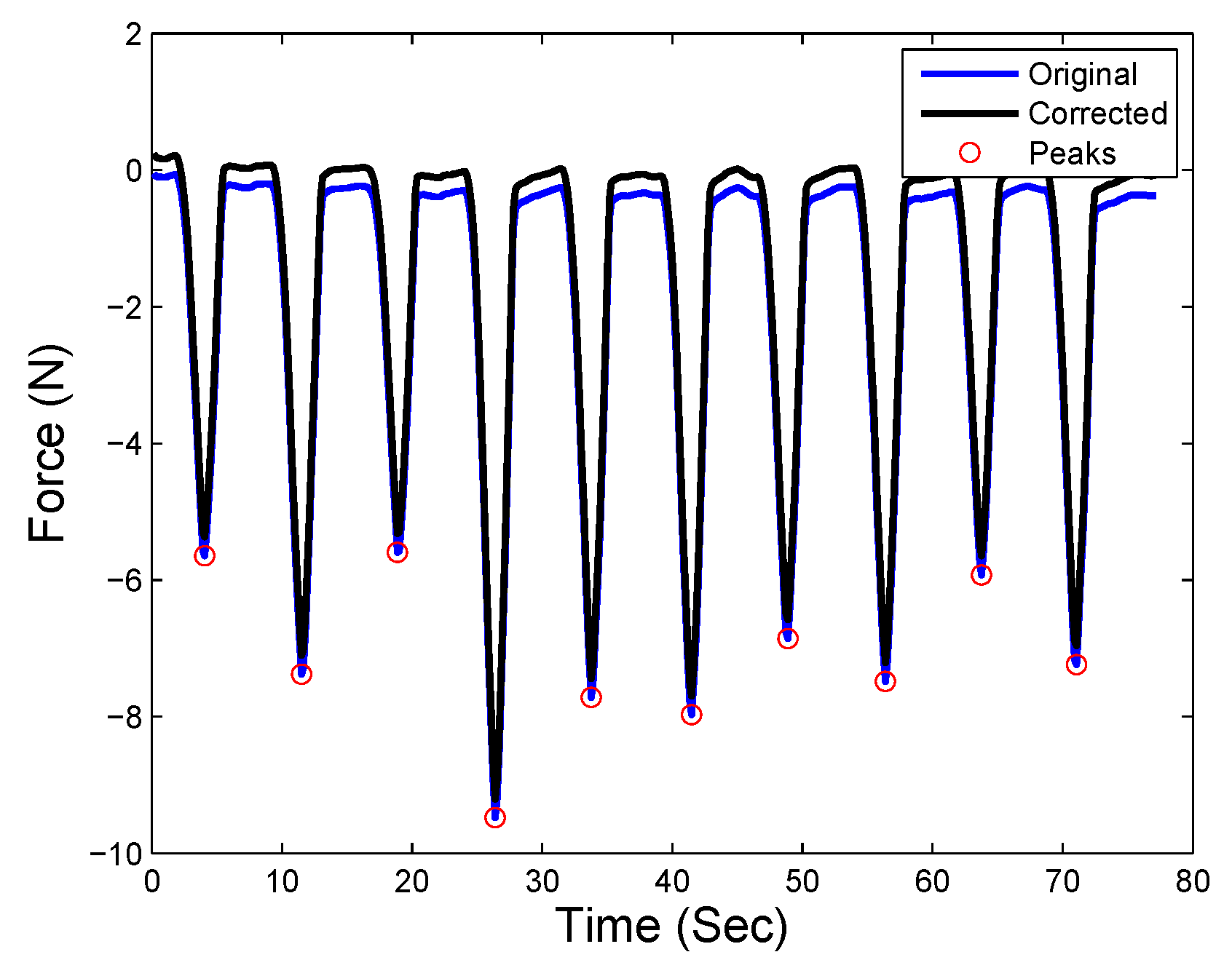
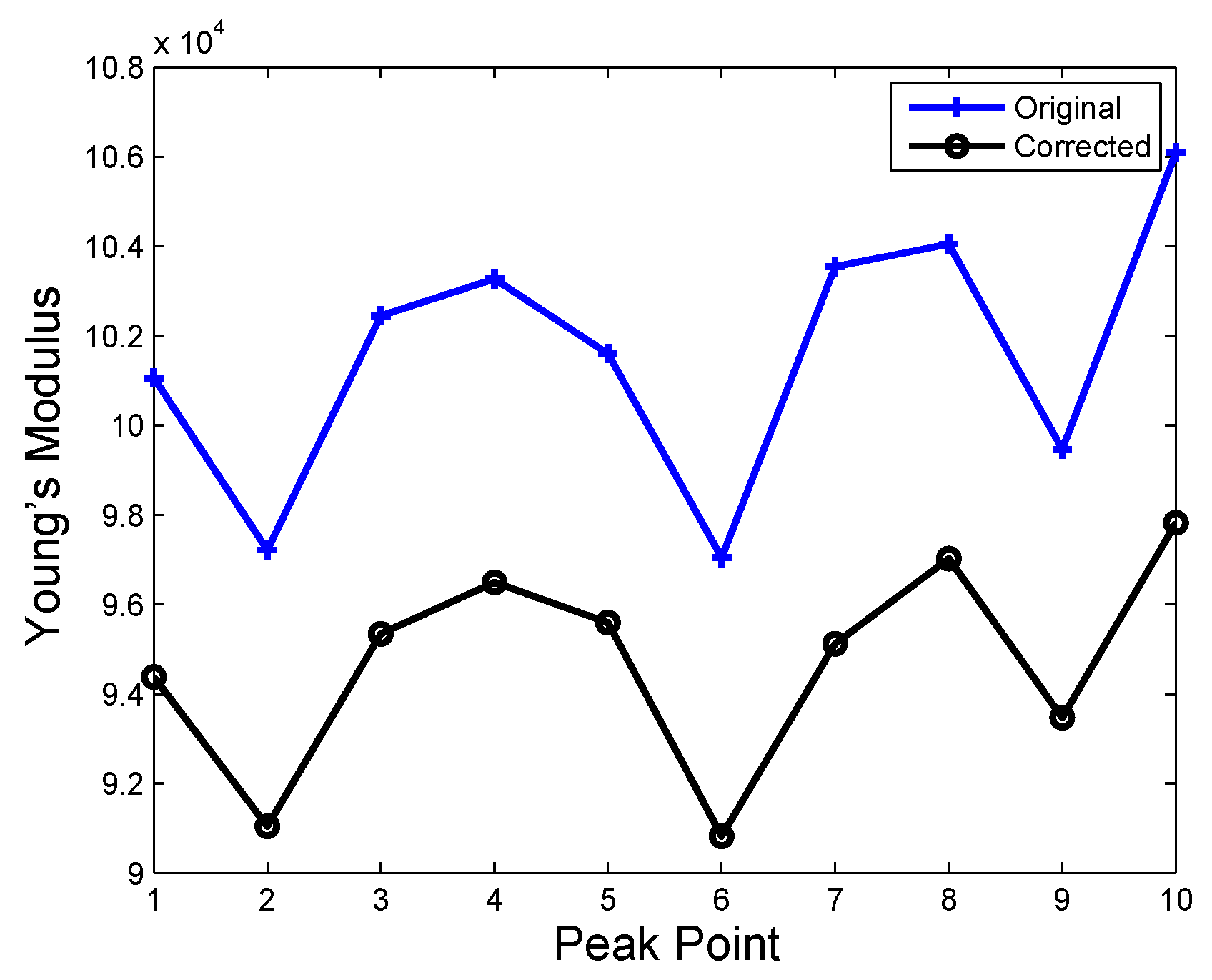
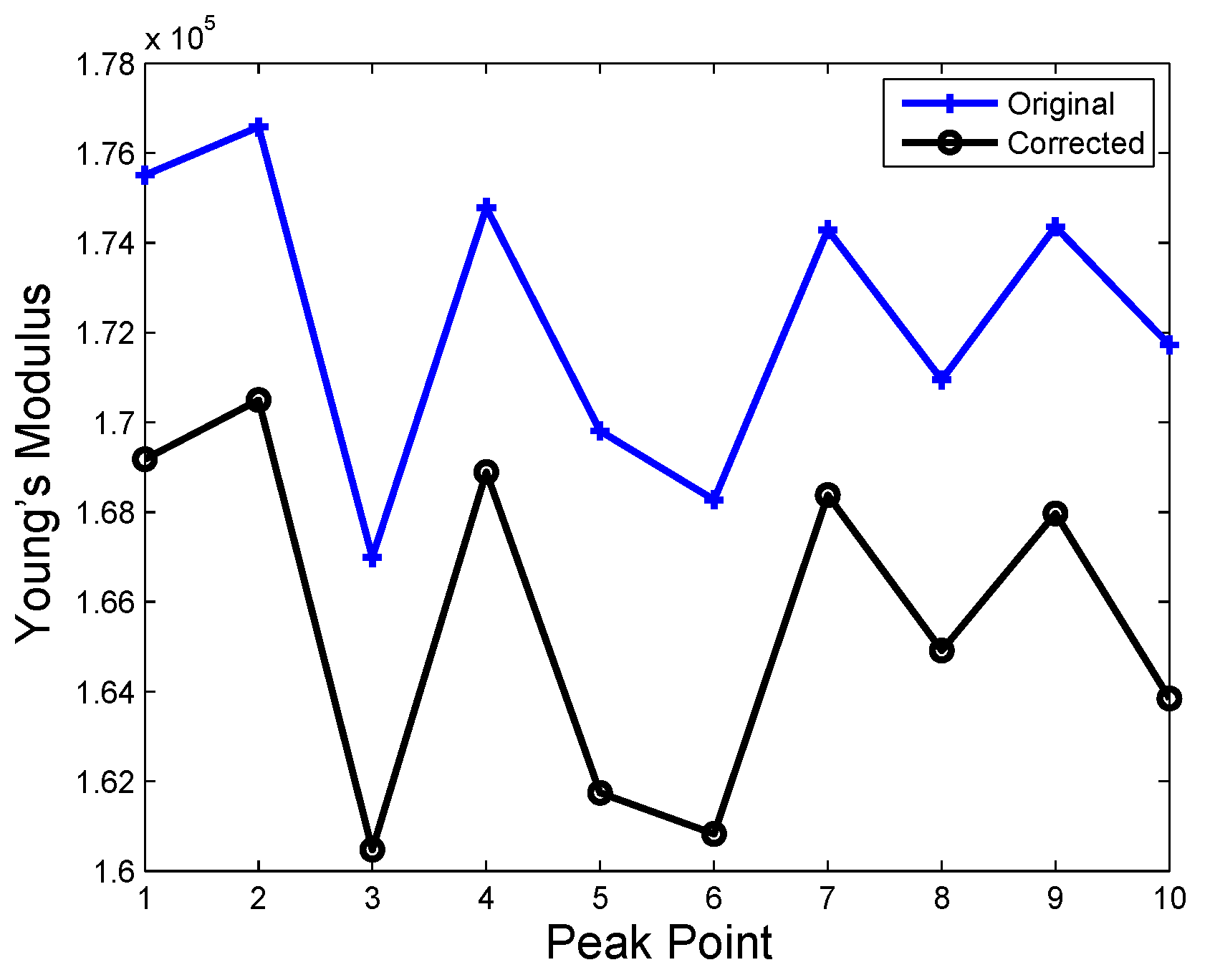
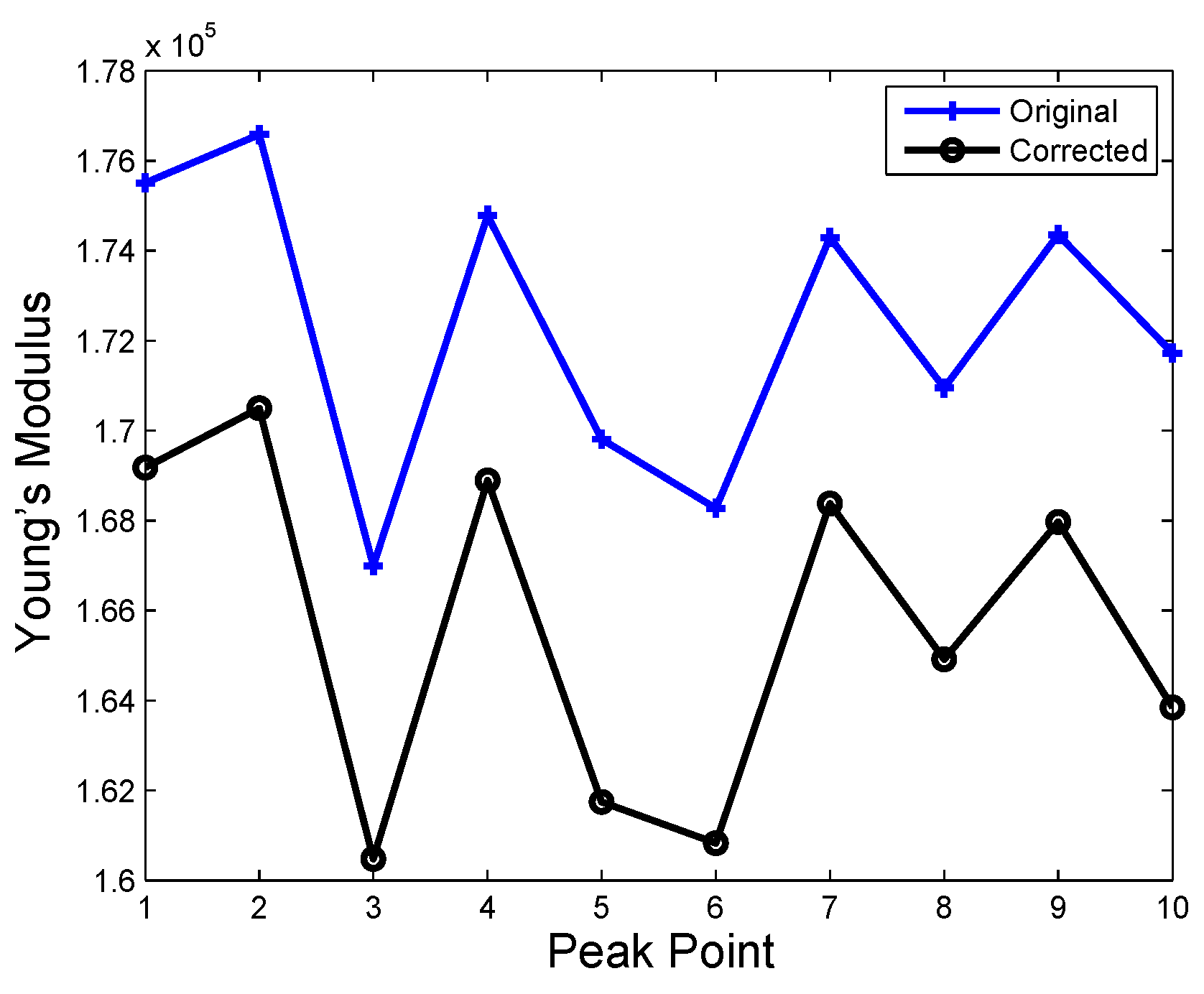
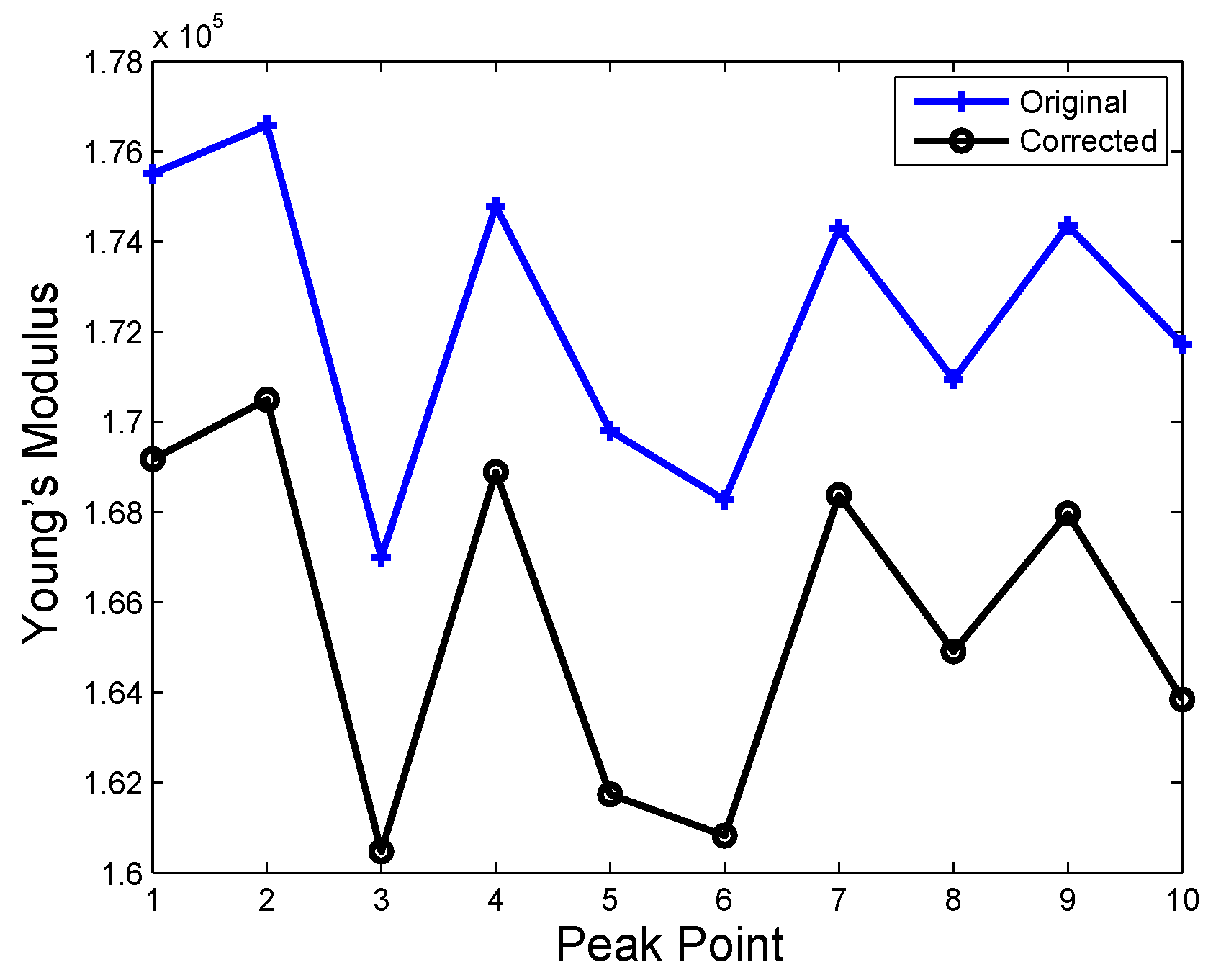
| Time | No Hard Inclusion | Hard Inclusion 5 mm | Hard Inclusion 8 mm | Hard Inclusion 10 mm |
|---|---|---|---|---|
| 1 | ( N and 3 mm) | ( N and 3 mm) | ( N and 3 mm) | ( N and 3 mm) |
| 2 | ( N and 4 mm) | ( N and 4 mm) | ( N and 4 mm) | ( N and 4 mm) |
| 3 | ( N and 5 mm) | ( N and 5 mm) | ( N and 5 mm) | ( N and 5 mm) |
| 4 | ( N and 6 mm) | ( N and 6 mm) | ( N and 6 mm) | ( N and 6 mm) |
| 5 | ( N and 7 mm) | ( N and 7 mm) | ( N and 7 mm) | ( N and 7 mm) |
| 6 | ( N and 8 mm) | ( N and 8 mm) | ( N and 8 mm) | ( N and 8 mm) |
| 7 | ( N and 9 mm) | ( N and 9 mm) | ( N and 9 mm) | ( N and 9 mm) |
| 8 | ( N and 10 mm) | ( N and 10 mm) | ( N and 10 mm) | ( N and 10 mm) |
| Palpation Cases | Original | Corrected | Static |
|---|---|---|---|
| No hard inclusion | |||
| Hard inclusion at 5 mm | |||
| Hard inclusion at 8 mm | |||
| Hard inclusion at 10 mm |
| Palpation Cases | ||
|---|---|---|
| No hard inclusion | ||
| Hard inclusion at 5 mm | ||
| Hard inclusion at 8 mm | ||
| Hard inclusion at 10 mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, J.; Xiao, B.; Ren, H. Compensating Uncertainties in Force Sensing for Robotic-Assisted Palpation. Appl. Sci. 2019, 9, 2573. https://doi.org/10.3390/app9122573
Guo J, Xiao B, Ren H. Compensating Uncertainties in Force Sensing for Robotic-Assisted Palpation. Applied Sciences. 2019; 9(12):2573. https://doi.org/10.3390/app9122573
Chicago/Turabian StyleGuo, Jing, Bo Xiao, and Hongliang Ren. 2019. "Compensating Uncertainties in Force Sensing for Robotic-Assisted Palpation" Applied Sciences 9, no. 12: 2573. https://doi.org/10.3390/app9122573
APA StyleGuo, J., Xiao, B., & Ren, H. (2019). Compensating Uncertainties in Force Sensing for Robotic-Assisted Palpation. Applied Sciences, 9(12), 2573. https://doi.org/10.3390/app9122573







