Mapping Areal Precipitation with Fusion Data by ANN Machine Learning in Sparse Gauged Region
Abstract
1. Introduction
2. Data and Methods
2.1. Study Area and Data Sources
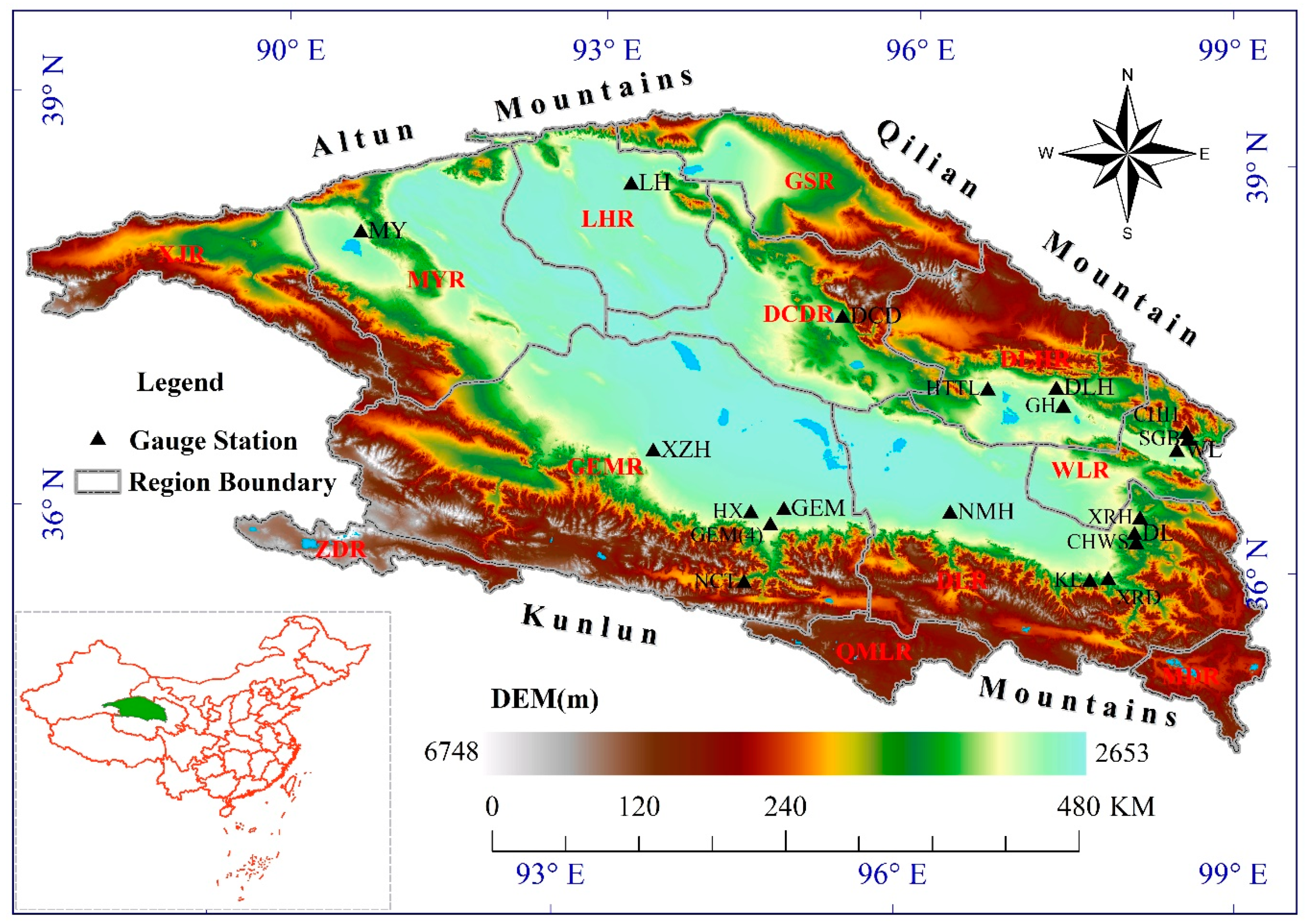
2.1.1. Study Area
2.1.2. Data Sources
2.2. Methodology
2.2.1. Evaluation of Remote Sensing Precipitation Precision
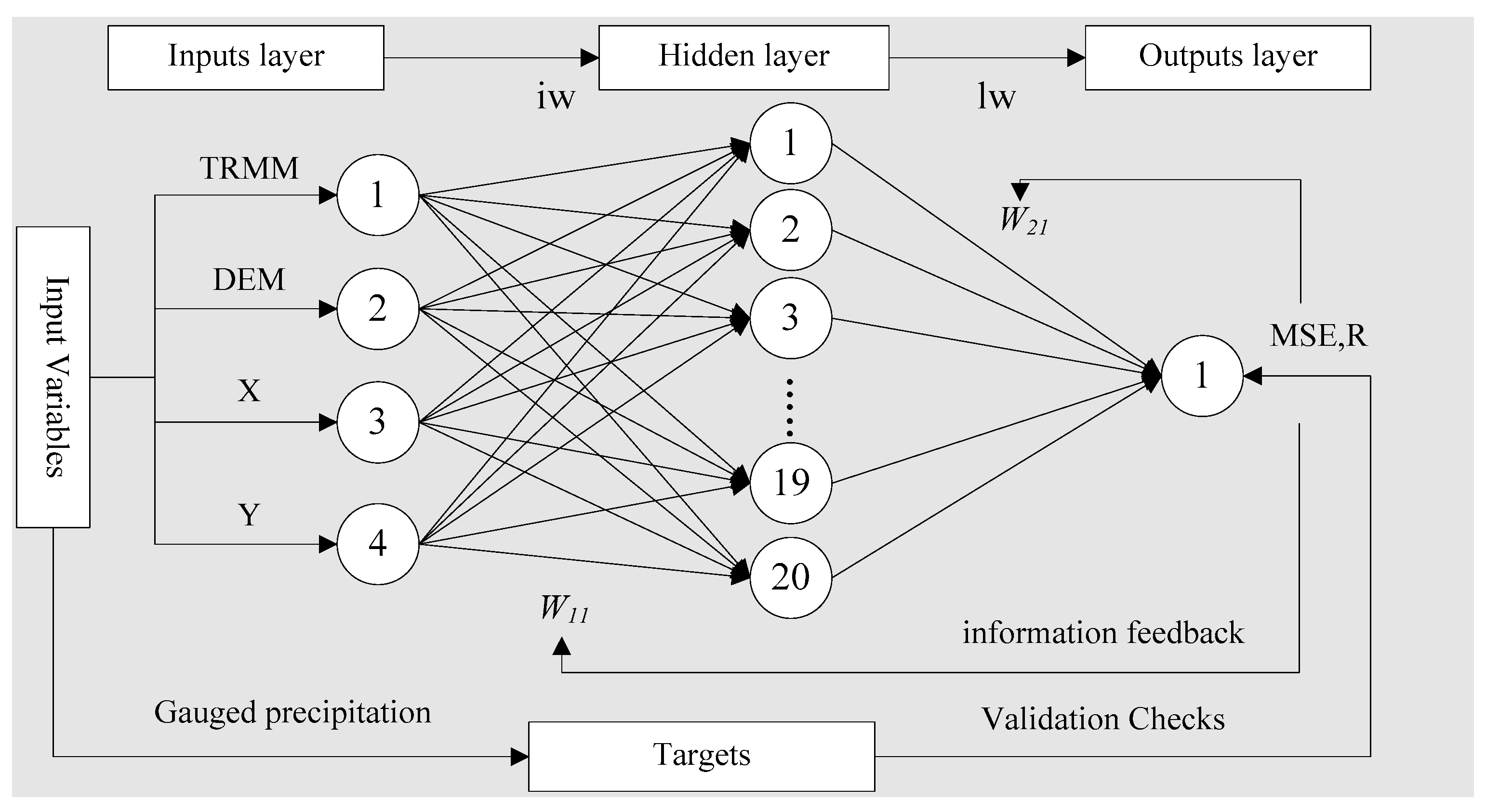
2.2.2. Correction of Remote Sensing Precipitation by ANN Model
2.2.3. Assessment of Rainwater Resources
3. Results and Discussion
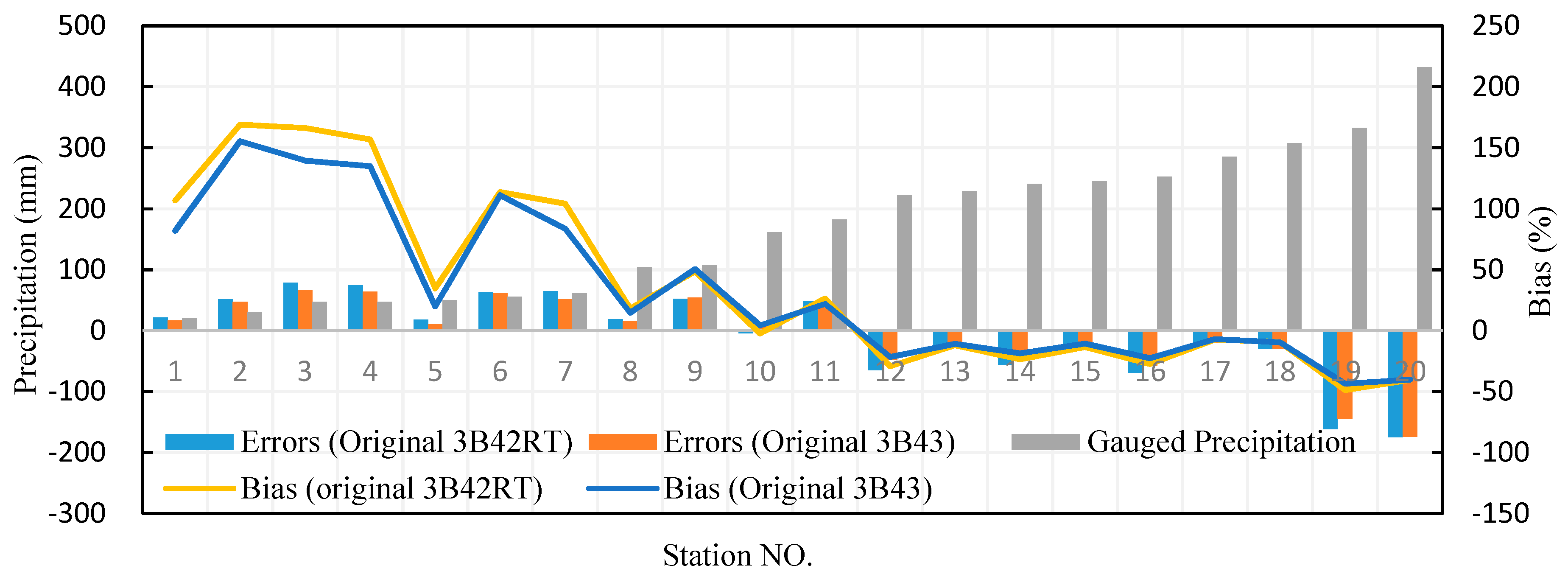
3.1. Precision of Original TRMM Products
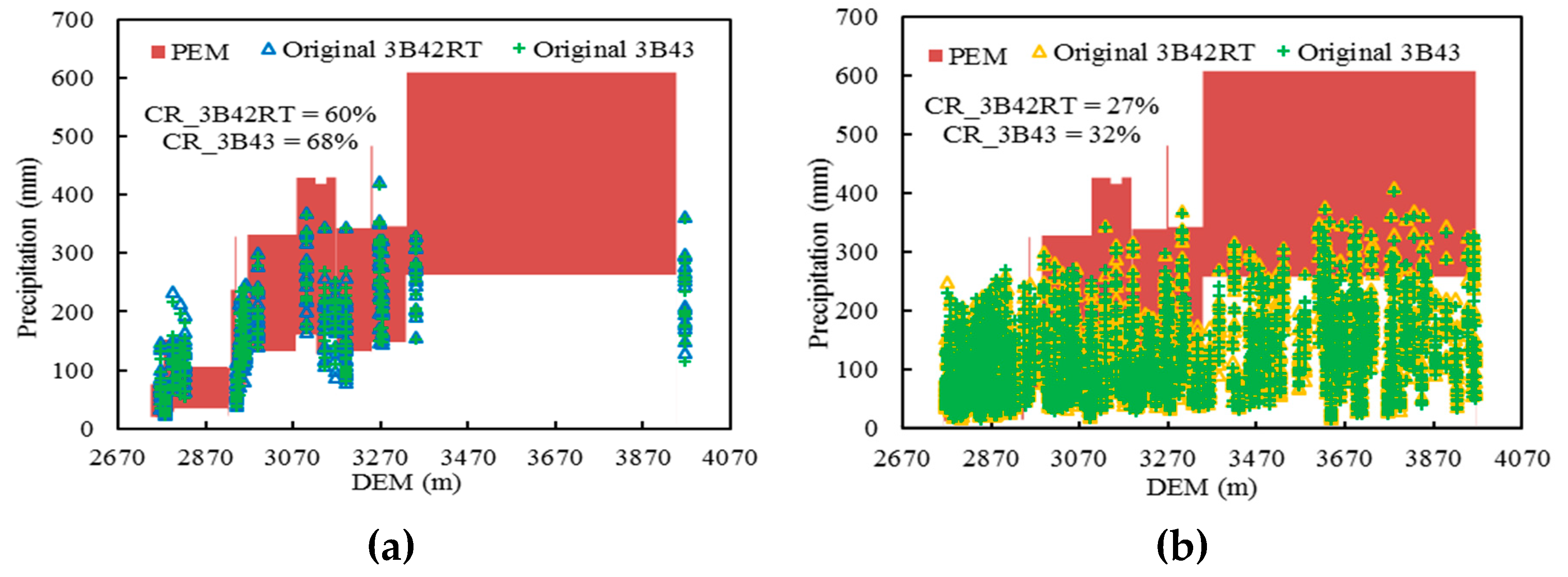
3.1.1. Grids with the Gauge Station
3.1.2. Grids without a Gauge Station
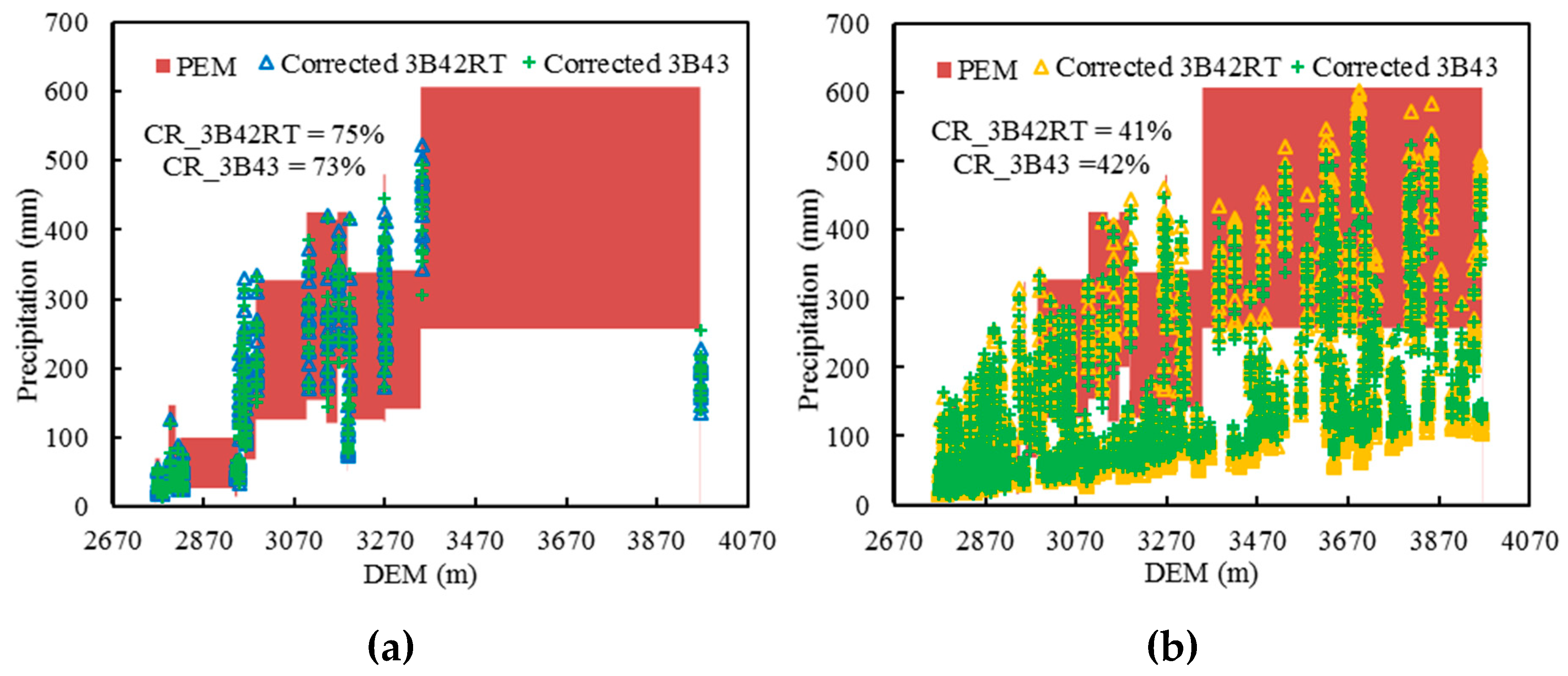
3.2. Correction of TRMM Products
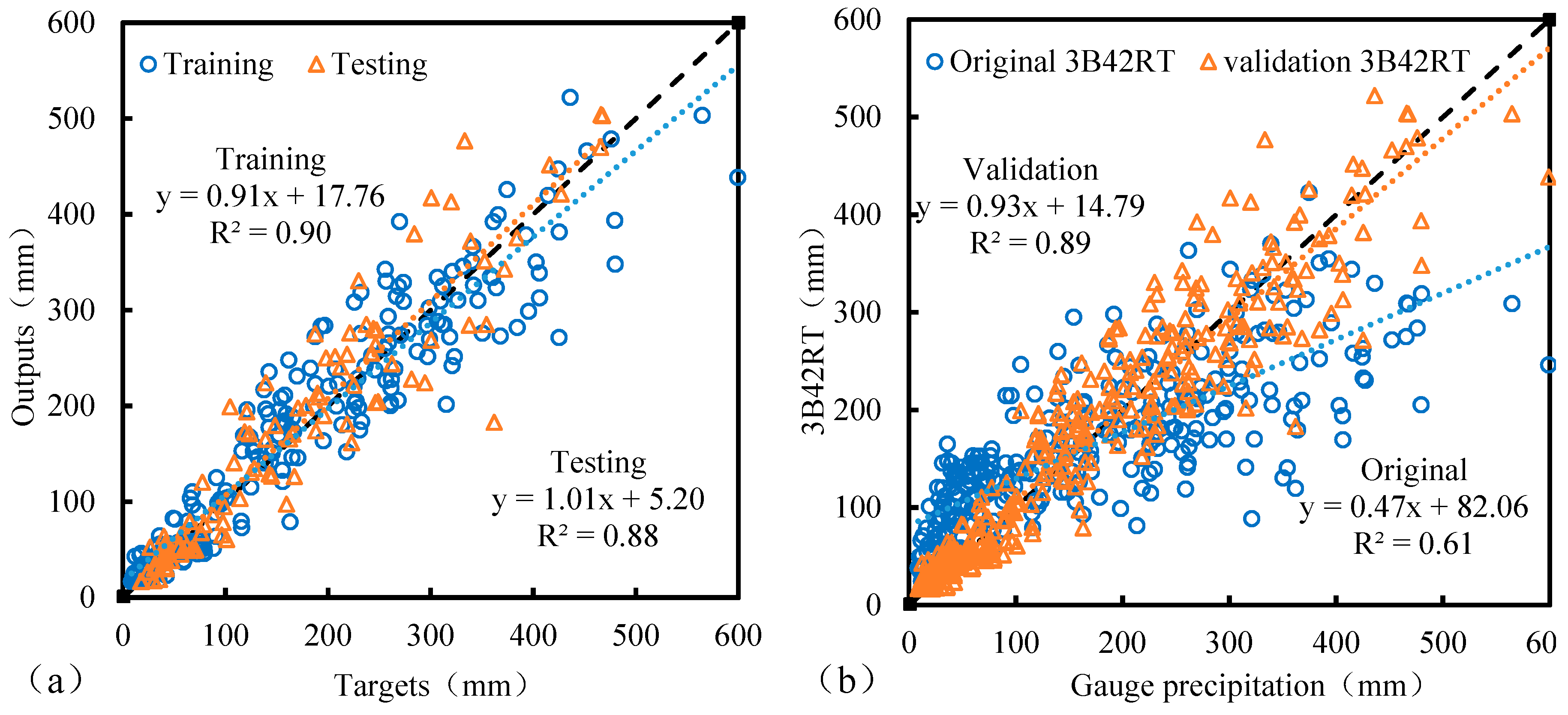
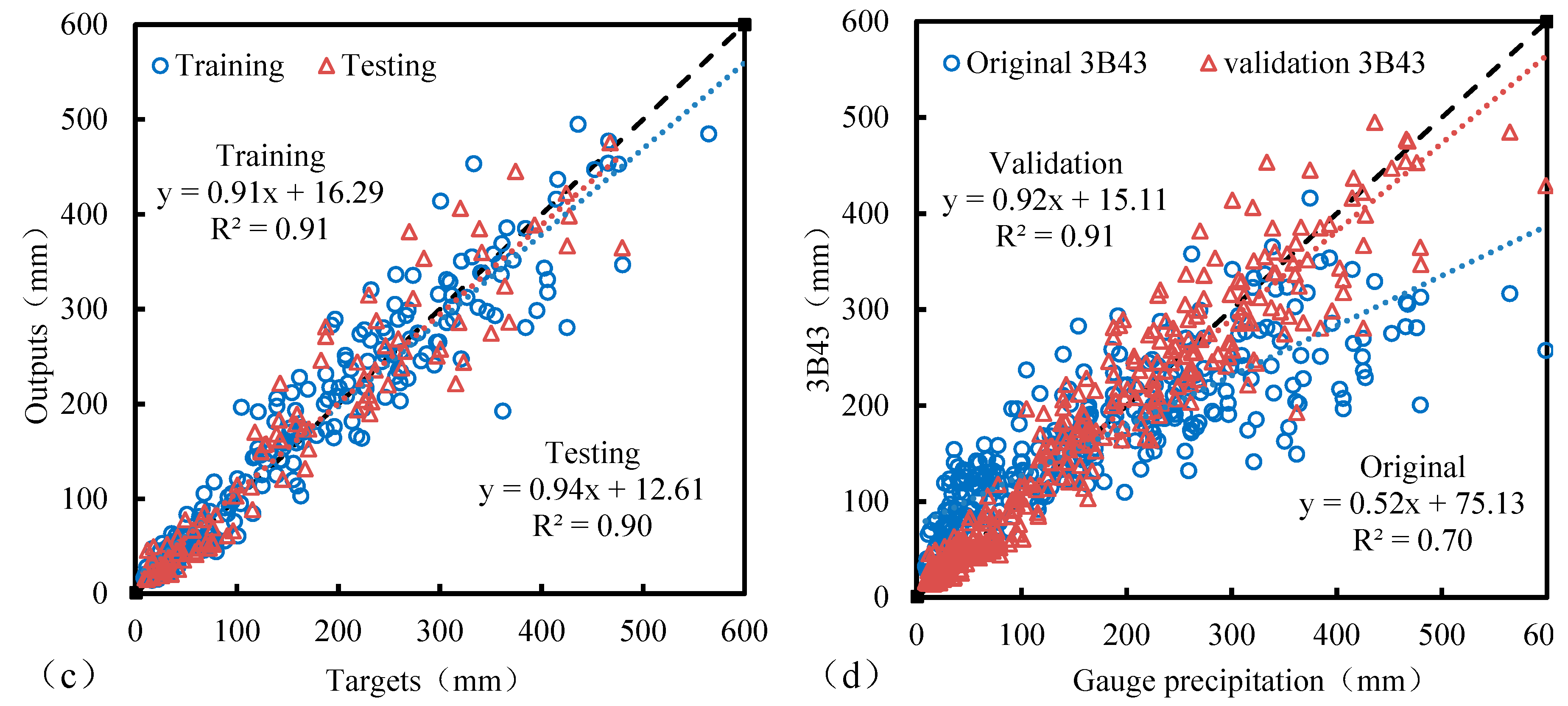
3.2.1. Calibration and Validation
3.2.2. The Precision of Corrected TRMM Products
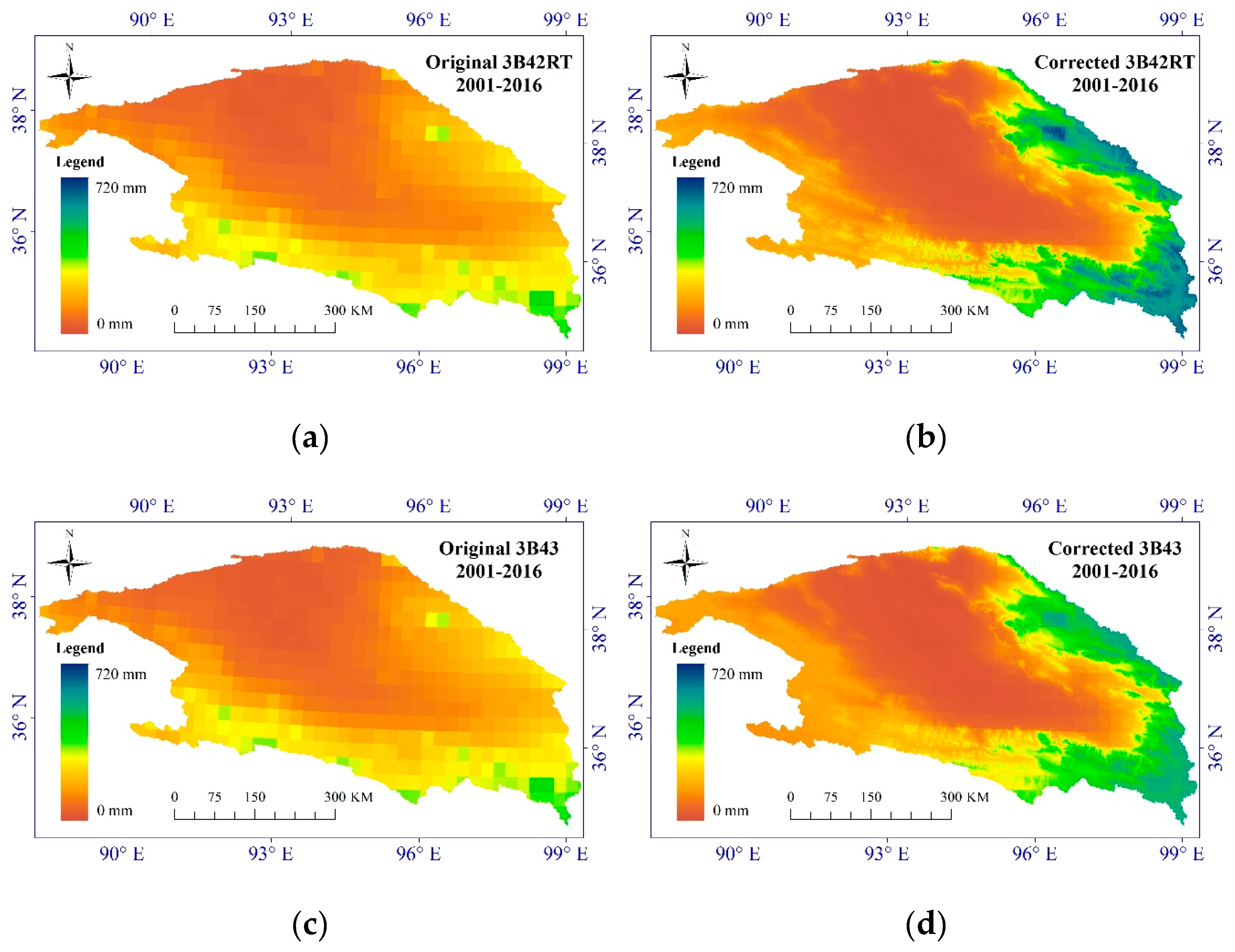
3.3. Assessment of Rainwater Resources of the Qaidam Basin
3.3.1. The Average Amount of Precipitation
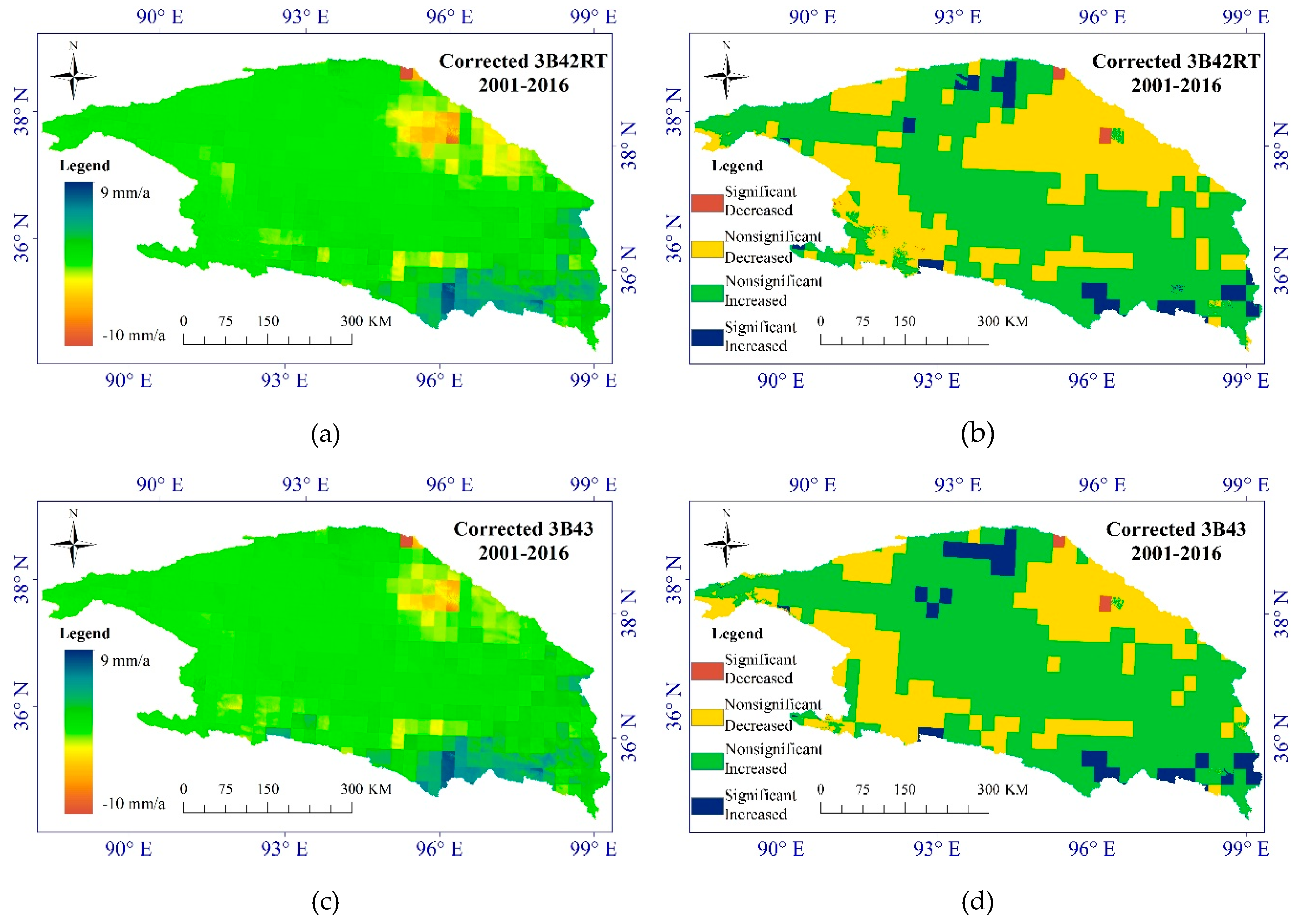
3.3.2. The Precipitation Variation Trend
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bohnenstengel, S.I.; Schlünzen, K.H.; Beyrich, F. Representativity of in situ precipitation measurements—A case study for the LITFASS area in North-Eastern Germany. J. Hydrol. 2011, 400, 387–395. [Google Scholar] [CrossRef]
- Marzano, F.S.; Cimini, D.; Montopoli, M. Investigating precipitation microphysics using ground-based microwave remote sensors and disdrometer data. Atmos. Res. 2010, 97, 583–600. [Google Scholar] [CrossRef]
- Zhuoqi, C.; Xiaogu, Z.; Shupeng, Z.; Tao, L. Mapping Daily Precipitation over China Based on TRMM Multisatellite Precipitation Analysis and Gauge Data. In Proceedings of the International Conference on Remote Sensing, Kyoto, Japan, 29 October–1 November 2012. [Google Scholar]
- XIE, P.; Arkin, P.A. Analyses of Global Monthly Precipitation Using Gauge Observations, Satellite Estimates, and Numerical Model Predictions. J. Clim. 1996, 9, 840–858. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Rudolf, B.; Schneider, U.; Keehn, P.R. Global Precipitation Estimates Based on a Technique for Combining Satellite-Based Estimates, Rain Gauge Analysis, and NWP Model Precipitation Information. J. Clim. 1995, 8, 1284–1295. [Google Scholar] [CrossRef]
- Vila, D.; Goncalves, L.; Toll, D.; Rozante, J.R. Statistical Evaluation of Combined Daily Gauge Observations and Rainfall Satellite Estimates over Continental South America. J. Hydrometeorol. 2009, 10, 533–543. [Google Scholar] [CrossRef]
- Rozante, J.R.; Moreira, D.S.; de Goncalves, L.G.G.; Vila, D.A. Combining TRMM and Surface Observations of Precipitation: Technique and Validation over South America. Weather 2010, 25, 885–894. [Google Scholar] [CrossRef]
- Shen, Y.; Zhao, P.; Pan, Y.; Yu, J. A high spatiotemporal gauge-satellite merged precipitation analysis over China. J. Geophys. Res. Atmos. 2014, 119, 3063–3075. [Google Scholar] [CrossRef]
- Huffman, G.J.; Robert, F.A.; David, T.B.; Nelkin, E.J.; Acheampong, M. The TRMM Multi-Satellite Precipitation Analysis (TMPA); Springer: Berlin, Germany, 2008. [Google Scholar]
- Kubota, T.; Ushio, T.; Shige, S.; Kida, S.; Kachi, M.; Okamoto, K. Verification of High-Resolution Satellite-Based Rainfall Estimates around Japan Using a Gauge-Calibrated Ground-Radar Dataset. J. Meteorol. Soc. Jpn. 2009, 87, 203–222. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.T.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104, 70–97. [Google Scholar] [CrossRef]
- Seto, S.; Iguchi, T.; Oki, T. The Basic Performance of a Precipitation Retrieval Algorithm for the Global Precipitation Measurement Mission’s Single/Dual-Frequency Radar Measurements. IEEE Trans. Geosci. Remote 2013, 51, 5239–5251. [Google Scholar] [CrossRef]
- Zhu, Z.; Yong, B.; Ke, L.; Wang, G.; Ren, L.; Chen, X. Tracing the Error Sources of Global Satellite Mapping of Precipitation for GPM (GPM-GSMaP) Over the Tibetan Plateau, China. IEEE J. Stars 2018, 11, 2181–2191. [Google Scholar] [CrossRef]
- Guo, H.; Chen, S.; Bao, A.; Behrangi, A.; Hong, Y.; Ndayisaba, F.; Hu, J.; Stepanian, P.M. Early assessment of Integrated Multi-satellite Retrievals for Global Precipitation Measurement over China. Atmos. Res. 2016, 176–177. [Google Scholar] [CrossRef]
- Haile, A.T.; Yan, F.; Habib, E. Accuracy of the CMORPH satellite-rainfall product over Lake Tana Basin in Eastern Africa. Atmos. Res. 2015, 163, 177–187. [Google Scholar] [CrossRef]
- Liu, S.; Yan, D.; Qin, T.; Weng, B.; Li, M. Correction of TRMM 3B42V7 Based on Linear Regression Models over China. Adv. Meteorol. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- Xia, T.; Wang, Z.; Zheng, H. Topography and Data Mining Based Methods for Improving Satellite Precipitation in Mountainous Areas of China. Atmosphere 2015, 6, 983–1005. [Google Scholar] [CrossRef]
- Zheng, X.; Zhu, J. A methodological approach for spatial downscaling of TRMM precipitation data in North China. Int. J. Remote Sens. 2015, 36, 144–169. [Google Scholar] [CrossRef]
- Tao, Z.; Yuanqing, H.; Jian, M.; Juan, P. Spatial and temporal distribution of precipitation based on corrected TRMM data around the Hexi Corridor, China. Sci. Cold Arid Reg. 2014, 6, 159–167. [Google Scholar]
- Shi, Y.; Song, L.; Xia, Z.; Lin, Y.; Myneni, R.; Choi, S.; Wang, L.; Ni, X.; Lao, C.; Yang, F. Mapping Annual Precipitation across Mainland China in the Period 2001–2010 from TRMM3B43 Product Using Spatial Downscaling Approach. Remote Sens. 2015, 7, 5849–5878. [Google Scholar] [CrossRef]
- Dinku, T.; Chidzambwa, S.; Ceccato, P.; Connor, S.J.; Ropelewski, C.F. Validation of high-resolution satellite rainfall products over complex terrain. Int. J. Remote Sens. 2008, 29, 4097–4110. [Google Scholar] [CrossRef]
- Bitew, M.M.; Gebremichael, M. Assessment of satellite rainfall products for streamflow simulation in medium watersheds of the Ethiopian highlands. Hydrol. Earth Syst. Sci. 2011, 15, 1147–1155. [Google Scholar] [CrossRef]
- Condom, T.; Rau, P.; Espinoza, J.C. Correction of TRMM 3B43 monthly precipitation data over the mountainous areas of Peru during the period 1998–2007. Hydrol. Process. 2011, 25, 1924–1933. [Google Scholar] [CrossRef]
- Darand, M.; Amanollahi, J.; Zandkarimi, S. Evaluation of the performance of TRMM Multi-satellite Precipitation Analysis (TMPA) estimation over Iran. Atmos. Res. 2017, 190, 121–127. [Google Scholar] [CrossRef]
- Romilly, T.G.; Gebremichael, M. Evaluation of satellite rainfall estimates over Ethiopian river basins. Hydrol. Earth Syst. Sci. 2011, 15, 1505–1514. [Google Scholar] [CrossRef]
- Moazami, S.; Golian, S.; Kavianpour, M.R.; Hong, Y. Uncertainty analysis of bias from satellite rainfall estimates using copula method. Atmos. Res. 2014, 137, 145–166. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, R.; Lai, C.; Chen, J. Evaluation of the GPM IMERG satellite-based precipitation products and the hydrological utility. Atmos. Res. 2017, 196, 151–163. [Google Scholar] [CrossRef]
- Lu, X.; Wei, M.; Tang, G.; Zhang, Y. Evaluation and correction of the TRMM 3B43V7 and GPM 3IMERGM satellite precipitation products by use of ground-based data over Xinjiang, China. Env. Earth Sci. 2018, 77, 209. [Google Scholar] [CrossRef]
- Lekula, M.; Lubczynski, M.W.; Shemang, E.M.; Verhoef, W. Validation of satellite-based rainfall in Kalahari. Phys. Chem. Earth Parts A/B/C 2018, 105, 84–97. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W.G.M. First results from Version 7 TRMM 3B43 precipitation product in combination with a new downscaling–calibration procedure. Remote Sens. Env. 2013, 131, 1–13. [Google Scholar] [CrossRef]
- Guofeng, Z.; Dahe, Q.; Yuanfeng, L.; Fenli, C.; Pengfei, H.; Dongdong, C.; Kai, W. Accuracy of TRMM precipitation data in the southwest monsoon region of China. Appl. Clim. 2017, 129, 353–362. [Google Scholar] [CrossRef]
- Jia, S.; Zhu, W.; Lű, A.; Yan, T. A statistical spatial downscaling algorithm of TRMM precipitation based on NDVI and DEM in the Qaidam Basin of China. Remote Sens. Env. 2011, 115, 3069–3079. [Google Scholar] [CrossRef]
- Liu, S.; Yan, D.; Wang, H.; Li, C.; Qin, T.; Weng, B.; Xing, Z. Evaluation of TRMM 3B42V7 at the basin scale over mainland China. Adv. Water Sci. 2016, 27, 639–651. [Google Scholar]
- Seyyedi, H.; Anagnostou, E.N.; Beighley, E.; McCollum, J. Satellite-driven downscaling of global reanalysis precipitation products for hydrological applications. Hydrol. Earth Syst. Sci. 2014, 18, 5077–5091. [Google Scholar] [CrossRef]
- Agatonovic-Kustrin, S.; Beresford, R. Basic Concepts of Artificial Neural Network (ANN) Modeling and its Application in Pharmaceutical Research. J. Pharm. Biomed. Anal. 2000, 22, 717–727. [Google Scholar] [CrossRef]
- Partridge, D.; Rae, S.; Wang, W.J. Artificial neural networks. J. Roy. Soc. Med. 1999, 92, 385. [Google Scholar] [CrossRef]
- Lyons, W.B.; Flanagan, C.; Lewis, E.; Ewald, H.; Lochmann, S. Interrogation of multipoint optical fibre sensor signals based on artificial neural network pattern recognition techniques. Sens. Actuators A Phys. 2004, 114, 7–12. [Google Scholar] [CrossRef]
- Lyons, W.; Fitzpatrick, C.; Flanagan, C.; Lewis, E. A novel multipoint luminescent coated ultra violet fibre sensor utilising artificial neural network pattern recognition techniques. Sens. Actuators A Phys. 2004, 115, 267–272. [Google Scholar] [CrossRef]
- Nissar, A.I.; Upadhyaya, S.J. Fault Diagnosis of Mixed Signal VLSI Systems Using Artificial Neural Networks. In Proceedings of the Southwest Symposium on Mixed-Signal Design (SSMSD 99), Tucson, AZ, USA, 11–13 April 1999; IEEE: Piscataway, NY, USA, 1999; pp. 93–98. [Google Scholar]
- Huesken, D.; Lange, J.; Mickanin, C.; Weiler, J.; Asselbergs, F.; Warner, J.; Meloon, B.; Engel, S.; Rosenberg, A.; Cohen, D.; et al. Design of a genome-wide siRNA library using an artificial neural network. Nat. Biotechnol. 2005, 23, 995–1001. [Google Scholar] [CrossRef]
- Aceto, G.; Ciuonzo, D.; Montieri, A.; Pescapé, A. Mobile Encrypted Traffic Classification Using Deep Learning. In Proceedings of the 2018 Network Traffic Measurement and Analysis Conference (TMA), Vienna, Austria, 26–29 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–8. [Google Scholar]
- Aceto, G.; Ciuonzo, D.; Montieri, A.; Pescape, A. Mobile Encrypted Traffic Classification Using Deep Learning: Experimental Evaluation, Lessons Learned, and Challenges. IEEE Trans. Netw. Serv. Manag. 2019. [Google Scholar] [CrossRef]
- Rucco, R.; Sorriso, A.; Liparoti, M.; Ferraioli, G.; Sorrentino, P.; Ambrosanio, M.; Baselice, F. Type and Location of Wearable Sensors for Monitoring Falls during Static and Dynamic Tasks in Healthy Elderly: A Review. Sensors 2018, 18, 1613. [Google Scholar] [CrossRef]
- Gardner, G.G.; Keating, D.; Williamson, T.H.; Elliott, A.T. Automatic detection of diabetic retinopathy using an artificial neural network: A screening tool. Brit. J. Ophthalmol. 1996, 80, 940–944. [Google Scholar] [CrossRef]
- Hsu, K.; Gupta, H.V.; Sorooshian, S. Artificial Neural Network Modeling of the Rainfall-Runoff Process. Water Resour. Res. 1995, 31, 2517–2530. [Google Scholar] [CrossRef]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Nasrollahi, N.; Habib, E. Accounting for Uncertainties of the TRMM Satellite Estimates. Remote Sens. 2009, 1, 606–619. [Google Scholar] [CrossRef]
- Heidinger, H.; Yarlequé, C.; Posadas, A.; Quiroz, R. TRMM rainfall correction over the Andean Plateau using wavelet multi-resolution analysis. Int. J. Remote Sens. 2012, 33, 4583–4602. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Teng, W.; Kempler, S. Tropical Rainfall Measuring Mission (TRMM) Precipitation Data and Services for Research and Applications. B Am. Meteorol. Soc. 2012, 93, 1317–1325. [Google Scholar] [CrossRef]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst. 2005, 19, 223–249. [Google Scholar] [CrossRef]
- Ji, T.; Yang, H.; Liu, R.; He, T.; Wu, J. Applicability analysis of the TRMM precipitation data in the Sichuan-Chongqing region. Prog. Geogr. 2014, 1375–1386. [Google Scholar]
- Wang, X.; Liu, H.; Bao, A. Applicability Research on TRMM Precipitation Data in Tianshan Mountains. J. China Hydrol. 2014, 58–64. [Google Scholar]
- Yongqing, B.; Juanle, W.; Yujie, W.; Xuehua, H.; Tsydypov, B.Z.; Ochir, A.; Davaasuren, D. Spatio-Temporal Distribution of Drought in the Belt and Road Area During 1998–2015 Based on TRMM Precipitation Data. J. Resour. Ecol. 2017, 8, 559–570. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Choudhury, B.J.; Garcia, M. Multitemporal Analysis of TRMM-Based Satellite Precipitation Products for Land Data Assimilation Applications. J. Hydrometeorol. 2007, 8, 1165–1183. [Google Scholar] [CrossRef]
- Bookhagen, B.; Burbank, D.W. Topography, relief, and TRMM-derived rainfall variations along the Himalaya. Geophys. Res. Lett. 2006, 33. [Google Scholar]
- Qu, W.; Lu, J.; Song, W.; Zhang, T.; Tan, Y.; Huang, P. Research on Accuracy Validation and Calibration Methods of TRMM Remote Sensing Precipitation Data in Irrawaddy Basin. Adv. Earth Sci. 2014, 1262–1270. [Google Scholar]
- Xu, R.; Tian, F.; Yang, L.; Hu, H.; Lu, H.; Hou, A. Ground validation of GPM IMERG and TRMM 3B42V7 rainfall products over southern Tibetan Plateau based on a high-density rain gauge network. J. Geophys. Res. Atmos. 2017, 122, 910–924. [Google Scholar] [CrossRef]
- Geographical Information Monitoring Cloud Platform. Available online: http://www.dsac.cn/ (accessed on 25 May 2018).
- National Aeronautics and Space Administration. Available online: https://mirador.gsfc.nasa.gov/ (accessed on 17 March 2018).
- National Meteorological Information Center. Available online: http://data.cma.cn/ (accessed on 9 May 2018).
- Qinghai Water Conservancy Bureau. Annual Hydrological Report P. R. China: Hydrological Data of Inland Rivers and Lakes, 1st ed.; Journal of Qinghai Water Conservancy Bureau: Xining, China, 2016; pp. 64–73. [Google Scholar]
- Marden, J.; Kendall, M.; Gibbons, J. Rank Correlation Methods (5th ed.). J. Am. Stat. Assoc. 1992, 87, 249. [Google Scholar] [CrossRef]
- Mann, H.B. Nonparametric Tests Against Trend. Econometrica 1945, 13, 245. [Google Scholar] [CrossRef]
- Burn, D.H.; Hag Elnur, M.A. Detection of hydrologic trends and variability. J. Hydrol. 2002, 255, 107–122. [Google Scholar] [CrossRef]
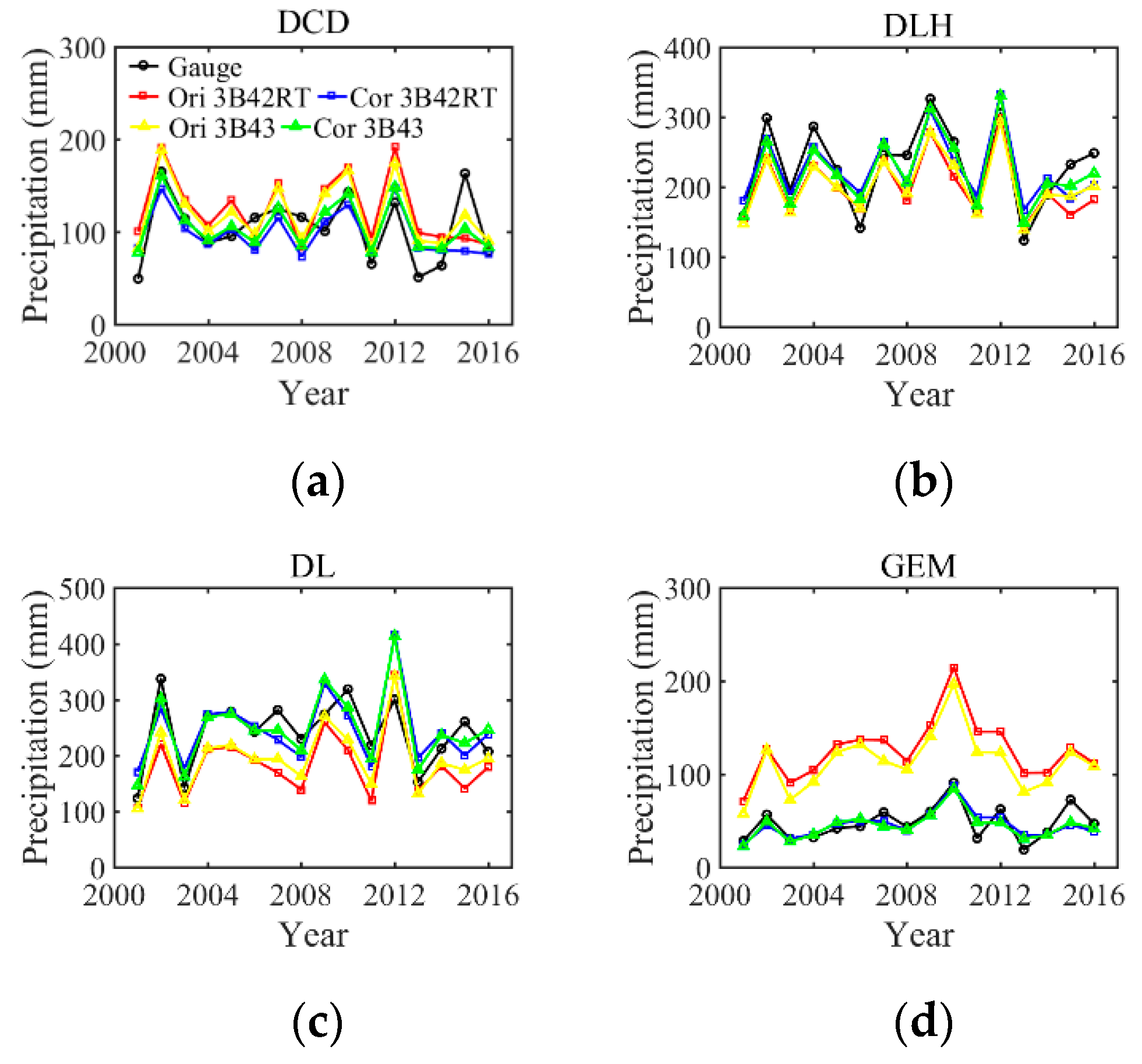
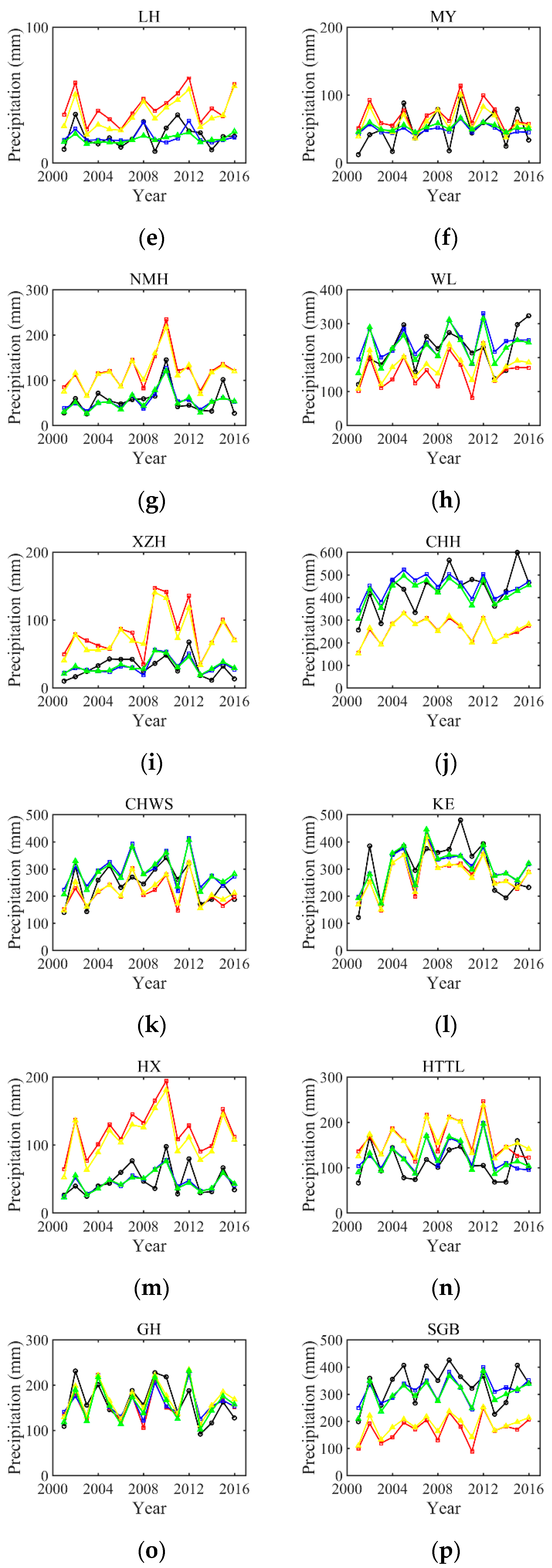
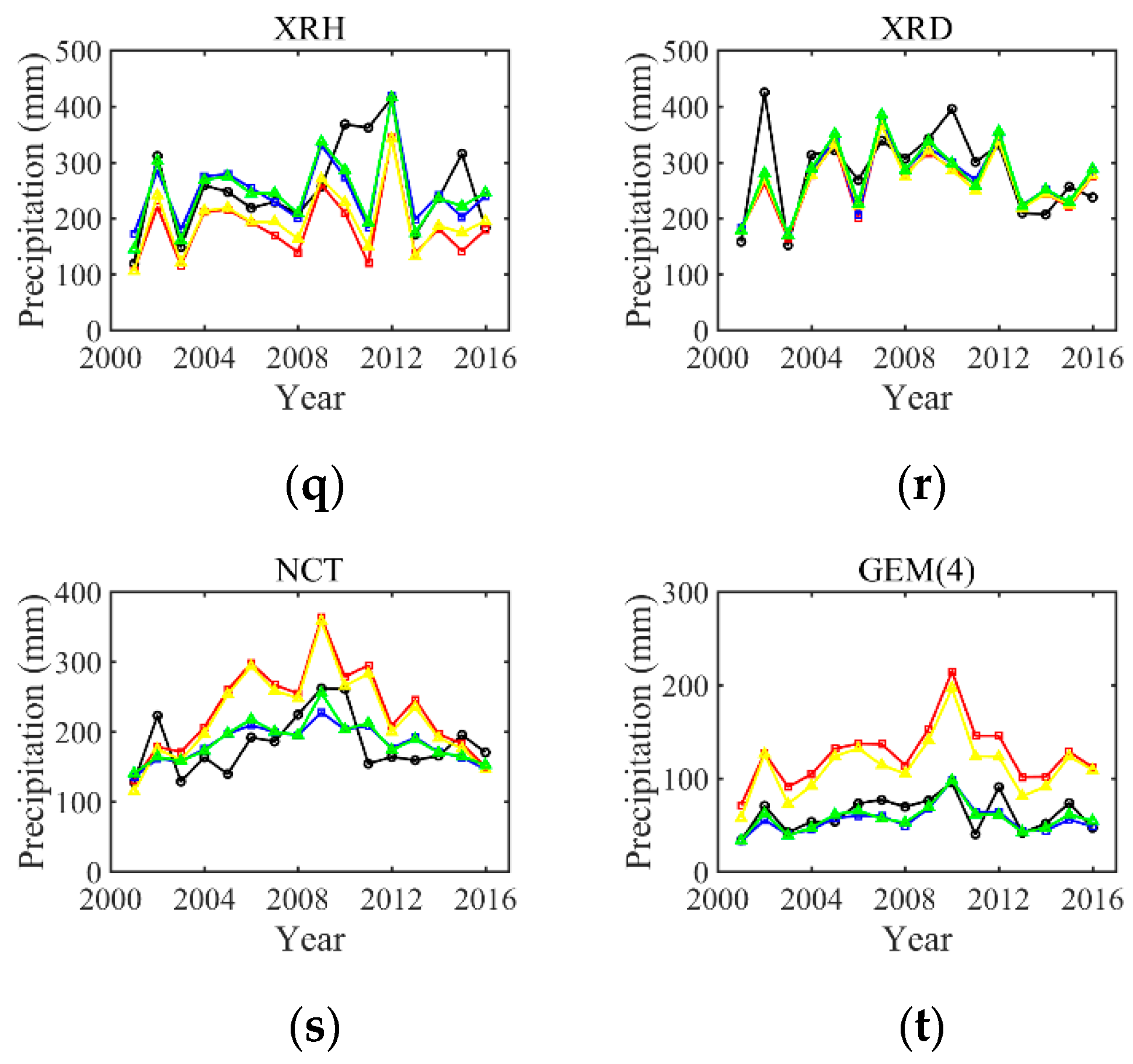
| Gauges | Original 3B42RT | Original 3B43 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| No. | Name | X (°) | Y (°) | DEM (m) | MAP (mm) | MAP (mm) | Bias (%) | RMSD (mm) | MAP (mm) | Bias (%) | RMSD (mm) |
| 1 | LH | 93.33 | 38.75 | 2777 | 19.88 | 41.10 | 106.79 | 23.17 | 36.19 | 82.07 | 18.42 |
| 2 | XZH | 93.68 | 36.80 | 2772 | 30.34 | 81.60 | 168.97 | 57.76 | 77.49 | 155.44 | 52.74 |
| 3 | GEM | 94.90 | 36.42 | 2812 | 47.32 | 126.01 | 166.30 | 81.28 | 113.31 | 139.46 | 68.68 |
| 4 | HX | 94.60 | 36.38 | 2822 | 47.34 | 121.63 | 156.91 | 77.60 | 111.21 | 134.89 | 68.22 |
| 5 | MY | 90.85 | 38.25 | 2942 | 50.16 | 68.37 | 34.55 | 26.85 | 60.59 | 19.79 | 20.07 |
| 6 | NMH | 96.42 | 36.43 | 2796 | 55.54 | 118.66 | 113.65 | 67.30 | 117.21 | 111.05 | 65.48 |
| 7 | GEM4 | 94.78 | 36.30 | 2957 | 61.76 | 126.01 | 104.05 | 67.61 | 113.31 | 83.48 | 55.44 |
| 8 | DCD | 95.37 | 37.85 | 3190 | 104.00 | 122.89 | 18.17 | 38.35 | 119.28 | 14.69 | 28.18 |
| 9 | HTTL | 96.73 | 37.35 | 2867 | 107.94 | 160.30 | 48.51 | 65.39 | 162.39 | 50.45 | 63.29 |
| 10 | GH | 97.43 | 37.23 | 2877 | 161.24 | 157.18 | −2.52 | 32.02 | 168.12 | 4.27 | 26.18 |
| 11 | NCT | 94.57 | 35.87 | 3966 | 182.31 | 230.40 | 26.38 | 70.91 | 222.21 | 21.89 | 65.31 |
| 12 | WL | 98.48 | 36.92 | 2959 | 222.26 | 157.31 | −29.22 | 83.38 | 174.37 | −21.55 | 66.26 |
| 13 | DLH | 97.37 | 37.37 | 2988 | 228.68 | 201.19 | −12.02 | 41.53 | 203.84 | −10.86 | 35.93 |
| 14 | DL | 98.10 | 36.30 | 3190 | 240.73 | 183.92 | −23.60 | 73.11 | 195.62 | −18.74 | 58.43 |
| 15 | CHWS | 98.12 | 36.23 | 3273 | 244.97 | 211.97 | −13.47 | 54.70 | 218.89 | −10.65 | 45.53 |
| 16 | XRH | 98.15 | 36.42 | 3143 | 252.91 | 183.92 | −27.28 | 95.16 | 195.62 | −22.65 | 81.60 |
| 17 | XRD | 97.87 | 35.97 | 3100 | 285.18 | 264.48 | −7.26 | 57.26 | 265.41 | −6.93 | 55.43 |
| 18 | KE | 97.70 | 35.95 | 3269 | 307.43 | 278.26 | −9.49 | 70.71 | 277.94 | −9.59 | 70.63 |
| 19 | SGB | 98.58 | 37.00 | 3168 | 332.05 | 170.04 | −48.79 | 171.22 | 187.25 | −43.61 | 151.87 |
| 20 | CHH | 98.57 | 37.05 | 3351 | 432.30 | 257.26 | –40.49 | 189.76 | 258.21 | –40.20 | 187.08 |
| -- | Average | -- | -- | -- | 170.72 | 163.12 | 36.51 | 72.25 | 163.92 | 31.63 | 64.24 |
| Gauges | Corrected 3B42RT | Corrected 3B43 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Name | X (°) | Y (°) | DEM (m) | MAP (mm) | MAP (mm) | Bias (%) | RMSD (mm) | MAP (mm) | Bias (%) | RMSD (mm) |
| LH | 93.33 | 38.75 | 2777 | 19.88 | 19.03 | −12.15 | 8.21 | 17.80 | −10.44 | 7.21 |
| XZH | 93.68 | 36.80 | 2772 | 30.34 | 31.60 | 4.15 | 11.71 | 32.25 | 6.32 | 12.21 |
| GEM | 94.90 | 36.42 | 2812 | 47.32 | 45.53 | −3.78 | 11.06 | 44.48 | −6.00 | 10.49 |
| HX | 94.60 | 36.38 | 2822 | 47.34 | 45.53 | −3.82 | 14.92 | 45.09 | −4.77 | 15.71 |
| MY | 90.85 | 38.25 | 2942 | 50.16 | 48.87 | −2.46 | 22.2 | 52.54 | 4.52 | 22.01 |
| NMH | 96.42 | 36.43 | 2796 | 55.54 | 54.30 | −2.23 | 17.24 | 53.51 | −3.66 | 17.53 |
| GEM4 | 94.78 | 36.30 | 2957 | 61.76 | 55.26 | −10.52 | 13.57 | 56.97 | −7.74 | 12.57 |
| DCD | 95.37 | 37.85 | 3190 | 104.00 | 98.31 | −5.47 | 29.43 | 105.38 | 1.33 | 23.10 |
| HTTL | 96.73 | 37.35 | 2867 | 107.94 | 123.67 | 14.57 | 38.85 | 123.21 | 14.15 | 35.36 |
| GH | 97.43 | 37.23 | 2877 | 161.24 | 160.28 | −0.60 | 31.44 | 158.83 | −1.50 | 26.12 |
| NCT | 94.57 | 35.87 | 3966 | 182.31 | 182.35 | 0.02 | 35.08 | 185.47 | 1.74 | 34.19 |
| WL | 98.48 | 36.92 | 2959 | 222.26 | 243.09 | 9.38 | 56.33 | 231.36 | 4.10 | 48.45 |
| DLH | 97.37 | 37.37 | 2988 | 228.68 | 226.20 | −1.08 | 31.62 | 223.36 | −2.32 | 24.75 |
| DL | 98.11 | 36.30 | 3190 | 240.73 | 246.18 | 2.26 | 48.60 | 247.77 | 2.93 | 40.58 |
| CHWS | 98.12 | 36.23 | 3273 | 244.97 | 290.87 | 18.74 | 63.93 | 289.24 | 18.07 | 58.15 |
| XRH | 98.15 | 36.42 | 3143 | 252.91 | 247.61 | −2.11 | 66.42 | 247.41 | −2.17 | 59.82 |
| XRD | 97.87 | 35.97 | 3100 | 285.18 | 271.46 | −4.81 | 54.38 | 275.56 | −3.37 | 52.80 |
| KE | 97.7 | 35.95 | 3269 | 307.43 | 304.7 | −0.89 | 62.78 | 308.31 | 0.29 | 63.06 |
| SGB | 98.58 | 37 | 3168 | 332.05 | 316.19 | −4.78 | 57.49 | 305.51 | −7.99 | 51.4 |
| CHH | 98.57 | 37.05 | 3351 | 432.3 | 449.37 | 3.95 | 74.96 | 426.29 | –1.27 | 68.8 |
| Average | -- | -- | -- | 170.72 | 173.02 | –0.08 | 37.51 | 171.52 | 0.11 | 34.22 |
| Region Name | Area (103 km2) | Interpolated Precipitation by Gauges | Original 3B42RT | Corrected 3B42RT | Original 3B43 | Corrected 3B43 |
|---|---|---|---|---|---|---|
| LE | 19.3 | 29.65 | 43.79 | 22.42 | 39.43 | 25.3 |
| MY | 31.3 | 42.43 | 67.72 | 55.27 | 62.22 | 62.48 |
| GEM | 69.4 | 65.64 | 162.73 | 118.69 | 157.5 | 114.27 |
| DCD | 21.3 | 69.55 | 100.92 | 128.46 | 97.61 | 126.22 |
| XJ | 17.4 | 74.31 | 114.1 | 131.95 | 108.28 | 133.53 |
| ZD | 4.8 | 83.98 | 239.7 | 171.39 | 238.79 | 141.03 |
| GS | 17.9 | 86.57 | 112.33 | 221.02 | 107.09 | 208.24 |
| QML | 6.5 | 157.57 | 275.74 | 363.65 | 273.22 | 321.82 |
| DLH | 22.7 | 168.45 | 190.01 | 369.43 | 192.47 | 343.08 |
| DL | 43.8 | 183.01 | 203.43 | 302.37 | 205.56 | 273.62 |
| WL | 10.4 | 259.57 | 171.17 | 299.41 | 185.38 | 288.63 |
| MD | 4.7 | 292.9 | 354.29 | 602.71 | 358.21 | 523.32 |
| The entire basin | 269.4 | 104.34 | 148.45 | 186.01 | 146.26 | 174.76 |
| Station Name | Gauged | Original 3B42RT | Corrected 3B42RT | Original 3B43 | Corrected 3B43 |
|---|---|---|---|---|---|
| GH | −2.21 | −0.23 | −0.18 | −0.27 | −0.85 |
| XRD | −1.32 | 0.01 | −0.02 | −0.06 | −0.07 |
| DCD | −0.63 | −1.55 | −0.75 | −1.07 | −0.77 |
| KE | −0.62 | −0.37 | −0.40 | −0.47 | −0.59 |
| DLH | −0.32 | −0.94 | −0.91 | −0.27 | −0.33 |
| HTTL | −0.15 | −1.05 | −0.63 | 0.13 | −0.10 |
| CHWS | 0.09 | 2.78 | 2.87 | 0.58 | 0.67 |
| LH | 0.13 | 0.91 | 0.05 | 1.10 | 0.26 |
| XZH | 0.14 | 1.44 | 0.39 | 1.94 | 0.57 |
| DL | 0.23 | 0.01 | 0.02 | 0.94 | 1.05 |
| GEM4 | 0.58 | 1.87 | 0.88 | 1.29 | 0.58 |
| NMH | 0.63 | 1.91 | 0.95 | 2.33 | 1.29 |
| HX | 0.89 | 2.08 | 0.69 | 2.23 | 0.85 |
| GEM | 0.93 | 1.87 | 0.84 | 1.29 | 0.54 |
| NCT | 1.31 | 0.63 | 0.32 | 0.86 | 0.35 |
| MY | 1.45 | 0.17 | 0.06 | 0.41 | 0.13 |
| SGB | 2.43 | 4.25 | 3.95 | 3.22 | 3.03 |
| WL | 4.71 | 3.14 | 2.77 | 2.28 | 2.69 |
| XRH | 3.21 | 2.21 | 2.29 | 2.94 | 3.06 |
| CHH | 10.45 | 0.19 | 0.18 | 1.16 | 1.78 |
| Average | 1.10 | 0.97 | 0.67 | 1.03 | 0.71 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Wang, Z.; Xia, T. Mapping Areal Precipitation with Fusion Data by ANN Machine Learning in Sparse Gauged Region. Appl. Sci. 2019, 9, 2294. https://doi.org/10.3390/app9112294
Xu G, Wang Z, Xia T. Mapping Areal Precipitation with Fusion Data by ANN Machine Learning in Sparse Gauged Region. Applied Sciences. 2019; 9(11):2294. https://doi.org/10.3390/app9112294
Chicago/Turabian StyleXu, Guoyin, Zhongjing Wang, and Ting Xia. 2019. "Mapping Areal Precipitation with Fusion Data by ANN Machine Learning in Sparse Gauged Region" Applied Sciences 9, no. 11: 2294. https://doi.org/10.3390/app9112294
APA StyleXu, G., Wang, Z., & Xia, T. (2019). Mapping Areal Precipitation with Fusion Data by ANN Machine Learning in Sparse Gauged Region. Applied Sciences, 9(11), 2294. https://doi.org/10.3390/app9112294





