A Critical Review of Spatial Predictive Modeling Process in Environmental Sciences with Reproducible Examples in R

Abstract

Spatial predictive methods are increasingly being used to generate predictions across various disciplines in environmental sciences. Accuracy of the predictions is critical as they form the basis for environmental management and conservation. Therefore, improving the accuracy by selecting an appropriate method and then developing the most accurate predictive model(s) is essential. However, it is challenging to select an appropriate method and find the most accurate predictive model for a given dataset due to many aspects and multiple factors involved in the modeling process. Many previous studies considered only a portion of these aspects and factors, often leading to sub-optimal or even misleading predictive models. This study evaluates a spatial predictive modeling process, and identifies nine major components for spatial predictive modeling. Each of these nine components is then reviewed, and guidelines for selecting and applying relevant components and developing accurate predictive models are provided. Finally, reproducible examples using spm, an R package, are provided to demonstrate how to select and develop predictive models using machine learning, geostatistics, and their hybrid methods according to predictive accuracy for spatial predictive modeling; reproducible examples are also provided to generate and visualize spatial predictions in environmental sciences.

1. Introduction

Spatial predictions of environmental variables are increasingly required in environmental sciences and management. Accurate spatially continuous data are required for environmental modeling, and for evidence-based environmental management and conservation. Such data are, however, usually not readily available and they are difficult and expensive to acquire, especially in areas that are difficult to access (e.g., mountainous or marine regions). In many cases, the spatial data of environmental variables are collected from point locations. Thus, spatial predictive methods are essential for generating spatially continuous predictions of environmental variables from the point samples. Moreover, predictive methods are increasingly being used to generate spatial predictions across various disciplines in environmental sciences [1,2,3,4,5,6] in parallel to recent advances in (1) computing technology and modeling techniques [7,8,9], and (2) data acquisition and data processing using remote-sensing techniques and geographic information systems. These advancements resulted in increasingly more environmental variables available for spatial predictive modeling. Consequently, more sophisticated spatial predictive modeling approaches are needed to deal with a large number of predictive variables.

Accuracy of spatial predictive model(s) is critical as it determines the quality of their predictions that form the scientific evidence to inform decision- and policy-making. Therefore, improving the accuracy by choosing an appropriate method and then identifying and developing the most accurate predictive model(s) is essential. It is often difficult to select an appropriate method for any given dataset because spatial predictive methods may be data- or even variable-specific and many factors need to be considered [10,11]. Although the development of hybrid methods of machine learning and geostatistics, and their application considerably improved predictive accuracy, these methods may also be data- or variable-specific [12,13,14]. For spatial predictive modeling, “no free lunch theorems” [15] are also applicable.

Furthermore, even with the right predictive method, it is a challenging task to identify and develop the most accurate predictive model(s). This is because the spatial predictive modeling process involves many factors or components [10,16,17]. In fact, only a portion of such factors were considered in many previous studies, which often led to sub-optimal or even misleading predictive models [11,18]. This not only presents an opportunity for scientists to develop and improve their predictive models, but also highlights the challenge of selecting relevant predictive variables from a large number of available predictive variables to form the most accurate predictive model. Heavy computations are often involved in identifying and selecting accuracy-improved predictive models for given datasets when the number of predictive variables is large, although high-performance computing facilities may be able to significantly alleviate this challenge.

This study aims to assist spatial modelers and scientists by critically reviewing the spatial predictive modeling process, developing guidelines for selecting the most appropriate spatial predictive methods and identifying and developing the most accurate predictive model to generate spatial predictions. In this study, I focus on spatial predictive models or spatial predictive modeling for generating spatially continuous predictions rather than on other models (e.g., inferential model) as discussed previously [19]. Consequently, the term accuracy in this study refers to the accuracy of predictive model(s) based on validation, and the term uncertainty refers to prediction uncertainty generated by predictive model(s). In this study, the term accuracy is used interchangeably with predictive accuracy. Furthermore, in this study, I mainly focus on the predictive methods for numerical data that are usually encountered in environmental sciences, with a brief discussion on categorical data. In this study, the following nine major components of spatial predictive modeling are identified and reviewed: (1) sampling design, sample quality control, and spatial reference systems; (2) selection of spatial predictive methods; (3) pre-selection of predictive variables; (4) exploratory analysis for variable selection; (5) parameter selection for relevant methods; (6) variable selection; (7) accuracy and error measures for predictive models (numerical vs. categorical); (8) model validation; and (9) spatial predictions, prediction uncertainty, and their visualization. In addition, reproducible examples using spm [20], an R package for machine learning, geostatistics, and their hybrid methods, are employed to demonstrate how to select and develop predictive models based on predictive accuracy for spatial predictive modeling; reproducible examples are also provided to generate and visualize spatial predictions in environmental sciences.

2. Sampling Design, Sample Quality Control, and Spatial Reference Systems

2.1. Sampling Design

Although samples are usually collected, stored, and ready to use for spatial predictive modeling, sometimes samples are not available and need to be collected. In the latter situation, a sampling design needs to be produced. In this study, I focus on sampling designs over space. To collect samples from a survey area for a certain survey purpose, a sampling design is an important step and must be created. A good sampling design ensures that data collected from a survey are capable of answering relevant research questions. Better designs, such as spatially stratified sampling designs, will also be as precise and efficient as possible [21,22]. Many methods were developed to generate sampling designs [23,24,25,26]. They typically fall into four main categories: (1) non-random sampling design; (2) unstratified random sampling design; (3) stratified random sampling design; and (4) stratified random sampling design with prior information.

The non-random sampling design can be ad hoc sampling based on expert knowledge, purely opportunistic when a certain type of environmental condition becomes available, or systematic sampling. This type of sampling design was applied to many surveys [27,28,29]. For spatial predictive modeling, this method is not recommended for future studies. However, an interesting comparison of non-random sampling designs was reported for spatial predictive modeling [26]; it may provide some useful clues for sampling designs (e.g., lattice plus close pairs) for spatial predictive modeling.

The unstratified random sampling design is that sampling locations are randomly selected. This can be (1) an unstratified equal probability design, or (2) an unstratified unequal probability design [30,31]. This type of sampling design is not recommended for spatial predictive modeling studies because (1) spatial information is available for sampling design and thus spatially stratified sampling design should be used as discussed below, and (2) it may even be over-performed by the non-random design (i.e., lattice design) [26].

The stratified random sampling design is often used when additional information is available. Such information can be spatial (or location) information, elevation, bathymetry, or geomorphological information. For spatial predictions, such information is important and should be considered when designing a survey for a region. A few recently developed randomized spatial sampling procedures were reviewed and compared using simple random sampling without replacement as a benchmark for comparison [22]. This study provided some empirical evidence for the improvement of sampling efficiency from using these designs and provided some guidance for choosing an appropriate spatial sampling design [22]. Furthermore, some R packages, such as spsurvey [31], GSIF [32], spcosa [33], clhs [34], and BalancedSampling [35], were developed for this type of sampling design. The stratified random sampling designs with spatial information (i.e., spatially stratified sampling design) are increasingly being used in practice [28,36,37].

The stratified random sampling design with prior information is a new development for sampling over a space. It incorporates the locations of legacy sites into new spatially balanced survey designs to ensure spatial balance among all sample locations [21]. It can be seen as a stratified unequal probability design. An R package, MBHdesign, was developed for this method [38].

2.2. Sample Quality Control

Sample quality is vitally important because samples provide the fundamental information for spatial predictive modeling. Many factors may affect sample quality and they are usually dataset-specific [39,40]. Consequently, relevant factors need to be identified for each dataset and then relevant data quality control (QC) criteria need to be developed to QC the dataset [39,40] prior to undertaking spatial predictive modeling. For example, in Geoscience Australia’s Marine Samples Database (MARS; http://dbforms.ga.gov.au/pls/www/npm.mars.search), seabed sediment samples were initially quality controlled prior to and after entering the database according to various criteria [12,41]. However, the quality of the samples was still affected by many factors, including data credibility (e.g., non-dredge), data accuracy (e.g., non-positive bathymetry), completeness (e.g., no missing values), etc.; hence, data quality control approaches were developed to QC the samples of seabed mud content and sand content [12,41]. These approaches may provide examples about how to identify relevant factors and develop possible data QC criteria for a given dataset. In some instances, data noise may result from repeated measurements, and certain rules may need to be developed to clean such samples based on professional knowledge [42]. Moreover, exploratory analysis can be used to further detect abnormal samples, as detailed in Section 5.

2.3. Spatial Reference Systems

To generate spatial predictions (i.e., spatially continuous data) for a region using spatial predictive models, two types of georeferenced data are required: (1) point samples of response and predictive variables; and (2) grid data of predictive variables. Such georeferenced data are often stored according to various spatial reference systems [43]. The spatial reference system used to project or store the spatial information is often assumed to have certain effects on the performance of predictive models; thus, in practice, various spatial reference systems were used to minimize such effects [43]. When a study area is small and within one particular UTM zone, spatial data are often projected using either the UTM zone or an appropriate projection system; when the study area is spanning multiple UTM zones, the existing geographic coordinate system (i.e., WGS84) or another appropriate projection system can be used.

Although the spatial reference system by which the spatial information is stored is often considered as a potential source of error for spatial predictive modeling, a series of studies demonstrated that the effects of spatial reference systems on the performance of spatial predictive methods (i.e., inverse distance weighting and ordinary kriging) are negligible for areas at various latitudinal locations (up to 70 dd) and spatial scales (i.e., regional and continental) [43,44,45]. Therefore, it was recommended that spatial reference system selection and re-projection can be removed for spatial predictive modeling for areas with latitude less than 70 dd, and spatial data can be modeled in WGS84 or the spatial projection system already used for the data. Although new spatial reference systems (e.g., DGGS [46]) may be developed to remedy various limitations of existing ones, the above recommendation may still be applicable as discussed previously on why the effects of spatial reference systems on the predictive accuracy are negligible [43,44,45].

3. Selection of Spatial Predictive Methods

3.1. Spatial Predictive Methods

For spatial predictive modeling, there are many methods available [3]. Previously, over 20 spatial predictive methods were grouped into (1) non-geostatistical methods (e.g., inverse distance weighting (IDW)), (2) geostatistical methods (e.g., ordinary kriging (OK)), and (3) combined or hybrid methods [10]. Collectively, these methods are largely non-machine learning methods and a small portion of these methods, like regression tree (RT) and linear regression models (LM), use secondary information.

When sufficient secondary information is available, a number of other methods could be used. These methods include traditional statistical methods, machine learning methods, the hybrid methods of traditional statistical methods and geostatistical methods, and the hybrid methods of machine learning and geostatistical methods (

Table 1. Spatial predictive methods using predictive variables [6,12,41,48,49,50,51,52,53,54,55].

Non-Machine Learning Method and Hybrid Methods		Machine Learning Method and Hybrid Methods
Non-machine learning method	Hybrid methods	Machine learning method	Hybrid methods
Generalized additive models		Cubist	Cubist and OK (cubistOK)
Generalized least squares trend estimation (GLS)	GLS and OK	Generalized boosted regression modeling (GBM)	GBM and IDS (GBMIDS)
Generalized linear models (GLM)	GLM and IDW (GLMIDW)		GBM and OK (GBMOK)
	GLM and OK (GLMOK)	General regression neural network (GRNN)	GRNN and IDS (GRNNIDS)
GLM with lasso or elastic net regularization			GRNN and OK (GRNNOK)
	Linear models and OK	Multivariate adaptive regression splines
	RT and IDS (RTIDS)	Naïve Bayes
	RT and OK (RTOK)	Random forest (RF)	RF and IDS (RKIDS)
			RF and OK (RKOK)
		Support vector machine (SVM)	SVM and OK (SVMOK)
			SVM and OK (SVMIDS)

). These methods were applied or compared in various spatial predictive modeling studies [12,41,47,48,49,50,51,52,53,54,55]. Of these methods, random forest (RF), hybrid method of RF and OK (RFOK), and hybrid method of RF and IDW (RFIDW) were among the most accurate methods in these applications. Generalized boosted regression modeling (GBM), hybrid method of GBM and OK (GBMOK), and hybrid method of GBM and IDW (GBMIDW) showed great potential based on our unpublished study. In the current study, these methods are presented in three main groups: (1) non-machine learning methods; (2) machine learning methods; and (3) the hybrid methods.

3.2. Selecting Spatial Predictive Methods

Selection of appropriate spatial predictive methods for a response variable (or dependent variable, or primary variable in geostatistics) is critical. For data without predictive variables, geostatistical methods are the only methods that can be used. Method selection was discussed and guidelines were developed for using geostatistical methods in various studies [16,56,57,58,59,60,61]. A decision tree was developed for selecting the most appropriate method from a pool of 25 spatial predictive methods according to the availability and nature of data and the expected predictions, together with the features of each method [10]. However, it was argued that there was no simple answer regarding the choice of appropriate geostatistical methods, because the hallmark of a good geostatistical modeling work is customization of the approach to the dataset at hand [56]. This suggests that “no free lunch theorems” [15] are also applicable for spatial predictive modeling using geostatistical methods. Joint application of two spatial predictive methods might produce additional benefits such as the combined procedures in previous studies [10,62,63,64].

For data with predictive variables, there are many options available. It is often difficult to select an appropriate method because the performance of spatial predictive methods depends on many factors, including the assumptions and properties of each method, the nature and spatial structure of data for the response variable, sample size and distribution, the availability of predictive variables, availability of software, computational demands, and many other factors [10,11]. All of these factors need to be considered when making an appropriate selection.

Moreover, if more than one method can be applied, model comparison techniques such as cross-validation in combination with the measures of predictive error or accuracy can be used to select a method. This selection technique not only selects the most appropriate method but also the most accurate predictive model that can maximize the predictive accuracy [12,65,66]. This selection technique can be applied to methods irrespective of whether they use predictive variables.

4. Pre-Selection of Predictive Variables

Predictive variables are termed predictor variables, independent variables, predictors, and features. They are also called secondary variables/information in geostatistics. They are essential for spatial predictive methods that use predictive variables.

4.1. Principles for Pre-Selection of Predictive Variables and Limitations

Principles for pre-selecting predictive variables may change with disciplines. For environmental sciences, the main principle is that predictive variables need to be closely related to the variable to be predicted (i.e., the response variable) [67,68]; ideally, they should be causal variables, or variables directly caused by the response variable (e.g., optical reflectance of vegetation types, backscatter of seabed substrates). They are usually identified based on expert or professional knowledge. However, in many cases, it is hard to know what the causal variable(s) is (are) for a response variable. Proxy (or surrogate) variables are often used instead of causal variable for spatial predictive modeling. Again, they are usually identified based on expert or professional knowledge [69]. Certainly, predictive models can use causal variables, proxy variables, or both if causal variables are not all available.

When the accuracy of a resultant predictive model is unexpectedly poor, then we may need to consider that we may have missed some important predictive variables, for which we may have no knowledge or even awareness (e.g., hidden variables [70]). Further actions are required to expand the professional knowledge pool in order to identify such possible predictive variables.

For spatial predictive modeling, the selection of potential predictive variables is even more challenging. This is because the selection could be constrained by certain factors. For example, predictive variables need to be continuously available for a target region. Spatial resolution is also a critical issue as the resolutions of various predictive variables need to meet the desired resolution for the final predictions, although they can be rescaled. Sometimes, even though we know the possible causal predictive variables based on expert or professional knowledge, they may not meet these requirements and cannot be used for spatial predictive modeling. This is particularly true in marine environmental sciences.

4.2. Predictive Variables for Environmental Sciences

For terrestrial environmental modeling, many predictive variables are available. Many previous applications provided examples of variables used for terrestrial environmental modeling [13,42,49,50,51,53,67,71,72].

In contrast, the information of predictive variables is often scarce for marine environmental modeling. In many cases, proxy variables are usually used for predictive modeling [69,73]. For example, to predict the spatial distribution of seabed sediments for Australian Exclusive Economic Zone (AEEZ) at a resolution of 0.01 or 0.0025 degrees, only a few predictive variables were available for the whole AEEZ [12,41,74] (

Table 2. A list of predictive variables used for some marine environmental variables.

No	Predictive Variables	Seabed Sediment/Grain Size	Seabed Hardness	Sponge Species Richness	Window/Kernel Size(s)
1	Longitude (long)	yes	yes	yes
2	Latitude (lat)	yes	yes	yes
3	Distance to coast (dist)	yes		yes
4	Bathymetry (bathy)	yes	yes	yes
5	Local Moran’s I from bathymetry	yes	yes	yes	yes
6	Mean curvature	yes			yes
7	Planar curvature	yes	yes	yes	yes
8	Profile curvature	yes	yes	yes	yes
9	Relief	yes	yes	yes	yes
10	Rugosity (or surface, surface complexity)	yes	yes	yes	yes
11	Slope	yes	yes	yes	yes
12	Topographic or bathymetric position index (tpi or bpi)	yes	yes	yes	yes
13	Fuzzy morphometric features	yes			yes
14	Backscatter (bs) 10–36	yes	yes	yes
15	Entropy from bs			yes	yes
16	Homogeneity from bs		yes	yes	yes
17	Local Moran’s I from bs		yes	yes	yes
18	Prock from bs		yes
19	Variance from bs		yes	yes	yes
20	Suspended particulate matter	yes
21	Mean tidal current velocity	yes
22	Peak orbital velocity of waves at seabed	yes
23	Roughness from bathy *	yes
24	Roughness from bs *	yes
25	Sobel filter from bathy #	yes

* The difference between the minimum and maximum of cell and its eight neighbors [48]. ^# A directional filter that emphasizes areas of large spatial frequency (edges) running horizontally (X) or vertically (Y) across the image [48].

). For spatial predictions over smaller areas, quite often more predictive variables became available at desired resolution such as for seabed sediment [4,75,76,77], seabed hardness [78,79,80], and sponge species richness [6,81] (Table 2). Bathymetry and backscatter were also used to predict seabed sediment at local scale [82]. Some derived information may be used as predictive variables. For example, in Table 2, predictive variables 5–13 were derived from bathymetry (bathy), while predictive variables 15–19 were derived from backscatter (bs). Some other variables were used for seabed grain size at small scale [48]. In addition, many variables were reviewed [69,83] and could be used for marine environmental modeling. Fuzzy geomorphic features were also used for spatial predictive modeling at local scales [77,84].

5. Exploratory Analysis for Variable Pre-Selection

5.1. Non-Machine Learning Methods

Exploratory analysis is often used to detect the relationships between the response variable and predictive variables for non-machine learning methods, such as LM, generalized linear models (GLM), and kriging with an external drift (KED). By applying such analysis, people intend to find data nature and structure [85]. Key issues may include the identification of (1) outliers, (2) homogeneity in variance of response variable, (3) data distribution of response variables including normality, (4) collinearity (i.e., the correlation among predictive variables), (5) relationships or response curves of response variable to predictive variables, (6) how strong the relationships are between response variable and predictive variables, (7) possible interactions among predictive variables, (8) independence of a response variable, whether temporally, spatially, or both, and (9) source of random errors, which may lead to a mixed-effect model or additional predictive variable(s) [71]. On the basis of the above analyses, certain actions can be taken to deal with relevant samples or variables. For instance, some predictive variables can be removed if their correlations with the response variable are low. However, it would be wise to let the variable selection process determine which variables should be removed because some variables may be important predictive variables even with low correlations. Highly correlated predictive variables, usually determined based on correlation coefficient (r) or variance inflation factor (VIF), can also be eliminated to reduce the collinearity, although caution should be taken for this exercise [9,86]. Relevant issues about collinearity were also discussed [87]. Some predictive variables may need to be specified to their second or third orders if a non-linear relationship is detected. Moreover, some interactions may need to be considered and tested.

5.2. Machine Learning Methods and Hybrid Methods

For machine learning methods, exploratory analysis is useful for understanding data and interpreting modeling results [78]. However, some roles of exploratory analysis for non-machine learning methods are no longer needed for machine learning methods. This is because machine learning methods, like RF, are free of assumptions on the data distribution and can handle non-linear relationships and interactive effects [88,89]. They can also handle highly correlated predictive variables [6,47]. Furthermore, the use of highly correlated predictive variables is encouraged for RF because they may be able to make a meaningful contribution to improving predictive accuracy [6].

5.3. Hybrid Methods

For the hybrid methods, exploratory analysis is as useful as for the aforementioned methods. The residuals of a detrending method (e.g., GLM, RF) are assumed to be normal if kriging methods are applied. Thus, the residuals need to be analyzed to check this assumption [12,41].

6. Parameter Selection

6.1. Parameter Selection for Non-Machine Learning Methods

For non-machine learning methods, I mainly focus on two commonly used methods [11], IDW and kriging (e.g., OK). For IDW, it is really dependent on the selection of appropriate values for a power parameter and the number of nearest observations, which can be selected based on their resultant predictive accuracy [41,90]. The smoothness of the estimated surface increases as the value of power parameter increases [91]; however, manipulating the power parameter to smooth the predictions and to produce visually pleasant maps does not warrant the quality of the resultant predictions and is not recommended.

For kriging methods, a number of parameters, including window size, and isotropy and anisotropy of data, need to be considered, as well as the variogram model and its parameters. Data transformation needs to be considered when the data are skewed and anisotropic. Three methods of data transformation (i.e., logarithms, standardized rank order, and normal scores) can be employed to reduce the skewness [74,92]. Some other methods, such as Box–Cox transformation [82], arcsine [88], square-root transformation [47], and double square root or square root and log [12], can be used to normalize the data. The selection of these transformation and normalization methods is largely data-dependent and careful examination should be taken. The selection can also be determined according to their effects on the predictive accuracy.

In addition, for anisotropy, non-stationary methods like KED should be used in cases with a general anisotropy or trend (i.e., drift) [75]. If different types of non-stationarity exist, application of different spatial predictive methods to each type may improve predictive accuracy [93].

The parameter selection for these methods can be determined according to the predictive accuracy of resultant predictive models. This is demonstrated in Section 11.

6.2. Parameter Selection for Machine Learning Methods

For machine learning methods, RF and GBM are considered. For RF, relevant parameters are mtry, ntree, and so on [94], while, for GBM, these include n.trees, learning.rate, interaction.depth, bag.fraction, and so on [95]. Some commonly used default parameter values can be used as they are quite often optimal [94,96], except the distribution parameter for GBM. The distribution parameter for GBM should be based on data type of the response variable; for example, Poisson should be used for count data. Relevant parameters can also be selected based on cross-validation [41,48,96].

6.3. Parameter Selection for Hybrid Methods

The parameter selections for the above non-machine learning methods and machine learning methods are equally applicable to relevant hybrid methods.

7. Variable Selection

For machine learning methods, variable selection is termed feature selection, while, for non-machine learning methods, it is often called model selection. However, model selection often leads to the most parsimonious fitted model rather than the most accurate predictive model [6]. In this study, we use the term “variable selection” for both non-machine learning and machine learning methods to identify and develop the most accurate spatial predictive model(s).

Variable selection is important for many predictive methods, although it is not required for all methods. For instance, classification and regression trees [97] and LIVES [98] are exempt from variable selection. However, as per all other methods, they assume that the predictive variables used are informative and not misleading because they treat each predictive variable as equally important. Thus, misleading predictive variables may considerably reduce predictive accuracy as discussed previously [98]. The variable selection procedure for machine learning methods and their hybrid methods is fundamentally different from the procedure for non-machine learning methods [47,79,99]. For geostatistical methods like IDW and OK, no variable selection is required, and it is really about the selection of appropriate values for relevant parameters, as discussed in Section 6. In this section, I focus on the following three methods: (1) GLM; (2) RF; and (3) GBM. This is because of their wide applications, robustness, or the recent developments in variable selection techniques for these methods.

For GLM, there are many methods available in R for variable selection [100,101,102,103]. These methods may include (1) stepAIC or step; (2) dropterm, drop1, or add1; (3) anova; (4) regsubsets; and (5) bestglm [100,102,103]. The application of these methods for spatial predictive modeling can be seen in recent studies [6,104]. Variables selected based on these methods may form the most parsimonious model, but the model may have low predictive accuracy or even be misleading [6,104], with the exception that bestglm is promising if cross-validation, instead of Akaike’s information criterion (AIC) or Bayesian information criterion (BIC), is used for information criteria [104]. Alternatively, the variable selection for GLM can also be based on variables selected by other method such as RF [71]. It was found that traditional variable selection methods are unsuitable for identifying GLM predictive models, and joint application of RF and AIC can select accuracy-improved predictive models [6]. This highlights the importance of differentiating variable selection for predictive modeling [6] from variable selection for hypothesis testing [99] or inferential modeling [19]. The common mistakes associated with incorrectly distinguishing data analytic types were briefly summarized and discussed previously [19].

For RF, variable selection methods may include (1) variable importance (VI) [78], (2) averaged variable importance (AVI) [79], (3) Boruta [105], (4) knowledge informed AVI (KIAVI) [6,79], (5) recursive feature selection (RFE) [106], and (6) variable selection using RF (VSURF) [107]. Of these methods, KIAVI is recommended because it outperforms all other variable selection methods [6,79,104,108].

For GBM, variables can be selected in terms of the relative influence [95,108]. The recursive feature selection [106] can also be used for variable selection.

Two concepts were proposed for variable selection: important and unimportant predictive variables based on the predictive accuracy [6,79]. They were defined as follows:

• Important variable based on the predictive accuracy (IVPA).
  This refers to the variable for which exclusion during the variable selection process would reduce the accuracy of a predictive model based on cross-validation. It may be more appropriate to call it predictive accuracy boosting variable (PABV).
• Unimportant variable based on the predictive accuracy (UVPA).
  This refers to variables for which exclusion during the variable selection process would increase the accuracy of a predictive model based on cross-validation [6,79]. It may be more precise to call it predictive accuracy reducing variable (PARV).

Application of relevant variable selection methods and concepts can further improve the accuracy of predictive models [6,79]; this is demonstrated in Section 11. Although these concepts were developed based on RF and its hybridization with geostatistical methods, they can be equally applied to any other predictive methods.

8. Accuracy and Error Measures for Predictive Models

8.1. Relationship between Observed, Predicted, and True Values

Predictive accuracy is about the differences between observed and predicted values that are derived based on validation methods [18]. However, it is often questioned what the differences between the predicted values and true values are. Since the true values are mostly unknown, the observed values are used to validate predictive models. For an observed value, it may be again different from its corresponding true value. The difference between the true value and observed value is the error associated with the observed value. Let us refer to this error as an observational error that is the sum of random error associated with observed variable, sampling error, and measuring error. The sampling and measuring errors are the sum of errors resulting from various factors that may affect the accuracy of observation (i.e., measurement) and change with the variable observed. Let us take seabed sediment as an example; the factors may include sampling design, the position accuracy of survey vessel, equipment used for sample collection, field operation, sample storage, sample processing procedure and analysis in laboratory, data entry, etc. However, how much error can be attributed to each of these factors is unknown in most cases. Hence, we have to use observed and predicted values to assess the predictive accuracy in practice.

8.2. Error and Accuracy Measures of Predictive Models

Many error and accuracy measures were developed to assess the accuracy of predictive models for numerical data [65,109,110]. Some of these error and accuracy measures were assessed and their limitations were previously discussed [3,18]. Of these error and accuracy measures, VEcv (i.e., variance explained by a predictive model based on cross-validation) measures how accurate the predictive model is and was proven to be independent of unit, scale, data mean, and variance [18,111], while root mean squared error (RMSE) measures how wrong the predictive model and the resultant predictions can be. Therefore, VEcv and RMSE are recommended for numerical predictions. Legates and McCabe’s E1 (E1) was recommended for numerical data as well [111]. The commonly used measure, r or r², is not recommended because it is an incorrect measure of predictive accuracy [111].

For categorical data, correct classification rate (CCR), kappa (kappa), sensitivity (sens), specificity (spec), and true skill statistic (TSS) are often recommended [112,113]. RMSE is also used for presence and absence data [114]. One commonly used measure, area under the curve (AUC) (or receiver operating characteristics (ROC)), is not recommended for reasons previously highlighted [112,115].

9. Model Validation

9.1. Model Validation Methods

The accuracy of predictive models is critical as it determines the quality of the resultant predictions. The accuracy is often assessed based on model validation methods that may include the following:

• Hold-out validation;
• K-fold cross-validation;
• Leave-one-out cross-validation;
• Leave-q-out cross-validation;
• Bootstrapping cross-validation;
• Using any new samples that are not used for model training.

In environmental sciences, the most commonly used validation methods are hold-out and leave-one-out [18]. However, of these validation methods, five- or 10-fold cross-validation was recommended [7,116].

9.2. Randomness Associated with Cross-Validation Methods

Although a five- or 10-fold cross-validation was recommended to evaluate the performance of spatial predictive models [116], the datasets are randomly generated for each fold of the cross-validation change when the process is repeated. Thus, the randomness associated with the cross-validation would produce predictive accuracy or error measures that change with each iteration of the cross-validation [47]. To reduce the influence of the randomness on predictive accuracy (i.e., to stabilize the resultant performance measures), the cross-validation needs to be repeated (e.g., 100 times) [47,74,78]. The choice of this iteration number is data-dependent and can be determined based on the method used in previous studies [47,78].

10. Spatial Predictions, Prediction Uncertainty, and Their Visualization

10.1. Spatial Predictions

In spatial predictive modeling, the goal is not only to develop the most accurate predictive model, but more importantly to generate spatial predictions. The spatial predictions are usually produced using the most accurate predictive model developed according to the above procedures. To make predictions, in addition to the spatial predictive model, we need relevant information of each model predictive variable to be available at each grid cell at a desired resolution. When all this information is prepared, the spatial predictions can then be generated. The predictions contain three columns, i.e., longitude, latitude, and predictions. Sometimes, uncertainty of the predictions can be produced.

10.2. Prediction Uncertainty

Prediction uncertainty in environmental modeling may refer to various aspects of the modeling process and is used to encompass many concepts [117,118,119,120]. It can result from various sources or factors as previously discussed [17,120,121]. In this study, the uncertainty which is produced by a predictive model is about spatial predictions. Prediction uncertainty is increasingly required for decision-making and many methods are used to produce such uncertainty. In this study, I focus on the uncertainty produced by some commonly used methods: OK, LM, and RF.

For OK, prediction variances can be produced [58]. However, it was shown that the variances produced are independent of the actual predicted values [122]. Thus, the resulting variances should not be used to measure uncertainty, although many studies used them for such purpose. Since they reflect the variations in spatial departures among samples, they can be used as good indicators where samples are sparse and, thus, may provide useful information for selecting future sampling locations.

For LM, prediction uncertainty (i.e., prediction intervals) produced are much wider than confidence intervals of a model fitted [101]. Such uncertainty, however, has little to do with the predictive accuracy of the model. For instance, it was found that the models developed according to goodness of fit could be misleading when they were used as predictive models [6]; hence, its prediction uncertainty could also be misleading, and further studies are recommended.

For RF, many types of uncertainty could be produced, which actually reflect the difference in sampling strategies [123,124,125,126]. For example, prediction uncertainty produced for RF in a previous study based on Monte Carlo resampling [127] was, in fact, measuring the variation in predictions among individual trees rather than by RF. A further example for RF is that an ensemble of equally probable realizations was generated and the differences amongst the realizations were used as a measure of uncertainty [128]. This type of uncertainty only measures the differences among the results of various runs of RF, that is, measuring the difference resulted from the randomness associated with each run. Hence, these values do not relate to predictive accuracy and do not measure prediction uncertainty.

In addition, for any of the spatial predictive methods above, predictive errors based on validation can be produced for a predictive model developed. However, this leads to only one error value, and all predictions would have the same uncertainty value if it is used as an uncertainty measurement [129].

It is apparent that the uncertainty values produced above are either not measuring prediction uncertainty, or they depend on various factors as discussed above. This consequently results in the need to question the uncertainty of uncertainty. In short, how to assess prediction uncertainty needs further study. Any uncertainty measures that can incorporate the information of predictive accuracy are worth further investigation and recommended for future studies.

10.3. Visualization

Spatial predictions can be visualized using various tools, most commonly ArcGIS and QGIS. The function, spplot, in R is often used to plot the distribution of spatially continuous predictions [59]. The R package, raster, can also be used for such purpose [130]. Joint application of R and Google Earth can be used to visualize the predictions. In this study, I demonstrate how to use the latter approach along with spplot to visualize the predictions as below.

11. Reproducible Examples for Spatial Predictive Modeling

In this section, reproducible examples using spm, an R package, are provided to demonstrate how to select and develop a predictive model according to the guidelines and recommendations provided in the previous sections for spatial predictive modeling in environmental sciences. The predictive model to be used was developed using RFOK [74], where data preparation, including pre-selection of predictive variables, relevant parameter selection, variable selection, and model validation, was detailed. Seabed gravel content samples in the Petrel sub-basin, northern Australia marine margin are used to demonstrate how to select relevant parameters, test the predictive accuracy, and generate and visualize spatial predictions. These examples for RFOK can be easily extended to other predictive methods including IDW, OK, RF, GBM, RFIDW, GBMOK, GBMIDW, RFOKRFIDW, and GBMOKGBMIDW by replacing rfokcv and its associated parameters with relevant functions and parameters for these methods in spm.

11.1. Accuracy of a Predictive Model for Seabed Gravel Content

In a previous predictive model [74], a spherical variogram model and a searching window size of 12 were used. The accuracy of this predictive model [74] can be shown using the rfokcv function in spm as shown below. To stabilize the accuracy derived, I repeat the cross-validation 100 times, which can be determined using the methods discussed in Section 9.2.

• > library(spm)
• > data(petrel)
• > names(petrel)
• [1] “long”   “lat”   “mud”   “sand”   “gravel”   “bathy”   “dist”   “relief”   “slope”
• > set.seed(1234)
• > n <- 100
• > rfokvecv1 <- NULL
• > for (i in 1:n) {
• +   rfokcv1 <- rfokcv(petrel[, c(1,2)], petrel[, c(1,2, 6:9)], petrel[, 5], predacc = “VEcv”)
• +   rfokvecv1 [i] <- rfokcv1
• + }
• > mean(rfokvecv1)
• [1] 37.44799

It suggests that the predictive accuracy is 37.4% in terms of VEcv.

11.2. Parameter Selection

The rfokcv function in spm is used to demonstrate how to select the best parameters for a predictive model (by using above predictive model as an example), and to check if the parameters used are optimal.

• > library(spm)
• > data(petrel)
• > nmax <- c(5:12); vgm.args <- c(“Sph”, “Mat”, “Ste”, “Log”)
• > rfokopt3 <- array(0, dim = c(length(nmax), length(vgm.args)))
• > set.seed(1234)
• > for (i in 1:length(nmax)) {
• +   for (j in 1:length(vgm.args)) {
• +   rfokcv1.1 <- NULL
• +     for (k in 1:100) {
• +     rfokcv1.1[k] <- rfokcv(petrel[, c(1, 2)], petrel[, c(1, 2, 6:9)], petrel[, 5], nmax = nmax[i],
• +     vgm.args = vgm.args[j], predacc = "VEcv") }
• +     rfokopt3[i, j] <- mean(rfokcv1.1) } }
• > which (rfokopt3 == max(rfokopt3, na.rm = T), arr.ind = T)
•     [1,]   6  4
• > vgm.args[4]; nmax[6]
•     [1] “Log”
•     [1] 10

The results suggest that the model would achieve the best predictive accuracy if “Log” is used for variogram modeling, and the 10 nearest samples are used for nmax. Of course, a different range may be used to choose the best nmax, and other variogram models can also be tested if needed.

We can use rfokcv in spm to assess the accuracy of RFOK by using the parameters identified above.

• > library(spm)
• > data(petrel)
• > set.seed(1234)
• > n <- 100
• > rfokvecv1 <- NULL
• > for (i in 1:n) {
• +   rfokcv1 <- rfokcv(petrel[, c(1, 2)], petrel[, c(1, 2, 6:9)], petrel[, 5], vgm.args = “Log”,
• +   nmax = 10,
• +   predacc = “VEcv”)
• +   rfokvecv1 [i] <- rfokcv1
• + }
• > mean(rfokvecv1)
• [1] 38.30175

This finding suggests that the overall averaged accuracy of the RFOK predictive model for seabed gravel content in terms of VEcv is 38.3%, higher than that of the previous model. This demonstrates that the parameters used previously are not optimal and that parameter selection improved predictive accuracy.

11.3. Predictive Variable Selection

In this study, we use the predictive variables previously identified [74], where the predictive variables were selected based on VI. Since then, more advanced variable selection methods for RF, RFOK, and RFIDW, such as AVI, KIAVI, PABV, and PARV [6,79], were developed. Application of these model selection methods and concepts may further improve the predictive accuracy of the model above. It is apparent that latitude (lat) is a PARV, as shown in the previous study [74]; thus, the removal of lat is expected to improve the predictive accuracy. This can be demonstrated below.

• > library(spm)
• > set.seed(1234)
• > rfokvecv1.1 <- NULL
• > for (i in 1:n) {
• >   rfokcv1 <- rfokcv(petrel[, c(1, 2)], petrel[, c(1, 6:9)], petrel[, 5], vgm.args = “Log”,
• +   nmax = 10,
• +   predacc = “Vecv”)
• +   rfokvecv1.1 [i] <- rfokcv1
• + }
• > mean(rfokvecv1.1, na.rm=T)
• [1] 39.00298

A further improvement in predictive accuracy is achieved after applying PARV. This further demonstrates the role of variable selection, especially the importance of newly developed variable selection methods.

11.4. Generation of Spatial Predictions

The predictive model developed above can be used to generate spatial predictions. The function rfokpred in spm is used to produce the predictions.

• > set.seed(1234)
• > library(spm)
• > data(petrel); data(petrel.grid)
• > rfokpred1 <- rfokpred(petrel[, c(1, 2)], petrel[, c(1, 6:9)], petrel[, 5], petrel.grid[, c(1, 2)],     +   petrel.grid, ntree = 500, nmax = 10, vgm.args = (“Log”))
• > names(rfokpred1)
• [1] “LON”   “LAT”   “Predictions”   “Variances”

The output dataset has four columns named longitude, latitude, predictions, and variances. Please note that the uncertainty information (i.e., variances) is produced for readers interested; however, be aware of the various limitations as discussed in Section 10 when using such information.

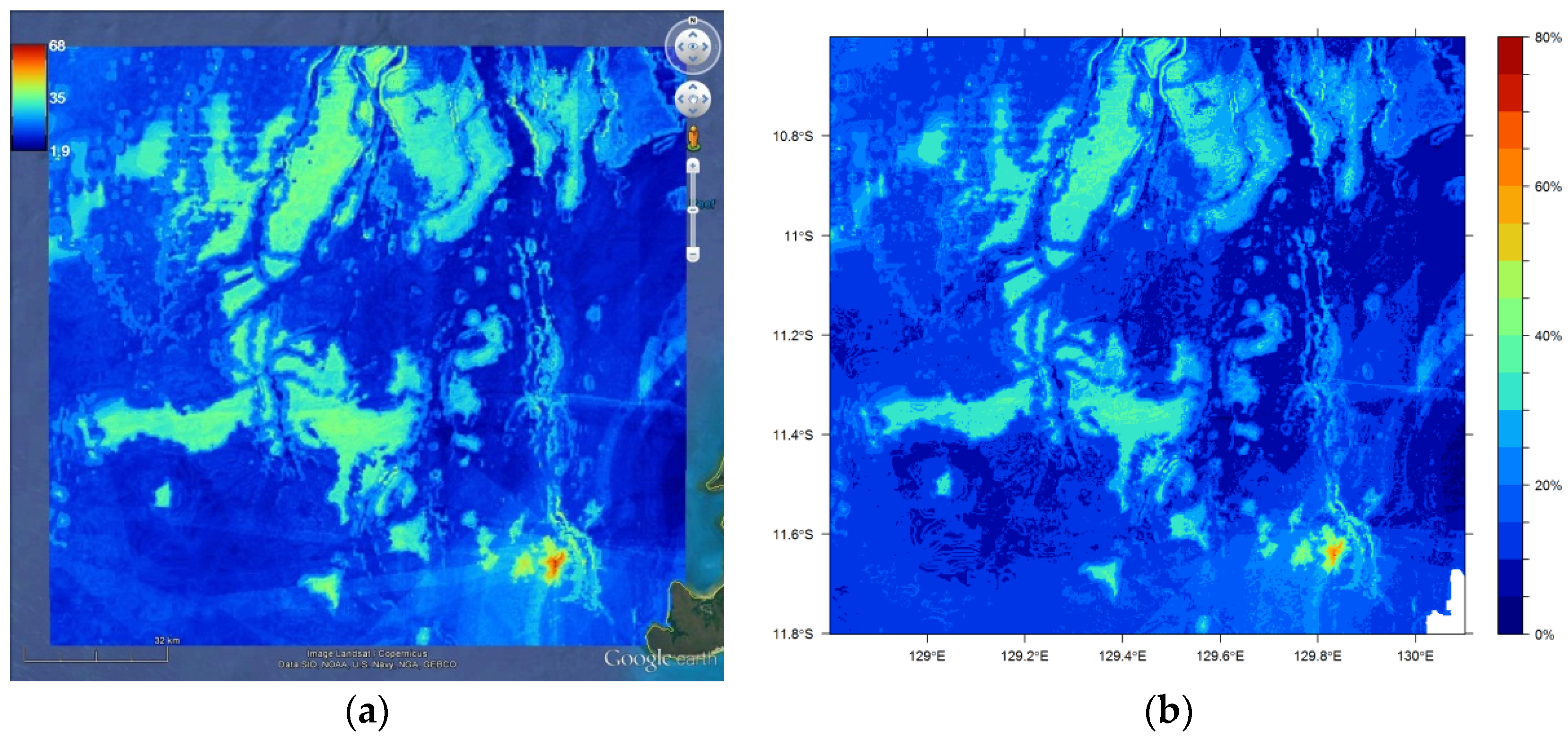
11.5. Visualisation of Spatial Predictions

Joint application of R and Google Earth can be used to visualize the predictions generated above.

• > library(sp); library(plotKML)
• > rfok1 <- rfokpred1
• > gridded(rfok1) <- ~ longitude + latitude
• > proj4string(rfok1) <- CRS(“+proj=longlat +datum=WGS84”)
• > plotKML(rfok1, colour_scale = SAGA_pal[[1]], grid2poly = TRUE)

The resultant map is shown in Figure 1a. One of the advantages of using R and Google Earth is that it can place the prediction map into the context map by Google Earth, which provides additional information to final users. However, the labels of longitude and latitude are hard to place in Figure 1a. If these labels are required, spplot can be applied to the above gridded data as shown below (Figure 1b).

• > par(font.axis=2, font.lab=2)
• > spplot(s1, c(“Predictions”), key.space=list(x=0.1,y=.95, corner=c(-1.2,2.8)),
• +  col.regions = SAGA_pal[[1]], # this requires plotKML
• +  scales=list(draw=T), colorkey = list(at = c(seq(0,80,5)), space=“right”,
• +  labels = c("0%“,” “,“”,“”,“20%”,“”,“”,“”,“40%”,“”,“”,“”,“60%”,“”,“”,“”,“80%”)),
• +  at=c(seq(0,80, 5)))

With regard to the prediction map, it is obvious that there are artefacts (e.g., sharp vertical changes associated with longitude) in the predictions. These artefacts may disappear or be alleviated if more variables could be used; in other words, different predictive variables should be tested according to the recently development in variable selection [6,79], as discussed in Section 7.

12. Summary

This study reviewed the modeling process for spatial predictive modeling in environmental sciences. The modeling process covers the following nine components:

• Sampling design and data preparation;
• Selection of predictive methods;
• Pre-selection of predictive variables;
• Exploratory analysis;
• Parameter selection;
• Variable selection;
• Accuracy assessment;
• Model validation;
• Spatial predictions, prediction uncertainty, and their visualization.

Each of these components plays a significant role in model development. Incorrect or inappropriate implementation of any components may lead to less accurate or even misleading predictive model(s). To select the most accurate predictive model, all components and relevant requirements and factors for each component need to be considered and carefully implemented by following the guidelines, suggestions, and recommendations provided under relevant components in this study. Reproducible examples were provided to demonstrate how to select and identify the most accurate spatial predictive model using spm, and to generate and visualize spatial predictions in environmental sciences. For a predictive model, predictive accuracy is a key criterion for model selection and is critical for subsequent spatial predictions. This modeling process is not only important for spatial predictive modeling, but also provides valuable reference to other predictive modeling fields. Although this study attempts to cover relevant components, which may contribute to the improvement of predictive accuracy, as completely as possible, the spatial predictive modeling field is too broad to allow that to be done comprehensively in this study. This is because different disciplines have their own specific features and requirements. Therefore, further studies are needed to identify factors in relevant components or additional components that can further improve the accuracy of predictive models in various disciplines. This study would be expected to not only boost applications of appropriate spatial predictive modeling processes, but also provide spatial predictive modeling tools for various modeling components to improve the quality of spatial predictions.