A Novel Neural Network-Based Method for Decoding and Detecting of the DS8-PSK Scheme in an OCC System
Abstract
:1. Introduction
2. Related Work
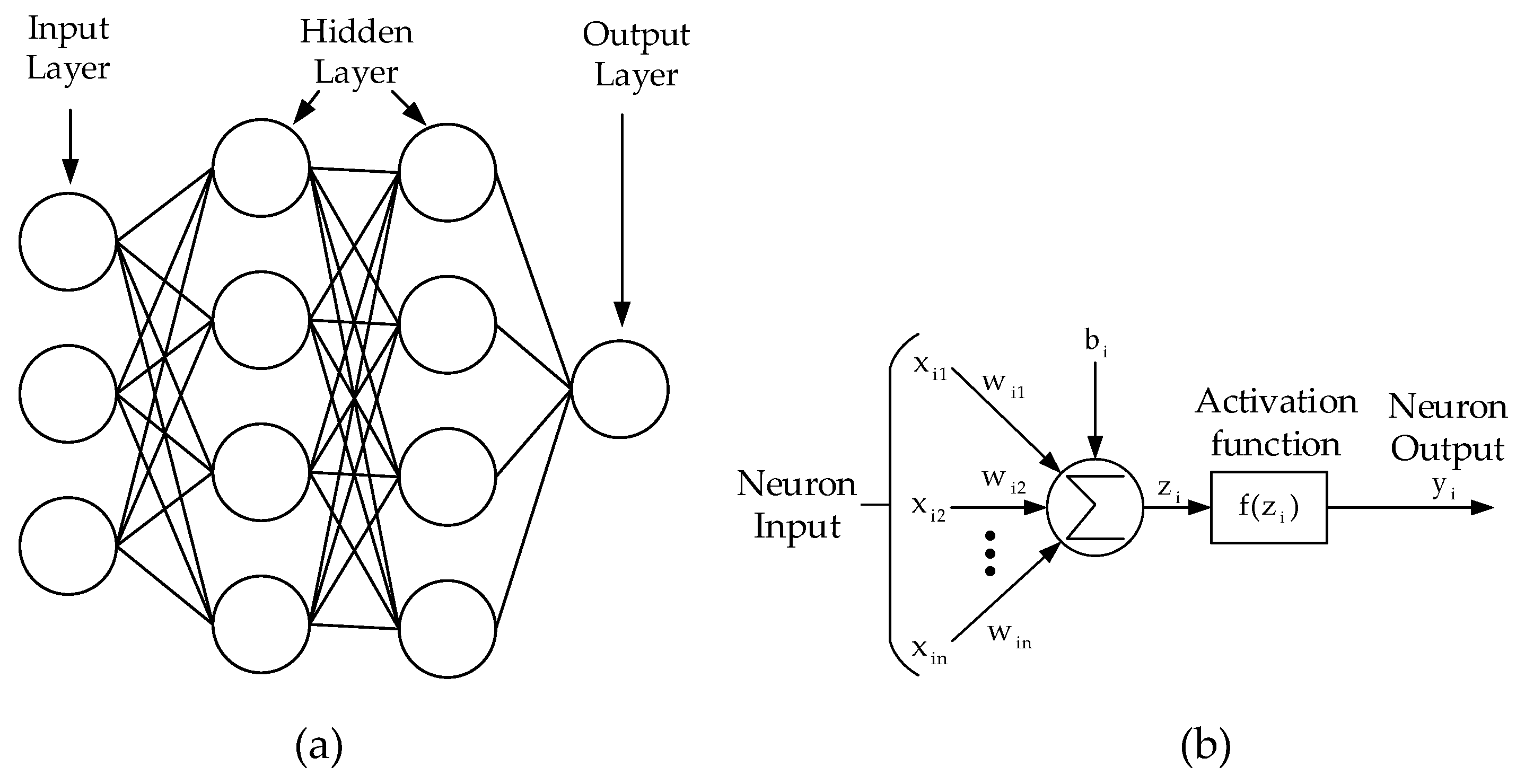
2.1. Fundamental AI
2.1.1. Loss Function
2.1.2. Optimization Algorithm
| The Adagrad algorithm |
|
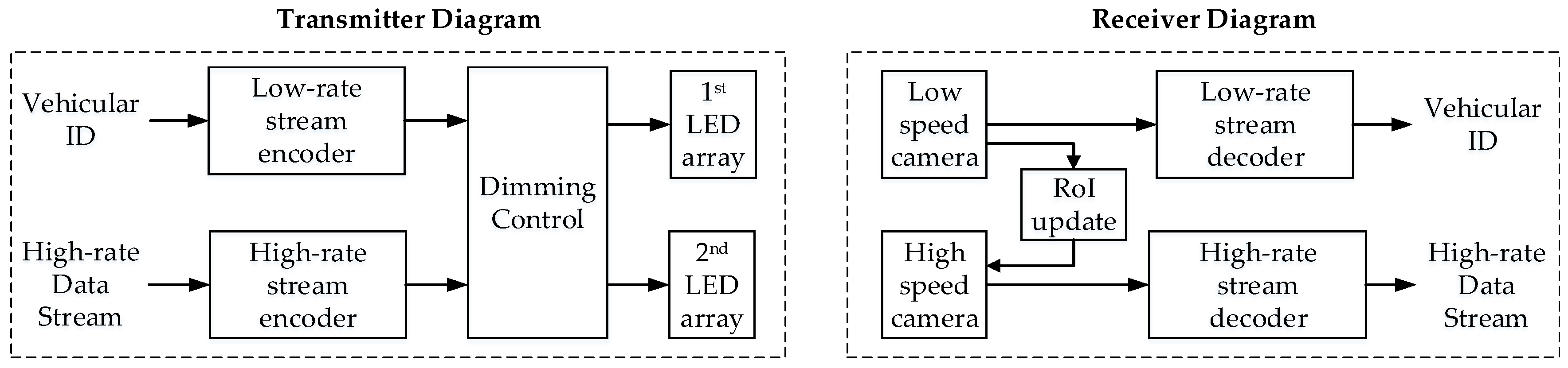
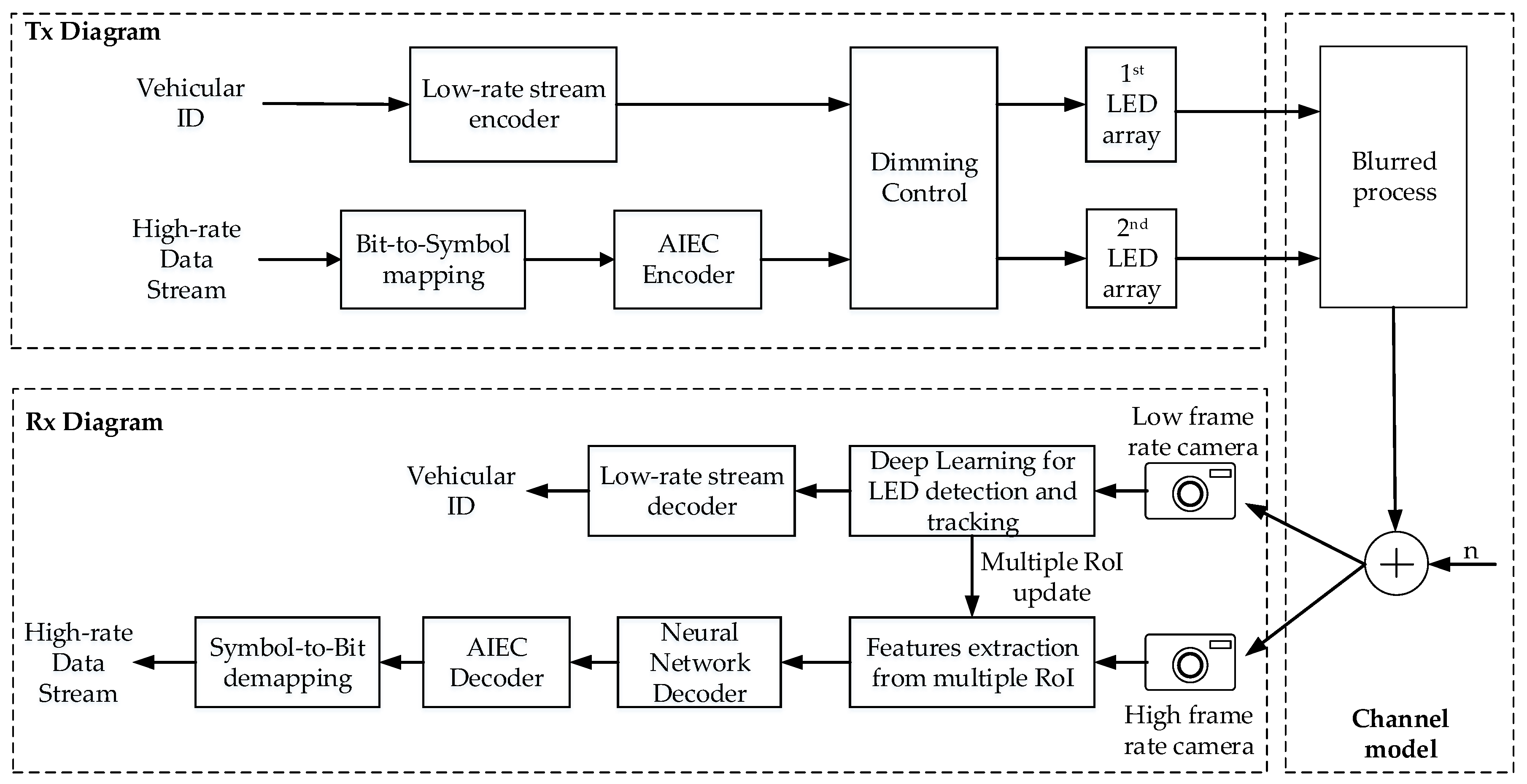
2.2. Reference Architecture of a Vehicular OCC System
3. Our contributions
- We define a novel channel model which can give the nearest approximation of the channel model in vehicular OCC system, considering the blur effect caused by a different type of environment condition, such as rainy, foggy, snowy, etc. The defined channel model is also designed to be able to simulate.
- We provide the principle of the blurred phenomenon on the image: How it affects the quality of the communication channel and the performance of the traditional decoder in an image sensor-based communication system.
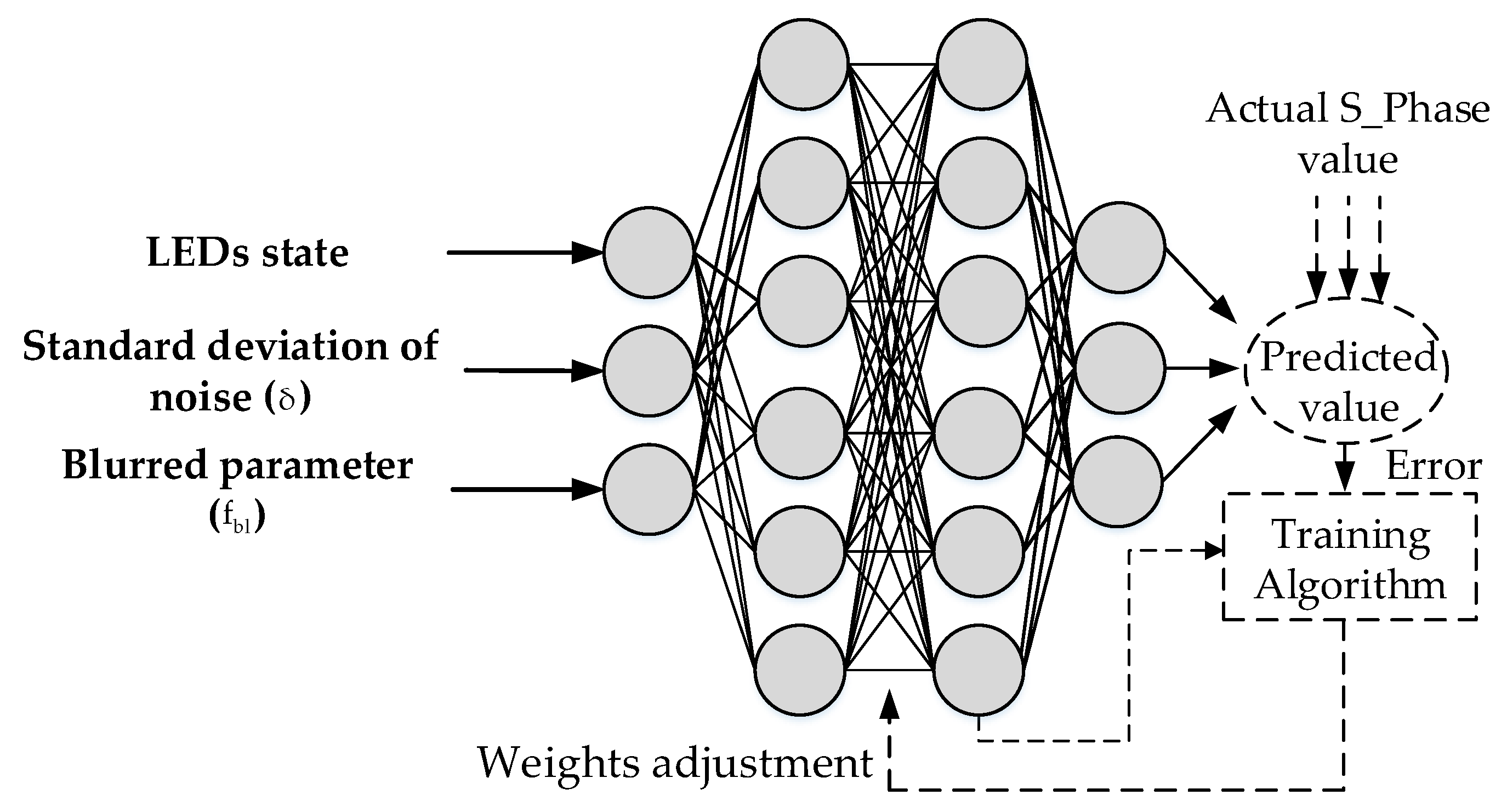
- We propose a new method of using deep learning and NN to decode the high-rate OCC waveform (DS8-PSK): The model architecture and dataset preparation for training and performance testing.
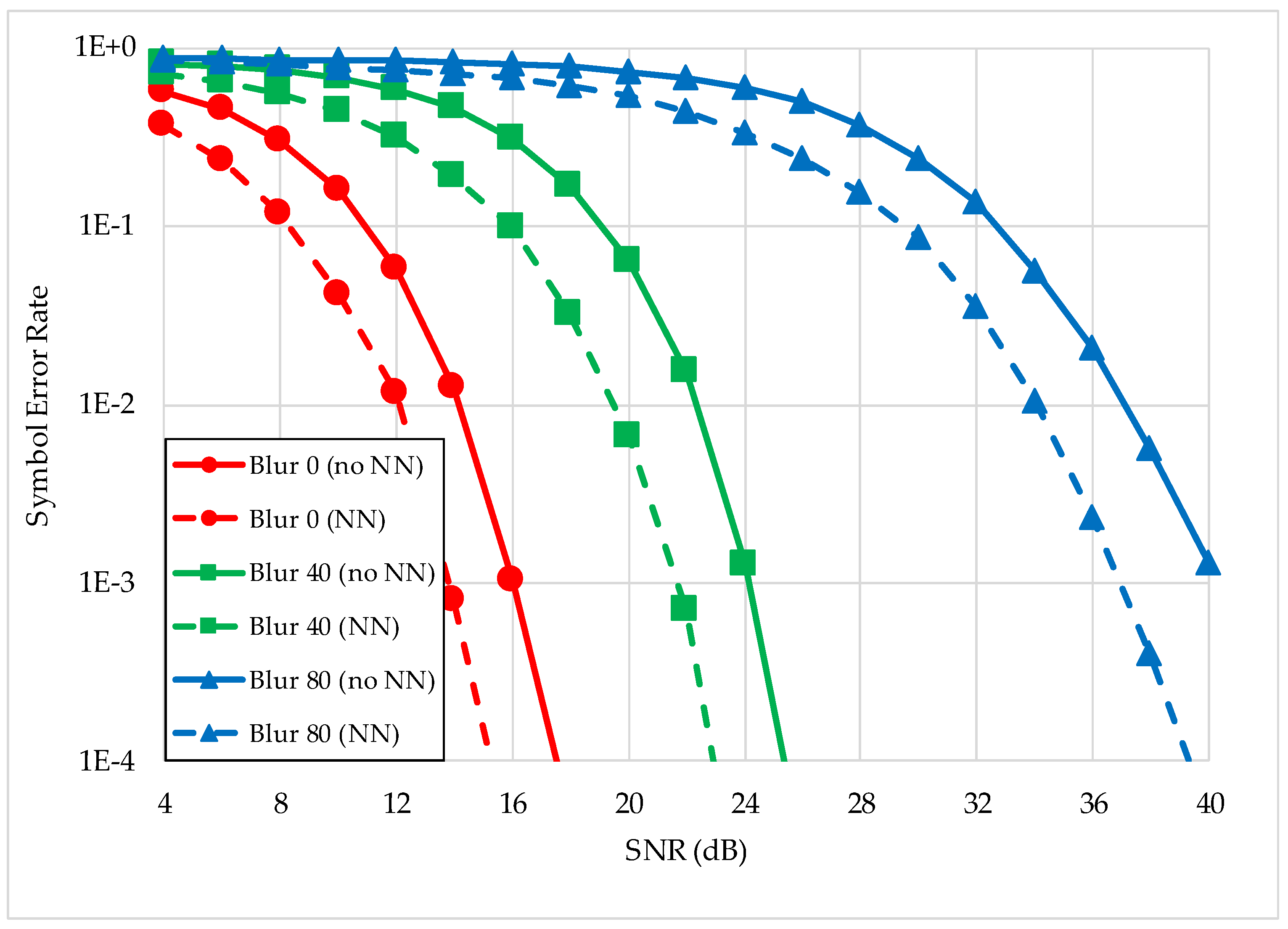
- We prove the robustness of a new AI-based decoder on a novel channel model by analyzing the SER performance of each decoding method. Thus, making a performance comparison between using the traditional decoder and our proposed AI-based decoder.
4. System Architecture and Performance Analysis
4.1. Reference High-rate Modulation Scheme
4.1.1. DS8-PSK Encoder
4.1.2. DS8-PSK Decoder
4.2. Proposed System Architecture
4.3. Performance Analysis
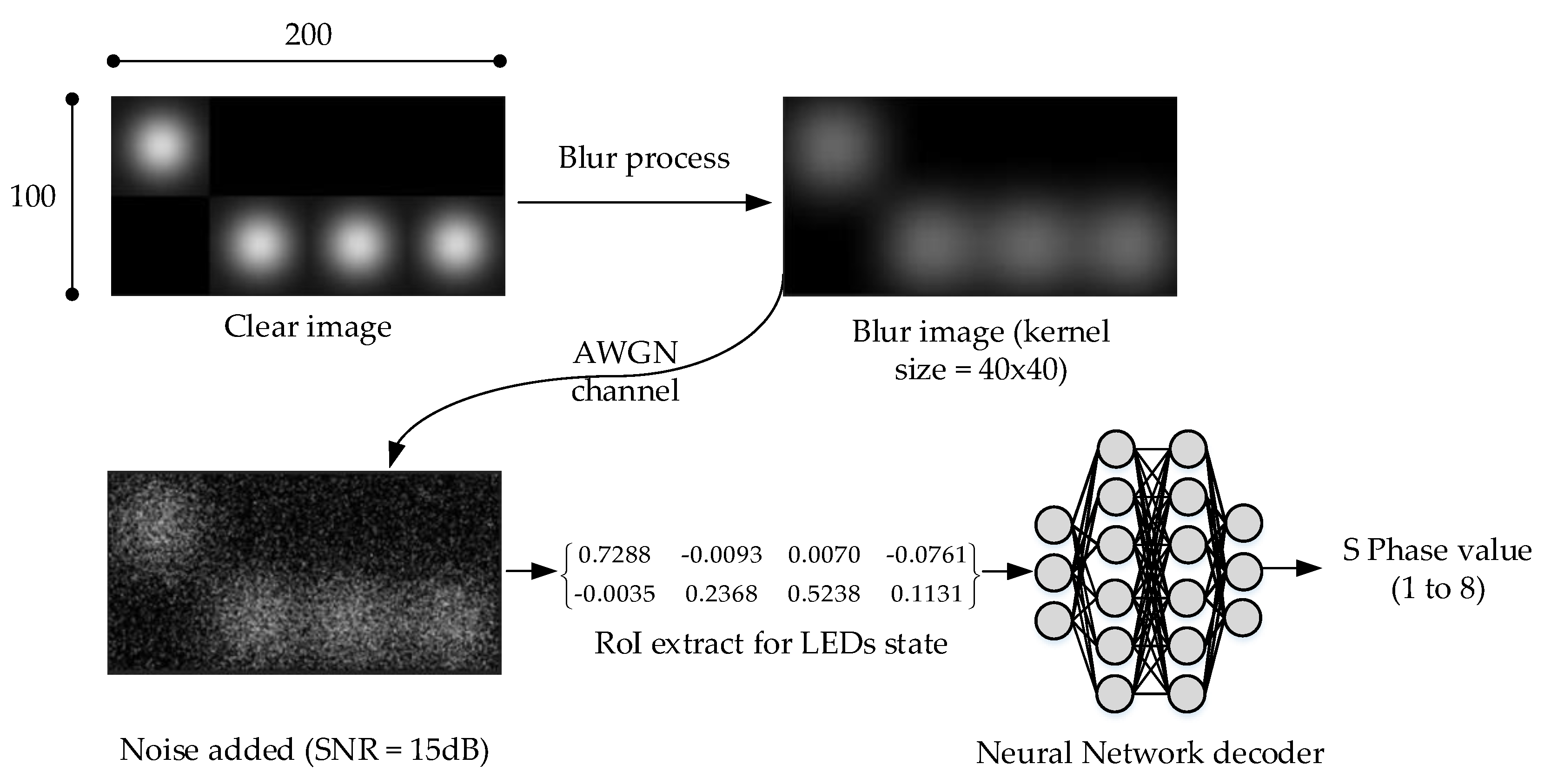
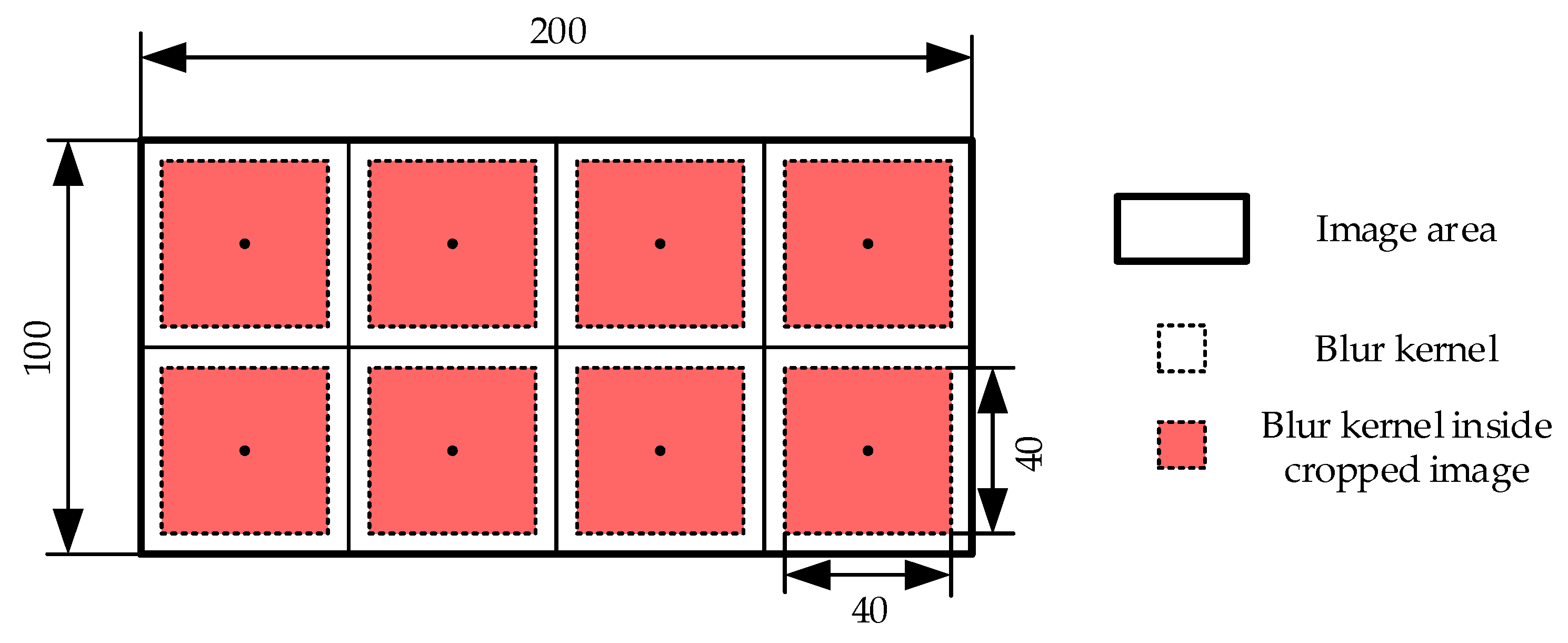
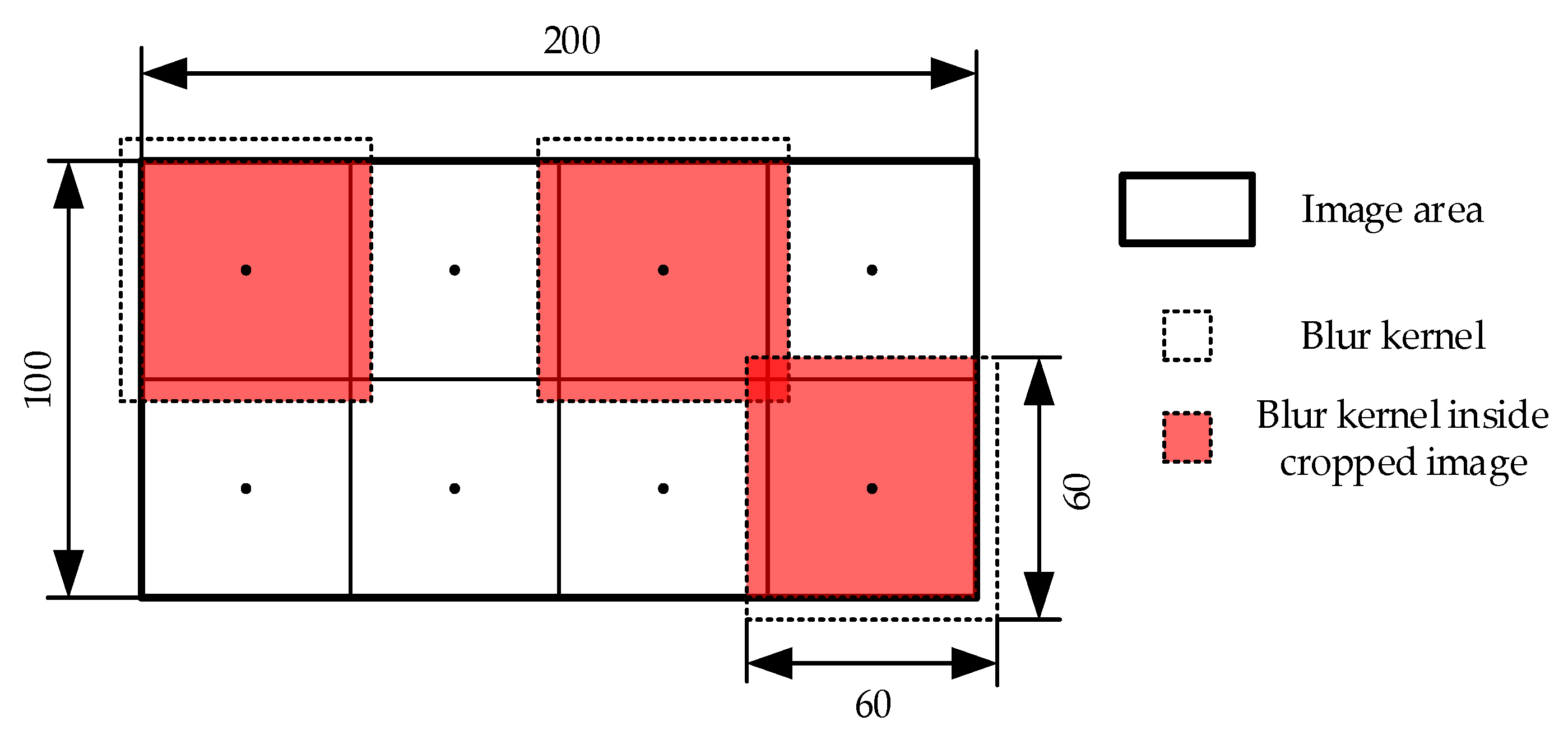
4.3.1. Blurred Image—Principle and Simulation Method
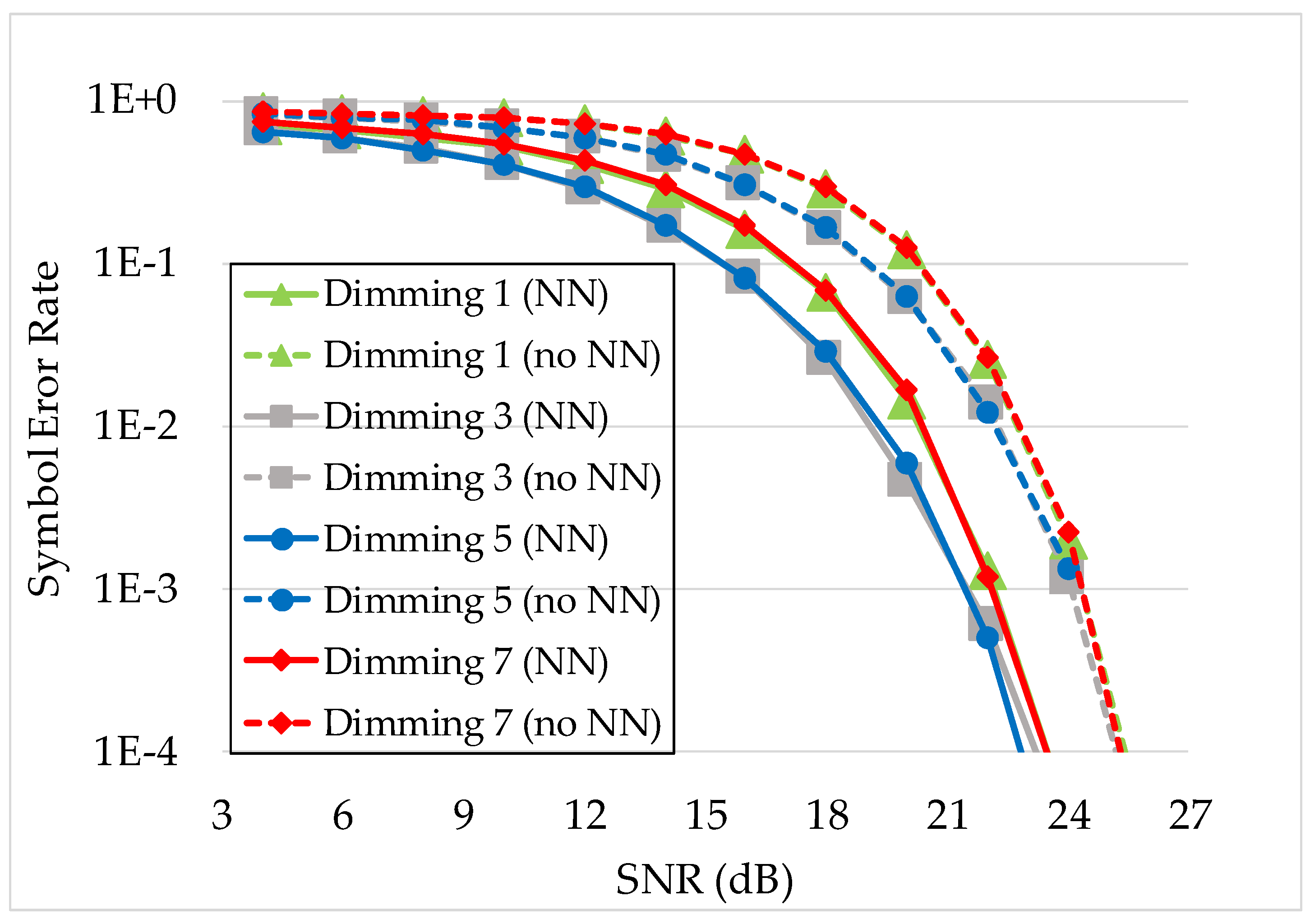
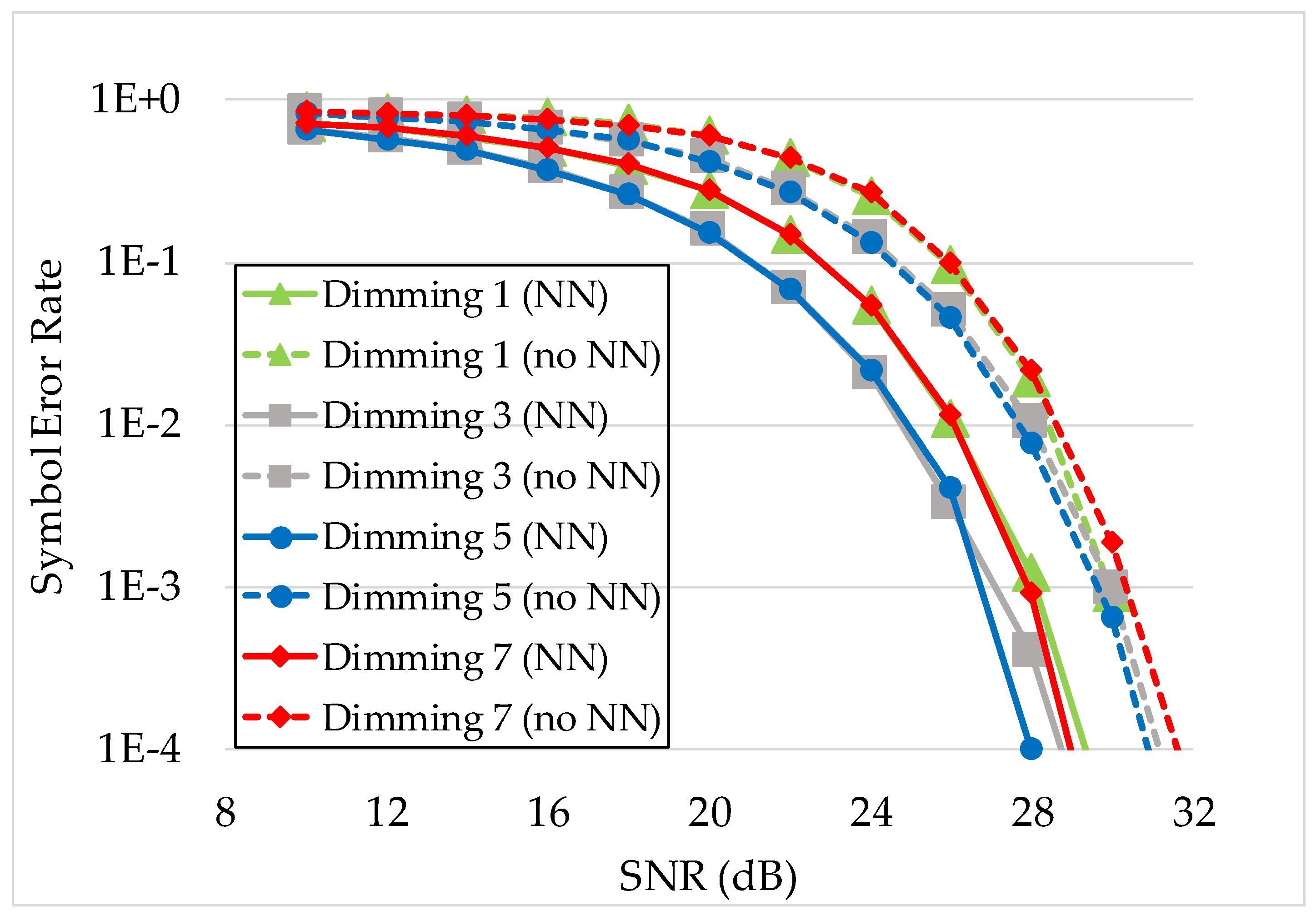
4.3.2. Performance Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Nagura, T.; Yamazato, T.; Katayama, M.; Yendo, T.; Fujii, T.; Okada, H. Improve decoding method of visible light communication system for ITS using LED array and high-speed camera. In Proceedings of the IEEE 71st Vehicular Technology Conference, Taipei, Taiwan, 16–19 May 2010. [Google Scholar]
- Pathak, P.H.; Feng, X.; Hu, P.; Mohapatra, P. Visible light communication networking and sensing: A survey potential and challenges. IEEE Commun. Surv. Tutor. 2015, 17, 2047–2077. [Google Scholar] [CrossRef]
- Rajagopal, S.; Roberts, R.D.; Lim, S.-K. IEEE 802.15.7 visible light communication: Modulation and dimming support. IEEE Commun. Mag. 2012, 50, 72–82. [Google Scholar] [CrossRef]
- Nguyen, T.; Islam, A.; Hossan, T.; Jang, Y.M. Current status and performance analysis of optical camera communication technologies for 5G networks. IEEE Access 2017, 5, 4574–4594. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Park, S.; Chae, Y.; Park, Y. VLC/OCC hybrid optical wireless systems for versatile indoor applications. IEEE Access 2019, 7, 22371–22376. [Google Scholar] [CrossRef]
- Lin, B.; Ghassemlooy, Z.; Lin, C.; Tang, X.; Li, Y.; Zhang, S. An indoor visible light positioning system based on optical camera communications. IEEE Photonics Technol. Lett. 2017, 29, 579–582. [Google Scholar] [CrossRef]
- Jiao, J.; Li, F.; Deng, Z.; Ma, W. A smartphone camera-based indoor positioning algorithm of crowded scenarios with the assistance of deep CNN. Sensors 2017, 17, 704. [Google Scholar] [CrossRef]
- Nguyen, T.; Islam, A.; Jang, Y.M. Region-of-interest signaling vehicular system using optical camera communications. IEEE Photonics J. 2017, 9. [Google Scholar] [CrossRef]
- Ji, P.; Tsai, H.M.; Wang, C.; Liu, F. Vehicular visible light communications with LED tail light and rolling shutter camera. In Proceedings of the IEEE 79th Vehicular Technology Conference (VTC Spring), Seoul, Korea, 18–21 May 2014; pp. 1–6. [Google Scholar]
- Tram, V.T.B.; Yoo, M. Vehicle-to-vehicle distance estimation using a low-resolution camera based on visible light communications. IEEE Access 2018, 6, 4521–4527. [Google Scholar] [CrossRef]
- Cailean, A.-M.; Dimian, M. Current challenges for visible light communications usage in vehicle applications: A survey. IEEE Commun. Surv. Tutor. 2017, 19, 2681–2703. [Google Scholar] [CrossRef]
- Khan, L.U. Visible light communication: Applications, architecture, standardization, and research challenges. Digit. Commun. Netw. 2017, 3, 78–88. [Google Scholar] [CrossRef]
- Kundur, D.; Hatzinakos, D.; Leung, H. Robust classification of blurred imagery. IEEE Trans. Image Process. 2000, 9, 9–243. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Chen, C.; Seff, A.; Kornhauser, A.; Xiao, J. DeepDriving: Learning affordance for direct perception in autonomous driving. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 2722–2730. [Google Scholar]
- Nachmani, E.; Be’ery, Y.; Burshtein, D. Learning to decode linear codes using deep learning. In Proceedings of the 54th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 27–30 September 2016; pp. 341–346. [Google Scholar]
- O’Shea, T.J.; Hoydis, J. An introduction to deep learning for the physical layer. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 563–575. [Google Scholar] [CrossRef]
- Cammerer, S.; Gruber, T.; Hoydis, J.; ten Brink, S. Scaling deep learning-based decoding of polar codes via partitioning. arXiv 2015, arXiv:1702.06901. [Google Scholar]
- Ye, H.; Li, G.Y.; Juang, B. Power of deep learning for channel estimation and signal detection in OFDM systems. IEEE Wirel. Commun. Lett. 2018, 7, 114–117. [Google Scholar] [CrossRef]
- Dörner, S.; Cammerer, S.; Hoydis, J.; Brink, S.T. Deep learning based communication over the air. IEEE J. Sel. Top. Signal. Process. 2018, 12, 12–132. [Google Scholar] [CrossRef]
- Liang, F.; Shen, C.; Wu, F. An iterative BP-CNN architecture for channel decoding. IEEE J. Sel. Top. Signal. Process. 2018, 12, 12–144. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Rajbhandari, S. Performance of diffused indoor optical wireless links employing neural and adaptive linear equalizers. In Proceedings of the 2007 6th International Conference on Information, Communications & Signal Processing, Singapore, 10–13 December 2007; pp. 1–6. [Google Scholar]
- Zhang Hao. Loss Functions in Neural Networks. Available online: https://isaacchanghau.github.io/post/loss_functions/ (accessed on 10 May 2019).
- Optimization techniques comparison in Julia: SGD, Momentum, Adagrad, Adadelta, Adam. Available online: https://int8.io/comparison-of-optimization-techniques-stochastic-gradient-descent-momentum-adagrad-and-adadelta/ (accessed on 17 April 2019).
- Duchi, J.; Hazan, E.; Singer, Y. Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 2011, 12, 2121–2159. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A.C. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Dean, J.; Corrado, G.; Monga, R.; Chen, K.; Devin, M.; Mao, M.; Ranzato, M.; Senior, A.; Tucker, P.; Yang, K.; et al. Large scale distributed deep networks. Neural Inf. Process. Syst. 2012, 1, 1232–1240. [Google Scholar]
- Ran, X.; Shan, Z.; Fang, Y.; Lin, C. Travel Time Prediction by Providing Constraints on a Convolutional Neural Network. IEEE Access 2018, 6, 6–59336. [Google Scholar] [CrossRef]
- Kookmin University PHY sub-proposal for ISC using Dimmable Spatial M-PSK (DSM-PSK). 2016. Available online: https://mentor.ieee.org/802.15/dcn/16/15-16-0015 -02-007a-kookmin-university-phy-sub-proposal-for-isc-using-dimmablespatial-m-psk-dsm-psk.pptx (accessed on 3 April 2019).
- Reeves, S.J.; Mersereau, R.M. Blur identification by the method of generalized cross-validation. IEEE Trans. Image Process. 1992, 1, 301–311. [Google Scholar] [CrossRef]
- Kundur, D.; Hatzinakos, D. Blind image deconvolution. IEEE Signal. Process. Mag. 1996, 13, 43–64. [Google Scholar] [CrossRef]
- Shan, Q.; Jia, J.; Agarwala, A. High-quality motion deblurring from a single image. ACM Trans. Graph. 2008, 27, 73. [Google Scholar] [CrossRef]
- Cai, J.-F.; Ji, H.; Liu, C.; Shen, Z. Blind motion deblurring using multiple images. J. Comput. Phys. 2009, 228, 5057–5071. [Google Scholar] [CrossRef]
- Zhang, H.; Wipf, D.; Zhang, Y. Multi-observation blind deconvolution with an adaptive sparse prior. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1628–1643. [Google Scholar] [CrossRef] [PubMed]
- Sroubek, F.; Milanfar, P. Robust multichannel blind deconvolution via fast alternating minimization. IEEE Trans. Image Process. 2012, 21, 1687–1700. [Google Scholar] [CrossRef] [PubMed]
- Lin, T.; Hou, L.; Liu, H.; Li, Y.; Truong, T. Reconstruction of single image from multiple blurry measured images. IEEE Trans. Image Process. 2018, 27, 27–2762. [Google Scholar] [CrossRef]
- Roberts, R.D. A MIMO protocol for camera communications (CamCom) using undersampled frequency shift ON-OFF keying (UFSOOK). In Proceedings of the IEEE Globecom Workshops (GC Wkshps), Atlanta, GA, USA, 9–13 December 2013; pp. 1052–1057. [Google Scholar]
- Roberts, R.D. Intel Proposal in IEEE 802.15.7r1, Slide 1-129. Available online: https://mentor.ieee. org/802.15/dcn/16/15-16-0006-01-007a-intel-occ-proposal.pdf (accessed on 3 April 2019).
- Redmon, J.; Divvala, S.K.; Girshick, R.B.; Farhadi, A. You only look once: Unified, real-time object detection. arXiv 2015, arXiv:1506.02640. [Google Scholar]
- Pham, T.L.; Nguyen, T.; Thieu, M.D.; Nguyen, H.; Nguyen, H.; Jang, Y.M. An Artificial Intelligence-based Error Correction for Optical Camera Communication. Presented at the 2019 Eleventh International Conference on Ubiquitous and Future Networks (ICUFN), Zagreb, Croatia, 2–5 July 2019. in press. [Google Scholar]
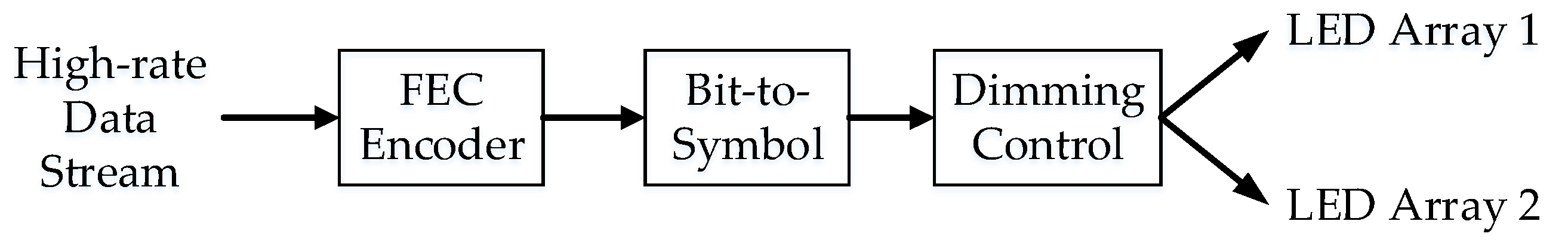
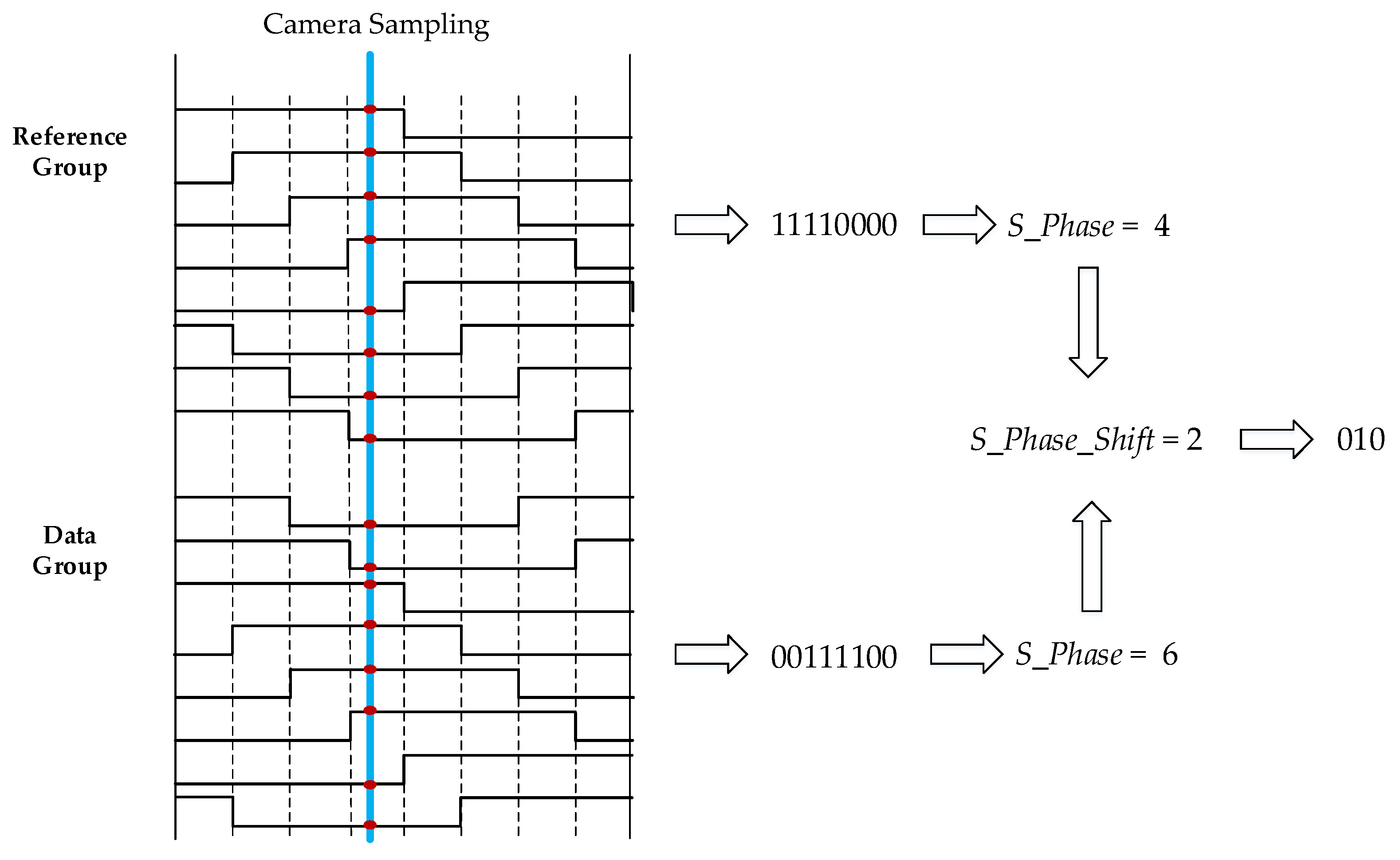

| 3 bits Input | S_Phase_Shift/(T/8) Output |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 8 States Input | S_Phase Output | ||||||
|---|---|---|---|---|---|---|---|
| Dimming 1/8 | Dimming 2/8 | Dimming 3/8 | Dimming 4/8 | Dimming 5/8 | Dimming 6/8 | Dimming 7/8 | |
| 10000000 | 10000001 | 10000011 | 10000111 | 10001111 | 10011111 | 10111111 | 1 |
| 01000000 | 11000000 | 11000001 | 11000011 | 11000111 | 11001111 | 11011111 | 2 |
| 00100000 | 01100000 | 11100000 | 11100001 | 11100011 | 11100111 | 11101111 | 3 |
| 00010000 | 00110000 | 01110000 | 11110000 | 11110001 | 11110011 | 11110111 | 4 |
| 00001000 | 00011000 | 00111000 | 01111000 | 11111000 | 11111001 | 11111011 | 5 |
| 00000100 | 00001100 | 00011100 | 00111100 | 01111100 | 11111100 | 11111101 | 6 |
| 00000010 | 00000110 | 00001110 | 00011110 | 00111110 | 01111110 | 11111110 | 7 |
| 00000001 | 00000011 | 00000111 | 00001111 | 00011111 | 00111111 | 01111111 | 8 |
| 8 States Input | S_Phase Output | ||||||
|---|---|---|---|---|---|---|---|
| Dimming 1/8 | Dimming 2/8 | Dimming 3/8 | Dimming 4/8 | Dimming 5/8 | Dimming 6/8 | Dimming 7/8 | |
| xx000000 | 1x00000x | 1x0000x1 | 1x000x11 | 1x00x111 | 1x0x1111 | 1xx11111 | 1 |
| 0xx00000 | x1x00000 | 11x0000x | 11x000x1 | 11x00x11 | 11x0x111 | 11xx1111 | 2 |
| 00xx0000 | 0x1x0000 | x11x0000 | 111x000x | 111x00x1 | 111x0x11 | 111xx111 | 3 |
| 000xx000 | 00x1x000 | 0x11x000 | x111x000 | 1111x00x | 1111x0x1 | 1111xx11 | 4 |
| 0000xx00 | 000x1x00 | 00x11x00 | 0x111x00 | x1111x00 | 11111x0x | 11111xx1 | 5 |
| 00000xx0 | 0000x1x0 | 000x11x0 | 00x111x0 | 0x1111x0 | x11111x0 | 111111xx | 6 |
| 000000xx | 00000x1x | 0000x11x | 000x111x | 00x1111x | 0x11111x | x111111x | 7 |
| x000000x | x00000x1 | x0000x11 | x000x111 | x00x1111 | x0x11111 | xx111111 | 8 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, T.L.; Nguyen, H.; Nguyen, T.; Jang, Y.M. A Novel Neural Network-Based Method for Decoding and Detecting of the DS8-PSK Scheme in an OCC System. Appl. Sci. 2019, 9, 2242. https://doi.org/10.3390/app9112242
Pham TL, Nguyen H, Nguyen T, Jang YM. A Novel Neural Network-Based Method for Decoding and Detecting of the DS8-PSK Scheme in an OCC System. Applied Sciences. 2019; 9(11):2242. https://doi.org/10.3390/app9112242
Chicago/Turabian StylePham, Tung Lam, Huy Nguyen, Trang Nguyen, and Yeong Min Jang. 2019. "A Novel Neural Network-Based Method for Decoding and Detecting of the DS8-PSK Scheme in an OCC System" Applied Sciences 9, no. 11: 2242. https://doi.org/10.3390/app9112242
APA StylePham, T. L., Nguyen, H., Nguyen, T., & Jang, Y. M. (2019). A Novel Neural Network-Based Method for Decoding and Detecting of the DS8-PSK Scheme in an OCC System. Applied Sciences, 9(11), 2242. https://doi.org/10.3390/app9112242






