Calibration of a Rotating or Revolving Platform with a LiDAR Sensor

Abstract

Perceiving its environment in 3D is an important ability for a modern robot. Today, this is often done using LiDARs which come with a strongly limited field of view (FOV), however. To extend their FOV, the sensors are mounted on driving vehicles in several different ways. This allows 3D perception even with 2D LiDARs if a corresponding localization system or technique is available. Another popular way to gain most information of the scanners is to mount them on a rotating carrier platform. In this way, their measurements in different directions can be collected and transformed into a common frame, in order to achieve a nearly full spherical perception. However, this is only possible if the kinetic chains of the platforms are known exactly, that is, if the LiDAR pose w.r.t. to its rotation center is well known. The manual measurement of these chains is often very cumbersome or sometimes even impossible to do with the necessary precision. Our paper proposes a method to calibrate the extrinsic LiDAR parameters by decoupling the rotation from the full six degrees of freedom transform and optimizing both separately. Thus, one error measure for the orientation and one for the translation with known orientation are minimized subsequently with a combination of a consecutive grid search and a gradient descent. Both error measures are inferred from spherical calibration targets. Our experiments with the method suggest that the main influences on the calibration results come from the the distance to the calibration targets, the accuracy of their center point estimation and the search grid resolution. However, our proposed calibration method improves the extrinsic parameters even with unfavourable configurations and from inaccurate initial pose guesses.

1. Introduction

In robotics, the perception of 3D information about the agent’s surroundings is important for many tasks, like planning robot arm movements, object and obstacle detection or 3D model reconstruction. Therefore, the increasing amount of available laser detection and ranging sensors (LiDAR), sometimes also referred to as laser range finder (LRF), together with falling device prices, caused an increasing usage of those for 3D perception. Although various sensor types and specifications [1,2,3] exist, all devices come with a strongly limited field of view and often with a low sampling resolution compared to other vision sensors. To compensate these disadvantages, many developments engaging different strategies of mounting them on various kinds of vehicles and robots are done. All of them try to gain as much information from the installed sensors as possible, by extending their field of view. This is solved through a specific mounting pose [4,5] or rotating the LiDARs on a sensor carrier [6,7]. Thus, there exists a variety of such sensor platforms.

A feature that all sensor platforms have in common is that the data perceived by the mounted sensors have to be combined during the continuous motion of the platform itself or of the whole vehicle. In order to achieve this, the data measured in each sensor’s frame has to be transformed into a common reference frame in real time. This requires accurate motion sensing of the platform and exact knowledge of each sensor’s pose with respect to the robot’s or sensor platform’s base link. The pose information, also referred as extrinsic parameters, can be used to build a kinematic chain modeling the necessary transformations. Erroneous transformations would result in artifacts, like duplicate sensing and lower accuracy, as illustrated in Figure 1. This can make the sensor data noisy, misleading or even useless.

Figure 1. Top-down view on a LiDAR scan of a building. (a) shows erroneous and (b) the correct transformed point cloud data.

Manually measuring the sensor pose is often not possible with appropriate precision. In particular, rotations are difficult to measure by hand and inaccuracies result in significant measurement errors when they are not known precisely. Therefore, calibration procedures for the extrinsic sensor parameters, suitable to the specific sensor arrangements, are required. They should identify or optimize the sensor pose information to reduce transformation errors of the sensor perceptions.

This work describes and evaluates a novel calibration method for the extrinsic parameters of rotating or revolving multi-beam LiDARs. Revolving sensors are shifted away from the actual rotation center, i.e., the sensor’s trajectory describes an orbit, while rotating ones turn around their own center. This is important because revolving sensors can be more challenging to calibrate. However, our method isolates the sensor’s orientation from its full pose information. This is a major step, since inaccurate knowledge of the sensor orientation leads to an error in the transformed data which is not just constant, but increases with the distance of the sampled data points to the sensing LiDAR. Furthermore, the orientation errors can not be measured or calculated directly, since they manifest in translational errors of the perceived data. Therefore, the orientation is optimized separately from the translation to avoid ambiguities between orientation and translation, and also to reduce the dimensionality of the original problem. Subsequently, the translation is also optimized using the previously determined rotation.

In Section 2, other relevant works about extrinsic parameter calibration for LiDARs are briefly described with short statements on how they are related to our proposal. Section 3 then outlines our method and its theoretical deduction in detail. To test the performance of our method during an actual calibration, Section 4 defines different settings for a calibration process of a specific exemplary sensor platform. In addition, a quality measure for 3D point clouds is defined, to get an idea of the improvements after the calibration. After a short discussion of the results, conclusions and possible further work on or around our proposal are illustrated in Section 5.

2. Related Work

There are many works on the extrinsic calibration between different sensors. Especially calibrating the pose of a LiDAR relative to a camera is a very popular topic. However, this and other works concern the extrinsic calibration of single sensors with respect to the construction they are mounted on. In general, these can be distinguished into two types of calibration methods. Both methods have their particular benefits and drawbacks. The first type requires previously known calibration targets, such as poles, spheres or planes inside the field of view of the used sensors. Moreover, it is often undesirable to use such objects, as this increases the required configuration effort. Therefore, a second, target-less type of calibration methods was developed. They use static environments and properties of their surroundings like big planar surfaces, which, however, are not always available.

2.1. Calibration Target Required

A representative of the first method type is described by Gao et al. [5]. It estimates the extrinsic parameters of a LiDAR scanner with respect to another LiDAR’s frame. Both are mounted on the top of the same car. Highly reflective patches are attached to pillars at the edge of a street track. While driving along this calibration track, the patches are detected by the reflection intensity of their LiDAR measurements and then reduced to a single feature point in both sensor frames. Using the known vehicle pose in a global reference frame, the error between patches from both sensors in a common frame is minimised. This is done by solving a second-order cone program which reformulates a more cost effective least-square problem. While the problem formulation is interesting, due to the reduction of computational costs, the proposed method requires a positioning system, and driving along a previously manipulated track. Both is not always feasible and may be error prone. Furthermore, the calibration results in knowing a sensor’s pose with respect to another sensor’s frame and not with respect to a part of the platform construction. This makes knowledge of the exact pose of the other LiDAR relative to the car necessary.

In contrast to more common numerical minimisation algorithms like in [5], a simple analytical method is proposed by Lin et al. [8]. The platform’s architecture obtains 3D point clouds from a 2D laser range finder by tilting it to different angles. Since the rotation center differs from the sensor center, it is important to know the radius exactly. Lin et al. [8] propose to measure points on a planar target, e.g., a wall, in different known tilt angles of the sensor. Using the vertical distances of those points, the radius can be inferred using angle and distance information in a triangle spanned by the rotation center and two of the LiDAR measurements. This method ignores all other dimensions of the sensor pose except the radius of the revolving LiDAR. However, these are important for many platforms and thus the proposed method is strongly bound to this specific architecture.

The method by Kang et al. [7] uses a target plane to estimate the pose of a 2D laser range finder orbiting a rotation center. The 3D scanline direction on the target is inferred to construct a cost function scoring the scanner’s orientation separately from its translation, which is optimised by a second cost function. These are used as objectives to minimize the distance between points on neighbouring scanlines of different platform orientations. The decoupling removes some ambiguities between translation and rotation of the scanner’s frame. Thus, rotations which compensate translations are removed from the search space of the objective functions. The decoupling is a clever approach not only to remove the ambiguities, but also to split up the optimisation problem into two functions with lower dimensionality. Some of our main ideas are based on this work. However, it is expected to depend on the device architecture of the LRF used on this platform.

2.2. Targetless Calibration

The method proposed by Levinson et al. [9] calibrates two sensor properties without any calibration targets: intrinsic LiDAR parameters, i.e., the internal laser arrangement, external LiDAR parameters specifying its pose relative to the robots’ base frame. To determine the internal and external parameters, a single energy function is formulated. This function rewards points of neighbouring laser beams if they lie on the same surface, i.e., having the same normal, while applying a penalty, if they do not. During a movement of the vehicle with tracked trajectory, the measured points can be transformed into a common frame. The external parameters minimising the energy function should be the true scanner pose. To avoid ambiguities and local minima, Levinson et al. [9] use a grid search instead of a Newton-based method, though the energy function would be contentious. They state that the search space is tractable. They also state not to make strong assumptions about their environment. However, the error formulation of their objective function implies planar surfaces. This is a relatively strong assumption, e.g., when thinking about urban rescue, forest, or underground environments. In addition, the requirement of a local positioning system is not always practical.

Sheehan et al. [10] constructed a sensor platform assembled from three independent 2D laser range finders mounted on a rotating plate. To calibrate the extrinsic parameters of all three scanners, they formulated a crispness function representing the sharpness of the resulting 3D point cloud, i.e., the neighbourhood distribution of the measured points. This measure consists of a Gaussian mixture model (GMM) of each individual point’s neighbourhood. The GMM gets more peaky as the deviation of nearby points in the neighbourhood of a point decreases, which happens if the transformation to the scanners approximate towards the true ones. To quantify this measure in a score that then can be maximised, the model is put into the Rényi Quadratic Entropy function [11]. The scanner transformations maximising the model’s entropy should be the ones sought.

Sheehan’s calibration method is tailored to their platform and only calibrates the relative position of the sensors to each other.

Maddern et al. [12] extend Sheehan’s method by the calibration of several other LiDAR or LRF sensors mounted on a vehicle. They require to drive a path, so that all sensors cover as much of the environment as possible. Utilising a positioning system with known covariance matrix, i.e., known measurement uncertainty, the sensor data can be transformed into a common coordinate system. This allows a comparison between the sensor data of the different sensors, especially between Sheehan’s platform and the other sensor data. To do so, Maddern et al. introduced another entropy based cross-sensor similarity measure. It integrates the Jensen–Rényi Divergence [13] in the crispness function of Sheehan et al. [10]. The new measure will reach its maximum with a transformation that results in the most similar sensor measures in the common frame. The requirement of driving and a working positioning system makes this method inapplicable in many situations. The necessary conditions prevail over the improvements made compared to Sheehan’s method.

While driving along a V-shaped track, the point clouds recorded by the LiDARs mounted on a vehicle should be aligned when they are transformed using the correct transformation $M_L$ between LiDARs and vehicle frame. To measure the alignment, He et al. [14] use the definition of a fitted plane and the pairwise distance between those planes, introduced in in He’s previous publication [15]. This allows He et al. [14] to formulate an error function depending on trajectory and LiDAR pose to transform the plane representations into a common frame and minimize its distance. Once a reference LiDAR is calibrated, other mounted LiDARs can be calibrated to minimize the distance between their fitted planes and the reference planes of the already calibrated sensor. Again, driving is required and the use of 2D-SLAM could cause additional transformation errors. It also requires extra hardware. Furthermore, the error based on the distance between the fitted planes is a good error measure, but assumes relatively large planar surfaces in the environment.

In [16], Oberländer et al. utilize the crispness introduced by Sheehan [10], and also the redundancy in the observation of a rotating or swivelling 2D laser range finder, mounted on their sensor platform, after a full rotation of the LRF. Given the case that the surrounding environment is static, the scanner has seen everything twice after a full revolution. Based on this fact, an objective function that represents the crispness of point clouds with this redundancy feature is formulated. To exploit this redundancy, the point cloud is separated into the two similar parts after a whole rotation. The objective function transforms the sample points into a common frame. Different to [10], the GMM of each point’s neighbourhood inside the other redundant point set, respectively, is calculated. The quantification is the same as in [10]. A high crispness, depending on the 6-DOF pose parameters of the scanner encodes a low deviation of points in their respective neighbourhood, which, in return, means, that point pairs in the redundant data are close together, or, in other words, represent the same surface patch. In both methods, Sheehan’s [10] and Oberländer’s [16], the crispness is optimised using iterative, numerical Newton-like algorithms. However, ambiguities emerge between translation and rotation when the sensors are rotated eccentrically on the platform, i.e., rotated around the center with a radius $r>0$. Furthermore, there are problems caused by different view angles of the redundant LiDAR measures. Nevertheless, the exploitation of redundancies in general is an elegant way to determine the scanner’s pose.

Nouira et al. [17] make use of the precise knowledge of the vehicle’s pose. They state that sample points on a planar surface of the same or a neighbouring scanline should be close together, if the transformations from navigation frame to the vehicle’s baselink and finally to the scanner’s frame are known and correct. Due to the fact that the pose is known by several sensors, Nouira et al. [17] were able to formulate an objective function which minimizes the Euclidean distance of neighbouring points on planar surfaces. This, however, requires several additional sensors and driving during the calibration process. Moreover, some of the required sensors, such as GPS are not always available. Besides the sensor requirements, there are difficulties exploiting the environments structure to avoid calibration targets. Planar surfaces are mostly found in artificial environments.

Some of the proposed methods require driving. This makes them inapplicable in many situations, for example, in stand-alone operation of sensing platforms. Others require additional localization information which are also often not available. Avoiding the use of calibration targets comes with strong assumptions about the agent’s environment. This will make recalibration sometimes difficult. Our novel calibration method does not require any additional localization nor does it make any assumptions about the scanner’s surroundings during the calibration process. Moreover, the majority of methods either optimize the sensor pose information with respect to other sensors, while our approach optimizes the extrinsic parameters with respect to static construction parts of the platform.

3. Calibration Method

On many sensing platforms, LiDARs are mounted on a rotating carrier, to enable the sensors to extend the field of view. Thus, it changes its direction while continuously scanning the environment in operation mode. The steady change of view direction makes a correct transformation of the drawn sample points more important because errors do not only result in a static rotated or shifted perception, but in many accumulated errors of this kind. The necessary transformation corresponds directly with the sensor’s pose with respect to the sensor carrier’s rotation center. This static transform is defined by the LiDAR’s extrinsic parameters.

The LiDAR is mounted in a way that its frustum is either tangential to the trajectory of the scanner rotation, as indicated by the coloured triangles in Figure 2 or the frustum is intersecting this trajectory, for example, when the scanner in Figure 2 is rotated by 90°. However, in both cases, there is a redundancy in the measurements done by the LiDAR after a full carrier rotation. The reason for this is that, at each carrier orientation, $R_i\in {\mathbb{R}}^{3\times 3}$, the LiDAR scans in opposite directions, simultaneously. These scans are depicted as blue and red lines in Figure 2. It also shows that a full perception of the platform’s surroundings is already completed after a 180° carrier rotation. Thus, there are two full, separable scans recorded after a 360° turn. However, if the transformation of the measured surface samples from the sensor’s frame into a common one is not configured with the true LiDAR pose, i.e., extrinsic parameters, the two resulting, redundant point clouds will differ. The magnitude of this divergence directly corresponds to the difference between the configured extrinsic parameters of the LiDAR and its real-world pose.

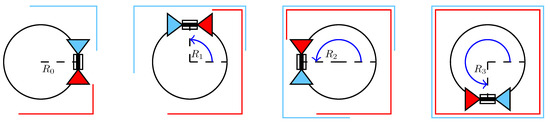
Figure 2. Perception redundancy after a full carrier rotation. The triangles in blue and red show the LiDAR’s frustums in a simplified manner. The lines, also in blue and red, are the measurement in the respective view direction. The figure shows four representative carrier orientations $R_i\in {\mathbb{R}}^{3\times 3},i=0,1,2,3$ with the revolving LiDAR and how its perceptions construct a full scan after a 180° carrier rotation.

Inspired by Oberländer’s approach [16], this is a key observation for the proposed method. The objective is to equalize the redundant measurements carried out by the sensor. This can, in principle, be achieved independently from any further tools, only by scanning the environment. However, some experiments with our sensing platform suggested that there are problems with different view points when inferring the LiDAR’s pose only from its bare measurements. This results from the fact that rotations with a positive radius, i.e., revolving or orbiting a rotation center, may measure the surroundings twice, like explained above. However, the two scans will differ slightly, since the same object scanned from different positions result in different occlusions, i.e., the shadows casted by the object on itself and other objects diverging. The different view points arise from the scanner’s translation relative to the rotation center. For example, the carrier orientations $R_0$ and $R_2$ in Figure 2 have overlap in the measurements, potentially observing the same surface, but from different positions. These problems are avoided by detecting spherical targets and using only their center points as artificial features to be aligned instead of the entire scanned environment. The estimation of the sphere center points is independent from the view angle onto, and the excerpt of the sphere seen by the LiDAR.

The targets are placed in pairs on opposite sides of the platform, thus two spheres of a pair are, and have to be, visible at the same time without any further platform rotation (Figure 3, top-left). As mentioned above, after a full carrier rotation, each pair of spherical targets has been seen twice. The redundant target pairs are depicted in Figure 3. This redundancy can be used to formulate error measures, which can then be minimised. Obviously, the sphere centers corresponding to the same sphere need to be congruent in the common rigid frame, even if they were seen from different carrier orientations, since they represent the same object. Thus, their divergence indicates how strong the error of a specific sensor pose is. However, since the sensor has six degrees of freedom, minimising the error can get computationally expensive, especially because all of them need to be optimised together, as long as they are hard coupled. In addition, there potentially arise combinations of orientations and translations compensating others, i.e., different extrinsic parameters could align the target center points. Inspired by Kang et.al. [7], this problem is approached by separating the sensor orientation from the translational part resulting in two error functions depending on the LiDAR’s extrinsic parameters.

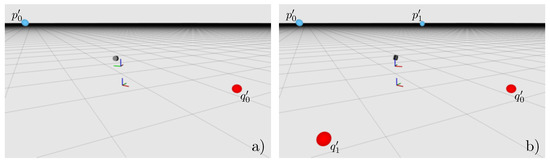
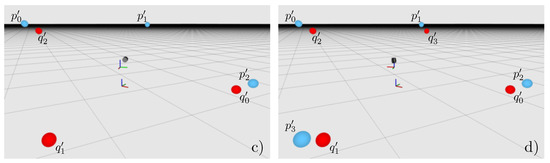
Figure 3. Sphere center points around the revolving LiDAR in the middle of the images. As in Figure 2, the spheres are coloured and denoted with $p_i,q_i,i=0,1,2,3$ according to their respective frustum-direction and the carrier’s i-th orientation $R_i$. From top-left to bottom-right, the sphere centers are estimated by the LiDAR measurements. (a) most clearly reveals the fact that two spheres can be seen by the LiDAR without further movement. (b) shows the scanner observing the second pair of spheres, after the carrier has turned by 90°. In the third image (c), the first target pair is detected a second time after another 90° rotation. Note that the different colors indicate that it is seen from a different carrier orientation. Furthermore, note that the center points are not aligned. This results from the actual transformation error between the sensor frame and the platforms base frame. Moreover, it clarifies that a redundant measurement of the surroundings begins after a 180° carrier rotation. Like (c), the last picture (d) shows the other redundant sphere detection after the carrier turns further 90°. In each picture’s center area, the revolving LiDAR is depicted in the coordinate system of the rotating sensor carrier. As can be seen, the LiDAR’s pose with respect to the carrier is static, i.e., it does not change over time.

The actual decoupling is deduced in Section 3.1. Finally, Section 3.2 derives a three-dimensional error measure for the orientation and another one for the translation, given that the orientation is already known. Minimising both with respect to the LiDAR’s extrinsic parameters aligns the sphere center points.

3.1. Decoupling

Minimising a function with six free parameters can be computationally expensive. Furthermore, in the case of transformation arguments, there are ambiguities between translation and orientation, i.e., some combinations of translations and rotations can compensate others. To tackle these challenges and especially to reduce the problem’s dimensionality, we decouple the rotational part from the full six degrees of freedom transformation. Inspired by [7], we formulate individual error functions for the rotational and translational part of the LiDAR’s extrinsic parameters. To do so, it is assumed that the LiDAR is able to see two spheres $S_{p_i}$ and $S_{q_i}$ in a single carrier position $R_i\in {\mathbb{R}}^{3\times 3}$ and that their respective center points $p_i$ and $q_i$ are estimated. We denote the scanner’s extrinsic parameters as translation $\overrightarrow{t}\in {\mathbb{R}}^3$ and orientation $R\in {\mathbb{R}}^{3\times 3}$. It will be the final objective to optimize the respective error functions with respect to $\overrightarrow{t}$ and R, separately.

The center points of $S_{p_i}$ and $S_{q_i}$ can be represented in the common, rigid frame of the sensing platform’s base, by transforming them with the sought sensor transformation $T_{R^{\prime }S}\in {\mathbb{R}}^{4\times 4}$, defined by the extrinsic parameters, into the carrier’s rotation center and subsequently applying the measured transformation of the sensor carrier $T_{R{R}^{\prime }}\in {\mathbb{R}}^{4\times 4}$. Since the translational component of $T_{R{R}^{\prime }}$ is always zero, its orientation is changing over time, it can be reduced to $R_i\in {\mathbb{R}}^{3\times 3}$. The index i denotes that the carrier orientation at of the i-th target pair can be detected:

$$\begin{array}{cc}\hfill {p^{\prime }}_i& =R_i\ast R\ast (p_i+\overrightarrow{t}),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill {q^{\prime }}_i& =R_i\ast R\ast (q_i+\overrightarrow{t}).\hfill \end{array}$$

(2)

Figure 4 depicts the transformed, estimated center points of a target pair ${p^{\prime }}_i$ and ${q^{\prime }}_i$ can be used to construct a vector ${\overrightarrow{d}}_i$ pointing from ${p^{\prime }}_i$ to ${q^{\prime }}_i$:

$${\overrightarrow{d}}_i={p^{\prime }}_i-{q^{\prime }}_i.$$

(3)

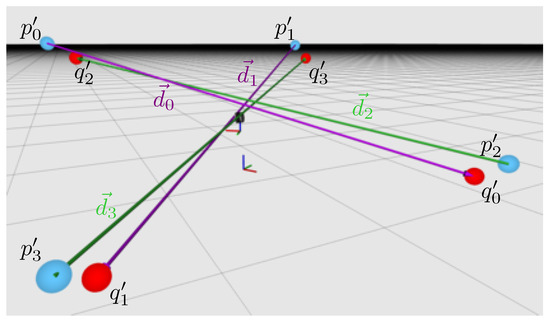
Figure 4. Direction-vectors between (e.g., ${\overrightarrow{d}}_1$ and ${\overrightarrow{d}}_3$) become anti-parallel if the rotation is well known. The picture shows an exemplary target arrangement using $M=4$ spheres. The depicted vectors indicate that the platform is not yet calibrated.

Inserting Equations (1) and (2) in Equation (3) results in

$$\begin{array}{cc}\hfill {\overrightarrow{d}}_i& =R_i\ast R\ast (p_i+\overrightarrow{t})-(R_i\ast R\ast (q_i+\overrightarrow{t}))\hfill \\ & =R_i\ast R\ast p_i+R_i\ast R\ast \overrightarrow{t}-(R_i\ast R\ast q_i+R_i\ast R\ast \overrightarrow{t})\hfill \\ & =R_i\ast R\ast p_i-R_i\ast R\ast q_i\hfill \\ & =R_i\ast R\ast (p_i-q_i).\hfill \end{array}$$

(4)

Thus, the vectors ${\overrightarrow{d}}_i$ between the center points of a pair of spheres, seen at a carrier orientation $R_i$ do not depend on the LiDAR’s translation relative to the carrier’s rotation center.

This leads to another observation of two such vectors ${\overrightarrow{d}}_i$ and ${\overrightarrow{d}}_j$ between the same pair of spheres, but seen with different carrier orientations $R_i$ and $R_j$, respectively, resulting in ${\overrightarrow{d}}_0$ and ${\overrightarrow{d}}_2$ as illustrated in Figure 4. Due to the redundancy in the LiDAR’s measurements, both vectors have to point in exactly opposite directions, when they are transformed into a common frame. This is because both measurements include the same spheres: $S_{p_i}$ on the left of the sensor and and $S_{q_i}$ from the other orientation. This means that

$${\overrightarrow{d}}_i=-{\overrightarrow{d}}_j$$

(5)

with $j=i+(M/2)$ has to hold, where M is the number of spheres. This insight is used in Section 3.2 to formulate a rotational error of the sensor’s pose.

3.2. Optimisation

As mentioned before, the LiDAR’s orientation is optimised separately from its translation. The vectors ${\overrightarrow{d}}_i$ and ${\overrightarrow{d}}_j$, between a pair of sphere centers estimated from two different carrier orientations $R_i$ and $R_j$, need to be anti-parallel when the configured extrinsic parameters of the sensor are close or equal to the true pose. This is exploited by formulating the error for a single pair of spheres as the magnitude of the cross-product of ${\overrightarrow{d}}_i$ and ${\overrightarrow{d}}_j$. Thus, the norm directly depends on the angle $\varphi$ between the two vectors ${\overrightarrow{d}}_i$ and ${\overrightarrow{d}}_j$, which should be anti-parallel, i.e., $\varphi =\pi$. This observation leads to an error function for a single pair of spheres:

$$\begin{array}{cc}\hfill E_{ij}\left(R\right)& =\Vert {\overrightarrow{d}}_i\times ({\overrightarrow{d}}_j)\Vert =\Vert R_i\ast R\ast (p_i-q_i)\times R_j\ast R\ast (p_j-q_j)\Vert .\hfill \end{array}$$

(6)

As can be seen in Equation (6) $R_i$, $p_i$, $q_i$, $R_j$, $p_j$ and $q_j$ are all measured quantities. Therefore, the error of the vector pair ${\overrightarrow{d}}_i$ and ${\overrightarrow{d}}_j$ only depends on the LiDAR orientation R. In addition, the cross product’s norm of two anti-parallel vectors becomes zero, so it works well as a minimisation objective in the first step. Thus, an overall error for the rotational part R of $T_{R^{\prime }S}$ can be formulated as

$$E\left(R\right)=\sum _{i=0}^{M/2}{E}_{ij}\left(R\right),$$

(7)

where, again, $j=i+\frac{M}{2}$ and M is the number of spheres. The orientation $R^{\ast }$ that minimizes $E\left(R\right)$ approximates the LiDAR’s actual orientation:

$$R^{\ast }=\underset{R}{argmin}\left[E\left(R\right)\right].$$

(8)

Afterwards, the translation is optimised separately. The sphere centers representing the same target can be used to formulate the error of a given sensor translation $\overrightarrow{t}$. As the orientation $R^{\ast }$ has been estimated previously, the translation error can be formulated as

$$\begin{array}{cc}\hfill E_{ij}(\overrightarrow{t})& =p_i^{\prime }-q_j^{\prime }=R_i\ast R^{\ast }\ast (p_i+\overrightarrow{t})-R_j\ast R^{\ast }\ast (q_j+\overrightarrow{t}).\hfill \end{array}$$

(9)

Again, $R_i$, $p_i$, $R_i$, and $q_j$ are measured. Furthermore, note that $R^{\ast }$ is assumed to be already estimated accurately. Therefore, $\overrightarrow{t}$ is the only independent variable. As already done for the LiDAR’s orientation, Equation (9) can be used to formulate a sum. This time as a least squares problem:

$$E(\overrightarrow{t})=\sum _{i=0}^{\frac{M}{2}}{E}_{ij}{(\overrightarrow{t})}^2,j=i+\frac{M}{2}.$$

(10)

The actual translation with respect to the carrier’s rotation center ${\overrightarrow{t}}^{\ast }$ is estimated as:

$${\overrightarrow{t}}^{\ast }=\underset{\overrightarrow{t}}{argmin}\left[E(\overrightarrow{t})\right].$$

(11)

Both error functions have to be minimised with respect to their respective argument. In our experiments, attempts to do this via classic gradient descent or trust region methods often converged to one of many local minima for the orientation, and thus did not result in the desired global minimum. A global minimisation approach seems to be better suited. A simple grid search to determine global minima gets tractable due to the reduction of the dimensionality of the original problem, achieved by decoupling the orientation and translation of the six degrees of freedom pose. However, this still leads to cubic complexity of both objective functions, if no further optimisations are performed.

A further dimension reduction is possible for the translation optimisation, since the z component of $\overrightarrow{t}$ can not be found. Changes in z will just lift or lower all measurements equally and therefore will have no effect on the error function. Ignoring $t_z$ will reduce the translation search to quadratic complexity.

However, the complexity of the optimisation of the sensor orientation remains cubic. It can get tractable, in practice, by reducing the range of the search space or the parameter grid’s resolution. The latter, however, is also a problem because the exact global minimum will probably be missed with a low grid resolution. Therefore, this is tackled with a subsequent local optimisation using a gradient descent solver using promising candidates resulting from the grid search as starting points.

4. Evaluation

The optimisation quality probably depends on the arrangement of the calibration targets. There are two quantities that could affect the calibration result: (1) is the distance between the targets and the LiDAR and (2) the angle between the direct lines corresponding to the pairs of spheres.

The distances $\Vert L_{02}\Vert$, $\Vert L_{13}\Vert$, $\Vert {L^{\prime }}_{02}\Vert$ and $\Vert {L^{\prime }}_{13}\Vert$ in Figure 5 have a direct influence on the sensitivity of the objective function for the orientation optimisation. The sensitivity of a function is the magnitude of the change of its response when its arguments are changed, that is, how steep the gradient is, relative to the change in a certain argument. Thus, the sensitivity has an influence on the optimisation behavior and should be high. For the distance, this means that the sensitivity with respect to $\varphi$ is of interest:

$$\begin{array}{cc}\hfill E_{ij}(R)& =\Vert \overrightarrow{d_i}\times (-\overrightarrow{d_j})\Vert =\Vert \overrightarrow{d_i}\Vert \ast \Vert -\overrightarrow{d_j}\Vert \ast sin(\varphi ),\varphi =\sphericalangle (\overrightarrow{d_i},(-\overrightarrow{d_j})),\hfill \\ \hfill \frac{d{E}_{ij}(R)}{d\varphi }& =\Vert \overrightarrow{d_i}\Vert \ast \Vert -\overrightarrow{d_j}\Vert \ast cos(\varphi ).\hfill \end{array}$$

(12)

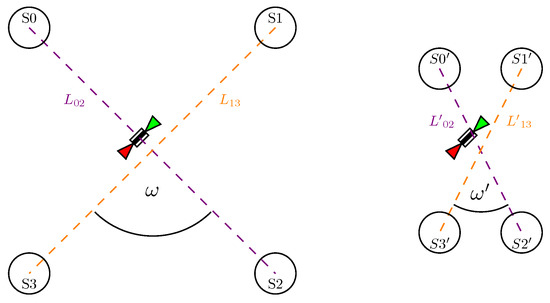
Figure 5. Two possible target arrangements. The left depicts an optimal placement with high target distances $L_{02}$ and $L_{13}$ as well as an angle between them of $\omega ={90}^{°}$. For the arrangement on the right, however, the targets are close to the LiDAR and an there is an angle ${\omega }^{\prime }\ne {90}^{°}$ between ${L^{\prime }}_{02}$ and ${L^{\prime }}_{13}$. The latter is expected to lead to suboptimal calibration results.

The derivative of $E_{ij}\left(R\right)$, with respect to the angle $\varphi$, in Equation (12) is scaled by the squared distance between the spheres of a pair. Therefore, we would expect that a larger distance between the platform and the targets is beneficial for the optimisation results.

The influence of the angles $\omega$ and ${\omega }^{\prime }$, however, does not directly affect the objective function. However, it affects the sensitivity of the coupling between two target pairs. If a change of the extrinsic parameters of the LiDAR results in a rotation of angle $\alpha$ around the direct line $L_{ij}$ between a certain pair of spheres, this does not change the residual contributed by this particular pair. Moreover, this rotation would increase the residual contributed by the other pairs. How strong this contribution gets is defined by the orthogonal portion $r_{kl}=\Vert L_{kl}\Vert sin\left(\omega \right)$, from one direct line $L_{ij}$ to another $L_{kl}$. Rotating around $L_{ij}$ would displace the spheres centers defining $L_{kl}$. The magnitude of the displacement can be described as an chord of length l:

$$\begin{array}{cc}\hfill l& =2r_{kl}sin\left(\alpha \right)=2(\Vert L_{kl}\Vert sin\left(\omega \right))sin\left(\alpha \right),\hfill \\ \hfill \frac{dl}{d\alpha }& =2(\Vert L_{kl}\Vert sin\left(\omega \right))cos\left(\alpha \right).\hfill \end{array}$$

(13)

The derivative, with respect to $\alpha$ in Equation (13), suggests that the coupling of two target pairs is more sensitive if $\omega \approx \pi$. Therefore, better optimisation results are expected if the direct lines between the pairs of spheres are orthogonal.

Further investigations about these expectations will be done in the following sections. To evaluate the calibration quality, a measure to rate recorded point clouds will be introduced in Section 4.1. The experiments in Section 4.2 will assess the calibration qualities of different target arrangements and calibration configurations followed by a discussion of the results in Section 4.3.

4.1. Quality Measures

The lack of knowledge about a ground truth real-world pose of the LiDAR makes it necessary to evaluate the quality of the optimised extrinsic parameters in an indirect way. In our experiments, this is done by rating the quality of recorded point clouds utilising the optimisation results from several calibration runs. Therefore, we introduce a quality measure to rate the recorded point clouds in an offline phase.

There would be an obvious quality measure of the resulting point cloud by comparing the points of the redundant measurements, e.g., by averaging the distance to their nearest redundant neighbour. However, since there is no correspondence between the single points of the different clouds defined, it is not possible to measure their distance or something like that. As the experiments are done in an artificial environment, there are many planar surfaces in the scene. How crisp or sharp a point cloud is can therefore be measured in a more semantic way. The effect on planar surfaces, like walls, were already shown in Figure 1 and thus the point cloud quality corresponds with how noisily those planar regions have been sampled.

To get this information, the largest planes are subsequently detected by fitting planes to the point cloud via a Random Sample Consensus (RANSAC) [18] method followed by a region growing taking only the Euclidean point distance into account. This separates planar unconnected patches lying in the same plane, such as several tables of the same height. This results in a set of smaller point clouds $P_k=\{{\overrightarrow{p}}_0,{\overrightarrow{p}}_1,\dots {\overrightarrow{p}}_{N_k-1}\},k=0,1,2,\cdots ,M-1$, each containing the samples of the respective planar surface patch. Afterwards, the centroid ${\overrightarrow{\mu }}_k$ of each patch is calculated as

$${\overrightarrow{\mu }}_k=\frac{1}{N_k}\sum _{i=0}^{N_k-1}{\overrightarrow{p}}_i,{\overrightarrow{p}}_i\in {\mathbb{R}}^{3\times 1},i=0,1,2,\cdots ,N_k-1$$

(14)

and used to compute the covariance matrix $C_k$ of this point set $P_k$ as

$$C_k=\frac{1}{N_k}\sum _{i=0}^{N_k-1}{({\overrightarrow{\mu }}_k-{\overrightarrow{p}}_i)}^T\ast ({\overrightarrow{\mu }}_k-{\overrightarrow{p}}_i),{\overrightarrow{\mu }}_k,{\overrightarrow{p}}_i\in {\mathbb{R}}^{3\times 1},i=0,1,2,\cdots ,N_k-1.$$

(15)

The covariance matrix $C_k$ encodes the squared deviations in the dataset with respect to ${\overrightarrow{\mu }}_k$. Since, the data points have three dimensions, $C_k$ also has three eigenvectors ${\overrightarrow{v}}_{k0},{\overrightarrow{v}}_{k1},{\overrightarrow{v}}_{k2}\in {\mathbb{C}}^{3\times 1}$, with

$$C_k\ast \overrightarrow{v_{ki}}={\lambda }_{ki}\ast \overrightarrow{v_{ki}},i=0,1,2,$$

(16)

where the eigenvalues ${\lambda }_{k0},{\lambda }_{k1},{\lambda }_{k2}\in \mathbb{C}$ with ${\lambda }_{k0}\ge {\lambda }_{k1}\ge {\lambda }_{k2}$ are associated with the eigenvectors ${\overrightarrow{v}}_{k0},{\overrightarrow{v}}_{k1},{\overrightarrow{v}}_{k2}$, and represent how strong the deviation in the respective direction is. Because a plane only expands in two dimensions, the eigenvector ${\overrightarrow{v}}_{k2}$, associated with the smallest eigenvalue ${\lambda }_{k2}$, is perpendicular to the plane, if the sampled data contains no additional systematic noise in other directions. In fact, the magnitude of change in this direction has to be the sensor noise or systematic deviations like they appear when points are erroneously transformed from sensor- to common frame (Figure 1). Summing up this error for every plane $P_k$ found in the scene and normalising it with the number of planes performs as a measure $E\left(P\right)$ for the cloud sharpness:

$$E\left(P\right)=\frac{1}{M}\sum _{k=0}^{M-1}{\lambda }_{k2}.$$

(17)

4.2. Experiments

The error caused by mistransformation in a point cloud is difficult to isolate, since there are different possible sources for errors. For example, there are errors caused by LiDAR noise or caused by the discrete measurement of the rotation encoder, resulting from angles which are actually between two encoder steps. Neither the source nor the respective portion of the sensory error can be distinguished from the residual error remaining after calibration. Furthermore, another problem prevents the direct analysis of the actual remaining transformation error. The data used during the calibration process are estimated sphere centers. These estimations are themselves erroneous and prevent the calculating the exact pose. Therefore, the quality measure described in Section 4.1 is applied to the uncalibrated LiDAR measurements and to all calibration results with the different target arrangements, parameter grid resolutions, and initial pose guesses. Rating the outcomes of the calibration in different conditions allows a reasoning about the method’s behavior.

During all experiments, the Velodyne VLP-16 of the SWAP platform [6] was calibrated. This is a suitable sensing platform since the mounted Velodyne is a revolving multi-beam LiDAR. The platform was placed in the hall of a building on our campus, i.e., in an environment with many planar surfaces that are not too close to the platform (ca. $5\mathrm{m}$ away). This is important, since errors caused by the orientation of the LiDAR increase with the distance of the sampled surface data. Moreover, the walls and floor, contained in the excerpt of the hall used to rate the calibration quality, have different orientations to ensure all dimensions of the sensor orientation are reflected by the orientation of the planar surfaces. The excerpt is depicted in Figure 6. Additionally, two objects, a cube (ca. 0.4 $\mathrm{m}$ side length) and a cylinder (ca. 0.4 $\mathrm{m}$ diameter and height), were placed in the scene to provide additional surface data and show concurrence of the redundant LiDAR measurements. The experiments can be split into two phases. The first phase records the calibration targets within the different arrangements discussed earlier and calibrates the extrinsic parameters using different configuration sets. The second phase takes the resulting LiDAR poses from the first phase and applies them to the platform configuration to record the environment, i.e., the building on our campus, in operation-mode. Finally, the proposed quality measure is applied to the record, in order to compare several calibration results.

Figure 6. Point cloud of the scene, recorded to compare calibration qualities with different configurations. The scene contains different oriented planar regions, about 3–5 $\mathrm{m}$ away. They cover the test of all orientation dimensions of the LiDAR. Moreover, a cube with about 0.4 $\mathrm{m}$ side length and a cylinder with ca. 0.4 $\mathrm{m}$ diameter and height are placed in the scene. They should be congruent after calibration.

In the first phase, the spherical calibration targets were placed around the LiDAR platform and were recorded in calibration mode. This means that the platform drives to several previously configured angles in sequence, from which the spheres can be scanned by the mounted Velodyne VLP-16 LiDAR to estimate their center points. These scans were recorded and passed to the calibration software, which optimizes the kinematic chain as explained earlier. We performed several calibration runs under different circumstances. First, the target arrangements were changed, i.e., the targets were placed at different distances of $2.0\mathrm{m}$, $3.0\mathrm{m}$, $3.5\mathrm{m}$ and $4.0\mathrm{m}$ from the sensor platform. This allows us to estimate how the sensitivity changes with the distance, as mentioned in Section 3.2. Furthermore, we, in addition, expected, that it is more beneficial to have a 90° angle between the $\overrightarrow{d}$-pairs. Therefore, the target pairs were additionally placed in a $\omega \approx {90}^{°}$ and a ${\omega }^{\prime }\approx {45}^{°}$ angle from each other (see Figure 5). In addition to the physical variations during the experiments, calibration parameters were also changed. The resolution of the search grid, used to find the global optimal orientation parameters, was configured to a $0.005$ step size in each dimension, to test a low resolution grid. To study a significantly higher resolution, the step size was also set to $0.00025$ in yaw, pitch and roll. Second, to investigate how the method behaves if the initial pose guess is far from the true pose, the actually measured pose was tested in comparison to one with an additional error of $+0.03$, added to all five dimensions.

The calibration runs result in different transformations that were used to record the surroundings in a second phase. While running the platform in operation mode, it was configured to rotate continuously with $0.0175\mathrm{Hz}$ (i.e., one full rotation in about a minute) to sample the environment. The records of the continuous runs were cropped to an excerpt of the room to avoid negative influence of clutter or salient structures of the building. The plane deviation measure was applied to each of these records to rate the quality of the respective point cloud. We set the parameters of the measure as followed. The RANSAC of the plane deviation has a parameter to set the allowed distance between the plane model and the data points to distinct plane inlier from other points. This was set to $2\sigma =0.06$, i.e., the doubled sensor noise, to prevent the potential over-segmentation of calibration results with low quality, i.e., high noise and thus also high point deviations. The same applies for the allowed point distance during the region growing. The qualities of the recorded point clouds are plotted against the different target distances in Figure 7.

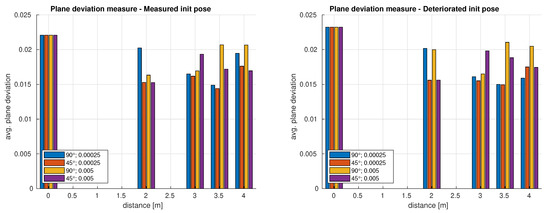
Figure 7. Results of experiments calibrating the LiDARs extrinsic parameters under different circumstances and with different quality measures. The graphs in the left diagram show the quality of recorded point clouds after calibration from a pose we actually measured at the platform construction, rated with the plane deviation (above) and the crispness measure (below). The graphs in the right diagram depict the same ratings but applied to results from an initial pose guess with an artificially upscaled error. All graphs contain ratings of calibration results produced from different target arrangements, each calibrated with a high ($0.00025$) and a relatively low ($0.005$) resolution of the pose parameter grid.

Additionally, to study the calibration runtime with different configurations, several calibration runs with static range limiting the search space and from a single initial pose guess were done. The runtime depends on the grid resolution, runtime of the local optimiser and the number of detected promising starting points for the gradient descent. All calibration runs to log the optimisation durations were performed on a Lenovo Thinkpad T460p laptop with an Intel(R) Core(TM) i7-6700HQ CPU. The CPU has four physical cores and another four logical ones. Each core is working at 2.60 GHz. Furthermore, the system has 16 GB of RAM and a 128 GB SSD storage. The logged runtimes are displayed in Table 1.

Table 1. Logged durations of the single optimisation steps with grid resolution in the first column. The second column shows the total durations composed from the time taken by the grid search (third column) and the subsequent local optimiser for the orientation and translation (last column). The resolutions used in experiments are bold.

Resolution [rad]	Total [s]	Grid [s]	Local [s]
0.005	7.588	0.618	0.018 + 6.951
0.0025	13.116	6.678	0.029 + 6.408
0.001	54.782	49.543	0.024 + 5.215
0.00075	106.638	101.075	0.008 + 5.554
0.0005	343.847	338.135	0.012 + 5.699
0.00025	2611.7	2606.2	0.024 + 5.462
0.000125	19359.7	19354.3	0.017 + 5.396
0.0001	38592.8	38586.3	0.013 + 6.488

4.3. Discussion

The plots in Figure 7 indicate an improvement of the extrinsic parameters compared to the respective initial guess, as measured with the plane deviation. The tendency to the optimal configuration goes to a sweet spot at a distance between sensor and targets of $3.5\mathrm{m}$ and a high resolution for the grid search (blue and red bars). This is indicated by a very low plane deviation for these configurations. Other configurations with close targets or a low resolution of the search grid also improve the initial pose, but scored less, compared to the sweet spot.

It is significant that targets placed at great distances lead to better results, at least for the promising grid configurations. The score gets better up to 3.5 m. Calibration runs with targets placed in $4.0\mathrm{m}$ range come up with worse scores. We believe that this is caused by the increasing error from sphere center estimation, dominating the benefit of targets placed farther away. In general, calibration runs with targets placed close to the platform result in less sharp point clouds. As predicted by our expectations, this can possibly be explained via the sensitivity of the objective function to optimize (see Section 3.2) and with the fact that a divergent angle has less effect at close range. This could possibly shift or widen minima to saddles to which the optimiser converges. This makes it necessary to place the targets as far as possible from the platform as long as an accurate sphere center estimation can be expected.

It was also expected to get better results using the higher resolution for the parameter grid used for the search of promising extrinsic parameter sets to start a gradient decent optimisation at. In fact, the results contain no evidence for a good result on low resolved search grids. Thus, a high resolution search seems to be not only beneficial, but also necessary.

Surprisingly, the angle between the target pairs (see Figure 5) had no strong or even any effect on the results. The fact that the 45° arrangement even scores best can arguably be explained by an inferior estimation of sphere centers when the data for the 90° arrangement were recorded. There is no theoretical reason for the acute-angle to be an advantage, known to us.

The plane deviation measure gives evidence that the initially guessed sensor pose does not need to be very accurate. The deteriorated initial pose parameters, shown in the right plot of Figure 7, result in similar qualities as the parameters estimated from the originally measured initial pose (left plot). Furthermore, Figure 8 supports this observation. The figure shows the point clouds recorded with the initial pose guesses in the first row—on the left side with the measured and on the right side with the deteriorated pose. The results with the best quality scores are shown below their respective initial guess. Both present fairly sharp point clouds. In addition, the objects, cube and cylinder placed in the scene got congruent. This is especially noticeable in the right column starting from the deteriorated initial pose.

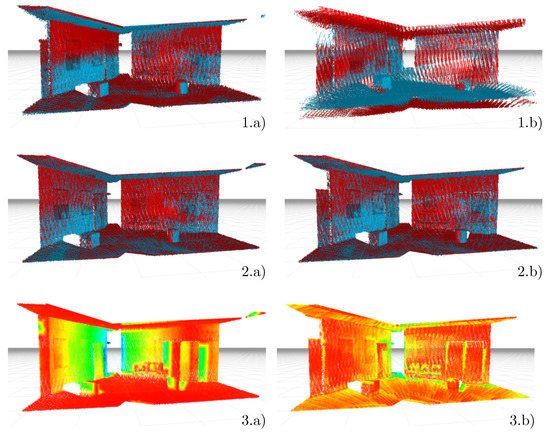
Figure 8. Point clouds sampling the excerpt of the test scene, the quality measure was applied to. The images (1.a,1.b) in the first row show the records done with the initial extrinsic parameter sets, used to study the influence of the initial pose the optimiser starts with. The cloud in (1.a) results from using the sensor pose parameters measured on the SWAP platform by hand. The one in (1.b) results from applying the transformation resulting from a deterioration of the measured transformation. Images (2.a,2.b) in the second row depict the resulting clouds after the parameter optimisation from the respective initial poses. The red and blue point colouring in the first two rows result from separating the two redundant measurements. The images (3.a,3.b) in the last row show the distances between the two clouds above. The intensity encodes the magnitude of changes with blue representing strong changes and reddish colors representing small changes.

As the data in the table on the left side in Table 1 suggest, most parts of the optimisation process have more or less constant runtime. Only the time taken by the grid search follows a cubic curve (shown in Figure 9), as the search space has three dimensions yaw, pitch and roll. However, working parallel reduced the duration by a factor of $\frac{1}{c}$, where c is the number of available hardware threads the used CPU can provide. The experimental runs discussed above resulting in the best extrinsic parameter configuration had a resolution of $0.00025$ and took about 43 minutes for the full configuration run excluding the time to perceive the target center points. This is a long time, but is still tractable, as the calibration is an offline process. However, runs with a doubled grid resolution will take $7.41$ times as long and thus will be hard compromise for a higher calibration accuracy.

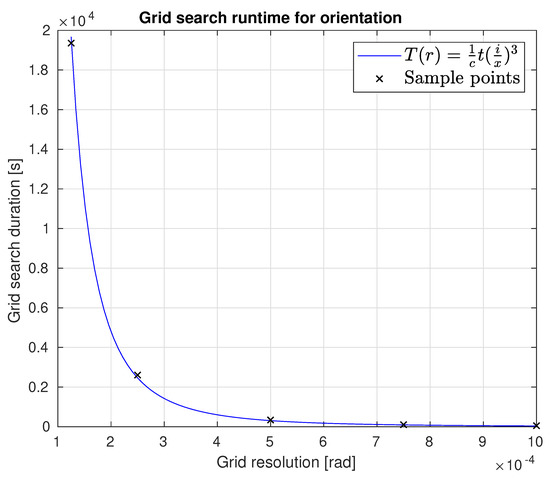
Figure 9. The plot shows the runtime behavior of the grid search with respect to the grid resolution. The curve in the graph is an approximation to the grid search durations in Table 1.

5. Conclusions and Future Work

In this work, we introduced a novel calibration method to optimize the extrinsic parameters of rotating or revolving multi-beam LiDARs. It is inspired by the work of Oberländer et al. [16] to exploit redundancies in the LiDAR measurements, and on the decoupling of pose components by Kang et al. [7]. This enabled us to deduce a theoretical method which allows the separate optimization of orientation and translation. The method was also tested with an exemplary sensor platform by Neuman et al. [6]. Revolving LiDARs theoretically come up with problems like the different view points of the redundant surface information. Therefore, the SWAP platform [6] with its revolving Velodyne VLP-16 was used in our experiments.

Our experiments indicated that the proposed method works, with restriction under the expected circumstances. Decoupling the LiDAR’s orientation from its translational shift relative to the carrier center allows a precise optimization of the five degrees of freedom pose in two steps, as long as a target pair can be detected by the LiDAR at a time and the sensor carrier orientation can be measured e.g., by a rotation encoder.

The calibration quality unfortunately strongly depends on the accuracy of the target detection, which correlates with the target distance. However, the experiments showed that the targets have to be as far away as possible and the resolution of the search grid needs to be relatively high, in order to achieve the optimal results. In particular, the latter can get inconvenient because it leads to longer calibration runtimes. This, however, could still be tractable, since the calibration process usually is not a time-critical application.

Nevertheless, the decoupling and separate optimization was the focus of this work and performed well, and thus the proposed method is a promising approach with potential for further improvements.

For future improvements, the target center issues probably can be addressed by using bigger spheres. Maybe the estimation accuracy for the sphere centers could also be increased if a better reflecting material is used for the calibration targets. This has to be tested in further experiments. Another approach to tackle center estimation errors could be to decrease the individual influence of each inaccuracy. It is possible that using more spheres could reduce the influence of each single one and thus also the influence of the error each one contributes to the sum of residuals. This possibility makes it worthwhile to test the calibration with additional target pairs placed around the platform—especially because the angle between the target pairs was shown to have less effect on the calibration quality. Moreover, for future applications, the sphere fitting method should be generalized. At the moment, our implementation is restricted to multi-beam LiDARs because a single scanline on a sphere has two equivalent fitting solutions. This can not actually be fixed, but maybe the right solution can be parameterized, e.g., by configuring if a certain scanline to be left or right of the sphere’s center point w.r.t. the LiDAR. This has to be implemented and tested.

Unfortunately, it is out of the scope of this work to decide if there are optimization algorithms that are better suited to the proposed problems i.e., more sophisticated global optimizers able to handle saddle regions. This also remains a topic for further research.

Furthermore, the restriction to LiDARs perceiving two calibration targets at a time could be slightly weakened by enabling a calibration, using another already calibrated sensor on the same platform. The alignment of the sphere centers detected by the calibrated LiDAR with the center points estimated by the uncalibrated sensor could also converge to optimized extrinsic parameters. However, this has to be implemented and tested. Although our method originally was developed to calibrate LiDARs mounted on a rotating sensor carrier, the theoretical background of our proposal allows for moving the LiDAR in six degrees of freedom e.g., by mounting it on a driving car to perceive the same target pairs from two different poses to achieve the redundant target measurements. Despite the requirement of an accurate localization system, this also could be a worthwhile application to extend the application of the proposed calibration method.