Dynamic Response Analysis of a Simply Supported Double-Beam System under Successive Moving Loads
Abstract
1. Introduction
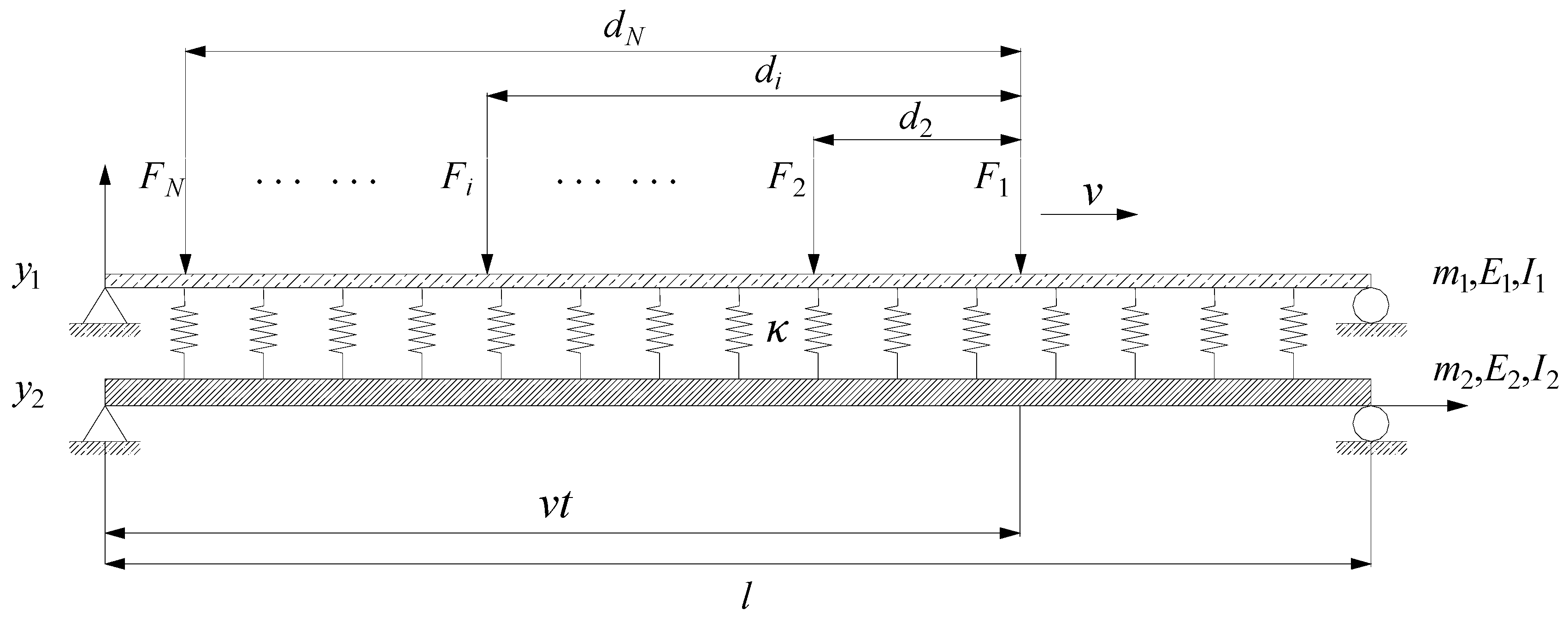
2. Vertical Dynamic Response of a Simply Supported Double-Beam System
2.1. Mathematical Model Building and Parameter Solving
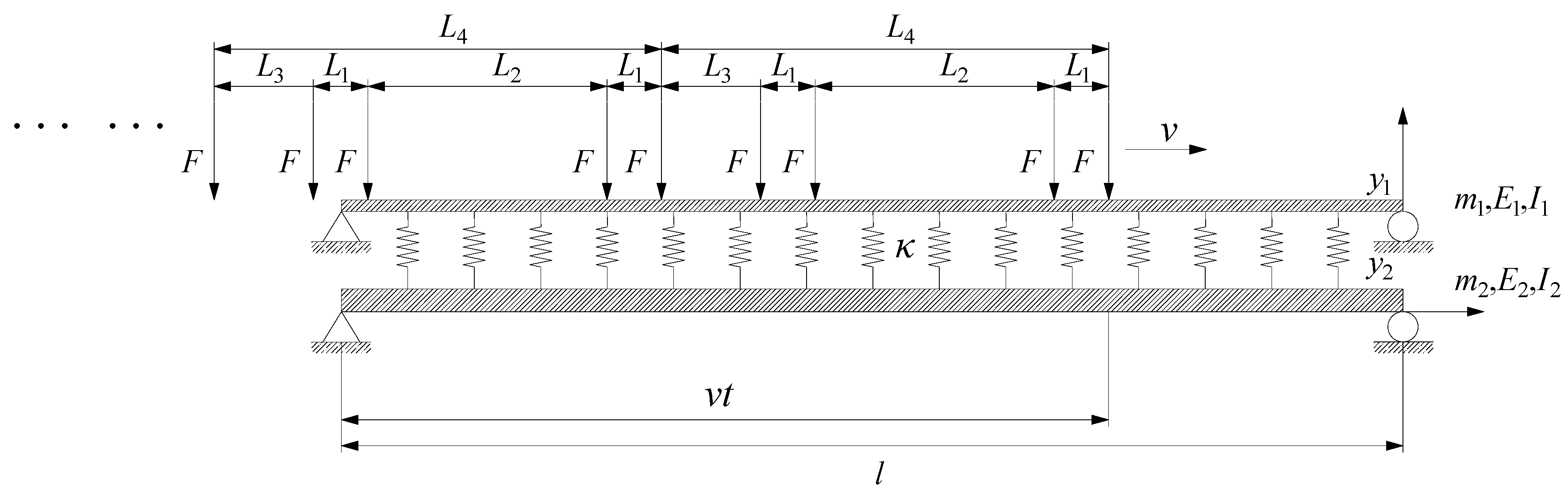
2.2. Expression of Fourier Series of Successive Moving Loads
2.3. Dynamic Response of Double-Beam Model Under Load Series
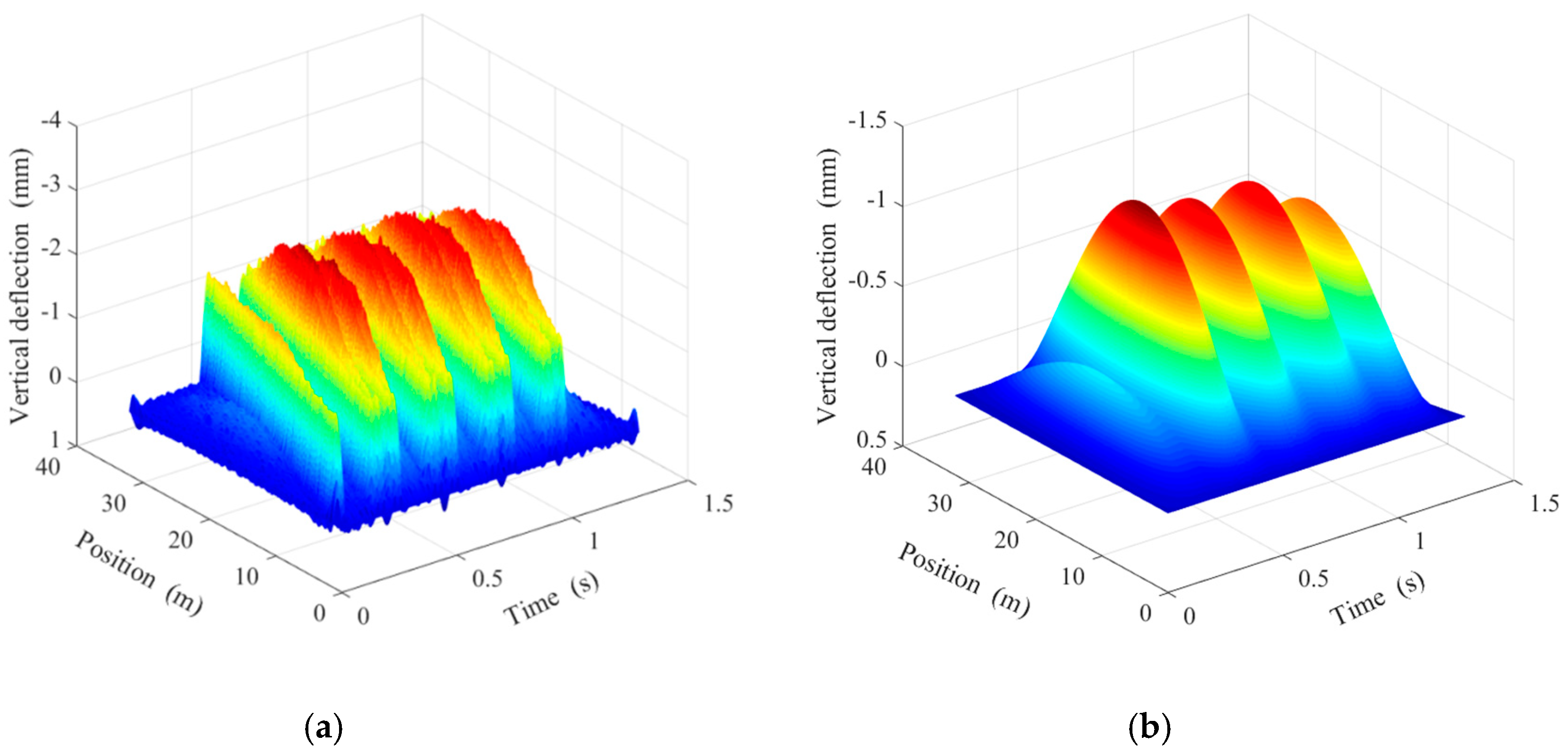
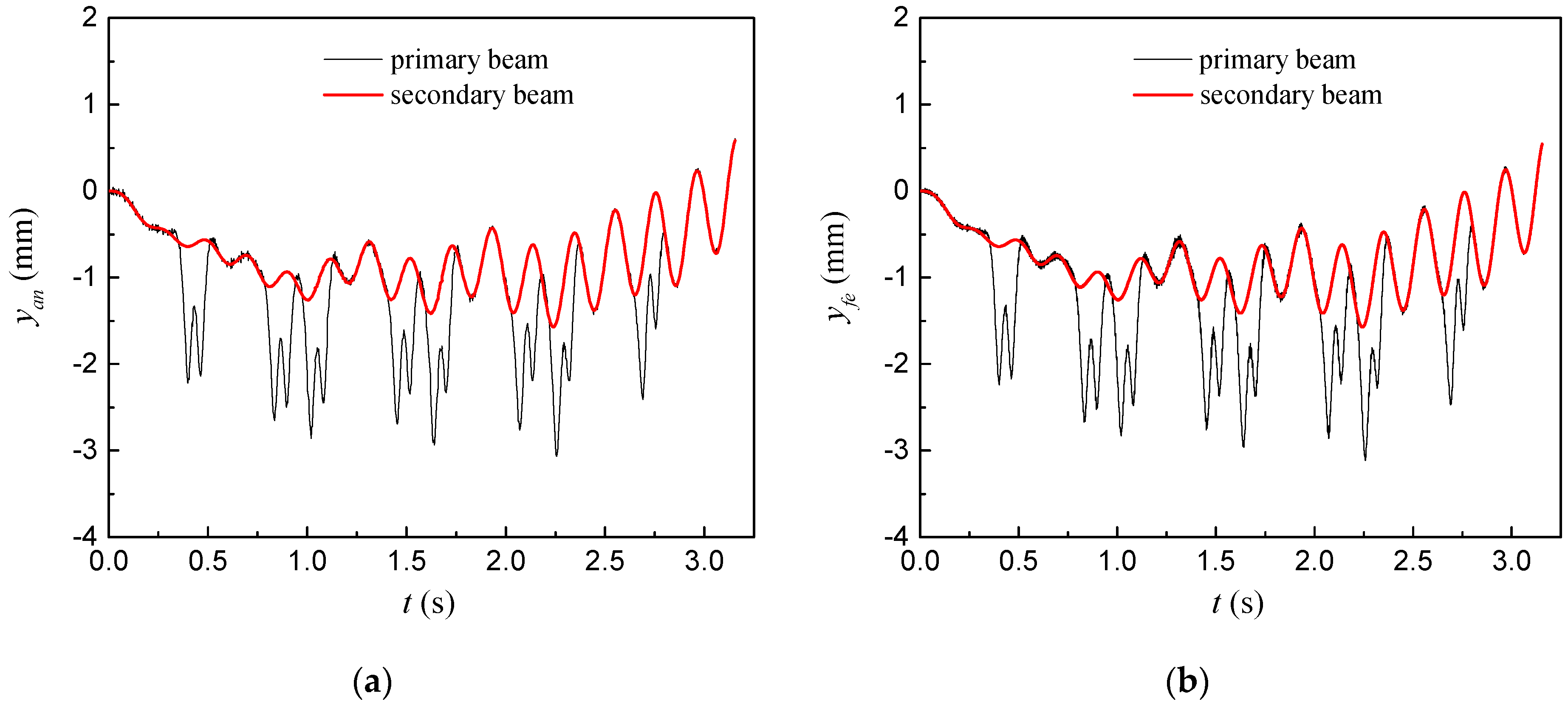
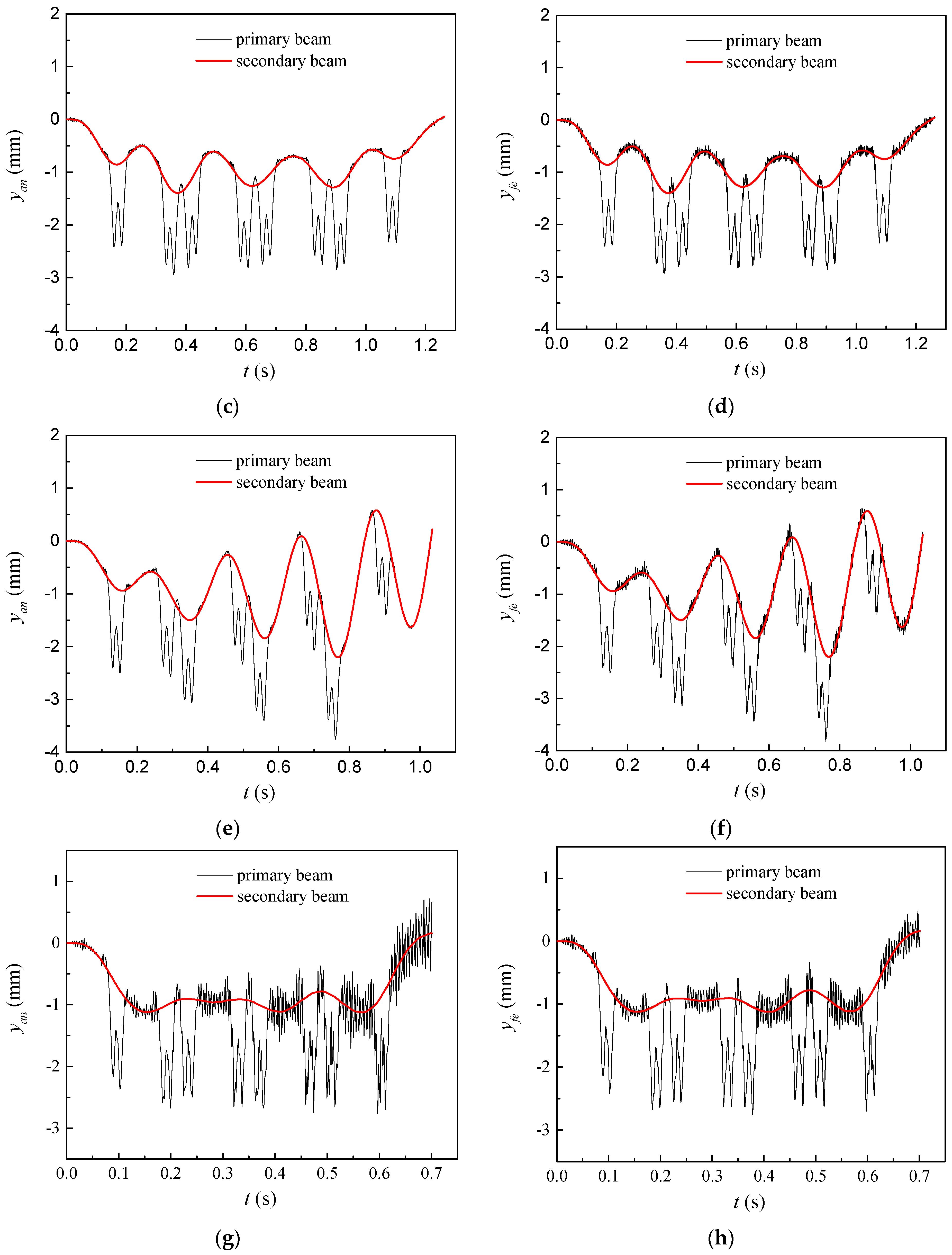
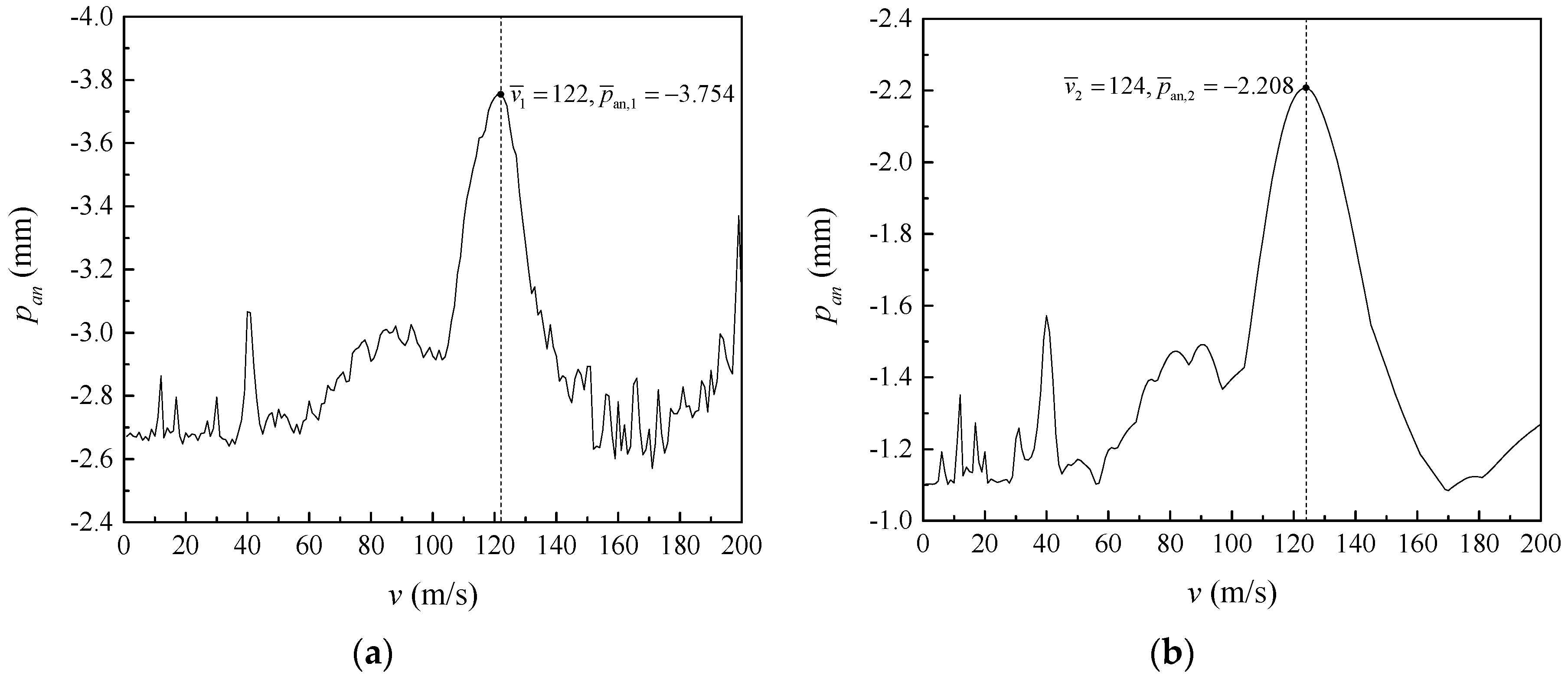
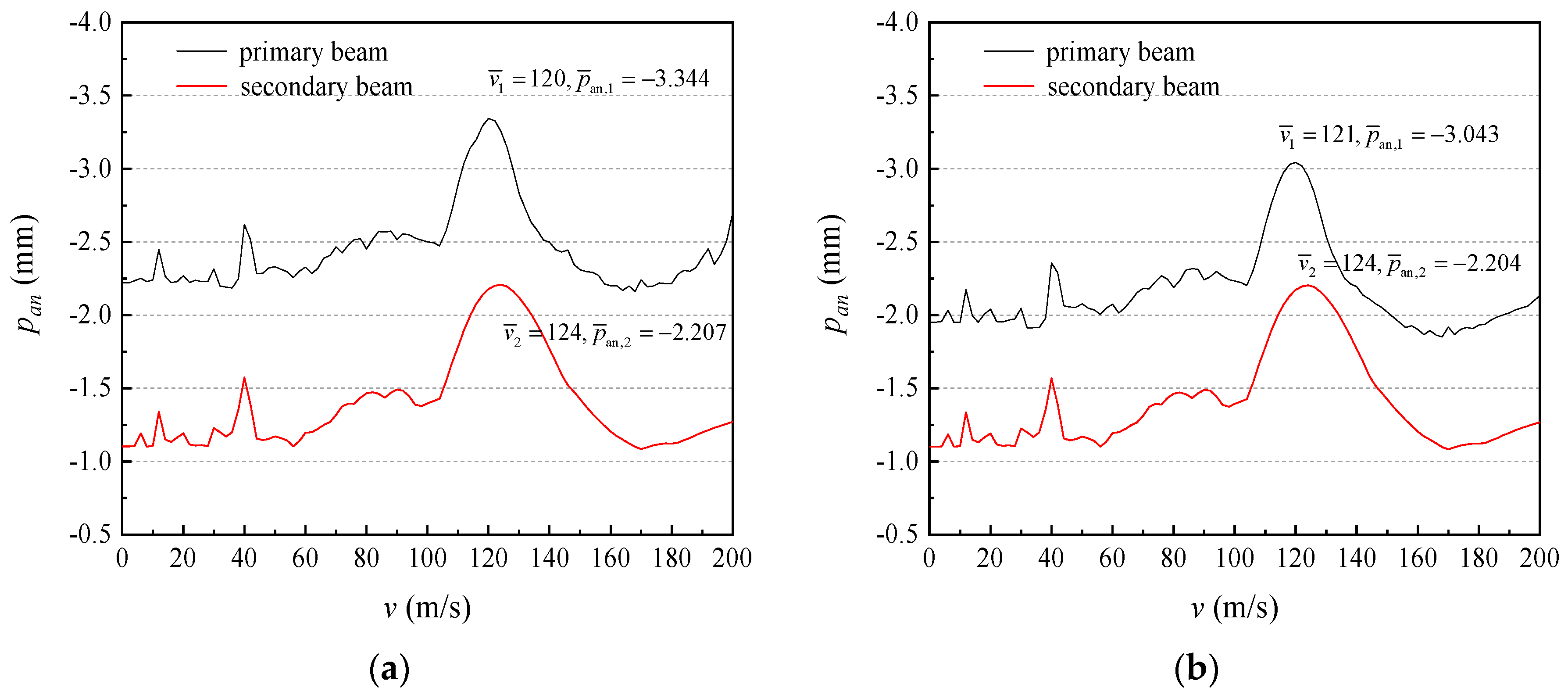
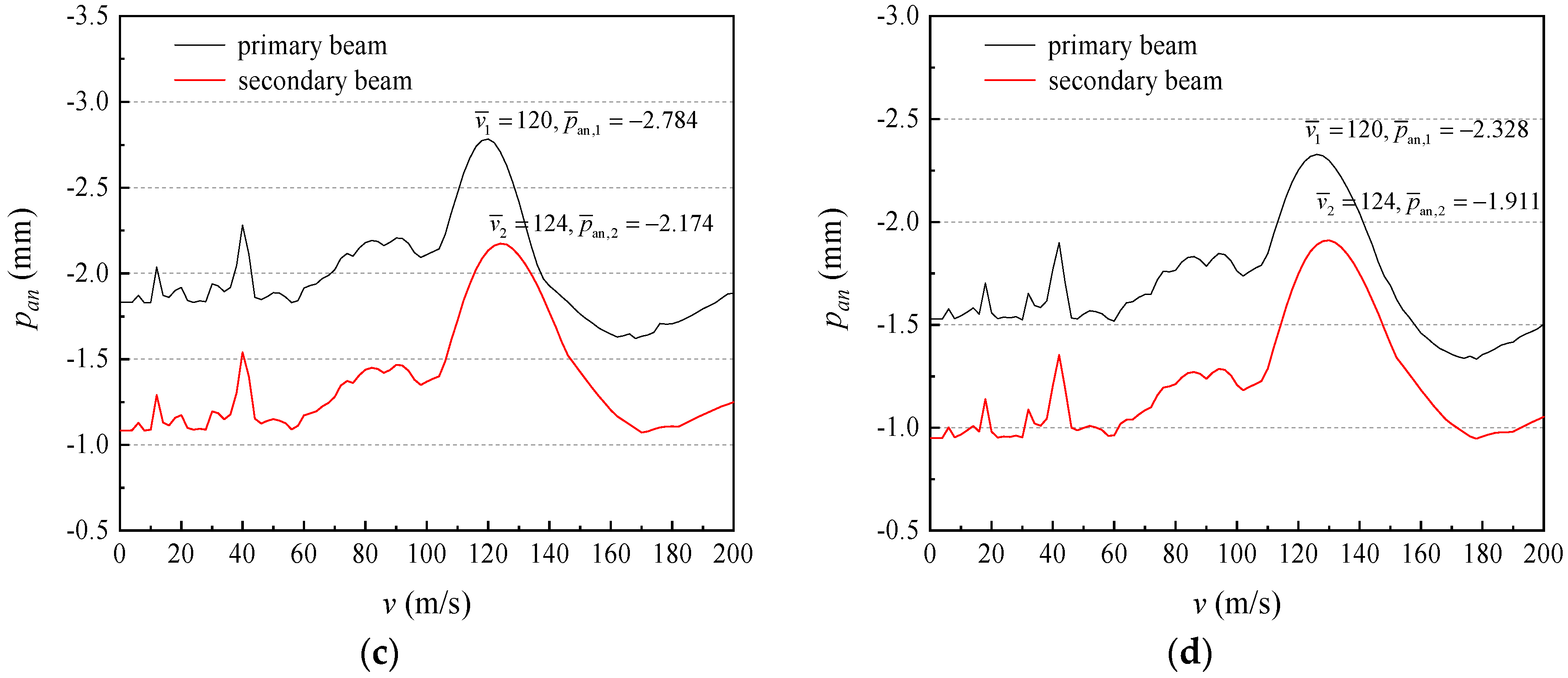
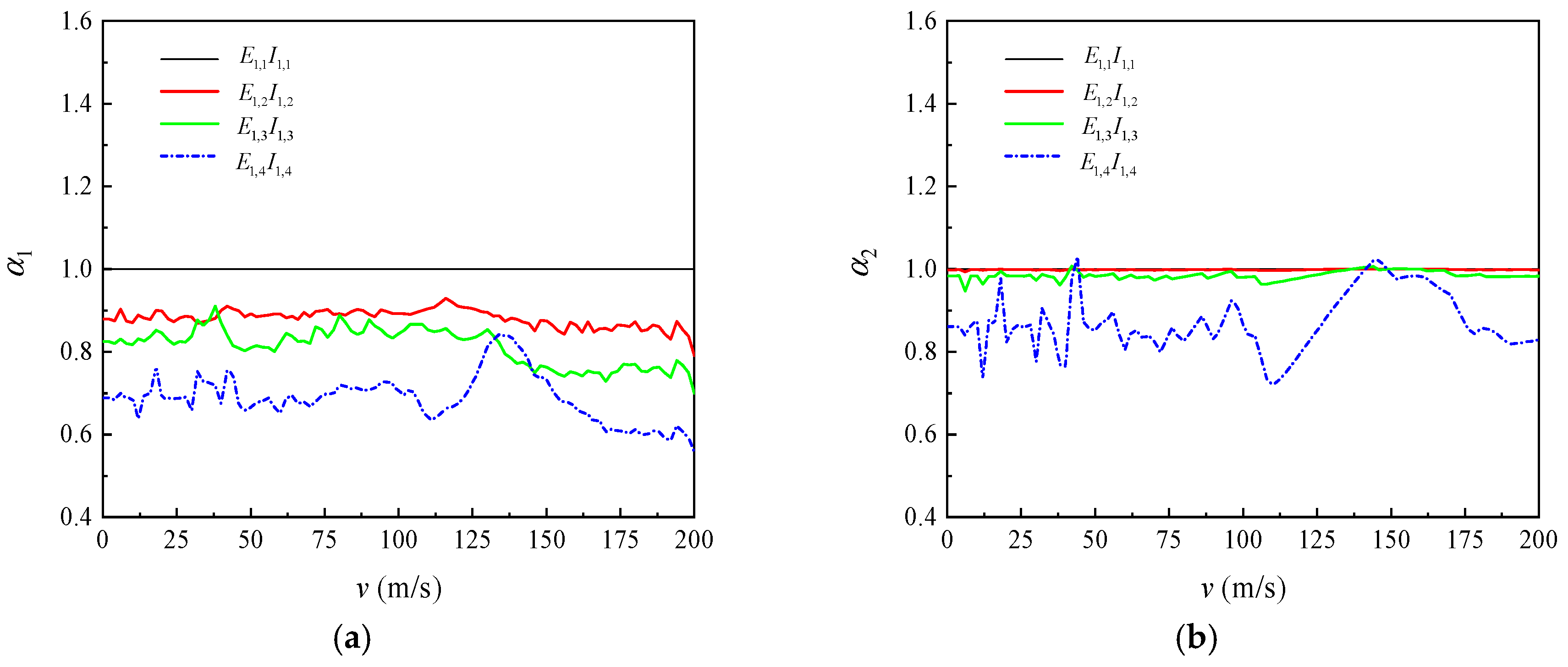
3. Analysis of Calculation Examples
3.1. Effect of Speed of Loads on Dynamic Response of Double-Beam System
3.2. Effect of Flexural Rigidity on Dynamic Response of Double-Beam System
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, D.Y.; Jia, H.Y.; Zheng, S.X.; Xie, W.C.; Pandey, M.D. A highly efficient and accurate stochastic seismic analysis approach for structures under tridirectional nonstationary multiple excitations. Comput. Struct. 2014, 145, 23–35. [Google Scholar] [CrossRef]
- Luo, N.; Jia, H.; Liao, H. Coupled wind-induced responses and equivalent static wind loads on long-span roof structures with the consistent load–response–correlation method. Adv. Struct. Eng. 2018, 21, 71–81. [Google Scholar] [CrossRef]
- Museros, P.; Moliner, E.; Martínez-Rodrigo, M.D. Free vibrations of simply-supported beam bridges under moving loads: Maximum resonance, cancellation and resonant vertical acceleration. J. Sound Vib. 2013, 332, 326–345. [Google Scholar] [CrossRef]
- Yau, J.D.; Frýba, L. Response of suspended beams due to moving loads and vertical seismic ground excitations. Eng. Struct. 2007, 29, 3255–3262. [Google Scholar] [CrossRef]
- Kurihara, M.; Shimogo, T. Stability of a Simply-Supported beam subjected to randomly spaced moving loads. J. Mech. Des. 1978, 100, 507–513. [Google Scholar] [CrossRef]
- Abu-Hilal, M. Vibration of beams with general boundary conditions due to a moving random load. Arch. Appl. Mech. 2003, 72, 637–650. [Google Scholar] [CrossRef]
- Kumar, C.P.S.; Sujatha, C.; Shankar, K. Vibration of simply supported beams under a single moving load: A detailed study of cancellation phenomenon. Int. J. Mech. Sci. 2015, 99, 40–47. [Google Scholar] [CrossRef]
- Chen, Y.H.; Sheu, J.T. Beam on Viscoelastic Foundation and Layered Beam. J. Eng. Mech. 1995, 121, 340–344. [Google Scholar] [CrossRef]
- Vu, H.V.; Ordonez, A.M.; Kaenopp, B.H. Vibration of a double-beam system. J. Sound Vib. 2000, 229, 807–822. [Google Scholar] [CrossRef]
- Rusin, J.Ł.; Śniady, P.Ł.; Śniady, P. Vibrations of double-string complex system under moving forces. Closed solutions. J. Sound Vib. 2011, 330, 404–415. [Google Scholar] [CrossRef]
- Wu, Y.; Gao, Y. Analytical solutions for simply supported viscously damped Double-Beam system under moving harmonic loads. J. Eng. Mech. 2015, 141, 4015004. [Google Scholar] [CrossRef]
- Oniszczuk, Z. Transverse vibrations of elastically connected double-string complex system—Part I: Free vibrations. J. Sound Vib. 2000, 232, 355–366. [Google Scholar] [CrossRef]
- Oniszczuk, Z. Forced transverse vibrations of an elastically connected complex simply supported double-beam system. J. Sound Vib. 2003, 264, 273–286. [Google Scholar] [CrossRef]
- Li, J.; Hua, H. Spectral finite element analysis of elastically connected double-beam systems. Finite Elem. Anal. Des. 2007, 43, 1155–1168. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Lu, Y.; Ma, G.W. Effect of compressive axial load on forced transverse vibrations of a double-beam system. Int. J. Mech. Sci. 2008, 50, 299–305. [Google Scholar] [CrossRef]
- Palmeri, A.; Adhikari, S. A Galerkin-type state-space approach for transverse vibrations of slender double-beam systems with viscoelastic inner layer. J. Sound Vib. 2011, 330, 6372–6386. [Google Scholar] [CrossRef]
- Stojanović, V.; Kozić, P. Forced transverse vibration of Rayleigh and Timoshenko double-beam system with effect of compressive axial load. Int. J. Mech. Sci. 2012, 60, 59–71. [Google Scholar] [CrossRef]
- Pavlović, R.; Kozić, P.; Pavlović, I. Dynamic stability and instability of a double-beam system subjected to random forces. Int. J. Mech. Sci. 2012, 62, 111–119. [Google Scholar] [CrossRef]
- Li, Y.X.; Hu, Z.J.; Sun, L.Z. Dynamical behavior of a double-beam system interconnected by a viscoelastic layer. Int. J. Mech. Sci. 2016, 105, 291–303. [Google Scholar] [CrossRef]
- Li, Y.X.; Sun, L.Z. Transverse vibration of an undamped elastically connected Double-Beam system with arbitrary boundary conditions. J. Eng. Mech. 2016, 142, 4015070. [Google Scholar] [CrossRef]
- Wu, Y.; Gao, Y. Dynamic response of a simply supported viscously damped double-beam system under the moving oscillator. J. Sound Vib. 2016, 384, 194–209. [Google Scholar] [CrossRef]
- Murmu, T.; Adhikari, S. Nonlocal transverse vibration of double-nanobeam-systems. J. Appl. Phys. 2010, 108, 83514. [Google Scholar] [CrossRef]
- Khaniki, H.B. On vibrations of nanobeam systems. Int. J. Eng. Sci. 2018, 124, 85–103. [Google Scholar] [CrossRef]
- Frank, I.W.; Lončar, M.; Mccutcheon, M.W.; Deotare, P.B. Programmable photonic crystal nanobeam cavities. Opt. Express 2010, 18, 8705–8712. [Google Scholar] [CrossRef]
- Murmu, T.; Adhikari, S. Axial instability of double-nanobeam-systems. Phys. Lett. A 2011, 375, 601–608. [Google Scholar] [CrossRef]
- şimşek, M. Nonlocal effects in the forced vibration of an elastically connected double-carbon nanotube system under a moving nanoparticle. Comput. Mater. Sci. 2011, 50, 2112–2123. [Google Scholar] [CrossRef]
- Cheng, Y.S.; Au, F.T.K.; Cheung, Y.K. Vibration of railway bridges under a moving train by using bridge-track-vehicle element. Eng. Struct. 2001, 23, 1597–1606. [Google Scholar] [CrossRef]
- Biondi, B.; Muscolino, G.; Sofi, A. A substructure approach for the dynamic analysis of train-track-bridge system. Comput. Struct. 2005, 83, 2271–2281. [Google Scholar] [CrossRef]
- Lou, P. A vehicle-track-bridge interaction element considering vehicle’s pitching effect. Finite Elem. Anal. Des. 2005, 41, 397–427. [Google Scholar] [CrossRef]
- Lou, P.; Yu, Z.; Au, F.T.K. Rail-bridge coupling element of unequal lengths for analysing train-track-bridge interaction systems. Appl. Math. Model. 2012, 36, 1395–1414. [Google Scholar] [CrossRef]
- Jia, H.Y.; Zhang, D.Y.; Zheng, S.X.; Xie, W.C.; Pandey, M.D. Local site effects on a high-pier railway bridge under tridirectional spatial excitations: Nonstationary stochastic analysis. Soil Dyn. Earthq. Eng. 2013, 52, 55–69. [Google Scholar] [CrossRef]
- Zhang, F.L.; Ni, Y.C.; Au, S.K.; Lam, H.F. Fast Bayesian approach for modal identification using free vibration data, Part I—Most probable value. Mech. Syst. Signal Process. 2016, 70–71, 209–220. [Google Scholar] [CrossRef]
- Hussein, M.F.M.; Hunt, H.E.M. Modelling of floating-slab tracks with continuous slabs under oscillating moving loads. J. Sound Vib. 2006, 297, 37–54. [Google Scholar] [CrossRef]
- Xin, T.; Gao, L. Reducing slab track vibration into bridge using elastic materials in high speed railway. J. Sound Vib. 2011, 330, 2237–2248. [Google Scholar] [CrossRef]
- Lai, Z.; Jiang, L.; Zhou, W. An analytical study on dynamic response of multiple simply supported beam system subjected to moving loads. Shock Vib. 2018, 2018, 2149251. [Google Scholar] [CrossRef]
| Layer | ||||
|---|---|---|---|---|
| 40 | Primary beam | −3.067 | −3.112 | −1.46% |
| Secondary beam | −1.572 | −1.571 | 0.06% | |
| λp | 1.950 | 1.981 | ||
| 100 | Primary beam | −2.922 | −2.933 | −0.40% |
| Secondary beam | −1.396 | −1.399 | −0.23% | |
| λp | 2.093 | 2.096 | ||
| 122 | Primary beam | −3.754 | −3.815 | −1.60% |
| Secondary beam | −2.201 | −2.200 | 0.04% | |
| λp | 1.706 | 1.734 | ||
| 180 | Primary beam | −2.769 | −2.754 | 0.53% |
| Secondary beam | −1.122 | −1.121 | 0.07% | |
| λp | 2.467 | 2.456 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, L.; Zhang, Y.; Feng, Y.; Zhou, W.; Tan, Z. Dynamic Response Analysis of a Simply Supported Double-Beam System under Successive Moving Loads. Appl. Sci. 2019, 9, 2162. https://doi.org/10.3390/app9102162
Jiang L, Zhang Y, Feng Y, Zhou W, Tan Z. Dynamic Response Analysis of a Simply Supported Double-Beam System under Successive Moving Loads. Applied Sciences. 2019; 9(10):2162. https://doi.org/10.3390/app9102162
Chicago/Turabian StyleJiang, Lizhong, Yuntai Zhang, Yulin Feng, Wangbao Zhou, and Zhihua Tan. 2019. "Dynamic Response Analysis of a Simply Supported Double-Beam System under Successive Moving Loads" Applied Sciences 9, no. 10: 2162. https://doi.org/10.3390/app9102162
APA StyleJiang, L., Zhang, Y., Feng, Y., Zhou, W., & Tan, Z. (2019). Dynamic Response Analysis of a Simply Supported Double-Beam System under Successive Moving Loads. Applied Sciences, 9(10), 2162. https://doi.org/10.3390/app9102162







