Multiscale Superpixelwise Locality Preserving Projection for Hyperspectral Image Classification
Abstract
1. Introduction
2. Related Work and Background
2.1. Locality Preserving Projection
2.2. Region Covariance Descriptor
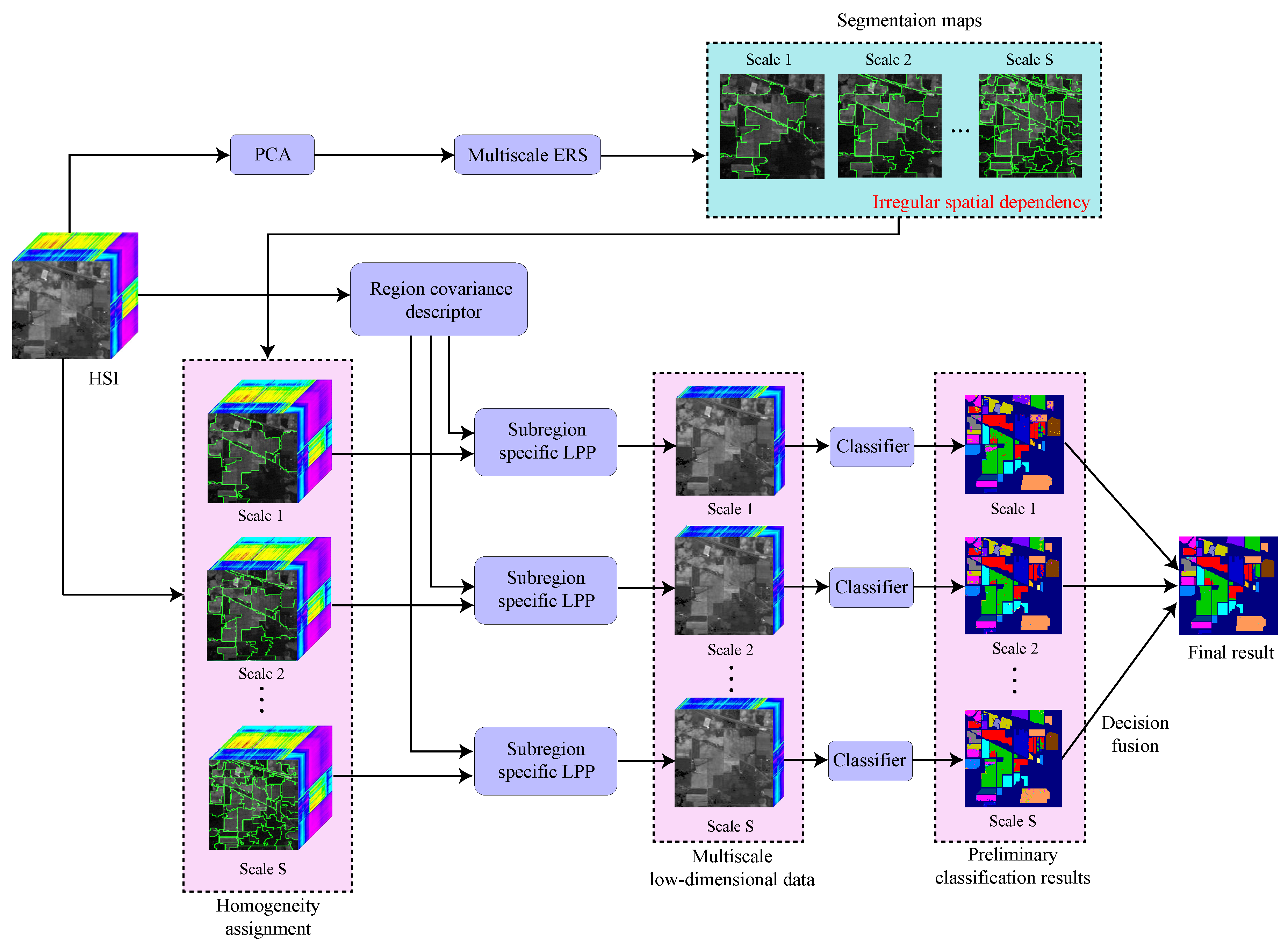
3. Proposed Method
3.1. Determination of Manifold Local Homogeneity with Multiscale Superpixel Segmentation
3.2. Divide-and-Conquer-Based LPP Classification
| Algorithm 1 MSuperLPP |
| Input: HSI ; scale set obtained by (8); window size . |
| Extract spectral-spatial covariance features using (5) and perform PCA to extract the first principle component . |
| for i = 1 to S do |
| Segment into homogeneous subregions using ERS with ; |
| for j = 1 to do |
| Perform LPP in each subregion , where the spectral-spatial covariance features are used to search for the k nearest neighbors. |
| end for |
| Combine the low-dimensional features of all the subregions on the same scale to form the low-dimensional data on this scale. Perform classification on the scales i to get preliminary output . |
| end for |
| Aggregate the classification results using (10) and (11). |
| Output: Final classification result T. |
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- He, L.; Li, J.; Liu, C.Y.; Li, S.T. Recent advances on spectral—Spatial hyperspectral image classification: An overview and new guidelines. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1579–1597. [Google Scholar] [CrossRef]
- Chang, C.I. Hyperspectral Data Exploitation: Theory And Applications; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Qiu, Z.; Chen, J.; Zhao, Y.; Zhu, S.; He, Y.; Zhang, C. Variety identification of single rice seed using hyperspectral imaging combined with convolutional neural network. Appl. Sci. 2018, 8, 212. [Google Scholar] [CrossRef]
- Hughes, G. On the mean accuracy of statistical pattern recognizers. IEEE Transa. Inf. Theory 1968, 14, 55–63. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Gumma, M.K.; Teluguntla, P.; Mohammed, I.A. Hyperspectral remote sensing of vegetation and agricultural crops. Photogramm. Eng. Remote Sens. 2014, 80, 697–723. [Google Scholar]
- Jiménez, L.O.; Rivera-Medina, J.L.; Rodríguez-Díaz, E.; Arzuaga-Cruz, E.; Ramírez-Vélez, M. Integration of spatial and spectral information by means of unsupervised extraction and classification for homogenous objects applied to multispectral and hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 844–851. [Google Scholar] [CrossRef]
- Ni, D.; Ma, H.B. Classification of hyperspectral image based on sparse representation in tangent space. IEEE Geosci. Remote Sens. Lett. 2015, 12, 786–790. [Google Scholar]
- Shao, Z.F.; Zhang, L. Sparse dimensionality reduction of hyperspectral image based on semi-supervised local Fisher discriminant analysis. Int. J. Appl. Earth Obs. Geoinf. 2014, 31, 122–129. [Google Scholar] [CrossRef]
- Zhang, L.P.; Zhong, Y.F.; Huang, B.; Gong, J.Y.; Li, P.X. Dimensionality reduction based on clonal selection for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2007, 45, 4172–4186. [Google Scholar] [CrossRef]
- Mojaradi, B.; Abrishami-Moghaddam, H.; Zoej, M.J.V.; Duin, R.P. Dimensionality reduction of hyperspectral data via spectral feature extraction. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2091–2105. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Fukunaga, K. Introduction to Statistical Pattern Recognition; Elsevier: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. Syst. 1987, 2, 37–52. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of hyperspectral images with regularized linear discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- He, X.F.; Niyogi, P. Locality preserving projections. In Proceedings of the Annual Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 8–13 December 2003; pp. 153–160. [Google Scholar]
- Wang, Z.Y.; He, B.B. Locality perserving projections algorithm for hyperspectral image dimensionality reduction. In Proceedings of the International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–4. [Google Scholar]
- Deng, Y.J.; Li, H.C.; Pan, L.; Emery, W.J. Tensor locality preserving projection for hyperspectral image classification. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017; pp. 771–774. [Google Scholar]
- Zhai, Y.; Zhang, L.; Wang, N.; Guo, Y.; Cen, Y.; Wu, T.; Tong, Q. A modified locality-preserving projection approach for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1059–1063. [Google Scholar] [CrossRef]
- Wang, R.; Nie, F.; Hong, R.; Chang, X.; Yang, X.; Yu, W. Fast and orthogonal locality preserving projections for dimensionality reduction. IEEE Trans. Image Process. 2017, 26, 5019–5030. [Google Scholar] [CrossRef]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; De, S.V.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Zhang, Z.Y.; Zha, H.Y. Nonlinear dimension reduction via local tangent space alignment. In Proceedings of the International Conference on Intelligent Data Engineering and Automated Learning, Hong Kong, China, 21–23 March 2003; pp. 477–481. [Google Scholar]
- Sun, H.; Ren, J.; Zhao, H.; Yan, Y.; Zabalza, J.; Marshall, S. Superpixel based feature specific sparse representation for spectral-spatial classification of hyperspectral images. Remote Sens. 2019, 11, 536. [Google Scholar] [CrossRef]
- Duan, W.; Li, S.; Fang, L. Spectral-spatial hyperspectral image classification using superpixel and extreme learning machines. In Proceedings of the Chinese Conference on Pattern Recognition, Changsha, China, 17–19 November 2014; pp. 159–167. [Google Scholar]
- Zhan, T.; Sun, L.; Xu, Y.; Yang, G.; Zhang, Y.; Wu, Z. Hyperspectral classification via superpixel kernel learning-based low rank representation. Remote Sens. 2018, 10, 1639. [Google Scholar] [CrossRef]
- Deng, Y.J.; Li, H.C.; Pan, L.; Shao, L.Y.; Du, Q.; Emery, W.J. Modified tensor locality preserving projection for dimensionality reduction of hyperspectral images. IEEE Geosci. Remote Sens. Lett. 2018, 15, 277–281. [Google Scholar] [CrossRef]
- Fang, L.; He, N.; Li, S.; Plaza, A.J.; Plaza, J. A new spatial-spectral feature extraction method for hyperspectral images using local covariance matrix representation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3534–3546. [Google Scholar] [CrossRef]
- He, N.; Paoletti, M.E.; Fang, L.; Li, S.; Plaza, A.; Plaza, J. Feature extraction with multiscale covariance maps for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1–15. [Google Scholar] [CrossRef]
- Qiao, L.; Chen, S.; Tan, X. Sparsity preserving projections with applications to face recognition. Pattern Recogn. 2010, 43, 331–341. [Google Scholar] [CrossRef]
- Tuzel, O.; Porikli, F.; Meer, P. Pedestrian detection via classification on riemannian manifolds. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1713–1727. [Google Scholar] [CrossRef]
- Xie, X.F.; Yu, Z.L.; Gu, Z.H.; Zhang, J.; Cen, L.; Li, Y.Q. Bilinear regularized locality preserving learning on Riemannian graph for motor imagery BCI. IEEE Trans. Neural Syst. Rehabil. Eng. 2018, 26, 698–708. [Google Scholar] [CrossRef]
- Wang, R.P.; Guo, H.M.; Davis, L.S.; Dai, Q.H. Covariance discriminative learning: A natural and efficient approach to image set classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 2496–2503. [Google Scholar]
- Guo, B.; Gunn, S.R.; Damper, R.I.; Nelson, J.D.B. Customizing kernel functions for SVM-based hyperspectral image classification. IEEE Trans. Image Process. 2008, 17, 622–629. [Google Scholar] [CrossRef]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Ma, L.; Crawford, M.M.; Tian, J. Local Manifold Learning-Based k-Nearest-Neighbor for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2010, 48, 4099–4109. [Google Scholar] [CrossRef]
- Liu, M.Y.; Tuzel, O.; Ramalingam, S.; Chellappa, R. Entropy rate superpixel segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 2097–2104. [Google Scholar]
- Jiang, J.J.; Ma, J.Y.; Chen, C.; Wang, Z.Y.; Cai, Z.H.; Wang, L.Z. SuperPCA: A superpixelwise PCA approach for unsupervised feature extraction of hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
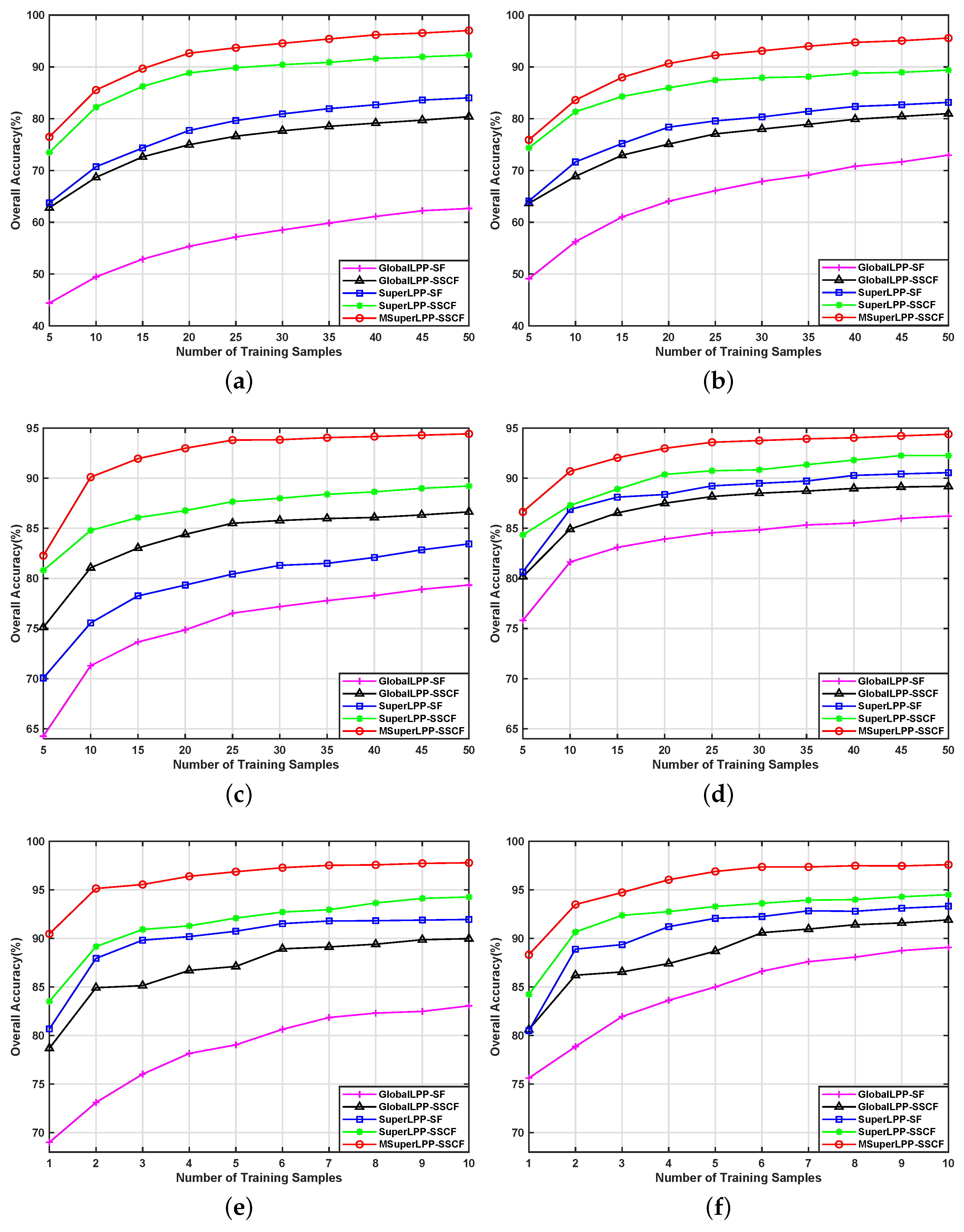
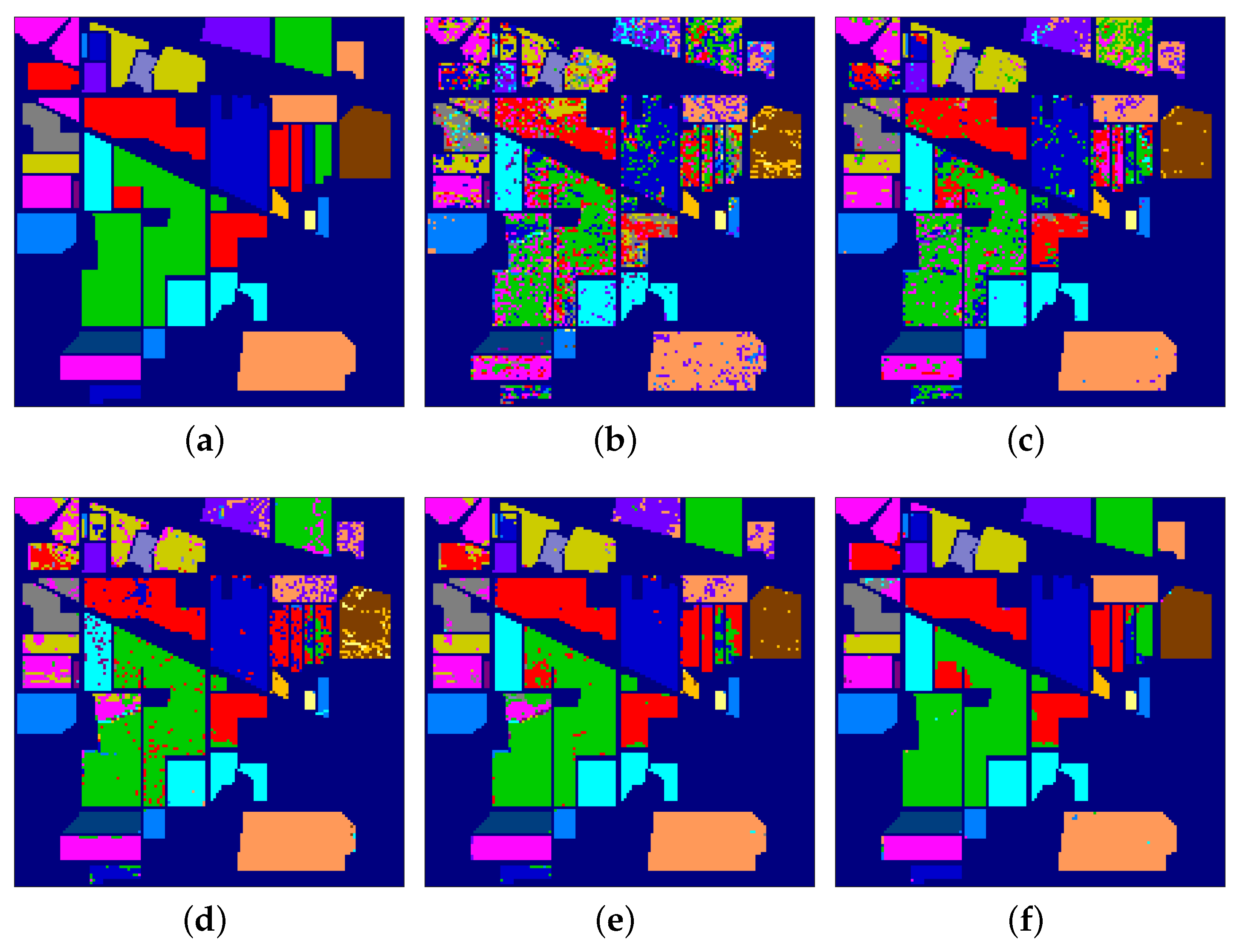
| Training Size | 5 | 10 | 30 | 50 | ||||
|---|---|---|---|---|---|---|---|---|
| Classifier | NN | SVM | NN | SVM | NN | SVM | NN | SVM |
| GlobalLPP-SF | 44.40 | 49.11 | 49.47 | 56.26 | 58.52 | 67.90 | 62.67 | 72.96 |
| GlobalLPP-SSCF | 62.81 | 63.65 | 68.67 | 68.87 | 77.66 | 77.99 | 80.39 | 80.98 |
| SuperLPP-SF | 63.74 | 64.10 | 70.73 | 71.65 | 80.92 | 80.33 | 84.03 | 83.14 |
| SuperLPP-SSCF | 73.50 | 74.37 | 82.23 | 81.35 | 90.43 | 87.91 | 92.28 | 89.38 |
| MSuperLPP | 76.49 | 75.91 | 85.53 | 83.60 | 94.55 | 93.10 | 97.02 | 95.57 |
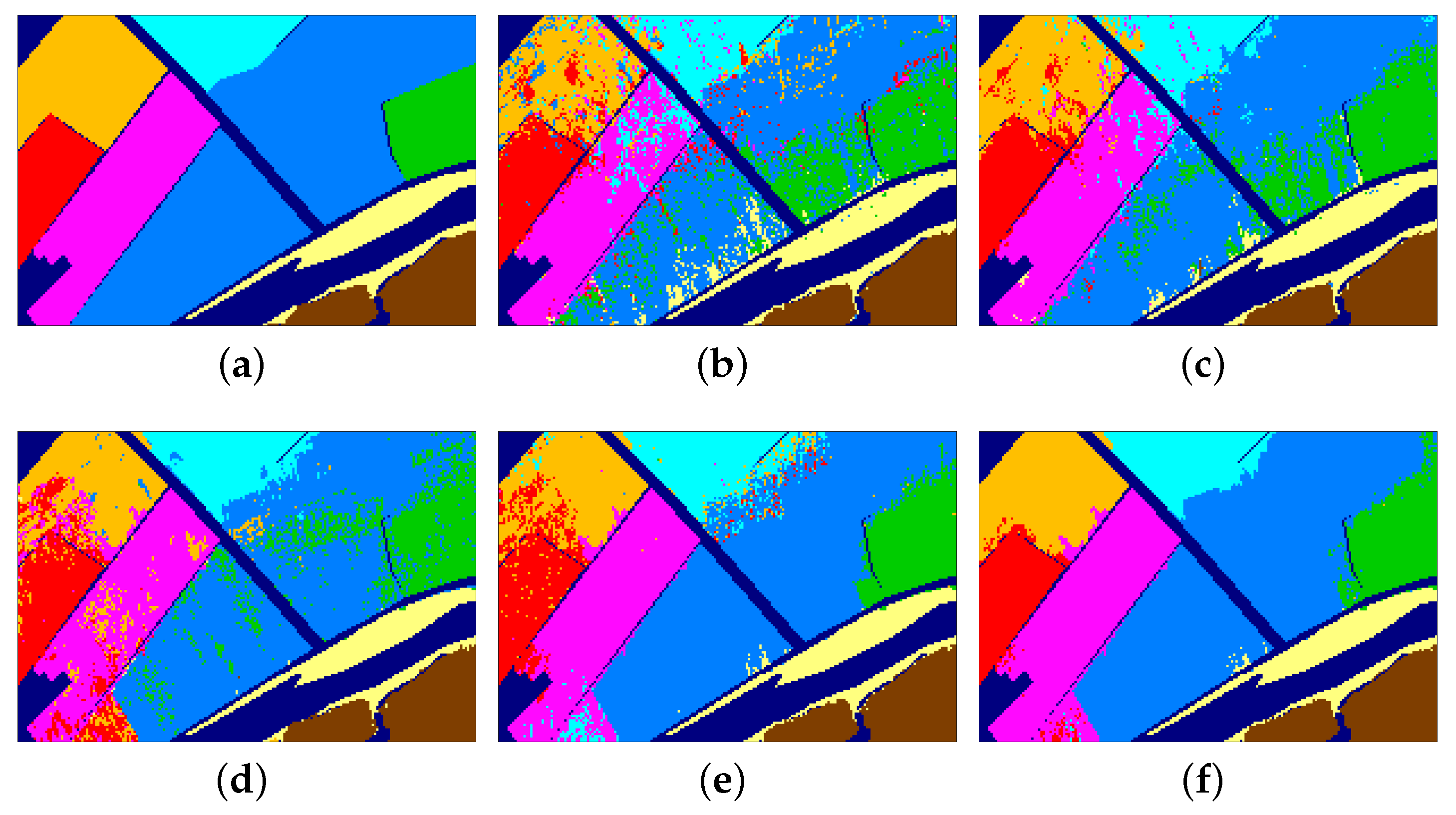
| Training Size | 5 | 10 | 30 | 50 | ||||
|---|---|---|---|---|---|---|---|---|
| Classifier | NN | SVM | NN | SVM | NN | SVM | NN | SVM |
| GlobalLPP-SF | 64.26 | 75.81 | 71.29 | 81.64 | 77.18 | 84.84 | 79.34 | 86.21 |
| GlobalLPP-SSCF | 75.12 | 80.18 | 81.06 | 84.92 | 85.77 | 88.50 | 86.63 | 89.19 |
| SuperLPP-SF | 70.06 | 80.65 | 75.56 | 86.88 | 81.30 | 89.48 | 83.44 | 90.55 |
| SuperLPP-SSCF | 80.81 | 84.34 | 84.79 | 87.28 | 88.00 | 90.83 | 89.22 | 92.26 |
| MSuperLPP | 82.27 | 86.64 | 90.10 | 90.68 | 93.83 | 93.75 | 94.42 | 94.39 |
| Training Size | 1 | 3 | 5 | 10 | ||||
|---|---|---|---|---|---|---|---|---|
| Classifier | NN | SVM | NN | SVM | NN | SVM | NN | SVM |
| GlobalLPP-SF | 69.00 | 75.61 | 76.02 | 81.95 | 79.04 | 85.00 | 83.05 | 89.07 |
| GlobalLPP-SSCF | 78.69 | 80.60 | 85.14 | 86.55 | 87.11 | 88.69 | 89.97 | 91.91 |
| SuperLPP-SF | 80.67 | 80.51 | 89.82 | 89.36 | 90.74 | 92.06 | 91.95 | 93.32 |
| SuperLPP-SSCF | 81.77 | 84.23 | 90.92 | 92.37 | 91.97 | 93.28 | 93.82 | 94.50 |
| MSuperLPP | 90.46 | 88.32 | 95.55 | 94.73 | 96.87 | 96.89 | 97.78 | 97.59 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, L.; Chen, X.; Li, J.; Xie, X. Multiscale Superpixelwise Locality Preserving Projection for Hyperspectral Image Classification. Appl. Sci. 2019, 9, 2161. https://doi.org/10.3390/app9102161
He L, Chen X, Li J, Xie X. Multiscale Superpixelwise Locality Preserving Projection for Hyperspectral Image Classification. Applied Sciences. 2019; 9(10):2161. https://doi.org/10.3390/app9102161
Chicago/Turabian StyleHe, Lin, Xianjun Chen, Jun Li, and Xiaofeng Xie. 2019. "Multiscale Superpixelwise Locality Preserving Projection for Hyperspectral Image Classification" Applied Sciences 9, no. 10: 2161. https://doi.org/10.3390/app9102161
APA StyleHe, L., Chen, X., Li, J., & Xie, X. (2019). Multiscale Superpixelwise Locality Preserving Projection for Hyperspectral Image Classification. Applied Sciences, 9(10), 2161. https://doi.org/10.3390/app9102161






