Establishment of a Numerical Model to Design an Electro-Stimulating System for a Porcine Mandibular Critical Size Defect
Abstract
1. Introduction
2. Materials and Methods
- setting up the anatomical and technical model, i.e., segmenting computer tomographic (CT) data and computer-aided design (CAD) modelling based on the segmentation.
- setting up the physical model, i.e., the anatomical and technical models are assigned their dielectric properties.
- setting up the corresponding boundary value problem, i.e., the needed equations for simulating the electric field distribution.
- solving the boundary value problem.
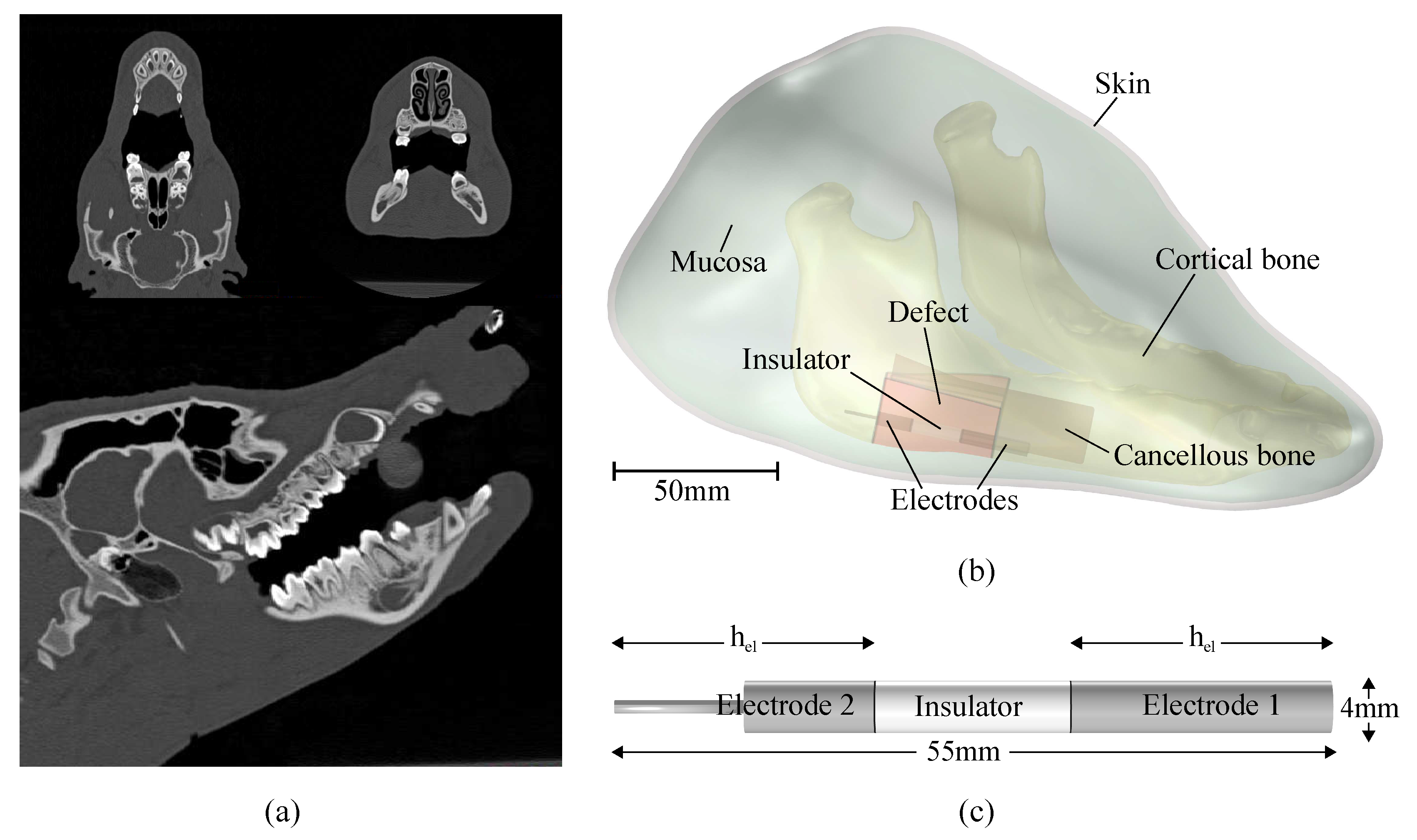
2.1. Anatomical and Technical Model Generation
2.2. Generation of the Physical Model
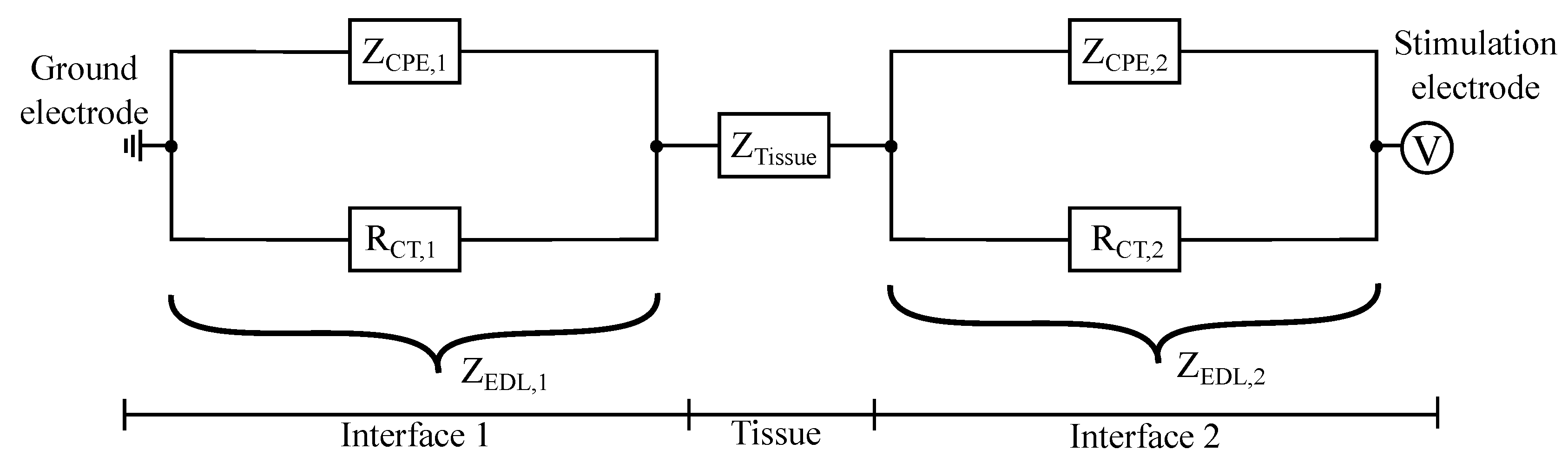
2.3. Modelling of the Electrode–Tissue Interface
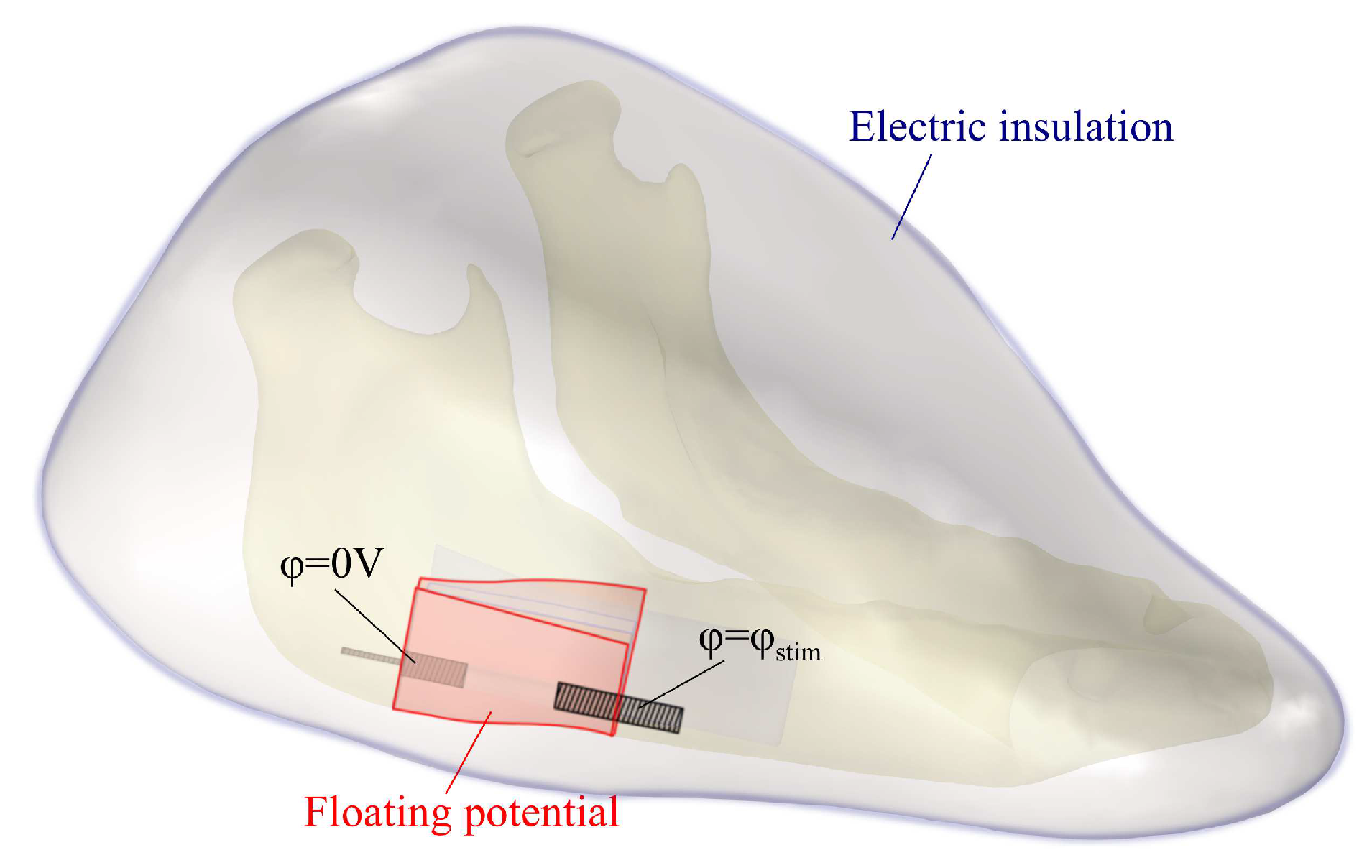
2.4. Electro-Quasistatic Boundary Value Problem
2.5. Optimization of the Stimulation Parameters
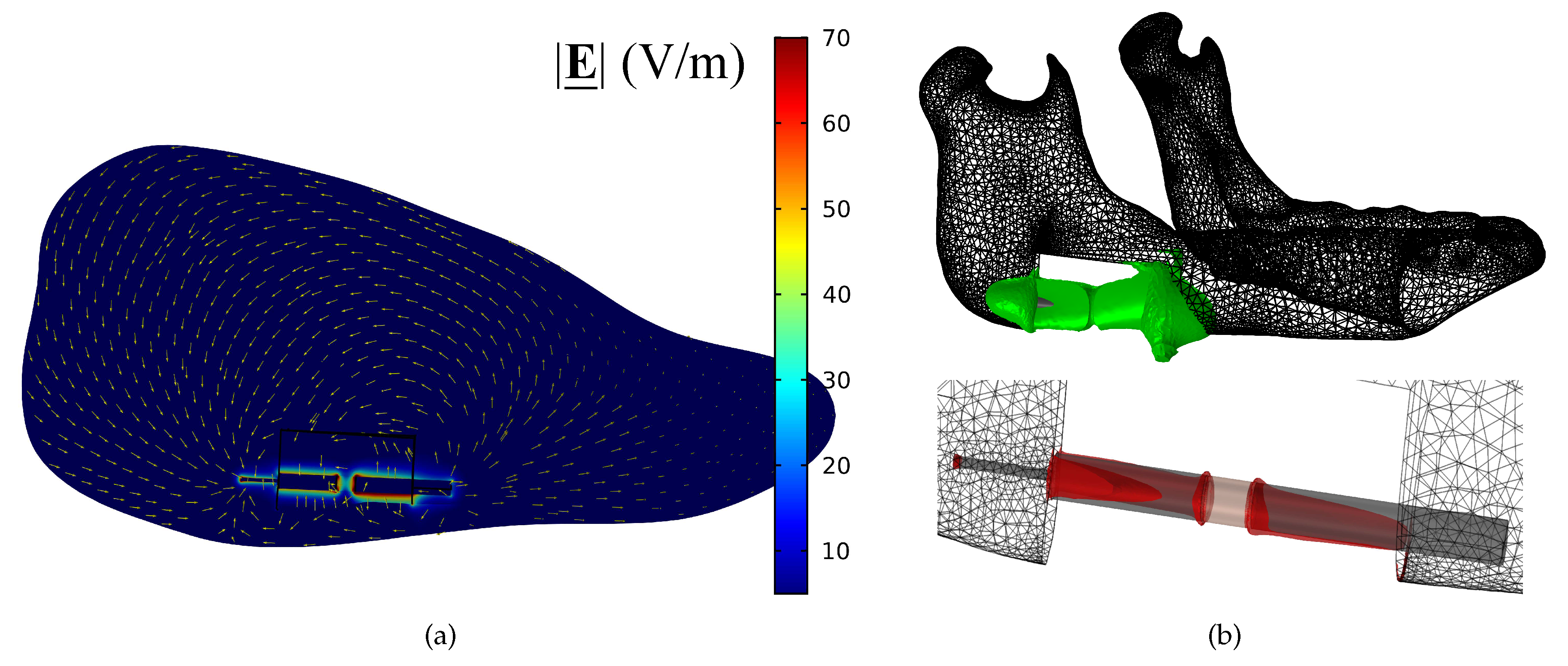
2.6. Finite-Element Simulation
3. Results
3.1. Electric Field Distribution
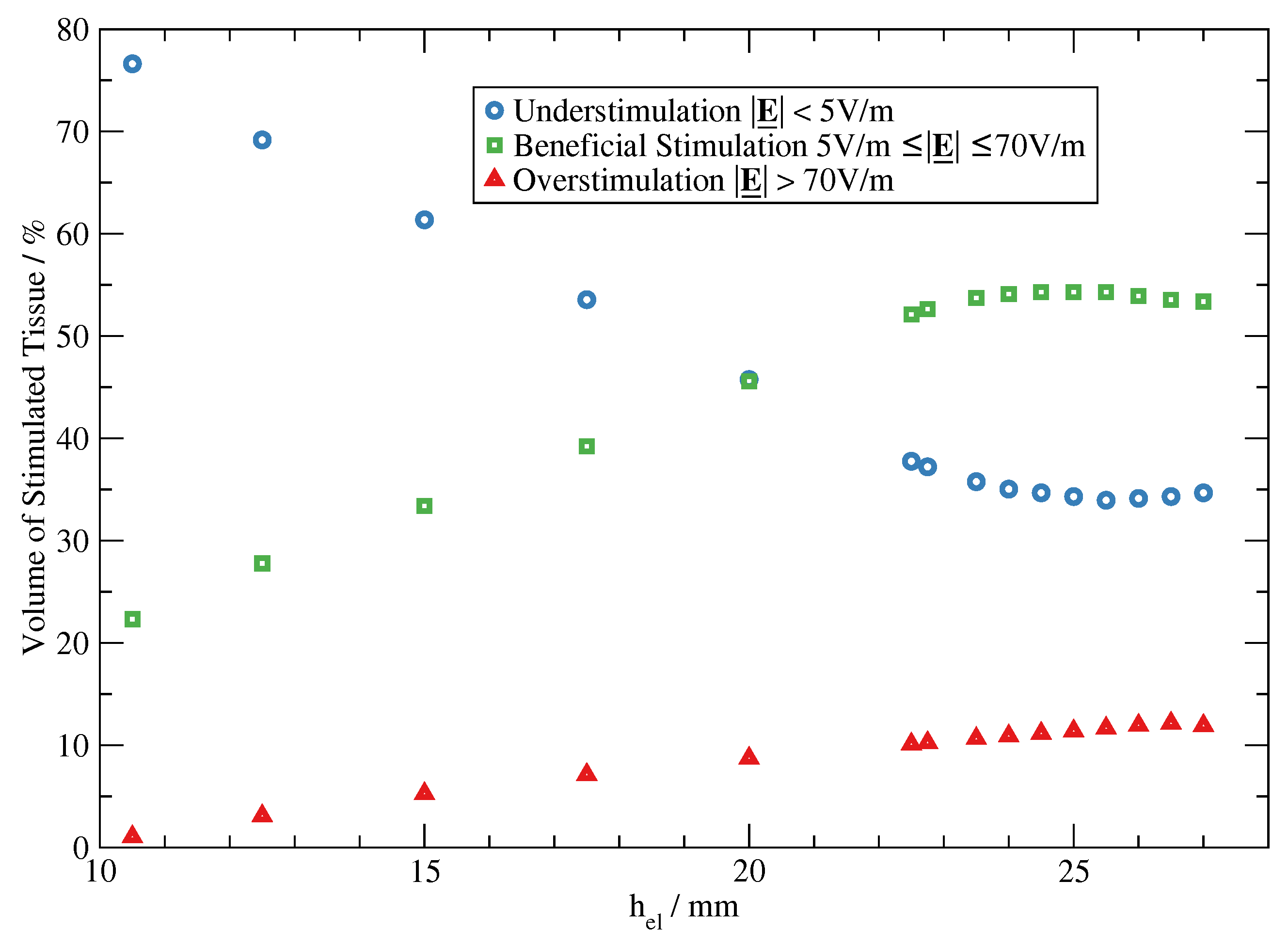
3.2. Optimized Electrode Parameters
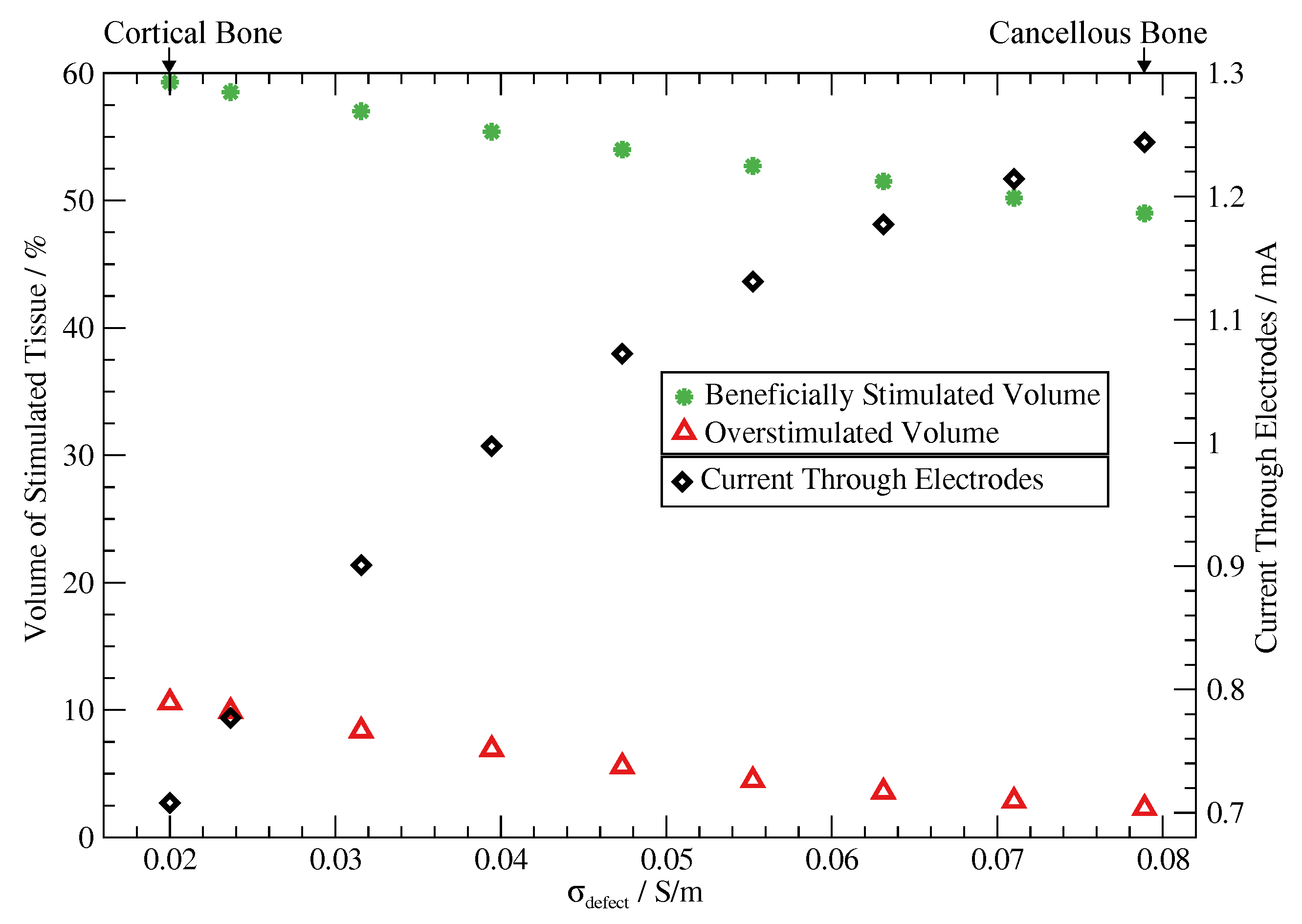
3.3. Impact of Varying Tissue Conductivity
4. Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bassett, C.A.; Pawluk, R.J.; Pilla, A.A. Acceleration of Fracture Repair by Electromagnetic Fields. A Surgically Noninvasive Method. Ann. N. Y. Acad. Sci. 1974, 238, 242–262. [Google Scholar] [CrossRef] [PubMed]
- Ryaby, J.T. Clinical Effects of Electromagnetic and Electric Fields on Fracture Healing. Clin. Orthop. Relat. Res. 1998, 355, S205–S215. [Google Scholar] [CrossRef]
- Brighton, C.T.; Hozack, W.J.; Brager, M.D.; Windsor, R.E.; Pollack, S.R.; Vreslovic, E.J.; Kotwick, J.E. Fracture Healing in the Rabbit Fibula when Subjected to Various Capacitively Coupled Electrical Fields. J. Orthop. Res. 1985, 3, 331–340. [Google Scholar] [CrossRef] [PubMed]
- Kuzyk, P.R.; Schemitsch, E.H. The Science of Electrical Stimulation Therapy for Fracture Healing. Indian J. Orthop. 2009, 43, 127–131. [Google Scholar]
- Daish, C.; Blanchard, R.; Fox, K.; Pivonka, P.; Pirogova, E. The Application of Pulsed Electromagnetic Fields (PEMFs) for Bone Fracture Repair: Past and Perspective Findings. Ann. Biomed. Eng. 2018, 46, 525–542. [Google Scholar] [CrossRef]
- Aaron, R.K.; Ciombor, D.M.; Simon, B.J. Treatment of Nonunions With Electric and Electromagnetic Fields. Clin. Orthop. Relat. Res. 2004, 419, 21–29. [Google Scholar] [CrossRef]
- Brighton, C.T.; Black, J.; Friedenberg, Z.B.; Esterhai, J.L.; Day, L.J.; Connolly, J.F. A Multicenter Study of the Treatment of Non-Union with Constant Direct Current. J. Bone Jt. Surg. Am. 1981, 63, 2–13. [Google Scholar] [CrossRef]
- Shandler, H.S.; Weinstein, S.; Nathan, L.E. Facilitated Healing of Osseous Lesions in the Canine Mandible after Electrical Stimulation. J. Oral Surg. 1979, 37, 787–792. [Google Scholar]
- Kohavi, D.; Pollack, S.R.; Brighton, C. Short-Term Effect of Guided Bone Regeneration and Electrical Stimulation on Bone Growth in a Surgically Modelled Resorbed Dog Mandibular Ridge. Biomater. Artif. Cells Immobil. Biotechnol. 1992, 20, 131–138. [Google Scholar]
- Leppik, L.; Zhihua, H.; Mobini, S.; Parameswaran, V.T.; Eischen-Loges, M.; Slavici, A.; Helbing, J.; Pindur, L.; Oliveira, K.M.; Bhavsar, M.B.; et al. Combining Electrical Stimulation and Tissue Engineering to Treat Large Bone Defects in a Rat Model. Sci. Rep. 2018, 8, 6307. [Google Scholar] [CrossRef] [PubMed]
- Schiegnitz, E.; Al-Nawas, B.; Kämmerer, P.W.; Grötz, K.A. Oral Rehabilitation with Dental Implants in Irradiated Patients: A Meta-Analysis on Implant Survival. Clin. Oral Investig. 2014, 18, 687–698. [Google Scholar] [CrossRef]
- Khojasteh, A.; Dehghan, M.M.; Nazeman, P. Immediate Implant Placement Following 1-Year Treatment with Oral Versus Intravenous Bisphosphonates: A Histomorphometric Canine Study on Peri-Implant Bone. Clin. Oral Investig. 2019, 23, 1803–1809. [Google Scholar] [CrossRef] [PubMed]
- Bassett, C.A.; Becker, R.O. Generation of Electric Potentials by Bone in Response to Mechanical Stress. Science 1962, 137, 1063–1064. [Google Scholar] [CrossRef] [PubMed]
- Cerquiglini, S.; Cignitti, M.; Marchetti, M.; Salleo, A. On the Origin of Electrical Effects Produced by Stress in the Hard Tissues of Living Organisms. Life Sci. 1967, 6, 2651–2660. [Google Scholar] [CrossRef]
- Pollack, S.R.; Petrov, N.; Salzstein, R.; Brankov, G.; Blagoeva, R. An Anatomical Model for Streaming Potentials in Osteons. J. Biomech. 1984, 17, 627–636. [Google Scholar] [CrossRef]
- Riddle, R.C.; Donahue, H.J. From Streaming-Potentials to Shear Stress: 25 Years of Bone Cell Mechanotransduction. J. Orthop. Res. 2009, 27, 143–149. [Google Scholar] [CrossRef]
- Fukada, E.; Yasuda, I. On the Piezoelectric Effect of Bone. J. Phys. Soc. Jpn. 1957, 12, 1158–1162. [Google Scholar] [CrossRef]
- Anderson, J.C.; Eriksson, C. Piezoelectric Properties of Dry and Wet Bone. Nature 1970, 227, 491–492. [Google Scholar] [CrossRef]
- Wieland, D.; Krywka, C.; Mick, E.; Willumeit-Römer, R.; Bader, R.; Kluess, D. Investigation of the Inverse Piezoelectric Effect of Trabecular Bone on a Micrometer Length Scale Using Synchrotron Radiation. Acta Biomater. 2015, 25, 339–346. [Google Scholar] [CrossRef]
- Ahn, A.C.; Grodzinsky, A.J. Relevance of Collagen Piezoelectricity to “Wolff’s Law”: A Critical Review. Med. Eng. Phys. 2009, 31, 733–741. [Google Scholar] [CrossRef]
- Min, S.; Lee, T.; Lee, S.H.; Hong, J. Theoretical Study of the Effect of Piezoelectric Bone Matrix on Transient Fluid Flow in the Osteonal Lacunocanaliculae. J. Orthop. Res. 2018. [Google Scholar] [CrossRef]
- Yasuda, I. The classic: Fundamental Aspects of Fracture Treatment by Iwao Yasuda, reprinted from J. Kyoto Med. Soc., 4:395–406, 1953. Clin. Orthop. Relat. Res. 1977, 124, 5–8. [Google Scholar]
- Shuai, C.; Yang, W.; Peng, S.; Gao, C.; Guo, W.; Lai, Y.; Feng, P. Physical Stimulations and their Osteogenesis-Inducing Mechanisms. Int. J. Bioprint. 2018, 4. [Google Scholar] [CrossRef]
- Massari, L.; Benazzo, F.; Falez, F.; Perugia, D.; Pietrogrande, L.; Setti, S.; Osti, R.; Vaienti, E.; Ruosi, C.; Cadossi, R. Biophysical Stimulation of Bone and Cartilage: State of the Art and Future Perspectives. Int. Orthop. 2019, 43, 539–551. [Google Scholar] [CrossRef] [PubMed]
- Soda, A.; Ikehara, T.; Kinouchi, Y.; Yoshizaki, K. Effect of Exposure to an Extremely Low Frequency-Electromagnetic Field on the Cellular Collagen with Respect to Signaling Pathways in Osteoblast-like Cells. J. Med. Investig. 2008, 55, 267–278. [Google Scholar] [CrossRef]
- Brighton, C.T.; Wang, W.; Seldes, R.; Zhang, G.; Pollack, S.R. Signal Transduction in Electrically Stimulated Bone Cells. J. Bone Jt. Surg. Am. 2001, 83-A, 1514–1523. [Google Scholar] [CrossRef]
- Wang, X.; Gao, Y.; Shi, H.; Liu, N.; Zhang, W.; Li, H. Influence of the Intensity and Loading Time of Direct Current Electric Field on the Directional Migration of Rat Bone Marrow Mesenchymal Stem Cells. Front. Med. 2016, 10, 286–296. [Google Scholar] [CrossRef]
- Grunert, P.; Jonitz-Heincke, A.; Su, Y.; Souffrant, R.; Hansmann, D.; Ewald, H.; Krüger, A.; Mittelmeier, W.; Bader, R. Establishment of a Novel in Vitro Test Setup for Electric and Magnetic Stimulation of Human Osteoblasts. Cell Biochem. Biophys. 2014, 70, 805–817. [Google Scholar] [CrossRef]
- Black, J. Electrical Stimulation: Its Role in Growth, Repair and Remodeling of the Musculoskeletal System; Greenwood Press: Westport, CT, USA, 1986; pp. 85–101. [Google Scholar]
- Griffin, M.; Bayat, A. Electrical Stimulation in Bone Healing: Critical Analysis by Evaluating Levels of Evidence. Eplasty 2011, 11, e34. [Google Scholar]
- Kraus, W. Magnetic Field Therapy and Magnetically Induced Electrostimulation in Orthopedics. Orthopaede 1984, 13, 78–92. [Google Scholar]
- Mittelmeier, W.; Lehner, S.; Kraus, W.; Matter, H.P.; Gerdesmeyer, L.; Steinhauser, E. BISS: Concept and Biomechanical Investigations of a New Screw System for Electromagnetically Induced Internal Osteostimulation. Arch. Orthop. Trauma Surg. 2004, 124, 86–91. [Google Scholar] [CrossRef]
- Dauben, T.J.; Ziebart, J.; Bender, T.; Zaatreh, S.; Kreikemeyer, B.; Bader, R. A Novel In Vitro System for Comparative Analyses of Bone Cells and Bacteria under Electrical Stimulation. BioMed Res. Int. 2016, 2016, 5178640. [Google Scholar] [CrossRef]
- Hiemer, B.; Ziebart, J.; Jonitz-Heincke, A.; Grunert, P.C.; Su, Y.; Hansmann, D.; Bader, R. Magnetically Induced Electrostimulation of Human Osteoblasts Results in Enhanced Cell Viability and Osteogenic Differentiation. Int. J. Mol. Med. 2016, 38, 57–64. [Google Scholar] [CrossRef]
- Klüß, D.; Souffrant, R.; Bader, R.; van Rienen, U.; Ewald, H.; Mittelmeier, W. A New Concept of an Electrostimulative Acetabular Revision System with Patient Individual Additional Fixation. In 4th European Conference of the International Federation for Medical and Biological Engineering; Vander Sloten, J., Verdonck, P., Nyssen, M., Haueisen, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1847–1850. [Google Scholar]
- Klüß, D.; Souffrant, R.; Ewald, E.; van Rienen, U.; Bader, R.; Mittelmeier, W. Acetabuläre Hüftendoprothese mit einer Vorrichtung zur Elektrostimulation des Knochens. Patent DE202008015661 U1, 20 May 2009. [Google Scholar]
- Potratz, C.; Kluess, D.; Ewald, H.; van Rienen, U. Multiobjective Optimization of an Electrostimulative Acetabular Revision System. IEEE Trans. Biomed. Eng. 2010, 57, 460–468. [Google Scholar] [CrossRef]
- Su, Y.; Souffrant, R.; Kluess, D.; Ellenrieder, M.; Mittelmeier, W.; van Rienen, U.; Bader, R. Evaluation of Electric Field Distribution in Electromagnetic Stimulation of Human Femoral Head. Bioelectromagnetics 2014, 35, 547–558. [Google Scholar] [CrossRef]
- Song, J.K.; Cho, T.H.; Pan, H.; Song, Y.M.; Kim, I.S.; Lee, T.H.; Hwang, S.J.; Kim, S.J. An Electronic Device for Accelerating Bone Formation in Tissues Surrounding a Dental Implant. Bioelectromagnetics 2009, 30, 374–384. [Google Scholar] [CrossRef]
- Delenda, B.; Bader, R.; van Rienen, U. Modeling and Simulation of Platelet Reaction and Diffusion towards an Electro-Stimulating Dental Implant. In Proceedings of the 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 2584–2587. [Google Scholar] [CrossRef]
- The Federal Health Monitoring System. Keyword “Operations and Procedures in Hospitals”. Available online: http://www.gbe-bund.de/gbe10/pkg_isgbe5.prc_isgbe?p_uid=gast&p_aid=0&p_sprache=E (accessed on 15 February 2019).
- Kämmerer, P.W.; Klein, M.O.; Moergel, M.; Gemmel, M.; Draenert, G.F. Local and Systemic Risk Factors Influencing the Long-Term Success of Angular Stable Alloplastic Reconstruction Plates of the Mandible. J. Craniomaxillofac. Surg. 2014, 42, e271–e276. [Google Scholar] [CrossRef]
- Sadr-Eshkevari, P.; Rashad, A.; Vahdati, S.A.; Garajei, A.; Bohluli, B.; Maurer, P. Alloplastic Mandibular Reconstruction: A Systematic Review and Meta-Analysis of the Current Century Case Series. Plast. Reconstr. Surg. 2013, 132, 413e–427e. [Google Scholar] [CrossRef]
- Maurer, P.; Eckert, A.W.; Kriwalsky, M.S.; Schubert, J. Scope and Limitations of Methods of Mandibular Reconstruction: A Long-Term Follow-Up. Br. J. Oral Maxillofac. Surg. 2010, 48, 100–104. [Google Scholar] [CrossRef]
- Raben, H.; Schmidt, C.; Sridhar, K.; Kämmerer, P.W.; van Rienen, U. Numerical Design Studies on a Novel Electrostimulative Osteosynthesis System for the Mandible. Curr. Dir. Biomed. Eng. 2017, 3, 613–617. [Google Scholar] [CrossRef]
- van Rienen, U.; Zimmermann, U.; Raben, H.; Kämmerer, P.W. Preliminary Numerical Study on Electrical Stimulation at Alloplastic Reconstruction Plates of the Mandible. Sci. Comput. Electr. Eng. 2018. [Google Scholar] [CrossRef]
- Ma, J.L.; Pan, J.L.; Tan, B.S.; Cui, F.Z. Determination of Critical Size Defect of Minipig Mandible. J. Tissue Eng. Regener. Med. 2009, 3, 615–622. [Google Scholar] [CrossRef]
- Raben, H.; van Rienen, U.; Kämmerer, P.W.; Bader, R. Data for: Establishment of a Numerical Model to Design an Electro-Stimulating System for a Porcine Mandibular Critical Size Defect. Dataset, May 2019, University Library, University of Rostock. Available online: http://purl.uni-rostock.de/rosdok/id00002450 (accessed on 23 May 2019). [CrossRef]
- Qvist, M.H.; Hoeck, U.; Kreilgaard, B.; Madsen, F.; Frokjaer, S. Evaluation of Göttingen Minipig Skin for Transdermal in vitro Permeation Studies. Eur. J. Pharm. Sci. 2000, 11, 59–68. [Google Scholar] [CrossRef]
- Gabriel, S.; Lau, R.W.; Gabriel, C. The Dielectric Properties of Biological Tissues: II. Measurements in the Frequency Range 10 Hz to 20 GHz. Phys. Med. Biol. 1996, 41, 2251–2269. [Google Scholar] [CrossRef] [PubMed]
- Lackovic, I.; Stare, Z. Low-Frequency Dielectric Properties of the Oral Mucosa. In 13th International Conference on Electrical Bioimpedance and the 8th Conference on Electrical Impedance Tomography; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar] [CrossRef]
- Dielectric Properties IT’IS Foundation Web Page. Available online: https://itis.swiss/virtual-population/tissue-properties/database/dielectric-properties/ (accessed on 9 January 2019).
- MatWeb Web Page on Titanium Ti-6Al-4V (Grade 5), Annealed. Available online: http://www.matweb.com/search/datasheet.aspx?MatGUID=a0655d261898456b958e5f825ae85390 (accessed on 21 March 2019).
- Mitsubishi Chemical Advanced Materials Web Page, Product Data Sheets. Available online: https://media.mcam.com/fileadmin/quadrant/documents/QEPP/Global/English/Product_Data_Sheets_AEP/Ketron_1000_PEEK_PDS_GLOB_E_19092016.pdf?_ga=2.7651570.1148302848.1554475020-1676376043.1553176436 (accessed on 5 April 2019).
- Rho, J.Y.; Kuhn-Spearing, L.; Zioupos, P. Mechanical Properties and the Hierarchical Structure of Bone. Med. Eng. Phys. 1998, 20, 92–102. [Google Scholar] [CrossRef]
- Richardot, A.; McAdams, E.T. Harmonic Analysis of Low-Frequency Bioelectrode Behavior. IEEE Trans. Med. Imag. 2002, 21, 604–612. [Google Scholar] [CrossRef] [PubMed]
- Lange, R.; Lüthen, F.; Beck, U.; Rychly, J.; Baumann, A.; Nebe, B. Cell-Extracellular Matrix Interaction and Physico-Chemical Characteristics of Titanium Surfaces Depend on the Roughness of the Material. Biomol. Eng. 2002, 19, 255–261. [Google Scholar] [CrossRef]
- Plonsey, R.; Heppner, D.B. Considerations of Quasi-Stationarity in Electrophysiological Systems. Bull. Math. Biophys. 1967, 29, 657–664. [Google Scholar] [CrossRef]
- van Rienen, U.; Flehr, J.; Schreiber, U.; Motrescu, V. Modeling, Simulation, and Optimization of Integrated Circuits; Volume 146 of International Series of Numerical Mathematics, Chapter Modeling and Simulation of Electro-Quasistatic Fields; Birkhäuser Verlag: Basel, Switzerland, 2003; pp. 17–31. [Google Scholar]
- Van Rienen, U.; Flehr, J.; Schreiber, U.; Schulze, S.; Gimsa, U.; Baumann, W.; Weiss, D.; Gimsa, J.; Benecke, R.; Pau, H.W. Electro-Quasistatic Simulations in Bio-Systems Engineering and Medical Engineering. Adv. Radio Sci. 2005, 3, 39–49. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Conn, A.R.; Scheinberg, K.; Vicente, L.N. Introduction to Derivative-Free Optimization; Number 8 in MPS-SIAM Series on Optimization; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]
- Doblare, M.; Garcia, J.M.; Gomez, M.J. Modelling Bone Tissue Fracture and Healing: A Review. Eng. Fract. Mech. 2004, 71, 1809–1840. [Google Scholar] [CrossRef]
- Gupta, K.; Gupta, P.; Singh, G.; Kumar, S.; Singh, R.; Srivastava, R. Changes in Electrical Properties of Bones as a Diagnostic Tool for Measurement of Fracture Healing. Hard Tissue 2013, 2, 3. [Google Scholar] [CrossRef][Green Version]
- Kumaravel, S.; Sundaram, S. Monitoring of Fracture Healing by Electrical Conduction: A New Diagnostic Procedure. Indian J. Orthop. 2012, 46, 384–390. [Google Scholar] [CrossRef]
- Liboff, A.R.; Rinaldi, R.A.; Lavine, L.S.; Shamos, M.H. On Electrical Conduction in Living Bone. Clin. Orthop. 1975, 106, 330–335. [Google Scholar] [CrossRef] [PubMed]
- IEC 2016. IEC 60479-1: Effects of Current on Human Beings and Livestock; International Electrotechnical Commission: Geneva, Switzerland, 2016. [Google Scholar]
- Kono, M.; Takahashi, T.; Nakamura, H.; Miyaki, T.; Rekimoto, J. Design Guideline for Developing Safe Systems that Apply Electricity to the Human Body. ACM Trans. Comput. Hum. Interact. 2018, 25, 19. [Google Scholar] [CrossRef]
- Schmidt, C.; Wagner, S.; Burger, M.; Rienen, U.V.; Wolters, C.H. Impact of Uncertain Head Tissue Conductivity in the Optimization of Transcranial Direct Current Stimulation for an Auditory Target. J. Neural Eng. 2015, 12, 046028. [Google Scholar] [CrossRef]
- Gabriel, C.; Gabriel, S.; Corthout, E. The Dielectric Properties of Biological Tissues: I. Literature Survey. Phys. Med. Biol. 1996, 41, 2231–2249. [Google Scholar] [CrossRef]
- McCann, H.; Pisano, G.; Beltrachini, L. Variation in Reported Human Head Tissue Electrical Conductivity Values. bioRxiv 2019. [Google Scholar] [CrossRef]
- Amin, B.; Elahi, M.A.; Shahzad, A.; Porter, E.; O’Halloran, M. A Review of the Dielectric Properties of the Bone for Low Frequency Medical Technologies. Biomed. Phys. Eng. Express 2019, 5, 022001. [Google Scholar] [CrossRef]
- Wendel, K.; Väisänen, J.; Seemann, G.; Hyttinen, J.; Malmivuo, J. The Influence of Age and Skull Conductivity on Surface and Subdermal Bipolar EEG Leads. Comput. Intell. Neurosci. 2010, 2010, 397272. [Google Scholar] [CrossRef] [PubMed]
- Amin, B.; Elahi, M.A.; Shahzad, A.; Parle, E.; McNamara, L.; O’Halloran, M. An Insight into Bone Dielectric Properties Variation: A Foundation for Electromagnetic Medical Devices. In Proceedings of the 2018 EMF-Med 1st World Conference on Biomedical Applications of Electromagnetic Fields (EMF-Med), Split, Croatia, 10–13 September 2018; pp. 1–2. [Google Scholar]
- Amin, B.; Elahi, M.A.; Shahzad, A.; Porter, E.; McDermott, B.; O’Halloran, M. Dielectric Properties of Bones for the Monitoring of Osteoporosis. Med. Biol. Eng. Comput. 2019, 57, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, C.; Zimmermann, U.; van Rienen, U. Modeling of an Optimized Electrostimulative Hip Revision System under Consideration of Uncertainty in the Conductivity of Bone Tissue. IEEE J. Biomed. Health Inf. 2015, 19, 1321–1330. [Google Scholar] [CrossRef] [PubMed]
- Römer, U.; Schmidt, C.; Van Rienen, U.; Schöps, S. Low-Dimensional Stochastic Modeling of the Electrical Properties of Biological Tissues. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Saturnino, G.B.; Thielscher, A.; Madsen, K.H.; Knösche, T.R.; Weise, K. A Principled Approach to Conductivity Uncertainty Analysis in Electric Field Calculations. Neuroimage 2018. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, U.; van Rienen, U. The Impact of Bone Microstructure on the Field Distribution of Electrostimulative Implants. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milan, Italy, 25–29 August 2015; pp. 3545–3548. [Google Scholar] [CrossRef]
- Chopard, B.; Borgdorff, J.; Hoekstra, A.G. A Framework for Multi-Scale Modelling. Philos. Trans. Ser. A Math. Phys. Eng. Sci. 2014, 372. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raben, H.; Kämmerer, P.W.; Bader, R.; van Rienen, U. Establishment of a Numerical Model to Design an Electro-Stimulating System for a Porcine Mandibular Critical Size Defect. Appl. Sci. 2019, 9, 2160. https://doi.org/10.3390/app9102160
Raben H, Kämmerer PW, Bader R, van Rienen U. Establishment of a Numerical Model to Design an Electro-Stimulating System for a Porcine Mandibular Critical Size Defect. Applied Sciences. 2019; 9(10):2160. https://doi.org/10.3390/app9102160
Chicago/Turabian StyleRaben, Hendrikje, Peer W. Kämmerer, Rainer Bader, and Ursula van Rienen. 2019. "Establishment of a Numerical Model to Design an Electro-Stimulating System for a Porcine Mandibular Critical Size Defect" Applied Sciences 9, no. 10: 2160. https://doi.org/10.3390/app9102160
APA StyleRaben, H., Kämmerer, P. W., Bader, R., & van Rienen, U. (2019). Establishment of a Numerical Model to Design an Electro-Stimulating System for a Porcine Mandibular Critical Size Defect. Applied Sciences, 9(10), 2160. https://doi.org/10.3390/app9102160






