Abstract
In this paper, we propose a numerical approach to simulate the degree of coherence (DOC) of a partially coherent beam (PCB) with a Schell-model correlator in any transverse plane during propagation. The approach is applicable for PCBs whose initial intensity distribution and DOC distribution are non-Gaussian functions, even for beams for which it is impossible to obtain an analytical expression for the cross-spectral density (CSD) function. Based on our approach, numerical examples for the distribution of the DOC of two types of PCBs are presented. One type is the partially coherent Hermite–Gaussian beam. The simulation results of the DOC agree well with those calculated from the analytical formula. The other type of PCB is the one for which it is impossible to obtain an analytical expression of CSD. The evolution of the DOC with the propagation distance and in the far field is studied in detail. Our numerical approach may find potential applications in optical encryption and information transfer.
1. Introduction
Over the past decades, partially coherent beams (PCBs) have attracted wide attention due to their important applications, such as particle trapping/manipulation, wide-field optical coherence tomography, laser material processing, optical metrology, 3D imaging and, so on [1,2,3,4,5,6,7,8,9]. Generally, PCBs are characterized by the so-called cross-spectral density (CSD) function in the space–frequency domain or mutual coherence function (MCF) in the space–time domain, and the coherence characteristics of PCBs are described by the degree of coherence (DOC) which can be obtained from the CSD function or the MCF. It is known that the DOC plays a central role in determining the beam propagation characteristics, image resolution, and effects of interaction with matter [10,11,12,13,14]. However, most studies are focused on the PCBs whose DOCs are of Gaussian function because it is a hard task to devise a physically realizable CSD function with arbitrary DOC. Recently, Gori and co-workers proposed a sufficient condition for mathematically devising a genuine CSD function [15,16]. Since then, researchers have turned their attention to study PCBs with special DOCs (non-Gaussian function) [17,18,19,20,21]. Owing to their special DOCs, these beams exhibit peculiar propagation features even in free space. For example, a non-uniformly correlated (NUC) beam displays “self-focusing” and lateral shift of intensity maxima during free-space propagation [17]. The multi-Gaussian-correlated beam and Laguerre–Gaussian (LG)-correlated beam will produce a flat-topped beam profile and ring-shaped beam profile in the far field, respectively [18,19]. In addition, the DOCs may carry the information of the beam itself or of the object with which the PCBs interact [22]. For example, by measuring the far-field DOC [23], the azimuthal and radial mode orders of a partially coherent LGpl beam can be determined. In [14], the authors point out that, when a PCB is obstructed by an opaque obstacle, its DOC can self-reconstruct. In addition, several methods have been proposed to experimentally generate the prescribed DOC of a PCB, for example by using a spatial light modulator, intra-cavity modulation and a deformable mirror, etc. [24,25,26,27]. However, the aforementioned studies are confined to PCBs whose initial intensity distributions have a Gaussian function.
On the other hand, PCBs with both initial non-Gaussian beam profiles and DOCs have also received considerable attention in recent years [28,29,30,31,32,33,34]. In the following text, we use the term general PCBs (GPCBs) to include a class of PCBs with non-Gaussian amplitudes and DOCs. Through controlling the DOCs and beam profiles in the source plane simultaneously, GPCBs can generate a far-field beam array with controllable forms [32,33], and the profile of each beamlet in the array is also adjustable, making them ideal sources for particle trapping and manipulation. Nevertheless, in these studies, the evolution properties of the DOC during propagation were neglected. Though other studies [35,36] presented the reciprocity relation between the initial beam profile and the DOC in the far filed, this is only applicable for special kinds of GPCBs, known as quasi-homogeneous beams. In such beams, the variation of the DOCs with the spatial point r is much faster than that of intensity distribution with r. Up to now, only few papers have dealt with the evolution of the DOCs during GPCBs passage through free space or paraxial optical systems, especially for those beams whose DOCs or initial intensity distributions are impossible to obtain using an analytical expression.
In this paper, we propose a numerical approach for calculating the DOC of a GPCB in any transverse plane perpendicular to the propagation axis during propagation in free space or paraxial optical systems. In this approach, we introduce white noises [37,38,39] into the convolution approach [40] to generate speckle patterns in any transverse plane of propagation. Then, the DOC is retrieved from the fourth-order correlation function of the speckle patterns. On the basis of this approach, we investigate the effects of source intensity distribution and coherence width on the DOC during propagation in free space through several numerical examples.
2. Theory
Let us consider a scalar, quasi-monochromatic, and statistically stationary optical beam, propagating along the z-direction. In the space–frequency domain, the second-order statistics of such GPCB are typically characterized by the CSD function , where E denotes the random electric field, and are two arbitrary position vectors in the transverse plane, the asterisk is the complex conjugate, and the angular brackets is the ensemble average over the field fluctuations. Assume that the GPCB we consider is a Schell-model beam whose DOC function is only dependent on the separation of two points. In this situation, the CSD function in the source plane (z = 0) can be written as [15,16]
where and are two arbitrary position vectors in the source plane, is a complex amplitude function, and is the DOC function. For a physically realizable CSD function, the DOC can be alternatively represented the following integral form [19]
with
The function p(v) in Equation (3) must be non-negative for any v to ensure that the CSD is genuine; denotes the Dirac function. In order to introduce our numerical approach, we rewrite the function in the follow form
where Cn(v) (n = 1, 2, 3, …) denotes the random complex function whose probability density functions of amplitude and phase of Cn obey the negative exponent and uniform distribution, respectively [39]. The angular bracket denotes the ensemble average. Here, Cn(v) can be viewed as the field of the white noise.
By substituting Equation (4) into Equations (1)–(3) and after some mathematical operations, Equation (1) turns out to be
with
where FT stands for the symbol of Fourier transform, Tn0 (r) (n = 1, 2, 3…) denotes the instantaneous electric fields, each of which represents one realization of a GPCB. In Equation (5), we use the incoherent superposition of instantaneous random realizations instead of ensemble averaging over the random fields, since we assume the beam is statistically stationary. If the number of realizations N is large enough, the incoherent realization superposition is a good approximation. The first term in Equation (6) is the complex amplitude, as we described above, and the second term contains the information of the DOC of the source. To synthesize the realization of Tn0 (r) numerically, one can use commercial software such as MATLAB to generate the random complex function Cn and then take the Fourier transform of the product of the function Cn and the square root of the p(v) function. Finally, one instantaneous electric filed is acquired by multiplying the Fourier result by the function . Note that the DOC is determined by the function p(v) in the simulation. Once each instantaneous electric field in the source plane is known, the relation between such fields in the source plane and in the output plane passing through a paraxial ABCD optical system is linked to the Collins integral formula, given by
where is the wavenumber associated with , which is the wavelength of the light, and denotes the arbitrary position vector in the output plane. A, B, D are the elements of the transfer matrix of an optical system. On Substituting Equation (6) into (7), we obtain the expression
After some rearrangement, Equation (8) can be written in the simple convolution form
where is the inverse Fourier transform of the new defined function , and denotes the convolution symbol. Equation (9) establishes the relation of an instantaneous field between the source plane and the output plane with the convolution form, which is the main result of this paper. It provides one convenient way to simulate the second-order statistics of a GPCB in the output plane.
Here, we describe the method for numerical simulating the instantaneous electric field using MATLAB. It follows from Equation (9) that the key point is to calculate the convolution term . According to the convolution theorem, such term can be expressed as , where denotes the symbol for inverse Fourier transform. The operations for the and in MATLAB are based on the fast Fourier transform (FFT) algorithm. In numerical simulation, each realization of any function is represented as a matrix with N1 × N1 number of elements. We first assume the function U has the physical dimensions L × L, where L is the length of the coordinate. The corresponding coordinate r = (x, y) for x or y is from −L/2 to L/2 with step L/N1. In order to match the coordinate (x, y), the function p (related to the DOC) must sample in the spatial frequency domain having dimensions N1/L × N1/L, and the corresponding coordinate fx or fy is from −N1/2L to N1/2L, with step 1/L [41]. The random complex function Cn is generated by [randn(N1) + i × randn(N1)]/sqrt(2), where randn(N1) is the build-in function returning the N1 × N1 matrix consisting of random numbers of normal distribution. Then, the Fourier transform function is multiplied by the function U, and, finally, is obtained by multiplying the inverse transform of the above results by the coefficient before the convolution shown in Equation (9). The corresponding coordinates for ρx or ρy in the out plane will be from −λBN1/2L to λBN1/2L, with step λB/L [41].
According to Equation (9), the average spectral density is calculated by the following formula
where is the instantaneous spectral density (one realization).
In order to evaluate the DOC, we first calculate the normalized intensity correlation (fourth-order correlation function) between points and , i.e.,
By applying the Gaussian moment theorem [1], the modulus of square of the DOC can be extracted from the normalized intensity correlation function, given by
It follows from Equation (12) that one can numerically calculate the DOC in the output plane from the normalized intensity correlation function. Note that Equation (12) is only valid for the GPCBs with a Schell-model type. Hence, the DOC is only a function of the separation of two points and , i.e., .
3. Simulation Results
In this section, to demonstrate the validity for the numerical approach, we first compare the results for the DOC obtained with our numerical approach with those derived from an analytical expression. Then, we present numerical examples for the evolution of the DOC with the propagation distance, using our numerical method. In this numerical case, it is impossible to obtain the analytical expression of the GPCB during propagation. In the following simulation, the number of elements N1 × N1 and N are chosen to be 512 × 512 and 104, respectively. Under this circumstance, it takes about 3.7 min for each plot. The computer is from Dell, Texas, USA, whose configurations used in the simulation are i7-8700 CPU @ 3.2GHz and 16GB RAM. Here, we want to stress that the advantage of our numerical approach is that it can deal with partially coherent beams that cannot be described by an analytical expression.
In order to demonstrate the validity of our simulation method, a typical Schell-model beam, named a partially coherent elegant Hermite–Gaussian (PCEHG) beam [42], is used to compare the evolution of DOC from the analytical results with that from the simulation results. The CSD function of the PCEHG beam in the source plane is expressed as
is the Hermite polynomial of order n, and are the beam waist size and the transverse coherence width, respectively. The analytical expression for the CSD function of the PCEHG beam at distance z in free-space propagation can be found in [42] (see Equation (17) in [42], where the elements of the transfer matrix are A = 1, B = z, and D = 1). Figure 1a1–e1 illustrates the evolution of the modulus of the square of the DOC with the propagation distance in free space calculated from the analytical formula. The beam parameters in the calculation are chosen to be n = 2, m = 0, , , and . For comparison, the corresponding results attained by our numerical approach are shown in Figure 1a2–e2. It can be seen that the simulation results agree reasonably well with those obtained from the analytical formula, implying that our method is valid and effective in simulating the evolution of the DOC during propagation.
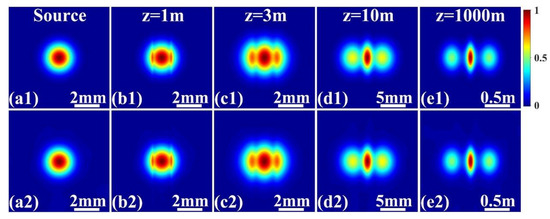
Figure 1.
Evolution of the square of the modulus of the degree of coherence of the partially coherent elegant Hermite–Gaussian beam with the propagation distance in free space. (a1–e1) Results obtained from the analytical formula; (a2–e2) the corresponding results obtained using our numerical approach.
As we state in Section 2, the advantage of the numerical approach is that it can deal with the evolution of the DOC of a GPCB whose CSD function during propagation is impossible to acquire by an analytical expression. In the following example, we assume that the function p(v) (Fourier transform of the DOC) is a soccer pattern, as shown in Figure 2a; the corresponding modulus of the square of the DOC is plotted in Figure 2c. The initial amplitude function we choose is the elegant Hermite–Gaussian distribution, as follows
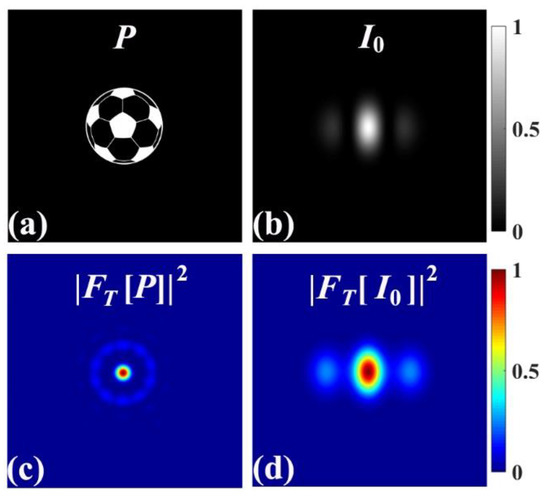
Figure 2.
(a) Soccer pattern as a function of p(v); (b) intensity distribution of the Hermite–Gaussian beam with n = 2, m = 0 in the source plane; (c) modulus of the square of the source degree of coherence, (d) modulus of the square of the Fourier transform of . The Fourier transform was performed by FFT in MATLAB.
Figure 2b,d presents the source intensity distribution of such GPCB and its modulus of the square of the Fourier transform, respectively. The relevant parameters are set as n = 2, m = 0, , and . If the source beam is assumed to be a quasi-homogeneous planar source [1,35,36], then, Figure 2d can be treated as the modulus of the square of the DOC in the far field.
Before presenting the simulation results, we want to determine the relationship between the initial coherence width and the size of the soccer pattern. As stated in [1,10,43], the source transverse coherence width is inversely proportional to the size of the function of p. Here, we assume that the transverse coherence width is where l denotes the size of the distribution of p(v) (radius of the soccer).
Figure 3 presents the simulation results of the DOC of the GPCB with different initial coherence width at several propagation distances. The parameters used in the simulation are n = 2, m = 0, ω0 = 1 mm, and λ = 532 nm. One can see that the DOC pattern can keep the profile similar to that in the source plane (see in Figure 2c), in a range from z = 0 to certain propagation distances, but this range is closely dependent on the initial coherence width. When the coherence width is large (), the DOC can keep its profile invariant at about 0.7 m (see Figure 3a3–c3]. In the case of , the profile of the DOC changes much faster compared to that in the case for and evolves into a shape similar to that in the far field at distance z = 1.0 m (see Figure 2d and Figure 3d1).
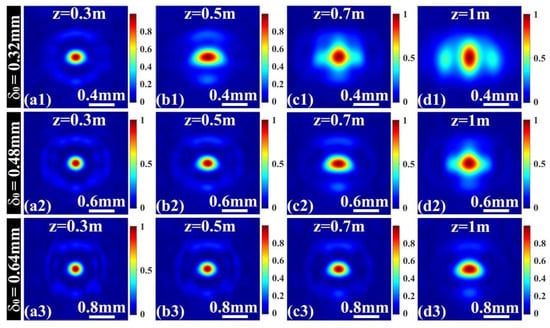
Figure 3.
Evolution of the modulus of the square of the degree of coherence of a general partially coherent beam with three different initial transverse coherences propagating in free space. The values of the initial coherence width δ0 in the first (a1–d1), second (a2–d2), and third (a3–d3) rows are 0.32 mm, 0.48 mm, and 0.64 mm, respectively. With the increase of δ0, the degree of coherence distribution remains invariant for a longer distance.
Let us now turn our attention on the influence of the initial coherence width on the DOC pattern of such GPCB in the far field. Figure 4a–c shows our numerical simulations of the DOC distributions at propagation distance z = 1000 m (far field) with different values of coherence width. The simulation parameters are the same as those used in Figure 3. For the case of (see Figure 4a), the DOC pattern is similar to that shown in Figure 2d, implying that the beam can be be considered as a quasi-homogeneous beam whose DOC in the far field is the Fourier transform of the source intensity distribution, independent of the DOC in the source plane. As the initial coherence width increases, the effects of the source DOC gradually appear. In this situation, the DOC pattern is determined by both the intensity distribution and the DOC function in the source plane. As the coherence width increases, the area of the side lobes becomes large. The enlargement of the side lobes in Figure 4b,c can be explained by the fact that, as the coherence width increases, the globe coherence in our calculation area, which is 2.0 mm × 2.0 mm, increases. As a result, the side lobes are enlarged in the high-coherence case (see in Figure 4b,c) compared with the low-coherence case (see in Figure 4a). It is also found that the distributions of the DOC in Figure 4 are left–right asymmetric, which may be caused by the fact that the p function (related to the DOC) has a slight left–right asymmetry, as shown in Figure 2a. To confirm our results, we choose as a circular function a p function, which is exactly circularly symmetric. The expression for a circular function is given by
where l is the radius of soccer defined previously. Figure 4d–f presents the corresponding numerical simulations of the DOC distributions at distance z = 1000 with the corresponding coherence width. The p function is shown in Equation (15). One can see that the intensities of the side lobes in the left side and the right side are the same.
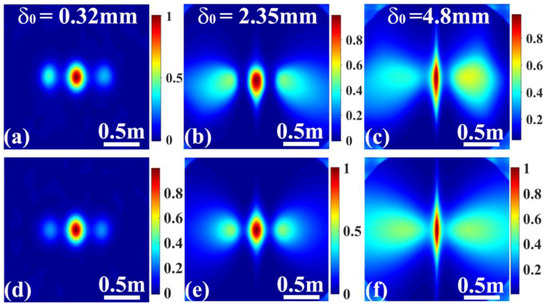
Figure 4.
Density plots of the modulus of the square of the degree of coherence of a general partially coherent beam at a propagation distance z = 1000 m, with the initial coherence width δ0 = 0.32 mm in (a,d), δ0 = 2.35 mm in (b,e), and δ0 = 4.8 mm in (c,f). The p function used in (a–c) is the soccer patter shown in Figure 2a, and the p function used in (d–f) is the circular function shown in Equation (15).
4. Conclusions
In summary, we have introduced a numerical approach to calculate the DOC distribution of a Schell-model type GPCB in any transverse plane perpendicular to the propagation axis during free-space propagation. This method first represents the GPCB as a sequence of random electric fields by introducing white noises into it. In this representation, each realization of random fields obeys the propagation law described by Huygens–Fresnel integral formula. Then, we use a convolution approach to obtain the corresponding realization of random fields in the output plane. At last, the information on DOC is acquired through evaluating the fourth-order correlation function of random fields in the output plane. The prominent advantage of this numerical approach is that it can conveniently calculate the DOC of any partially coherent Schell-mode beam, even when it is impossible to obtain using analytical expressions for the CSD function. Two numerical examples of the evolution of DOCs for two types of GPCBs with propagation distance were investigated in detail. One demonstrated that our approach is valid, by comparing our results with those obtained with the analytical formula. The other example showed the influence of the initial field amplitude and correlation function on the evolution of the DOC. The analytical formula for the CSD function cannot be applied to the beam in the second example. Our method can also deal with the DOC of a GPCB propagation through a paraxial ABCD optical system or atmospheric turbulence. We believe that this numerical approach may find applications in optical communication and optical encryption.
Author Contributions
P.M. (Data curation and Writing—Original Draft); B.K. (Writing—Review); R.K. (Data curation); C.L. (Supervision and investigation); J.Z. (software); X.P. (investigation); C.M. (formal analysis); Y.E.M. (software); Y.Z. (formal analysis and validation); F.W. (Supervision, Writing—Review, Editing and validation); Y.C. (Supervision, Writing—Review, Editing and validation).
Funding
This research was funded by the National Natural Science Foundation of China (NSFC) (91750201, 11874046, 11525418); Project of the Priority Academic Program Development of Jiangsu Higher Education Institutions; Qing Lan Project of Jiangsu Province; Postgraduate Research & Practice Innovation Program of Jiangsu Province (KYCX17_2024). China Scholarship Council (CSC) (201706920085).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: New York, NY, USA, 1995; ISBN 9780521417112. [Google Scholar]
- Wolf, E. Introduction to the Theory of Coherence and Polarization of Light; Cambridge University Press: New York, NY, USA, 2007; ISBN 9780521822114. [Google Scholar]
- Cai, Y.; Wang, F.; Zhao, C.; Zhu, S.; Wu, G.; Dong, Y. Partially Coherent Vector Beams: From Theory to Experiment. In Vectorial Optical Fields: Fundamentals and Applications; Zhen, Q., Ed.; World Scientific: Singapore, 2013; ISBN 9789814449885. Chapter 7; pp. 221–273. [Google Scholar]
- Gbur, G.; Visser, T.D. The Structure of Partially Coherent Fields. Prog. Opt. 2010, 55, 285–341. [Google Scholar]
- Karamata, B.; Lambelet, P.; Laubscher, M.; Salathé, R.; Lasser, T. Spatially Incoherent Illumination as a Mechanism for Cross-Talk Suppression in Wide-Field Optical Coherence Tomography. Opt. Lett. 2004, 29, 736–738. [Google Scholar] [CrossRef]
- Zhao, C.; Cai, Y.; Lu, X.; Eyyuboğlu, H.T. Radiation Force of Coherent and Partially Coherent Flat-Topped Beams on a Rayleigh Particle. Opt. Express 2009, 17, 1753–1765. [Google Scholar] [CrossRef] [PubMed]
- Kato, Y.; Mima, K.; Miyanaga, N.; Arinaga, S.; Kitagawa, Y.; Nakatsuka, M.; Yamanaka, C. Random Phasing of High-Power Lasers for Uniform Target Acceleration and Plasma-Instability Suppression. Phys. Rev. Lett. 1984, 53, 1057–1060. [Google Scholar] [CrossRef]
- Douglass, K.M.; Sieben, C.; Archetti, A.; Lambert, A.; Manley, S. Super-Resolution Imaging of Multiple Cells by Optimised Flat-Field Epi-Illumination. Nat. Photonics 2016, 10, 705–708. [Google Scholar] [CrossRef] [PubMed]
- Van Dijk, T.; Fischer, D.G.; Visser, T.D.; Wolf, E. Effects of Spatial Coherence on the Angular Distribution of Radiant Intensity Generated by Scattering on a Sphere. Phys. Rev. Lett. 2010, 104, 173902. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Chen, Y.; Wang, F. Generation and Propagation of Partially Coherent Beams with Nonconventional Correlation Functions: A Review [Invited]. J. Opt. Soc. Am. A 2014, 31, 2083–2096. [Google Scholar] [CrossRef]
- Liang, C.; Wu, G.; Wang, F.; Li, W.; Cai, Y.; Ponomarenko, S.A. Overcoming the Classical Rayleigh Diffraction Limit by Controlling Two-Point Correlations of Partially Coherent Light Source. Opt. Express 2017, 25, 28352–28362. [Google Scholar] [CrossRef]
- Brown, D.P.; Brown, T.G. Partially Correlated Azimuthal Vortex Illumination: Coherence and Correlation Measurements and Effects in Imaging. Opt. Express 2008, 16, 20418–20426. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y.; Liu, X.; Cai, Y.; Ponomarenko, S.A. Self-Reconstruction of Partially Coherent Light Beams Scattered by Opaque Obstacles. Opt. Express 2016, 24, 23735–23746. [Google Scholar] [CrossRef]
- Liu, X.; Peng, X.; Liu, L.; Wu, G.; Zhao, C.; Wang, F.; Cai, Y. Self-Reconstruction of the Degree of Coherence of a Partially Coherent Vortex Beam Obstructed by an Opaque Obstacle. Appl. Phys. Lett. 2017, 110, 181104. [Google Scholar] [CrossRef]
- Gori, F.; Santarsiero, M. Devising Genuine Spatial Correlation Functions. Opt. Lett. 2007, 32, 3531–3533. [Google Scholar] [CrossRef]
- Gori, F.; Ramírez-Sánchez, V.; Santarsiero, M.; Shirai, T. On Genuine Cross-Spectral Density Matrices. J. Opt. A Pure Appl. Opt. 2009, 11, 085706. [Google Scholar] [CrossRef]
- Lajunen, H.; Saastamoinen, T. Propagation Characteristics of Partially Coherent Beams with Spatially Varying Correlations. Opt. Lett. 2011, 36, 4104–4106. [Google Scholar] [CrossRef]
- Sahin, S.; Korotkova, O. Light Sources Generating Far Fields with Tunable Flat Profiles. Opt. Lett. 2012, 37, 2970–2972. [Google Scholar] [CrossRef]
- Wang, F.; Liu, X.; Yuan, Y.; Cai, Y. Experimental Generation of Partially Coherent Beams with Different Complex Degrees of Coherence. Opt. Lett. 2013, 38, 1814–1816. [Google Scholar] [CrossRef]
- Ma, L.; Ponomarenko, S.A. Optical Coherence Gratings and Lattices. Opt. Lett. 2014, 39, 6656–6659. [Google Scholar] [CrossRef]
- Chen, Y.; Norrman, A.; Ponomarenko, S.A.; Friberg, A.T. Coherence Lattices in Surface Plasmon Polariton Fields. Opt. Lett. 2018, 43, 3429–3432. [Google Scholar] [CrossRef]
- Chen, Y.; Ponomarenko, S.A.; Cai, Y. Experimental Generation of Optical Coherence Lattices. Appl. Phys. Lett. 2016, 109, 061107. [Google Scholar] [CrossRef]
- Liu, X.; Wu, T.; Liu, L.; Zhao, C.; Cai, Y. Experimental Determination of the Azimuthal and Radial Mode Orders of a Partially Coherent LGpl Beam. Chin. Opt. Lett. 2017, 15, 030002. [Google Scholar]
- Hyde, M.; Bose-Pillai, S.; Voelz, D.G.; Xiao, X. Generation of Vector Partially Coherent Optical Sources Using Phase-Only Spatial Light Modulators. Phys. Rev. Appl. 2016, 6, 064030. [Google Scholar] [CrossRef]
- Chriki, R.; Nixon, M.; Pal, V.; Tradonsky, C.; Barach, G.; Friesem, A.A.; Davidson, N. Manipulating the Spatial Coherence of a Laser Source. Opt. Express 2015, 23, 12989–12997. [Google Scholar] [CrossRef]
- Lehtolahti, J.; Kuittinen, M.; Turunen, J.; Tervo, J. Coherence Modulation by Deterministic Rotating Diffusers. Opt. Express 2015, 23, 10453–10466. [Google Scholar] [CrossRef]
- Hyde, M.; Bose-Pillai, S.; Wood, R.A. Synthesis of Non-Uniformly Correlated Partially Coherent Sources Using a Deformable Mirror. Appl. Phys. Lett. 2017, 111, 101106. [Google Scholar] [CrossRef]
- Wu, T.; Liang, C.; Wang, F.; Cai, Y. Shaping the Intensity and Degree of Coherence of a Partially Coherent Beam by a 4f Optical System with an Amplitude Filter. J. Opt. 2017, 19, 124010. [Google Scholar] [CrossRef]
- Visser, T.D.; Agrawal, G.P.; Milonni, P.W. Fourier Processing with Partially Coherent Fields. Opt. Lett. 2017, 42, 4600–4602. [Google Scholar] [CrossRef]
- Liang, C.; Mi, C.; Wang, F.; Zhao, C.; Cai, Y.; Ponomarenko, S.A. Vector Optical Coherence Lattices Generating Controllable Far-Field Beam Profiles. Opt. Express 2017, 25, 9872–9885. [Google Scholar] [CrossRef]
- Zhu, S.; Wang, J.; Liu, X.; Cai, Y.; Li, Z. Generation of Arbitrary Radially Polarized Array Beams by Manipulating Correlation Structure. Appl. Phys. Lett. 2016, 109, 161904. [Google Scholar] [CrossRef]
- Mei, Z.; Korotkova, O. Sources for Random Arrays with Structured Complex of Coherence. Opt. Lett. 2018, 43, 2676–2679. [Google Scholar] [CrossRef]
- Liang, C.; Zhu, X.; Mi, C.; Peng, X.; Wang, F.; Cai, Y.; Ponomarenko, S.A. High-Quality Partially Coherent Bessel Beam Array Generation. Opt. Lett. 2018, 43, 3188–3191. [Google Scholar] [CrossRef]
- Liu, X.; Liu, L.; Peng, X.; Liu, L.; Wang, F.; Gao, Y.; Cai, Y. Partially coherent vortex beam with periodical coherence properties. J. Quant. Spectrosc. Radiat. Transf. 2019, 222–223, 138–144. [Google Scholar] [CrossRef]
- Carter, W.H.; Wolf, E. Coherence and Radiometry with Quasihomogeneous Planar Sources. J. Opt. Soc. Am. 1977, 67, 785–796. [Google Scholar] [CrossRef]
- Raghunathan, S.B.; Visser, T.D.; Wolf, E. Far-Zone Properties of Electromagnetic Beams Generated by Quasi-Homogeneous Sources. Opt. Commun. 2013, 295, 11–16. [Google Scholar] [CrossRef]
- Voelz, D.; Xiao, X.; Korotkova, O. Numerical Modeling of Schell-Model Beams with Arbitrary Far-Field Patterns. Opt. Lett. 2015, 40, 352–355. [Google Scholar] [CrossRef]
- Goodman, J.W. Statistical Optics, 2nd ed.; Wiley: New York, NY, USA, 1985; ISBN 9781119009450. [Google Scholar]
- Dainty, J.C. Laser Speckle and Related Phenomena; Spring-Verlag: Berlin, Germany, 1975; ISBN 9783662432051. [Google Scholar]
- Wang, F.; Korotkova, O. Convolution Approach for Beam Propagation in Random Media. Opt. Lett. 2016, 41, 1546–1549. [Google Scholar] [CrossRef]
- Schmidt, J.D. Numerical Simulation of Optical Wave Propagation with Examples in MATLAB; SPIE Press: Washington, DC, USA, 2010; ISBN 9780819483263. [Google Scholar]
- Wang, F.; Cai, Y.; Eyyuboğlu, H.T.; Baykal, Y.; Çil, C.Z. Partially Coherent Elegant Hermite-Gaussian Beams. Appl. Phys. B 2010, 100, 617–626. [Google Scholar] [CrossRef]
- Pauwels, J.; Verschaffelt, G. Speckle Reduction in Laser Projection Using Microlens-Array Screens. Opt. Express 2017, 25, 3180–3195. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).