Framework for Fast Experimental Testing of Autonomous Navigation Algorithms
Abstract
:1. Introduction
- A generic navigation framework. We propose a conceptual structure for navigation problems that permits to implement complete autonomous navigation systems in a fast and easy way (although demonstrated in a ground vehicle, these implementations can be tailored to different kind of robots, whether it be terrestrial, marine or aerial). This framework permits us to easily arrange the system complexity, enabling researchers to focus on their topics of interest while generating minimal but complete applications suitable for real-world experimental testing. This feature improves the research productivity and is a direct consequence of the proposed architecture.
- A Kalman filter (KF)-based 2D SLAM and GNSS fusion module. To demonstrate how easy is to replace any module using the proposed framework, we developed a new localization module that became a contribution itself. This module is based on a Kalman filter that fuses the poses generated by two complementary localization sources as 2D SLAM and GNSS are. This module permits to recover the SLAM localization after exploring unmapped areas, so mixed navigation on-map/off-map can be performed.
- A set of tools for basic system implementation. In addition to the conceptual framework, we provide a set of tools that brings the basic functionalities required to implement a fully operative terrestrial autonomous navigation system. It comprises planning, car-like control, and reactive safety modules.
2. Related Work
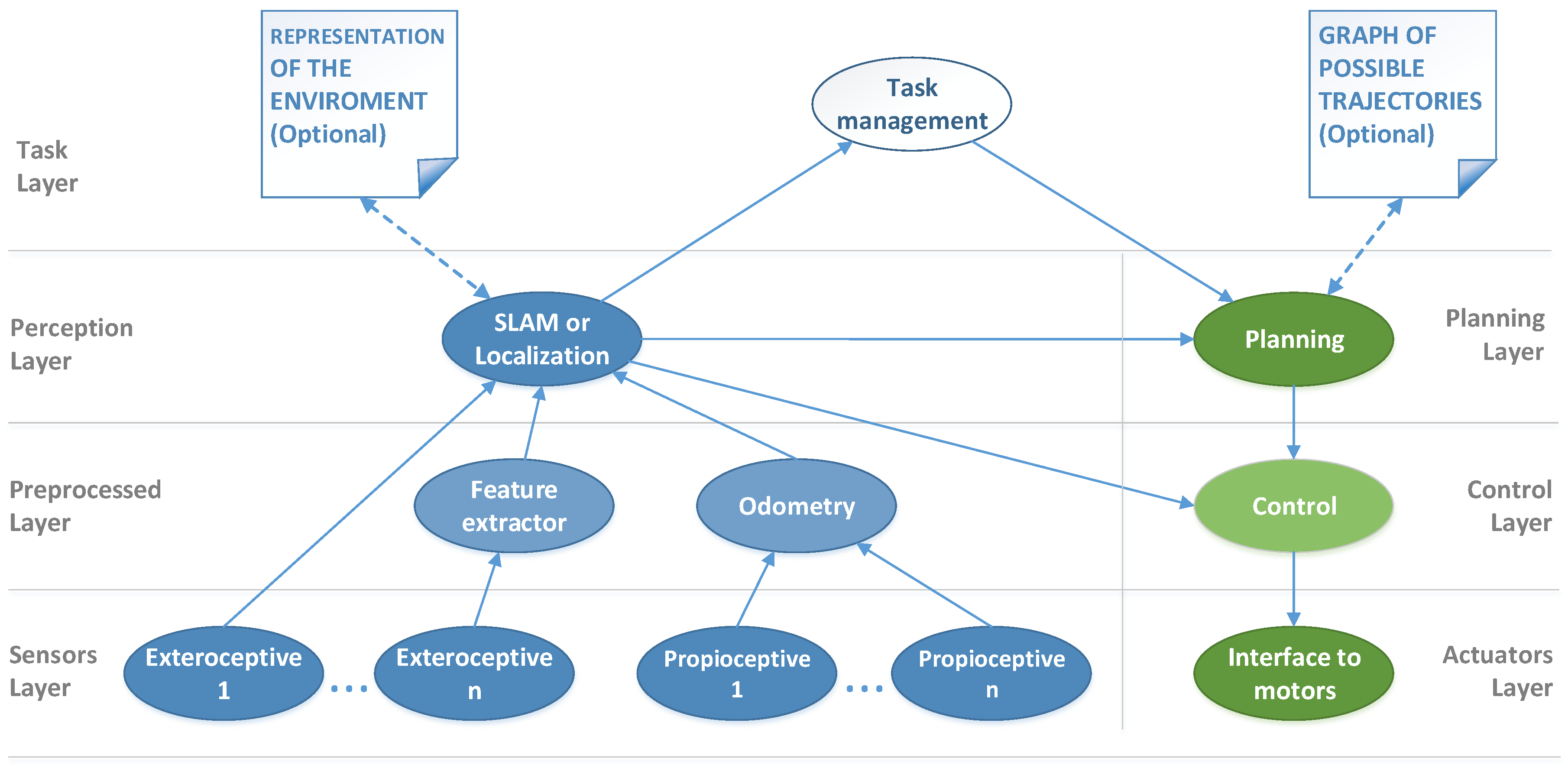
3. Framework Design
- Our planning is independent of the environment representation. In the navigation stack, global planning depends on a grid map, making it difficult to use alternative representations of the environment. On the contrary, following our approach any planning module must be independent of the environment representation, as can be seen in Figure 1. This favors modularity and eliminates conversions and other undesired extra processes required to integrate alternative environment representations with the navigation stack. An example of this can be found in [36], where the authors explain the integration of a graph-based visual SLAM system with the navigation stack planning and control modules. The authors report that they had to create a grid map from their native graph representation and that this extra process introduced additional problems that even forced to discard two of the three scenarios for the path-planning experiments carried out for the paper.
- Every ROS node belongs to a single module. The navigation stack does not follow this rule, which makes difficult the substitution of certain components. For example, the move_base node fuses planning and control, which makes it rigid in its operation [26]. In contrast, replacing modules in our framework is as easy as changing a single line in the ROS launch file. This makes the produced systems flexible and easy to adapt to different specifications (e.g., different robot kinematics, highlighted as a ROS navigation stack limitation in [24,35]) because only the related nodes need to be modified or substituted.
- Our framework follows a clear conceptual structure. In [37] we see an example of how developing a complex system using the navigation stack can lead to an intricate architecture. On the contrary, we follow a conceptual structure based on abstraction levels to make the applications clear, organized and scalable. Moreover, a neat division in conceptually different sub-problems makes easier to keep the research focus on the topics of interest without giving up the advantages that a complete system in real-world operation provides for experimental testing, as happens when using datasets or simulators.
3.1. Framework Requirements
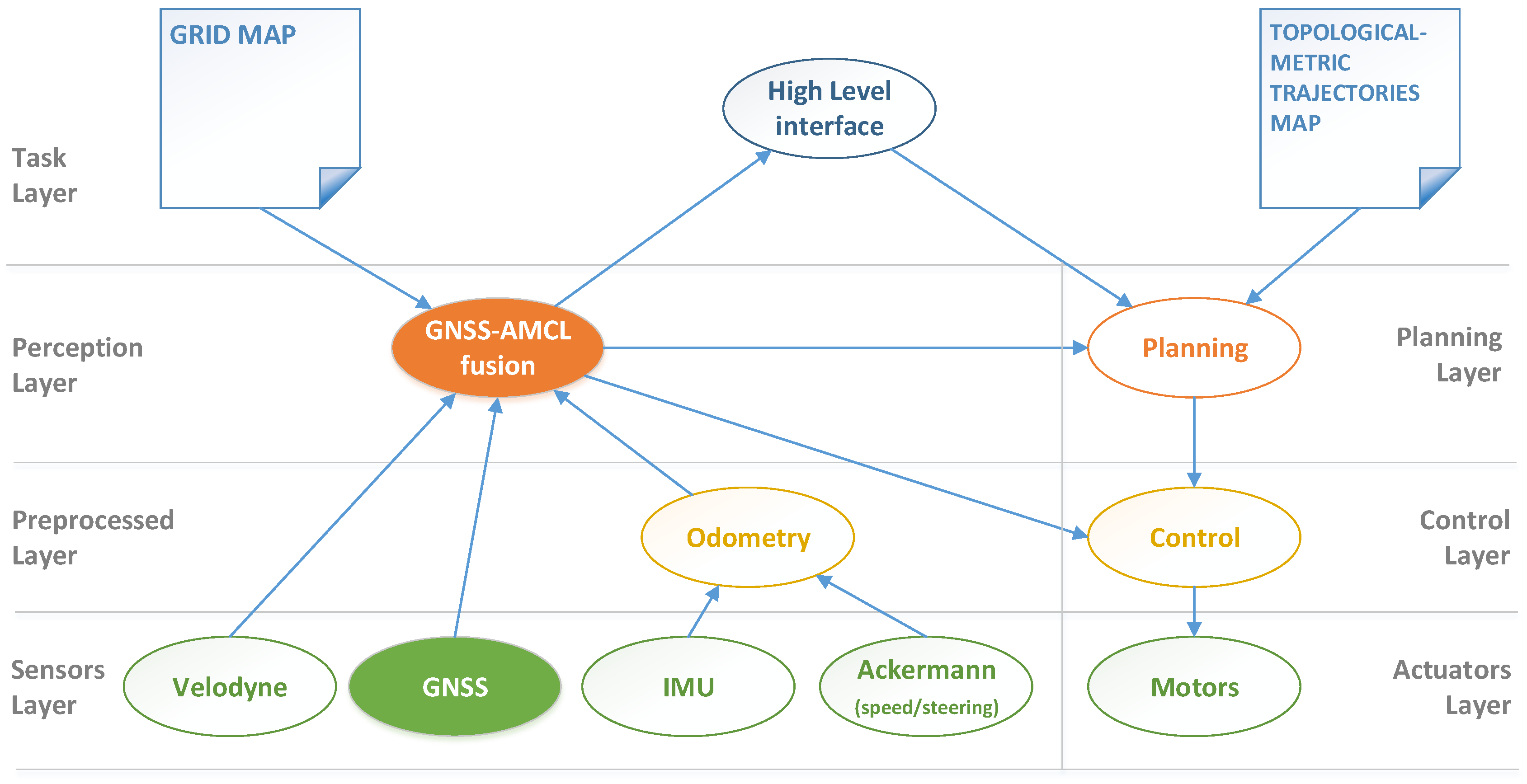
3.2. Proposed Approach
3.2.1. Perception
3.2.2. Motion
3.2.3. High Level
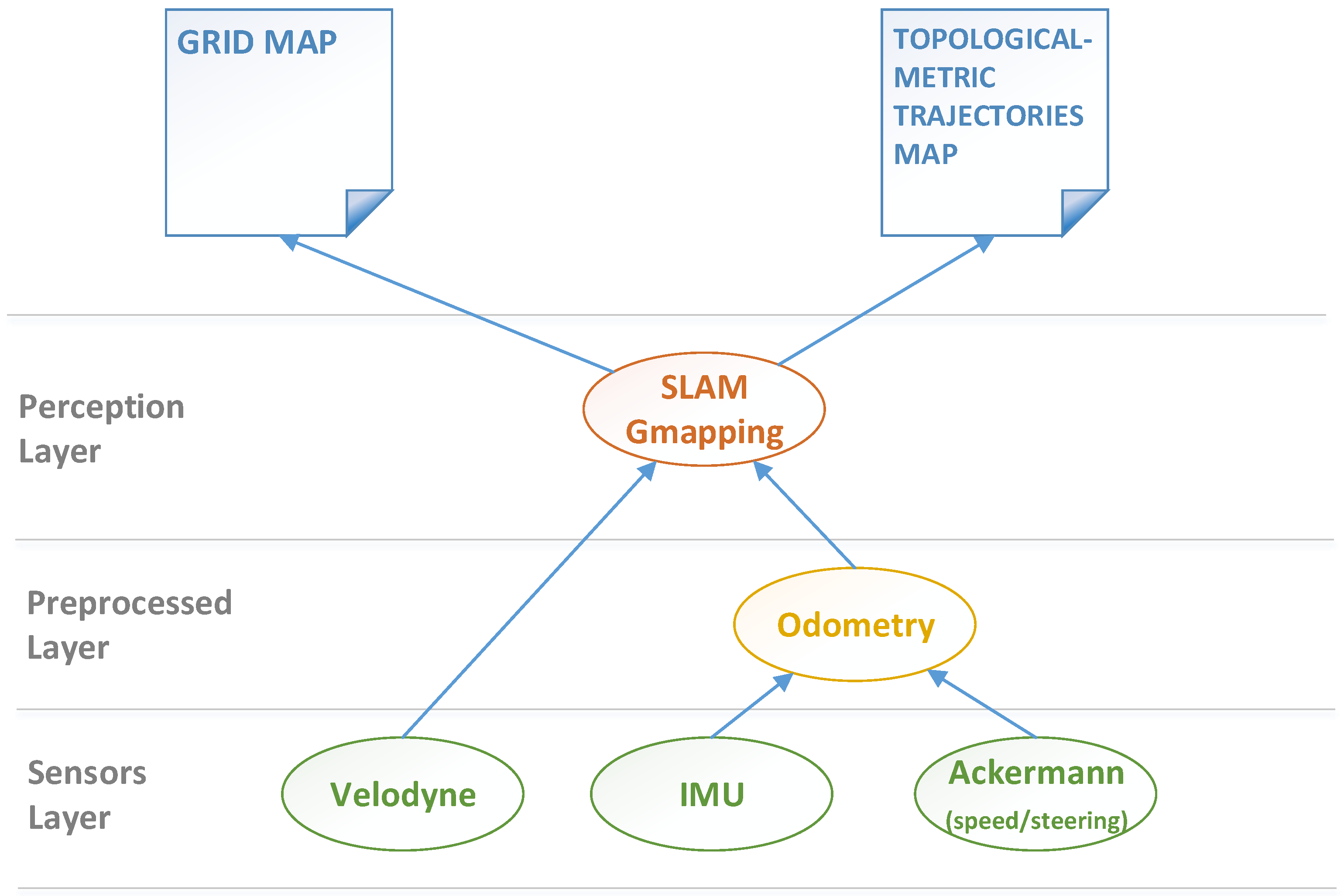
4. Initial Framework Implementation
4.1. Pre-Execution Phase
4.2. Execution Phase
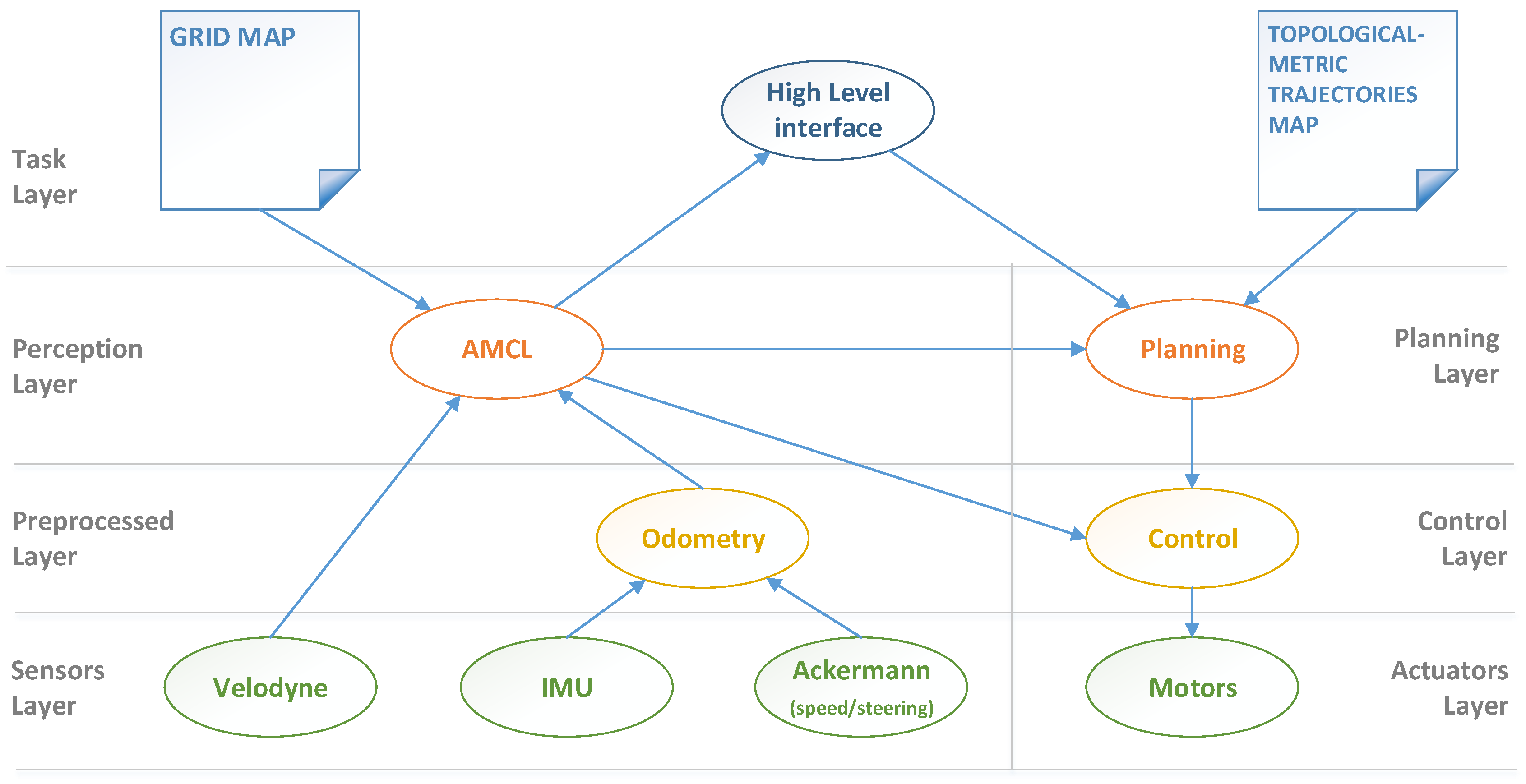
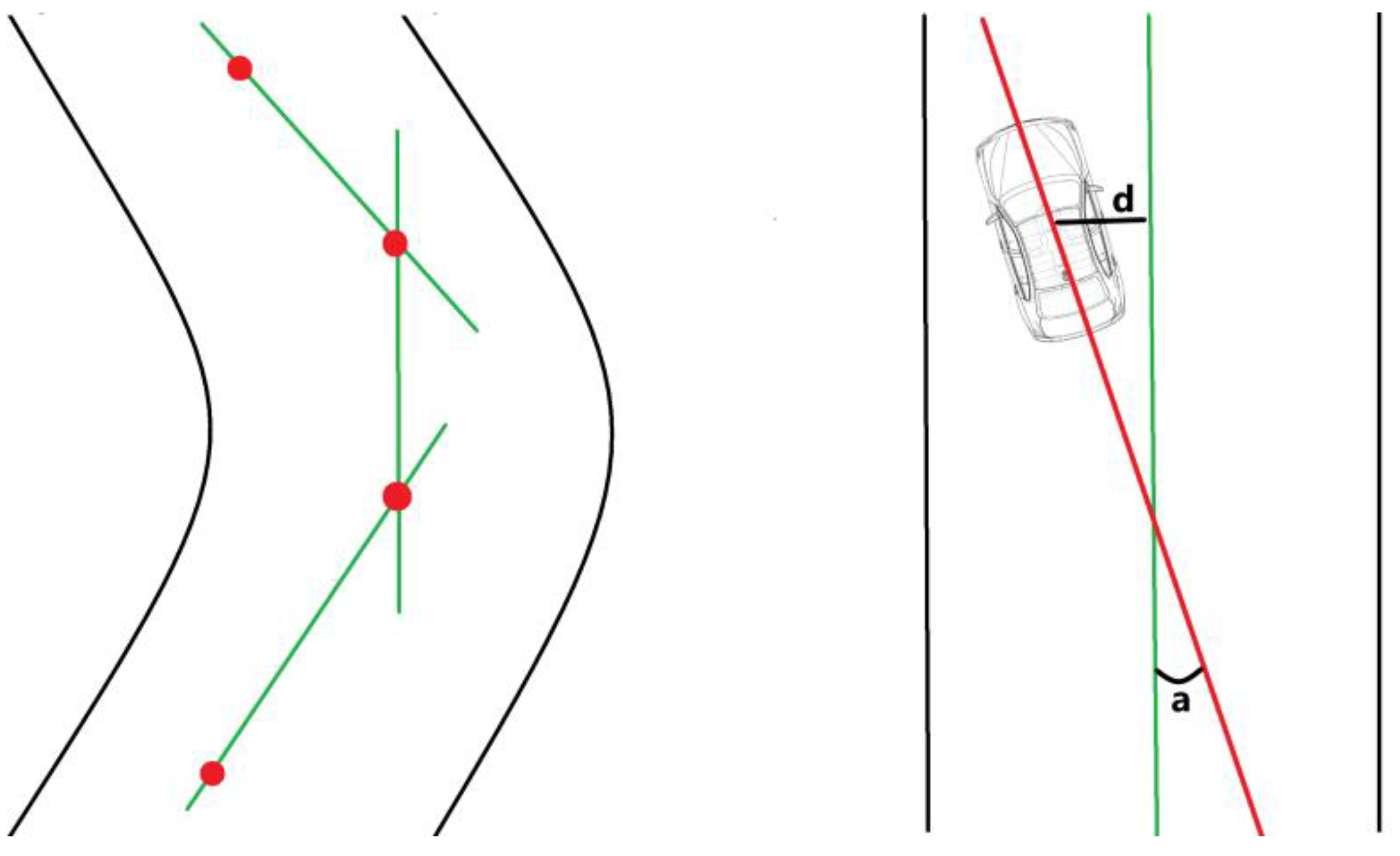
4.2.1. Localization Module: AMCL
4.2.2. Planning
4.2.3. Control
4.2.4. Safety
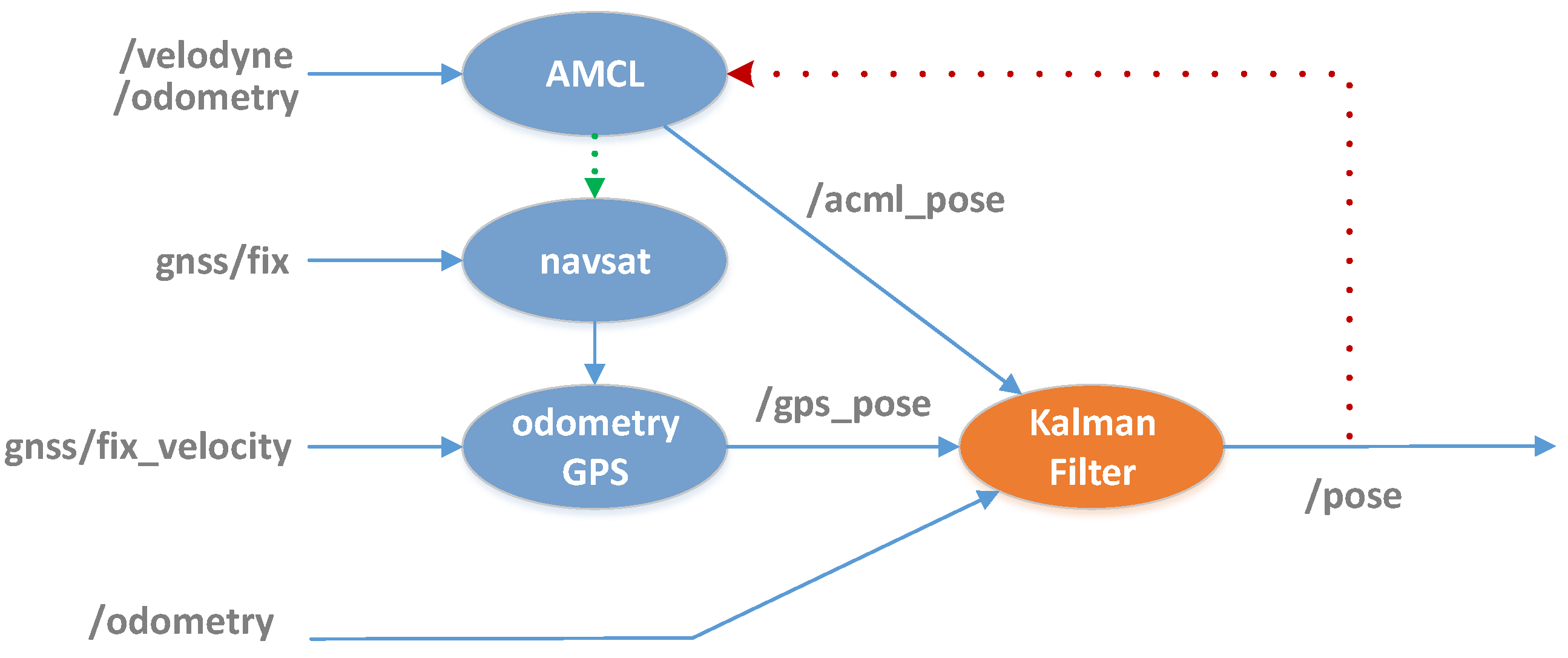
5. New Localization Module: GNSS/SLAM Fusion
5.1. AMCL Subsystem
5.2. GNSS Subsystem
5.3. Odometry
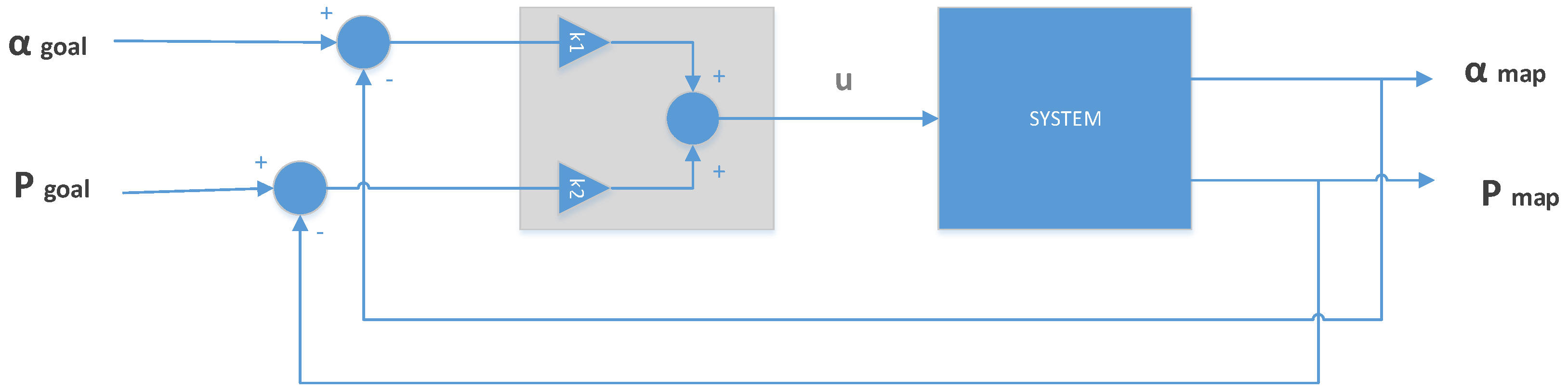
5.4. Kalman Filter
5.5. Integrity Monitoring
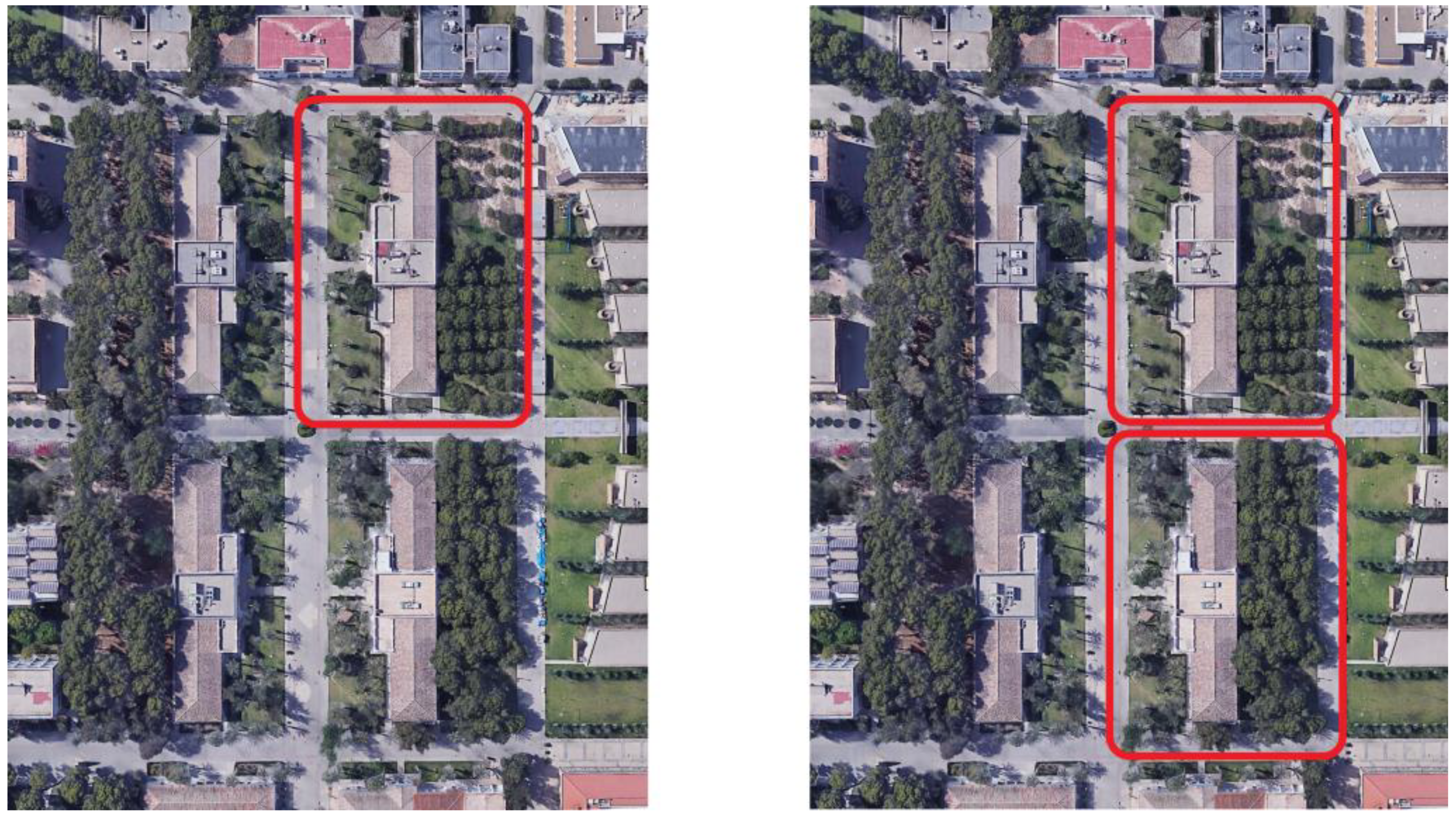
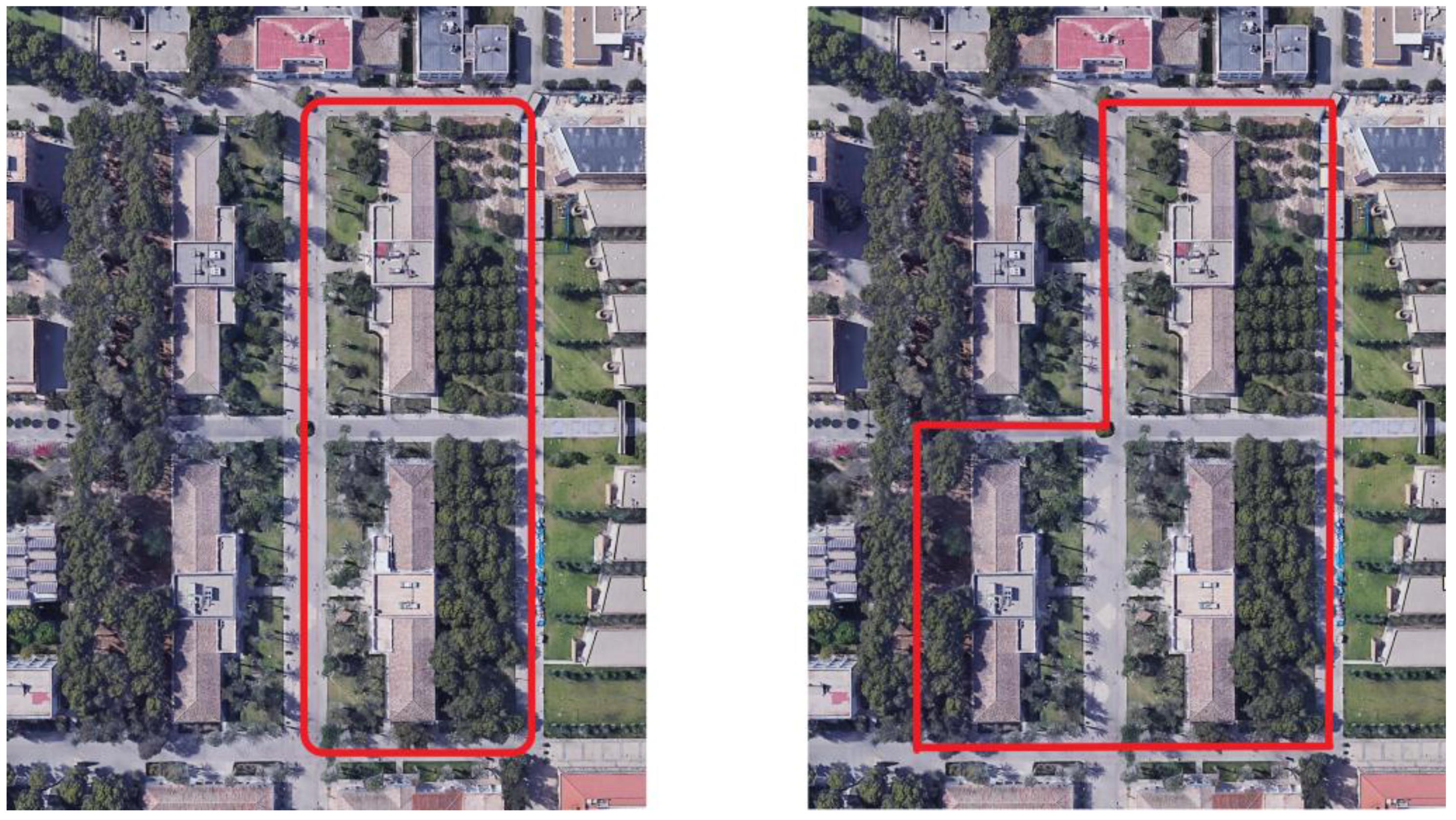
6. Experiments
6.1. Experimental Platform
6.2. Settings
6.3. Initial Framework Experiments
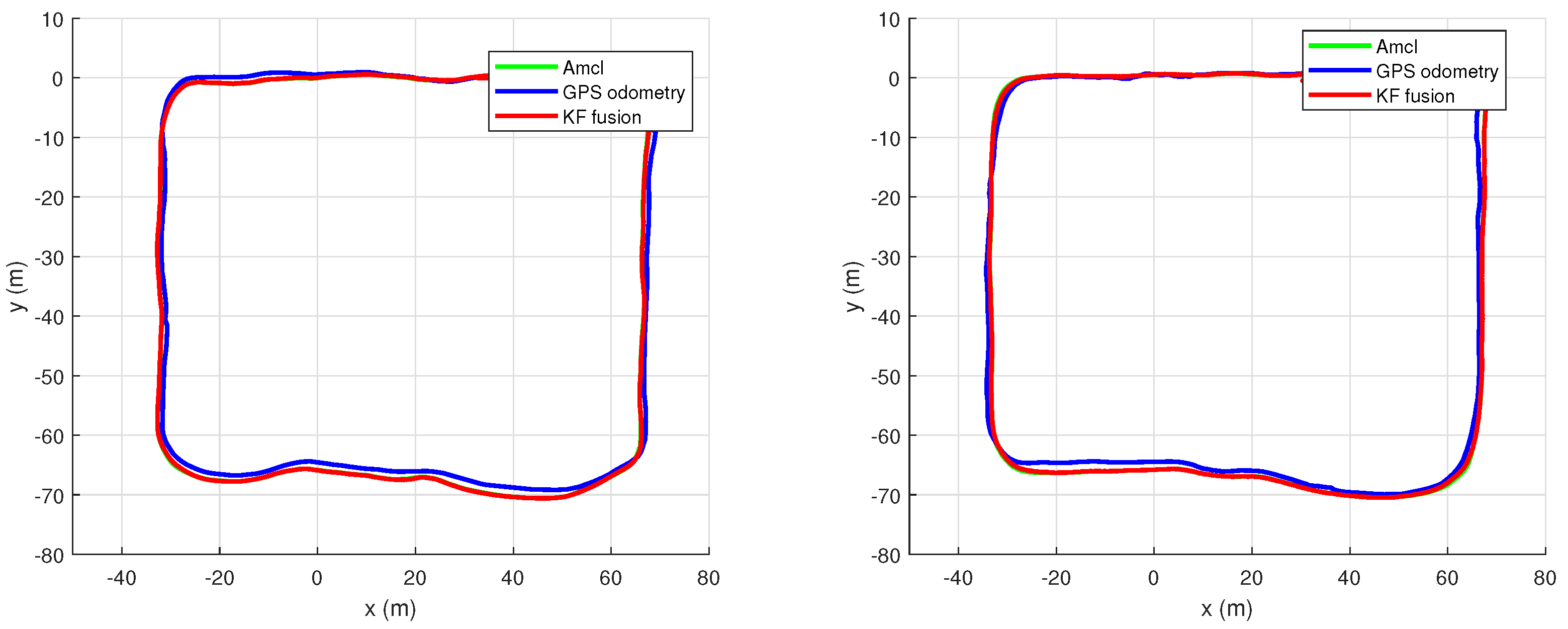
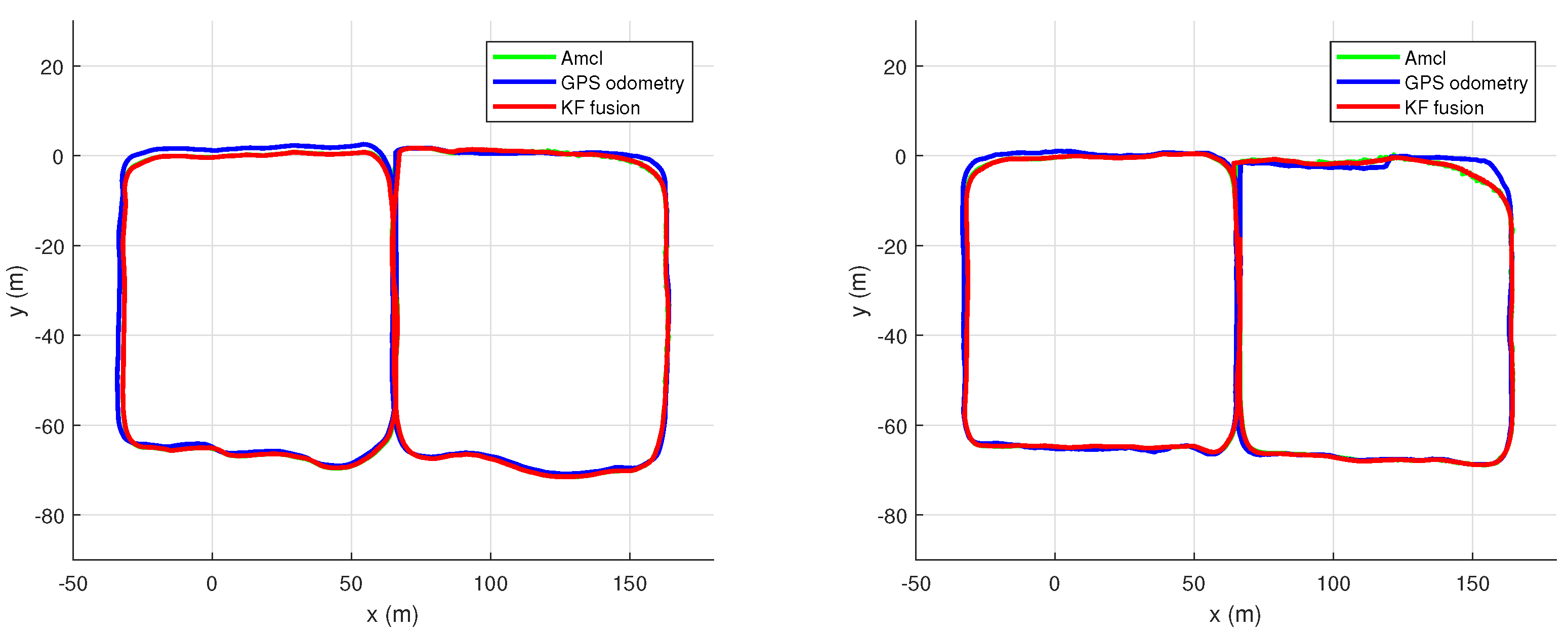
6.4. GNSS/SLAM Fusion Framework Experiments
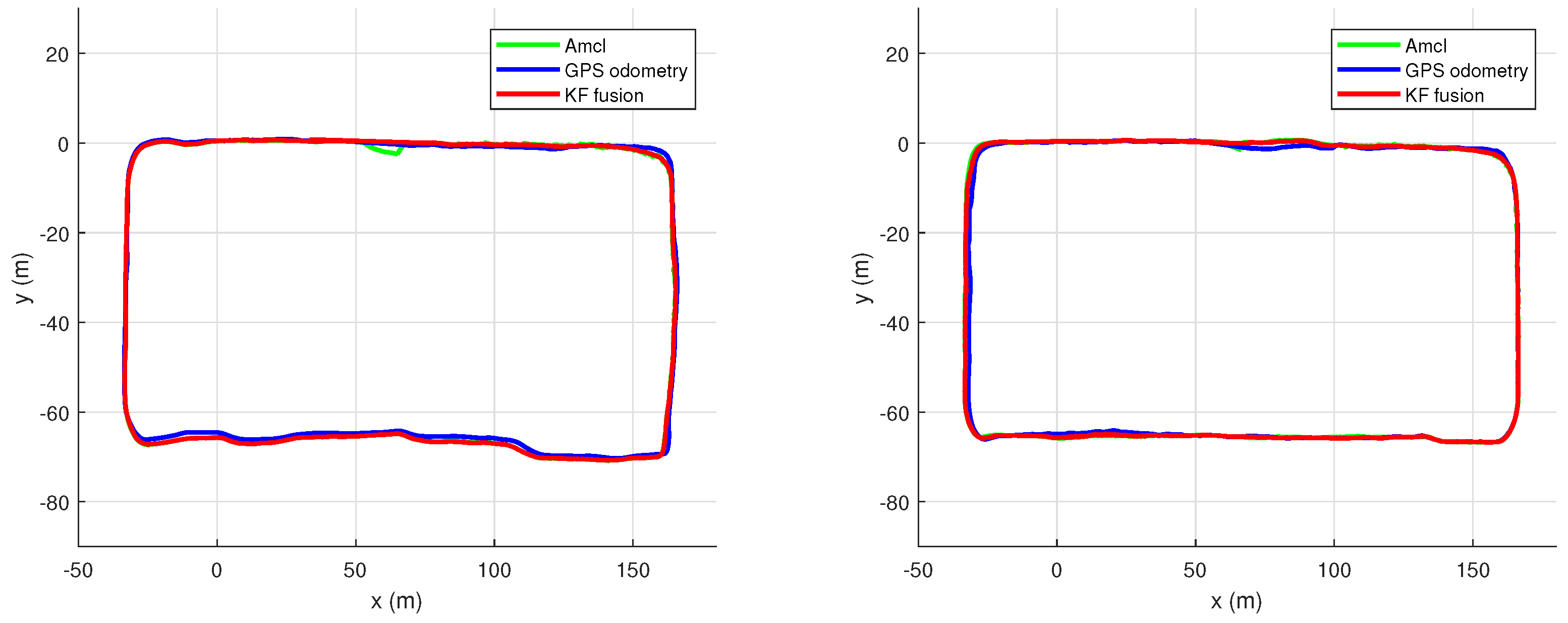
6.4.1. Localization
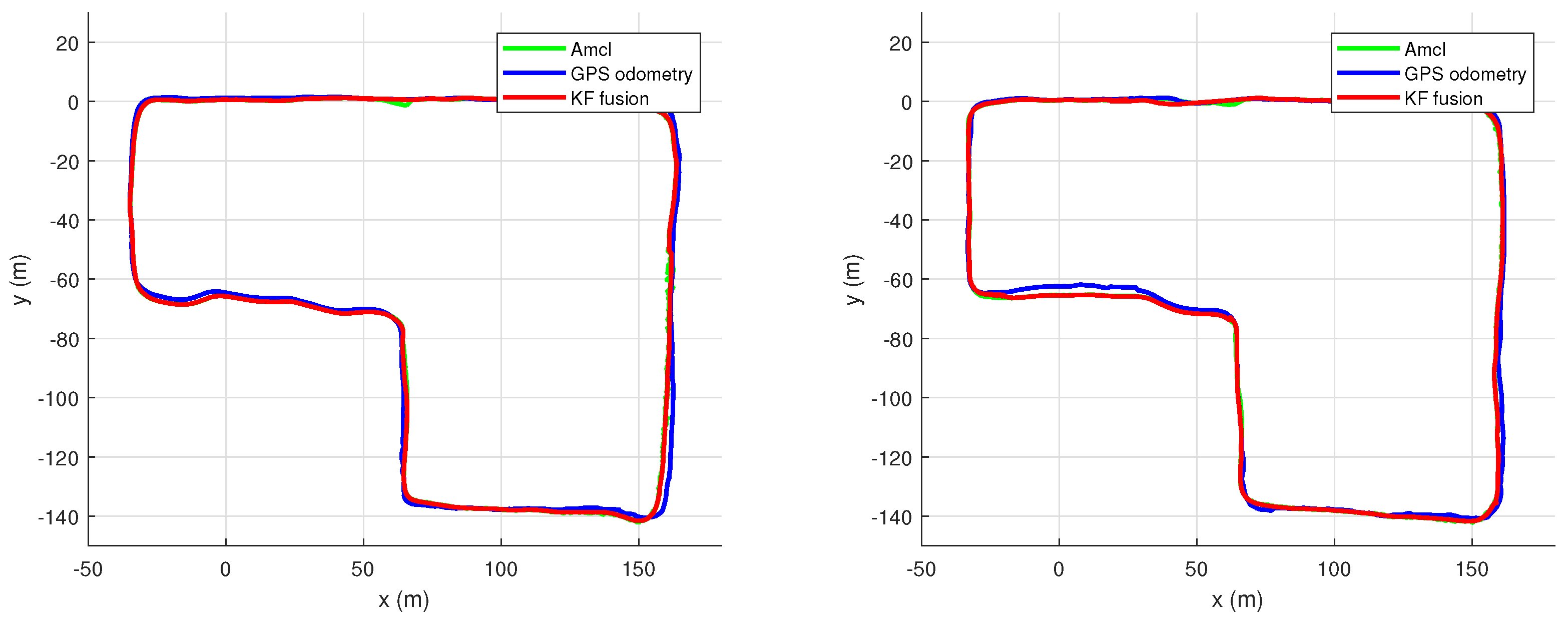
6.4.2. Autonomous Navigation
7. Conclusions and Future Work
Supplementary Files
Supplementary File 1Author Contributions
Funding
Conflicts of Interest
References
- Niemueller, T.; Lakemeyer, G.; Ferrein, A. The RoboCup logistics league as a benchmark for planning in robotics. In Proceedings of the International Conference on Automated Planning and Scheduling (ICAPS)—WS on Planning and Robotics (PlanRob), Jerusalem, Israel, 7–11 June 2015; Association for the Advancement of Artificial Intelligence (AAAI): Palo Alto, CA, USA, 2015. [Google Scholar]
- King, A. The future of agriculture. Nature 2017, 544, S21–S23. [Google Scholar] [CrossRef] [PubMed]
- Milanés, V.; Bergasa, L.M. Introduction to the Special Issue on “New Trends towards Automatic Vehicle Control and Perception Systems”. Sensors 2013, 13, 5712–5719. [Google Scholar] [CrossRef] [PubMed]
- Nilsson, N.J. A Mobile Automaton: An Application of Artificial Intelligence Techniques. In Proceedings of the 1st International Joint Conference on Artificial intelligence (IJCAI’69), Washington, DC, USA, 7–9 May 1969; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1969; pp. 509–520. [Google Scholar]
- Carrio, A.; Sampedro, C.; Rodriguez-Ramos, A.; Campoy, P. A review of deep learning methods and applications for unmanned aerial vehicles. J. Sens. 2017, 2017, 3296874. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- Gomes, L. When will Google’s self-driving car really be ready? It depends on where you live and what you mean by “ready” [News]. IEEE Spectr. 2016, 53, 13–14. [Google Scholar] [CrossRef]
- Canedo-Rodríguez, A.; Alvarez-Santos, V.; Regueiro, C.V.; Iglesias, R.; Barro, S.; Presedo, J. Particle filter robot localisation through robust fusion of laser, WiFi, compass, and a network of external cameras. Inf. Fusion 2016, 27, 170–188. [Google Scholar] [CrossRef]
- Castro-Toscano, M.J.; Rodríguez-Quiñonez, J.C.; Hernández-Balbuena, D.; Rivas-Lopez, M.; Sergiyenko, O.; Flores-Fuentes, W. Obtención de Trayectorias Empleando el Marco Strapdown INS/KF: Propuesta Metodológica. Rev. Iberoam. De Automática E Informática Ind. 2018, 15, 391–403. [Google Scholar] [CrossRef]
- Alami, R.; Chatila, R.; Fleury, S.; Ghallab, M.; Ingrand, F. An architecture for autonomy. Int. J. Robot. Res. 1998, 17, 315–337. [Google Scholar] [CrossRef]
- Thrun, S.; Montemerlo, M.; Dahlkamp, H.; Stavens, D.; Aron, A.; Diebel, J.; Fong, P.; Gale, J.; Halpenny, M.; Hoffmann, G.; et al. Stanley: The robot that won the DARPA Grand Challenge. J. Field Robot. 2006, 23, 661–692. [Google Scholar] [CrossRef]
- Sanchez-Lopez, J.L.; Pestana, J.; de la Puente, P.; Campoy, P. A reliable open-source system architecture for the fast designing and prototyping of autonomous multi-uav systems: Simulation and experimentation. J. Intell. Robot. Syst. 2016, 84, 779–797. [Google Scholar] [CrossRef]
- Siegwart, R.; Nourbakhsh, I.R.; Scaramuzza, D. Introduction to Autonomous Mobile Robots; MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- The Robotics Data Set Repository (Radish). Available online: http://radish.sourceforge.net (accessed on 5 May 2019).
- Koenig, N.; Howard, A. Design and use paradigms for gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2004), Sendai, Japan, 28 September–2 October 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Calisi, D.; Iocchi, L.; Nardi, D. A unified benchmark framework for autonomous mobile robots and vehicles motion algorithms (MoVeMA benchmarks). In Proceedings of the Workshop on Experimental Methodology and Benchmarking in Robotics Research (RSS 2008), Zurich, Switzerland, 26–30 June 2008. [Google Scholar]
- Kweon, I.S.; Goto, Y.; Matsuzaki, K.; Obatake, T. CMU sidewalk navigation system: A blackboard-based outdoor navigation system using sensor fusion with colored-range images. In Proceedings of the Fall Joint Computer Conference, Dallas, TX, USA, 2–6 November 1986; IEEE: Piscataway, NJ, USA, 1986. [Google Scholar]
- Goto, Y.; Stentz, A. Mobile robot navigation: The CMU system. IEEE Expert 1987, 2, 44–54. [Google Scholar] [CrossRef]
- Buehler, M.; Iagnemma, K.; Singh, S. The 2005 DARPA Grand Challenge: The Great Robot Race; Springer: Berlin, Germany, 2007; Volume 36. [Google Scholar]
- Buehler, M.; Iagnemma, K.; Singh, S. The DARPA Urban Challenge: Autonomous Vehicles in City Traffic; Springer: Berlin, Germany, 2009; Volume 56. [Google Scholar]
- Montemerlo, M.; Becker, J.; Bhat, S.; Dahlkamp, H.; Dolgov, D.; Ettinger, S.; Haehnel, D.; Hilden, T.; Hoffmann, G.; Huhnke, B.; et al. Junior: The stanford entry in the urban challenge. J. Field Robot. 2008, 25, 569–597. [Google Scholar] [CrossRef]
- Urmson, C.; Anhalt, J.; Bagnell, D.; Baker, C.; Bittner, R.; Clark, M.; Dolan, J.; Duggins, D.; Galatali, T.; Geyer, C.; et al. Autonomous driving in urban environments: Boss and the urban challenge. J. Field Robot. 2008, 25, 425–466. [Google Scholar] [CrossRef]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 17 May 2009; Volume 3, p. 5. [Google Scholar]
- Guimarães, R.L.; de Oliveira, A.S.; Fabro, J.A.; Becker, T.; Brenner, V.A. ROS navigation: Concepts and tutorial. In Robot Operating System (ROS); Springer International Publishing: Cham, Switzerland, 2016; Volume 1, pp. 121–160. [Google Scholar]
- Rösmann, C.; Hoffmann, F.; Bertram, T. Kinodynamic trajectory optimization and control for car-like robots. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 5681–5686. [Google Scholar]
- Conner, D.C.; Willis, J. Flexible navigation: Finite state machine-based integrated navigation and control for ROS enabled robots. In Proceedings of the SoutheastCon 2017, Charlotte, NC, USA, 30 March–2 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–8. [Google Scholar]
- Brahimi, S.; Tiar, R.; Azouaoui, O.; Lakrouf, M.; Loudini, M. Car-like mobile robot navigation in unknown urban areas. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1727–1732. [Google Scholar]
- Vivacqua, R.; Vassallo, R.; Martins, F. A low cost sensors approach for accurate vehicle localization and autonomous driving application. Sensors 2017, 17, 2359. [Google Scholar] [CrossRef] [PubMed]
- Ferrer, G.; Zulueta, A.G.; Cotarelo, F.H.; Sanfeliu, A. Robot social-aware navigation framework to accompany people walking side-by-side. Auton. Robot. 2017, 41, 775–793. [Google Scholar] [CrossRef]
- Dove, R.; Schindel, B.; Scrapper, C. Agile systems engineering process features collective culture, consciousness, and conscience at SSC Pacific Unmanned Systems Group. INCOSE Int. Symp. 2016, 26, 982–1001. [Google Scholar] [CrossRef]
- Li, X.; Sun, Z.; Cao, D.; Liu, D.; He, H. Development of a new integrated local trajectory planning and tracking control framework for autonomous ground vehicles. Mech. Syst. Signal Process. 2017, 87, 118–137. [Google Scholar] [CrossRef]
- Hernádez Juan, S.; Herrero Cotarelo, F. Autonomous Navigation Framework for a Car-Like Robot (Technical Report IRI-TR-15-07); Institut de Robòtica i Informàtica Industrial (IRI): Barcelona, Spain, 2015. [Google Scholar]
- Rodrigues, M.; McGordon, A.; Gest, G.; Marco, J. Developing and testing of control software framework for autonomous ground vehicle. In Proceedings of the 2017 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Coimbra, Portugal, 26–28 April 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 4–10. [Google Scholar]
- Stateczny, A.; Burdziakowski, P. Universal autonomous control and management system for multipurpose unmanned surface vessel. Pol. Marit. Res. 2019, 26, 30–39. [Google Scholar] [CrossRef]
- Huskić, G.; Buck, S.; Zell, A. GeRoNa: Generic Robot Navigation. J. Intell. Robot. Syst. 2018, 1–24. [Google Scholar] [CrossRef]
- Hartmann, J.; Klüssendorff, J.H.; Maehle, E. A unified visual graph-based approach to navigation for wheeled mobile robots. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1915–1922. [Google Scholar]
- Guzmán, R.; Ariño, J.; Navarro, R.; Lopes, C.; Graça, J.; Reyes, M.; Barriguinha, A.; Braga, R. Autonomous hybrid GPS/reactive navigation of an unmanned ground vehicle for precision viticulture-VINBOT. In Proceedings of the 62nd German Winegrowers Conference, Stuttgart, Germany, 27–30 November 2016. [Google Scholar]
- Romay, A.; Kohlbrecher, S.; Stumpf, A.; von Stryk, O.; Maniatopoulos, S.; Kress-Gazit, H.; Schillinger, P.; Conner, D.C. Collaborative Autonomy between High-level Behaviors and Human Operators for Remote Manipulation Tasks using Different Humanoid Robots. J. Field Robot. 2017, 34, 333–358. [Google Scholar] [CrossRef]
- OpenSLAM: GMapping Algorithm. Available online: https://openslam-org.github.io (accessed on 5 May 2019).
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Moore, T.; Stouch, D. A generalized extended kalman filter implementation for the robot operating system. In Proceedings of the 13th International Conference IAS-13 (Intelligent Autonomous Systems 13), Padova, Italy, 15–18 July 2014; Springer International Publishing: Cham, Switzerland, 2016; pp. 35–348. [Google Scholar]
- del Pino, I.; Muñoz-Bañon, M.Á.; Cova-Rocamora, S.; Contreras, M.Á.; Candelas, F.A.; Torres, F. Deeper in BLUE. J. Intell. Robot. Syst. 2019, 1–19. [Google Scholar] [CrossRef]
- del Pino, I.; Muñoz Bañón, M.A.; Contreras, M.Á.; Cova, S.; Candelas, F.A.; Torres, F. Speed Estimation for Control of an Unmanned Ground Vehicle Using Extremely Low Resolution Sensors. In Proceedings of the 15th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Portu, Portugal, 29–31 July 2018. [Google Scholar]
- Gmapping in ROS. Available online: http://wiki.ros.org/gmapping (accessed on 5 May 2019).
- Amcl in ROS. Available online: http://wiki.ros.org/amcl (accessed on 5 May 2019).



| Module | Parameter | Value | Units |
|---|---|---|---|
| GMapping | Grid resolution | 0.05 | m |
| Maximum map dimensions | 100 × 100 | m | |
| Number of particles | 30 | none | |
| AMCL | 1.12 | none | |
| 0.1 | none | ||
| 1.05 | none | ||
| 0.1 | none | ||
| Planning | Subsampling distance | 2.0 | m |
| Control | Constant | 8.0 | none |
| Constant | 0.5 | none | |
| Maximum speed | 1.0 | m/s | |
| Minimum speed | 0.6 | m/s | |
| Maximun steering | 25.0 | deg | |
| Kalman filter | Noise model for components | 0.05 | m |
| Noise model for component | 0.58 | deg | |
| Integrity monitoring | Mahalanobis distance threshold | 3.0 | none |
| AMCL correction threshold for components | 3.0 | m | |
| AMCL correction threshold for component | 10 | deg |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muñoz–Bañón, M.Á.; del Pino, I.; Candelas, F.A.; Torres, F. Framework for Fast Experimental Testing of Autonomous Navigation Algorithms. Appl. Sci. 2019, 9, 1997. https://doi.org/10.3390/app9101997
Muñoz–Bañón MÁ, del Pino I, Candelas FA, Torres F. Framework for Fast Experimental Testing of Autonomous Navigation Algorithms. Applied Sciences. 2019; 9(10):1997. https://doi.org/10.3390/app9101997
Chicago/Turabian StyleMuñoz–Bañón, Miguel Á., Iván del Pino, Francisco A. Candelas, and Fernando Torres. 2019. "Framework for Fast Experimental Testing of Autonomous Navigation Algorithms" Applied Sciences 9, no. 10: 1997. https://doi.org/10.3390/app9101997
APA StyleMuñoz–Bañón, M. Á., del Pino, I., Candelas, F. A., & Torres, F. (2019). Framework for Fast Experimental Testing of Autonomous Navigation Algorithms. Applied Sciences, 9(10), 1997. https://doi.org/10.3390/app9101997







