Evaluation of Cracks in Metallic Material Using a Self-Organized Data-Driven Model of Acoustic Echo-Signal
Abstract
1. Introduction
2. The Consensus Self-Organizing Models (COSMO)
3. Crack Identification Based on COSMO
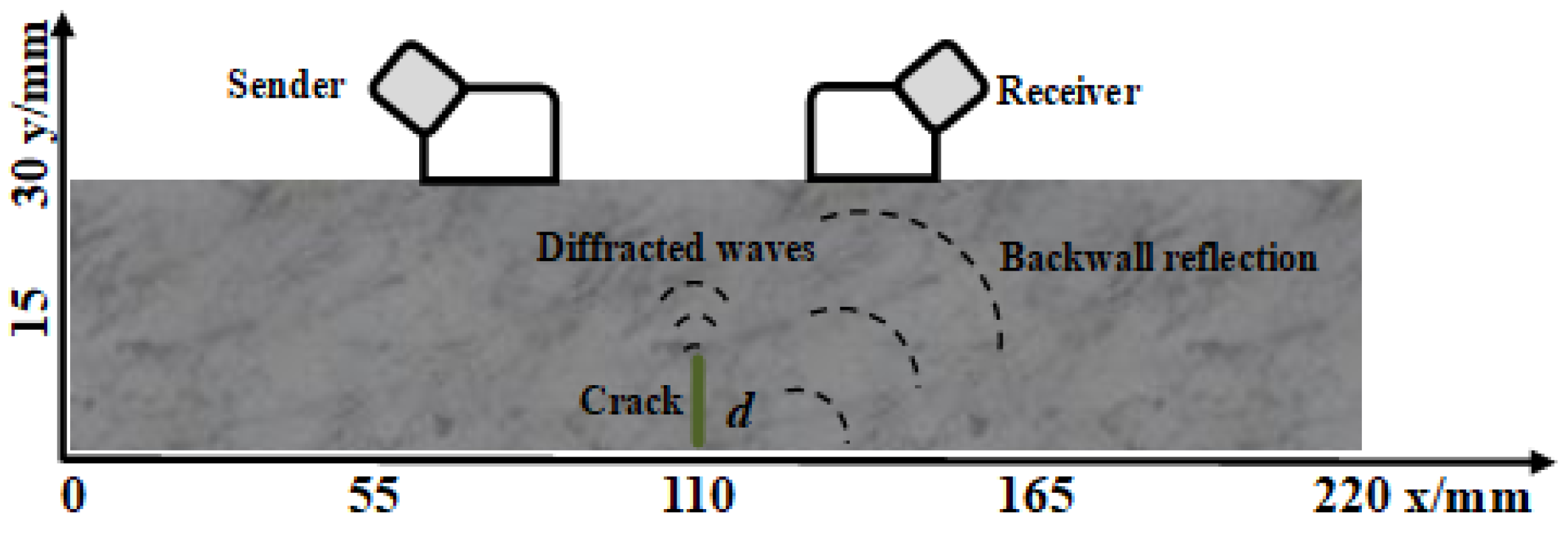
3.1. Numerical Simulation
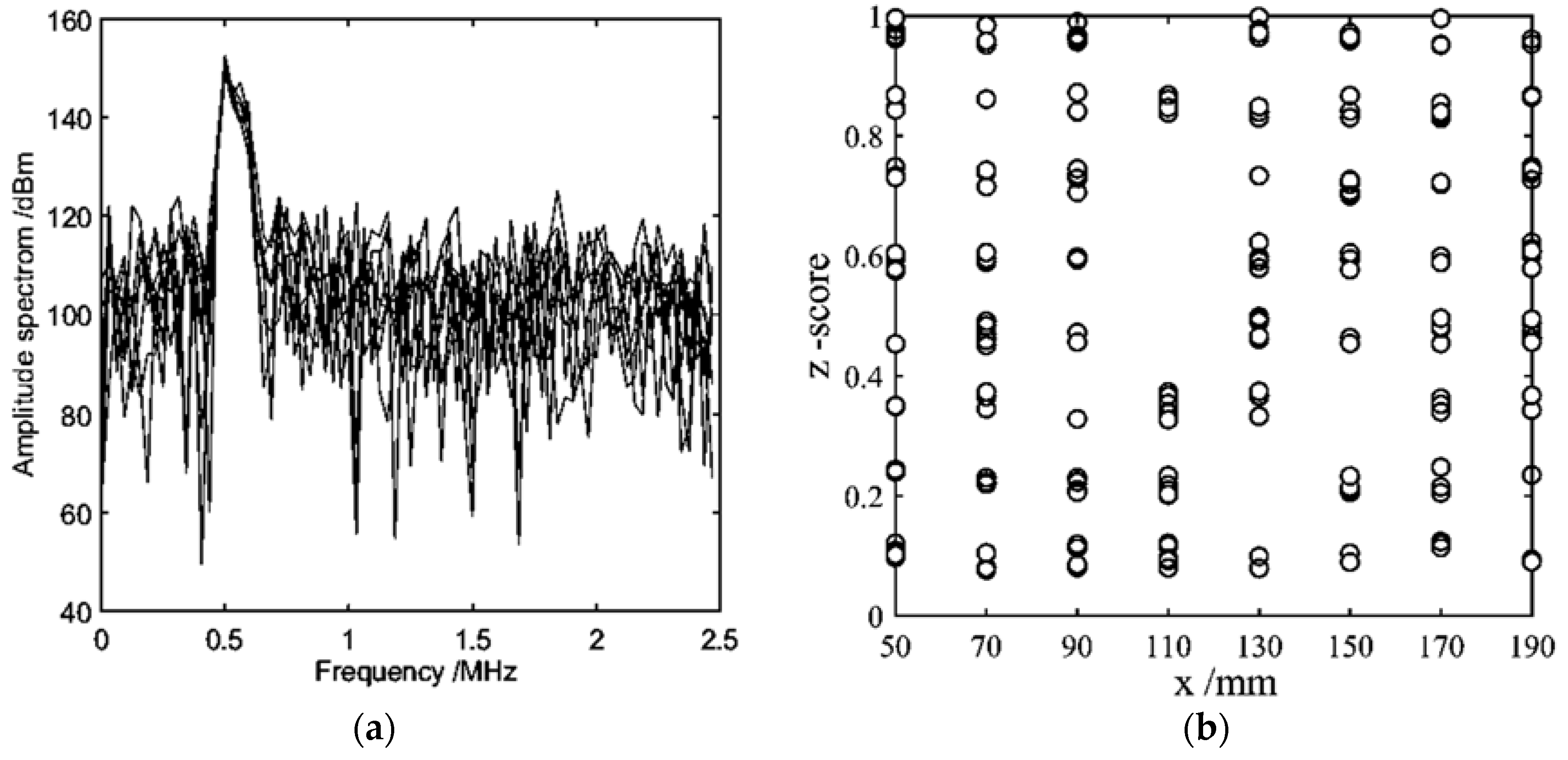
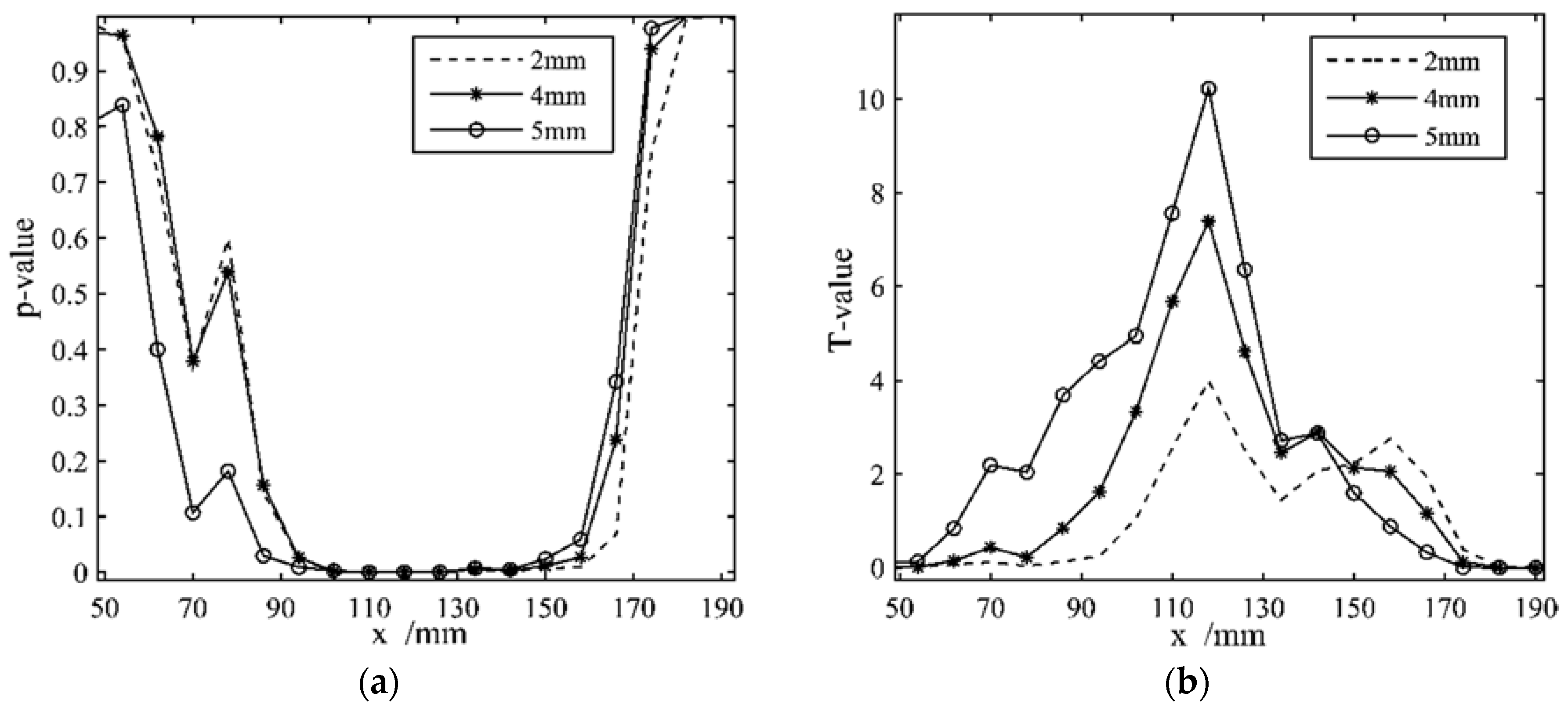
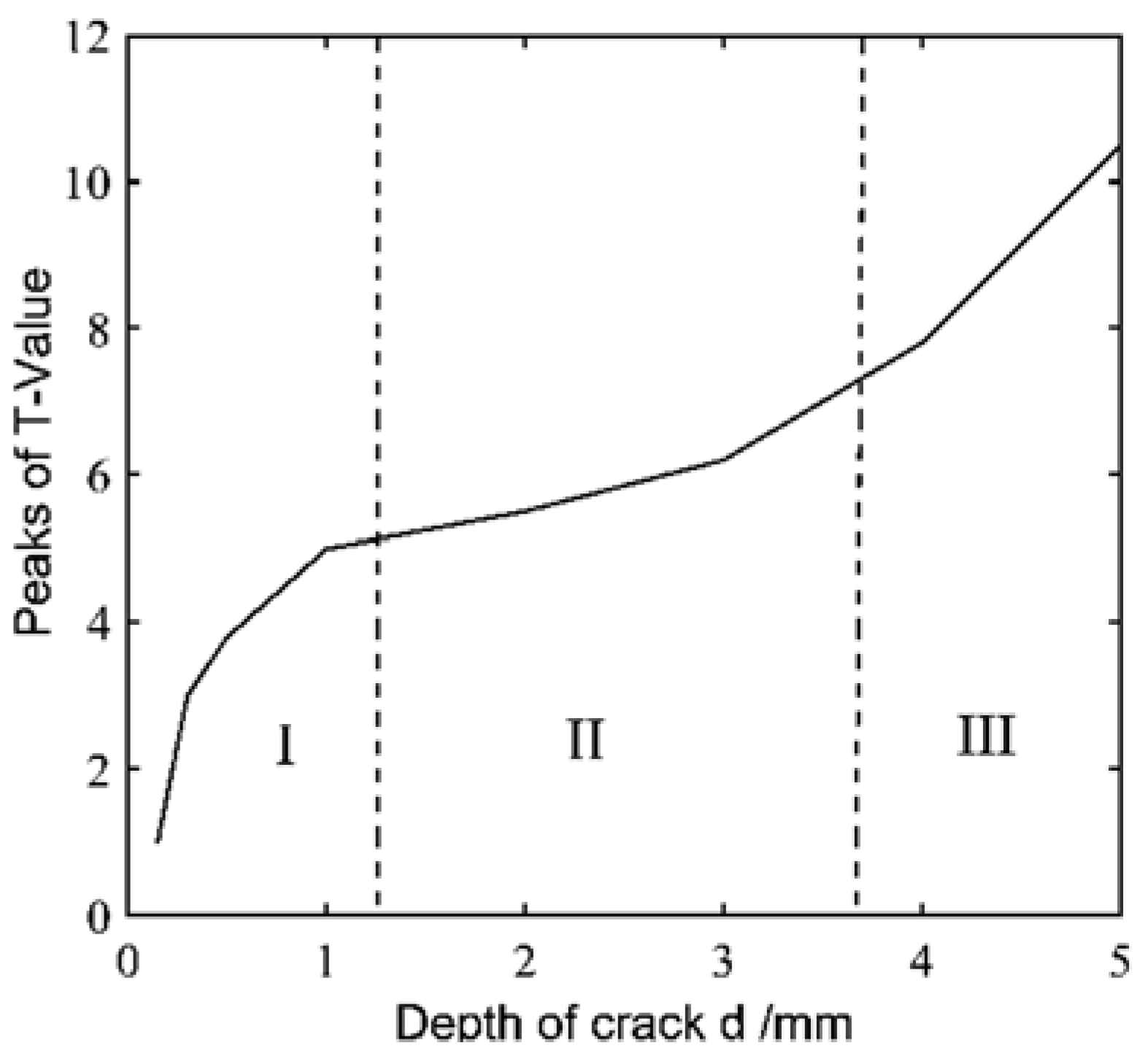
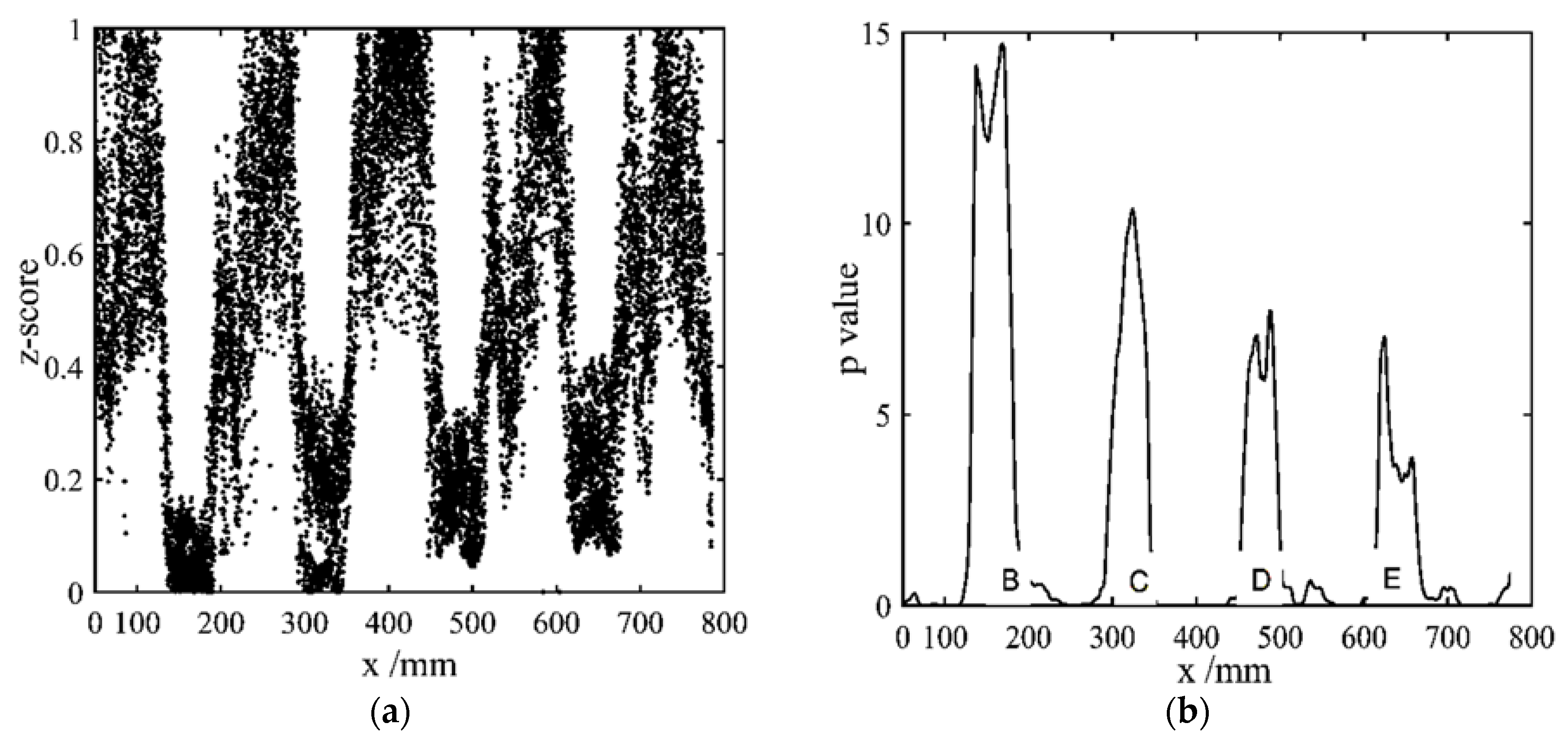
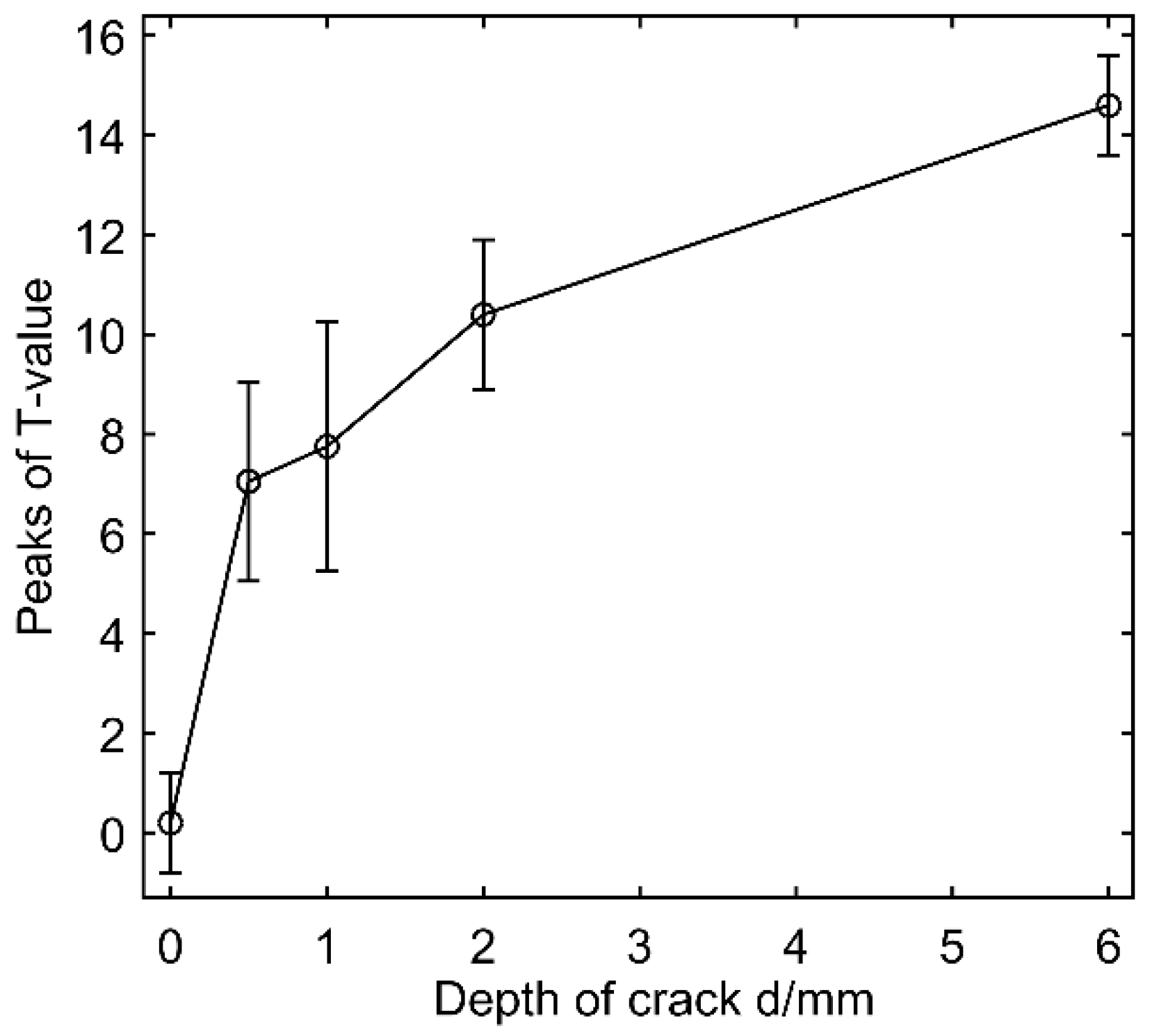
3.2. Experimental Measurement
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Broda, D.; Staszewski, W.J.; Martowicz, A.; Uhl, T.; Silberschmidt, V.V. Modelling of nonlinear crack–wave interactions for damage detection based on ultrasound—A review. J. Sound Vib. 2014, 333, 1097–1118. [Google Scholar] [CrossRef]
- Novak, A.; Bentahar, M.; Tournat, V.; Guerjouma, R.; Simon, L. Nonlinear acoustic characterization of micro-damaged materials through higher harmonic resonance analysis. NDT E Int. 2012, 45, 1–8. [Google Scholar]
- Donskoy, D.; Sutin, A.; Ekimov, A. Nonlinear acoustic interaction on contact interfaces and its use for nondestructive testing. NDT E Int. 2001, 34, 231–238. [Google Scholar]
- Nagy, P.B. Fatigue damage assessment by nonlinear ultrasonic materials characterization. Ultrasonics 1998, 36, 375–381. [Google Scholar] [CrossRef]
- Dos Santos, S.; Vejvodova, S.; Prevorovsky, Z. Nonlinear signal processing for ultrasonic imaging of material complexity. Proc. Est. Acad. Sci. 2010, 59, 108–117. [Google Scholar] [CrossRef]
- Jhang, K.Y. Nonlinear ultrasonic techniques for nondestructive assessment of micro damage in material: A review. Int. J. Precis. Eng. Manuf. 2009, 10, 123–135. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, D.; Zhang, J. Detection of fatigue-induced micro-cracks in a pipe by using time-reversed nonlinear guidedwaves: A three-dimensional model study. Ultrasonics 2012, 52, 912–919. [Google Scholar] [CrossRef]
- Blanloeuil, P.; Rose, L.F.; Veidt, M.; Wang, C.H. Time reversal invariance for a nonlinear scatterer exhibiting contactacoustic nonlinearity. J. Sound Vib. 2018, 417, 413–431. [Google Scholar] [CrossRef]
- Ostrovsky, L.A.; Johnson, P.A. Dynamic nonlinear elasticity in geomaterials. La Rivista Del Nuovo Cimento 2008, 24, 1–46. [Google Scholar]
- Hall, D.A. Review Nonlinearity in piezoelectric ceramics. J. Mater. Sci. 2001, 36, 4575–4601. [Google Scholar] [CrossRef]
- Zhenggan, Z.; Siming, L. Nonlinear Ultrasonic Techniques Used in Nondestructive Testing: A Review. J. Mech. Eng. 2011, 47, 2–9. [Google Scholar]
- Gang, Q.; Steven, F.W. A Framework of Data-Enabled Science for Evaluation of Material Damage Based on Acoustic Emission. J. Nondestruct. Eval. 2014, 33, 597–615. [Google Scholar]
- Sollier, T.; Blain, C. IRSN preliminary analysis on statistical methods for NDE performances assessment. In Proceedings of the 12th International Conference on Non-Destructive Evaluation in Relation to Structural Integrity for Nuclear and Pressurized Components, Dubrovnik, Croatia, 4–6 October 2016; pp. 1–10. [Google Scholar]
- Keprate, A.; Ratnayake, R.M.C. Probability of Detection as a Metric for Quantifying NDE Reliability: The State of The Art. J. Pipeline Eng. 2015, 14, 199–209. [Google Scholar]
- Schneider, C.R.A.; Rudlin, J.R. Review of statistical methods used in quantifying NDT reliability. Insight-Non-Destruct. Test. Cond. Monit. (INSIGHT) 2004, 46, 77–79. [Google Scholar]
- Lu, C.J.; Meeker, W.Q. Using Degradation Measures to Estimate a Time-to-Failure Distribution. Technometrics 1993, 35, 161–174. [Google Scholar] [CrossRef]
- Wu, S.; Tsai, T. Estimation of time-to-failure distribution derived from a degradation model using fuzzy clustering. Qual. Reliab. Eng. Int. 2015, 16, 261–267. [Google Scholar] [CrossRef]
- Batzel, T.D.; Swanson, D.C. Prognostic Health Management of Aircraft Power Generators. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 473–482. [Google Scholar] [CrossRef]
- Lakhtakia, A. Transition from Nondestructive Testing (NDT) to Structural Health Monitoring (SHM): Potential and challenges. SPIE Smart Struct. Nondestruct. Eval. 2014, 9055, 90550Z. [Google Scholar]
- Gebraeel, N.Z.; Lawley, M.A.; Li, R. Residual-Life Distributions from Component Degradation Signals: A Bayesian Approach. IIE Trans. 2005, 37, 543–557. [Google Scholar] [CrossRef]
- Zhou, W.; Zh, L.V.; Wang, Y.R. Acoustic Response and Micro-Damage Mechanism of Fiber Composite Materials under Mode-II Delamination. Chin. Phys. Lett. 2015, 32, 046201. [Google Scholar] [CrossRef]
- Kůs, V.; Tláskal, J.; Farová, Z.; Santos, D.S. Signal detection, separation & classification under random noise background. In Proceedings of the 13th Biennial Baltic Electronics Conference, Tallinn, Estonia, 3–5 October 2012; pp. 287–290. [Google Scholar]
- RÖgnvaldsson, T.; Norrman, H.; Byttner, S.; Järpe, E. Estimating p-values for deviation detection. In Proceedings of the IEEE Eighth International Conference on Self-Adaptive and Self-Organizing Systems, London, UK, 8–12 September 2014; pp. 100–109. [Google Scholar]
- Fan, Y.T.; Nowaczyk, S.; RÖgnvaldsson, T. Evaluation of Self-Organized Approach for Predicting Compressor Faults in a City Bus Fleet. Procedia Comput. Sci. 2015, 53, 447–456. [Google Scholar] [CrossRef]
- Teng, X.; Fan, Y.; Nowaczyk, S. Evaluation of micro-flaws in metallic material based on a self-organized data-driven approach. In Proceedings of the 2016 IEEE International Conference on Prognostics and Health Management (ICPHM), Ottawa, ON, Canada, 20–22 June 2016; pp. 1–5. [Google Scholar]
- Kim, J.Y.; Yakovlev, V.A.; Rokhlin, S.I. Parametric modulation mechanism of surface acoustic wave on a partially closed crack. Appl. Phys. Lett. 2003, 82, 3203–3205. [Google Scholar] [CrossRef]
- Krüger, S.E.; Rebello, J.M.A.; Camargo, P.C. Hydrogen damage detection by ultrasonic spectral analysis. NDT E Int. 1999, 32, 275–281. [Google Scholar]
- Hillis, A.J.; Neild, S.A.; Drinkwa, B.W.; Wilcoxter, P.D. Global crack detection using bispectral analysis. Proc. R. Soc. A 2006, 462, 1515–1530. [Google Scholar] [CrossRef]

| Grade | Elements (%) | Yield Strength (MPa) | Tensile Strength (MPa) | Elongation (%) | ||||
|---|---|---|---|---|---|---|---|---|
| C | Mn | Si | P | S | ||||
| Q235A | 0.14~0.22 | 0.30~0.65 | 0.30 | 0.045 | 0.030 | 235 | 375~460 | 21–26 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teng, X.; Zhang, X.; Fan, Y.; Zhang, D. Evaluation of Cracks in Metallic Material Using a Self-Organized Data-Driven Model of Acoustic Echo-Signal. Appl. Sci. 2019, 9, 95. https://doi.org/10.3390/app9010095
Teng X, Zhang X, Fan Y, Zhang D. Evaluation of Cracks in Metallic Material Using a Self-Organized Data-Driven Model of Acoustic Echo-Signal. Applied Sciences. 2019; 9(1):95. https://doi.org/10.3390/app9010095
Chicago/Turabian StyleTeng, Xudong, Xin Zhang, Yuantao Fan, and Dong Zhang. 2019. "Evaluation of Cracks in Metallic Material Using a Self-Organized Data-Driven Model of Acoustic Echo-Signal" Applied Sciences 9, no. 1: 95. https://doi.org/10.3390/app9010095
APA StyleTeng, X., Zhang, X., Fan, Y., & Zhang, D. (2019). Evaluation of Cracks in Metallic Material Using a Self-Organized Data-Driven Model of Acoustic Echo-Signal. Applied Sciences, 9(1), 95. https://doi.org/10.3390/app9010095





