A Novel Heart Rate Robust Method for Short-Term Electrocardiogram Biometric Identification
Abstract
1. Introduction
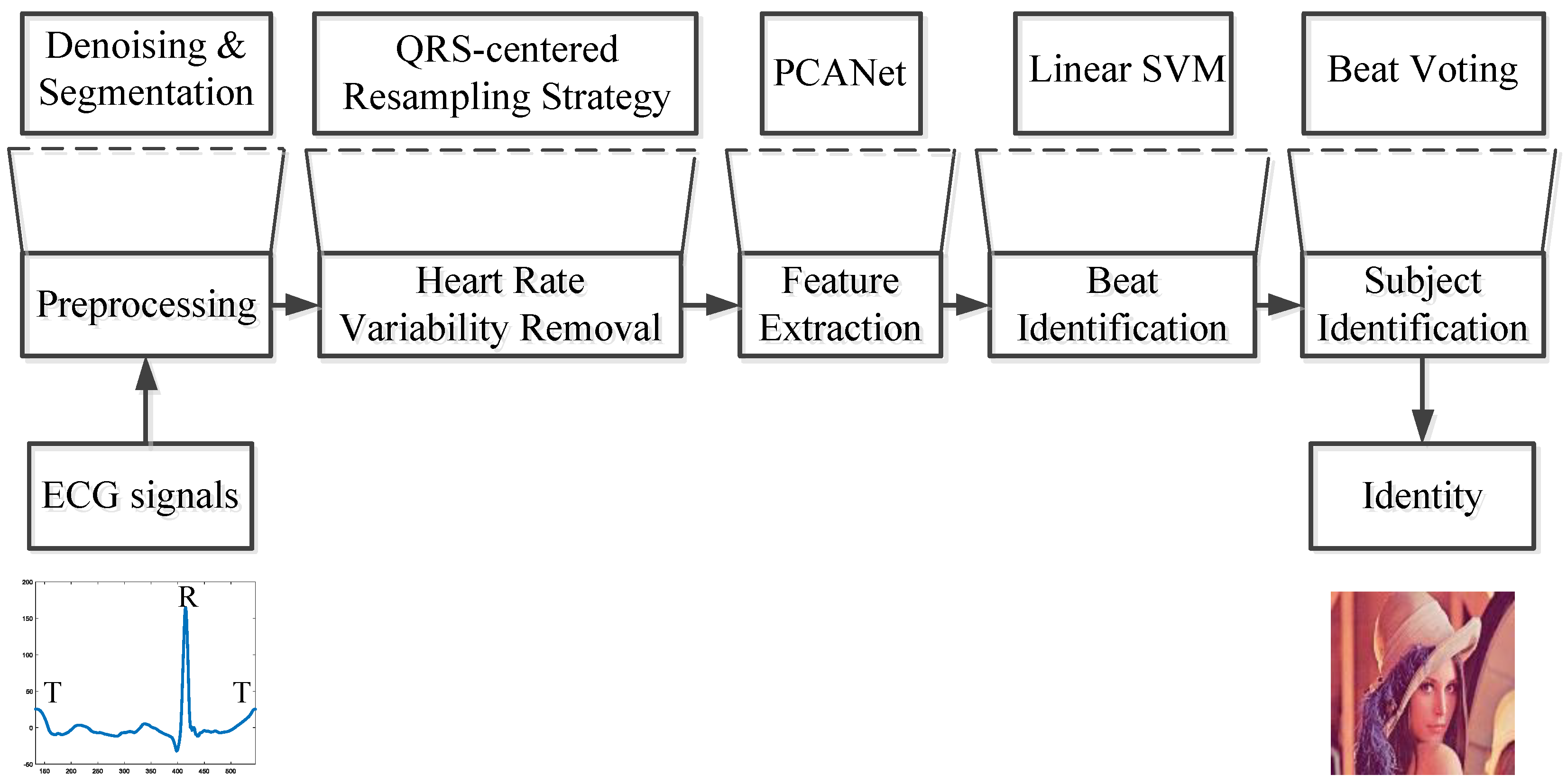
2. Methods
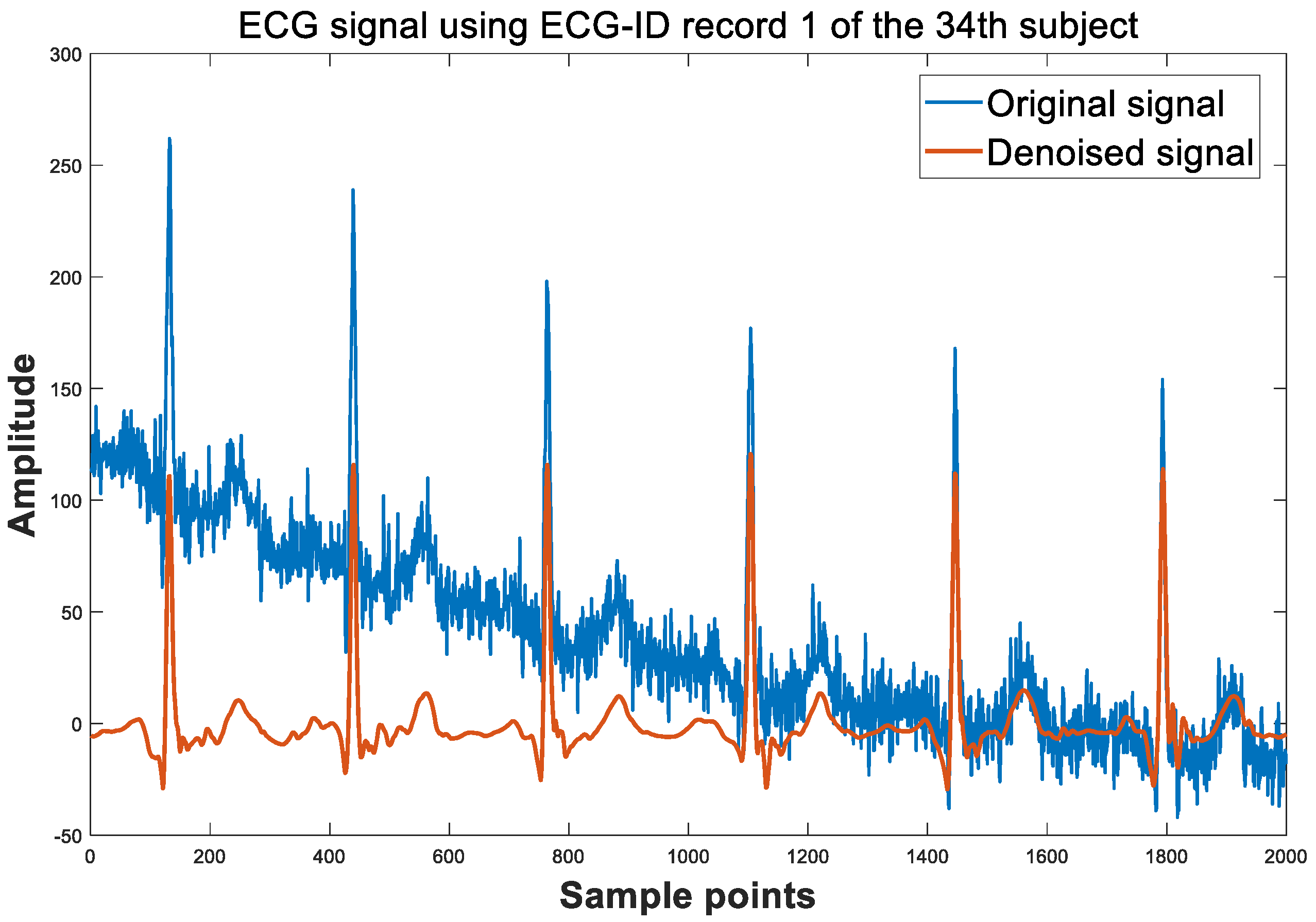
2.1. Preprocessing
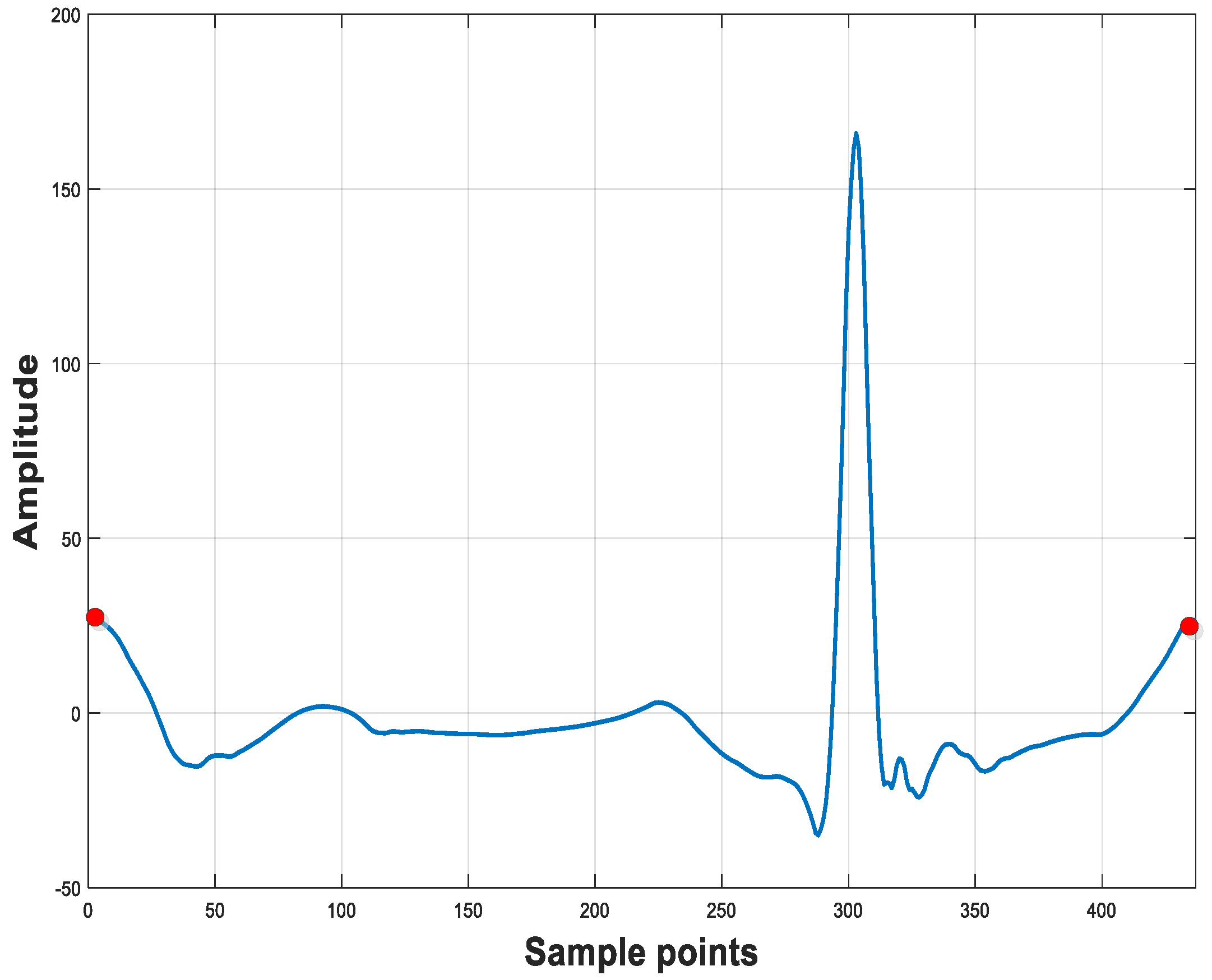
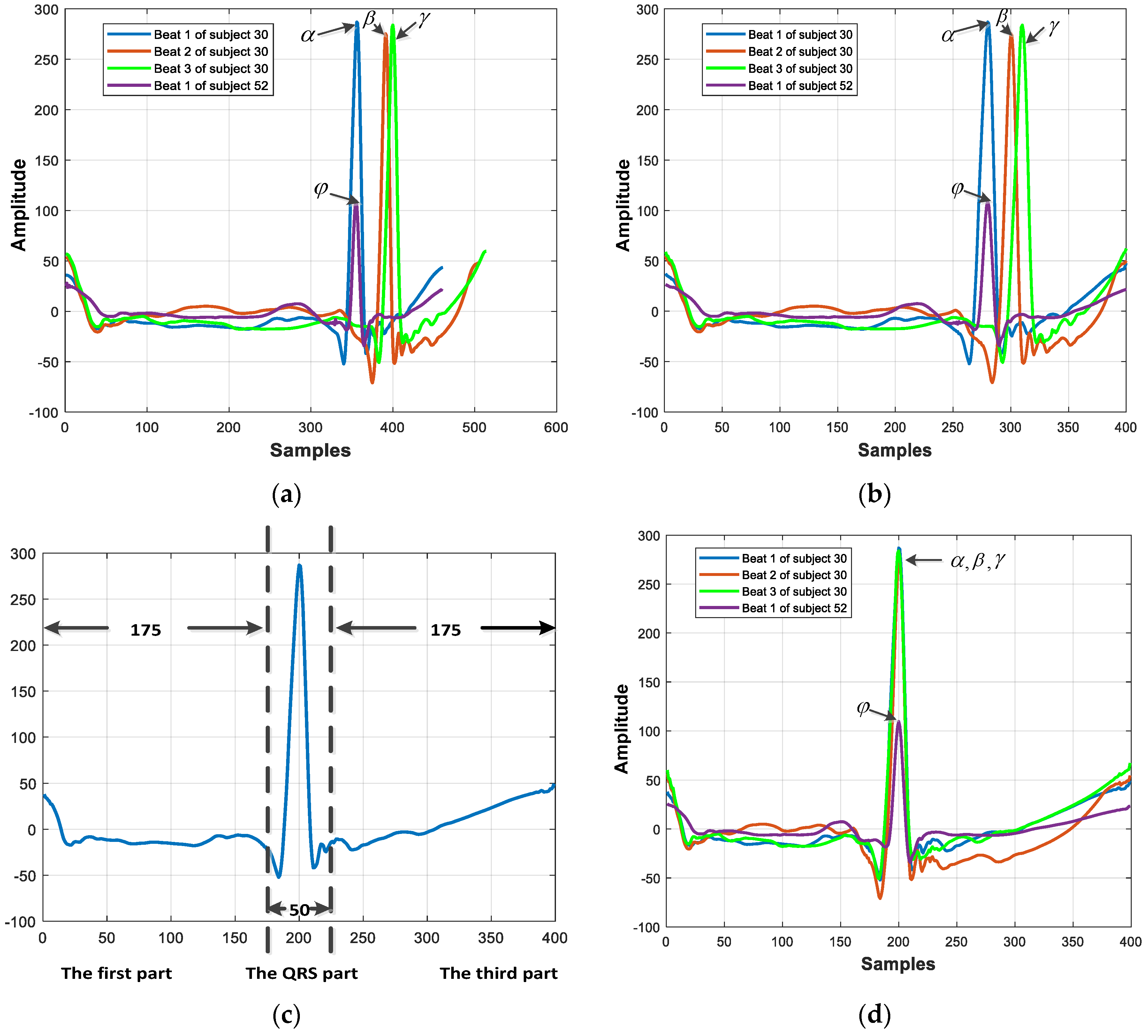
2.2. QRS-Centered Resampling Strategy
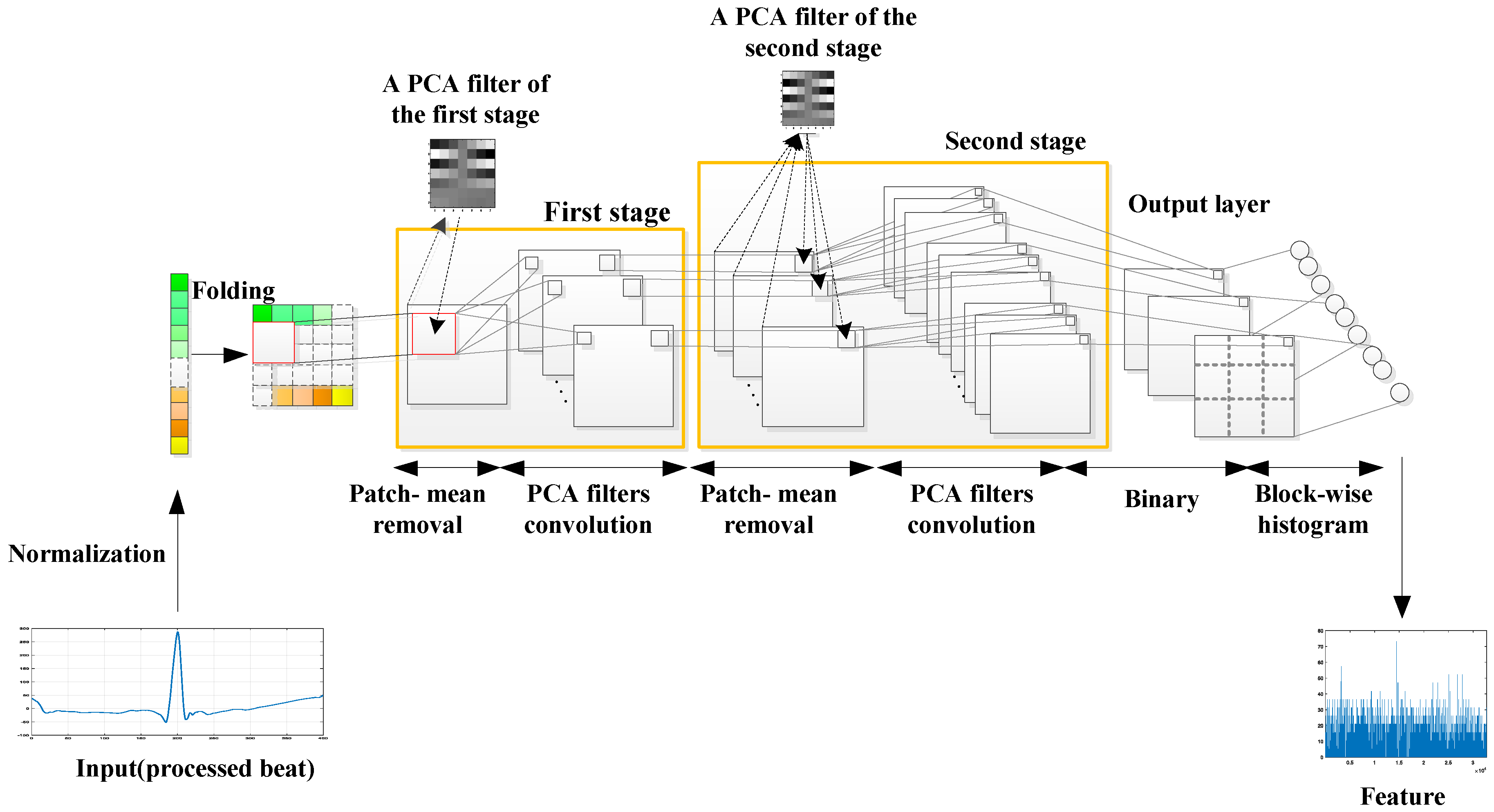
2.3. PCANet
2.3.1. Normalization
2.3.2. Input Layer
2.3.3. The First Stage (PCA)
2.3.4. The Second Stage (PCA)
2.3.5. Output Stage
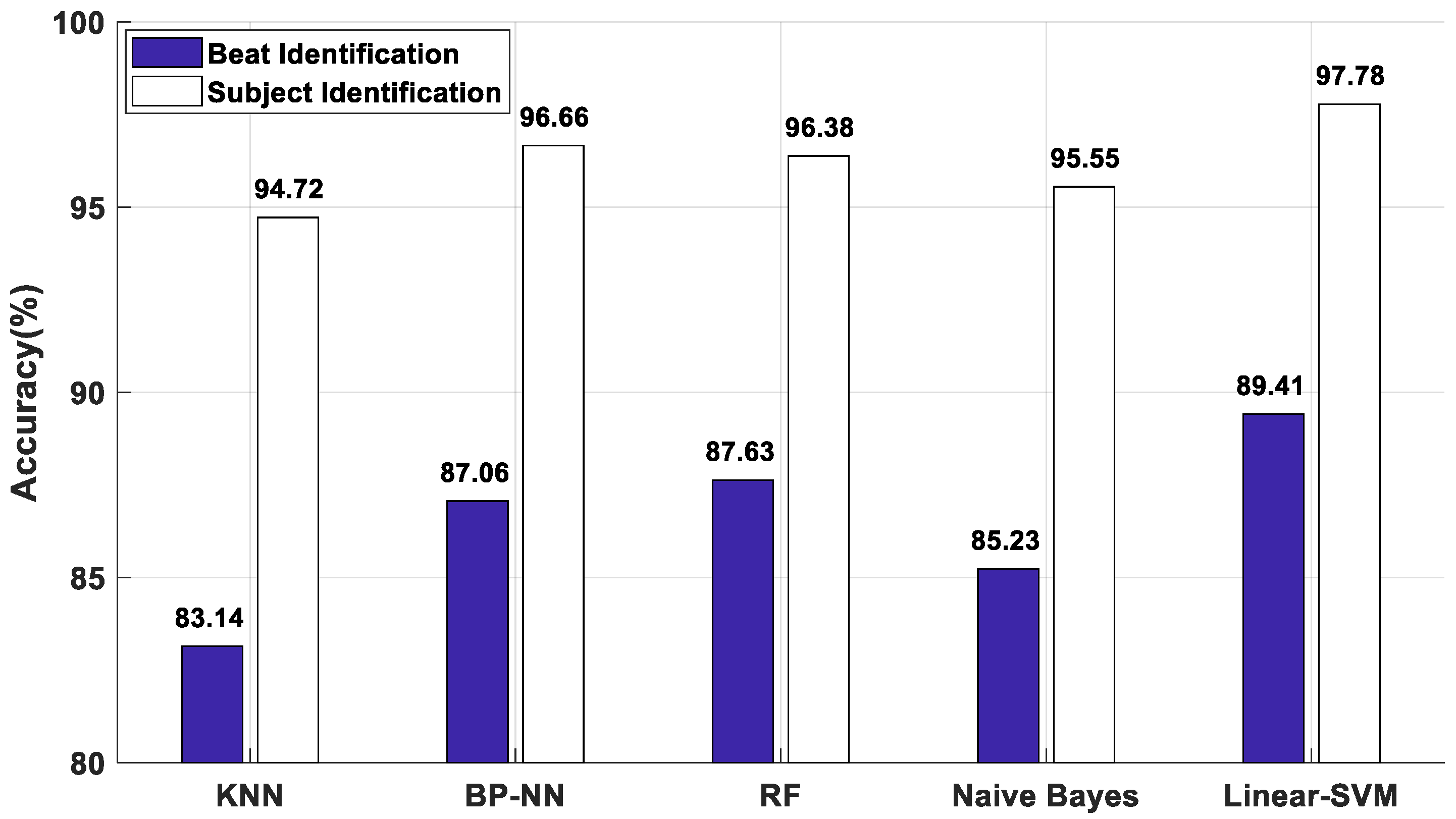
2.4. Classifier
2.4.1. K-Nearest Neighbor (KNN)
2.4.2. Back Propagation Neural Network (BP-NN)
2.4.3. Random Forest (RF)
2.4.4. Naive Bayes Classifier
2.4.5. Support Vector Machines (SVM)
2.5. Signal Identification
3. Results
3.1. Database
3.2. Experimental Setup
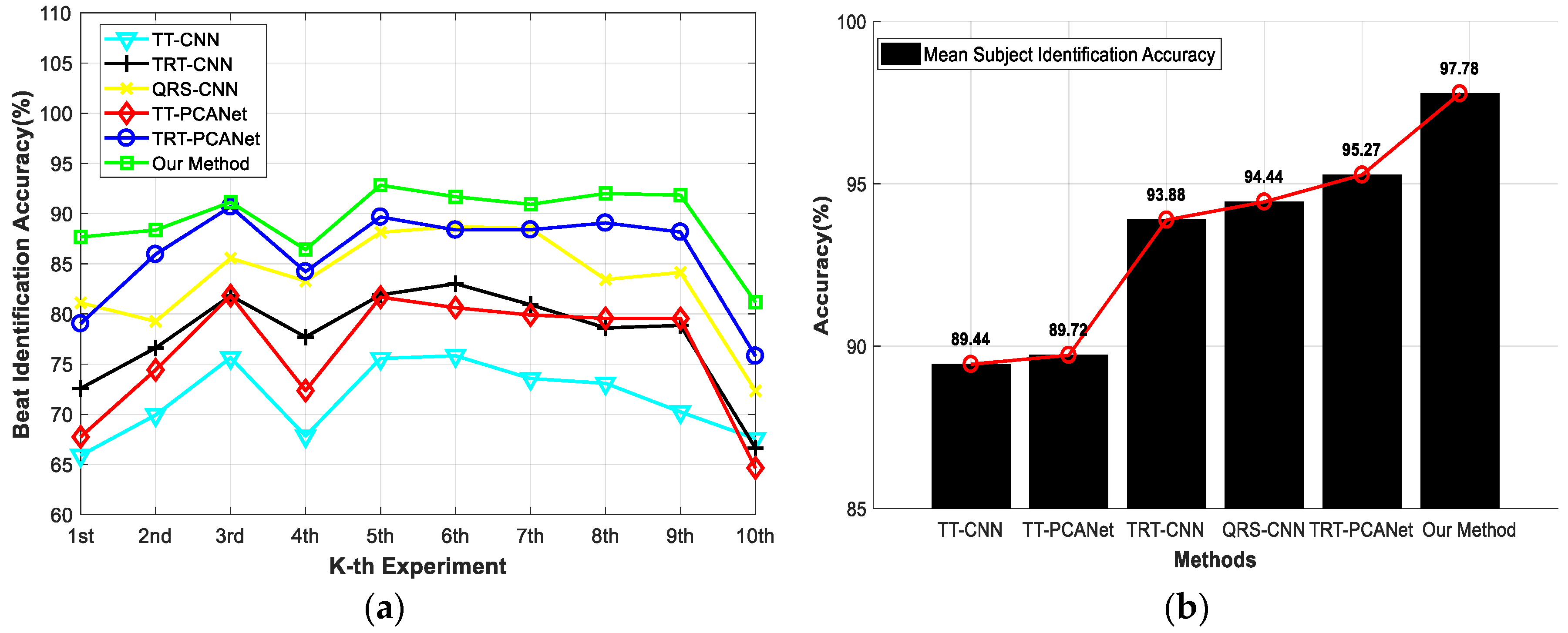
3.3. Experimental Results
3.3.1. Experiment 1
3.3.2. Experiment 2
3.3.3. Experiment 3
3.3.4. Experiment 4
3.3.5. Experiment 5
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Komeili, M.; Armanfard, N.; Hatzinakos, D. Liveness Detection and Automatic Template Updating Using Fusion of ECG and Fingerprint. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1810–1822. [Google Scholar] [CrossRef]
- Belgacem, N.; Fournier, R.; Nait-Ali, A.; Bereksi-Reguig, F. A novel biometric authentication approach using ECG and EMG signals. J. Med. Eng. Technol. 2015, 39, 226–238. [Google Scholar] [CrossRef] [PubMed]
- Fang, S.C.; Chan, H.L. QRS detection-free electrocardiogram biometrics in the reconstructed phase space. Pattern Recognit. Lett. 2013, 34, 595–602. [Google Scholar] [CrossRef]
- Karimian, N.; Guo, Z.M.; Tehranipoor, M.; Forte, D. Highly Reliable Key Generation From Electrocardiogram (ECG). IEEE Trans. Biomed. Eng. 2017, 64, 1400–1411. [Google Scholar] [CrossRef]
- Tuerxunwaili; Nor, R.M.; Rahman, A.W.B.A.; Sidek, K.A.; Ibrahim, A.A. Electrocardiogram Identification: Use a Simple Set of Features in QRS Complex to Identify Individuals. In Proceedings of the 12th International Conference on Computing and Information Technology (IC2IT), Khon-Kaen, Thailand, 7–8 July 2016; Springer: Cham, Switzerland, 2016; pp. 139–148. [Google Scholar] [CrossRef]
- Ghongade, R.; Ghatol, A. An effective feature set for ECG pattern classification. In Proceedings of the International Conference on Medical Biometrics, Hong Kong, China, 4–5 January 2008; pp. 25–32. [Google Scholar] [CrossRef]
- Liu, S.-H.; Cheng, D.-C.; Lin, C.-M. Arrhythmia Identification with Two-Lead Electrocardiograms Using Artificial Neural Networks and Support Vector Machines for a Portable ECG Monitor System. Sensors 2013, 13, 813–828. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Yang, L.; Chen, D.; Luo, Y. A Human ECG Identification System Based on Ensemble Empirical Mode Decomposition. Sensors 2013, 13, 6832–6864. [Google Scholar] [CrossRef] [PubMed]
- Salloum, R.; Kuo, C.C.J. ECG-based biometrics using recurrent neural networks. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, 5–9 March 2017; pp. 2062–2066. [Google Scholar] [CrossRef]
- Dar, M.N.; Akram, M.U.; Usman, A.; Khan, S.A. ECG Biometric Identification for General Population Using Multiresolution Analysis of DWT Based Features. In Proceedings of the Second International Conference on Information Security and Cyber Forensics (InfoSec), Cape Town, South Africa, 15–17 November 2015; pp. 5–10. [Google Scholar] [CrossRef]
- Tseng, K.-K.; Lee, D.; Hurst, W.; Lin, F.-Y.; Ip, W.H. Frequency Rank Order Statistic with Unknown Neural Network for ECG Identification System. In Proceedings of the 4th International Conference on Enterprise Systems (ES), Melbourne, VIC, Australia, 2–3 November 2016; pp. 160–167. [Google Scholar] [CrossRef]
- Page, A.; Kulkarni, A.; Mohsenin, T. Utilizing Deep Neural Nets for an Embedded ECG-based Biometric Authentication System. In Proceedings of the 2015 IEEE Biomedical Circuits and Systems Conference (BioCAS), Atlanta, GA, USA, 22–24 October 2015; pp. 346–349. [Google Scholar] [CrossRef]
- Peimankar, A.; Puthusserypady, S. Ensemble Learning for Detection of Short Episodes of Atrial Fibrillation. In Proceedings of the 2018 26th European Signal Processing Conference (EUSIPCO), Roma, Italy, 3–7 September 2018; pp. 66–70. [Google Scholar] [CrossRef]
- Poree, F.; Kervio, G.; Carrault, G. ECG biometric analysis in different physiological recording conditions. Signal Image Video Process. 2016, 10, 267–276. [Google Scholar] [CrossRef]
- Nemirko, A.; Lugovaya, T. Biometric human identification based on electrocardiogram. In Proceedings of the XIIIth Russian Conference on Mathematical Methods of Pattern Recognition, Moscow, Russian, 20–26 June 2005; pp. 387–390. [Google Scholar] [CrossRef]
- Gargiulo, F.; Fratini, A.; Sansone, M.; Sansone, C. Subject identification via ECG fiducial-based systems: Influence of the type of QT interval correction. Comput. Meth. Prog. Biomed. 2015, 121, 127–136. [Google Scholar] [CrossRef]
- Tawfik, M.M.; Selim, H.; Kamal, T. Human identification using time normalized QT signal and the QRS complex of the ECG. In Proceedings of the 7th International Symposium on Communication Systems, Networks & Digital Signal Processing (CSNDSP 2010), Newcastle upon Tyne, UK, 21–23 July 2010; pp. 755–759. [Google Scholar]
- Patro, K.K.; Kumar, P.R. Effective Feature Extraction of ECG for Biometric Application. In Proceedings of the 7th International Conference on Advances in Computing & Communications (ICACC-2017), Cochin, India, 22–24 August 2017; pp. 296–306. [Google Scholar] [CrossRef]
- Chen, C.-L.; Chuang, C.-T. A QRS Detection and R Point Recognition Method for Wearable Single-Lead ECG Devices. Sensors 2017, 17, 1969. [Google Scholar] [CrossRef]
- Lee, W.; Kim, S.; Kim, D. Individual Biometric Identification Using Multi-Cycle Electrocardiographic Waveform Patterns. Sensors 2018, 18, 1005. [Google Scholar] [CrossRef]
- Matveev, M.; Christov, I.; Krasteva, V.; Bortolan, G.; Simov, D.; Mudrov, N.; Jekova, I. Assessment of the stability of morphological ECG features and their potential for person verification/identification. In Proceedings of the 21st International Conference on Circuits, Systems, Communications and Computers (CSCC 2017), Crete Island, Greece, 14–17 July 2017. [Google Scholar] [CrossRef]
- Acharya, U.R.; Fujita, H.; Lih, O.S.; Hagiwara, Y.; Tan, J.H.; Adam, M. Automated detection of arrhythmias using different intervals of tachycardia ECG segments with convolutional neural network. Inf. Sci. 2017, 405, 81–90. [Google Scholar] [CrossRef]
- Acharya, U.R.; Oh, S.L.; Hagiwara, Y.; Tan, J.H.; Adam, M.; Gertych, A.; Tan, R.S. A deep convolutional neural network model to classify heartbeats. Comput. Biol. Med. 2017, 89, 389–396. [Google Scholar] [CrossRef] [PubMed]
- Andersen, R.S.; Peimankar, A.; Puthusserypady, S. A deep learning approach for real-time detection of atrial fibrillation. Expert Syst. Appl. 2019, 115, 465–473. [Google Scholar] [CrossRef]
- Yang, W.; Si, Y.; Wang, D.; Guo, B. Automatic recognition of arrhythmia based on principal component analysis network and linear support vector machine. Comput. Biol. Med. 2018, 101, 22–32. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.-H.; Jia, K.; Gao, S.; Lu, J.; Zeng, Z.; Ma, Y. PCANet: A Simple Deep Learning Baseline for Image Classification? IEEE Trans. Image Process. 2015, 24, 5017–5032. [Google Scholar] [CrossRef] [PubMed]
- Jané, R.; Laguna, P.; Thakor, N.V.; Caminal, P. Adaptive baseline wander removal in the ECG: Comparative analysis with cubic spline technique. In Proceedings of the Computers in Cardiology, Durham, NC, USA, 11–14 October 1992; pp. 143–146. [Google Scholar] [CrossRef]
- Date, A.A.; Ghongade, R.B. Performance of Wavelet Energy Gradient Method for QRS Detection. In Proceedings of the 4th International Conference on Intelligent and Advanced Systems (ICIAS2012), Kuala Lumpur, Malaysia, 12–14 June 2012; pp. 876–881. [Google Scholar] [CrossRef]
- Rakshit, M.; Das, S. An efficient ECG denoising methodology using empirical mode decomposition and adaptive switching mean filter. Biomed. Signal Process. Control 2018, 40, 140–148. [Google Scholar] [CrossRef]
- Li, J.; Si, Y.; Lang, L.; Liu, L.; Xu, T. A Spatial Pyramid Pooling-Based Deep Convolutional Neural Network for the Classification of Electrocardiogram Beats. Appl. Sci.-Basel 2018, 8, 1590. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, J.M. Ideal spatial adaptation by wavelet shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Yao, C.; Si, Y. ECG P, T wave complex detection algorithm based on lifting wavelet. J. Jilin. U Techno Ed. 2013, 43, 177–182. [Google Scholar] [CrossRef]
- Goldberger, A.L.; Amaral, L.A.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.-K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef]
- Wei, J.J.; Chang, C.J.; Chou, N.K.; Jan, G.J. ECG data compression using truncated singular value decomposition. IEEE Trans. Biomed. Eng. 2001, 5, 290–299. [Google Scholar] [CrossRef]
- PCANet Code. Available online: http://mx.nthu.edu.tw/~tsunghan (accessed on 5 December 2018).
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Naive Bayes Code. Available online: https://github.com/andreeas26/NaiveBayesClassifier-Matlab (accessed on 28 December 2018).
- Fan, R.-E.; Chang, K.-W.; Hsieh, C.-J.; Wang, X.-R.; Lin, C.-J. LIBLINEAR: A Library for Large Linear Classification. J. Mach. Learn. Res. 2008, 9, 1871–1874. [Google Scholar] [CrossRef]
- Dar, M.N.; Akram, M.U.; Shaukat, A.; Khan, M.A. Ieee. ECG Based Biometric Identification for Population with Normal and Cardiac Anomalies Using Hybrid HRV and DWT Features. In Proceedings of the 2015 5th International Conference on IT Convergence and Security (ICITCS), Kuala Lumpur, Malaysia, 24–27 August 2015. [Google Scholar] [CrossRef]
- Rezgui, D.; Lachiri, Z. ECG Biometric Recognition Using SVM-Based Approach. IEEJ Trans. Electr. Electron. Eng. 2016, 11, S94–S100. [Google Scholar] [CrossRef]
- Tan, R.; Perkowski, M. ECG Biometric Identification Using Wavelet Analysis Coupled with Probabilistic Random Forest. In Proceedings of the 2016 15th IEEE International Conference on Machine Learning and Applications (ICMLA), Anaheim, CA, USA, 18–20 December 2016; pp. 182–187. [Google Scholar] [CrossRef]
- Yu, J.; Si, Y.; Liu, X.; Wen, D.; Luo, T.; Lang, L. ECG Identification Based on PCA-RPROP. In Proceedings of the International Conference on Digital Human Modeling and Applications in Health, Safety, Ergonomics and Risk Management, Vancouver, BC, Canada, 9–14 July 2017; pp. 419–432. [Google Scholar] [CrossRef]
- Lynn, H.M.; Yeom, S.; Kim, P. ECG-based biometric human identification based on backpropagation neural network. In Proceedings of the 2018 Conference Research in Adaptive and Convergent Systems (RACS 2018), Honolulu, HI, USA, 9–12 October 2018; pp. 6–10. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, Y.; Deng, Y.; Zhang, X. ECG authentication system design incorporating a convolutional neural network and generalized S-Transformation. Comput. Biol. Med. 2018, 102, 168–179. [Google Scholar] [CrossRef]
- Bassiouni, M.M.; El-Dahshan, E.-S.A.; Khalefa, W.; Salem, A.M. Intelligent hybrid approaches for human ECG signals identification. Signal Image Video Process. 2018, 12, 941–949. [Google Scholar] [CrossRef]
- Sun, Z.; Chiong, R.; Hu, Z.-P. An extended dictionary representation approach with deep subspace learning for facial expression recognition. Neurocomputing 2018, 316, 1–9. [Google Scholar] [CrossRef]
- Wu, J.; Qiu, S.; Kong, Y.; Jiang, L.; Chen, Y.; Yang, W.; Senhadji, L.; Shu, H. PCANet: An energy perspective. Neurocomputing 2018, 313, 271–287. [Google Scholar] [CrossRef]
- Chun, S.Y. Single Pulse ECG-based Small Scale User Authentication using Guided Filtering. In Proceedings of the IEEE International Conference on Biometrics (ICB), Halmstad, Sweden, 13–16 June 2016. [Google Scholar] [CrossRef]
- Bendale, A.; Boult, T.E. Towards Open Set Deep Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1563–1572. [Google Scholar] [CrossRef]
- Mendes Junior, P.R.; de Souza, R.M.; Werneck, R.d.O. Nearest neighbors distance ratio open-set classifier. Mach. Learn. 2017, 106, 359–386. [Google Scholar] [CrossRef]
| Steps | Project | Parameter |
|---|---|---|
| Input | Heartbeat matrix size | 20 × 20 |
| The first stage | Patch size () | 7 × 7 |
| The number of filters of the first stage () | 8 | |
| The second stage | Patch size () | 7 × 7 |
| The number of filters of the second stage () | 8 | |
| Output | Histogram block size () | 7 × 7 |
| Block overlap ratio () | 0.5 |
| Subject Number | Heartbeat Number & Estimated Heart Rate (beat/min) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Record-1 | Record-2 | Record-3 | Record-4 | Record-5 | ||||||
| 3 | 25 | 75 | 25 | 75 | 24 | 72 | 23 | 69 | 23 | 69 |
| 10 | 28 | 84 | 27 | 81 | 28 | 84 | 33 | 99 | 24 | 72 |
| 24 | 24 | 72 | 25 | 75 | 25 | 75 | 21 | 63 | 18 | 54 |
| 25 | 24 | 72 | 24 | 72 | 23 | 69 | 19 | 57 | 23 | 69 |
| 30 | 23 | 69 | 24 | 72 | 21 | 63 | 21 | 63 | 19 | 57 |
| 32 | 22 | 66 | 22 | 66 | 23 | 69 | 24 | 72 | 23 | 69 |
| 34 | 31 | 93 | 30 | 90 | 27 | 81 | 29 | 87 | 30 | 90 |
| 36 | 19 | 57 | 20 | 60 | 23 | 69 | 25 | 75 | 23 | 69 |
| 52 | 25 | 75 | 26 | 78 | 28 | 84 | 29 | 87 | 31 | 93 |
| 53 | 26 | 78 | 27 | 81 | 27 | 81 | 30 | 90 | 27 | 81 |
| 59 | 25 | 75 | 28 | 84 | 33 | 99 | 21 | 63 | 20 | 60 |
| 72 | 24 | 72 | 25 | 75 | 20 | 60 | 37 | 111 | 34 | 102 |
| Main Operating | TT-CNN | TRT-CNN | QRS-CNN | TT-PCANet | TRT-PCANet | Proposed Method | |
|---|---|---|---|---|---|---|---|
| Heartbeat Resampling Manner | TT | Y | N | N | Y | N | N |
| TRT | N | Y | N | N | Y | N | |
| QRS-centered | N | N | Y | N | N | Y | |
| Feature Extraction | CNN | Y | Y | Y | N | N | N |
| PCANet | N | N | N | Y | Y | Y | |
| Layers | Type | Number of Neurons (Output Layer) | Kernel Size | Stride |
|---|---|---|---|---|
| 0–1 | Convolution | 16 × 16 × 6 | 5 × 5 | 1 |
| 1–2 | Max-pooling | 8 × 8 × 6 | 2 × 2 | 2 |
| 2–3 | Convolution | 4 × 4 × 12 | 5 × 5 | 1 |
| 3–4 | Max-pooling | 2 × 2 × 12 | 2 × 2 | 2 |
| Method | ECG Length (in Number of Heartbeats) | Average Subject Identification Accuracy (10 Experiments) |
|---|---|---|
| TT-CNN | 1 | 71.51% |
| TT-CNN | 3 | 77.57% |
| TT-CNN | 5 | 85.22% |
| TT-PCANet | 1 | 77.22% |
| TT-PCANet | 3 | 80.85% |
| TT-PCANet | 5 | 85.82% |
| TRT-CNN | 1 | 77.86% |
| TRT-CNN | 3 | 83.46% |
| TRT-CNN | 5 | 87.71% |
| TRT-PCANet | 1 | 85.93% |
| TRT-PCANet | 3 | 90.28% |
| TRT-PCANet | 5 | 91.96% |
| QRS-CNN | 1 | 83.44% |
| QRS-CNN | 3 | 88.96% |
| QRS-CNN | 5 | 91.89% |
| Our Method | 1 | 89.41% |
| Our Method | 3 | 92.49% |
| Our Method | 5 | 94.40% |
| Target Class | Classification Class | Accuracy | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 24 | 25 | 30 | 32 | 34 | 36 | 52 | 53 | 59 | 72 | ||
| 3 | 19 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 90.48% |
| 10 | 0 | 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 90.48% |
| 24 | 3 | 1 | 16 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 76.19% |
| 25 | 0 | 0 | 0 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| 30 | 0 | 0 | 0 | 0 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| 32 | 0 | 0 | 0 | 0 | 0 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| 34 | 2 | 0 | 0 | 1 | 0 | 0 | 18 | 0 | 0 | 0 | 0 | 0 | 85.71% |
| 36 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 17 | 0 | 0 | 2 | 0 | 80.95% |
| 52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 21 | 0 | 0 | 0 | 100% |
| 53 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 21 | 0 | 0 | 100% |
| 59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 17 | 3 | 80.95% |
| 72 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 7 | 13 | 61.90% |
| Target Class | Classification Class | Accuracy | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 24 | 25 | 30 | 32 | 34 | 36 | 52 | 53 | 59 | 72 | ||
| 3 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| 10 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| 24 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| 25 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| 30 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| 32 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 0 | 100% |
| 34 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 100% |
| 36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 100% |
| 52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | 100% |
| 53 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | 100% |
| 59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | 100% |
| 72 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 2 | 1 | 33.33% |
| S. No | Performance Parameter | Value [18] | Value (Our Method) |
|---|---|---|---|
| 1 | True_Positive Rate (Beat Identification) | 80.5556% | 88.8889% |
| 2 | True_Positive Rate (Subject Identification) | 88.8889% | 94.4444% |
| 3 | Overall_Accuracy | 98.1481% | 99.0741% |
| 4 | Overall_Recall | 88.8889% | 94.4444% |
| 5 | Overall_Specificity | 98.9899% | 99.4949% |
| 6 | Overall_Precision | 93.750% | 96.6667% |
| 7 | Overall_F1 Score | 88.5317% | 93.7500% |
| Methods | ECG-ID: 89 | MIT-BIH: 47 | ||
|---|---|---|---|---|
| ECG Length (in Number of Heartbeats) | SI | ECG Length (in Number of Heartbeats) | SI | |
| RNN [9] | 18 | 91.7% | 18 | 93.3% |
| GRU [9] | 18 | 94.4% | 18 | 95.7% |
| LSTM [9] | 18 | 100% | 18 | 100% |
| Proposed method | 18 | 97.75% | 18 | 100% |
| Proposed method | 7 | 95.25% | 7 | 97.85% |
| Proposed method | 5 | 92.36% | 5 | 97.80% |
| Proposed method | 3 | 89.97% | 3 | 96.96% |
| Proposed method | 1 | 84.50% | 1 | 90.45% |
| Methods | Year | Feature Extraction (Type) | Decision | ECG Dataset | Performance |
|---|---|---|---|---|---|
| Page et al. [12] | 2015 | QRS complex segments (Fiducial) | NN | ECG-ID: 90 | SI: 99.93% |
| Dar et al. [40] | 2015 | Haar Transform/GBFS (Non-fiducial) | KNN | ECG-ID: 90 MIT-BIH: 47 | SI: 83.2% SI: 95.9% |
| Dar et al. [10] | 2015 | Haar Transform and HRV/GBFS (Non-fiducial) | Random Forest | ECG-ID: 90 MIT-BIH: 47 | SI: 83.9% SI: 93.1% |
| Dhou-ha et al. [41] | 2016 | 21 temporal and amplitude features and 10 morphological descriptors (Fiducial) | SVM | MIT-BIH: 44 | SI: 98.8% |
| Tan et al. [42] | 2017 | Temporal, amplitude, and angle fid. + DWT coefficients (Fiducial) | Random Forests + WDIST KNN | ECG-ID: 89 MIT-BIH: 47 | SI: 100% SI: 100% |
| Yu et al. [43] | 2017 | PCA (Non-fiducial) | RPROP | ECG-ID: 89 | SI: 96.60% |
| Lynn et al. [44] | 2018 | Temporal and amplitude features (Fiducial) | BP-NN | ECG-ID: 3 10 20 | SI: 98.24% SI: 96.20% SI: 94.00% |
| Zhao et al. [45] | 2018 | Generalized S-transformation (Non-fiducial) | CNN | ECG-ID:50 | SI: 96.63% |
| Mahmoud et al. [46] | 2018 | Mean P-QRS-T fragment + DWT (Fusion of fiducial and non-fiducial) | SVM | ECG-ID: 90 MIT-BIH: 47 | SI: 99% SI: 100% |
| Proposed Method | - | QRS-centered resampling strategy + PCANet (partial-fiducial) | Linear-SVM | ECG-ID: 12 89 MIT-BIH: 47 | SI: 97.78% SI: 97.75% SI: 100% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Si, Y.; Yang, W.; Zhang, G.; Liu, T. A Novel Heart Rate Robust Method for Short-Term Electrocardiogram Biometric Identification. Appl. Sci. 2019, 9, 201. https://doi.org/10.3390/app9010201
Wang D, Si Y, Yang W, Zhang G, Liu T. A Novel Heart Rate Robust Method for Short-Term Electrocardiogram Biometric Identification. Applied Sciences. 2019; 9(1):201. https://doi.org/10.3390/app9010201
Chicago/Turabian StyleWang, Di, Yujuan Si, Weiyi Yang, Gong Zhang, and Tong Liu. 2019. "A Novel Heart Rate Robust Method for Short-Term Electrocardiogram Biometric Identification" Applied Sciences 9, no. 1: 201. https://doi.org/10.3390/app9010201
APA StyleWang, D., Si, Y., Yang, W., Zhang, G., & Liu, T. (2019). A Novel Heart Rate Robust Method for Short-Term Electrocardiogram Biometric Identification. Applied Sciences, 9(1), 201. https://doi.org/10.3390/app9010201




