A State of Charge Estimator Based Extended Kalman Filter Using an Electrochemistry-Based Equivalent Circuit Model for Lithium-Ion Batteries
Abstract
:1. Introduction
1.1. Literature Review
1.2. Main Contributions
- (1)
- Four typical ECMs and four improved ECMs considering partial electrochemical properties are compared under the new European Driving Cycle (NEDC) and the dynamic stress test (DST) working conditions to obtain a more suitable battery model for the entire SOC area.
- (2)
- A subarea parameter-identification method based on PSO is proposed to improve the global model accuracy in the entire SOC area.
- (3)
- A SOC estimator based on extended kalman filter (EKF) for our proposed model is developed, and its accuracy and robustness are verified by experiments.
1.3. Organization of the Paper
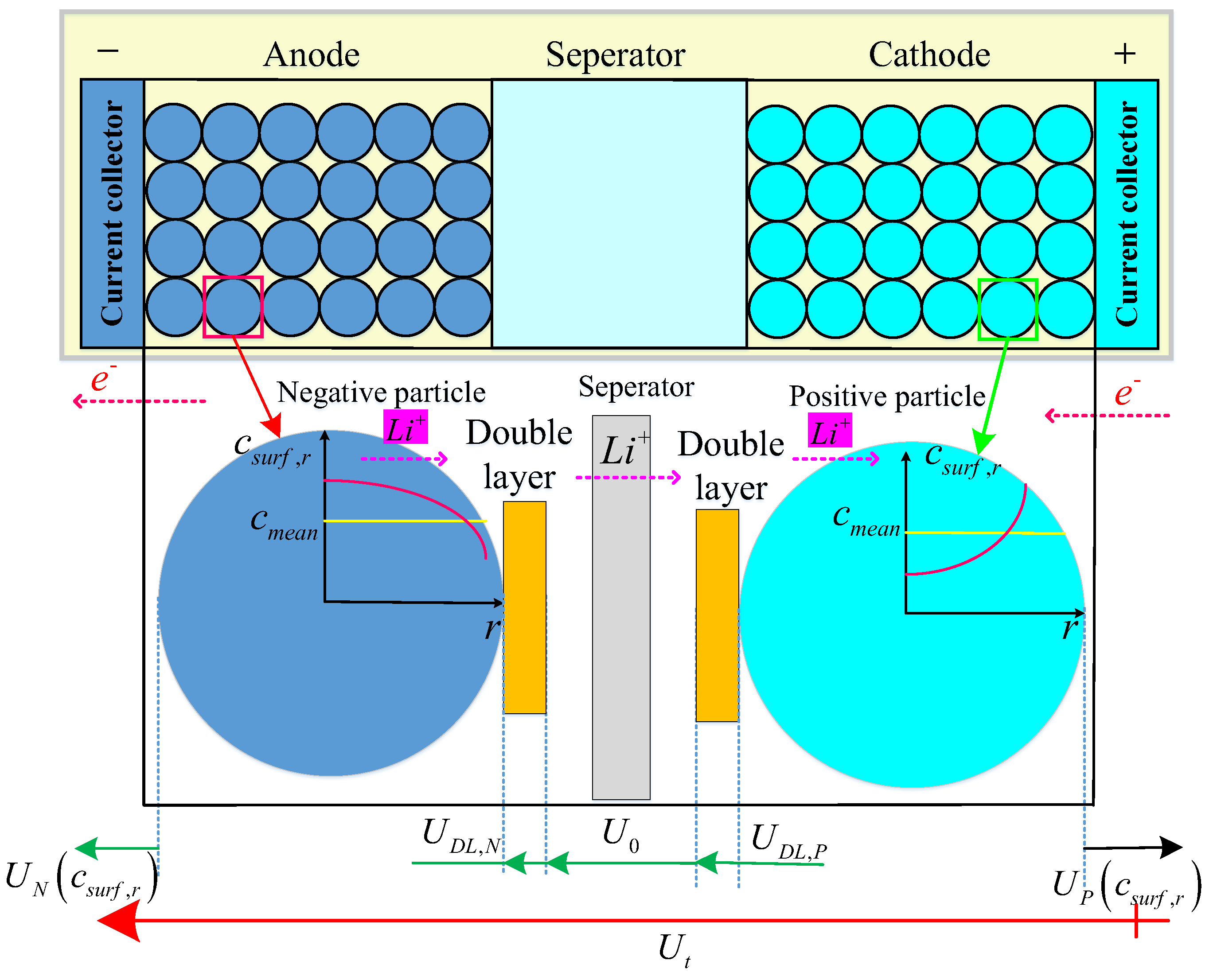
2. Electrochemistry-Based Equivalent Circuit Model
2.1. Single-Particle Model
2.2. ECM Considering Electrochemical Properties
3. Model Parameter Identification and Comparison
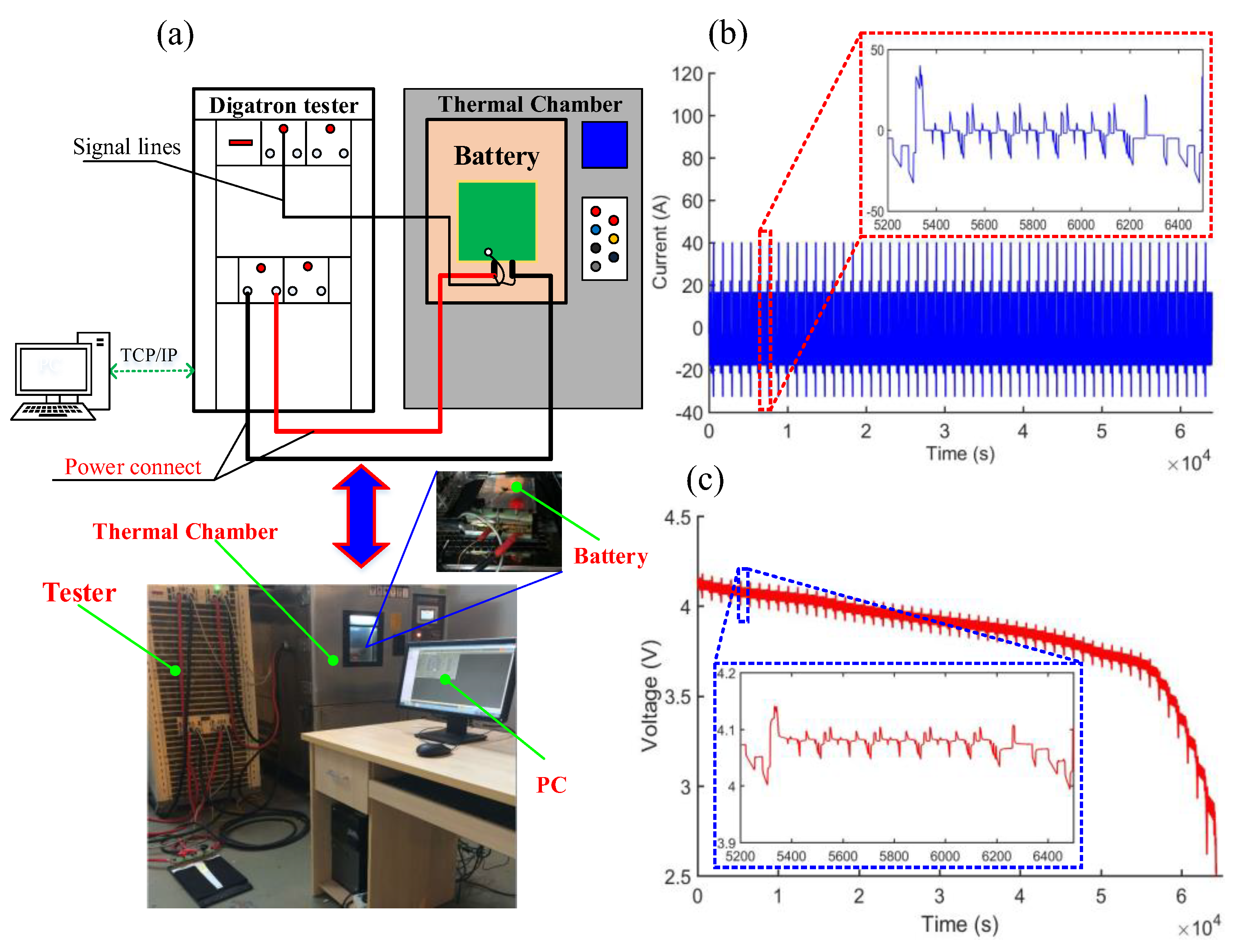
3.1. Experiments
3.2. Model Parameter Identification Using PSO
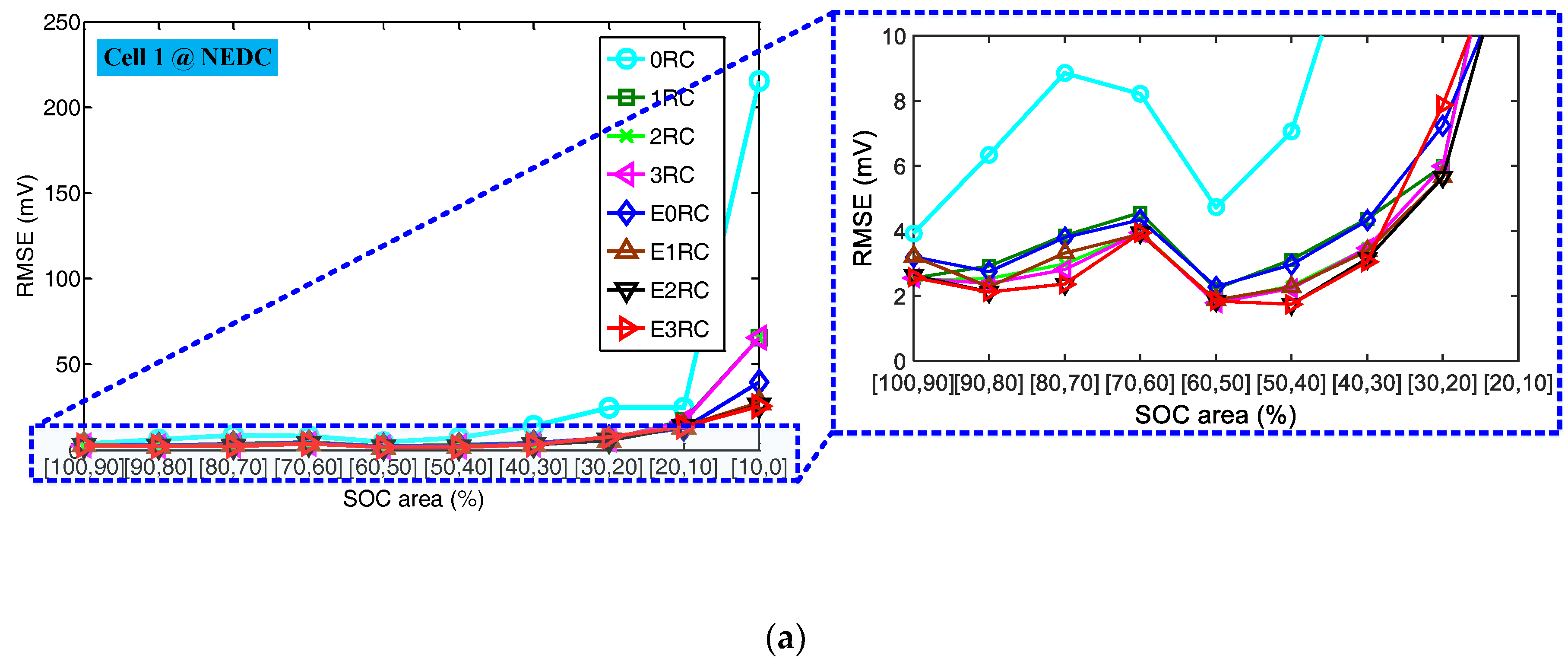
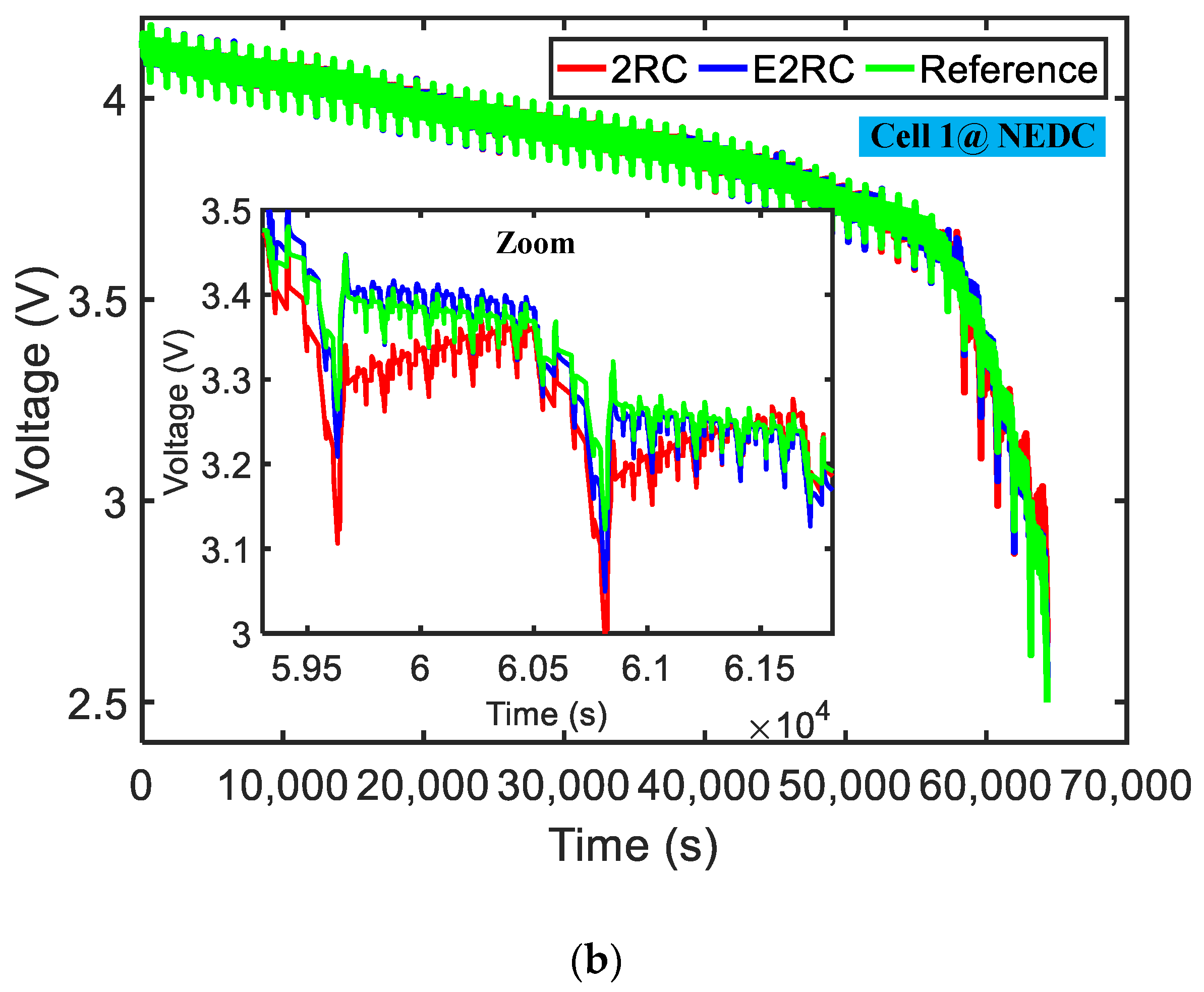
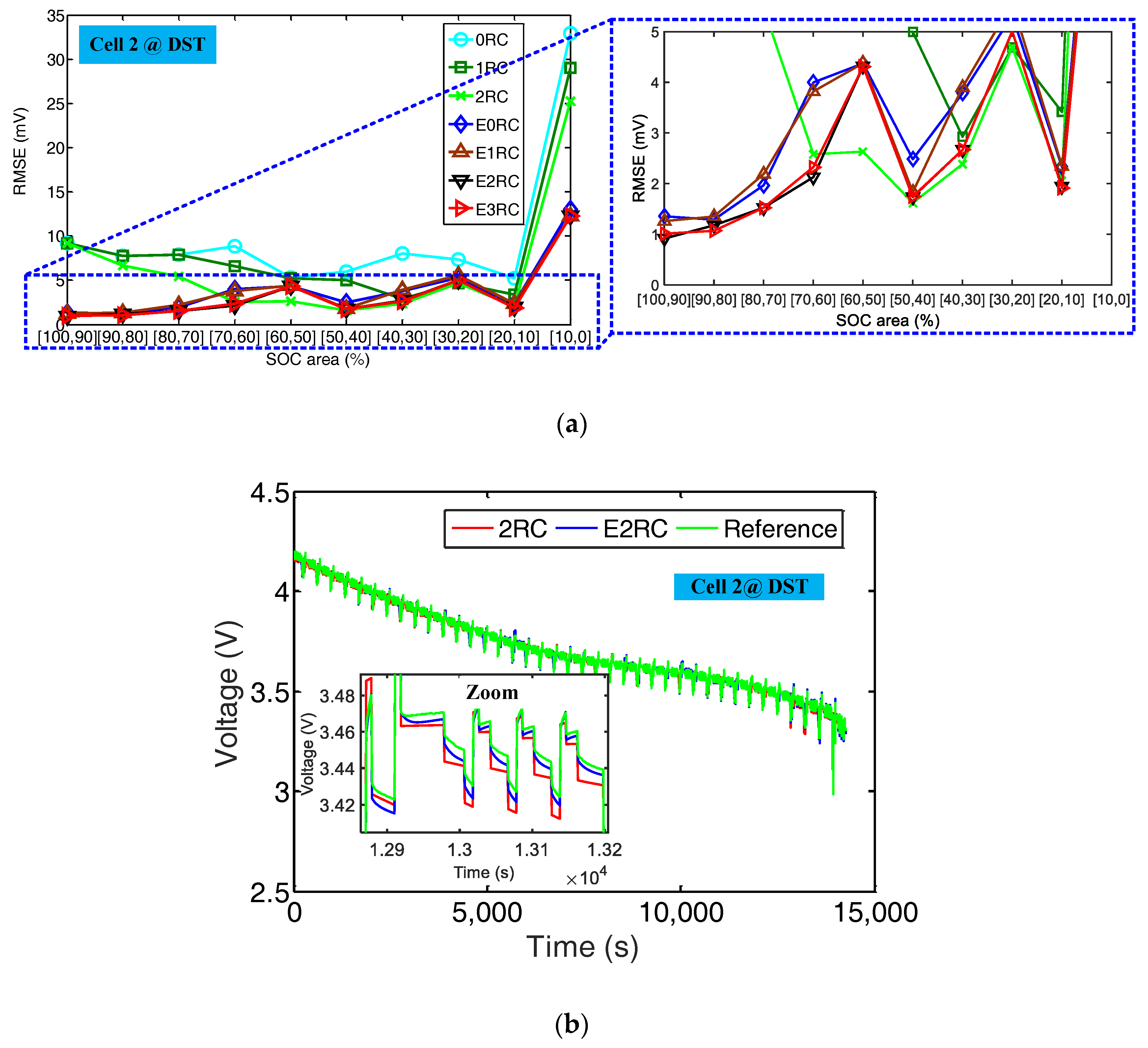
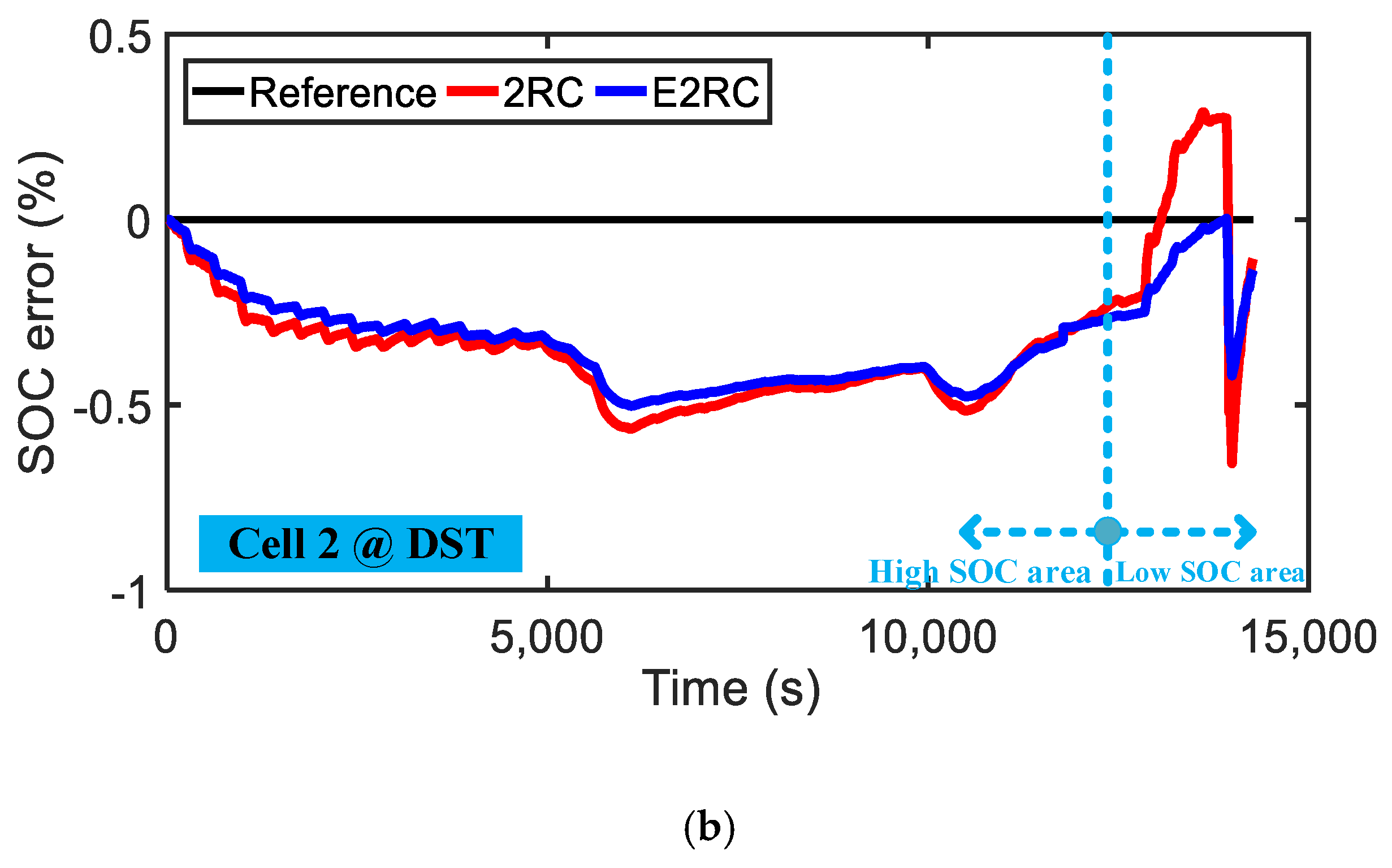
3.3. Results and Discussion
4. SOC Estimation in the Entire SOC Area
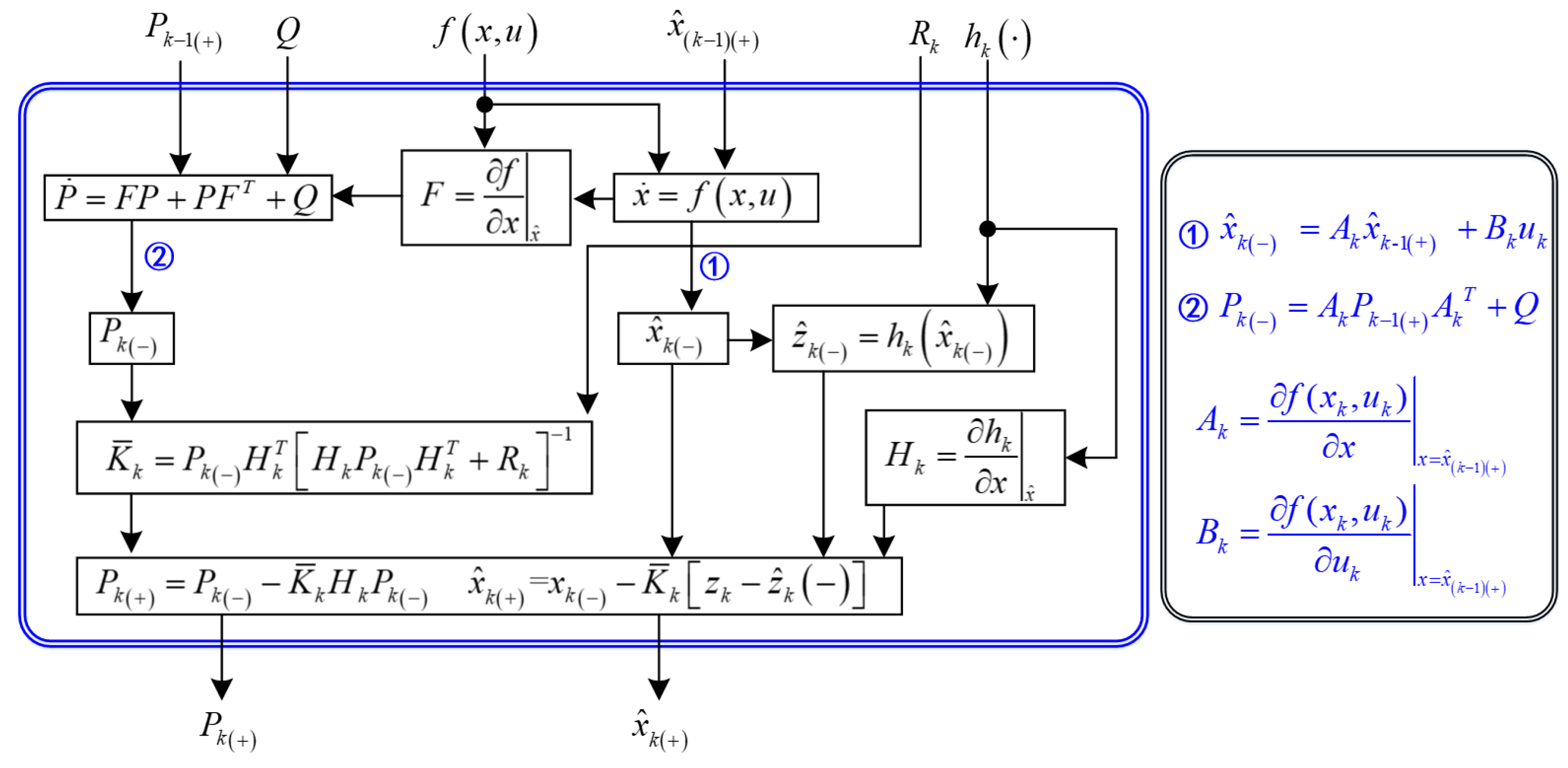
4.1. EKF-Based SOC Estimator
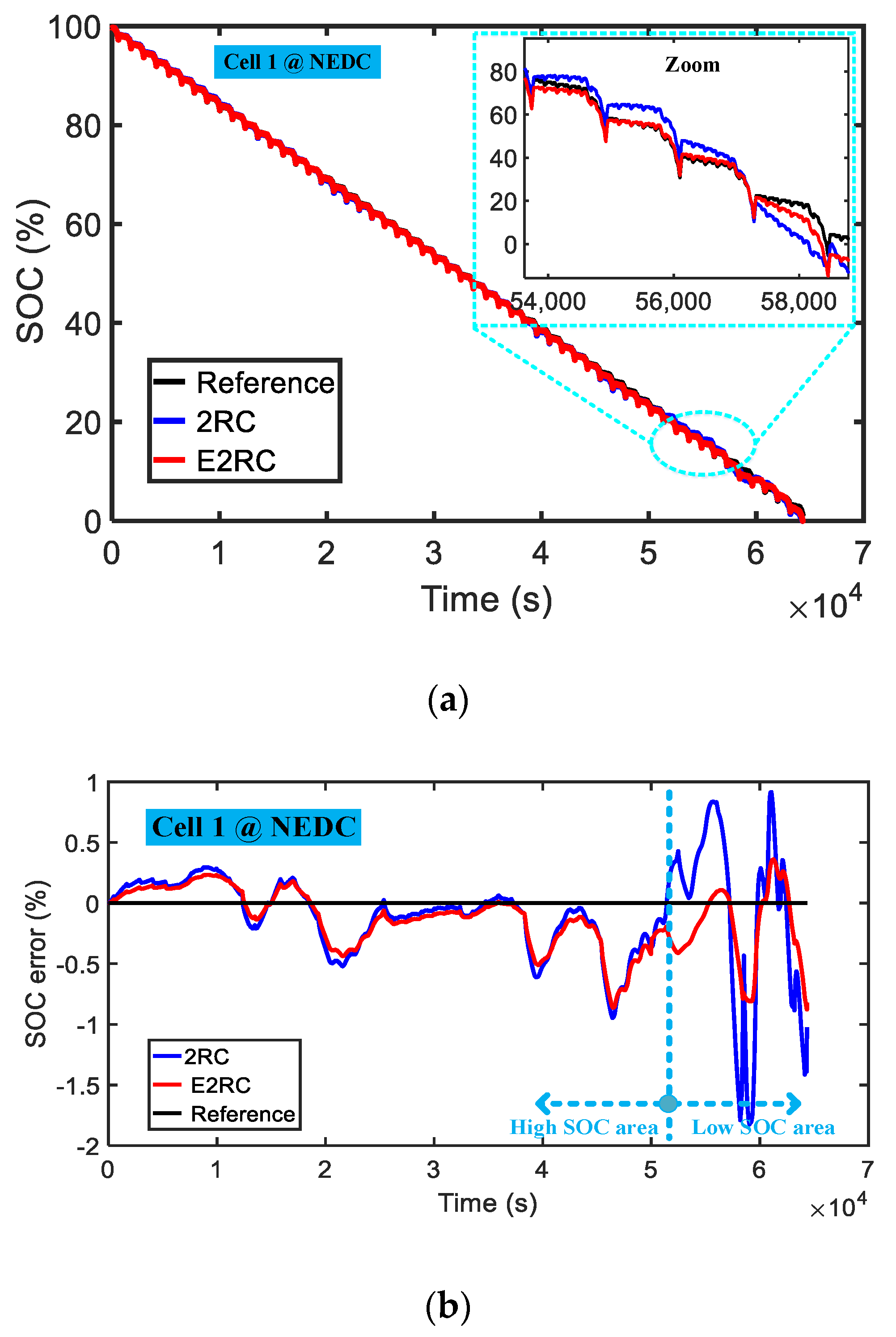
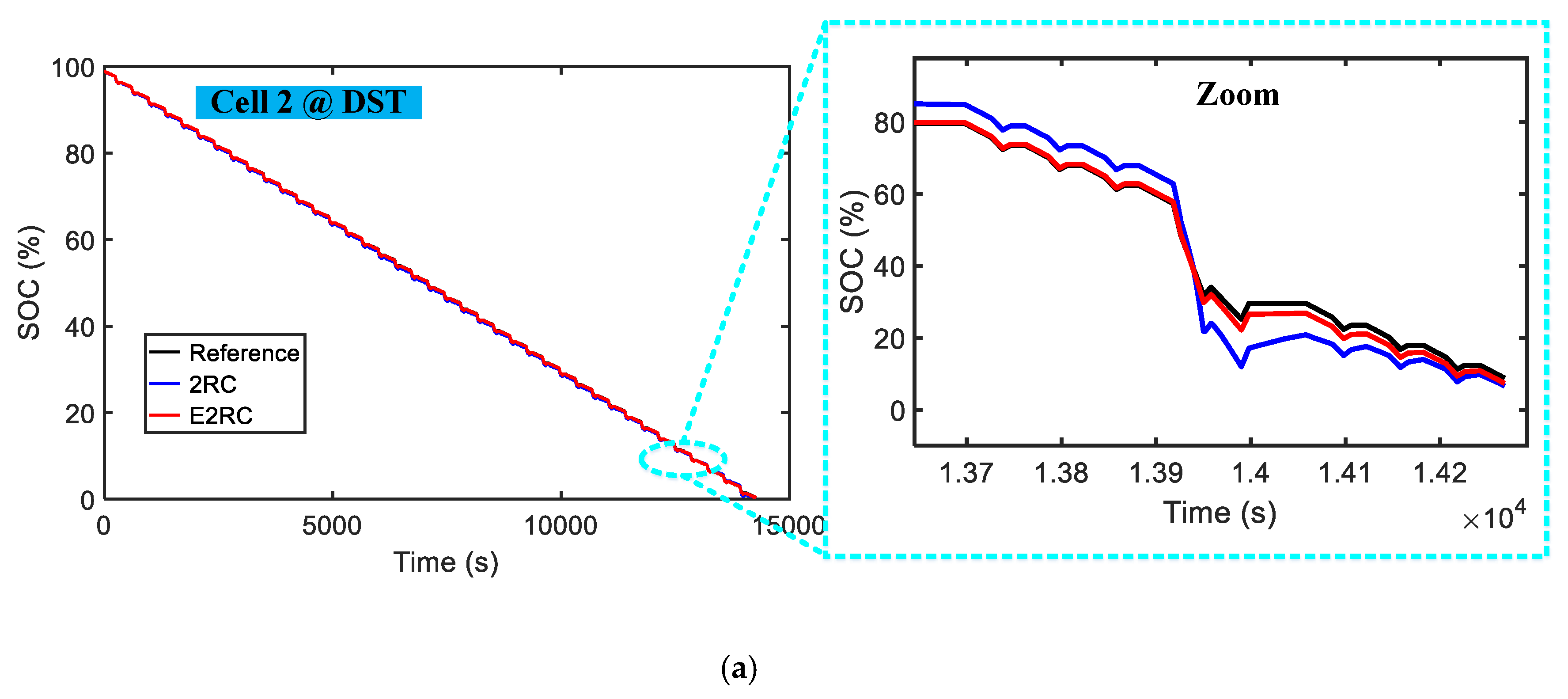
4.2. Results and Discussion
5. Conclusions
- (1)
- Comparative studies show that E2RC model is the best choice. The accuracy of the proposed model is one times higher than that of the traditional ECM in the low SOC area, and slightly better than that of the ECM in the high SOC area.
- (2)
- An EKF-based SOC estimator using our proposed model has higher SOC estimation accuracy than the ECM, especially in low SOC area. The SOC estimation error is less than 1% in the entire SOC area.
- (3)
- The proposed battery model and SOC estimation algorithm have satisfactory accuracy and robustness with low computational complexity.
Author Contributions
Funding
Conflicts of Interest
References
- Dong, G.Z.; Wei, J.W.; Chen, Z.H. Constrained bayesian dual-filtering for state of charge estimation of lithium-ion batteries. Int. J. Electr. Power Energy Syst. 2018, 99, 516–524. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Ouyang, M.G.; Han, X.B.; Lu, L.G.; Li, J.Q. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Z.Z.; Lu, Z.Q.; Li, J.Z.; Ji, B.; Wei, H.Y.; Pan, H.H. A novel state-of-charge estimation method of lithium-ion batteries combining the grey model and genetic algorithms. IEEE Trans. Power Electron. 2018, 33, 8797–8807. [Google Scholar] [CrossRef]
- Sahinoglu, G.O.; Pajovic, M.; Sahinoglu, Z.; Wang, Y.B.; Orlik, P.V.; Wada, T. Battery state-of-charge estimation based on regular/recurrent gaussian process regression. IEEE Trans. Ind. Electron. 2018, 65, 4311–4321. [Google Scholar] [CrossRef]
- Ladpli, P.; Kopsaftopoulos, F.; Chang, F.K. Estimating state of charge and health of lithium-ion batteries with guided waves using built-in piezoelectric sensors/actuators. J. Power Sources 2018, 384, 342–354. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.J.; Zhou, L.; Gao, W.K. Electrical behavior of overdischarge-induced internal short circuit in lithium-ion cells. Electrochim. Acta 2018, 278, 245–254. [Google Scholar] [CrossRef]
- Wei, Z.B.; Zou, C.F.; Leng, F.; Soong, B.H.; Tseng, K.J. Online model identification and state-of-charge estimate for lithium-ion battery with a recursive total least squares-based observer. IEEE Trans. Ind. Electron. 2018, 65, 1336–1346. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long short-term memory networks for accurate state-of-charge estimation of li-ion batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Panchal, S.; Mcgrory, J.; Kong, J.; Fraser, R.; Fowler, M.; Dincer, I.; Agelin-Chaab, M. Cycling degradation testing and analysis of a lifepo4 battery at actual conditions. Int. J. Energy Res. 2017, 41, 2565–2575. [Google Scholar] [CrossRef]
- Liu, C.Z.; Liu, W.Q.; Wang, L.Y.; Hu, G.D.; Ma, L.P.; Ren, B.Y. A new method of modeling and state of charge estimation of the battery. J. Power Sources 2016, 320, 1–12. [Google Scholar] [CrossRef]
- He, H.W.; Xiong, R.; Guo, H.Q.; Li, S.C. Comparison study on the battery models used for the energy management of batteries in electric vehicles. Energy Convers. Manag. 2012, 64, 113–121. [Google Scholar] [CrossRef]
- Ma, Y.; Duan, P.; Sun, Y.S.; Chen, H. Equalization of lithium-ion battery pack based on fuzzy logic control in electric vehicle. IEEE Trans. Ind. Electron. 2018, 65, 6762–6771. [Google Scholar] [CrossRef]
- Lai, X.; Zheng, Y.J.; Sun, T. A comparative study of different equivalent circuit models for estimating state-of-charge of lithium-ion batteries. Electrochim. Acta 2018, 259, 566–577. [Google Scholar] [CrossRef]
- Han, X.B.; Ouyang, M.G.; Lu, L.G.; Li, J.Q. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part i: Diffusion simplification and single particle model. J. Power Sources 2015, 278, 802–813. [Google Scholar] [CrossRef]
- Ouyang, M.G.; Liu, G.M.; Lu, L.G.; Li, J.Q.; Han, X.B. Enhancing the estimation accuracy in low state-of-charge area: A novel onboard battery model through surface state of charge determination. J. Power Sources 2014, 270, 221–237. [Google Scholar] [CrossRef]
- Zhang, C.P.; Jiang, J.C.; Gao, Y.; Zhang, W.G.; Liu, Q.J.; Hu, X.S. Charging optimization in lithium-ion batteries based on temperature rise and charge time. Appl. Energy 2017, 194, 569–577. [Google Scholar] [CrossRef]
- Tian, Y.; Li, D.; Tian, J.D.; Xia, B.Z. State of charge estimation of lithium-ion batteries using an optimal adaptive gain nonlinear observer. Electrochim. Acta 2017, 225, 225–234. [Google Scholar] [CrossRef]
- Lim, K.; Bastawrous, H.A.; Duong, V.H.; See, K.W.; Zhang, P.; Dou, S.X. Fading kalman filter-based real-time state of charge estimation in lifepo4 battery-powered electric vehicles. Appl. Energy 2016, 169, 40–48. [Google Scholar] [CrossRef]
- Sturm, J.; Ennifar, H.; Erhard, S.V.; Rheinfeld, A.; Kosch, S.; Jossen, A. State estimation of lithium-ion cells using a physicochemical model based extended kalman filter. Appl. Energy 2018, 223, 103–123. [Google Scholar] [CrossRef]
- Deng, Z.W.; Yang, L.; Deng, H.; Cai, Y.S.; Li, D.D. Polynomial approximation pseudo-two-dimensional battery model for online application in embedded battery management system. Energy 2018, 142, 838–850. [Google Scholar] [CrossRef]
- Allam, A.; Onori, S. An interconnected observer for concurrent estimation of bulk and surface concentration in the cathode and anode of a lithium-ion battery. IEEE Trans. Ind. Electron. 2018, 65, 7311–7321. [Google Scholar] [CrossRef]
- Meng, J.H.; Luo, G.Z.; Ricco, M.; Swierczynski, M.; Stroe, D.I.; Teodorescu, R. Overview of lithium-ion battery modeling methods for state-of-charge estimation in electrical vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Liu, G.M.; Ouyang, M.G.; Lu, L.G.; Li, J.Q.; Han, X.B. Online estimation of lithium-ion battery remaining discharge capacity through differential voltage analysis. J. Power Sources 2015, 274, 971–989. [Google Scholar] [CrossRef]
- Farmann, A.; Sauer, D.U. Comparative study of reduced order equivalent circuit models for on-board state-of-available-power prediction of lithium-ion batteries in electric vehicles. Appl. Energy 2018, 225, 1102–1122. [Google Scholar] [CrossRef]
- Panchal, S.; Rashid, M.; Long, F.; Mathew, M.; Fraser, R.; Fowler, M. Degradation testing and modeling of 200 ah LiFePO4 battery. SAE Tech. Pap. 2018. [Google Scholar] [CrossRef]
- Ma, Z.Y.; Wang, Z.P.; Xiong, R.; Jiang, J.C. A mechanism identification model based state-of-health diagnosis of lithium-ion batteries for energy storage applications. J. Clean Prod. 2018, 193, 379–390. [Google Scholar] [CrossRef]
- Altinoz, O.T.; Yilmaz, A.E.; Duca, A.; Ciuprina, G. Incorporating the avoidance behavior to the standard particle swarm optimization 2011. Adv. Electr. Comput. Eng. 2015, 15, 51–58. [Google Scholar] [CrossRef]
- Lin, X.F. Theoretical analysis of battery soc estimation errors under sensor bias and variance. IEEE Trans. Ind. Electron. 2018, 65, 7138–7148. [Google Scholar] [CrossRef]
- Wei, J.W.; Dong, G.Z.; Chen, Z.H.; Kang, Y. System state estimation and optimal energy control framework for multicell lithium-ion battery system. Appl. Energy 2017, 187, 37–49. [Google Scholar] [CrossRef]
- Lu, L.G.; Han, X.B.; Li, J.Q.; Hua, J.F.; Ouyang, M.G. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]


| Model Name | Discretization Equations (Discharge Is Negative) | Number of Parameters |
|---|---|---|
| 0RC | 2 | |
| E0RC | 4 | |
| nRC: 1RC 2RC 3RC | 1RC: 4 2RC: 6 3RC: 8 | |
| EnRC: E1RC E2RC E3RC | E1RC: 6 E2RC: 8 E3RC: 10 |
| Type | Nominal Capacity (Ah) | Lower Cut-Off Voltage (V) | Upper Cut-Off Voltage (V) | Maximum Charge Current (A) |
|---|---|---|---|---|
| Cell #1 | 32.5 | 2.5 | 4.15 | 65 |
| Cell #2 | 40 | 2.8 | 4.2 | 100 |
| Step 1: Initialize the variables, randomly generate a particle swarm, and calculate the particle fitness values; |
| Step 2: Repeat the following steps until the termination criterion is satisfied (the error is sufficiently small, or the maximum loop count is reached): |
| Implement the following operations on each individual: |
| Update the velocity and position state (according to Equations (10) and (11)); Update the variable representing the individual’s best position; |
| Step 3: Output the optimization results. |
| Model Name | Identification Time (s) |
|---|---|
| 0RC | 1.7796 |
| E0RC | 4.0983 |
| 1RC | 5.2645 |
| E1RC | 5.9482 |
| 2RC | 5.9897 |
| E2RC | 6.1520 |
| 3RC | 8.5727 |
| E3RC | 11.3445 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, X.; Qin, C.; Gao, W.; Zheng, Y.; Yi, W. A State of Charge Estimator Based Extended Kalman Filter Using an Electrochemistry-Based Equivalent Circuit Model for Lithium-Ion Batteries. Appl. Sci. 2018, 8, 1592. https://doi.org/10.3390/app8091592
Lai X, Qin C, Gao W, Zheng Y, Yi W. A State of Charge Estimator Based Extended Kalman Filter Using an Electrochemistry-Based Equivalent Circuit Model for Lithium-Ion Batteries. Applied Sciences. 2018; 8(9):1592. https://doi.org/10.3390/app8091592
Chicago/Turabian StyleLai, Xin, Chao Qin, Wenkai Gao, Yuejiu Zheng, and Wei Yi. 2018. "A State of Charge Estimator Based Extended Kalman Filter Using an Electrochemistry-Based Equivalent Circuit Model for Lithium-Ion Batteries" Applied Sciences 8, no. 9: 1592. https://doi.org/10.3390/app8091592
APA StyleLai, X., Qin, C., Gao, W., Zheng, Y., & Yi, W. (2018). A State of Charge Estimator Based Extended Kalman Filter Using an Electrochemistry-Based Equivalent Circuit Model for Lithium-Ion Batteries. Applied Sciences, 8(9), 1592. https://doi.org/10.3390/app8091592






