Review of Auxetic Materials for Sports Applications: Expanding Options in Comfort and Protection
Abstract
1. Introduction
2. Introduction to Sporting Protective Equipment
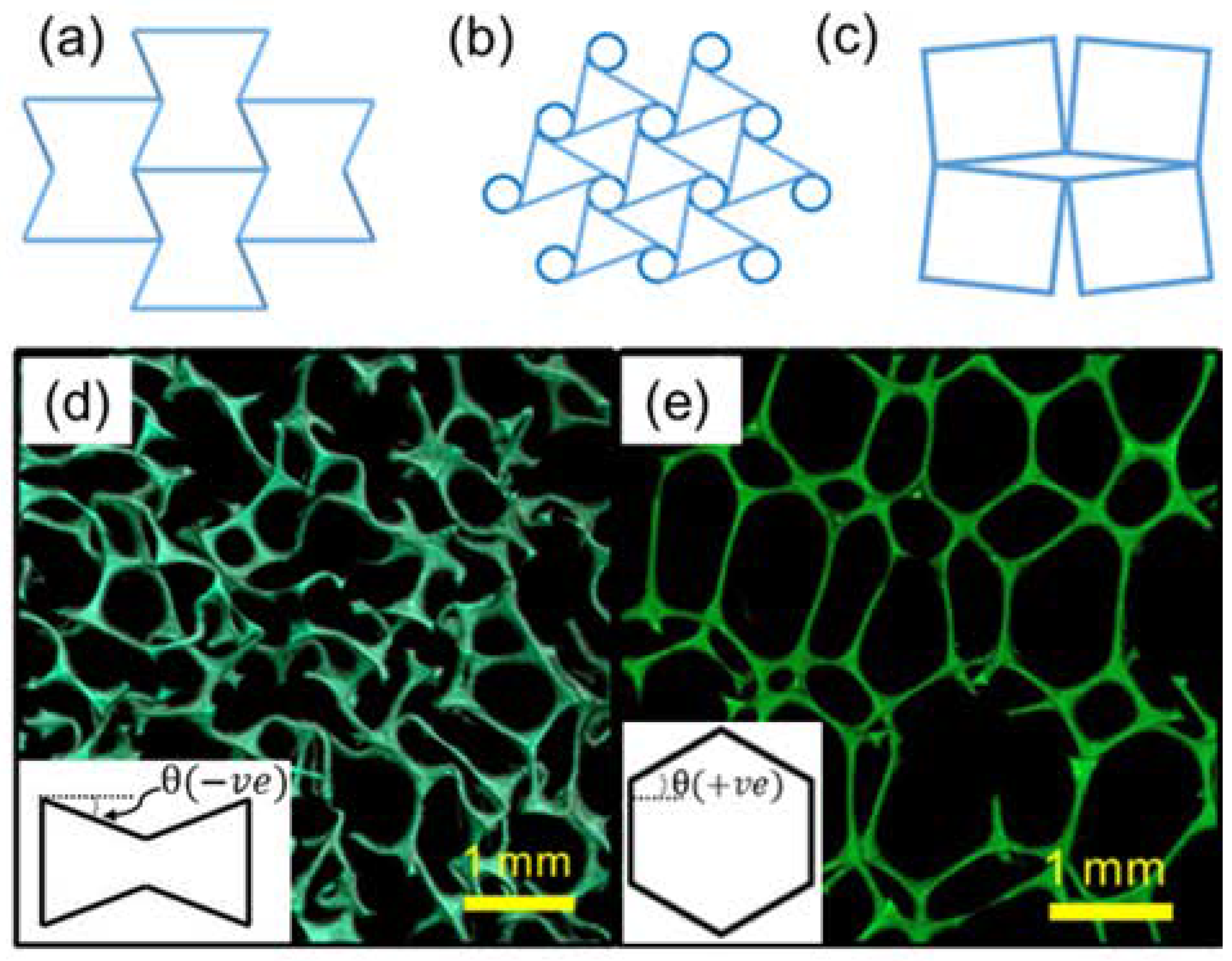
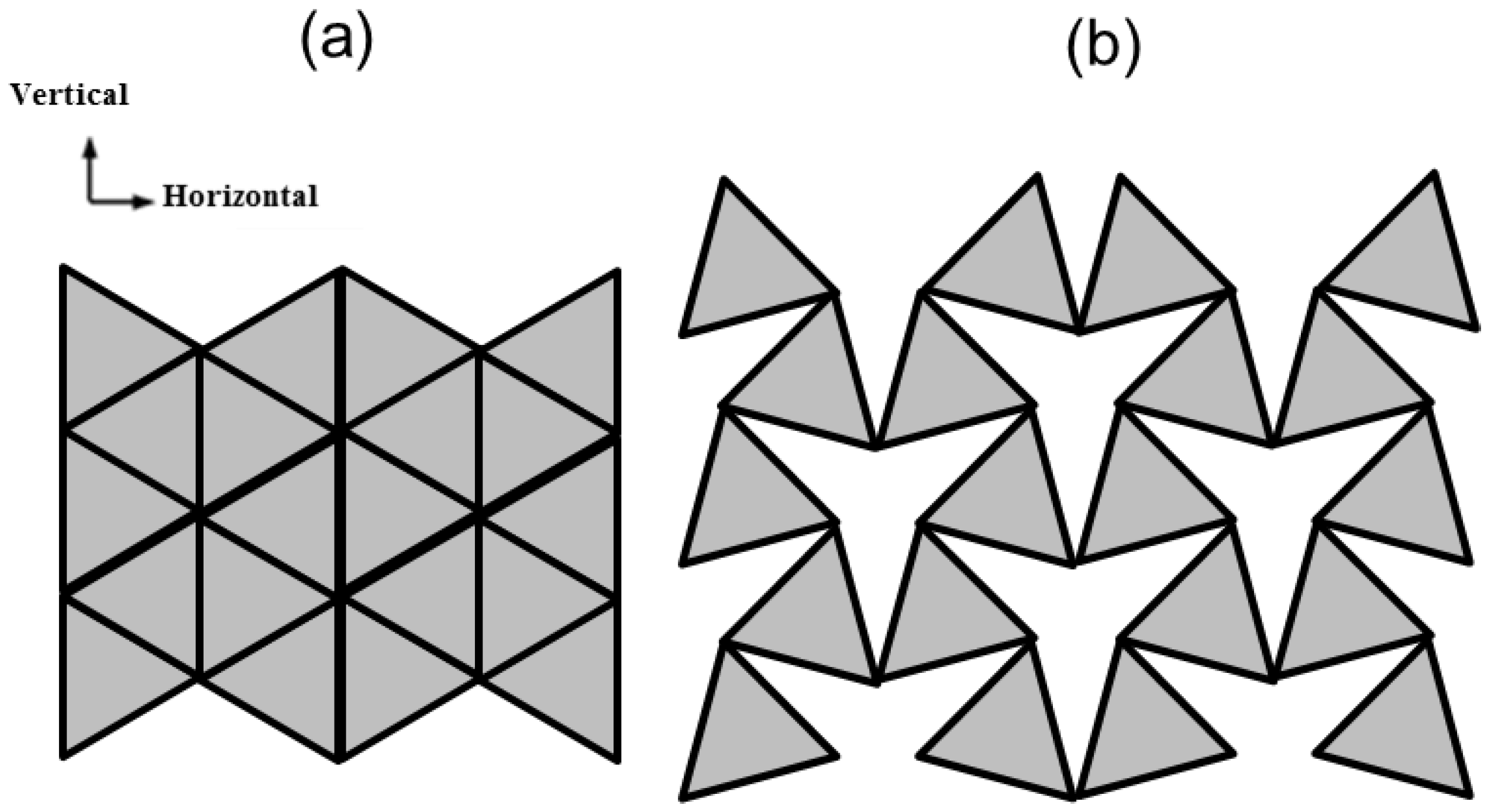
3. Common Auxetic Materials and Structures
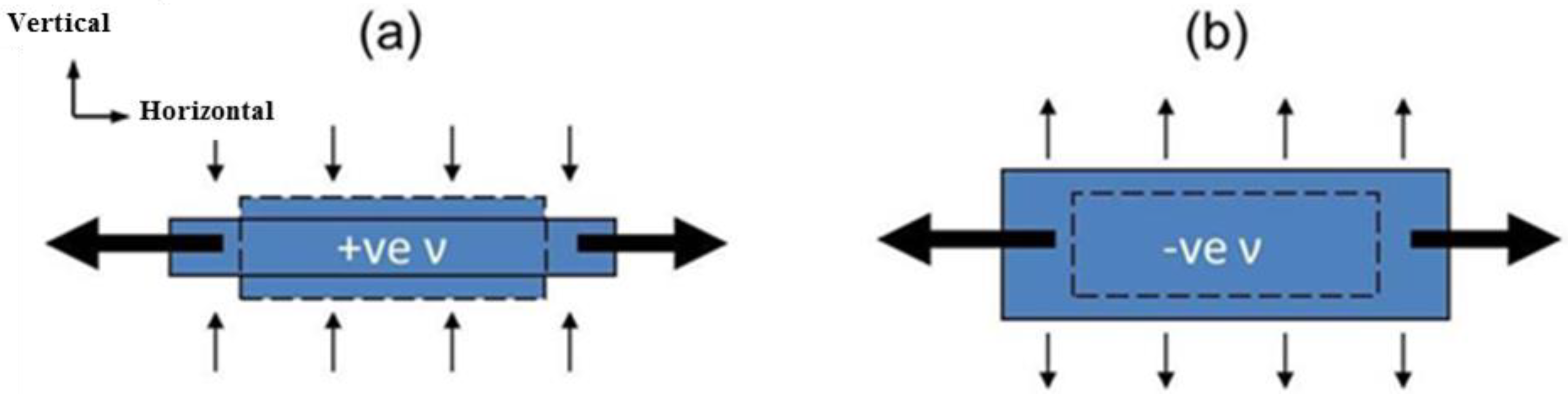
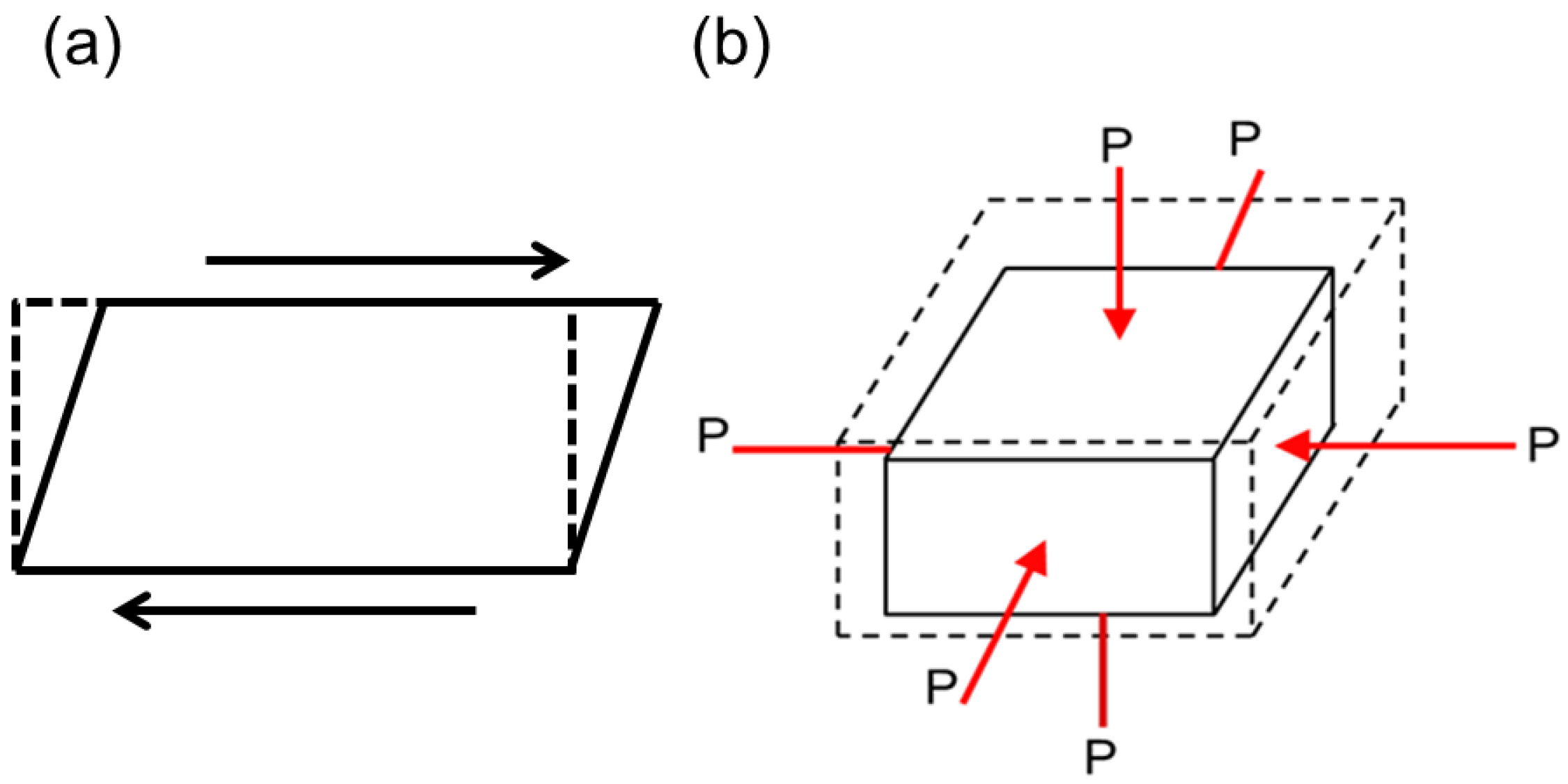
3.1. Modelling Auxetic Materials and Structures
3.2. Fabricating and Characterising Auxetic Foam
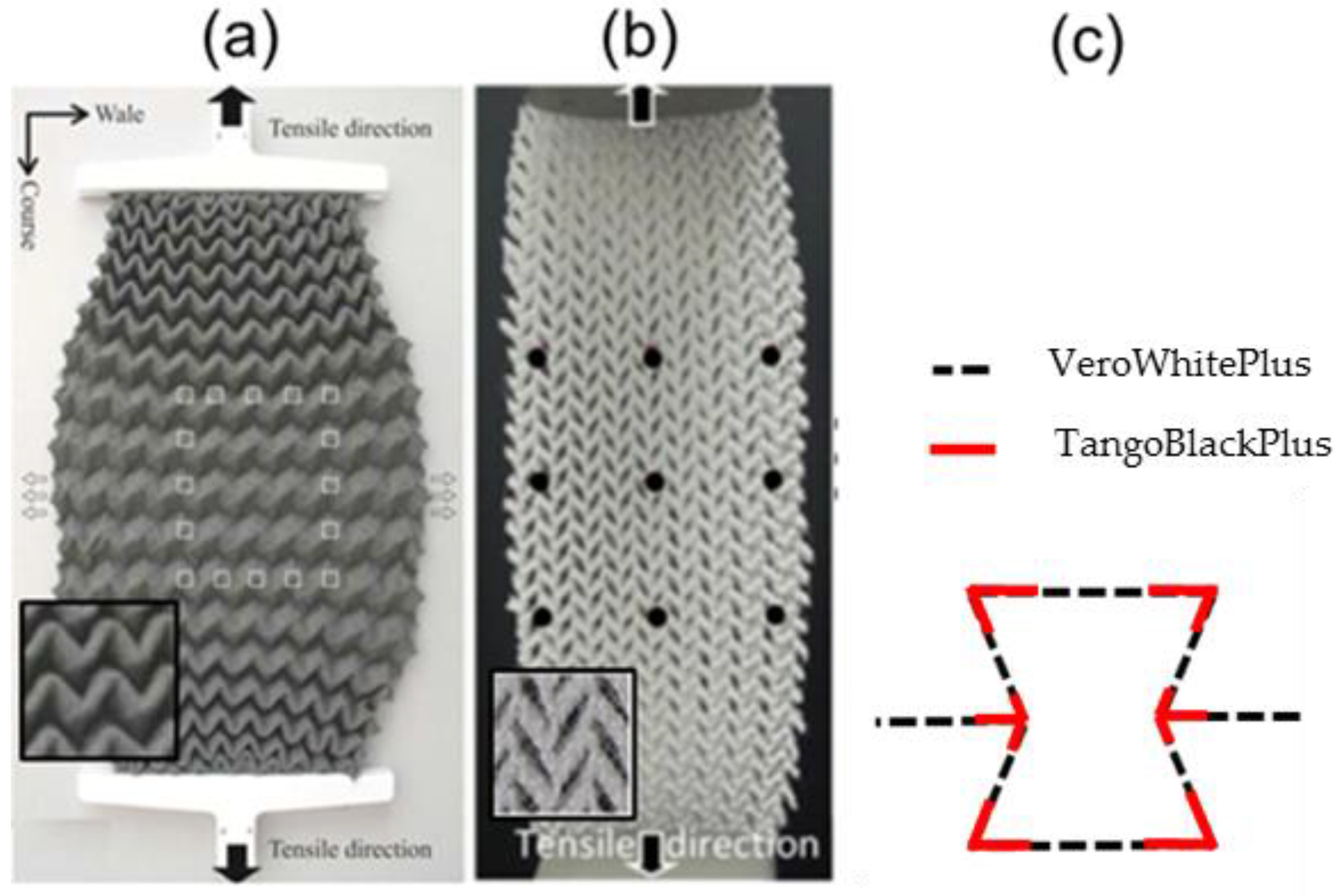
3.3. Fabricating Auxetic Textiles
3.4. Additively Manufactured Auxetic Materials and Structures
3.5. Gradient Materials
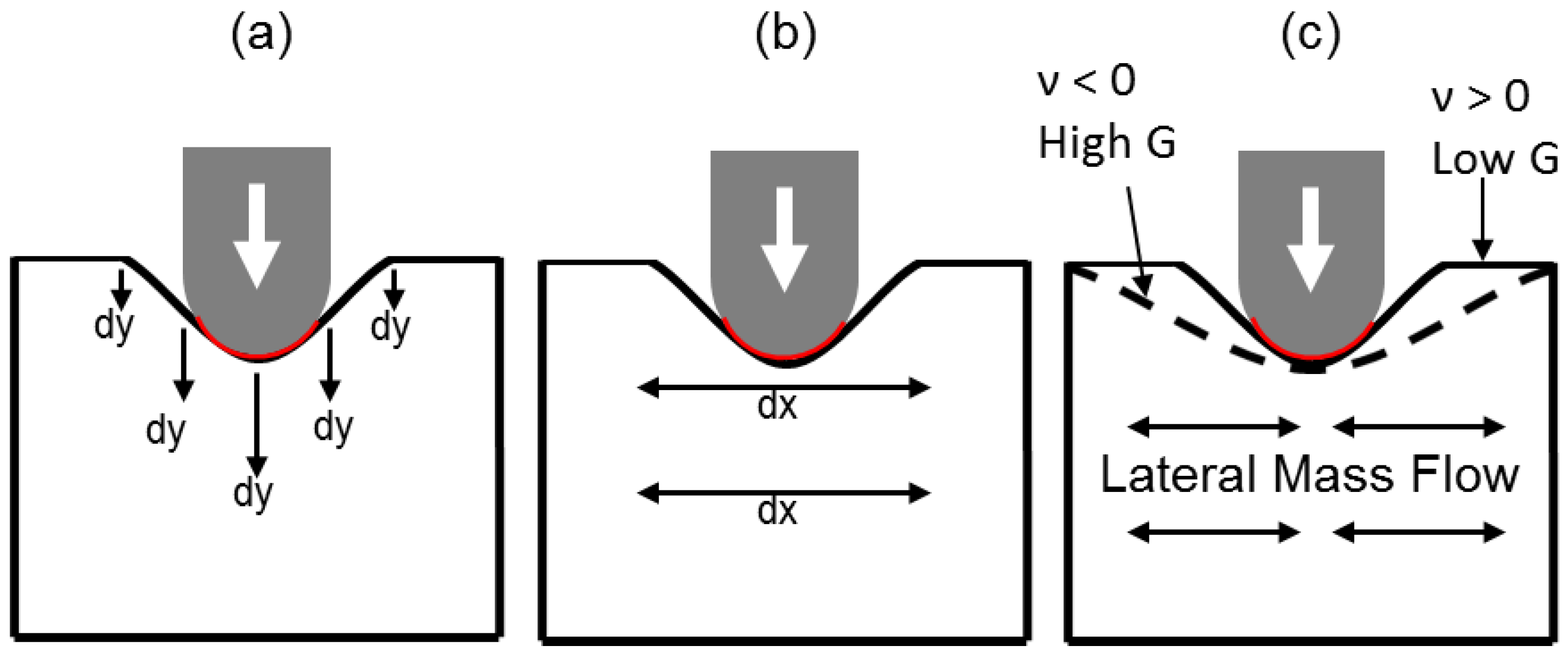
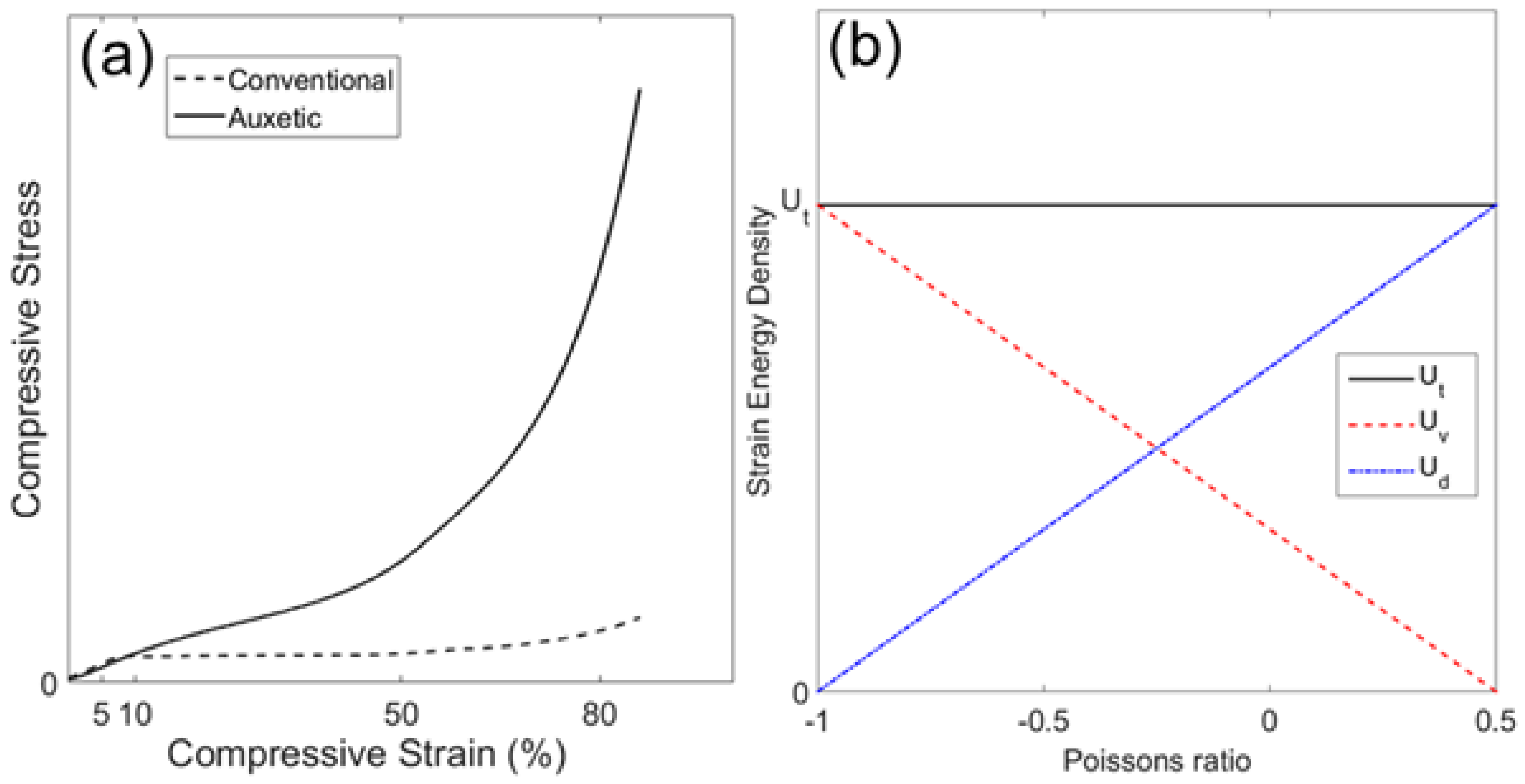
4. Expected Characteristics and Supporting Evidence
5. The Potential for Auxetic Materials in Sports Products
6. Conclusions
Conflicts of Interest
References
- Evans, K.E. Auxetic polymers: A new range of materials. Endeavour 1991, 15, 170–174. [Google Scholar] [CrossRef]
- Lisiecki, J.; Błazejewicz, T.; Kłysz, S.; Gmurczyk, G.; Reymer, P.; Mikułowski, G. Tests of polyurethane foams with negative Poisson’s ratio. Phys. Status Solidi Basic Res. 2013, 250, 1988–1995. [Google Scholar] [CrossRef]
- Allen, T.; Shepherd, J.; Hewage, T.A.M.; Senior, T.; Foster, L.; Alderson, A. Low-kinetic energy impact response of auxetic and conventional open-cell polyurethane foams. Phys. Status Solidi Basic Res. 2015, 9, 1631–1639. [Google Scholar] [CrossRef]
- Duncan, O.; Foster, L.; Senior, T.; Alderson, A.; Allen, T. Quasi-static characterisation and impact testing of auxetic foam for sports safety applications. Smart Mater. Struct. 2016, 25, 54014. [Google Scholar] [CrossRef]
- Zhou, L.; Zeng, J.; Jiang, L.; Hu, H. Low-velocity impact properties of 3D auxetic textile composite. J. Mater. Sci. 2017, 53, 3899–3914. [Google Scholar] [CrossRef]
- Taha, Z.; Hassan, M.H.A. Parametric Analysis of the Influence of Elastomeric Foam on the Head Response during Soccer Heading Manoeuvre. Procedia Eng. 2016, 147, 139–144. [Google Scholar] [CrossRef]
- Allen, T.; Duncan, O.; Foster, L.; Senior, T.; Zampieri, D.; Edeh, V.; Alderson, A. Auxetic foam for snowsport safety devices. In Snow Sports Trauma and Safety, Proceedings of the International Society of Skiing Safety; Springer: Cham, Switzerland, 2016; pp. 145–159. [Google Scholar]
- Duncan, O.; Foster, L.; Senior, T.; Allen, T.; Alderson, A. A Comparison of Novel and Conventional Fabrication Methods for Auxetic Foams for Sports Safety Applications. Procedia Eng. 2016, 147, 384–389. [Google Scholar] [CrossRef]
- Lakes, R.S. Foam Structures with a Negative Poisson’s Ratio. Science 1987, 235, 1038–1041. [Google Scholar] [CrossRef] [PubMed]
- Evans, K.E.; Alderson, A. Auxetic materials: Functional materials and structures from lateral thinking! Adv. Mater. 2000, 12, 617–628. [Google Scholar] [CrossRef]
- Yang, W.; Li, Z.M.; Shi, W.; Xie, B.H.; Yang, M.B. On auxetic materials. J. Mater. Sci. 2004, 39, 3269–3279. [Google Scholar] [CrossRef]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef] [PubMed]
- Critchley, R.; Corni, I.; Wharton, J.A.; Walsh, F.C.; Wood, R.J.K.; Stokes, K.R. A review of the manufacture, mechanical properties and potential applications of auxetic foams. Phys. Status Solidi Basic Res. 2013, 250, 1963–1982. [Google Scholar] [CrossRef]
- Prawoto, Y. Seeing auxetic materials from the mechanics point of view: A structural review on the negative Poisson’s ratio. Comput. Mater. Sci. 2012, 58, 140–153. [Google Scholar] [CrossRef]
- Kolken, H.M.A.; Zadpoor, A.A. Auxetic mechanical metamaterials. RSC Adv. 2017, 7, 5111–5129. [Google Scholar] [CrossRef]
- Lakes, R.S. Negative-Poisson’s-Ratio Materials: Auxetic Solids. Annu. Rev. Mater. Res. 2017, 47, 63–81. [Google Scholar] [CrossRef]
- Ren, X.; Das, R.; Tran, P.; Ngo, T.D.; Xie, Y.M. Auxetic metamaterials and structures: A review. Smart Mater. Struct. 2018, 27, 23001. [Google Scholar] [CrossRef]
- Schmitt, K.U.; Liechti, B.; Michel, F.I.; Stämpfli, R.; Brühwiler, P.A. Are current back protectors suitable to prevent spinal injury in recreational snowboarders? Br. J. Sports Med. 2010, 44, 822–826. [Google Scholar] [CrossRef] [PubMed]
- Mcintosh, A.S. Biomechanical considerations in the design of equipment to prevent sports injury. Proc. Inst. Mech. Eng. Part P 2011, 226, 193–199. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, C. On the successful fabrication of auxetic polyurethane foams: Materials requirement, processing strategy and conversion mechanism. Polymer 2016, 87, 98–107. [Google Scholar] [CrossRef]
- Li, Y.; Zeng, C. Room-Temperature, Near-Instantaneous Fabrication of Auxetic Materials with Constant Poisson’s Ratio over Large Deformation. Adv. Mater. 2016, 28, 2822–2826. [Google Scholar] [CrossRef] [PubMed]
- Sanami, M.; Alderson, A.; Alderson, K.L.; McDonald, S.A.; Mottershead, B.; Withers, P.J. The production and characterization of topologically and mechanically gradient open-cell thermoplastic foams. Smart Mater. Struct. 2014, 23, 55016. [Google Scholar] [CrossRef]
- Duncan, O.; Allen, T.; Foster, L.; Senior, T.; Alderson, A. Fabrication, characterisation and modelling of uniform and gradient auxetic foam sheets. Acta Mater. 2017, 126, 426–437. [Google Scholar] [CrossRef]
- Gatt, R.; Attard, D.; Farrugia, P.S.; Azzopardi, K.M.; Mizzi, L.; Brincat, J.P.; Grima, J.N. A realistic generic model for anti-tetrachiral systems. Phys. Status Solidi Basic Res. 2013, 250, 2012–2019. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Modeling of uniaxial compression in a 3D periodic re-entrant lattice structure. J. Mater. Sci. 2013, 48, 1413–1422. [Google Scholar] [CrossRef]
- Scarpa, F.; Panayiotou, P.; Tomlinson, G. Numerical and experimental uniaxial loading on in-plane auxetic honeycombs Numerical and experimental uniaxial loading on in-plane auxetic honeycombs. J. Strain Anal. Eng. Des. 2000, 35, 383–388. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, Z.D.; Wang, L. A finite element stratification method for a polyurethane jounce bumper. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 983–992. [Google Scholar] [CrossRef]
- Toronjo, A. Articles of Apparel Including Auxetic Materials. U.S. Patent 20140059734 A1, 6 March 2014. [Google Scholar]
- Liu, Y.; Hu, H.; Lam, J.K.C.; Liu, S. Negative Poisson’s Ratio Weft-knitted Fabrics. Text. Res. J. 2010, 80, 856–863. [Google Scholar]
- Chan, N.; Evans, K.E. Indentation resilience of conventional and auxetic foams. J. Cell. Plast. 1998, 34, 231–260. [Google Scholar] [CrossRef]
- Alderson, K.L.; Pickles, A.P.; Neale, P.J.; Evans, K.E. Auxetic polyethylene: The effect of a negative poisson’s ratio on hardness. Acta Metall. Mater. 1994, 42, 2261–2266. [Google Scholar] [CrossRef]
- Alderson, K.L.; Simkins, V.R.; Coenen, V.L.; Davies, P.J.; Alderson, A.; Evans, K.E. How to make auxetic fibre reinforced composites. Phys. Status Solidi Basic Res. 2005, 242, 509–518. [Google Scholar] [CrossRef]
- Ge, C. A comparative study between felted and triaxial compressed polymer foams on cushion performance. J. Cell. Plast. 2013, 49, 521–533. [Google Scholar] [CrossRef]
- Cross, T.M.; Hoffer, K.W.; Jones, D.P.; Kirschner, P.B.; Meschter, J.C. Auxetic Structures and Footwear with Soles Having Auxetic Structures. U.S. Patent 2015/0075034 A1, 19 March 2015. [Google Scholar]
- Martin, P.G. Filtering Face-Piece Respirator Having an Auxetic Mesh in the Mask Body. U.S. Patent 2011/0155137 A1, 30 June 2011. [Google Scholar]
- Wang, Z.; Hu, H. 3D auxetic warp-knitted spacer fabrics. Phys. Status Solidi Basic Res. 2014, 251, 281–288. [Google Scholar] [CrossRef]
- Sanami, M.; Ravirala, N.; Alderson, K.; Alderson, A. Auxetic materials for sports applications. Procedia Eng. 2014, 72, 453–458. [Google Scholar] [CrossRef]
- Alderson, A.; Evans, K.E.; Rasburn, J. Separation Process and Apparatus. WO Patent 1999022838A1, 14 May 1999. [Google Scholar]
- Alderson, A.; Rasburn, J.; Evans, K.E. An Auxetic Filter: A Tuneable Filter Displaying Enhanced Size Selectivity or Defouling Properties. Ind. Eng. Chem. Res. 2000, 39, 654–665. [Google Scholar] [CrossRef]
- Alderson, A.; Rasburn, J.; Evans, K.E. Mass transport properties of auxetic (negative Poisson’s ratio) foams. Phys. Status Solidi 2007, 244, 817–827. [Google Scholar] [CrossRef]
- Hou, Y.; Neville, R.; Scarpa, F.; Remillat, C.; Gu, B.; Ruzzene, M. Graded conventional-auxetic Kirigami sandwich structures: Flatwise compression and edgewise loading. Compos. Part B Eng. 2014, 59, 33–42. [Google Scholar] [CrossRef]
- Hou, Y.; Tai, Y.H.; Lira, C.; Scarpa, F.; Yates, J.R.; Gu, B. The bending and failure of sandwich structures with auxetic gradient cellular cores. Compos. Part A Appl. Sci. Manuf. 2013, 49, 119–131. [Google Scholar] [CrossRef]
- Hrysomallis, C.; Morrison, W.; He, J. Assessing the shock absorption of thigh pads. J. Sci. Med. 1999, 2, 49. [Google Scholar] [CrossRef]
- Payne, T.; Mitchell, S.; Halkon, B.; Bibb, R. A systematic approach to the characterisation of human impact injury scenarios in sport. BMJ Open Sport Exerc. Med. 2016, 2, e000017. [Google Scholar] [CrossRef] [PubMed]
- Schmikli, S.L.; Backx, F.J.G.; Kemler, H.J.; Van Mechelen, W. National survey on sports injuries in the netherlands: Target populations for sports injury prevention programs. Clin. J. Sport Med. 2009, 19, 101–106. [Google Scholar] [CrossRef] [PubMed]
- Statista. Sporting Goods Industry—Statistics & Facts [Internet]. 2018. Available online: https://www.statista.com/topics/961/sporting-goods/ (accessed on 1 May 2018).
- Ankrah, S.; Mills, N.J. Analysis of ankle protection in Association football. Sport Eng. 2004, 7, 41–52. [Google Scholar] [CrossRef]
- Ankrah, S.; Mills, N.J. Performance of football shin guards for direct stud impacts. Sport Eng. 2003, 6, 207–219. [Google Scholar] [CrossRef]
- Hrysomallis, C. Surrogate thigh model for assessing impact force attenuation of protective pads. J. Sci. Med. Sport 2009, 12, 35–41. [Google Scholar] [CrossRef] [PubMed]
- Michel, F.I.; Schmitt, K.U.; Liechti, B.; Stämpfli, R.; Brühwiler, P. Functionality of back protectors in snow sports concerning safety requirements. Procedia Eng. 2010, 2, 2869–2874. [Google Scholar] [CrossRef]
- Adams, C.; James, D.; Senior, T.; Allen, T.; Hamilton, N. Development of a Method for Measuring Quasi-static Stiffness of Snowboard Wrist Protectors. Procedia Eng. 2016, 147, 378–383. [Google Scholar] [CrossRef]
- Mills, N.J. The biomechanics of hip protectors. Proc. Inst. Mech. Eng. Part H 1996, 210, 259–266. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, M. Materials in Sports Equipment; Woodhead Publishing Ltd.: Cambridge, UK, 2007; Volume 2, pp. 138–139. [Google Scholar]
- American Society for Testing and Materials. ASTM F2040-02: Standard Specification for Helmets Used for Recreational Snow Sports; ASTM International: West Conshohocken, PA, USA, 2002; Volume 15, pp. 1–4. [Google Scholar]
- British Standards Institution. BS 6183-3:2000-Protective Equipment for Cricketers; British Standards Institution: London, UK, 2000. [Google Scholar]
- British Standards Institution. Helmets for Alpine Skiers and Snowboarders; BS EN 1077:2007; British Standards Institution: London, UK, 2007; Volume 3. [Google Scholar]
- European Committee for Standardization. Protective Clothing—Shin Guards for Association Football Players—Requirements and Test Methods; BS EN: 13061:2009; European Committee for Standardization: Brussels, Belgium, 2009. [Google Scholar]
- World Fightsport & Martial Arts Council. Official Rulebook. 2010. Available online: www.wfmc-kickboxing.com (accessed on 29 June 2017).
- Lyn, G.; Mills, N.J. Design of foam crash mats for head impact protection. Sport. Eng. 2001, 4, 153–163. [Google Scholar] [CrossRef]
- British Standards Institution. Sports Mats, Part 1: Gymnastic Mats, Safety Requirements; British Standards Institution: London, UK, 2013. [Google Scholar]
- European Committee for Standardization. Protective Clothing—Wrist, Palm, Knee and Elbow Protectors for Users of Roller Sports Equipment—Requirements and Test Methods; EN 14120:2003; European Committee for Standardization: Brussels, Belgium, 2003. [Google Scholar]
- European Committee for Standardization. Motorradfahrer Schutzkleidung Teil 2 Rückenprotektoren; EN 1621-2: 2003; European Committee for Standardization: Brussels, Belgium, 2003. [Google Scholar]
- Dickson, T.J.; Trathen, S.; Terwiel, F.A.; Waddington, G.; Adams, R. Head injury trends and helmet use in skiers and snowboarders in Western Canada, 2008–2009 to 2012–2013: An ecological study. Scand. J. Med. Sci. Sports 2017, 27, 236–244. [Google Scholar] [CrossRef] [PubMed]
- Ekeland, A.; Rødven, A.; Heir, S. Injury Trends in Recreational Skiers and Boarders in the 16-Year Period 1996–2012. In Snow Sports Trauma and Safety; Scher, I.S., Greenwald, R.M., Petrone, N., Eds.; Springer: Cham, Switzerland, 2017; pp. 3–16. [Google Scholar]
- Mez, J.; Daneshvar, D.H.; Kiernan, P.T.; Abdolmohammadi, B.; Alvarez, V.E.; Huber, B.R.; Alosco, M.L.; Solomon, T.M.; Nowinski, C.J.; McHale, L.; et al. Clinicopathological Evaluation of Chronic Traumatic Encephalopathy in Players of American Football. JAMA 2017, 318, 360–370. [Google Scholar] [PubMed]
- King, A.I.; Yang, K.H.; Zhang, L.; Hardy, W.; Viano, D. Is Head Injury Caused by Linear or Angular Acceleration? In Proceedings of the IRCOBI Conference, Lisbon, Portugal, 25–26 September 2003; pp. 1–12. [Google Scholar]
- Rowson, S.; Duma, S.M. Brain injury prediction: Assessing the combined probability of concussion using linear and rotational head acceleration. Ann. Biomed. Eng. 2013, 41, 873–882. [Google Scholar] [CrossRef] [PubMed]
- National Operating Committee on Standards for Athletic Equipment (NOCSAE). Standard Test Method and Equipment Used in Evaluating the Performance Characteristics of Protective Headgear/Equipment; DOC. 001-13m15; NOCSAE: Overland Park, KS, USA, 2011. [Google Scholar]
- Mcintosh, A.S.; Andersen, T.E.; Bahr, R.; Greenwald, R.; Kleiven, S.; Turner, M.; Varese, M.; McCrory, P. Sports helmets now and in the future. Br. J. Sports Med. 2011, 45, 1258–1265. [Google Scholar] [CrossRef] [PubMed]
- Casson, I.R.; Viano, D.C.; Powell, J.W.; Pellman, E.J. Twelve years of National Football League concussion data. Sports Health 2010, 2, 471–483. [Google Scholar] [CrossRef] [PubMed]
- British Standards Institution. Protective Helmets for Vehicle Users; BS 6658:1985; British Standards Institution: London, UK, 1985. [Google Scholar]
- British Standards Institution. Specification for Head Protectors for Cricketers; BS 7928:2013; British Standards Institution: London, UK, 2013. [Google Scholar]
- McIntosh, A.S.; Janda, D. Evaluation of cricket helmet performance and comparison with baseball and ice hockey helmets. Br. J. Sports Med. 2003, 37, 325–330. [Google Scholar] [CrossRef] [PubMed]
- Van Bekkum, J.E.; Williams, J.M.; Morris, P.G. Cycle commuting and perceptions of barriers: Stages of change, gender and occupation. Health Educ. 2011, 111, 476–497. [Google Scholar] [CrossRef]
- Heinen, E.; Maat, K.; Van Wee, B. The role of attitudes toward characteristics of bicycle commuting on the choice to cycle to work over various distances. Transp. Res. Part D 2011, 16, 102–109. [Google Scholar] [CrossRef]
- Willinger, R.; Deck, C.; Halldin, P.; Otte, D. Towards advanced bicycle helmet test methods. In Proceedings of the International Cycling Safety Conference, Göteborg, Sweden, 18–19 November 2014; pp. 1–11. [Google Scholar]
- Zuzarte, P. Protective Helmet. U.S. Patent 6,658,671 B1, 9 December 2003. [Google Scholar]
- Aare, M.; Kleiven, S.; Halldin, P. Injury tolerances for oblique impact helmet testing. Int. J. Crashworthiness 2004, 9, 15–23. [Google Scholar] [CrossRef]
- Kleiven, S. Influence of impact direction on the human head in prediction of subdural hematoma. J. Neurotrauma 2003, 20, 365–379. [Google Scholar] [CrossRef] [PubMed]
- Kleiven, S. Evaluation of head injury criteria using a finite element model validated against experiments on localized brain motion, intracerebral acceleration, and intracranial pressure. Int. J. Crashworthiness 2006, 11, 65–79. [Google Scholar] [CrossRef]
- Kleiven, S.; Hardy, W.N. Correlation of an FE Model of the Human Head with Local Brain Motion—Consequences for Injury Prediction. Stapp Car Crash J. 2002, 46, 123–144. [Google Scholar] [PubMed]
- Dura, J.V.; Garcia, A.C.; Solaz, J. Testing shock absorbing materials: The application of viscoelastic linear model. Sport Eng. 2002, 5, 9–14. [Google Scholar] [CrossRef]
- Hayes, S.G.; Venkatraman, P. Materials and Technology for Sportswear and Performance Apparel; CRC Press: Boca Raton, FL, USA, 2016; p. 314. [Google Scholar]
- Adams, C.; James, D.; Senior, T.; Allen, T.; Hamilton, N. Effect of surrogate design on the measured stiffness of snowboarding wrist protectors. Sport Eng. 2018, 1, 1–9. [Google Scholar]
- Michel, F.I.; Schmitt, K.U.; Greenwald, R.M.; Russell, K.; Simpson, F.I.; Schulz, D.; Langran, M. White Paper: Functionality and efficacy of wrist protectors in snowboarding-towards a harmonized international standard. Sport Eng. 2013, 16, 197–210. [Google Scholar] [CrossRef]
- Payne, T.; Mitchell, S.; Halkon, B.; Bibb, R.; Waters, M. Development of a synthetic human thigh impact surrogate for sports personal protective equipment testing. Proc. Inst. Mech. Eng. Part P 2016, 230, 5–16. [Google Scholar] [CrossRef]
- Petrone, N.; Carraro, G.; Dal Castello, S.; Broggio, L.; Koptyug, A.; Backstrom, M. A novel instrumented human head surrogate for the impact evaluation of helmets. Proceedings 2018, 2, 269. [Google Scholar] [CrossRef]
- Nakamura, K.E.N.I.; Wada, M.; Kuga, S.; Okano, T. Poisson’s Ratio of Cellulose Iβ and Cellulose II. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 1206–1211. [Google Scholar] [CrossRef]
- Caddock, B.D.; Evans, K.E. Microporous materials with negative Poisson’s ratios. I. Microstructure and mechanical properties. J. Phys. D. Appl. Phys. 1989, 22, 1877–1882. [Google Scholar] [CrossRef]
- Dominec, J.; Vase, P.; Svoboda, P.; Plechacek, V.; Laermans, C. Elastic Moduli for Three Superconducting Phases of Bi-Sr-Ca-Cu-O. Mod. Phys. Lett. B 1992, 6, 1049. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafstro, S. Negative Poisson’s ratios as a common feature of Cubic Metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Clarke, J.F.; Duckett, R.A.; Hine, P.J.; Hutchinson, I.J.; Ward, I.M. Negative Poisson’s ratios in angle-ply laminates: Theory and experiment. Composites 1994, 25, 863–868. [Google Scholar] [CrossRef]
- Barthelat, F.; Tang, H.; Zavattieri, P.D.; Li, C.M.; Espinosa, H.D. On the mechanics of mother-of-pearl: A key feature in the material hierarchical structure. J. Mech. Phys. Solids 2007, 55, 306–337. [Google Scholar] [CrossRef]
- Rad, M.S.; Mohsenizadeh, S.; Ahmad, Z. Finite element approach and mathematical formulation of viscoelastic auxetic honeycomb structures for impact mitigation. J. Eng. Sci. Technol. 2017, 12, 471–490. [Google Scholar]
- Gibson, L.J.; Ashby, M.F.; Schajer, G.S.; Robertson, C.I. The mechanics of two-dimensional cellular materials. Proc. R. Soc. Lond. A 1982, 382, 25–42. [Google Scholar] [CrossRef]
- Masters, I.G.; Evans, K.E. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Whitty, J.P.M.; Nazare, F.; Alderson, A. Modelling the effects of density variations on the in-plane Poisson’s ratios and Young’s moduli of periodic conventional and re-entrant honeycombs—Part 1: Rib thickness variations. Cell. Polym. 2002, 21, 69–98. [Google Scholar]
- Nkansah, M.A.; Evans, K.E.; Hutchinson, I.J. Modelling the mechanical properties of an auxetic molecular network. Model. Simul. Mater. Sci. Eng. 1994, 2, 337–352. [Google Scholar] [CrossRef]
- Strek, T.; Maruszewski, B.; Narojczyk, J.W.; Wojciechowski, K.W. Finite element analysis of auxetic plate deformation. J. Non-Cryst. Solids 2008, 354, 4475–4480. [Google Scholar] [CrossRef]
- Ge, Z.; Hu, H.; Liu, Y. A finite element analysis of a 3D auxetic textile structure for composite reinforcement. Smart Mater. Struct. 2013, 22, 84005. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, G.; Wang, Z.; Ruan, D.; Alomarah, A.; Durandet, Y. Large deformation of an auxetic structure in tension: Experiments and finite element analysis. Compos. Struct. 2018, 184, 92–101. [Google Scholar] [CrossRef]
- Almgren, R.F. An isotropic three-dimensional structure with Poisson’s ratio = −1. J. Elast. 1985, 15, 427–430. [Google Scholar]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Prall, D.; Lakes, R.S. Properties of A Chiral Honeycomb with A Poisson’s Ratio of—1. Int. J. Mech. Sci. 1997, 39, 305–314. [Google Scholar] [CrossRef]
- Grima, J.N.; Evans, K.E. Auxetic behavior from rotating squares. J. Mater. Sci. Lett. 2000, 19, 1563–1565. [Google Scholar] [CrossRef]
- Grima, J.N.; Alderson, A.; Evans, K.E. Auxetic behaviour from rotating rigid units. Phys. Status Solidi Basic Res. 2005, 242, 561–575. [Google Scholar] [CrossRef]
- Grima, J.N.; Farrugia, P.S.; Gatt, R.; Zammit, V. Connected Triangles Exhibiting Negative Poisson’s Ratios and Negative Thermal Expansion. J. Phys. Soc. Jpn. 2007, 76, 025001. [Google Scholar] [CrossRef]
- Attard, D.; Grima, J.N. A three-dimensional rotating rigid units network exhibiting negative Poisson’s ratios. Phys. Status Solidi Basic Res. 2012, 249, 1330–1338. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Ravirala, N.; Alderson, A.; Evans, K.E. Negative Poisson’s ratios in cellular foam materials. Mater. Sci. Eng. A 2006, 423, 214–218. [Google Scholar] [CrossRef]
- Smith, C.W.; Grima, J.N.; Evans, K.E. Novel mechanism for generating auxetic behaviour in reticulated foams: Missing rib foam model. Acta Mater. 2000, 48, 4349–4356. [Google Scholar] [CrossRef]
- Bertoldi, K. Harnessing Instabilities to Design Tunable Architected Cellular Materials. Annu. Rev. Mater. Res. 2017, 47, 51–61. [Google Scholar] [CrossRef]
- Alderson, A.; Evans, K.E. Modelling concurrent deformation mechanisms in auxetic microporous polymers. J. Mater. Sci. 1997, 32, 2797–2809. [Google Scholar] [CrossRef]
- Bertoldi, K.; Reis, P.M.; Willshaw, S.; Mullin, T. Negative poisson’s ratio behavior induced by an elastic instability. Adv. Mater. 2010, 22, 361–366. [Google Scholar] [CrossRef] [PubMed]
- Overvelde, J.T.B.; Shan, S.; Bertoldi, K. Compaction through buckling in 2D periodic, soft and porous structures: Effect of pore shape. Adv. Mater. 2012, 24, 2337–2342. [Google Scholar] [CrossRef] [PubMed]
- Overvelde, J.T.B.; Bertoldi, K. Relating pore shape to the non-linear response of periodic elastomeric structures. J. Mech. Phys. Solids 2014, 64, 351–366. [Google Scholar] [CrossRef]
- Babaee, S.; Shim, J.; Weaver, J.C.; Chen, E.R.; Patel, N.; Bertoldi, K. 3D soft metamaterials with negative poisson’s ratio. Adv. Mater. 2013, 25, 5044–5049. [Google Scholar] [CrossRef] [PubMed]
- Javid, F.; Smith-Roberge, E.; Innes, M.C.; Shanian, A.; Weaver, J.C.; Bertoldi, K. Dimpled elastic sheets: A new class of non-porous negative Poisson’s ratio materials. Sci. Rep. 2015, 5, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.J.; Ashby, M.F. Cellular Solids. Structure and Properties; Cambridge University Press: Cambridge, UK, 1997; pp. 67, 176–183, 259–264, 286, 498. [Google Scholar]
- Choi, J.B.; Lakes, R.S. Analysis of elastic modulus of conventional foams and of re-entrant foam materials with a negative Poisson’s ratio. Int. J. Mech. Sci. 1995, 37, 51–59. [Google Scholar] [CrossRef]
- Evans, K.E.; Alderson, A.; Christian, F.R. Auxetic Two-dimensional Polymer Networks. J. Chem. Soc. Faraday Trans. 1995, 91, 2671–2680. [Google Scholar] [CrossRef]
- Alipour, M.M.; Shariyat, M. Analytical zigzag formulation with 3D elasticity corrections for bending and stress analysis of circular/annular composite sandwich plates with auxetic cores. Compos. Struct. 2015, 132, 175–197. [Google Scholar] [CrossRef]
- Wu, W.; Song, X.; Liang, J.; Xia, R.; Qian, G.; Fang, D. Mechanical properties of anti-tetrachiral auxetic stents. Compos. Struct. 2018, 185, 381–392. [Google Scholar] [CrossRef]
- Abramovitch, H.; Burgard, M.; Edery-Azulay, L.; Evans, K.E.; Hoffmeister, M.; Miller, W.; Scarpa, F.; Smith, C.W.; Tee, K.F. Smart tetrachiral and hexachiral honeycomb: Sensing and impact detection. Compos. Sci. Technol. 2010, 70, 1072–1079. [Google Scholar] [CrossRef]
- Grima, J.N.; Attard, D.; Ellul, B.; Gatt, R. An improved analytical model for the elastic constants of auxetic and conventional hexagonal honeycombs. Cell. Polym. 2011, 30, 287–310. [Google Scholar]
- Hughes, T.P.; Marmier, A.; Evans, K.E. Auxetic frameworks inspired by cubic crystals. Int. J. Solids Struct. 2010, 47, 1469–1476. [Google Scholar] [CrossRef]
- Wang, X.T.; Li, X.W.; Ma, L. Interlocking assembled 3D auxetic cellular structures. Mater. Des. 2016, 99, 467–476. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, G.; Ruan, D.; Wang, Z. Tensile behavior of an auxetic structure: Analytical modeling and finite element analysis. Int. J. Mech. Sci. 2018, 136, 143–154. [Google Scholar] [CrossRef]
- Dirrenberger, J.; Forest, S.; Jeulin, D. Elastoplasticity of auxetic materials. Comput. Mater. Sci. 2012, 64, 57–61. [Google Scholar] [CrossRef]
- Najarian, F.; Alipour, R.; Shokri Rad, M.; Nejad, A.F.; Razavykia, A. Multi-objective optimization of converting process of auxetic foam using three different statistical methods. Meas. J. Int. Meas. Confed. 2018, 119, 108–116. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J. Auxetic Foams: Modelling Negative Poisson’s Ratios. Acta Metall. Mater. 1994, 42, 1289–1294. [Google Scholar] [CrossRef]
- Crespo, J.; Montáns, F.J. A continuum approach for the large strain finite element analysis of auxetic materials. Int. J. Mech. Sci. 2018, 135, 441–457. [Google Scholar] [CrossRef]
- Ciambella, J.; Bezazi, A.; Saccomandi, G.; Scarpa, F. Nonlinear elasticity of auxetic open cell foams modeled as continuum solids. J. Appl. Phys. 2015, 117, 184902. [Google Scholar] [CrossRef]
- Lee, J.; Choi, J.B.; Choi, K. Application of homogenization FEM analysis to regular and re-entrant honeycomb structures. J. Mater. Sci. 1996, 31, 4105–4110. [Google Scholar] [CrossRef]
- Huang, F.-Y.; Yan, B.-H.; Yang, D.U. The effects of material constants on the micropolar elastic honeycomb structure with negative Poisson’s ratio using the finite element method. Eng. Comput. 2002, 19, 742–763. [Google Scholar] [CrossRef]
- Yang, D.U.; Lee, S.; Huang, F.Y. Geometric effects on micropolar elastic honeycomb structure with negative Poisson’s ratio using the finite element method. Finite Elem. Anal. Des. 2003, 39, 187–205. [Google Scholar]
- Liu, W.; Wang, N.; Huang, J.; Zhong, H. The effect of irregularity, residual convex units and stresses on the effective mechanical properties of 2D auxetic cellular structure. Mater. Sci. Eng. A 2014, 609, 26–33. [Google Scholar] [CrossRef]
- Yang, C.; Vora, H.D.; Chang, Y.B. Application of Auxetic Polymeric Structures for Body Protection. In Proceedings of the ASME 2016 Conference on Smart Materials, Adaptive Structures & Intelligent Systems, Stowe, VT, USA, 28–30 September 2016; pp. 1–5. [Google Scholar]
- Strek, T.; Jopek, H.; Idczak, E.; Wojciechowski, K.W. Computational modelling of structures with non-intuitive behaviour. Materials 2017, 10, 1386. [Google Scholar] [CrossRef] [PubMed]
- Bezazi, A.; Scarpa, F.; Remillat, C. A novel centresymmetric honeycomb composite structure. Compos. Struct. 2005, 71, 356–364. [Google Scholar] [CrossRef]
- Mousanezhad, D.; Ebrahimi, H.; Haghpanah, B.; Ghosh, R.; Ajdari, A.; Hamouda, A.M.S.; Vaziri, A. Spiderweb honeycombs. Int. J. Solids Struct. 2015, 66, 218–227. [Google Scholar] [CrossRef]
- Grima, J.N.; Cauchi, R.; Gatt, R.; Attard, D. Honeycomb composites with auxetic out-of-plane characteristics. Compos. Struct. 2013, 106, 150–159. [Google Scholar] [CrossRef]
- Silva, T.A.A.; Panzera, T.H.; Brandão, L.C.; Lauro, C.H.; Boba, K.; Scarpa, F. Preliminary investigations on auxetic structures based on recycled rubber. Phys. Status Solidi Basic Res. 2012, 249, 1353–1358. [Google Scholar] [CrossRef]
- Milton, G.W. Composite materials with poisson’s ratios close to—1. J. Mech. Phys. Solids 1992, 40, 1105–1137. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J. Modelling Negative Poisson Ratio Effects in Network-Embedded Composites. Acta Metall. Mater. 1992, 40, 2463–2469. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Maruszewski, B.T.; Nienartowicz, M. Computational analysis of sandwich-structured composites with an auxetic phase. Phys. Status Solidi Basic Res. 2014, 251, 354–366. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Nienartowicz, M. Dynamic response of sandwich panels with auxetic cores. Phys. Status Solidi Basic Res. 2015, 252, 1540–1550. [Google Scholar] [CrossRef]
- Poźniak, A.A.; Wojciechowski, K.W.; Grima, J.N.; Mizzi, L. Planar auxeticity from elliptic inclusions. Compos. Part B Eng. 2016, 94, 379–388. [Google Scholar] [CrossRef]
- Strek, T.; Jopek, H.; Idczak, E. Computational design of two-phase auxetic structures. Phys. Status Solidi Basic Res. 2016, 253, 1387–1394. [Google Scholar] [CrossRef]
- Jopek, H.; Strȩk, T. Thermoauxetic behavior of composite structures. Materials 2018, 11, 294. [Google Scholar] [CrossRef] [PubMed]
- Jopek, H.; Strek, T. Thermal and structural dependence of auxetic properties of composite materials. Phys. Status Solidi Basic Res. 2015, 252, 1551–1558. [Google Scholar] [CrossRef]
- Doyoyo, M.; Wan Hu, J. Plastic failure analysis of an auxetic foam or inverted strut lattice under longitudinal and shear loads. J. Mech. Phys. Solids 2006, 54, 1479–1492. [Google Scholar] [CrossRef]
- Qiao, J.X.; Chen, C.Q. Impact resistance of uniform and functionally graded auxetic double arrowhead honeycombs. Int. J. Impact Eng. 2015, 83, 47–58. [Google Scholar] [CrossRef]
- Qiao, J.; Chen, C.Q. Analyses on the In-Plane Impact Resistance of Auxetic Double Arrowhead Honeycombs. J. Appl. Mech. 2015, 82, 51007. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, Q.; Li, X.; Yang, Z. Elastic properties of two novel auxetic 3D cellular structures. Int. J. Solids Struct. 2017, 124, 46–56. [Google Scholar] [CrossRef]
- Shufrin, I.; Pasternak, E.; Dyskin, A.V. Negative Poisson’s ratio in hollow sphere materials. Int. J. Solids Struct. 2015, 54, 192–214. [Google Scholar] [CrossRef]
- Spadoni, A.; Ruzzene, M. Elasto-static micropolar behavior of a chiral auxetic lattice. J. Mech. Phys. Solids 2012, 60, 156–171. [Google Scholar] [CrossRef]
- Qi, C.; Remennikov, A.; Pei, L.Z.; Yang, S.; Yu, Z.H.; Ngo, T.D. Impact and close-in blast response of auxetic honeycomb-cored sandwich panels: Experimental tests and numerical simulations. Compos. Struct. 2017, 180, 161–178. [Google Scholar] [CrossRef]
- Wang, X.T.; Wang, B.; Li, X.W.; Ma, L. Mechanical properties of 3D re-entrant auxetic cellular structures. Int. J. Mech. Sci. 2017, 131, 396–407. [Google Scholar] [CrossRef]
- Ranga, D.; Strangwood, M. Finite element modelling of the quasi-static and dynamic behaviour of a solid sports ball based on component material properties. Procedia Eng. 2010, 2, 3287–3292. [Google Scholar] [CrossRef]
- Jiang, L.; Hu, H. Low-velocity impact response of multilayer orthogonal structural composite with auxetic effect. Compos. Struct. 2017, 169, 62–68. [Google Scholar] [CrossRef]
- Miller, W.; Smith, C.W.; Scarpa, F.; Evans, K.E. Flatwise buckling optimization of hexachiral and tetrachiral honeycombs. Compos. Sci. Technol. 2010, 70, 1049–1056. [Google Scholar] [CrossRef]
- Novak, N.; Vesenjak, M.; Ren, Z. Computational Simulation and Optimization of Functionally Graded Auxetic Structures Made from Inverted Tetrapods. Phys. Status Solidi Basic Res. 2017, 254, 1–7. [Google Scholar] [CrossRef]
- Safikhani Nasim, M.; Etemadi, E. Three dimensional modeling of warp and woof periodic auxetic cellular structure. Int. J. Mech. Sci. 2018, 136, 475–481. [Google Scholar] [CrossRef]
- Carta, G.; Brun, M.; Baldi, A. Design of a porous material with isotropic negative Poisson’s ratio. Mech. Mater. 2016, 97, 67–75. [Google Scholar] [CrossRef]
- Scarpa, F.; Blain, S.; Lew, T.; Perrott, D.; Ruzzene, M.; Yates, J.R. Elastic buckling of hexagonal chiral cell honeycombs. Compos. Part A Appl. Sci. Manuf. 2007, 38, 280–289. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H. A finite element analysis of an auxetic warp-knitted spacer fabric structure. Text. Res. J. 2015, 85, 404–415. [Google Scholar] [CrossRef]
- Gao, Q.; Wang, L.; Zhou, Z.; Ma, Z.D.; Wang, C.; Wang, Y. Theoretical, numerical and experimental analysis of three-dimensional double-V honeycomb. Mater. Des. 2018, 139, 380–391. [Google Scholar] [CrossRef]
- Farhan, M.; Shahid, M. Negative Poissons ratio behavior of idealized elastomeric auxetic cellular structures for various carbon black nanoparticles loadings. J. Elastomers Plast. 2015, 47, 479–487. [Google Scholar] [CrossRef]
- Javadi, A.A.; Faramarzi, A.; Farmani, R. Design and optimization of microstructure of auxetic materials. Eng. Comput. 2012, 29, 260–276. [Google Scholar] [CrossRef]
- Lee, D.; Shin, S. Evaluation of Optimized Topology Design of Cross-Formed Structures with a Negative Poisson’s Ratio. Iran. J. Sci. Technol. Trans. Civ. Eng. 2016, 40, 109–120. [Google Scholar] [CrossRef]
- Vogiatzis, P.; Chen, S.; Wang, X.; Li, T.; Wang, L. Topology optimization of multi-material negative Poisson’s ratio metamaterials using a reconciled level set method. Comput. Aided Des. 2017, 83, 15–32. [Google Scholar] [CrossRef]
- Ren, X.; Shen, J.; Tran, P.; Ngo, T.D.; Xie, Y.M. Design and characterisation of a tuneable 3D buckling-induced auxetic metamaterial. Mater. Des. 2018, 139, 336–342. [Google Scholar] [CrossRef]
- Li, H.; Luo, Z.; Gao, L.; Walker, P. Topology optimization for functionally graded cellular composites with metamaterials by level sets. Comput. Methods Appl. Mech. Eng. 2017, 328, 340–364. [Google Scholar] [CrossRef]
- Qin, H.; Yang, D.; Ren, C. Modelling theory of functional element design for metamaterials with arbitrary negative Poisson’s ratio. Comput. Mater. Sci. 2018, 150, 121–133. [Google Scholar] [CrossRef]
- Yang, S.; Qi, C.; Guo, D.M.; Wang, D. Energy absorption of an re-entrant honeycombs with negative Poisson’s ratio. Appl. Mech. Mater. 2012, 148, 992–995. [Google Scholar] [CrossRef]
- Hou, X.; Deng, Z.; Zhang, K. Dynamic Crushing Strength Analysis of Auxetic Honeycombs. Acta Mech. Solida Sin. 2016, 29, 490–501. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, L.; Ma, Z.D.; Wang, T. A negative Poisson’s ratio suspension jounce bumper. Mater. Des. 2016, 103, 90–99. [Google Scholar] [CrossRef]
- Imbalzano, G.; Tran, P.; Ngo, T.D.; Lee, P.V.S. Three-dimensional modelling of auxetic sandwich panels for localised impact resistance. J. Sandw. Struct. Mater. 2017, 19, 291–316. [Google Scholar] [CrossRef]
- Imbalzano, G.; Tran, P.; Ngo, T.D.; Lee, P.V.S. A numerical study of auxetic composite panels under blast loadings. Compos. Struct. 2016, 135, 339–352. [Google Scholar] [CrossRef]
- Critchley, R.; Corni, I.; Stokes, K.; Walsh, F.C.; Wharton, J.; Wood, R.J.K. High Strain Materials for Body Armour Inspired from Nature High Strain Materials for Body Armour Inspired from Nature. 2014. Available online: https://www.researchgate.net/publication/267261907 (accessed on 4 June 2018).
- Bryson, A.; Smith, L. Impact response of sports materials. Procedia Eng. 2010, 2, 2961–2966. [Google Scholar] [CrossRef]
- Mills, N.J.; Gilchrist, A. Oblique impact testing of bicycle helmets. Int. J. Impact Eng. 2008, 35, 1075–1086. [Google Scholar] [CrossRef]
- Scarpa, F.; Giacomin, J.; Zhang, Y.; Pastorino, P. Mechanical performance of auxetic polyurethane foam for antivibration glove applications. Cell. Polym. 2005, 24, 253–268. [Google Scholar]
- Choi, J.B.; Lakes, R.S. Nonlinear Analysis of the Poisson’s Ratio of Negative Poisson’s Ratio Foams. J. Compos. Mater. 1994, 29, 113–128. [Google Scholar] [CrossRef]
- Chan, N.; Evans, K.E. Fabrication methods for auxetic foams. J. Mater. Sci. 1997, 32, 5945–5953. [Google Scholar] [CrossRef]
- Loureiro, M.A.; Lakes, R.S. Scale-up of transformation of negative Poisson’s ratio foam: Slabs. Cell. Polym. 1997, 16, 349–363. [Google Scholar]
- Bianchi, M.; Scarpa, F.; Banse, M.; Smith, C.W. Novel generation of auxetic open cell foams for curved and arbitrary shapes. Acta Mater. 2011, 59, 686–691. [Google Scholar] [CrossRef]
- Allen, T.; Hewage, T.; Newton-Mann, C.; Wang, W.; Duncan, O.; Alderson, A. Fabrication of Auxetic Foam Sheets for Sports Applications. Phys. Status Solidi Basic Res. 2017, 254, 1700596. [Google Scholar] [CrossRef]
- Choi, J.B.; Lakes, R.S. Nonlinear properties of polymer cellular materials with a negative Poisson’s ratio. Mater. Sci. 1992, 27, 4678–4684. [Google Scholar] [CrossRef]
- Alderson, A.; Davies, P.J.; Alderson, K.; Smart, G.M. The Effects of Processing on the Topology and Mechanical Properties of Negative Poisson’s Ratio Foams. In Proceedings of the 2005 ASME International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005; pp. 1–8. [Google Scholar]
- Gatt, R.; Attard, D.; Manicaro, E.; Chetcuti, E.; Grima, J.N. On the effect of heat and solvent exposure on the microstructure properties of auxetic foams: A preliminary study. Phys. Status Solidi Basic Res. 2011, 248, 39–44. [Google Scholar] [CrossRef]
- Bianchi, M.; Frontoni, S.; Scarpa, F.; Smith, C.W. Density change during the manufacturing process of PU-PE open cell auxetic foams. Phys. Status Solidi Basic Res. 2011, 248, 30–38. [Google Scholar] [CrossRef]
- Scarpa, F.; Pastorino, P.; Garelli, A.; Patsias, S.; Ruzzene, M. Auxetic compliant flexible PU foams: Static and dynamic properties. Phys. Status Solidi Basic Res. 2005, 242, 681–694. [Google Scholar] [CrossRef]
- Duncan, O.; Allen, T.; Foster, L.; Gatt, R.; Grima, J.N.; Alderson, A. Controlling Density and Modulus in Auxetic Foam Fabrications—Implications for Impact and Indentation Testing. Proceedings 2018, 2, 250. [Google Scholar] [CrossRef]
- Boba, K.; Bianchi, M.; McCombe, G.; Gatt, R.; Griffin, A.C.; Richardson, R.M.; Scarpa, F.; Hamerton, I.; Grima, J. Blocked shape memory effect in negative Poisson’s ratio polymer metamaterials. ACS Appl. Mater. Interfaces 2016, 8, 20319–20328. [Google Scholar] [CrossRef] [PubMed]
- Grima, J.N.; Attard, D.; Gatt, R.; Cassar, R.N. A novel process for the manufacture of auxetic foams and for their re-conversion to conventional form. Adv. Eng. Mater. 2009, 11, 533–535. [Google Scholar] [CrossRef]
- Lowe, A.; Lakes, R.S. Negative Poisson’s ratio foam as seat cushion material. Cell. Polym. 2000, 19, 157–167. [Google Scholar]
- Chan, N.; Evans, K.E. Microscopic examination of the microstructure and deformation of conventional and auxetic foams. J. Mater. Sci. 1997, 2, 5725–5736. [Google Scholar] [CrossRef]
- Martz, E.O.; Lee, T.; Lakes, R.S.; Goel, V.K.; Park, J.B. Re-entrant transformation methods in closed cell foams. Cell. Polym. 1996, 15, 229–249. [Google Scholar]
- Quadrini, F.; Bellisario, D.; Ciampoli, L.; Costanza, G.; Santo, L. Auxetic epoxy foams produced by solid state foaming. J. Cell. Plast. 2015, 52, 441–454. [Google Scholar] [CrossRef]
- Xu, T.; Li, G. A shape memory polymer based syntactic foam with negative Poisson’ s ratio. Mater. Sci. Eng. A 2011, 528, 6804–6811. [Google Scholar] [CrossRef]
- Wang, K.; Chang, Y.H.; Chen, Y.; Zhang, C.; Wang, B. Designable dual-material auxetic metamaterials using three-dimensional printing. Mater. Des. 2015, 67, 159–164. [Google Scholar] [CrossRef]
- McDonald, S.A.; Ravirala, N.; Withers, P.J.; Alderson, A. In situ three-dimensional X-ray microtomography of an auxetic foam under tension. Scr. Mater. 2009, 60, 232–235. [Google Scholar] [CrossRef]
- Lisiecki, J.; Klysz, S.; Blazejewicz, T.; Gmurczyk, G.; Reymer, P. Tomographic examination of auxetic polyurethane foam structures. Phys. Status Solidi Basic Res. 2013, 251, 314–320. [Google Scholar] [CrossRef]
- American Society for Testing and Materials. ASTM-D412-15a: Standard Test Methods for Vulcanized Rubber and Thermoplastic Elastomers—Tension; ASTM International: West Conshohocken, PA, USA, 2015; Volume 9, pp. 1–14. [Google Scholar]
- Miller, W.; Hook, P.B.; Smith, C.W.; Wang, X.; Evans, K.E. The manufacture and characterisation of a novel, low modulus, negative Poisson’s ratio composite. Compos. Sci. Technol. 2009, 69, 651–655. [Google Scholar] [CrossRef]
- Miller, W.; Ren, Z.; Smith, C.W.; Evans, K.E. A negative Poisson’s ratio carbon fibre composite using a negative Poisson’s ratio yarn reinforcement. Compos. Sci. Technol. 2012, 72, 761–766. [Google Scholar] [CrossRef]
- Bhattacharya, S.; Zhang, G.H.; Ghita, O.; Evans, K.E. The variation in Poisson’s ratio caused by interactions between core and wrap in helical composite auxetic yarns. Compos. Sci. Technol. 2014, 102, 87–93. [Google Scholar] [CrossRef]
- Zhang, G.; Ghita, O.R.; Evans, K.E. Dynamic thermo-mechanical and impact properties of helical auxetic yarns. Compos. Part B Eng. 2016, 99, 494–505. [Google Scholar] [CrossRef]
- Zhang, G.H.; Ghita, O.; Evans, K.E. The fabrication and mechanical properties of a novel 3-component auxetic structure for composites. Compos. Sci. Technol. 2015, 117, 257–267. [Google Scholar] [CrossRef]
- Zhang, G.; Ghita, O.R.; Lin, C.; Evans, K.E. Large-scale manufacturing of helical auxetic yarns using a novel semi-coextrusion process. Text. Res. J. 2017, 1–12. [Google Scholar] [CrossRef]
- Ge, Z.; Hu, H.; Liu, S. A novel plied yarn structure with negative Poisson’s ratio. J. Text. Inst. 2016, 107, 578–588. [Google Scholar] [CrossRef]
- Lim, T.C. Semi-auxetic yarns. Phys. Status Solidi Basic Res. 2014, 251, 273–280. [Google Scholar] [CrossRef]
- Liu, S.; Pan, X.; Zheng, D.; Du, Z.; Liu, G.; Yang, S. Study on the structure formation and heat treatment of helical auxetic complex yarn. Text. Res. J. 2018. [Google Scholar] [CrossRef]
- Sloan, M.R.; Wright, J.R.; Evans, K.E. The helical auxetic yarn—A novel structure for composites and textiles; Geometry, manufacture and mechanical properties. Mech. Mater. 2011, 43, 476–486. [Google Scholar] [CrossRef]
- McAfee, J.; Faisal, N.H. Parametric sensitivity analysis to maximise auxetic effect of polymeric fibre based helical yarn. Compos. Struct. 2017, 162, 1–12. [Google Scholar] [CrossRef]
- Wright, J.R.; Burns, M.K.; James, E.; Sloan, M.R.; Evans, K.E. On the design and characterisation of low-stiffness auxetic yarns and fabrics. Text. Res. J. 2012, 82, 645–654. [Google Scholar] [CrossRef]
- Alderson, K.L.; Alderson, A.; Smart, G.; Simkins, V.R.; Davies, P.J. Auxetic polypropylene fibres: Part 1—Manufacture and characterisation. Plast Rubber Compos. 2002, 31, 344–349. [Google Scholar] [CrossRef]
- Ravirala, N.; Alderson, A.; Alderson, K.L.; Davies, P.J. Auxetic polypropylene films. Polym. Eng. Sci. 2005, 45, 517–528. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K. Expanding materials and applications: Exploiting auxetic textiles. Tech. Text. Int. 2005, 14, 29–34. [Google Scholar]
- Simkins, V.R.; Alderson, A.; Davies, P.J.; Alderson, K.L. Single fibre pullout tests on auxetic polymeric fibres. J. Mater. Sci. 2005, 40, 4355–4364. [Google Scholar] [CrossRef]
- Ng, W.S.; Hu, H. Woven fabrics made of auxetic plied yarns. Polymers 2018, 10, 226. [Google Scholar]
- Alderson, A. Smart Solutions from Auxetic Materials; Med-Tech Innovation: Chester, UK, 2011. [Google Scholar]
- Verma, P.; Shofner, M.L.; Lin, A.; Wagner, K.B.; Griffin, A.C. Induction of auxetic response in needle-punched nonwovens: Effects of temperature, pressure, and time. Phys. Status Solidi 2016, 253, 1270–1278. [Google Scholar] [CrossRef]
- Verma, P.; Shofner, M.L.; Lin, A.; Wagner, K.B.; Griffin, A.C. Inducing out-of-plane auxetic behavior in needle-punched nonwovens. Phys. Status Solidi Basic Res. 2015, 252, 1455–1464. [Google Scholar] [CrossRef]
- Zulifqar, A.; Hua, T.; Hu, H. Development of UNI-stretch woven fabrics with zero and negative Poisson’s ratio. Text. Res. J. 2017. [Google Scholar] [CrossRef]
- Alderson, K.; Alderson, A.; Anand, S.; Simkins, V.; Nazare, S.; Ravirala, N. Auxetic warp knit textile structures. Phys. Status Solidi Basic Res. 2012, 249, 1322–1329. [Google Scholar] [CrossRef]
- Ma, P.; Chang, Y.; Jiang, G. Design and fabrication of auxetic warp-knitted structures with a rotational hexagonal loop. Text. Res. J. 2016, 86, 2151–2157. [Google Scholar] [CrossRef]
- Ugbolue, S.C.; Kim, Y.K.; Warner, S.B.; Fan, Q.; Yang, C.L.; Kyzymchuk, O.; Feng, Y.; Lord, J. The formation and performance of auxetic textiles. Part II: Geometry and structural properties. J. Text. Inst. 2011, 102, 424–433. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H.; Xiao, X. Deformation behaviors of three-dimensional auxetic spacer fabrics. Text. Res. J. 2014, 84, 1361–1372. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H. Tensile and forming properties of auxetic warp-knitted spacer fabrics. Text. Res. J. 2017, 87, 1925–1937. [Google Scholar] [CrossRef]
- Chang, Y.; Ma, P. Fabrication and property of auxetic warp-knitted spacer structures with mesh. Text. Res. J. 2017. [Google Scholar] [CrossRef]
- Chang, Y.; Ma, P.; Jiang, G. Energy absorption property of warp-knitted spacer fabrics with negative Possion’s ratio under low velocity impact. Compos. Struct. 2017, 182, 471–477. [Google Scholar] [CrossRef]
- Chang, Y.; Ma, P. Energy absorption and Poisson’s ratio of warp-knitted spacer fabrics under uniaxial tension. Text. Res. J. 2018. [Google Scholar] [CrossRef]
- Hu, H.; Wang, Z.; Liu, S. Development of auxetic fabrics using flat knitting technology. Text. Res. J. 2011, 81, 1493–1502. [Google Scholar]
- Steffens, F.; Oliveira, F.R.; Mota, C.; Fangueiro, R. High-performance composite with negative Poisson’s ratio. J. Mater. Res. 2017, 32, 3477–3484. [Google Scholar] [CrossRef]
- Goto, K.; Arai, M.; Matsuda, T.; Kubo, G. Elasto-viscoplastic analysis for negative through-the-thickness Poisson’s ratio of woven laminate composites based on homogenization theory. Int. J. Mech. Sci. 2017. [Google Scholar] [CrossRef]
- Ge, Z.; Hu, H.; Liu, Y. Numerical analysis of deformation behavior of a 3D textile structure with negative Poisson’s ratio under compression. Text. Res. J. 2015, 85, 548–557. [Google Scholar] [CrossRef]
- Ge, Z.; Hu, H. A theoretical analysis of deformation behavior of an innovative 3D auxetic textile structure. J. Text. Inst. 2015, 106, 101–109. [Google Scholar] [CrossRef]
- Nava-Gómez, G.G.; Camacho-Montes, H.; Sabina, F.J.; Rodríguez-Ramos, R.; Fuentes, L.; Guinovart-Díaz, R. Elastic properties of an orthotropic binary fiber-reinforced composite with auxetic and conventional constituents. Mech. Mater. 2012, 48, 1–25. [Google Scholar] [CrossRef]
- Liaqat, M.; Samad, H.A.; Hamdani, S.T.A.; Nawab, Y. The development of novel auxetic woven structure for impact applications. J. Text. Inst. 2017, 108, 1264–1270. [Google Scholar] [CrossRef]
- American Society for Testing and Materials. D6110-17: Standard Test Method for Determining the Charpy Impact Resistance of Notched Specimens of Plastics; ASTM International: West Conshohocken, PA, USA, 2010; pp. 1–17. [Google Scholar]
- Zhou, L.; Jiang, L.; Hu, H. Auxetic composites made of 3D textile structure and polyurethane foam. Phys. Status Solidi Basic Res. 2016, 257, 1331–1341. [Google Scholar] [CrossRef]
- Jiang, L.; Gu, B.; Hu, H. Auxetic composite made with multilayer orthogonal structural reinforcement. Compos. Struct. 2016, 135, 23–29. [Google Scholar] [CrossRef]
- Wang, Z.; Hu, H. Auxetic materials and their potential applications in textiles. Text. Res. J. 2014, 84, 1600–1611. [Google Scholar] [CrossRef]
- Ma, P.; Chang, Y.; Boakye, A.; Jiang, G. Review on the knitted structures with auxetic effect. J. Text. Inst. 2017, 108, 947–961. [Google Scholar] [CrossRef]
- Yuan, S.; Shen, F.; Bai, J.; Chua, C.K.; Wei, J.; Zhou, K. 3D soft auxetic lattice structures fabricated by selective laser sintering: TPU powder evaluation and process optimization. Mater. Des. 2017, 120, 317–327. [Google Scholar] [CrossRef]
- Lantada, A.D.; De Blas Romero, A.; Schwentenwein, M.; Jellinek, C.; Homa, J. Lithography-based ceramic manufacture (LCM) of auxetic structures: Present capabilities and challenges. Smart Mater. Struct. 2016, 25, 054015. [Google Scholar] [CrossRef]
- Critchley, B.R.; Corni, I.; Wharton, J.A.; Walsh, F.C.; Wood, R.J.K.; Stokes, K.R. The Preparation of Auxetic Foams by Three-Dimensional Printing and Their Characteristics. Adv. Eng. Mater. 2013, 15, 980–985. [Google Scholar] [CrossRef]
- Hengsbach, S.; Lantada, A.D. Direct laser writing of auxetic structures: Present capabilities and challenges. Smart Mater. Struct. 2014, 23, 085033. [Google Scholar] [CrossRef]
- Yang, L.; Harrysson, O.; West, H.; Cormier, D. Mechanical properties of 3D re-entrant honeycomb auxetic structures realized via additive manufacturing. Int. J. Solids Struct. 2015, 69, 475–490. [Google Scholar] [CrossRef]
- Li, T.; Wang, L. Bending behavior of sandwich composite structures with tunable 3D-printed core materials. Compos. Struct. 2017, 175, 46–57. [Google Scholar] [CrossRef]
- Li, D.; Ma, J.; Dong, L.; Lakes, R.S. Stiff square structure with a negative Poisson’s ratio. Mater. Lett. 2017, 188, 149–151. [Google Scholar] [CrossRef]
- Ma, Q.; Peel, L.D. Development of spiral auxetic structures. Compos. Struct. 2018, 192, 310–316. [Google Scholar] [CrossRef]
- Boldrin, L.; Hummel, S.; Scarpa, F.; Di Maio, D.; Lira, C.; Ruzzene, M.; Remillat, C.; Lim, T.; Rajasekaran, R.; Patsias, S. Dynamic behaviour of auxetic gradient composite hexagonal honeycombs. Compos. Struct. 2016, 149, 114–124. [Google Scholar] [CrossRef]
- Huang, H.H.; Wong, B.L.; Chou, Y.C. Design and properties of 3D-printed chiral auxetic metamaterials by reconfigurable connections. Phys. Status Solidi Basic Res. 2016, 253, 1557–1564. [Google Scholar] [CrossRef]
- Saxena, K.K.; Calius, E.P.; Das, R. Tailoring Cellular Auxetics For Wearable Applications with Multimaterial 3D Printing. In Proceedings of the ASME 2016 International Mechanical Engineering Congress & Exposition, Phoenix, AZ, USA, 11–17 November 2016. [Google Scholar]
- Saxena, K.K.; Das, R.; Calius, E.P. 3D printable multimaterial cellular auxetics with tunable stiffness. arXiv, 2017; arXiv:1707.04486. [Google Scholar]
- Jiang, Y.; Li, Y. Novel 3D-Printed Hybrid Auxetic Mechanical Metamaterial with Chirality-Induced Sequential Cell Opening Mechanisms. Adv. Eng. Mater. 2018, 20, 1–9. [Google Scholar] [CrossRef]
- Jiang, Y.; Li, Y. 3D Printed Auxetic Mechanical Metamaterial with Chiral Cells and Re-entrant Cores. Sci. Rep. 2018, 8, 2397. [Google Scholar] [CrossRef] [PubMed]
- Brighenti, R. Smart behaviour of layered plates through the use of auxetic materials. Thin-Walled Struct. 2014, 84, 432–442. [Google Scholar] [CrossRef]
- Ingrole, A.; Hao, A.; Liang, R. Design and modeling of auxetic and hybrid honeycomb structures for in-plane property enhancement. Mater. Des. 2017, 117, 72–83. [Google Scholar] [CrossRef]
- Li, X.; Lu, Z.; Yang, Z.; Yang, C. Directions dependence of the elastic properties of a 3D augmented re-entrant cellular structure. Mater. Des. 2017, 134, 151–162. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, D. Mechanical properties of auxetic cellular material consisting of re-entrant hexagonal honeycombs. Materials 2016, 9, 900. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Dong, L.; Lakes, R.S. A unit cell structure with tunable Poisson’s ratio from positive to negative. Mater. Lett. 2016, 164, 456–459. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Mousanezhad, D.; Nayeb-Hashemi, H.; Norato, J.; Vaziri, A. 3D cellular metamaterials with planar anti-chiral topology. Mater. Des. 2018, 145, 226–231. [Google Scholar] [CrossRef]
- Fu, M.; Liu, F.; Hu, L. A novel category of 3D chiral material with negative Poisson’s ratio. Compos. Sci. Technol. 2018, 160, 111–118. [Google Scholar] [CrossRef]
- Hanifpour, M.; Petersen, C.F.; Alava, M.J.; Zapperi, S. Mechanics of disordered auxetic metamaterials. arXiv, 2017; arXiv:1704.00943. [Google Scholar]
- Yang, C.; Vora, H.D.; Chang, Y.B. Evaluation of Auxetic Polymeric Structures for Use in Protective Pads. In Proceedings of the ASME 2016 International Mechanical Engineering Congress & Exposition, Phoenix, AZ, USA, 11–17 November 2016. [Google Scholar]
- Yang, C.; Vora, H.; Chang, Y. Behavior of Auxetic Structures Under Compression and Impact Forces. Smart Mater. Struct. 2017, 27, 025012. [Google Scholar] [CrossRef]
- Bates, S.R.G.; Farrow, I.R.; Trask, R.S. 3D printed polyurethane honeycombs for repeated tailored energy absorption. Mater. Des. 2016, 112, 172–183. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; McDonald, S.A.; Mottershead, B.; Nazare, S.; Withers, P.J.; Yao, Y. Piezomorphic materials. Macromol. Mater. Eng. 2013, 298, 318–327. [Google Scholar] [CrossRef]
- Zorzetto, L.; Ruffoni, D. Re-entrant inclusions in cellular solids: From defects to reinforcements. Compos. Struct. 2017, 176, 195–204. [Google Scholar] [CrossRef]
- Lakes, R.S.; Elms, K. Indentability of conventional and negative Poisson’s ratio foams. J. Compos. Mater. 1993, 27, 1193–1202. [Google Scholar] [CrossRef]
- Scarpa, F.; Yates, J.R.; Ciffo, L.G.; Patsias, S. Dynamic crushing of auxetic open-cell polyurethane foam. Proc. Inst. Mech. Eng. Part C 2002, 216, 1153–1156. [Google Scholar] [CrossRef]
- Bocquet, C. Bra with Variable-Volume Straps. WO Patent 2006045935A, 4 May 2006. [Google Scholar]
- Timishenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Budynas. R.G. Advanced Strength and Applied Stress Analysis; WCB/McGraw-Hill: New York, NY, USA, 1999; pp. 21, 80. [Google Scholar]
- Roark, R.J.; Young, W.C. Formulas for Stress and Strain; McGraw-Hill: New York, NY, USA, 2012; pp. 20–22, 48–50. [Google Scholar]
- Lempriere, B.M. Poisson’s ratio in orthotropic materials. AIAA J. 1968, 6, 2226–2227. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Remarks on “Poisson ratio beyond the limits of the elasticity theory”. J. Phys. Soc. Jpn. 2003, 72, 1819–1820. [Google Scholar] [CrossRef]
- Lakes, R.S. Design Considerations for Materials with Negative Poisson’s Ratios. J. Mech. Des. 1993, 115, 696. [Google Scholar] [CrossRef]
- Alderson, K.L.; Fitzgerald, A.; Evans, K.E. The strain dependent indentation resilience of auxetic microporous polyethylene. J. Mater. Sci. 2000, 35, 4039–4047. [Google Scholar] [CrossRef]
- Lin, D.C.; Shreiber, D.I.; Dimitriadis, E.K.; Horkay, F. Spherical indentation of soft matter beyond the Hertzian regime: Numerical and experimental validation of hyperelastic models. Biomech. Model. Mechanobiol. 2009, 8, 345–358. [Google Scholar] [CrossRef] [PubMed]
- Argatov, I.I.; Guinovart-Díaz, R.; Sabina, F.J. On local indentation and impact compliance of isotropic auxetic materials from the continuum mechanics viewpoint. Int. J. Eng. Sci. 2012, 54, 42–57. [Google Scholar] [CrossRef]
- Wang, Y.C.; Lakes, R. Analytical parametric analysis of the contact problem of human buttocks and negative Poisson’s ratio foam cushions. Int. J. Solids Struct. 2002, 39, 4825–4838. [Google Scholar] [CrossRef]
- Waters, N.E. The indentation of thin rubberer sheets by cylindrical indetors. Br. J. Appl. Phys. 1965, 16, 1387–1392. [Google Scholar] [CrossRef]
- Photiou, D.; Sarris, E.; Constantinides, G. On the conical indentation response of elastic auxetic materials: Effects of Poisson’s ratio, contact friction and cone angle. Int. J. Solids Struct. 2017, 1, 33–42. [Google Scholar] [CrossRef]
- Photiou, D.; Sarris, E.; Constantinides, G. Erratum to “On the conical indentation response of elastic auxetic materials: Effects of Poisson’s ratio, contact friction and cone angle” [Int. J. Solids Struct. 81 (2016) 33–42]. Int. J. Solids Struct. 2017, 110–111, 404. [Google Scholar] [CrossRef]
- Guo, X.; Jin, F.; Gao, H. Mechanics of non-slipping adhesive contact on a power-law graded elastic half-space. Int. J. Solids Struct. 2011, 48, 2565–2575. [Google Scholar] [CrossRef]
- Li, S.; Al-Badani, K.; Gu, Y.; Lake, M.; Li, L.; Rothwell, G.; Ren, J. The Effects of Poisson’s Ratio on the Indentation Behavior of Materials with Embedded System in an Elastic Matrix. Phys. Status Solidi Basic Res. 2017, 254, 1–8. [Google Scholar] [CrossRef]
- Aw, J.; Zhao, H.; Norbury, A.; Li, L.; Rothwell, G.; Ren, J. Effects of Poisson’s ratio on the deformation of thin membrane structures under indentation. Phys. Status Solidi Basic Res. 2015, 252, 1526–1532. [Google Scholar] [CrossRef]
- Morris, D.J.; Cook, R.F. Indentation fracture of low-dielectric constant films: Part II. Indentation fracture mechanics model. J. Mater. Res. 2008, 23, 2429–2442. [Google Scholar] [CrossRef]
- Argatov, I.I.; Sabina, F.J. Small-scale indentation of an elastic coated half-space: The effect of compliant substrate. Int. J. Eng. Sci. 2016, 104, 87–96. [Google Scholar] [CrossRef]
- Chan, N.; Evans, K.E. The mechanical properties of conventional and auxetic foams. Part I: Compression and tension. J. Cell. Plast. 1999, 35, 130–165. [Google Scholar] [CrossRef]
- Adam, M.M.; Berger, J.R.; Martin, P.A. Singularities in auxetic elastic bimaterials. Mech. Res. Commun. 2013, 47, 102–105. [Google Scholar] [CrossRef]
- Kwon, K.; Phan, A.V. Symmetric-Galerkin boundary element analysis of the dynamic T-stress for the interaction of a crack with an auxetic inclusion. Mech. Res. Commun. 2015, 69, 91–96. [Google Scholar] [CrossRef]
- Song, F.; Zhou, J.; Xu, X.; Xu, Y.; Bai, Y. Effect of a negative poisson ratio in the tension of ceramics. Phys. Rev. Lett. 2008, 100, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Mohsenizadeh, S.; Alipour, R.; Shokri Rad, M.; Farokhi Nejad, A.; Ahmad, Z. Crashworthiness assessment of auxetic foam-filled tube under quasi-static axial loading. Mater. Des. 2015, 88, 258–268. [Google Scholar] [CrossRef]
- Bezazi, A.; Scarpa, F. Mechanical behaviour of conventional and negative Poisson’s ratio thermoplastic polyurethane foams under compressive cyclic loading. Int. J. Fatigue. 2007, 29, 922–930. [Google Scholar] [CrossRef]
- Pastorino, P.; Scarpa, F.; Patsias, S.; Yates, J.R.; Haake, S.J.; Ruzzene, M. Strain rate dependence of stiffness and Poisson’s ratio of auxetic open cell PU foams. Phys. Status Solidi Basic Res. 2007, 244, 955–965. [Google Scholar] [CrossRef]
- Nakonieczna, P.; Wierzbicki, Ł.; Śladowska, B.; Leonowicz, M.; Lisiecki, J. Composites with Impact Absorption Ability Based on Shear Thickening Fluids and Auxetic Foams. Compos. Theory Pract. 2017, 2, 67–72. [Google Scholar]
- Qi, C.; Yang, S.; Wang, D.; Yang, L.J. Ballistic resistance of honeycomb sandwich panels under in-plane high-velocity impact. Sci. World J. 2013, 2013, 892781. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Wang, N.; Luo, T.; Lin, Z. In-plane dynamic crushing of re-entrant auxetic cellular structure. Mater. Des. 2016, 100, 84–91. [Google Scholar] [CrossRef]
- Yang, S.; Chalivendra, V.B.; Kim, Y.K. Impact behaviour of auxetic Kevlar®/epoxy composites. IOP Conf. Ser. Mater. Sci. Eng. 2017, 254, 042031. [Google Scholar] [CrossRef]
- Yang, S.; Chalivendra, V.B.; Kim, Y.K. Fracture and impact characterization of novel auxetic Kevlar®/Epoxy laminated composites. Compos. Struct. 2017, 168, 120–129. [Google Scholar] [CrossRef]
- Alderson, K.L.; Coenen, V.L. The low velocity impact response of auxetic carbon fibre laminates. Phys. Status Solidi 2008, 245, 489–496. [Google Scholar] [CrossRef]
- Coenen, V.L.; Alderson, K.L. Mechanisms of failure in the static indentation resistance of auxetic carbon fibre laminates. Phys. Status Solidi Basic Res. 2011, 248, 66–72. [Google Scholar] [CrossRef]
- International Organization for Standardization. Mechanical Vibration and Shock—Hand-Arm Vibration—Method for Measuring the Vibration Transmissibility of Resilient Materials When Loaded by the Hand-Arm System; ISO 13753:1999; ISO: Geneva, Switzerland, 1999. [Google Scholar]
- Chen, C.P.; Lakes, R.S. Dynamic wave dispersion and loss properties of conventional and negative Poisson’s ratio polymeric cellular materials. Cell. Polym. 1989, 8, 343–369. [Google Scholar]
- Lisiecki, J.; Nowakowski, D.; Reymer, P. Fatigue Properties of Polyurethane Foams, With Special Emphasis on Auxetic Foams, Used for Helicopter Pilot Seat Cushion Inserts. Fatigue Aircr. Struct. 2014, 1, 72–78. [Google Scholar] [CrossRef]
- Evans, K.E. The design of doubly curved sandwich panels with honeycomb cores. Compos. Struct. 1991, 17, 95–111. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Chirima, G.; Ravirala, N.; Zied, K.M. The in-plane linear elastic constants and out-of-plane bending of 3-coordinated ligament and cylinder-ligament honeycombs. Compos. Sci. Technol. 2010, 70, 1034–1041. [Google Scholar] [CrossRef]
- Mehta, R. A nose for auxetics. Mater. World 2010, 18, 9–12. [Google Scholar]
- Bianchi, M.; Scarpa, F.; Smith, C.W.; Whittell, G.R. Physical and thermal effects on the shape memory behaviour of auxetic open cell foams. J. Mater. Sci. 2010, 45, 341–347. [Google Scholar] [CrossRef]
- Allen, T.; Martinello, N.; Zampieri, D.; Hewage, T.; Senior, T.; Foster, L.; Alderson, A. Auxetic foams for sport safety applications. Procedia Eng. 2015, 112, 104–109. [Google Scholar] [CrossRef]
- Lim, T.C.; Alderson, A.; Alderson, K.L. Experimental studies on the impact properties of auxetic materials. Phys. Status Solidi. 2014, 251, 307–313. [Google Scholar] [CrossRef]
- D3O. Trust Helmet Pad System [Internet]. Web Page. 2018. Available online: https://www.d3o.com/products/trust-helmet-pad-system/ (accessed on 25 January 2018).
- Xu, K.; Tan, Y.; Xin, J.H.; Liu, Y.; Lu, C.; Deng, Y.; Han, C.; Hu, H.; Wang, P. A novel impact hardening polymer with negative Poisson’s ratio for impact protection. Mater. Today Commun. 2015, 5, 50–59. [Google Scholar] [CrossRef]
- Foster, L.; Peketi, P.; Allen, T.; Senior, T.; Duncan, O.; Alderson, A. Application of Auxetic Foam in Sports Helmets. Appl. Sci. 2018, 8, 354. [Google Scholar] [CrossRef]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duncan, O.; Shepherd, T.; Moroney, C.; Foster, L.; Venkatraman, P.D.; Winwood, K.; Allen, T.; Alderson, A. Review of Auxetic Materials for Sports Applications: Expanding Options in Comfort and Protection. Appl. Sci. 2018, 8, 941. https://doi.org/10.3390/app8060941
Duncan O, Shepherd T, Moroney C, Foster L, Venkatraman PD, Winwood K, Allen T, Alderson A. Review of Auxetic Materials for Sports Applications: Expanding Options in Comfort and Protection. Applied Sciences. 2018; 8(6):941. https://doi.org/10.3390/app8060941
Chicago/Turabian StyleDuncan, Olly, Todd Shepherd, Charlotte Moroney, Leon Foster, Praburaj D. Venkatraman, Keith Winwood, Tom Allen, and Andrew Alderson. 2018. "Review of Auxetic Materials for Sports Applications: Expanding Options in Comfort and Protection" Applied Sciences 8, no. 6: 941. https://doi.org/10.3390/app8060941
APA StyleDuncan, O., Shepherd, T., Moroney, C., Foster, L., Venkatraman, P. D., Winwood, K., Allen, T., & Alderson, A. (2018). Review of Auxetic Materials for Sports Applications: Expanding Options in Comfort and Protection. Applied Sciences, 8(6), 941. https://doi.org/10.3390/app8060941






