Refractive Index Variation of Magnetron-Sputtered a-Si1−xGex by “One-Sample Concept” Combinatory
Abstract
:1. Introduction
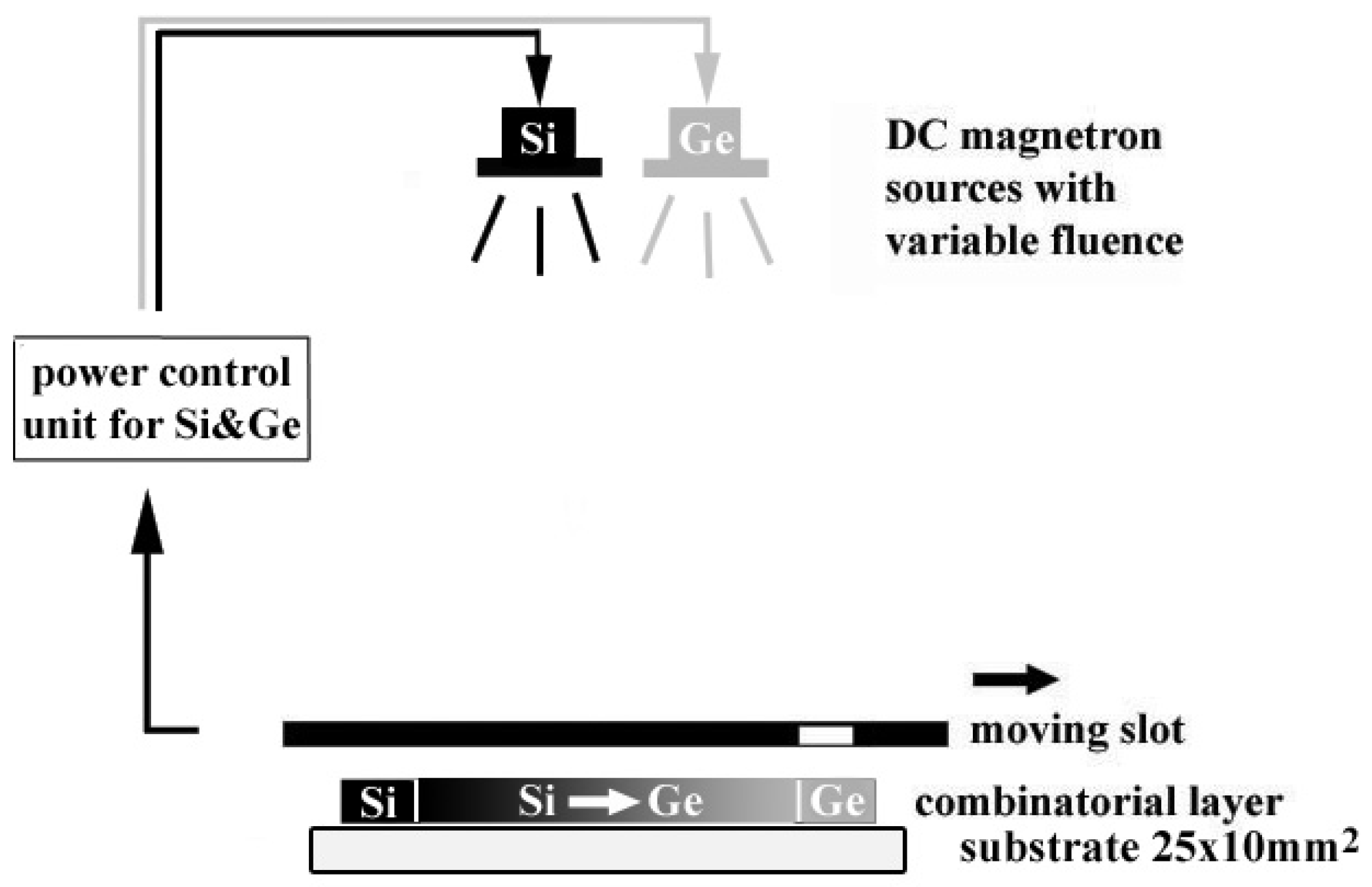
2. ’One-Sample’ Combinatory
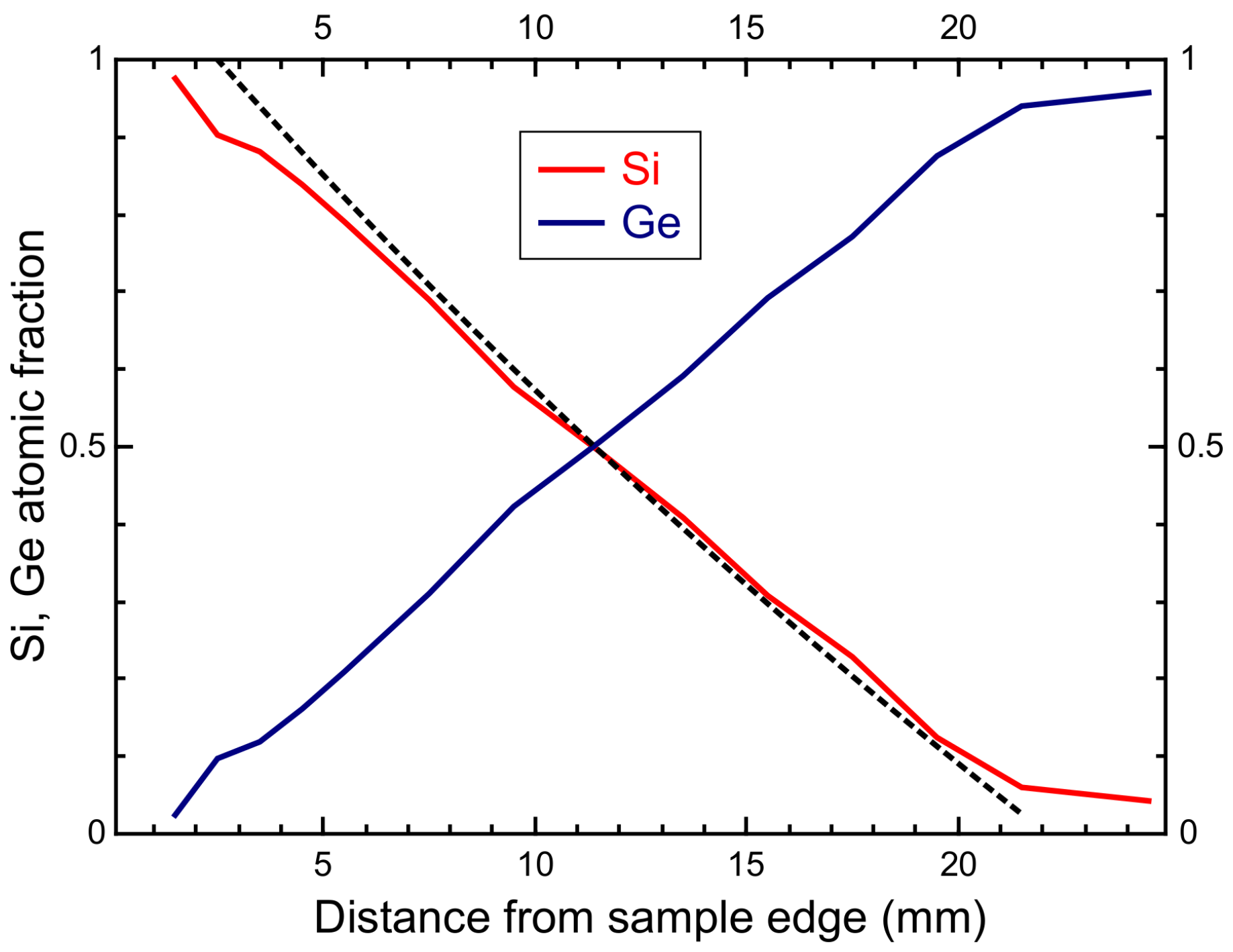
3. Distribution of Si and Ge Atomic Fractions
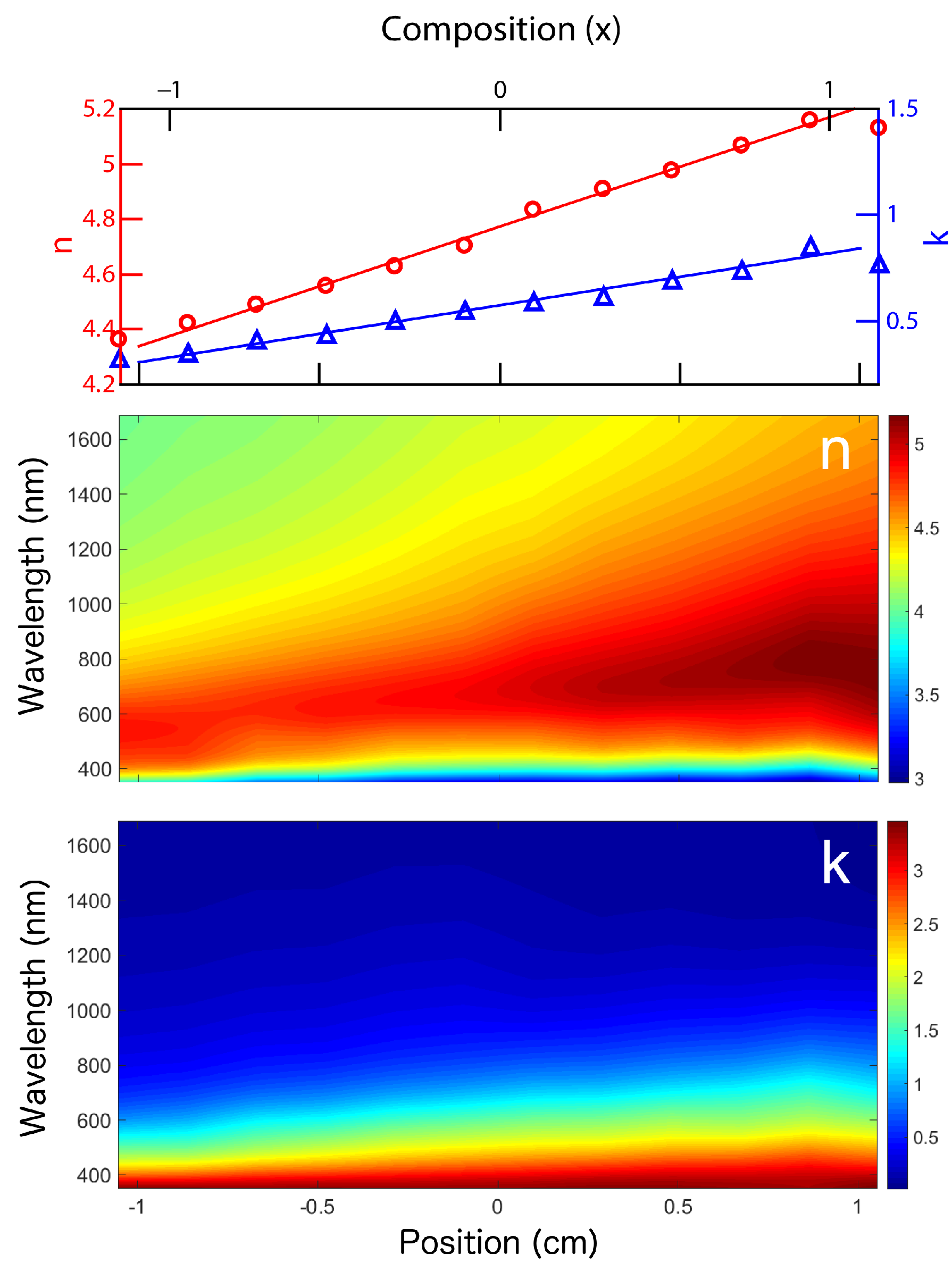
4. Distribution of the Optical Properties
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Ferrieu, F. Refined model for spectroscopic ellipsometry analysis of SixGe1−x/Si strained heterostructures. Appl. Phys. Lett. 2000, 76, 2023–2025. [Google Scholar]
- Hoffmann, L.; Bech Nielsen, B.; Nylandsted Larsen, A.; Leary, P.; Jones, R.; Briddon, P.; Öberg, S. Substitutional carbon in Si1−xGex. Phys. Rev. B 1999, 60, 13573–13581. [Google Scholar] [CrossRef]
- Engvall, J.; Nagesh, V.; Grimmeiss, H.; Schreiber, H.U.; Kasper, E. Electrical characterization of SiGe heterostructure bipolar transistors. Thin Solid Films 1992, 222, 154–156. [Google Scholar] [CrossRef]
- Pfeiffer, U.; Mishra, C.; Rassel, R.; Pinkett, S.; Reynolds, S. Schottky barrier diode circuits in silicon for future millimeter-wave and terahertz applications. IEEE Trans. Microw. Theory Tech. 2008, 56, 364–371. [Google Scholar] [CrossRef]
- Rogalski, A. Recent progress in infrared detector technologies. Infrared Phys. Technol. 2011, 54, 136–154. [Google Scholar] [CrossRef]
- Sinobad, M.; Monat, C.; Luther-davies, B.; Ma, P.; Madden, S.; Moss, D.J.; Mitchell, A.; Allioux, D.; Orobtchouk, R.; Boutami, S.; et al. Mid-infrared octave spanning supercontinuum generation to 85 µm in silicon-germanium waveguides. Optica 2018, 5, 360. [Google Scholar] [CrossRef]
- Rogalski, A. Heterostructure infrared photovoltaic detectors. Infrared Phys. Technol. 2000, 41, 213–238. [Google Scholar] [CrossRef]
- Pickering, C.; Carline, R. Dielectric function spectra of strained and relaxed Si1−xGex alloys (x = 0–0.25). J. Appl. Phys. 1994, 75, 4642–4647. [Google Scholar] [CrossRef]
- Kosarev, A.; Torres, A.; Hernandez, Y.; Ambrosio, R.; Zuniga, C.; Felter, T.; Asomoza, R.; Kudriavtsev, Y.; Silva-Gonzalez, R.; Gomez-Barojas, E.; et al. Silicon-germanium films deposited by low-frequency plasma-enhanced chemical vapor deposition: Effect of H2 and Ar dilution. J. Mater. Res. 2006, 21, 88–104. [Google Scholar] [CrossRef]
- Liu, Y.; Dalal, V.L. Properties of amorphous silicon-germanium films and devices deposited at higher growth rates. Mater. Res. Soc. Symp. 2002, 715, 515–520. [Google Scholar] [CrossRef]
- Soref, R. Mid-infrared photonics in silicon and germanium. Nat. Photonics 2010, 4, 495–497. [Google Scholar] [CrossRef]
- Brun, M.; Labeye, P.; Grand, G.; Hartmann, J.M.; Boulila, F.; Carras, M.; Nicoletti, S. Low loss SiGe graded index waveguides for mid-IR applications. Opt. Express 2014, 22, 508–518. [Google Scholar] [CrossRef] [PubMed]
- Ramirez, J.M.; Vakarin, V.; Frigerio, J.; Chaisakul, P.; Chrastina, D.; Le Roux, X.; Ballabio, A.; Vivien, L.; Isella, G.; Marris-Morini, D. Ge-rich graded-index Si_1-xGex waveguides with broadband tight mode confinement and flat anomalous dispersion for nonlinear mid-infrared photonics. Opt. Express 2017, 25, 6561–6567. [Google Scholar] [CrossRef] [PubMed]
- Carletti, L.; Sinobad, M.; Ma, P.; Yu, Y.; Allioux, D.; Orobtchouk, R.; Brun, M.; Ortiz, S.; Labeye, P.; Hartmann, J.M.; et al. Nonlinear optical response of low loss silicon germanium waveguides in the mid-infrared. Opt. Express 2015, 23, 8261–8271. [Google Scholar] [CrossRef] [PubMed]
- Grochla, D.; Siegel, A.; Hamann, S.; Buenconsejo, P.J.; Kieschnick, M.; Brunken, H.; König, D.; Ludwig, A. Time- and space-resolved high-throughput characterization of stresses during sputtering and thermal processing of Al-Cr-N thin films. J. Phys. D 2013, 46, 084011. [Google Scholar] [CrossRef]
- Kadletz, P.; Motemani, Y.; Iannotta, J.; Salomon, S.; Khare, C.; Grossmann, L.; Maier, H.; Ludwig, A.; Schmahl, W. Crystallographic Structure Analysis of a Ti-Ta Thin Film Materials Library Fabricated by Combinatorial Magnetron Sputtering. ACS Comb. Sci. 2018, 20, 137–150. [Google Scholar] [CrossRef] [PubMed]
- Mao, F.; Nyberg, T.; Thersleff, T.; Andersson, A.; Jansson, U. Combinatorial magnetron sputtering of AgFeO2 thin films with the delafossite structure. Mater. Des. 2016, 91, 132–142. [Google Scholar] [CrossRef]
- Kovács, A.; Barna, P.B.; Lábár, J.L. The nucleation and growth of intermetallic Al-Pt phases in co-deposited thin films. Thin Solid Films 2003, 433, 78–81. [Google Scholar] [CrossRef]
- Hung, L.S.; Nastase, M.; Gyulai, J.; Mayer, J.W. Ioninduced amorphous and crystalline phase formation in Al/Ni, Al/Pd, and Al/Pt thin films. Appl. Phys. Lett. 1983, 42, 672–674. [Google Scholar] [CrossRef]
- Sáfrán, G. ‘One-sample concept’ micro-combinatory for high throughput TEM of binary films. Ultramicroscopy 2018, 187, 50–55. [Google Scholar] [CrossRef] [PubMed]
- Humlíček, J.; Garriga, M.; Alonso, M.I.; Cardona, M. Optical spectra of SixGe1−x alloys. J. Appl. Phys. 1989, 65, 2827–2832. [Google Scholar] [CrossRef]
- Schmidt, J.; Eilert, M.; Peters, S.; Wietler, T.F. Characterization of thin SiGe layers on Si (001) by spectroscopic ellipsometry for Ge fractions from 0 to 100%. Appl. Surf. Sci. 2017, 421, 2827–2832. [Google Scholar] [CrossRef]
- Pászti, F.; Manuaba, A.; Hajdu, C.; Melo, A.A.; Silva, M.F.D. Current measurement on MeV energy ion beams. Nucl. Instrum. Methods 1990, 47, 187–192. [Google Scholar] [CrossRef]
- Kótai, E. Computer methods for analysis and simulation of RBS and ERDA spectra. Nucl. Instrum. Methods B 1994, 85, 588–596. [Google Scholar] [CrossRef]
- Jellison, G.E.; Modine, F. Parameterization of the optical functions of amorphous materials in the interband region. Appl. Phys. Lett. 1996, 69, 371–373. [Google Scholar] [CrossRef]
- Collins, R.W.; Windischmann, H.; Cavese, J.M.; Gonzalez-Hernandez, J. Optical properties of dense thin-film Si and Ge prepared by ion-beam sputtering. J. Appl. Phys. 1985, 58, 954–957. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lohner, T.; Kalas, B.; Petrik, P.; Zolnai, Z.; Serényi, M.; Sáfrán, G. Refractive Index Variation of Magnetron-Sputtered a-Si1−xGex by “One-Sample Concept” Combinatory. Appl. Sci. 2018, 8, 826. https://doi.org/10.3390/app8050826
Lohner T, Kalas B, Petrik P, Zolnai Z, Serényi M, Sáfrán G. Refractive Index Variation of Magnetron-Sputtered a-Si1−xGex by “One-Sample Concept” Combinatory. Applied Sciences. 2018; 8(5):826. https://doi.org/10.3390/app8050826
Chicago/Turabian StyleLohner, Tivadar, Benjamin Kalas, Peter Petrik, Zsolt Zolnai, Miklós Serényi, and György Sáfrán. 2018. "Refractive Index Variation of Magnetron-Sputtered a-Si1−xGex by “One-Sample Concept” Combinatory" Applied Sciences 8, no. 5: 826. https://doi.org/10.3390/app8050826
APA StyleLohner, T., Kalas, B., Petrik, P., Zolnai, Z., Serényi, M., & Sáfrán, G. (2018). Refractive Index Variation of Magnetron-Sputtered a-Si1−xGex by “One-Sample Concept” Combinatory. Applied Sciences, 8(5), 826. https://doi.org/10.3390/app8050826




