A Nonlinear Beamformer Based on p-th Root Compression—Application to Plane Wave Ultrasound Imaging
Abstract
1. Introduction
2. Methods and Materials
2.1. Methods
2.1.1. Conventional DAS for Plane Wave Imaging
2.1.2. FDMAS Beamforming
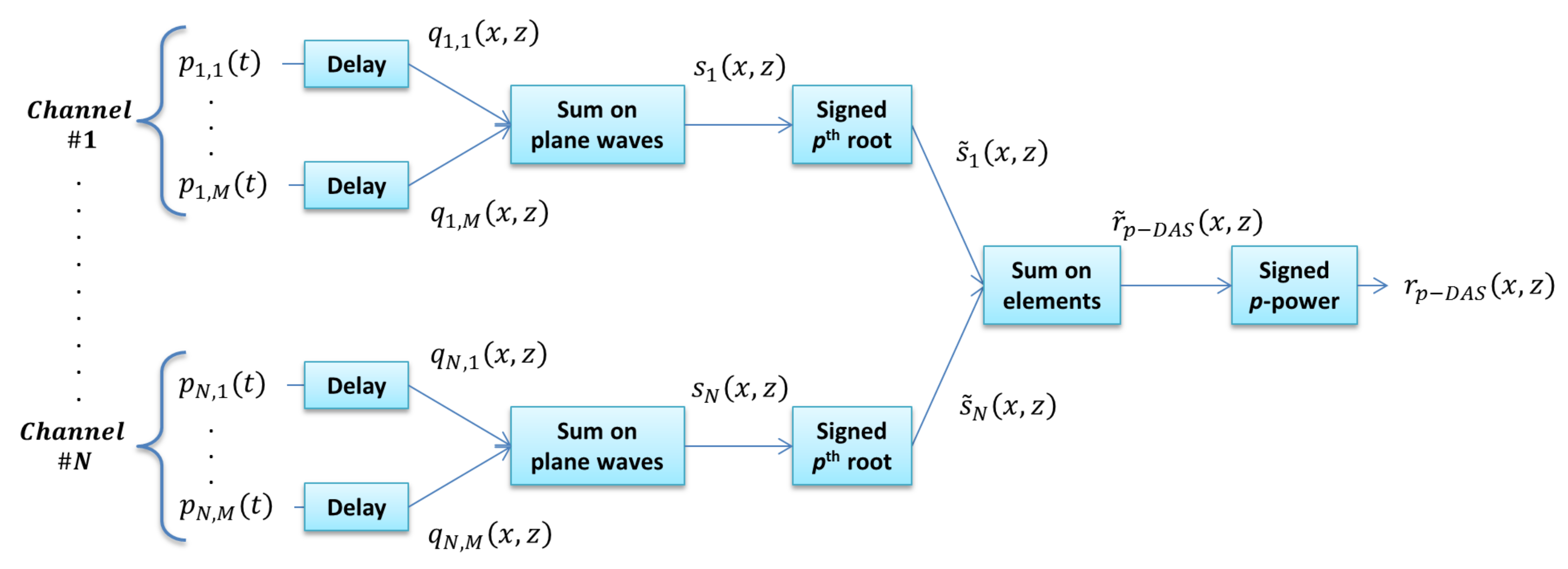
2.1.3. Proposed Method: p-DAS Beamforming
2.2. Materials
2.2.1. Beamforming Parameters
2.2.2. Image Quality Metrics
3. Results and Discussion
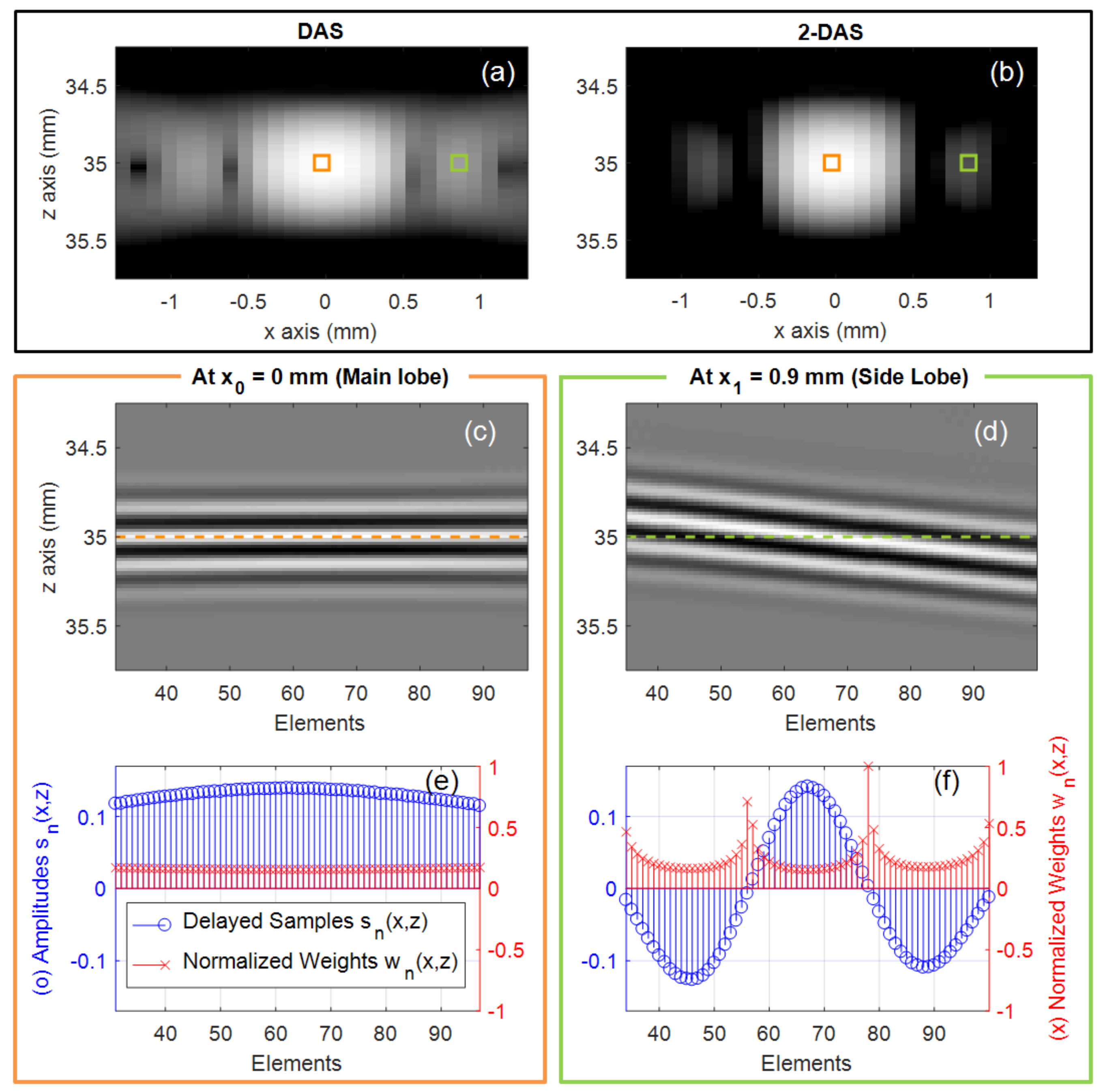
3.1. Analysis on the Principle of p-DAS
3.2. Performances Evaluation of p-DAS on Image Quality
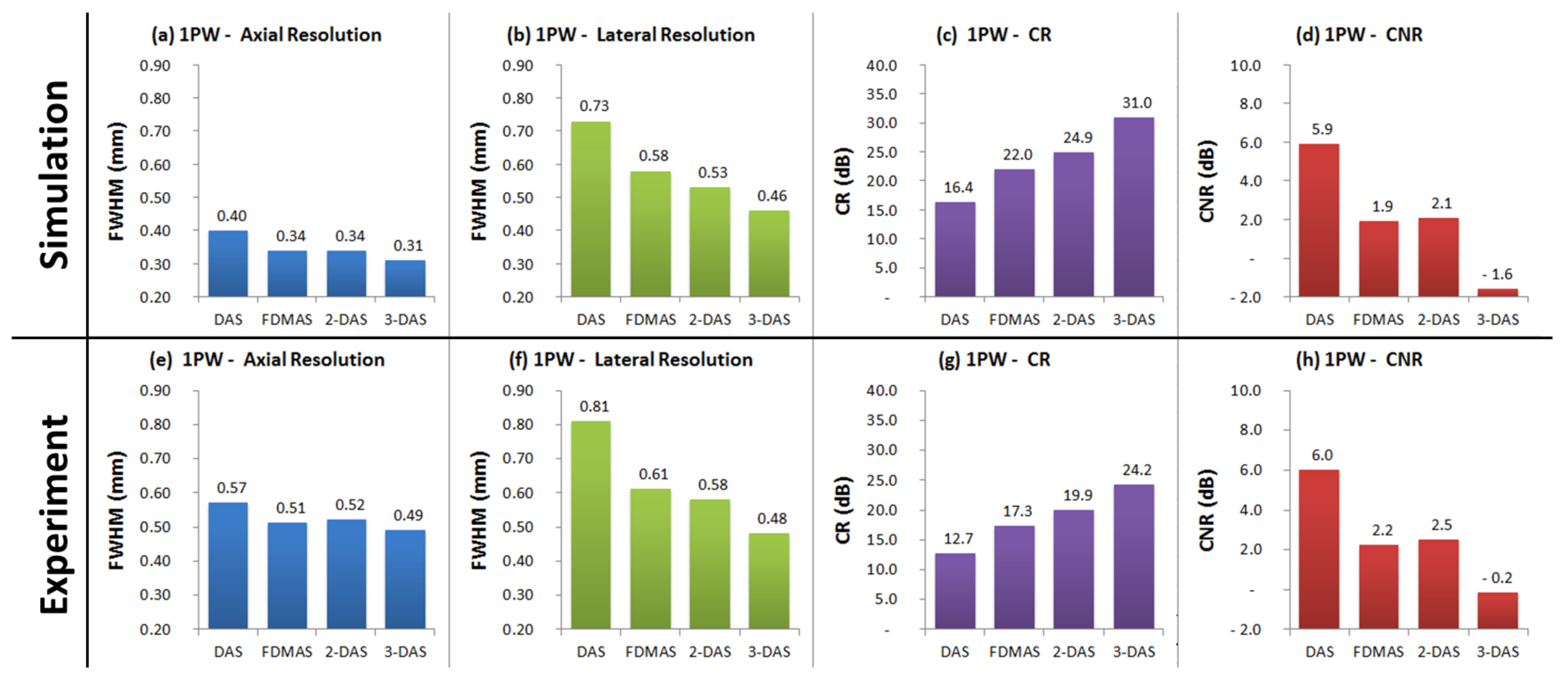
3.2.1. Single Plane Wave Imaging
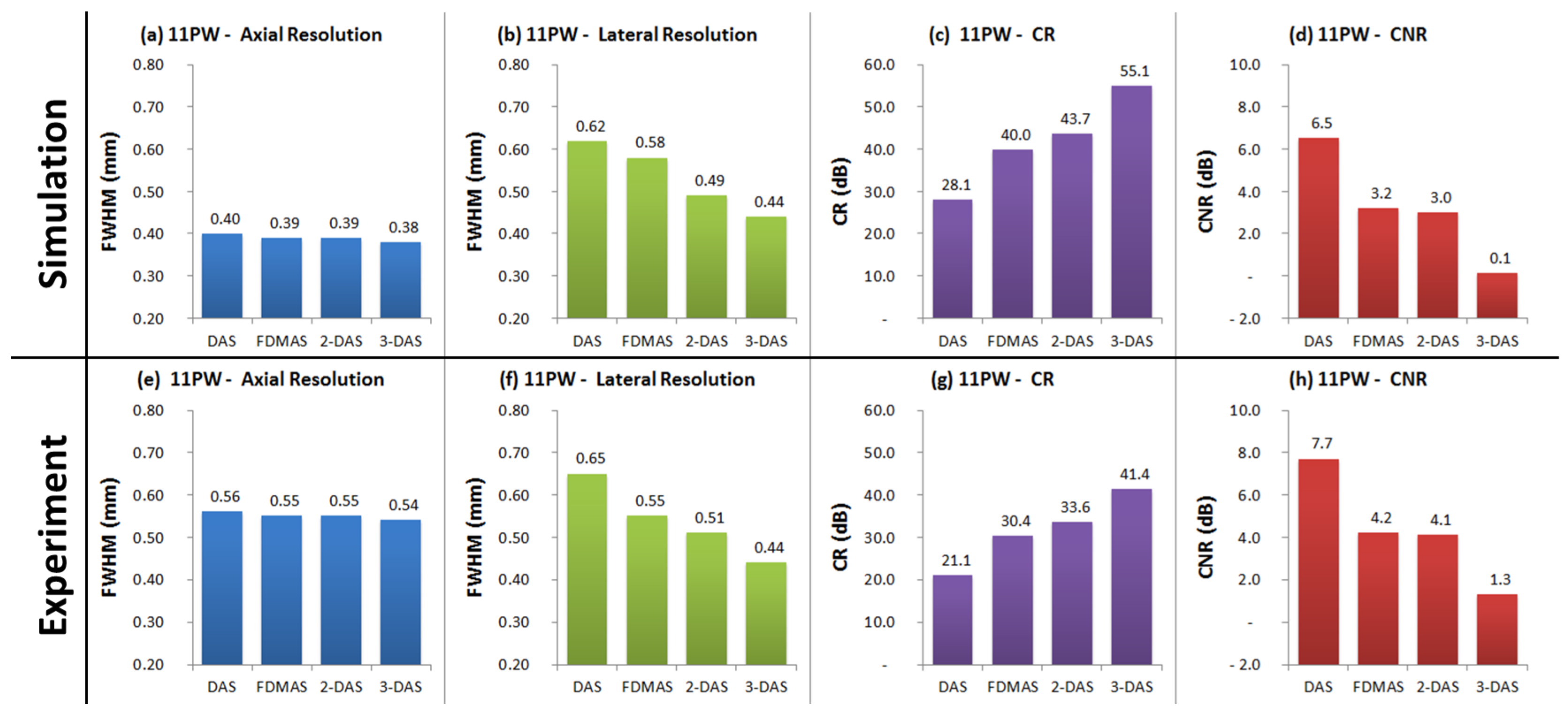
3.2.2. Eleven Plane Wave Imaging
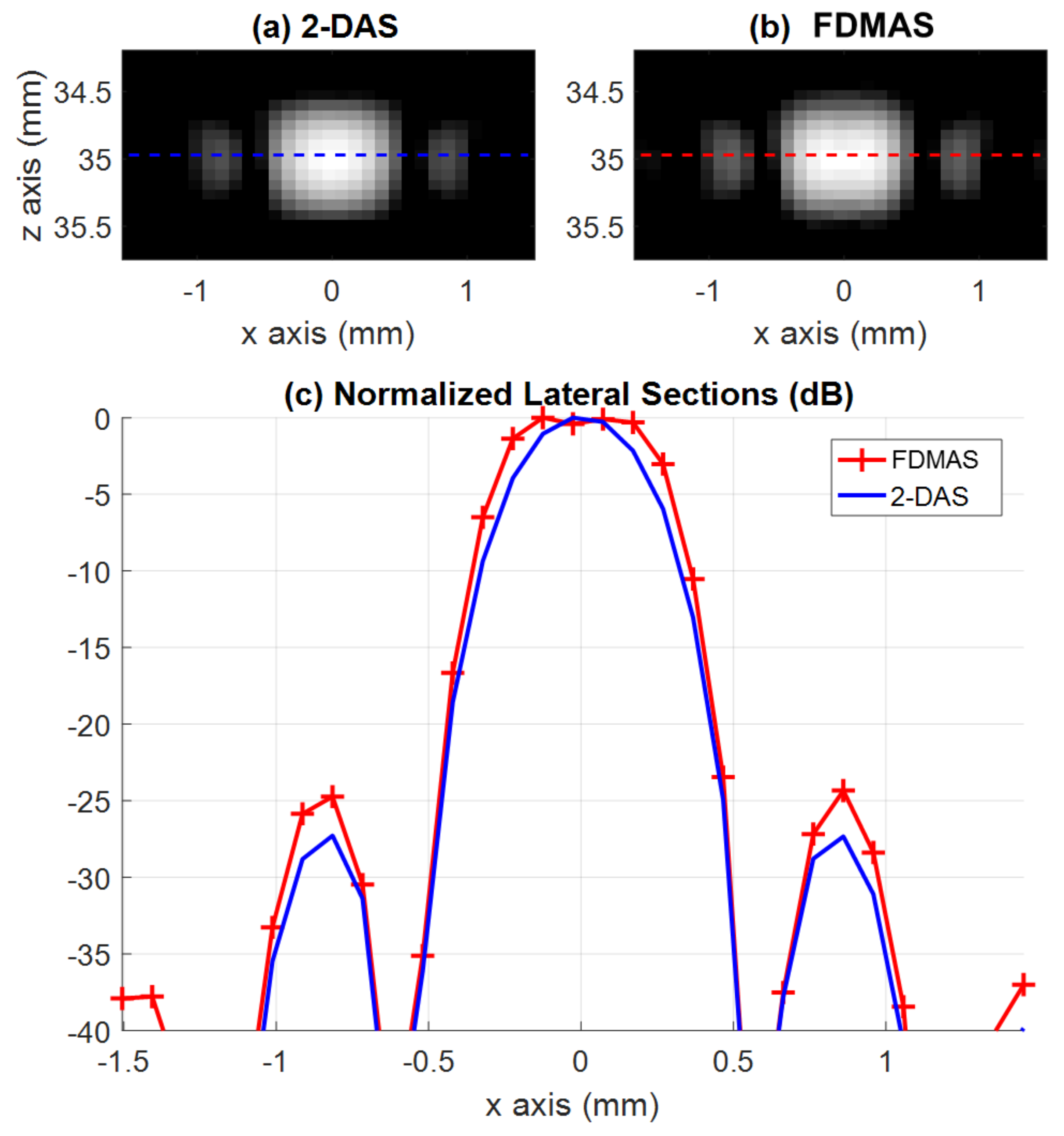
3.3. Comparison between FDMAS and p-DAS
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tanter, M.; Fink, M. Ultrafast imaging in biomedical ultrasound. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2014, 61, 102–119. [Google Scholar] [CrossRef] [PubMed]
- Petrusca, L.; Varray, F.; Souchon, R.; Bernard, A.; Chapelon, J.Y.; Liebgott, H.; N’Djin, W.A.; Viallon, M. Fast Volumetric Ultrasound B-Mode and Doppler Imaging with a New High-Channels Density Platform for Advanced 4D Cardiac Imaging/Therapy. Appl. Sci. 2018, 8, 200. [Google Scholar] [CrossRef]
- Tong, L.; Gao, H.; Choi, H.F.; D’hooge, J. Comparison of conventional parallel beamforming with plane wave and diverging wave imaging for cardiac applications: A simulation study. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2012, 59, 1654–1663. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Gao, H.; D’hooge, J. Multi-transmit beam forming for fast cardiac imaging-a simulation study. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1719–1731. [Google Scholar] [CrossRef] [PubMed]
- Montaldo, G.; Tanter, M.; Bercoff, J.; Benech, N.; Fink, M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 489–506. [Google Scholar] [CrossRef] [PubMed]
- Synnevag, J.; Austeng, A.; Holm, S. Adaptive beamforming applied to medical ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2007, 54, 1606. [Google Scholar] [CrossRef] [PubMed]
- Holfort, I.K.; Gran, F.; Jensen, J.A. Broadband minimum variance beamforming for ultrasound imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 314–325. [Google Scholar] [CrossRef] [PubMed]
- Synnevag, J.F.; Austeng, A.; Holm, S. A low-complexity data-dependent beamformer. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 281–289. [Google Scholar] [CrossRef] [PubMed]
- Li, P.C.; Li, M.L. Adaptive imaging using the generalized coherence factor. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 128–141. [Google Scholar] [PubMed]
- Camacho, J.; Parrilla, M.; Fritsch, C. Phase coherence imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56. [Google Scholar] [CrossRef] [PubMed]
- Matrone, G.; Savoia, A.S.; Caliano, G.; Magenes, G. The delay multiply and sum beamforming algorithm in ultrasound B-mode medical imaging. IEEE Trans. Med. Imaging 2015, 34, 940–949. [Google Scholar] [CrossRef] [PubMed]
- Matrone, G.; Ramalli, A.; Savoia, A.S.; Tortoli, P.; Magenes, G. High frame-rate, high resolution ultrasound imaging with multi-line transmission and filtered-delay multiply and sum beamforming. IEEE Trans. Med. Imaging 2017, 36, 478–486. [Google Scholar] [CrossRef] [PubMed]
- Prieur, F.; Rindal, O.M.H.; Holm, S.; Austeng, A. Influence of the Delay-Multiply-And-Sum beamformer on the ultrasound image amplitude. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017. [Google Scholar]
- Polichetti, M.; Varray, F.; Matrone, G.; Savoia, A.S.; Béra, J.C.; Cachard, C.; Nicolas, B. A computationally efficient nonlinear beamformer based on p-th root signal compression for enhanced ultrasound B-mode imaging. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017. [Google Scholar]
- Liebgott, H.; Rodriguez-Molares, A.; Cervenansky, F.; Jensen, J.A.; Bernard, O. Plane-wave imaging challenge in medical ultrasound. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016. [Google Scholar]
- Matrone, G.; Savoia, A.S.; Magenes, G. Filtered Delay Multiply And Sum beamforming in plane-wave ultrasound imaging: Tests on simulated and experimental data. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016. [Google Scholar]
- Varray, F.; Bernard, O.; Assou, S.; Cachard, C.; Vray, D. Hybrid strategy to simulate 3D nonlinear radio-frequency ultrasound using a variant spatial PSF. IIEEE Trans. Ultrason. Ferroelectr. Freq. Control 2016, 63, 1390–1398. [Google Scholar] [CrossRef] [PubMed]
- Rindal, O.M.H.; Rodriguez-Molares, A.; Austeng, A. The dark region artifact in adaptive ultrasound beamforming. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017. [Google Scholar]
- Thijssen, J.M. Ultrasonic speckle formation, analysis and processing applied to tissue characterization. Pattern Recognit. Lett. 2003, 24, 659–675. [Google Scholar] [CrossRef]
- Hverven, S.M.; Rindal, O.M.H.; Rodriguez-Molares, A.; Austeng, A. The influence of speckle statistics on contrast metrics in ultrasound imaging. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017. [Google Scholar]
- Ramalli, A.; Scaringella, M.; Matrone, G.; Dallai, A.; Boni, E.; Savoia, A.S.; Bassi, L.; Hine, G.E.; Tortoli, P. High dynamic range ultrasound imaging with real-time filtered-delay multiply and sum beamforming. In Proceedings of the 2017 IEEE International Ultrasonics Symposium (IUS), Washington, DC, USA, 6–9 September 2017. [Google Scholar]
- Errico, C.; Pierre, J.; Pezet, S.; Desailly, Y.; Lenkei, Z.; Couture, O.; Tanter, M. Ultrafast ultrasound localization microscopy for deep super-resolution vascular imaging. Nature 2015, 527, 499–502. [Google Scholar] [CrossRef] [PubMed]
- Boulos, P.; Varray, F.; Poizat, A.; Kalkhoran, M.A.; Gilles, B.; Bera, J.; Cachard, C. Passive cavitation imaging using different advanced beamforming methods. In Proceedings of the 2016 IEEE International Ultrasonics Symposium (IUS), Tours, France, 18–21 September 2016. [Google Scholar]


| Number of Elements N | 128 | Excitation (number of cycles) | 2.5 |
| Pitch (mm) | 0.3 | Transmit frequency (MHz) | 5.2 |
| Element width (mm) | 0.27 | Sampling Frequency (MHz) | 20.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polichetti, M.; Varray, F.; Béra, J.-C.; Cachard, C.; Nicolas, B. A Nonlinear Beamformer Based on p-th Root Compression—Application to Plane Wave Ultrasound Imaging. Appl. Sci. 2018, 8, 599. https://doi.org/10.3390/app8040599
Polichetti M, Varray F, Béra J-C, Cachard C, Nicolas B. A Nonlinear Beamformer Based on p-th Root Compression—Application to Plane Wave Ultrasound Imaging. Applied Sciences. 2018; 8(4):599. https://doi.org/10.3390/app8040599
Chicago/Turabian StylePolichetti, Maxime, François Varray, Jean-Christophe Béra, Christian Cachard, and Barbara Nicolas. 2018. "A Nonlinear Beamformer Based on p-th Root Compression—Application to Plane Wave Ultrasound Imaging" Applied Sciences 8, no. 4: 599. https://doi.org/10.3390/app8040599
APA StylePolichetti, M., Varray, F., Béra, J.-C., Cachard, C., & Nicolas, B. (2018). A Nonlinear Beamformer Based on p-th Root Compression—Application to Plane Wave Ultrasound Imaging. Applied Sciences, 8(4), 599. https://doi.org/10.3390/app8040599





