Spatial Coherence of Backscattered Signals in Multi-Line Transmit Ultrasound Imaging and Its Effect on Short-Lag Filtered-Delay Multiply and Sum Beamforming
Abstract
1. Introduction
2. Materials and Methods
2.1. Spatial Coherence
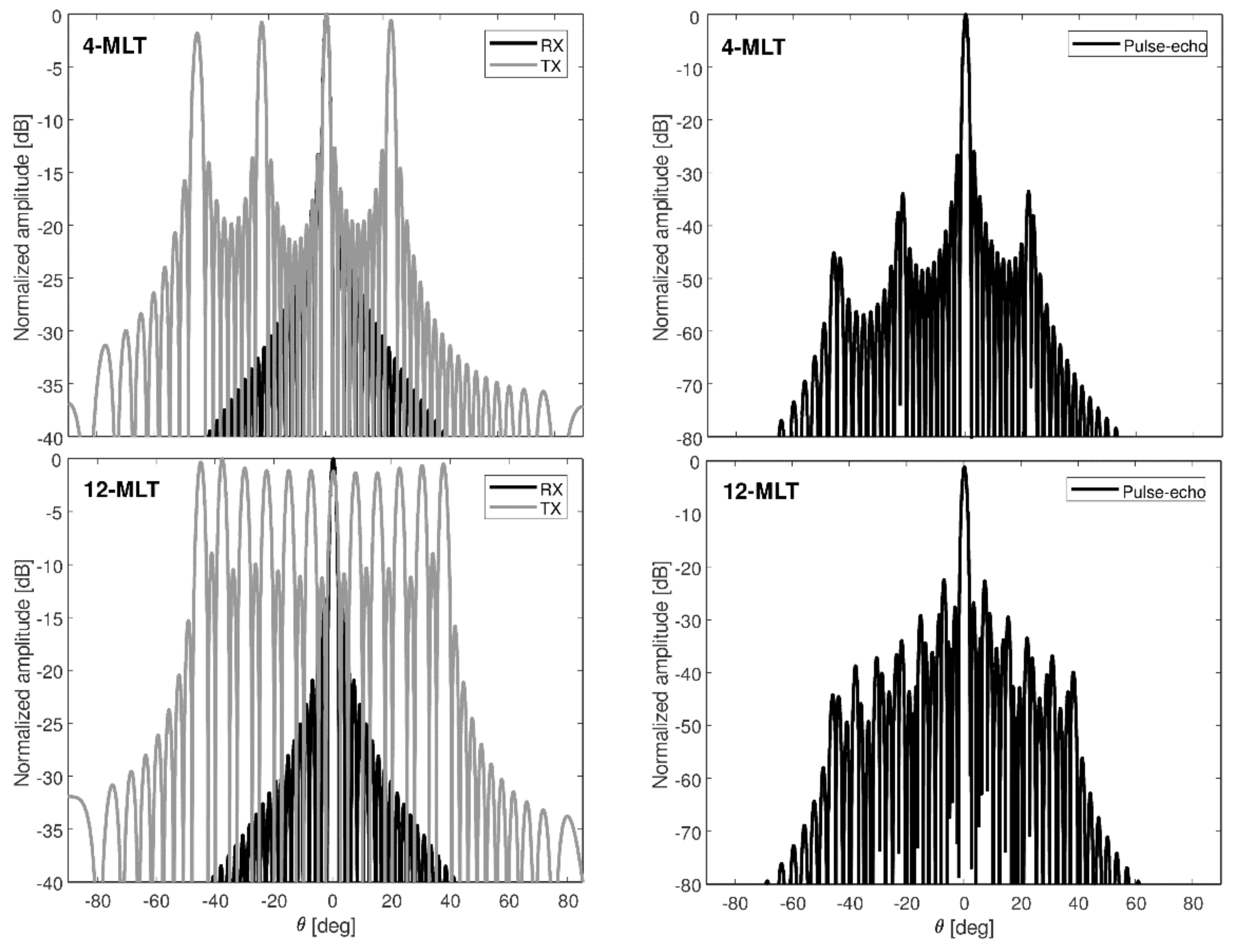
2.2. Multi-Line Transmission
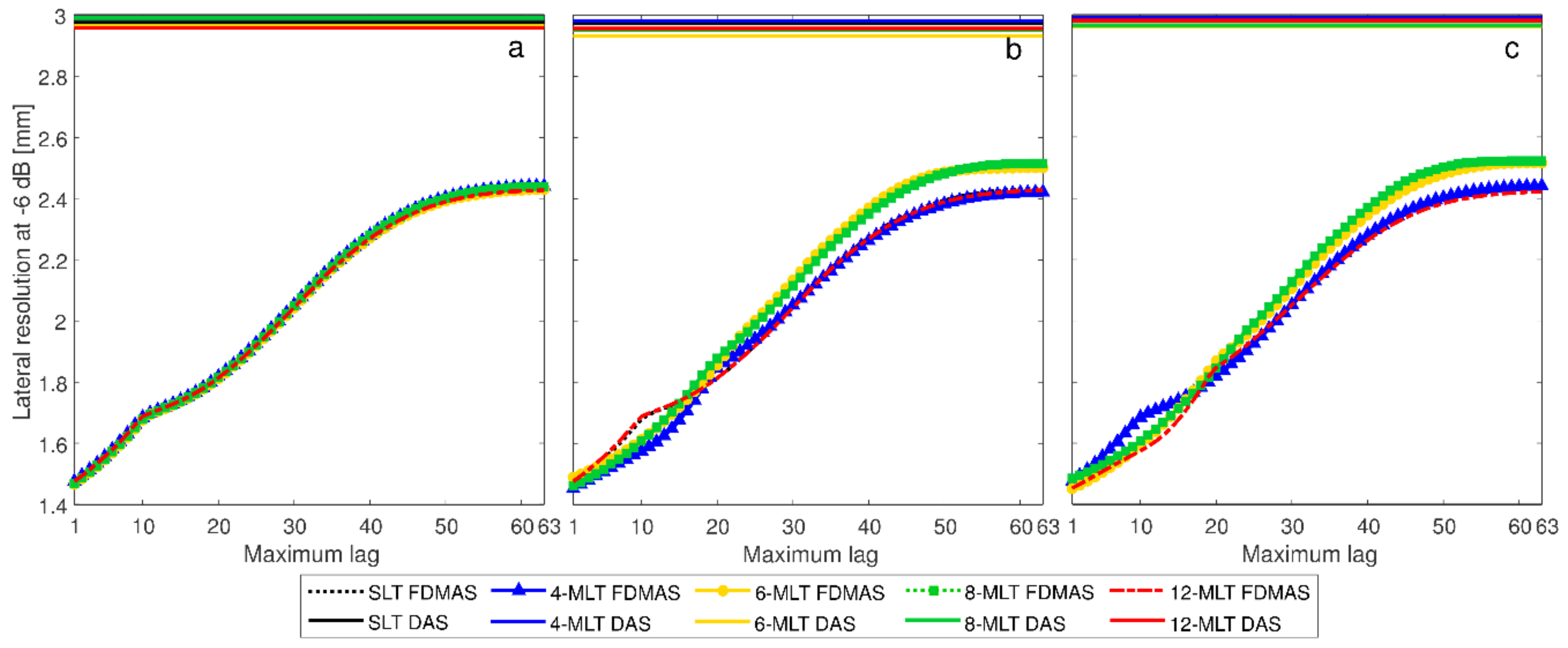
2.3. Short-Lag Filtered-Delay Multiply and Sum Beamforming
2.4. Simulation Setup and Study Organization
- the number of MLT beams varies (i.e., NTX = 1/4/6/8/12), but the total image sector is fixed (θSECT = 90°), as well as the number of lines (192); consequently, the angle among the TX beams (θTX = θSECT/NTX) changes together with the number of beams (usually, this is the classic MLT implementation);
- the number of MLT beams varies (i.e., NTX = 1/4/6/8/12), but the same angle (θTX) among the beams is used in all configurations; in particular, this angle was set to be equal to the one that would be obtained applying 12-MLT to scan a 90° sector (i.e., θ12). Thus, in this case, the total image sector also changes in the different MLT configurations;
- the number of beams is fixed (i.e., NTX = 4), while the angle among them changes, as it would do in 4/6/8/12-MLT when a 90° sector is acquired. Thus, also here, the total image sector changes in each case.
3. Results and Discussion
3.1. Spatial Coherence Trends in MLT Images of a Homogeneous Phantom
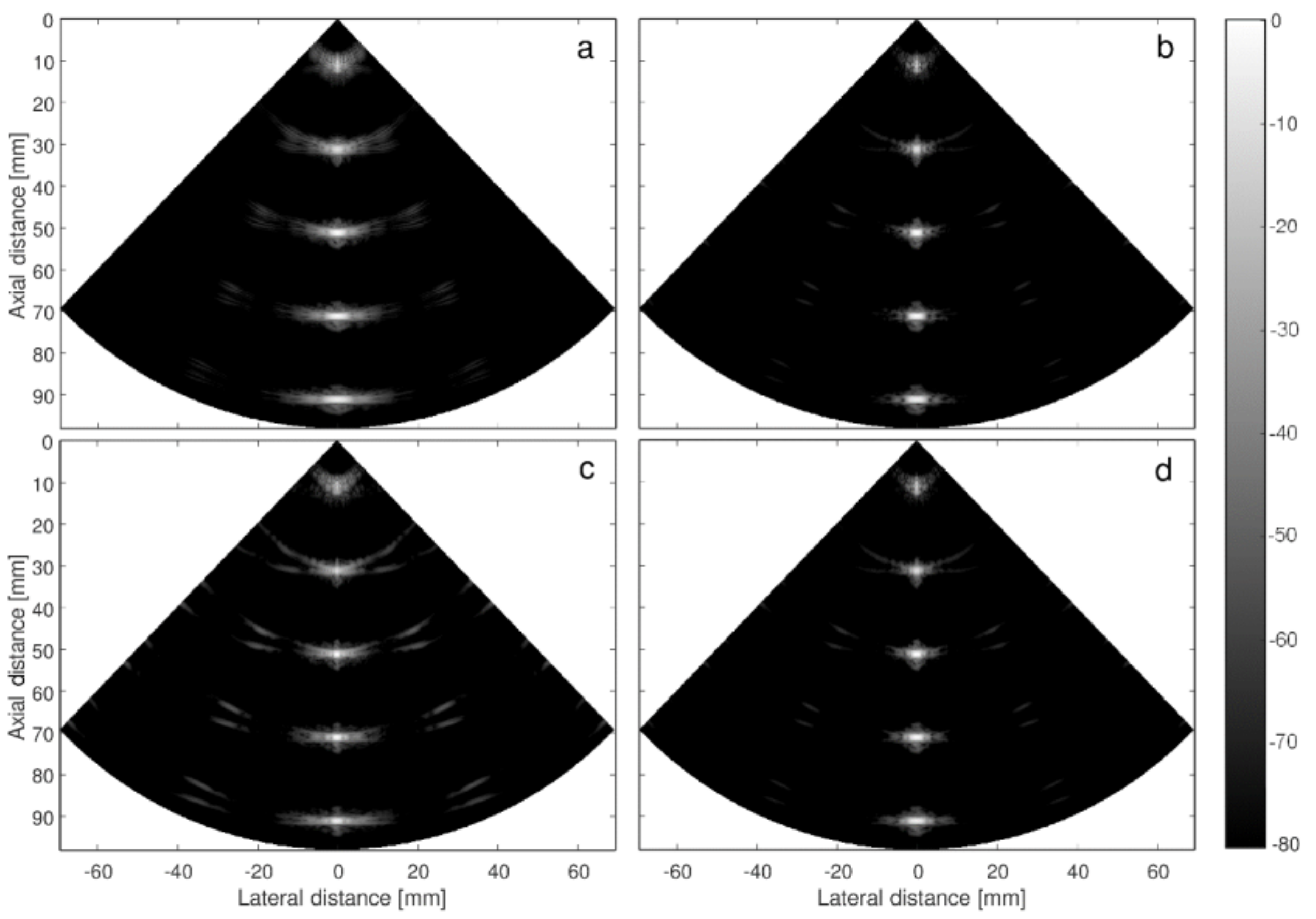
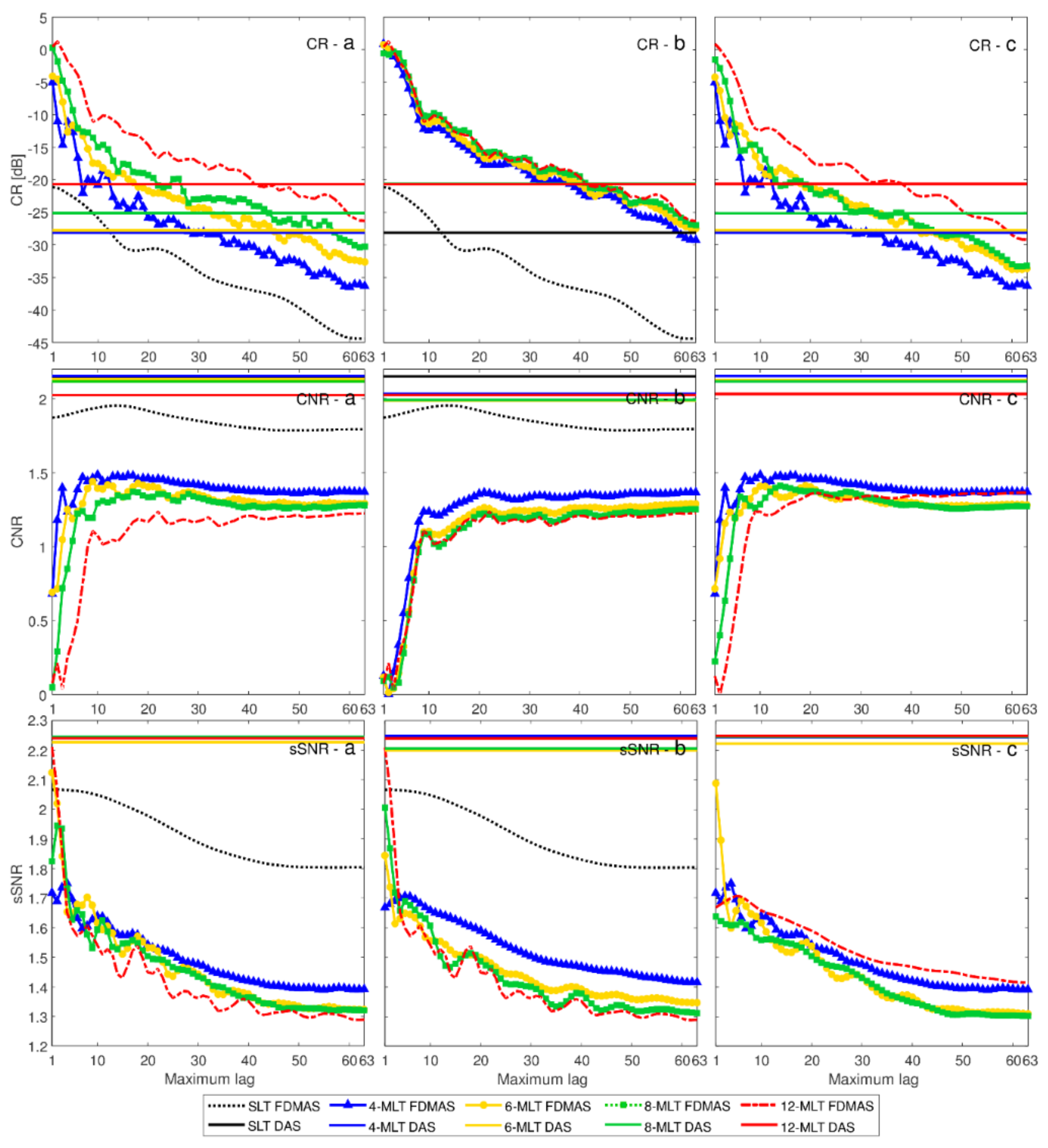
3.2. Simulated Images with MLT and Short-Lag F-DMAS
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Mallart, R.; Fink, M. The Van Cittert-Zernike theorem in pulsed ultrasound. Implications for ultrasound imaging. In Proceedings of the IEEE Ultrasonics Symposium, Honolulu, HI, USA, 4–7 December 1990; pp. 1603–1607. [Google Scholar]
- Mallart, R.; Fink, M. Adaptive focusing in scattering media through sound-speed inhomogeneities: The Van Cittert Zernike approach and focusing criterion. J. Acoust. Soc. Am. 1994, 96, 3721–3732. [Google Scholar] [CrossRef]
- Mallart, R.; Fink, M. The van Cittert–Zernike theorem in pulse echo measurements. J. Acoust. Soc. Am. 1991, 90, 2718–2727. [Google Scholar] [CrossRef]
- Liu, D.-L.; Waag, R.C. About the application of the Van Cittert-Zernike theorem in ultrasonic imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1995, 42, 590–601. [Google Scholar]
- Li, P.-C.; Li, M.-L. Adaptive imaging using the generalized coherence factor. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2003, 50, 128–142. [Google Scholar] [PubMed]
- Chen, J.F.; Zagzebski, J.A.; Dong, F.; Madsen, E.L. Estimating the spatial autocorrelation function for ultrasound scatterers in isotropic media. Med. Phys. 1998, 25, 648–655. [Google Scholar] [CrossRef] [PubMed]
- Camacho, J.; Parrilla, M.; Fritsch, C. Phase coherence imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 958–974. [Google Scholar] [CrossRef] [PubMed]
- Matrone, G.; Savoia, A.S.; Caliano, G.; Magenes, G. The Delay Multiply and Sum beamforming algorithm in ultrasound B-mode medical imaging. IEEE Trans. Med. Imaging 2015, 34, 940–949. [Google Scholar] [CrossRef] [PubMed]
- Lediju, M.A.; Trahey, G.E.; Byram, B.C.; Dahl, J.J. Short-Lag Spatial Coherence of backscattered echoes: imaging characteristics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2011, 58, 1377–1388. [Google Scholar] [CrossRef] [PubMed]
- Dahl, J.J.; Hyun, D.; Lediju, M.; Trahey, G.E. Lesion detectability in diagnostic ultrasound with short-lag spatial coherence imaging. Ultrason. Imaging 2011, 33, 119–133. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.-Y. 2D and 3D high frame-rate imaging with limited diffraction beams. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1997, 44, 839–856. [Google Scholar] [CrossRef]
- Montaldo, G.; Tanter, M.; Bercoff, J.; Benech, N.; Fink, M. Coherent plane-wave compounding for very high frame rate ultrasonography and transient elastography. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 489–506. [Google Scholar] [CrossRef] [PubMed]
- Shattuck, D.P.; Weinshenker, M.D.; Smith, S.W.; von Ramm, O.T. Explososcan: A parallel processing technique for high speed ultrasound imaging with linear phased arrays. J. Acoust. Soc. Am. 1984, 75, 1273–1282. [Google Scholar] [CrossRef] [PubMed]
- Mallart, R.; Fink, M. Improved imaging rate through simultaneous transmission of several ultrasound beams. Proc. SPIE 1992, 1773, 120–130. [Google Scholar]
- Tong, L.; Ramalli, A.; Jasaityte, R.; Tortoli, P.; D’hooge, J. Multi-transmit beam forming for fast cardiac imaging-Experimental Validation and in vivo application. IEEE. Trans. Med. Imaging 2014, 33, 1205–1219. [Google Scholar] [CrossRef] [PubMed]
- Prieur, F.; Dénarié, B.; Austeng, A.; Torp, H. Multi-line transmission in medical imaging using the second-harmonic signal. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 2682–2692. [Google Scholar] [CrossRef] [PubMed]
- Rabinovich, A.; Feuer, A.; Friedman, Z. Multi-line transmission combined with minimum variance beamforming in medical ultrasound imaging. IEEE. Trans. Ultrason. Ferroelectr. Freq. Control 2015, 62, 814–827. [Google Scholar] [CrossRef] [PubMed]
- Zurakhov, G.; Tong, L.; Ramalli, A.; Tortoli, P.; D’hooge, J.; Friedman, Z.; Adam, D. Multi line transmit beamforming combined with adaptive apodization. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2018. [Google Scholar] [CrossRef]
- Matrone, G.; Ramalli, A.; Savoia, A.S.; Tortoli, P.; Magenes, G. High frame-rate, high resolution ultrasound imaging with multi-line transmission and Filtered-Delay Multiply and Sum beamforming. IEEE Trans. Med. Imaging 2017, 36, 478–486. [Google Scholar] [CrossRef] [PubMed]
- Matrone, G.; Savoia, A.S.; Caliano, G.; Magenes, G. Depth-of-field enhancement in Filtered-Delay Multiply and Sum beamformed images using synthetic aperture focusing. Ultrasonics 2017, 75, 216–225. [Google Scholar] [CrossRef] [PubMed]
- Matrone, G.; Ramalli, A.; Tortoli, P.; Magenes, G. Experimental evaluation of ultrasound higher-order harmonic imaging with Filtered-Delay Multiply And Sum (F-DMAS) non-linear beamforming. Ultrasonics 2018, 86, 59–68. [Google Scholar] [CrossRef] [PubMed]
- Tong, L.; Gao, H.; D’hooge, J. Multi-transmit beam forming for fast cardiac imaging—A simulation study. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1719–1731. [Google Scholar] [CrossRef] [PubMed]
- Bottenus, N.; Byram, B.C.; Dahl, J.J.; Trahey, G.E. Synthetic Aperture Focusing for Short-Lag Spatial Coherence Imaging. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2013, 60, 1816–1826. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Szabo, T.L. Diagnostic Ultrasound Imaging: Inside Out; Elsevier Academic Press: Hartford, CT, USA, 2004. [Google Scholar]
- Lim, H.B.; Nhung, N.T.; Li, E.P.; Thang, N.D. Confocal Microwave Imaging for Breast Cancer Detection: Delay-Multiply-and-Sum Image Reconstruction Algorithm. IEEE Trans. Biomed. Eng. 2008, 55, 1697–1704. [Google Scholar] [PubMed]
- Jensen, J.A.; Svendsen, N.B. Calculation of pressure fields from arbitrarily shaped, apodized, and excited ultrasound transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1992, 39, 262–267. [Google Scholar] [CrossRef] [PubMed]
- Jensen, J.A. Field: A program for simulating ultrasound systems. Med. Biol. Eng. Comput. 1996, 34, 351–353. [Google Scholar]
- Tong, L.; Ramalli, A.; Tortoli, P.; Fradella, G.; Caciolli, S.; Luo, J.; D’hooge, J. Wide-Angle Tissue Doppler Imaging at High Frame Rate Using Multi-Line Transmit Beamforming: An Experimental Validation In Vivo. IEEE Trans. Med. Imaging 2016, 35, 521–528. [Google Scholar] [CrossRef] [PubMed]
- Pedrosa, J.; Queiros, S.; Bernard, O.; Engvall, J.; Edvardsen, T.; Nagel, E.; D’hooge, J. Fast and Fully Automatic Left Ventricular Segmentation and Tracking in Echocardiography Using Shape-Based B-Spline Explicit Active Surfaces. IEEE Trans. Med. Imaging 2017, 36, 2287–2296. [Google Scholar] [CrossRef] [PubMed]





| Scenario 1 | Scenario 2 | Scenario 3 | |||
|---|---|---|---|---|---|
| NTX | θTX | NTX | θTX | NTX | θTX |
| 1 | θ1 = 90° | 1 | θ12 | - | - |
| 4 | θ4 = θ1/4 | 4 | θ12 | 4 | θ4 |
| 6 | θ6 = θ1/6 | 6 | θ12 | 4 | θ6 |
| 8 | θ8 = θ1/8 | 8 | θ12 | 4 | θ8 |
| 12 | θ12 = θ1/12 | 12 | θ12 | 4 | θ12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matrone, G.; Ramalli, A. Spatial Coherence of Backscattered Signals in Multi-Line Transmit Ultrasound Imaging and Its Effect on Short-Lag Filtered-Delay Multiply and Sum Beamforming. Appl. Sci. 2018, 8, 486. https://doi.org/10.3390/app8040486
Matrone G, Ramalli A. Spatial Coherence of Backscattered Signals in Multi-Line Transmit Ultrasound Imaging and Its Effect on Short-Lag Filtered-Delay Multiply and Sum Beamforming. Applied Sciences. 2018; 8(4):486. https://doi.org/10.3390/app8040486
Chicago/Turabian StyleMatrone, Giulia, and Alessandro Ramalli. 2018. "Spatial Coherence of Backscattered Signals in Multi-Line Transmit Ultrasound Imaging and Its Effect on Short-Lag Filtered-Delay Multiply and Sum Beamforming" Applied Sciences 8, no. 4: 486. https://doi.org/10.3390/app8040486
APA StyleMatrone, G., & Ramalli, A. (2018). Spatial Coherence of Backscattered Signals in Multi-Line Transmit Ultrasound Imaging and Its Effect on Short-Lag Filtered-Delay Multiply and Sum Beamforming. Applied Sciences, 8(4), 486. https://doi.org/10.3390/app8040486






