A Topological View on Optical and Phononic Fabry–Perot Microcavities through the Su–Schrieffer–Heeger Model
Abstract
:1. Introduction
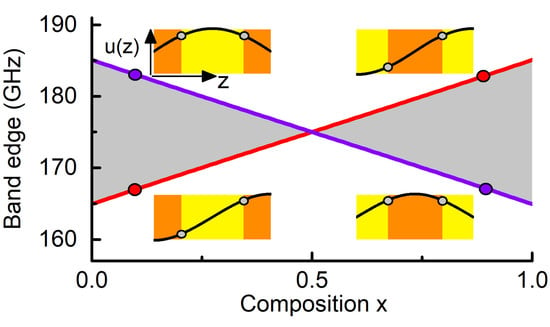
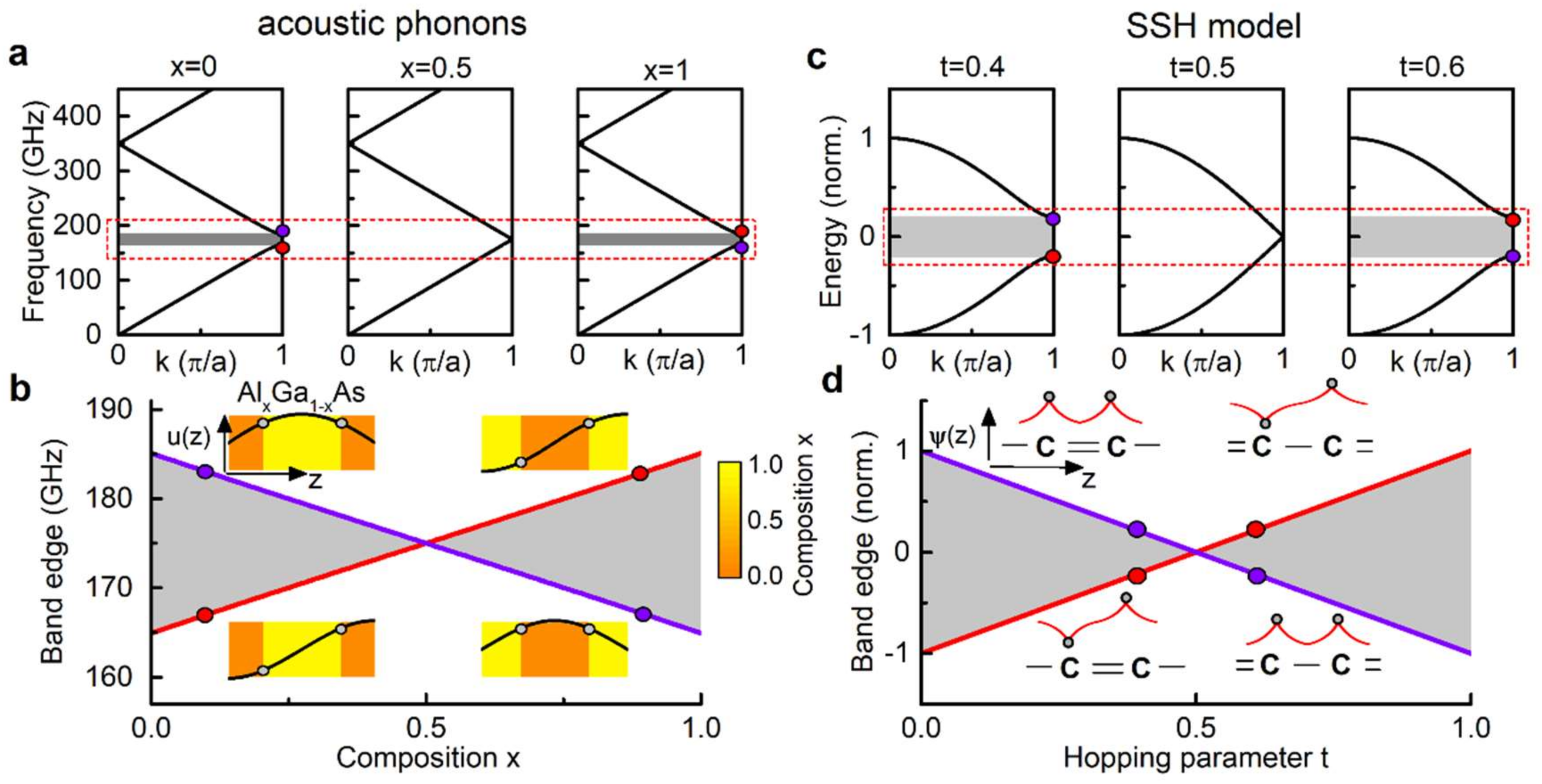
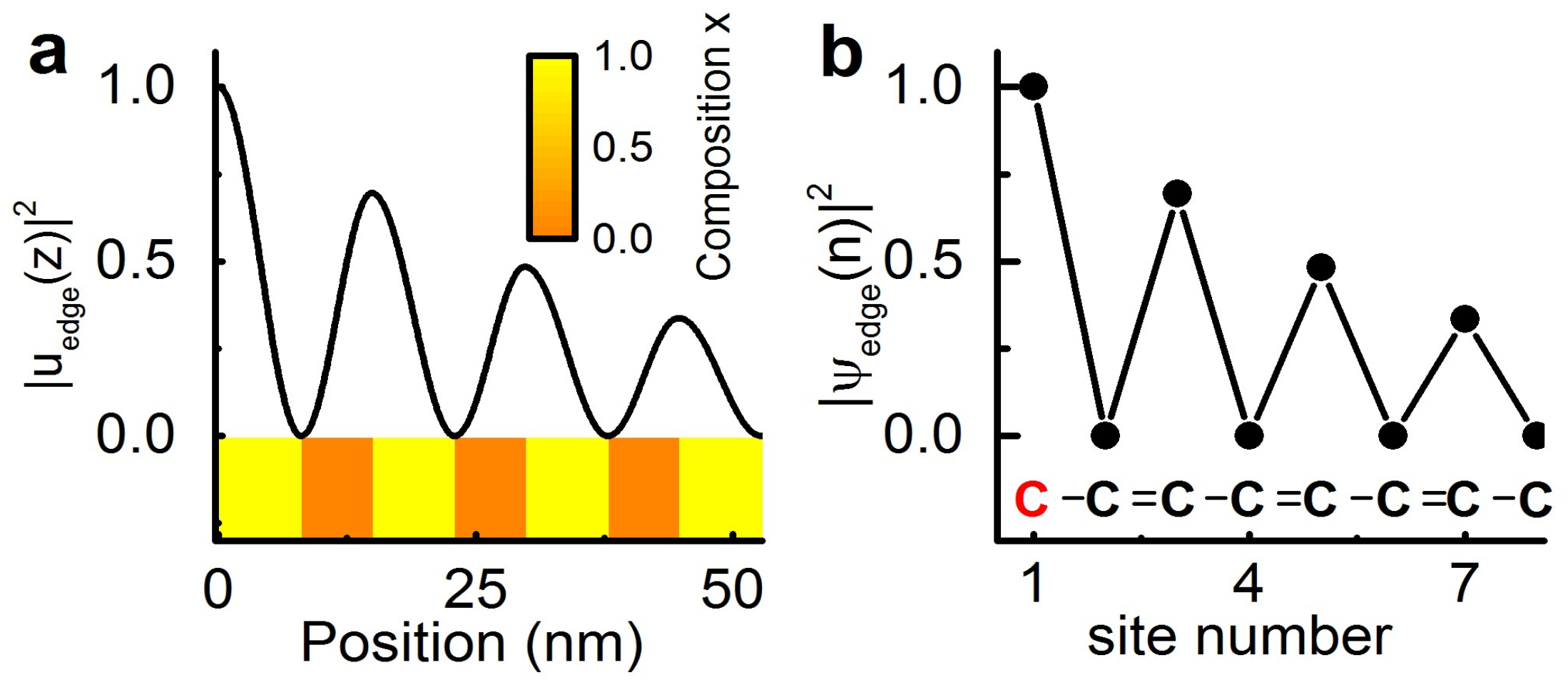
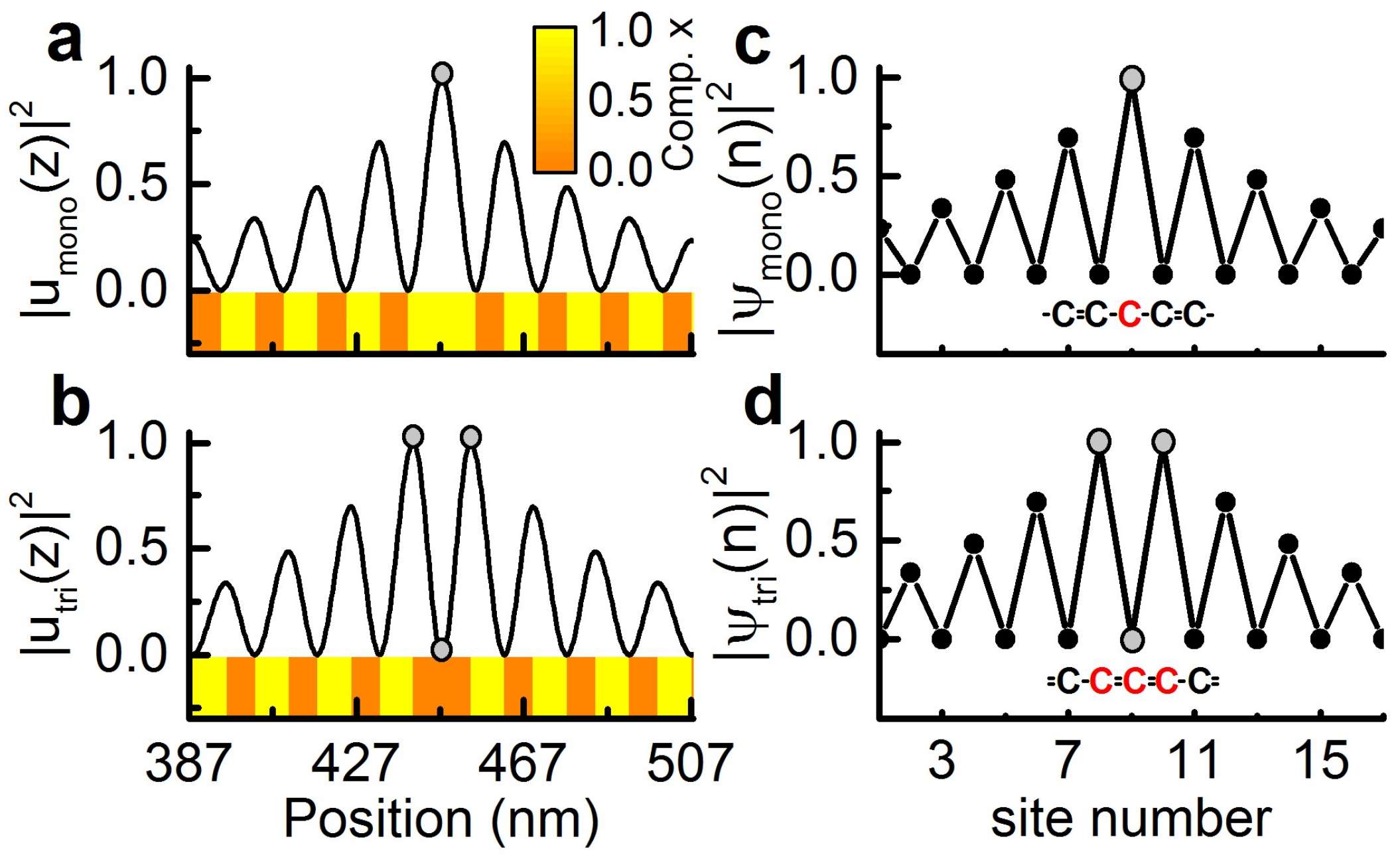
2. Interface Modes through Material Composition Tuning
3. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Adachi, S. GaAs, AlAs, and AlxGa1−xAs: Material parameters for use in research and device applications. J. Appl. Phys. 1985, 58, R1. [Google Scholar] [CrossRef]
- Anguiano, S.; Bruchhausen, A.E.; Jusserand, B.; Favero, I.; Lamberti, F.R.; Lanco, L.; Sagnes, I.; Lemaître, A.; Lanzillotti-Kimura, N.D.; Senellart, P.; et al. Micropillar Resonators for Optomechanics in the Extremely High 19–95-GHz Frequency Range. Phys. Rev. Lett. 2017, 118, 263901. [Google Scholar] [CrossRef] [PubMed]
- Bajoni, D.; Senellart, P.; Wertz, E.; Sagnes, I.; Miard, A.; Lemaître, A.; Bloch, J. Polariton Laser Using Single Micropillar GaAs−GaAlAs Semiconductor Cavities. Phys. Rev. Lett. 2008, 100, 47401. [Google Scholar] [CrossRef] [PubMed]
- Galbiati, M.; Ferrier, L.; Solnyshkov, D.; Tanese, D.; Wertz, E.; Amo, A.; Abbarchi, M.; Senellart, P.; Sagnes, I.; Lemaître, A.; et al. Polariton Condensation in Photonic Molecules. Phys. Rev. Lett. 2012, 108, 126403. [Google Scholar] [CrossRef] [PubMed]
- Jacqmin, T.; Carusotto, I.; Sagnes, I.; Abbarchi, M.; Solnyshkov, D.D.; Malpuech, G.; Galopin, E.; Lemaître, A.; Bloch, J.; Amo, A. Direct Observation of Dirac Cones and a Flatband in a Honeycomb Lattice for Polaritons. Phys. Rev. Lett. 2014, 112, 116402. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.S.; Gerace, D.; Carusotto, I.; Sanvitto, D.; Galopin, E.; Lemaître, A.; Sagnes, I.; Bloch, J.; Amo, A. Acoustic Black Hole in a Stationary Hydrodynamic Flow of Microcavity Polaritons. Phys. Rev. Lett. 2015, 114, 36402. [Google Scholar] [CrossRef] [PubMed]
- Somaschi, N.; Giesz, V.; Santis, L.D.; Loredo, J.C.; Almeida, M.P.; Hornecker, G.; Portalupi, S.L.; Grange, T.; Antón, C.; Demory, J.; et al. Near-optimal single-photon sources in the solid state. Nat. Photonics 2016, 10, 340–345. [Google Scholar] [CrossRef]
- Giesz, V.; Somaschi, N.; Hornecker, G.; Grange, T.; Reznychenko, B.; de Santis, L.; Demory, J.; Gomez, C.; Sagnes, I.; Lemaître, A.; et al. Coherent manipulation of a solid-state artificial atom with few photons. Nat. Commun. 2016, 7, 11986. [Google Scholar] [CrossRef] [PubMed]
- Trigo, M.; Bruchhausen, A.; Fainstein, A.; Jusserand, B.; Thierry-Mieg, V. Confinement of Acoustical Vibrations in a Semiconductor Planar Phonon Cavity. Phys. Rev. Lett. 2002, 89, 227402. [Google Scholar] [CrossRef] [PubMed]
- Huynh, A.; Lanzillotti-Kimura, N.; Jusserand, B.; Perrin, B.; Fainstein, A.; Pascual-Winter, M.; Peronne, E.; Lemaître, A. Subterahertz Phonon Dynamics in Acoustic Nanocavities. Phys. Rev. Lett. 2006, 97, 115502. [Google Scholar] [CrossRef] [PubMed]
- Fainstein, A.; Lanzillotti-Kimura, N.D.; Jusserand, B.; Perrin, B. Strong Optical-Mechanical Coupling in a Vertical GaAs/AlAs Microcavity for Subterahertz Phonons and Near-Infrared Light. Phys. Rev. Lett. 2013, 110, 37403. [Google Scholar] [CrossRef] [PubMed]
- Lanzillotti-Kimura, N.; Fainstein, A.; Balseiro, C.; Jusserand, B. Phonon engineering with acoustic nanocavities: Theoretical considerations on phonon molecules, band structures, and acoustic Bloch oscillations. Phys. Rev. B 2007, 75, 24301. [Google Scholar] [CrossRef]
- Winter, M.F.P.; Rozas, G.; Fainstein, A.; Jusserand, B.; Perrin, B.; Huynh, A.; Vaccaro, P.O.; Saravanan, S. Selective Optical Generation of Coherent Acoustic Nanocavity Modes. Phys. Rev. Lett. 2007, 98, 265501. [Google Scholar] [CrossRef] [PubMed]
- Villafañe, V.; Soubelet, P.; Bruchhausen, A.E.; Lanzillotti-Kimura, N.D.; Jusserand, B.; Lemaître, A.; Fainstein, A. Slow light and slow acoustic phonons in optophononic resonators. Phys. Rev. B 2016, 94, 205308. [Google Scholar] [CrossRef]
- Rozas, G.; Winter, M.; Jusserand, B.; Fainstein, A.; Perrin, B.; Semenova, E.; Lemaître, A. Lifetime of THz Acoustic Nanocavity Modes. Phys. Rev. Lett. 2009, 102, 15502. [Google Scholar] [CrossRef] [PubMed]
- Lanzillotti-Kimura, N.; Fainstein, A.; Perrin, B.; Jusserand, B.; Soukiassian, A.; Xi, X.; Schlom, D. Enhancement and Inhibition of Coherent Phonon Emission of a Ni Film in a BaTiO3/SrTiO3 Cavity. Phys. Rev. Lett. 2010, 104, 187402. [Google Scholar] [CrossRef] [PubMed]
- Lanzillotti-Kimura, N.D.; Fainstein, A.; Jusserand, B. Towards GHz–THz cavity optomechanics in DBR-based semiconductor resonators. Ultrasonics 2015, 56, 80–89. [Google Scholar] [CrossRef] [PubMed]
- Kimura, N.D.L.; Fainstein, A.; Jusserand, B. Phonon Bloch oscillations inacoustic-cavity structures. Phys. Rev. B 2005, 71, 41305. [Google Scholar] [CrossRef]
- Lanzillotti-Kimura, N.D.; Fainstein, A.; Perrin, B.; Jusserand, B.; Mauguin, O.; Largeau, L.; Lemaître, A. Bloch Oscillations of THz Acoustic Phonons in Coupled Nanocavity Structures. Phys. Rev. Lett. 2010, 104, 197402. [Google Scholar] [CrossRef] [PubMed]
- Jäger, J.V.; Scherbakov, A.V.; Glavin, B.A.; Salasyuk, A.S.; Campion, R.P.; Rushforth, A.W.; Yakovlev, D.R.; Akimov, A.V.; Bayer, M. Resonant driving of magnetization precession in a ferromagnetic layer by coherent monochromatic phonons. Phys. Rev. B 2015, 92, 20404. [Google Scholar] [CrossRef]
- Brüggemann, C.; Akimov, A.V.; Scherbakov, A.V.; Bombeck, M.; Schneider, C.; Höfling, S.; Forchel, A.; Yakovlev, D.R.; Bayer, M. Laser mode feeding by shaking quantum dots in a planar microcavity. Nat. Photonics 2012, 6, 30–34. [Google Scholar] [CrossRef]
- Beardsley, R.P.; Akimov, A.V.; Henini, M.; Kent, A.J. Coherent Terahertz Sound Amplification and Spectral Line Narrowing in a Stark Ladder Superlattice. Phys. Rev. Lett. 2010, 104, 85501. [Google Scholar] [CrossRef] [PubMed]
- Maryam, W.; Akimov, A.V.; Campion, R.P.; Kent, A.J. Dynamics of a vertical cavity quantum cascade phonon laser structure. Nat. Commun. 2013, 4, 2184. [Google Scholar] [CrossRef] [PubMed]
- Villafañe, V.; Bruchhausen, A.E.; Jusserand, B.; Senellart, P.; Lemaître, A.; Fainstein, A. Confinement of gigahertz sound and light in Tamm plasmon resonators. Phys. Rev. B 2015, 92, 165308. [Google Scholar] [CrossRef]
- Lamberti, F.R.; Esmann, M.; Lemaître, A.; Carbonell, C.G.; Krebs, O.; Favero, I.; Jusserand, B.; Senellart, P.; Lanco, L.; Lanzillotti-Kimura, N.D. Nanomechanical resonators based on adiabatic periodicity-breaking in a superlattice. Appl. Phys. Lett. 2017, 111, 173107. [Google Scholar] [CrossRef]
- Lamberti, F.R.; Yao, Q.; Lanco, L.; Nguyen, D.T.; Esmann, M.; Fainstein, A.; Sesin, P.; Anguiano, S.; Villafañe, V.; Bruchhausen, A.; et al. Optomechanical properties of GaAs/AlAs micropillar resonators operating in the 18 GHz range. Opt. Express 2017, 25, 24437–24447. [Google Scholar] [CrossRef] [PubMed]
- Esmann, M.; Lamberti, F.R.; Senellart, P.; Favero, I.; Krebs, O.; Lanco, L.; Carbonell, C.G.; Lemaitre, A.; Lanzillotti-Kimura, N.D. Topological nanophononic states by band inversion. arxiv, 2018; arXiv:1802.08870. [Google Scholar]
- Xiao, M.; Ma, G.; Yang, Z.; Sheng, P.; Zhang, Z.Q.; Chan, C.T. Geometric phase and band inversion in periodic acoustic systems. Nat. Phys. 2015, 11, 240–244. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Z.Q.; Chan, C.T. Surface Impedance and Bulk Band Geometric Phases in One-Dimensional Systems. Phys. Rev. X 2014, 4, 21017. [Google Scholar] [CrossRef]
- Rhim, J.-M.; Behrends, J.; Bardarson, J.H. Bulk-boundary correspondence from the inter-cellular Zak phase. Phys. Rev. B 2017, 95, 35421. [Google Scholar] [CrossRef]
- Amo, A.; Lemaître, A.; Galopin, E.; Sagnes, I.; Bloch, J.; Gratiet, L.L.; St-Jean, P.; Ozawa, T.; Goblot, V. Lasing in topological edge states of a one-dimensional lattice. Nat. Photonics 2017, 11, 651–656. [Google Scholar]
- Heeger, A.J. Nobel Lecture: Semiconducting and metallic polymers:The fourth generation of polymeric materials. Rev. Mod. Phys. 2001, 73, 681. [Google Scholar] [CrossRef]
- Su, W.; Schrieffer, J.R.; Heeger, A.J. Solitons in Polyacetylene. Phys. Rev. Lett. 1979, 42, 1698. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [PubMed]
- Zak, J. Berry’s phase for energy bands in solids. Phys. Rev. Lett. 1989, 62, 2747. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.-G.; Geng, Z.-G.; Zhu, X.-F. Topologically protected bound states in one-dimensional Floquet acoustic waveguide systems. J. Appl. Phys. 2018, 123, 91716. [Google Scholar] [CrossRef]
- Jusserand, B.; Cardona, M. Light Scatt. Solids V; Springer: Berlin/Heidelberg, Germany, 1989; pp. 49–152. [Google Scholar]
- Su, W.-P.; Schrieffer, J.R.; Heeger, A.J. Soliton excitations in polyacetylene. Phys. Rev. B 1980, 22, 2099. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Lanzillotti-Kimura, N.D.; Fainstein, A.; Jusserand, B.; Lemaître, A. Resonant Raman scattering of nanocavity-confined acoustic phonons. Phys. Rev. B 2009, 79, 35404. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmann, M.; Lanzillotti-Kimura, N.D. A Topological View on Optical and Phononic Fabry–Perot Microcavities through the Su–Schrieffer–Heeger Model. Appl. Sci. 2018, 8, 527. https://doi.org/10.3390/app8040527
Esmann M, Lanzillotti-Kimura ND. A Topological View on Optical and Phononic Fabry–Perot Microcavities through the Su–Schrieffer–Heeger Model. Applied Sciences. 2018; 8(4):527. https://doi.org/10.3390/app8040527
Chicago/Turabian StyleEsmann, Martin, and Norberto Daniel Lanzillotti-Kimura. 2018. "A Topological View on Optical and Phononic Fabry–Perot Microcavities through the Su–Schrieffer–Heeger Model" Applied Sciences 8, no. 4: 527. https://doi.org/10.3390/app8040527
APA StyleEsmann, M., & Lanzillotti-Kimura, N. D. (2018). A Topological View on Optical and Phononic Fabry–Perot Microcavities through the Su–Schrieffer–Heeger Model. Applied Sciences, 8(4), 527. https://doi.org/10.3390/app8040527