Three-Dimensional Modeling of a Robotic Fish Based on Real Carp Locomotion
Abstract
:1. Introduction
2. Three Dimensional Dynamic Model and Motion Equations of the Robotic Fish
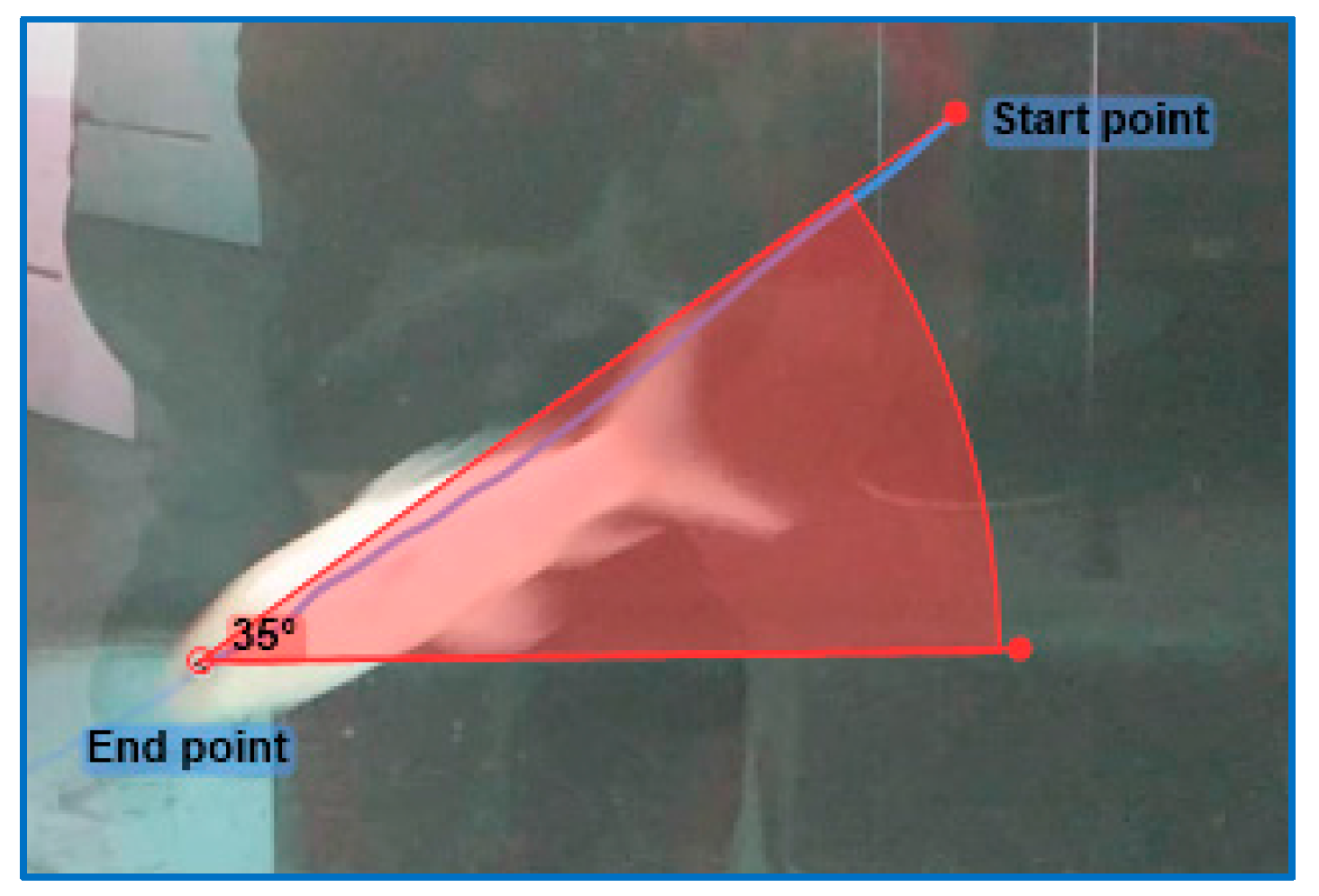
2.1. Carp Locomotion
2.2. Swimming Motion of the Robotic Fish
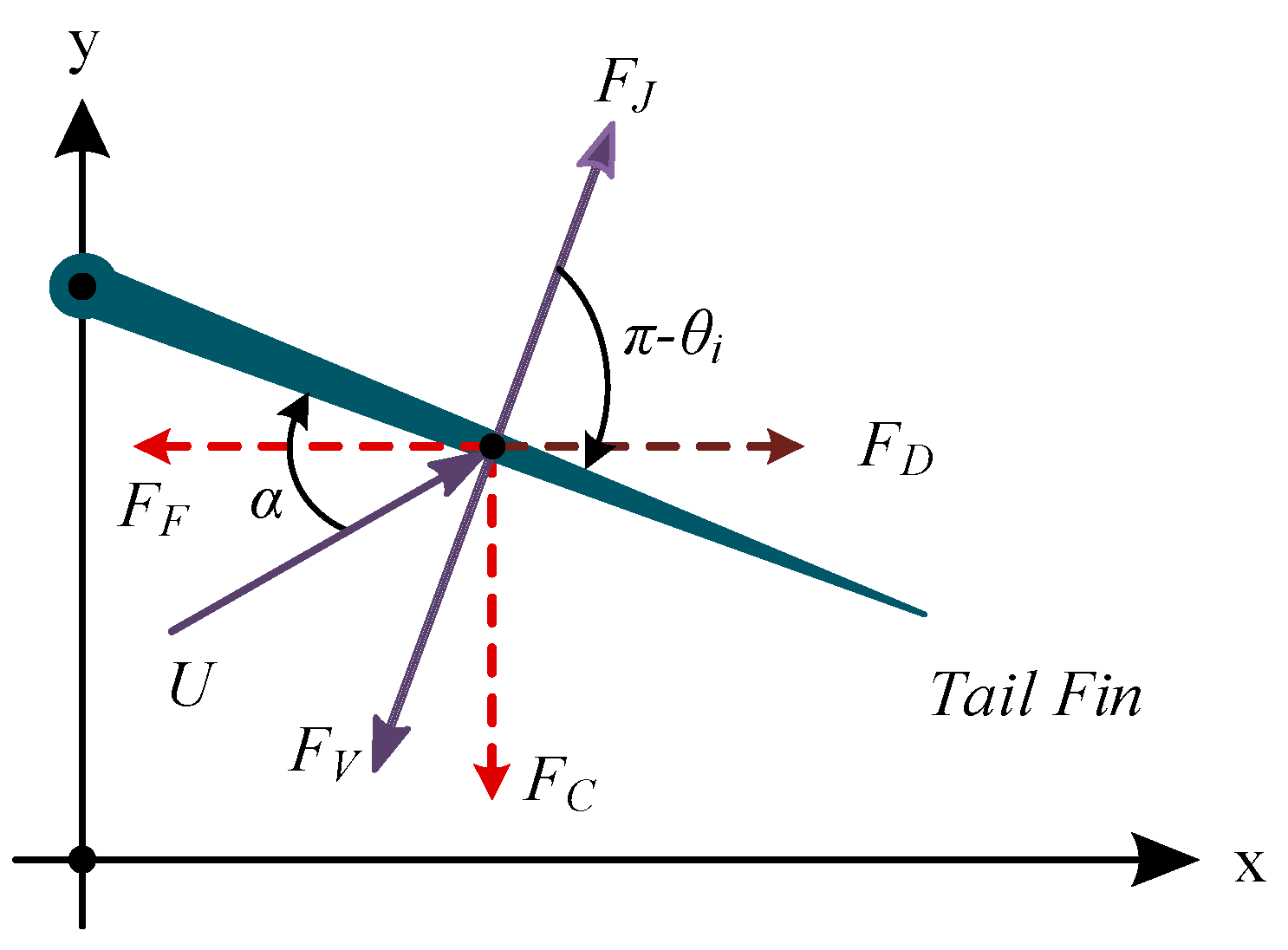
2.3. Hydrodynamic Forces Acting on the Tail
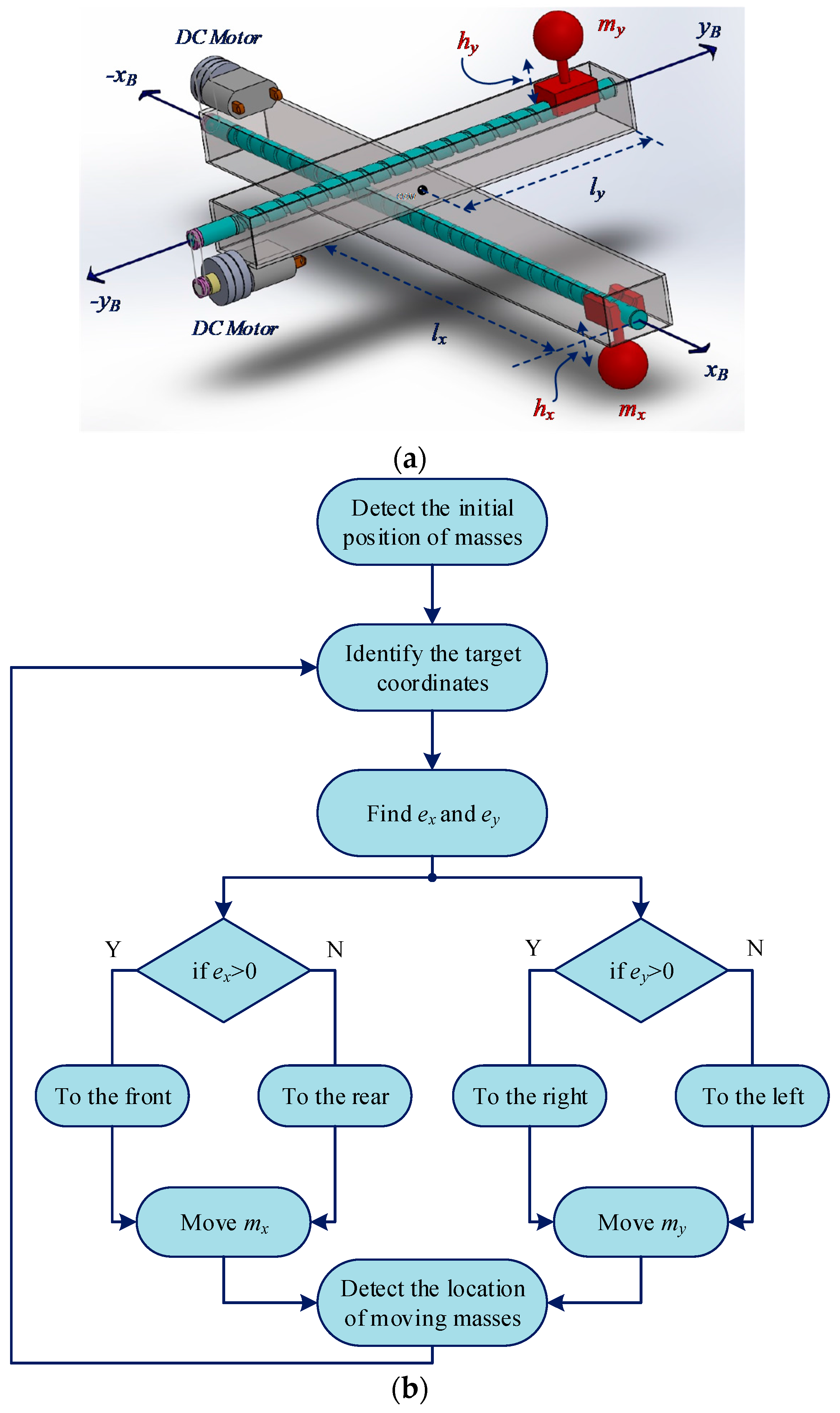
2.4. Modeling of the Up-Down Motion Mechanism
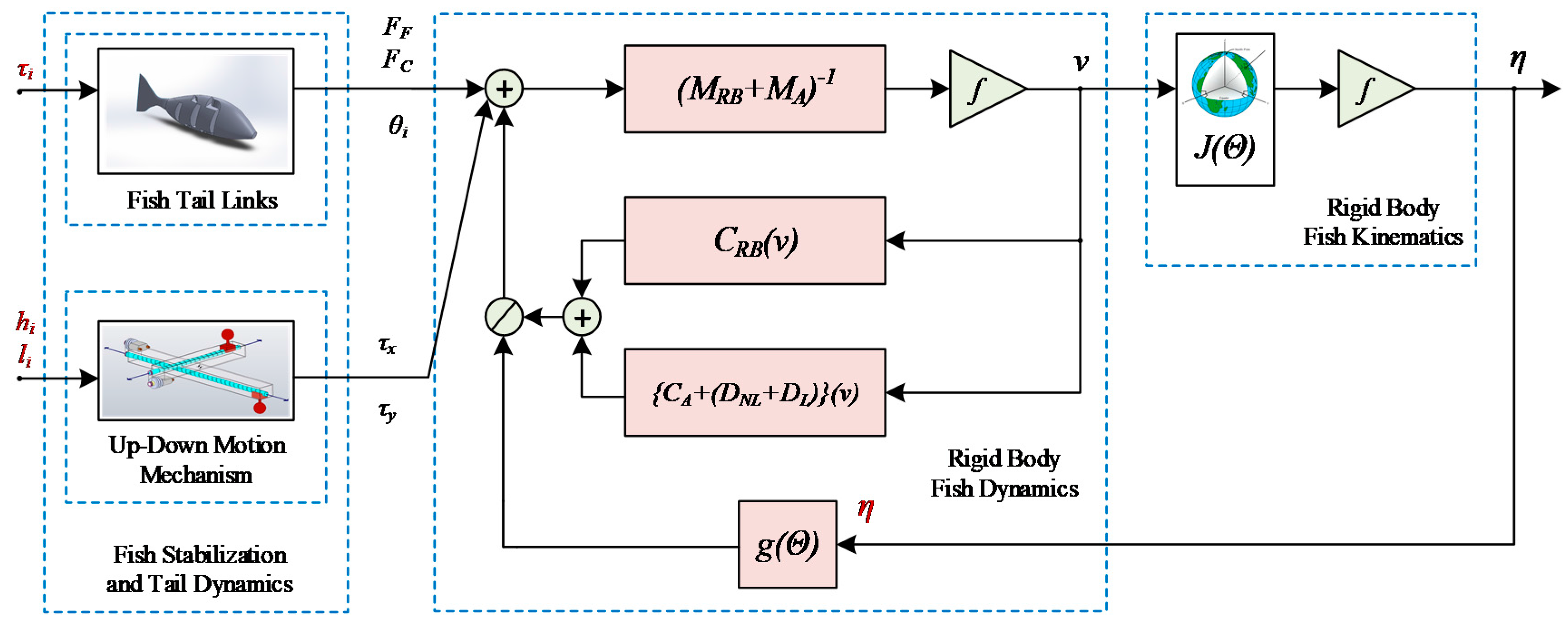
2.5. Three Dimensional Model Equations of Motion
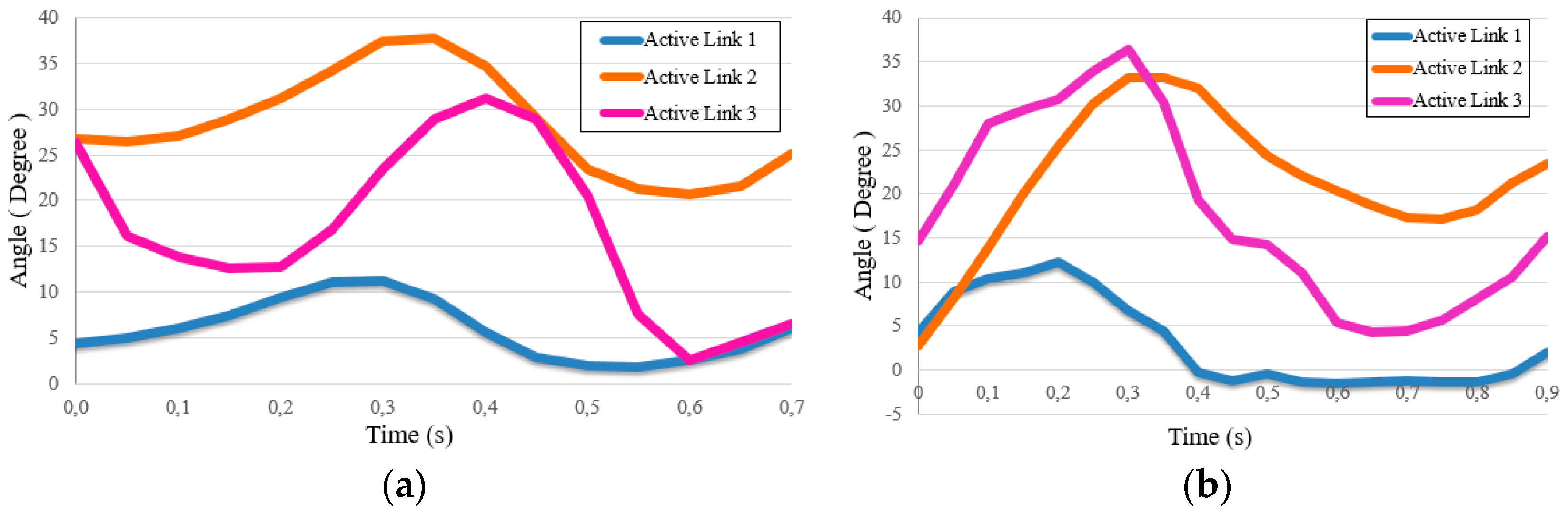
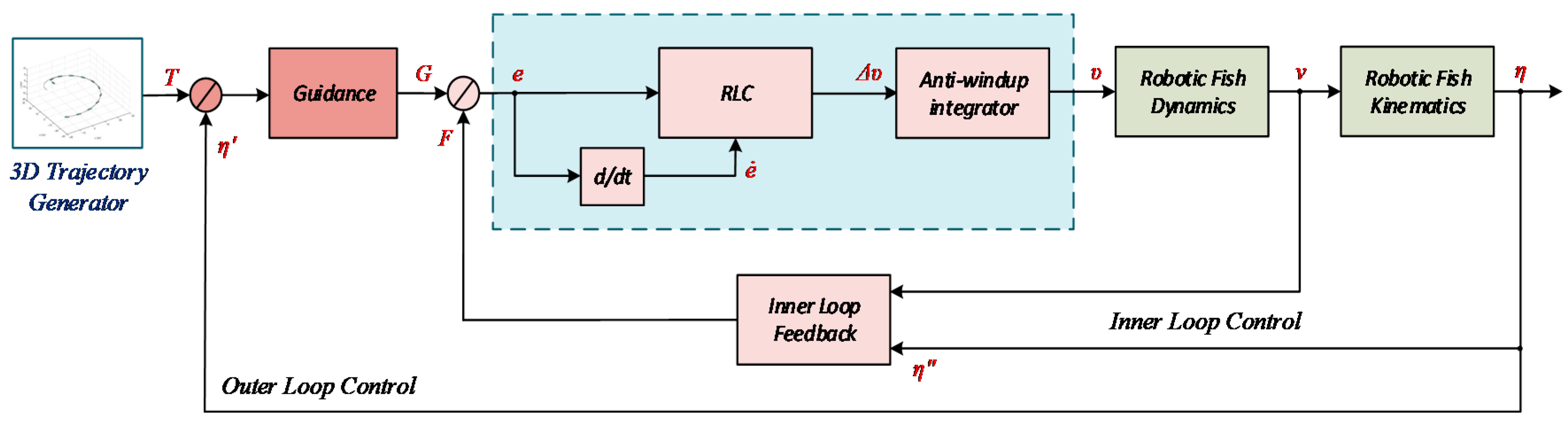
3. Implementations of the Fish-Like Motion
- Proportional optimum link lengths according to actual size,
- Flapping frequency,
- Swimming speed performance,
- Proportional physical parameters according to the carp,
- Trajectory tracking.
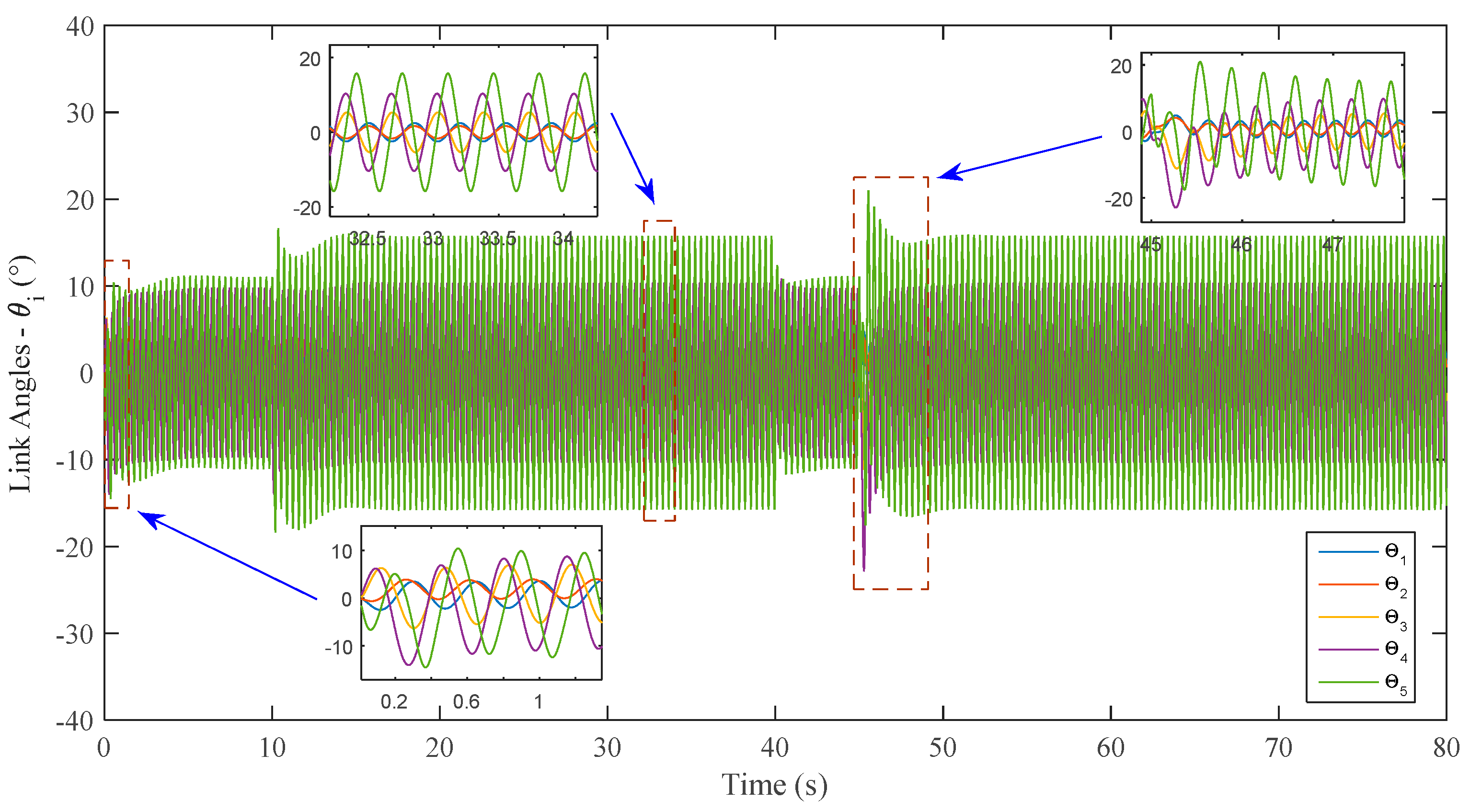
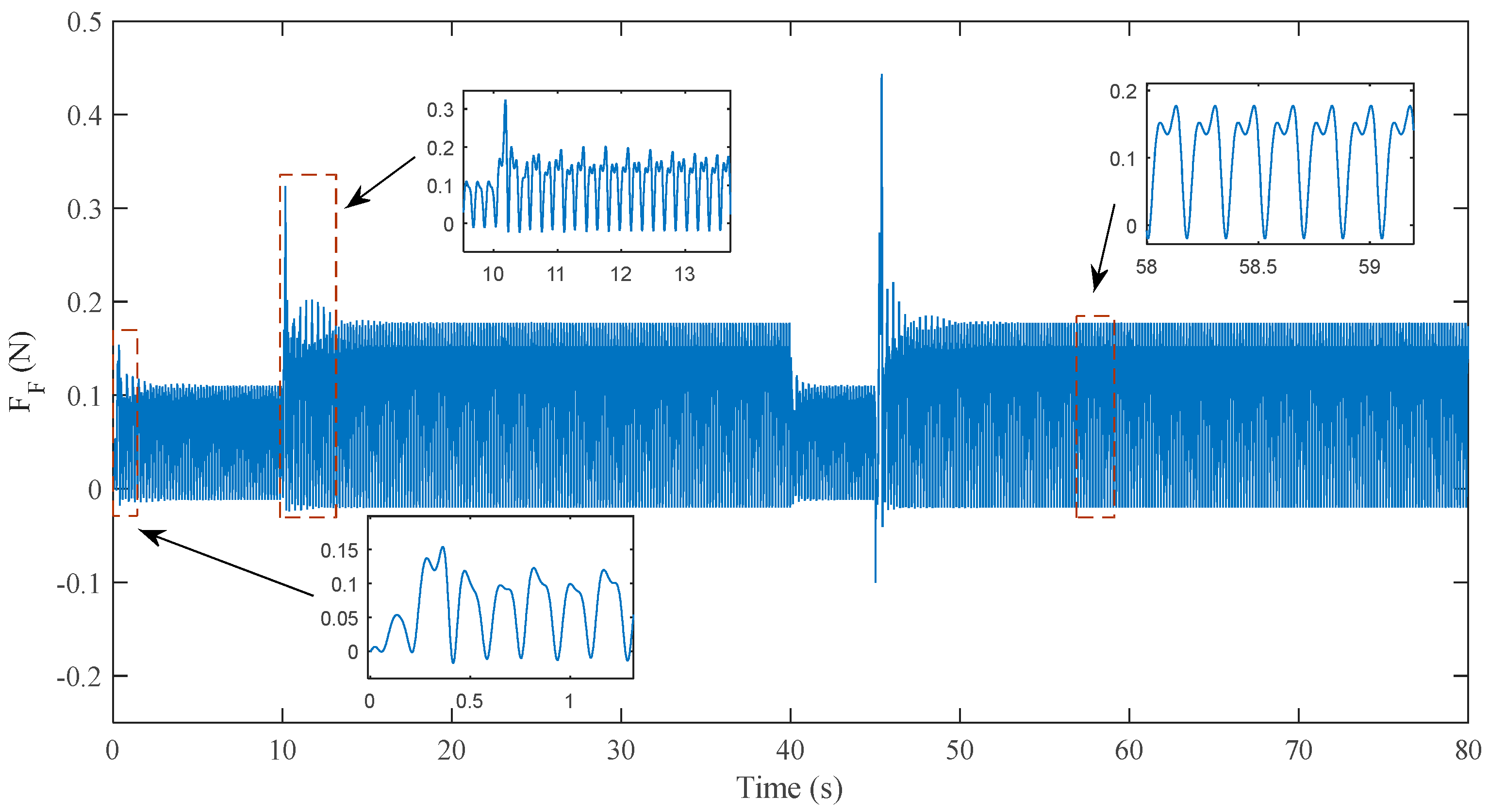
3.1. Ability of the Fish-Like Motion
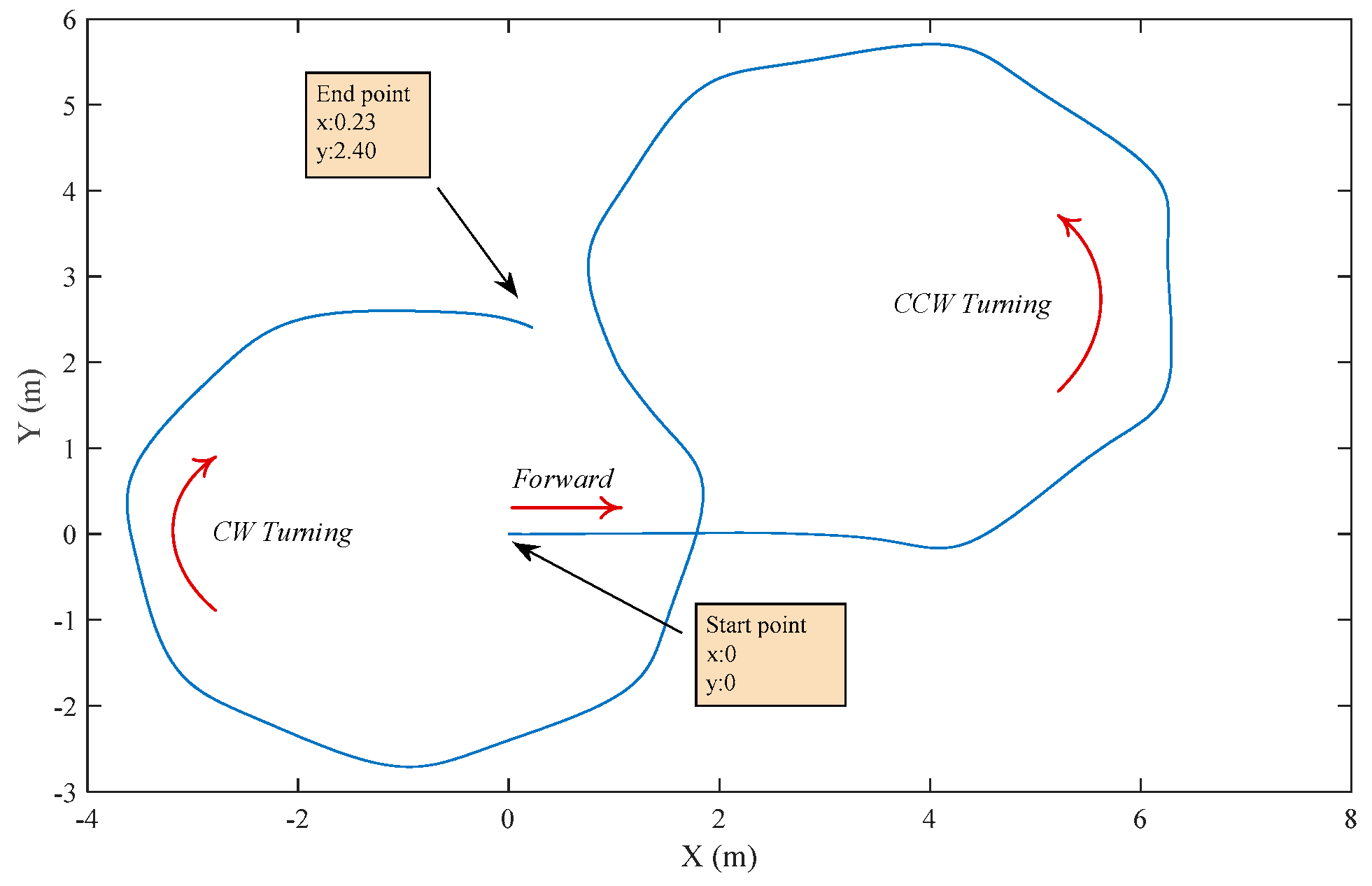
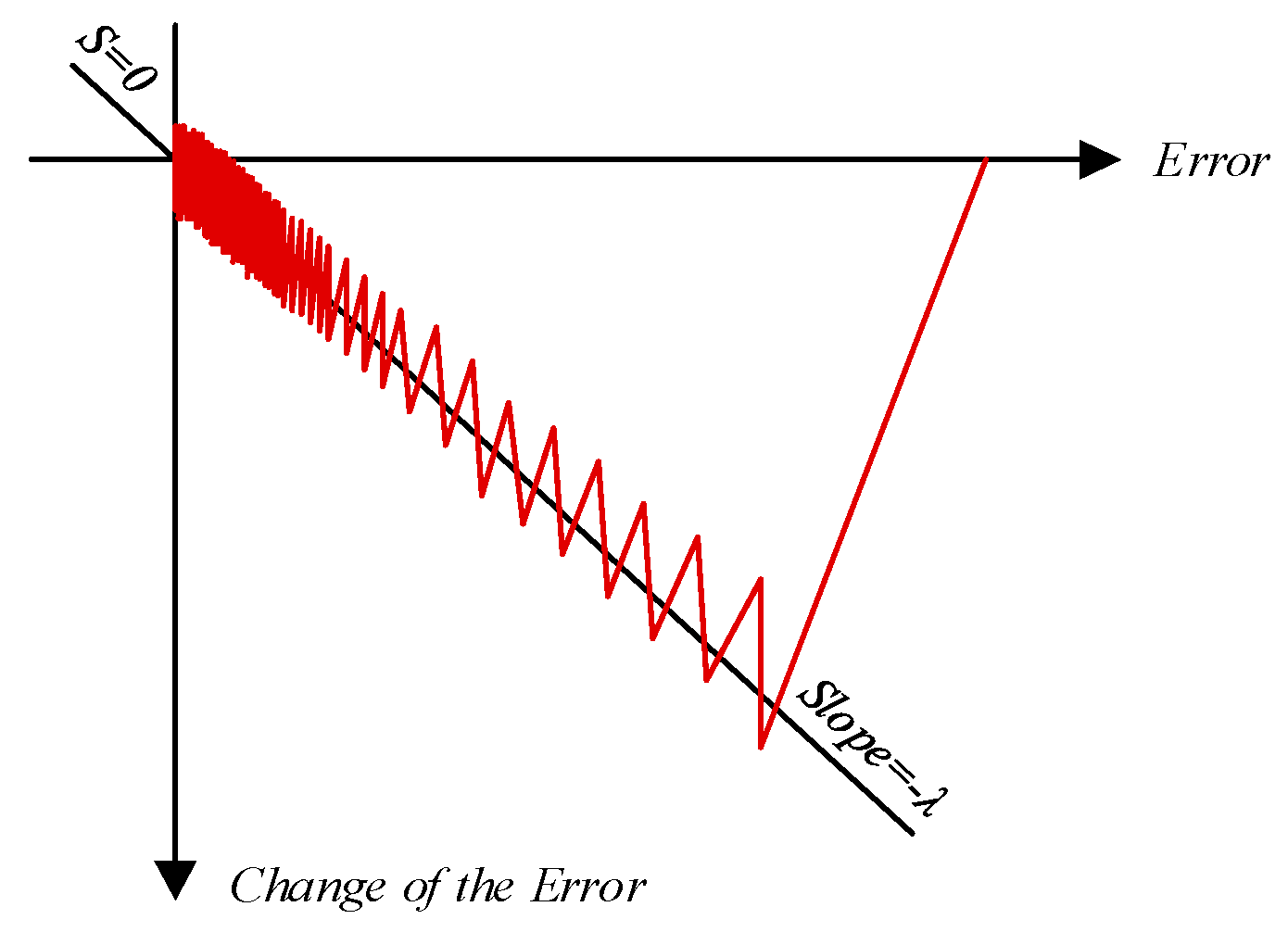
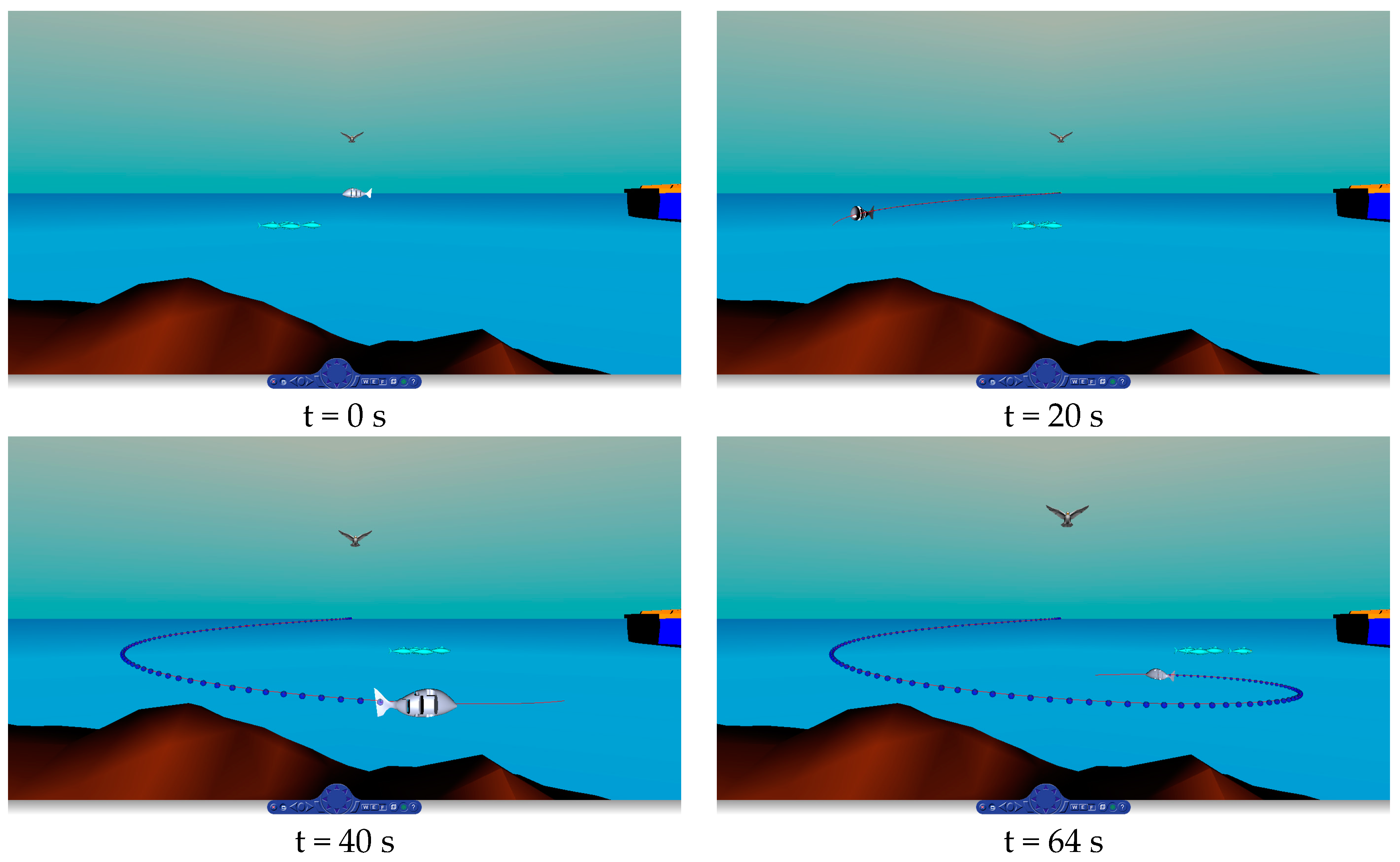
3.2. Guidance and Trajectory Tracking
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yu, J.; Wang, M.; Su, Z.; Tan, M.; Zhang, J. Dynamic modeling of a CPG-governed multijoint robotic fish. Adv. Robot. 2013, 27, 275–285. [Google Scholar] [CrossRef]
- Ding, R.; Yu, J.; Yang, Q.; Tan, M.; Zhang, J. Dolphin-like swimming modeling for a biomimetic amphibious robot. IFAC Proc. Vol. 2011, 18, 9367–9372. [Google Scholar] [CrossRef]
- Zhou, C.; Cao, Z.; Wang, S.; Tan, M. A marsupial robotic fish team: Design, motion and cooperation. Sci. China Technol. Sci. 2010, 53, 2896–2904. [Google Scholar] [CrossRef]
- Lauder, G.V.; Madden, P.G.A. Learning from fish: Kinematics and experimental hydrodynamics for roboticists. Int. J. Autom. Comput. 2006, 3, 325–335. [Google Scholar] [CrossRef]
- Zhang, F.; Tan, X. Three-Dimensional Spiral Tracking Control for Gliding Robotic Fish. In Proceedings of the 2014 IEEE 53rd Annual Conference on Decision and Control (CDC), Los Angeles, CA, USA, 15–17 December 2014; pp. 5340–5345. [Google Scholar]
- Yang, G.H.; Choi, W.; Lee, S.H.; Kim, K.S.; Lee, H.J.; Choi, H.S.; Ryuh, Y.S. Control and Design of a 3 DOF Fish Robot ‘ICHTUS’. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics (ROBIO), Karon Beach, Phuket, Thailand, 7–11 December 2011; pp. 2108–2113. [Google Scholar]
- Zhou, C.; Tan, M.; Cao, Z.; Wang, S.; Creighton, D.; Gu, N.; Nahavandi, S. Kinematic Modeling of a Bio-Inspired Robotic Fish. In Proceedings of the IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 695–699. [Google Scholar]
- Suebsaiprom, P.; Lin, C.L. Fish-Tail Modeling for Fish Robot. In Proceedings of the 2012 International Symposium on Computer, Consumer and Control (IS3C), Taichung, Taiwan, 4–6 June 2012; pp. 548–551. [Google Scholar]
- Ryuh, Y.S.; Yang, G.H.; Liu, J.; Hu, H. A school of robotic fish for mariculture monitoring in the sea coast. J. Bionic Eng. 2015, 12, 37–46. [Google Scholar] [CrossRef]
- Masoomi, S.F.; Gutschmidt, S.; Chen, X.; Sellier, M. The Kinematics and Dynamics of Undulatory Motion of a Tuna-mimetic Robot. Int. J. Adv. Robot. Syst. 2015, 12, 83. [Google Scholar] [CrossRef]
- Liu, J.; Hu, H. Biological Inspiration: From Carangiform Fish to Multi-Joint Robotic Fish. J. Bionic Eng. 2010, 7, 35–48. [Google Scholar] [CrossRef]
- Niu, X.; Xu, J.; Ren, Q.; Wang, Q. Locomotion learning for an anguilliform robotic fish using central pattern generator approach. IEEE Trans. Ind. Electron. 2014, 61, 4780–4787. [Google Scholar] [CrossRef]
- Li, G.; Deng, Y.; Osen, O.L.; Bi, S.; Zhang, H. A Bio-Inspired Swimming Robot for Marine Aquaculture Applications: From Concept-Design to Simulation. In Proceedings of the Oceans 2016—Shanghai, Shanghai, China, 10–13 April 2016; pp. 1–7. [Google Scholar]
- Sfakiotakis, M. Review of Fish Swimming Modes for Aquatic Locomotion. IEEE J. Ocean. Eng. 1998, 24, 237–252. [Google Scholar] [CrossRef]
- Suebsaiprom, P.; Lin, C.L. Maneuverability modeling and trajectory tracking for fish robot. Control Eng. Pract. 2015, 45, 22–36. [Google Scholar] [CrossRef]
- Chowdhury, A.R.; Prasad, B.; Kumar, V.; Kumar, R.; Panda, S.K. Design, Modeling and Open-Loop Control of a BCF Mode Bio-Mimetic Robotic Fish. In Proceedings of the 2011 International Siberian Conference on Control and Communications (SIBCON), Krasnoyarsk, Russia, 15–16 September 2011; pp. 226–231. [Google Scholar]
- Hu, Y.H.; Zhao, W.; Wang, L. Vision-Based Target Tracking and Collision Avoidance for Two Autonomous Robotic Fish. IEEE Trans. Ind. Electron. 2009, 56, 1401–1410. [Google Scholar]
- Yu, J.; Wang, S.; Tan, M. A simplified propulsive model of bio-mimetic robot fish and its realization. Robotica 2005, 23, 101–107. [Google Scholar] [CrossRef]
- Yu, J.Z.; Liu, L.Z.; Tan, M. Three-dimensional dynamic modelling of robotic fish: simulations and experiments. Trans. Inst. Meas. Control 2008, 30, 239–258. [Google Scholar]
- Wang, W.; Xie, G.; Shi, H. Dynamic Modeling of an Ostraciiform Robotic Fish Based on Angle of Attack Theory. In Proceedings of the 2014 International Joint Conference on Neural Networks (IJCNN), Beijing, China, 6–11 July 2014; pp. 3944–3949. [Google Scholar]
- Li, G.; Zhang, H.; Zhang, J.; Bye, R.T. Development of adaptive locomotion of a caterpillar-like robot based on a sensory feedback CPG model. Adv. Robot. 2014, 28, 389–401. [Google Scholar] [CrossRef]
- Li, G.; Zhang, H.; Li, W.; Hildre, H.P.; Zhang, J. Design of Neural Circuit for Sidewinding of Snake-Like Robots. In Proceedings of the 2014 IEEE International Conference on Information and Automation (ICIA), Hailar, China, 28–30 July 2014; pp. 333–338. [Google Scholar]
- Ijspeert, A.J. Central pattern generators for locomotion control in animals and robots: A review. Neural Netw. 2008, 21, 642–653. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Hu, H. A 3D simulator for autonomous robotic fish. Int. J. Autom. Comput. 2004, 1, 42–50. [Google Scholar] [CrossRef]
- Yu, J.Y.J.; Liu, L.L.L.; Wang, L.W.L. Dynamic Modeling of Robotic Fish Using Schiehien’s Method. In Proceedings of the 2006 IEEE International Conference on Robotics and Biomimetics, Kunming, China, 17–20 December 2006; pp. 457–462. [Google Scholar]
- Liu, L.; Yu, J.; Wang, L. Dynamic Modeling of Three-Dimensional Swimming for Biomimetic Robotic Fish. In Proceedings of the IEEE International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006; pp. 3916–3921. [Google Scholar]
- Zhou, C.; Cao, Z.; Wang, S.; Tan, M. The Dynamic Analysis of the Backward Swimming Mode for Biomimetic Carangiform Robotic Fish. In Proceedings of the IROS 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, 22–26 September 2008; pp. 3072–3076. [Google Scholar]
- Nakashima, M.; Ohgishi, N.; Ono, K. A study on the propulsive mechanism of a double jointed fish robot utilizing self-excitation control. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2003, 46, 982–990. [Google Scholar] [CrossRef]
- Kim, H.; Lee, B.; Kim, R. A Study on the motion mechanism of articulated fish robot. In Proceedings of the 2007 IEEE International Conference on Mechatronics and Automation (ICMA), Harbin, China, 5–8 August 2007; pp. 485–490. [Google Scholar]
- Suebsaiprom, P.; Lin, C.L. 2-DOF Barycenter Mechanism for Stabilization of Fish-Robots. In Proceedings of the 2013 IEEE 8th Conference on Industrial Electronics and Applications (ICIEA), Melbourne, VIC, Australia, 19–21 June 2013; pp. 1119–1122. [Google Scholar]
- Yu, J.; Wang, L.; Tan, M. Geometric optimization of relative link lengths for biomimetic robotic fish. IEEE Trans. Robot. 2007, 23, 382–386. [Google Scholar] [CrossRef]
- Bal, C.; Korkmaz, D.; Koca, G.O.; Ay, M.; Akpolat, Z.H. Link Length Optimization of A Biomimetic Robotic Fish Based on Big Bang—Big Crunch Algorithm. In Proceedings of the 21st International Conference on Methods and Models in Automation and Robotics (MMAR), Miedzyzdroje, Poland, 29 August–1 September 2016; pp. 189–193. [Google Scholar]
- Yu, J.; Tan, M.; Chen, J.; Zhang, J. A survey on CPG-inspired control models and system implementation. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 441–456. [Google Scholar] [PubMed]
- Ozmen Koca, G.; Korkmaz, D.; Bal, C.; Akpolat, Z.H.; Ay, M. Implementations of the route planning scenarios for the autonomous robotic fish with the optimized propulsion mechanism. Measurement 2016, 93, 232–242. [Google Scholar] [CrossRef]
- Vo, T.Q.; Kim, H.S.; Lee, B.R. Smooth gait optimization of a fish robot using the genetic-hill climbing algorithm. Robotica 2012, 30, 257–278. [Google Scholar] [CrossRef]
- Gao, W.B.; Wang, Y.F.; Homaifa, A. Discrete-Time Variable-Structure Control-Systems. IEEE Trans. Ind. Electron. 1995, 42, 117–122. [Google Scholar]
- Akpolat, Z.; Gokbulut, M. Discrete time adaptive reaching law speed control of electrical drives. Electr. Eng. 2003, 85, 53–58. [Google Scholar] [CrossRef]
- Akpolat, Z.H.; Guldemir, H. Trajectory following sliding mode control of induction motors. Electr. Eng. 2003, 85, 205–209. [Google Scholar] [CrossRef]






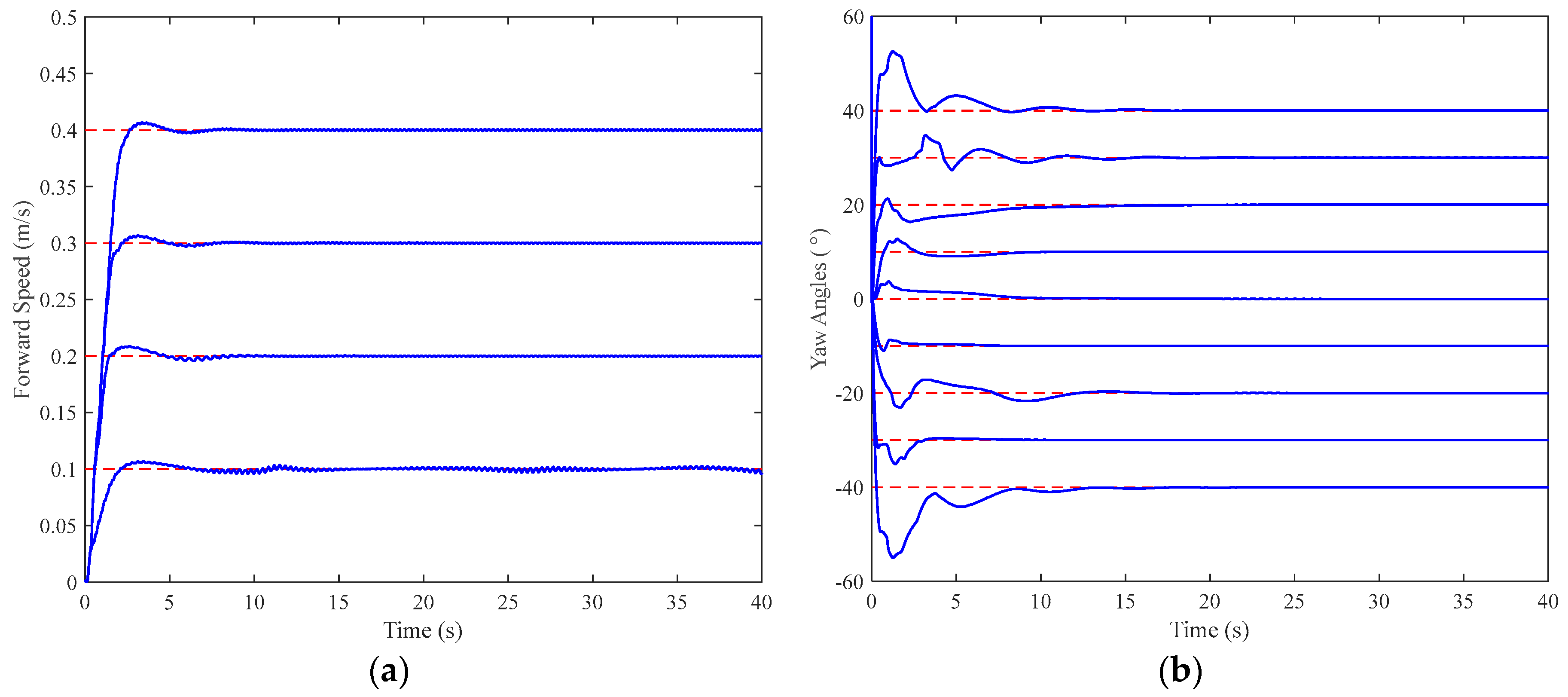
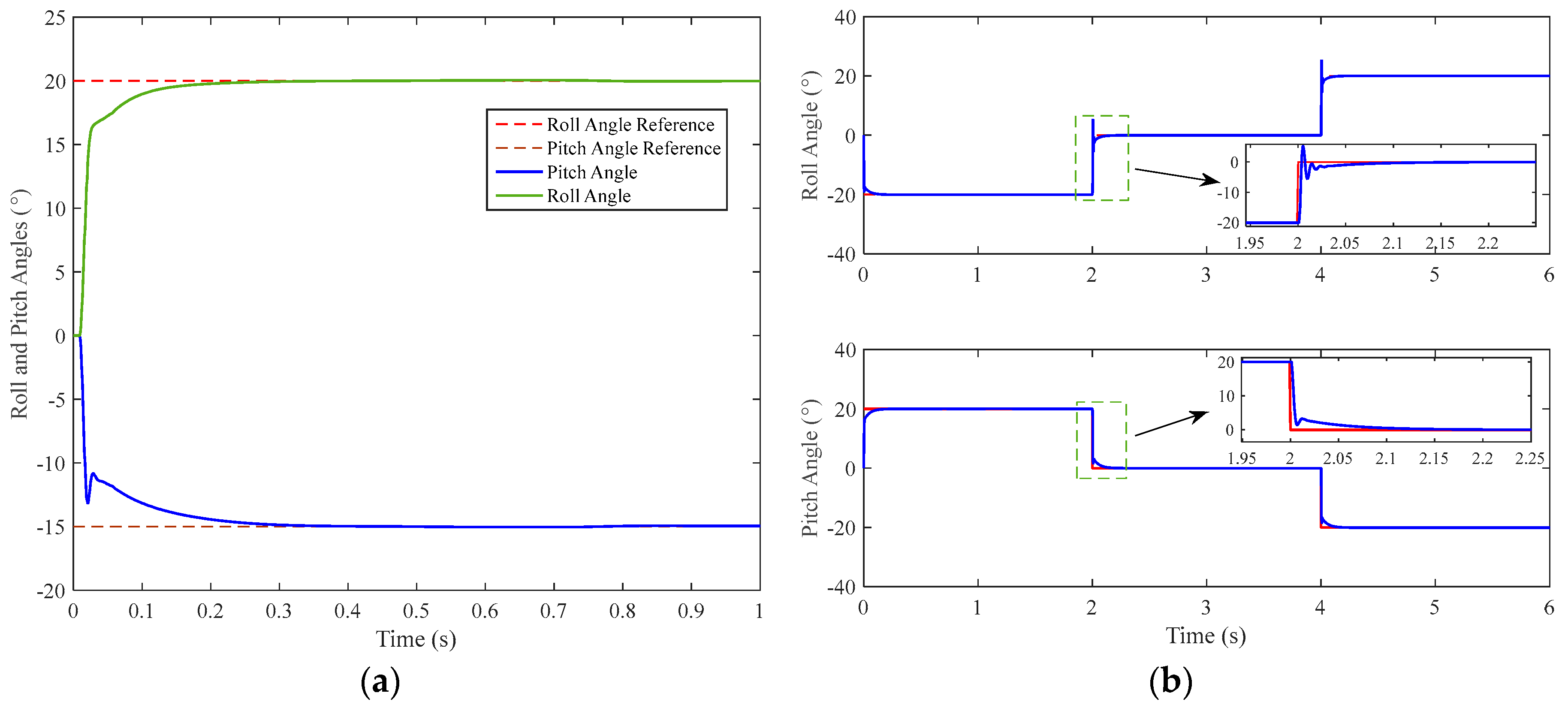

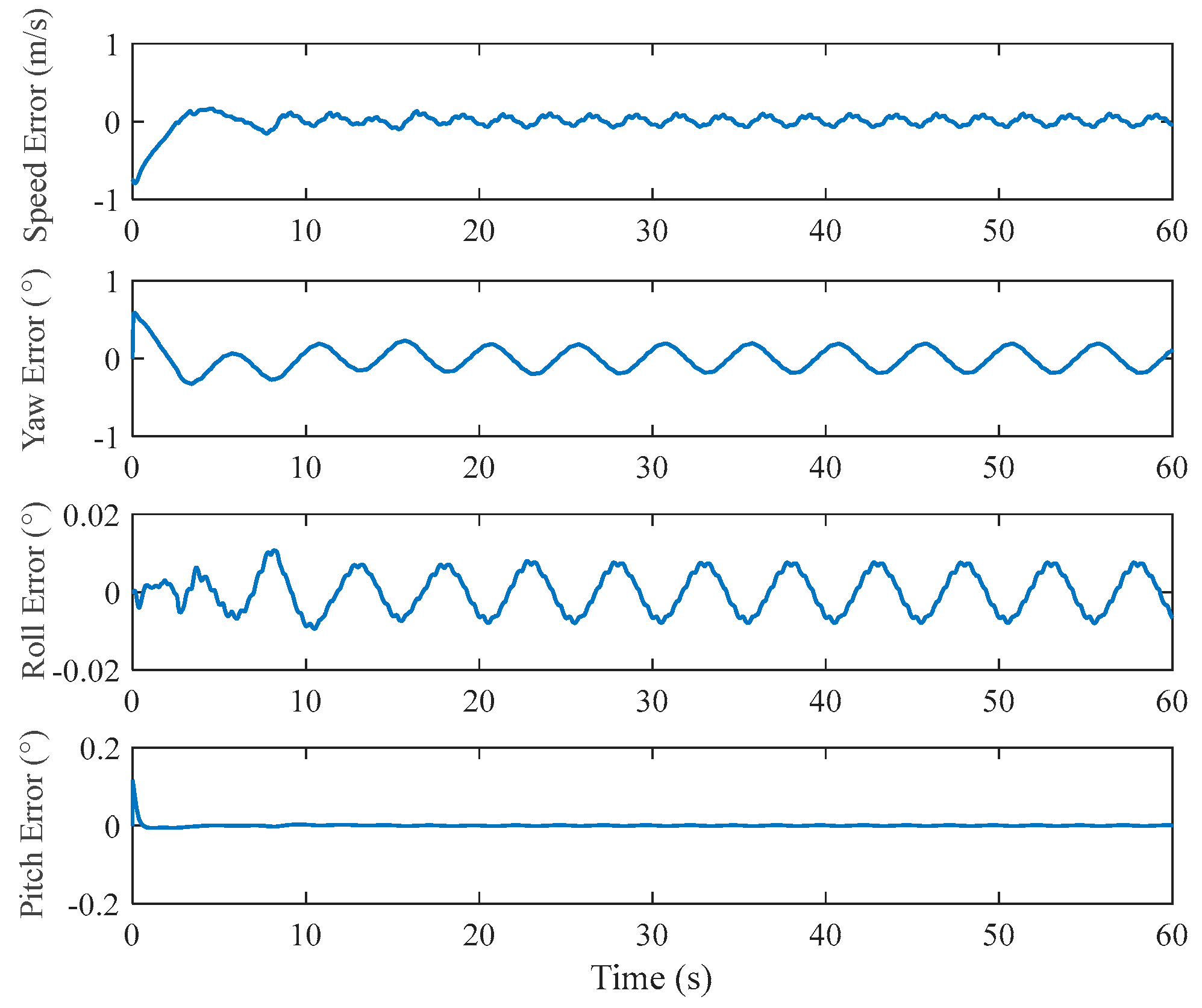


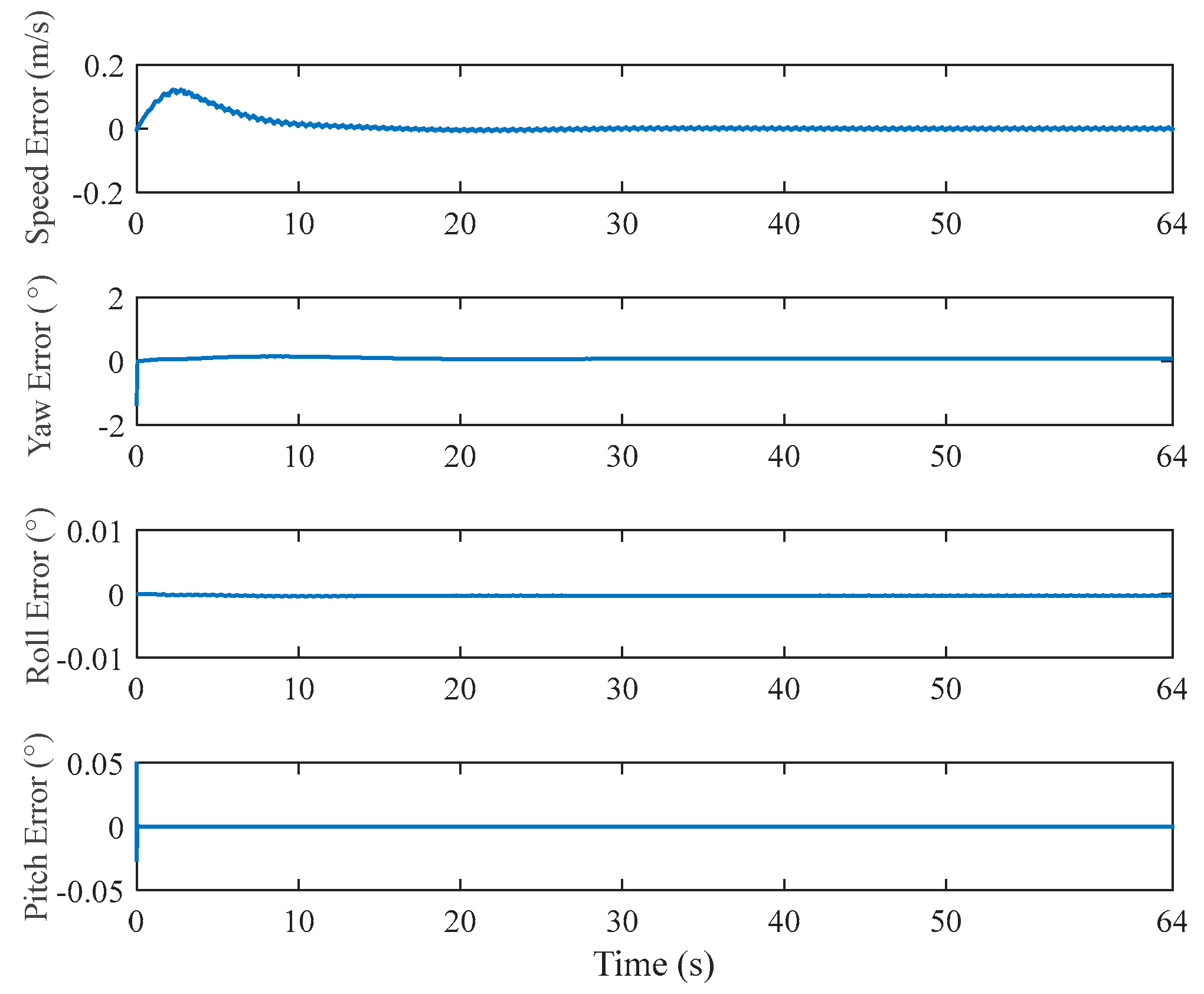
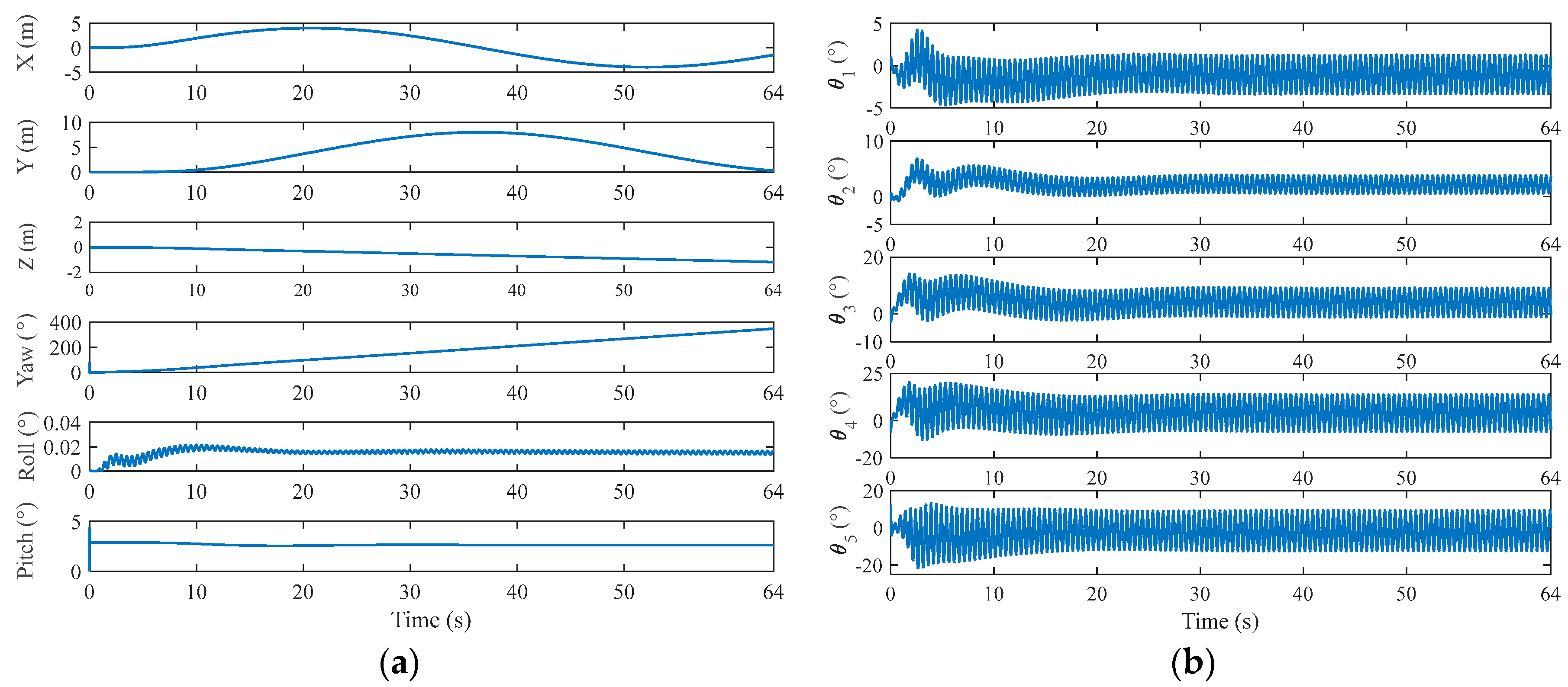
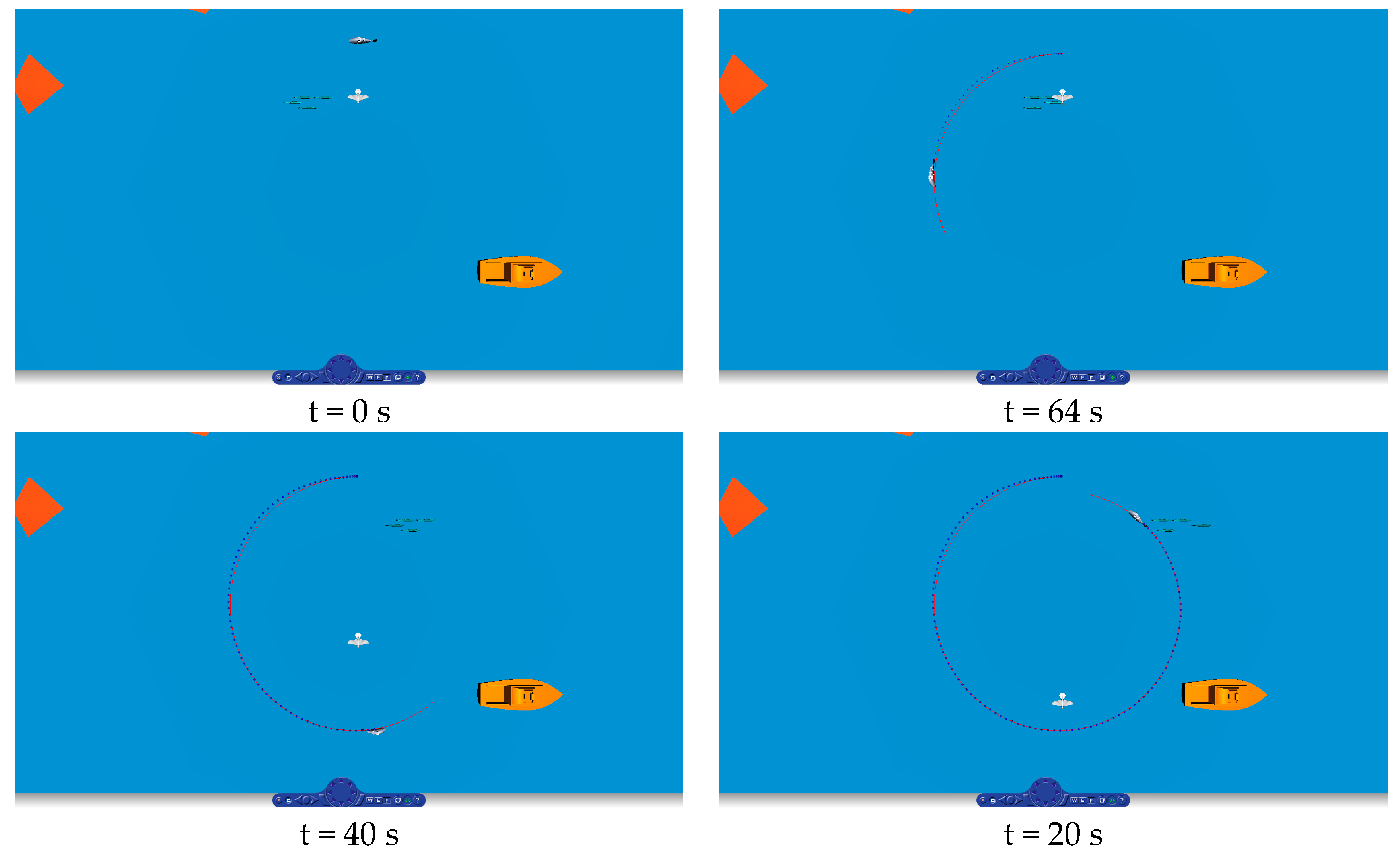
| Interval | Maximum Overshoot (%) | Settling Time (s) | |
|---|---|---|---|
| Forward Speed (m/s) | 0.1 | 6.80 | 16.30 |
| 0.2 | 4.40 | 11.80 | |
| 0.3 | 2.23 | 15.40 | |
| 0.4 | 1.65 | 12.20 | |
| Yaw Angles (°) | −40 | 37.50 | 18.30 |
| −30 | 16.66 | 8.80 | |
| −20 | 15 | 16.65 | |
| −10 | 10 | 8.20 | |
| 0 | 36 | 14.50 | |
| 10 | 27.50 | 10.80 | |
| 20 | 6.50 | 21.50 | |
| 30 | 15 | 17.60 | |
| 40 | 31.25 | 18.90 |
| Criteria | Step | Stairs | ||||||
|---|---|---|---|---|---|---|---|---|
| Value (°) | 20 | −15 | −20 | 0 | 20 | |||
| Motion | Roll | Pitch | Roll | Pitch | Roll | Pitch | Roll | Pitch |
| Maximum Overshoot (%) | - | - | - | - | 27 | - | 27.50 | - |
| Settling Time (s) | 0.38 | 0.37 | 0.20 | 0.24 | 0.18 | 0.26 | 0.19 | 0.24 |
| Trajectory | ex (m) | ey (m) | ez (m) |
|---|---|---|---|
| P1 | 0.0968 | 0.0131 | 0.1058 |
| P2 | 0.0827 | 0.0107 | 0.0920 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozmen Koca, G.; Bal, C.; Korkmaz, D.; Bingol, M.C.; Ay, M.; Akpolat, Z.H.; Yetkin, S. Three-Dimensional Modeling of a Robotic Fish Based on Real Carp Locomotion. Appl. Sci. 2018, 8, 180. https://doi.org/10.3390/app8020180
Ozmen Koca G, Bal C, Korkmaz D, Bingol MC, Ay M, Akpolat ZH, Yetkin S. Three-Dimensional Modeling of a Robotic Fish Based on Real Carp Locomotion. Applied Sciences. 2018; 8(2):180. https://doi.org/10.3390/app8020180
Chicago/Turabian StyleOzmen Koca, Gonca, Cafer Bal, Deniz Korkmaz, Mustafa Can Bingol, Mustafa Ay, Zuhtu Hakan Akpolat, and Seda Yetkin. 2018. "Three-Dimensional Modeling of a Robotic Fish Based on Real Carp Locomotion" Applied Sciences 8, no. 2: 180. https://doi.org/10.3390/app8020180
APA StyleOzmen Koca, G., Bal, C., Korkmaz, D., Bingol, M. C., Ay, M., Akpolat, Z. H., & Yetkin, S. (2018). Three-Dimensional Modeling of a Robotic Fish Based on Real Carp Locomotion. Applied Sciences, 8(2), 180. https://doi.org/10.3390/app8020180





