Digital Shearography for NDT: Phase Measurement Technique and Recent Developments
Abstract
:1. Introduction
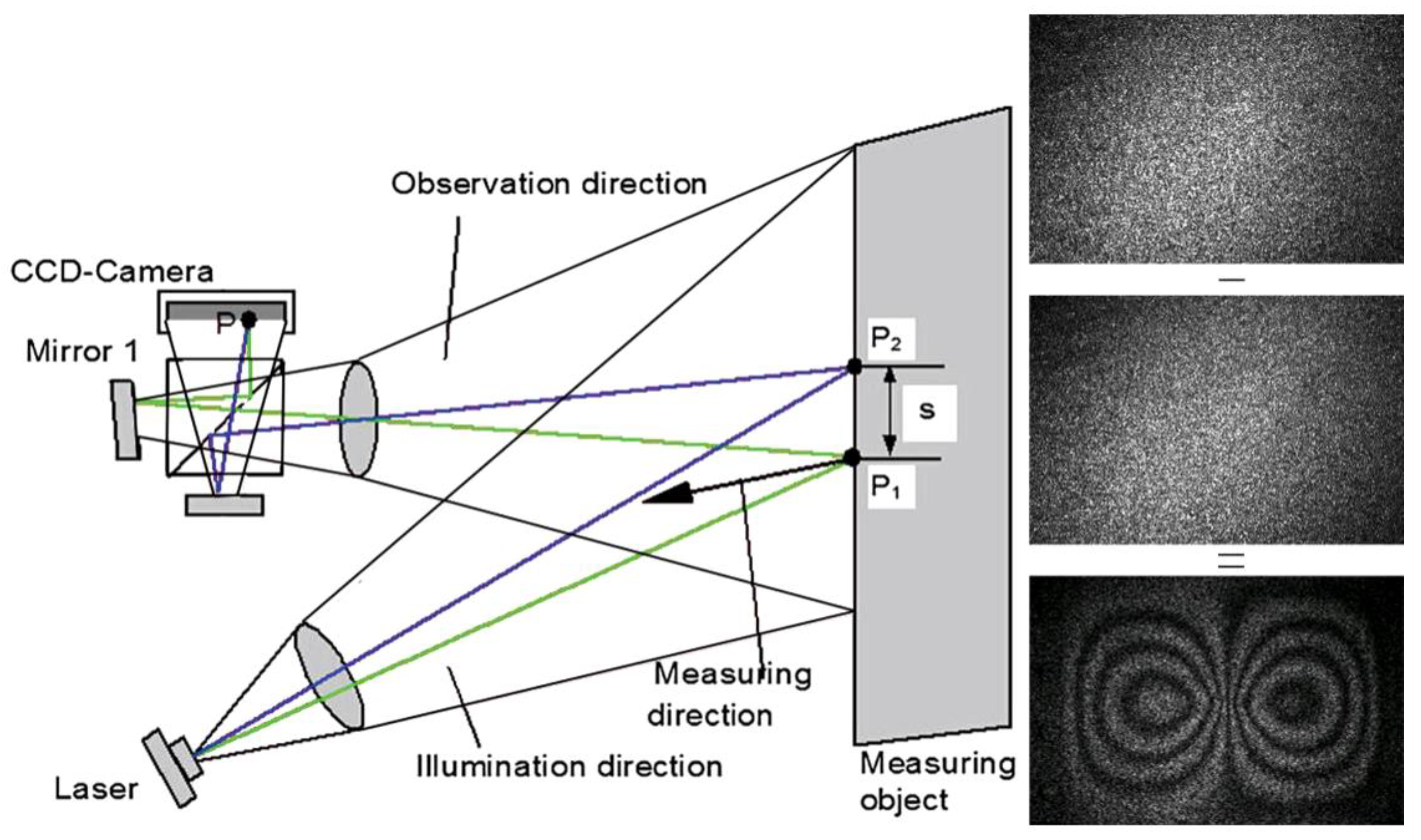
2. Brief Review of Digital Shearography
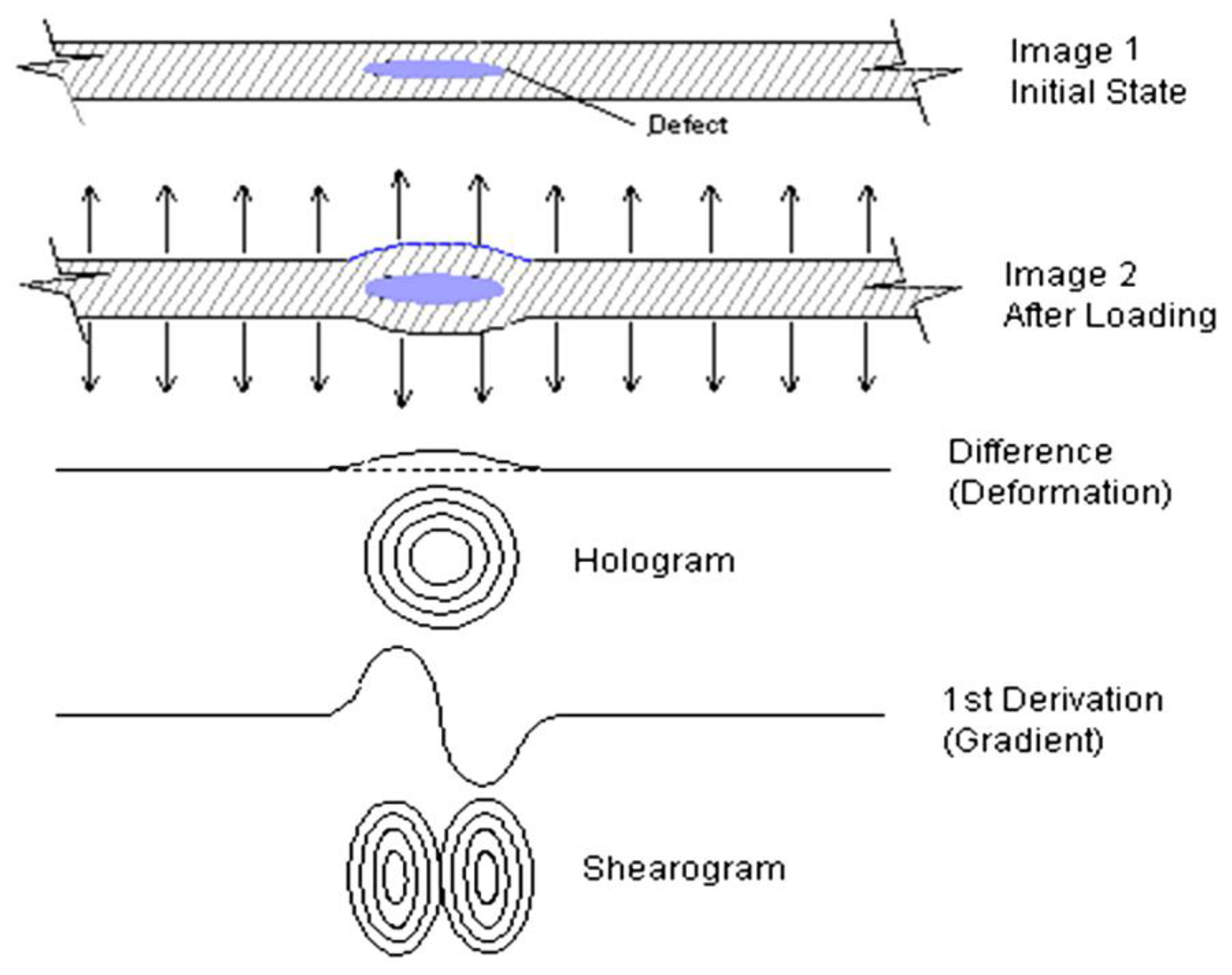
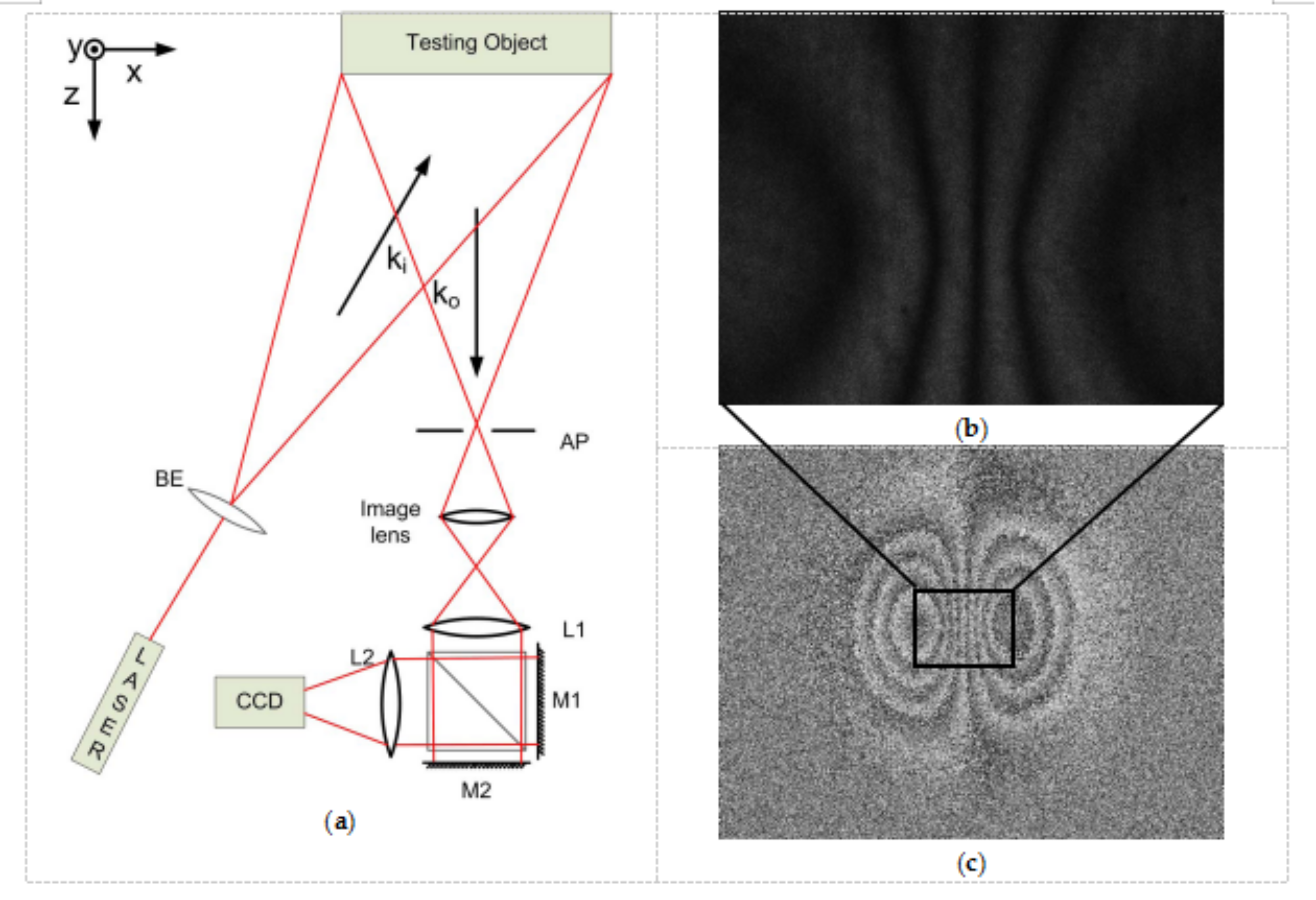
2.1. Formation of Fringes in Digital Shearography
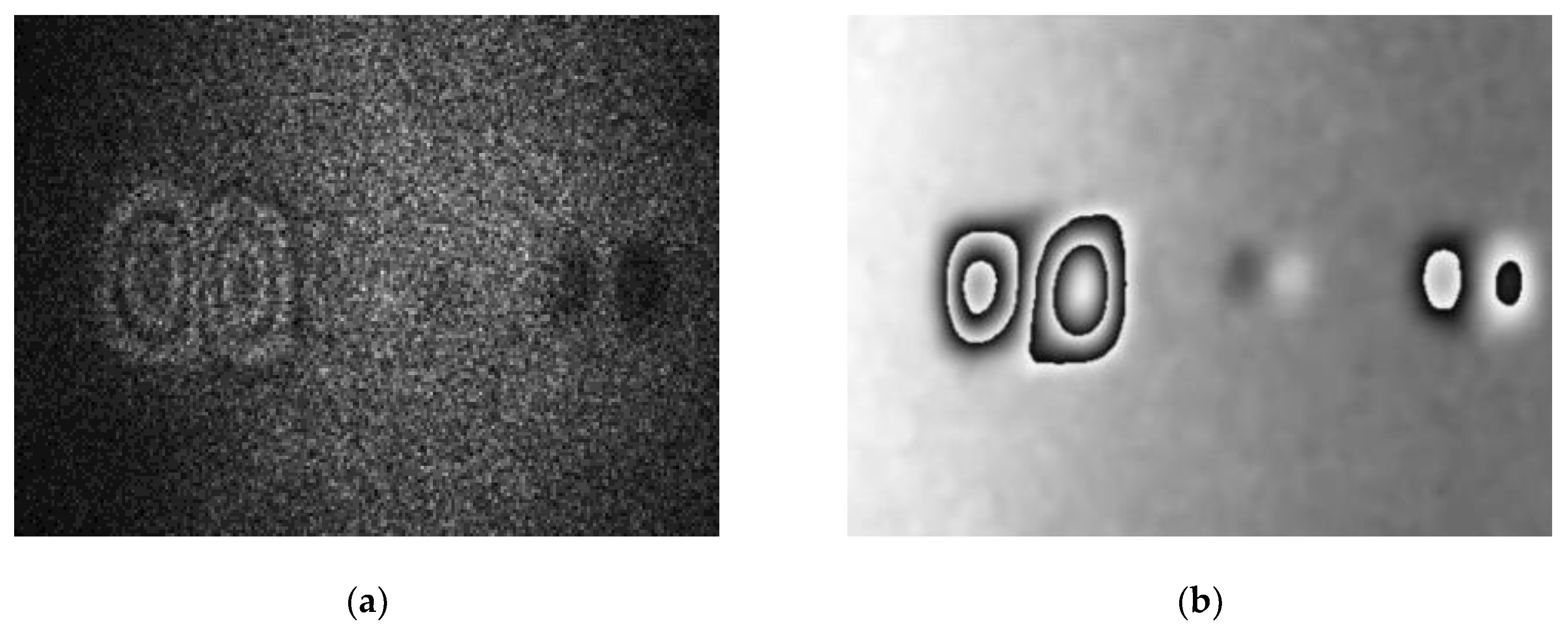
2.2. Interpretation of Fringes in Digital Shearography
3. Phase Measurement Technique
3.1. Phase Measurement Technique: Temporal Phase-Shift Shearography
3.2. Phase Measurement Technique: Spatial Phase-Shift Shearography
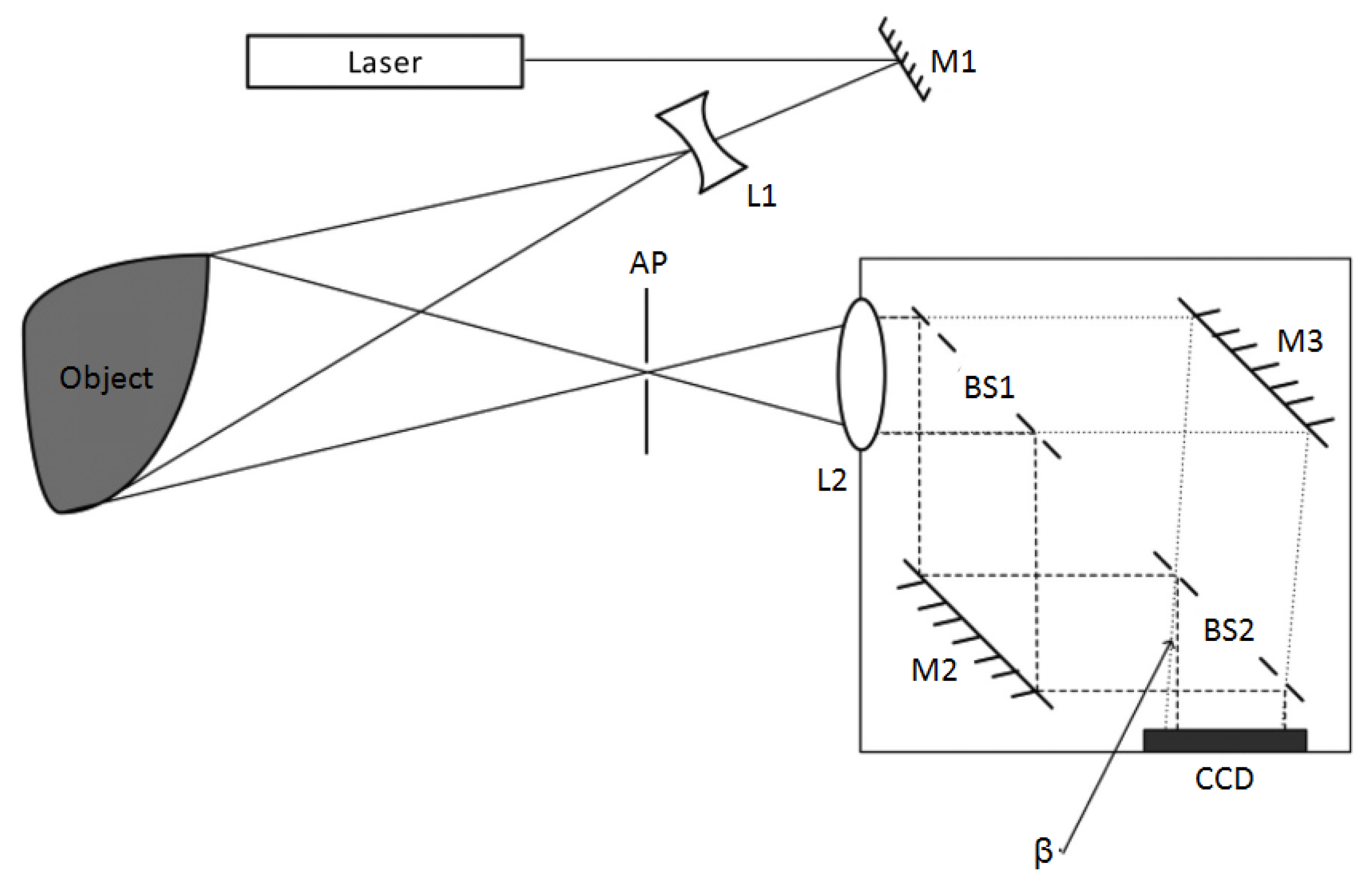
3.2.1. Multichannel Spatial Phase-Shift Shearography
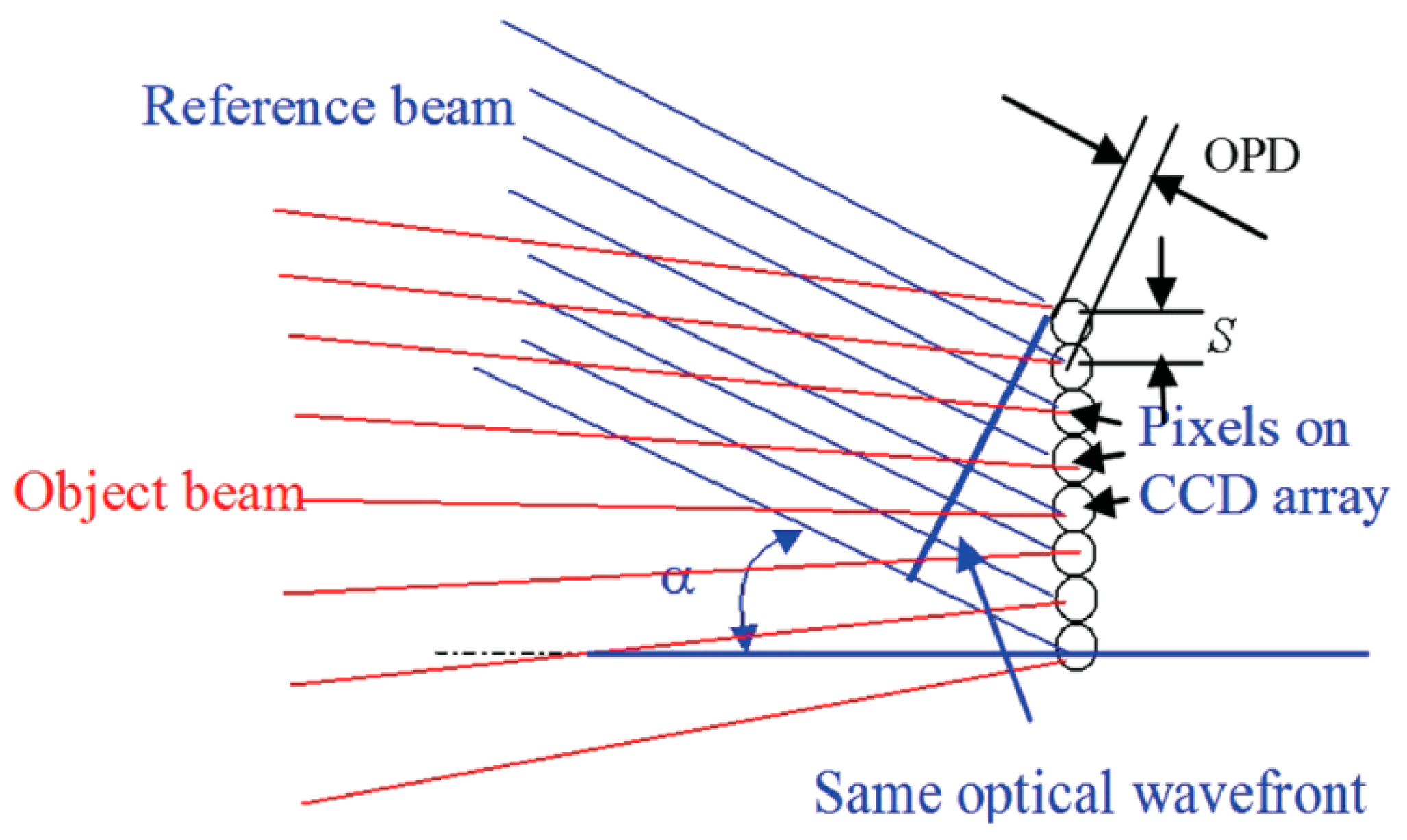
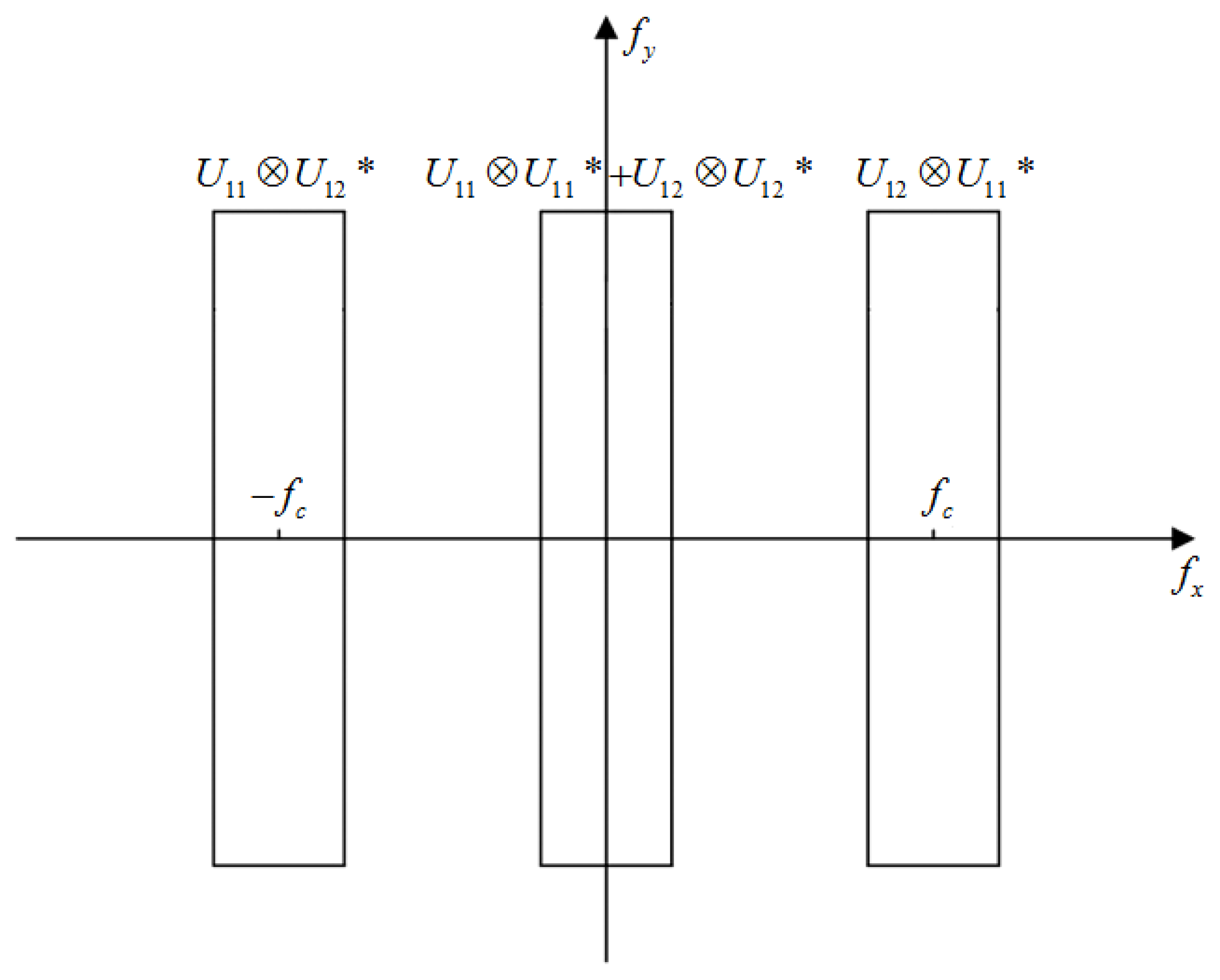
3.2.2. Carrier-Frequency Spatial Phase-Shift Shearography
4. Recent Developments of Shearographic NDT
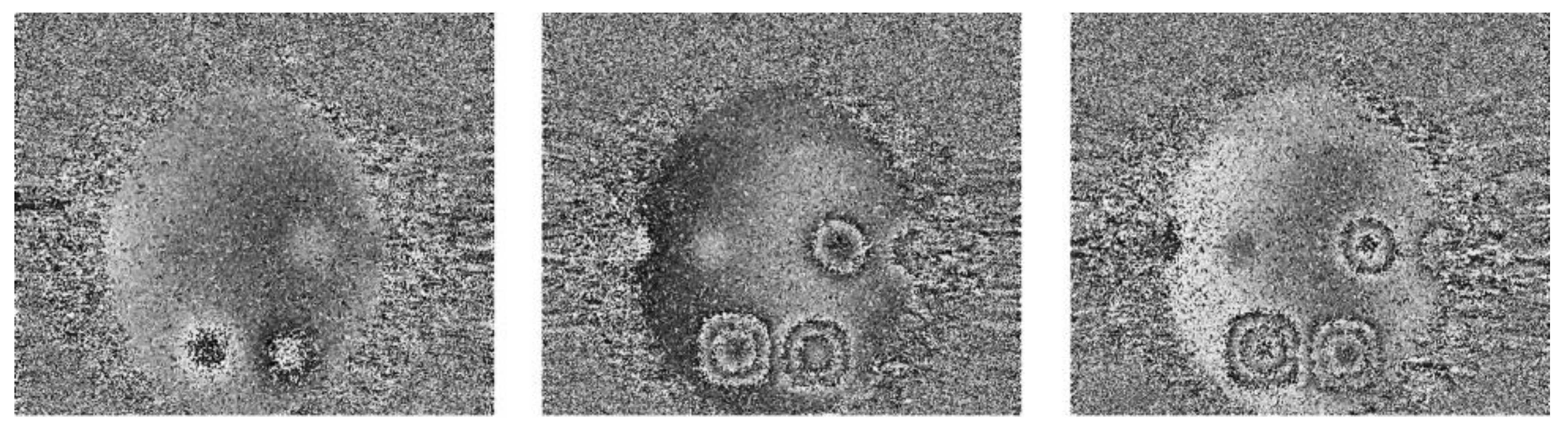
4.1. Simultaneous Measurement of Deformation and the First Derivative
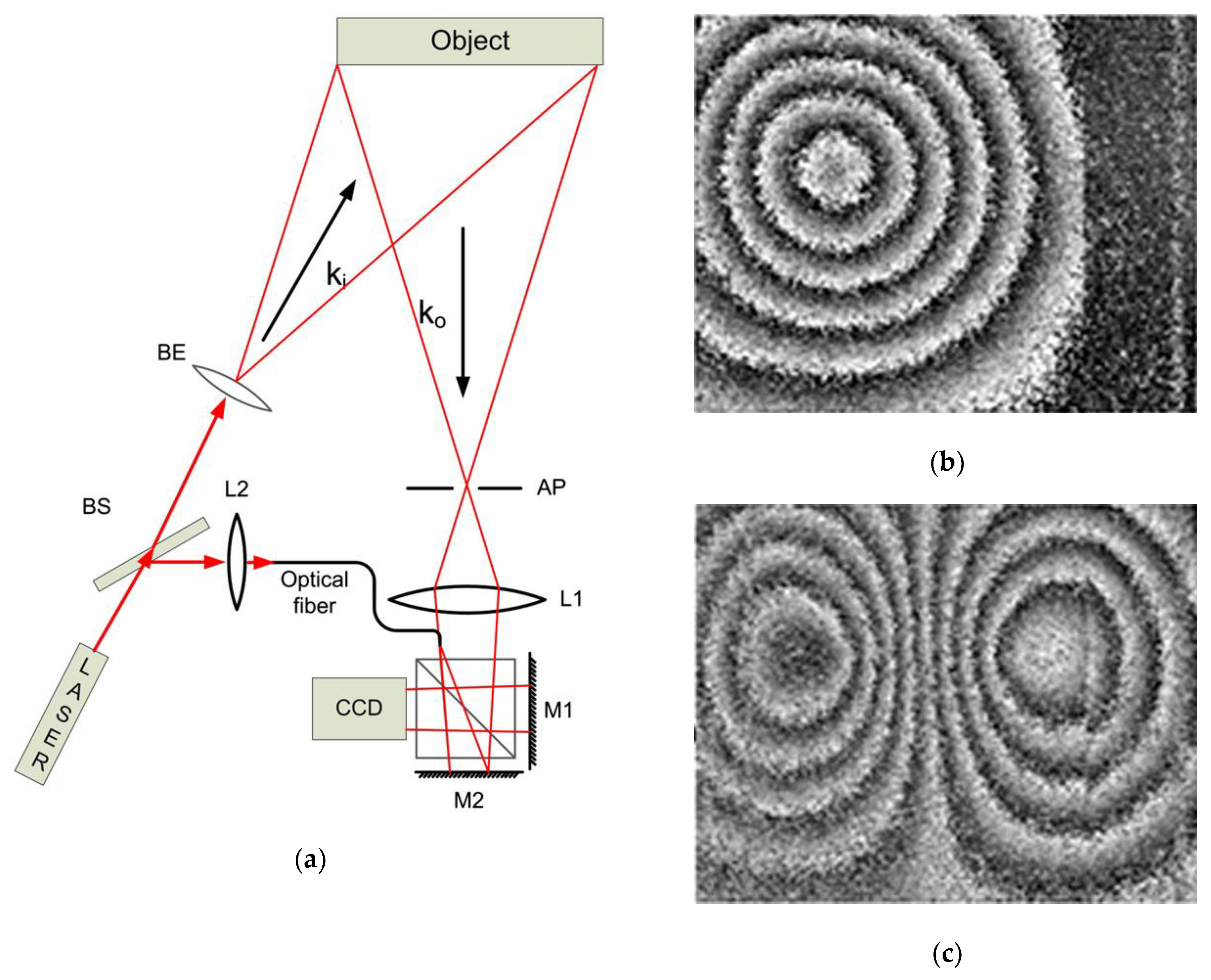
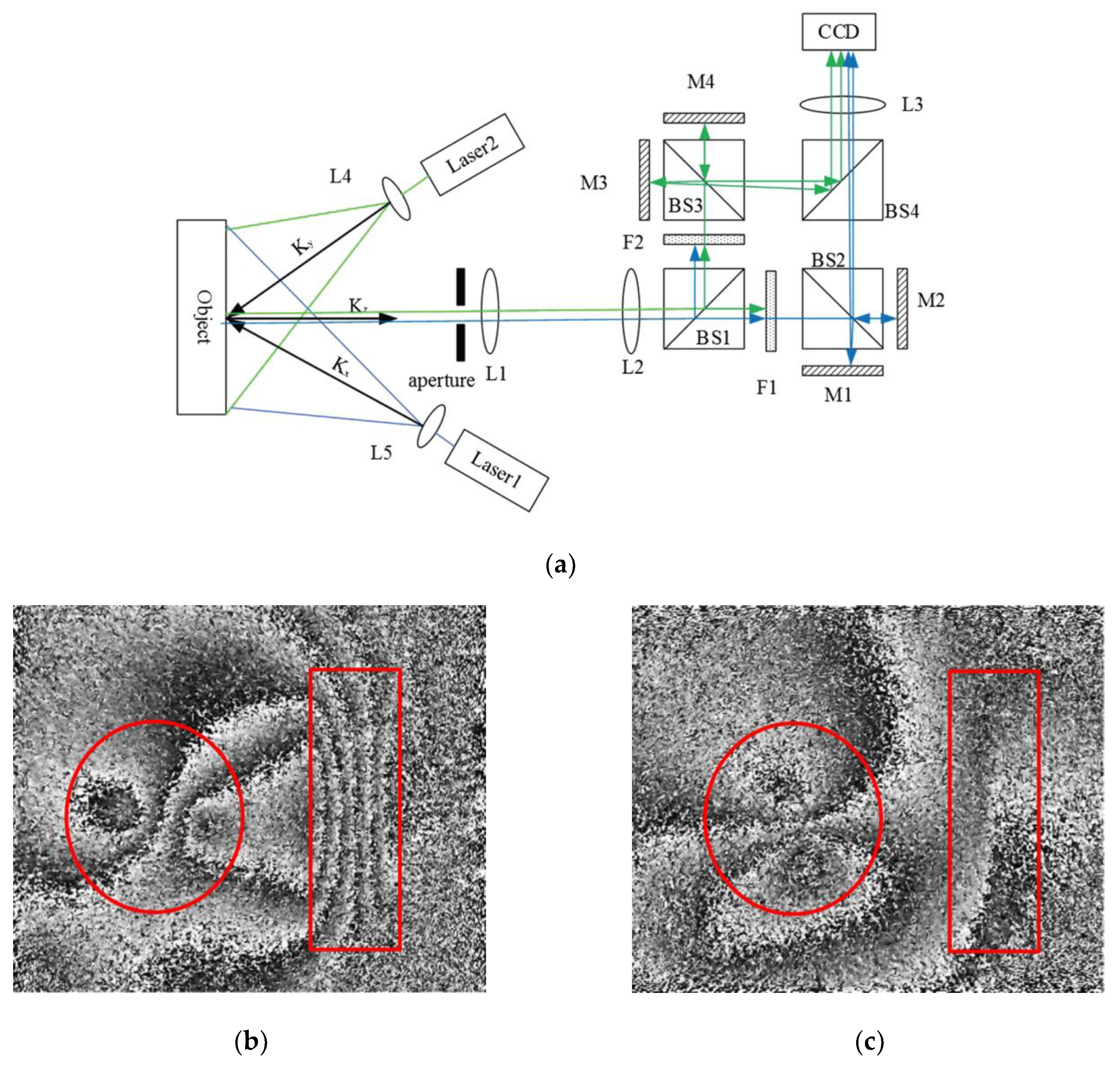
4.2. Multidirectional Sheared SPS-DS
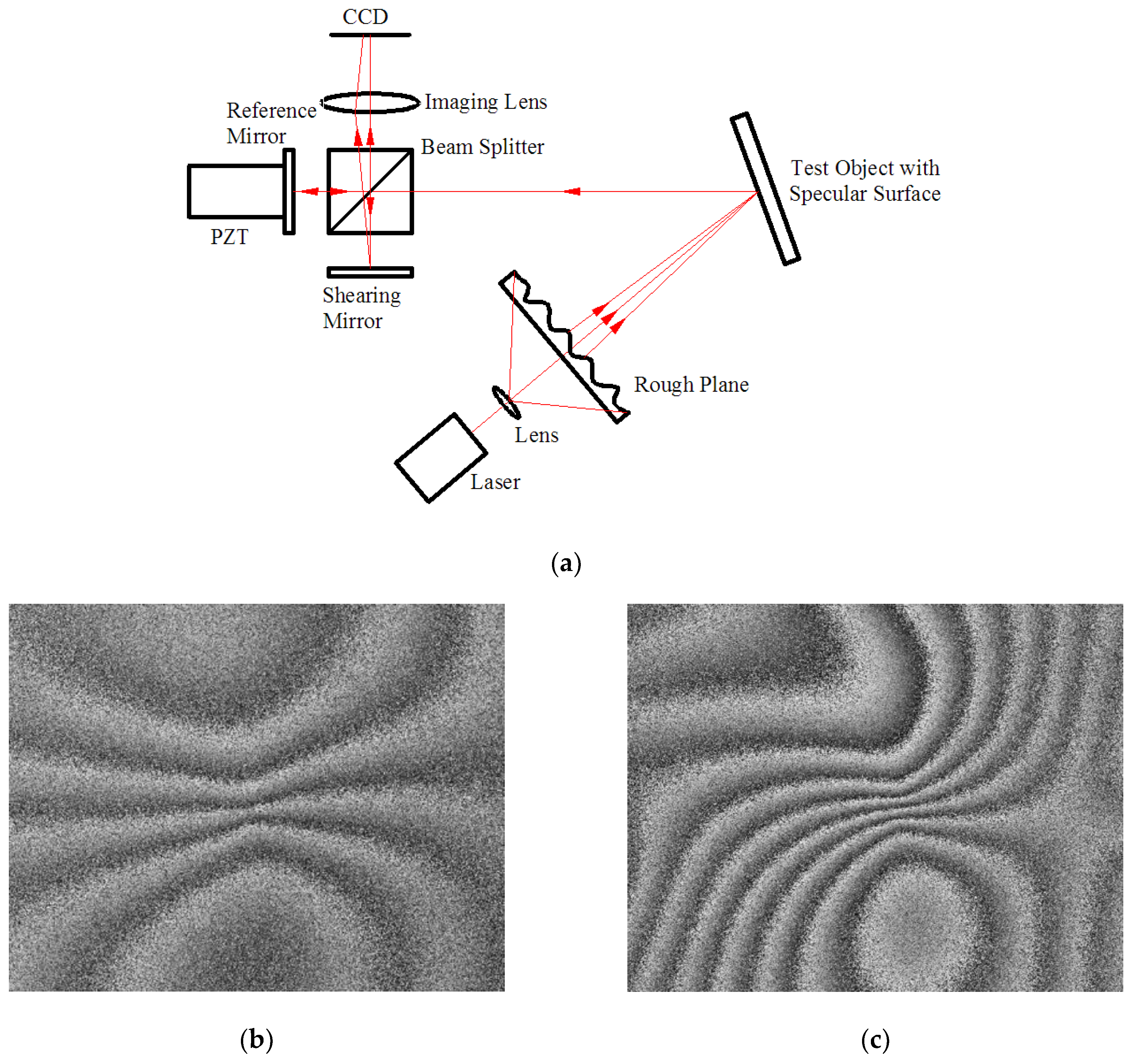
4.3. Shearographic NDT on Specular Surface Materials
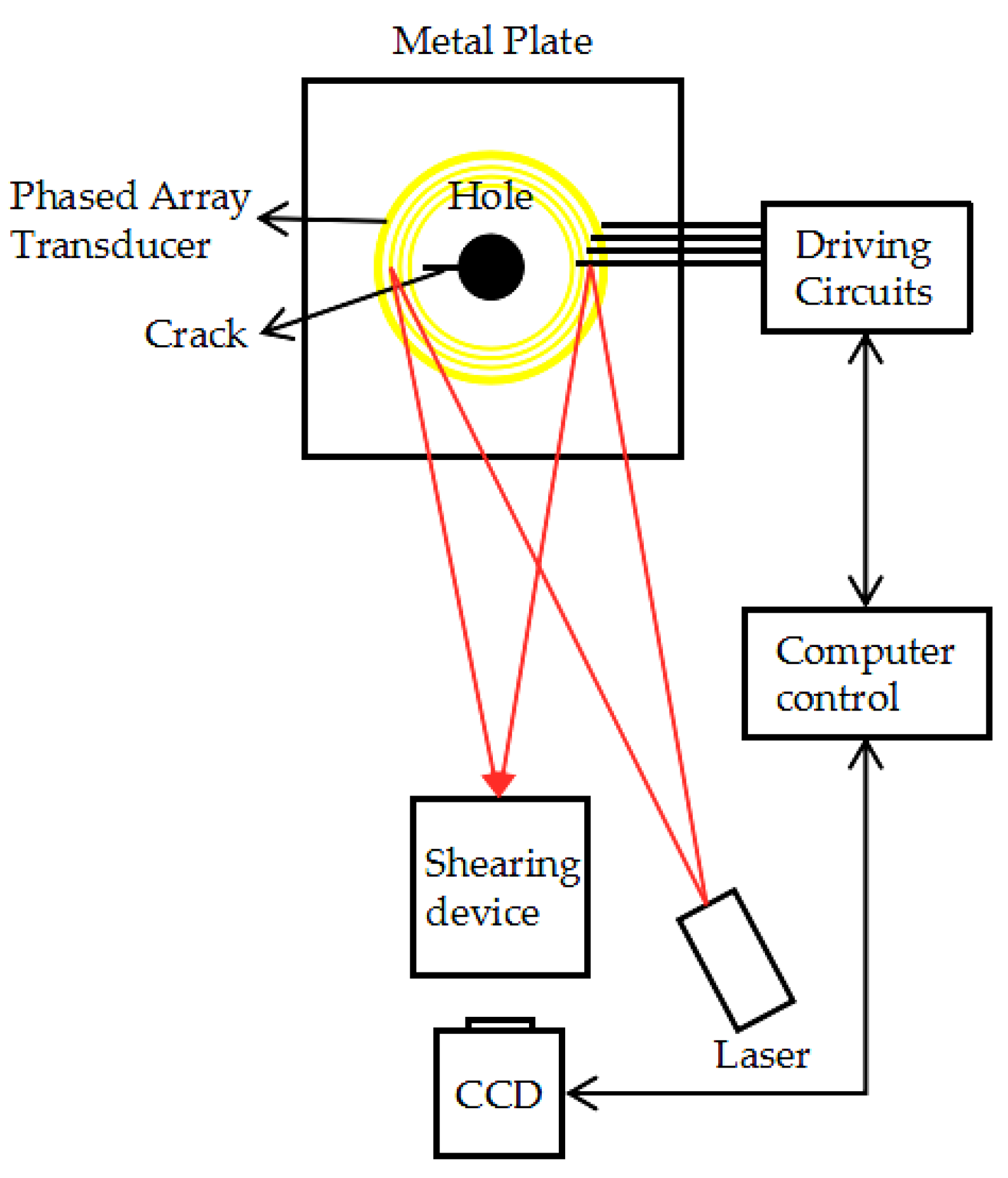
4.4. Directed Acoustic Shearography for Subsurface Crack
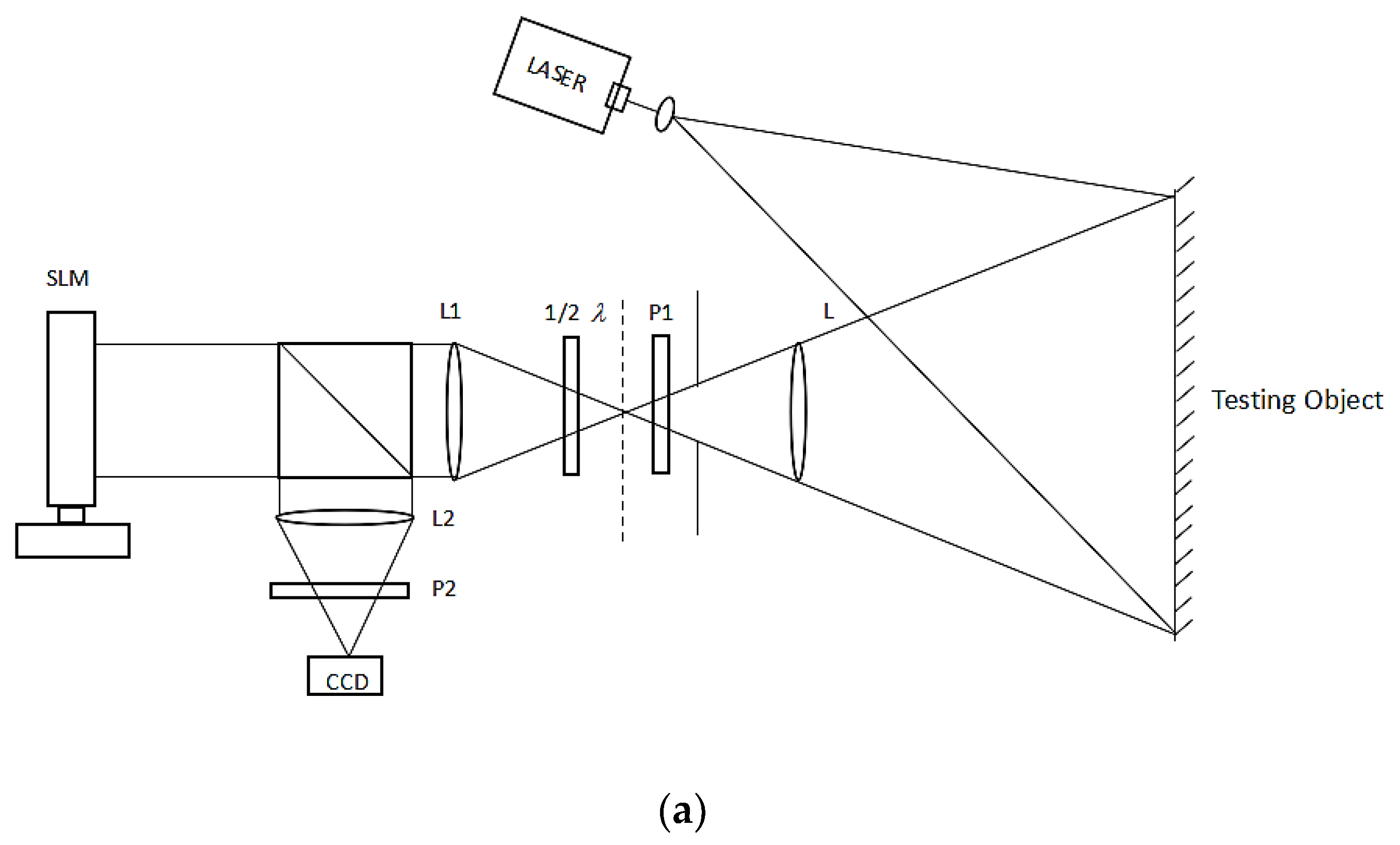
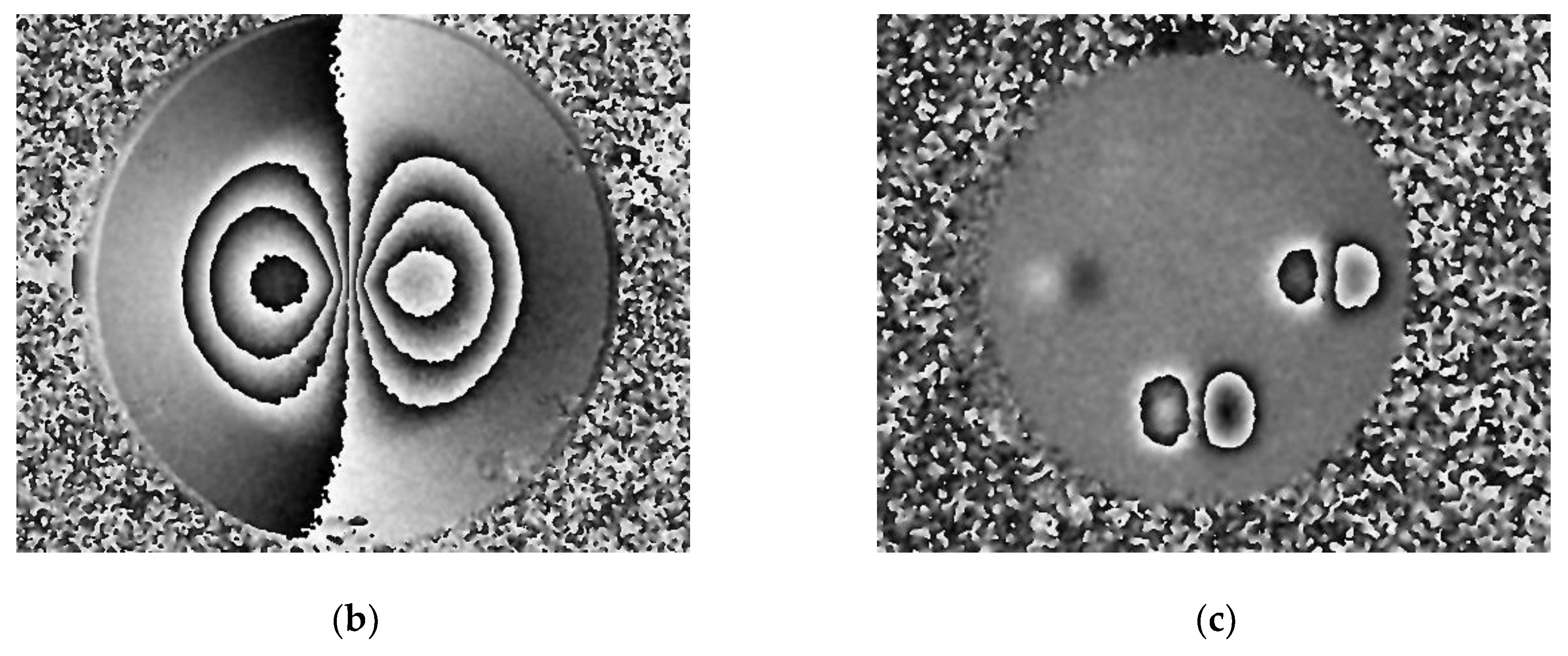
4.5. New Shearographic System with SLM
4.6. Recent Applications of Shearographic NDT
5. Potentials and Limitations
5.1. Potentials
- Digital shearography has all of the advantages of the optical NDT technique; it is full-field, noncontact, highly sensitive, and robust.
- Compared to noncoherent measurement methods (such as DIC), digital shearography has a much higher measurement sensitivity. Combined with the phase-shift technique, digital shearography can achieve measurement sensitivity at dozens of nanometer levels.
- Compared to other coherent measurement methods (such as holographic interferometry and ESPI), digital shearography is more robust and well suited for practical applications. This is because digital shearography directly measures the first derivative of deformation, which is the strain information. Therefore, digital shearography is less sensitive to environmental disturbances than other coherent methods.
- Digital shearography simplifies the optical system using a self-reference interferometric device. At the same time, the self-reference interferometric device does not require a coherence length of the laser source and can be illuminated with a low-cost laser diode.
5.2. Limitations
- It is difficult to measure defects away from the object surface using digital shearography. Although directed acoustic shearography can detect subsurface defects, the defects away from the object surface are difficult to detect because they cannot be loaded to produce enough abnormality on the surface that can be detected by shearography.
- Although a new digital shearography system has been developed for specular surface materials, the measurement field is limited by the size of the rough surface in the optical path.
- As an interference-based technique, digital shearography is still sensitive to environmental disturbances. Large rigid-body motions, strong thermal air currents, etc. will all affect the measurement results.
- The phase map obtained by digital shearography still contains lots of noise, which will affect the detection of defects. How to effectively improve the quality of the phase map during dynamic measurement is a problem.
6. Conclusion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Talreja, R. Damage and fatigue in composites-A personal account. Sci. Technol. 2008, 68, 2585–2591. [Google Scholar] [CrossRef]
- Haider, M.F.; Majumdar, P.K.; Angeloni, S.; Reifsnider, K.L. Nonlinear anisotropic electrical response of carbon fiber-reinforced polymer composites. J. Compos Mater. 2018, 52, 1017–1032. [Google Scholar] [CrossRef]
- Majumdar, P.K.; Haider, M.F.; Reifsnider, K. Multi-Physics Response of Structural Composites and Framework for Modeling using Material Geometry. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, NJ, USA, 8–11 April 2013. [Google Scholar]
- Miller, A. The Boeing 787 Dreamliner. In Proceedings of the 22nd American Society for Composites Technical Conference, Seattle, WA, USA, 17–19 September 2007. [Google Scholar]
- Reifsnider, K.L.; Case, S.W. Damage Tolerance and Durability of Material Systems; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Yang, L.X.; Chen, F.; Steinchen, W.; Hung, M.Y. Digital Shearography for Nondestructive Testing: Potentials, Limitations, and Applications. J. Hologr. Speckle 2004, 1, 69–79. [Google Scholar] [CrossRef]
- Vest, C.M. Holographic Interferometry; John Wiley and Sons: Hoboken, NJ, USA, 1979. [Google Scholar]
- Lokberg, O.J.; Malmo, J.T. Long-distance electronic speckle pattern interferometry. Opt. Eng. 1988, 27, 150–156. [Google Scholar] [CrossRef]
- Leendertz, J.A.; Butters, J.N. An image-shearing speckle-pattern interferometer for measuring bending moments. J. Phys. E 1973, 6, 1107–1110. [Google Scholar] [CrossRef]
- Yamaguchi, I. A laser-speckle strain gauge. J. Phys. E Sci. Instrum. 1981, 14, 1270–1273. [Google Scholar] [CrossRef]
- Hung, Y.Y. Shearography for non-destructive evaluation of composite structures. Opt. Lasers Eng. 1996, 24, 161–182. [Google Scholar] [CrossRef]
- Yang, L.X.; Hung, Y.Y. Digital shearography for nondestructive evaluation and application in automotive and aerospace industries. In Proceedings of the 16th WCNDT, Montreal, QC, Canada, 1 January 2004. [Google Scholar]
- Hung, Y.Y.; Yang, L.X.; Huang, Y.H. Non-destructive evaluation (NDE) of composites: Digital shearography. In Non-Destructive Evaluation (NDE) of Polymer Matrix Composites; Karbhari, V.M., Woodhead, Eds.; Woodhead Publishing Limited: Sawston, Cambridge, 2013; pp. 84–115. [Google Scholar]
- Hung, Y.Y. Shearography: A new optical method for strain measurement and nondestructive testing. Opt. Eng. 1982, 21, 391–395. [Google Scholar] [CrossRef]
- Steinchen, W.; Yang, L.X.; Schuth, M.; Kupfer, G. Electronic shearography (ESPSI) for direct measurement of strains. In Proceedings of the Optical Measurements and Sensors for the Process Industries, Optics for Productivity in Manufacturing, Frankfurt, Germany, 15 November 1994. [Google Scholar]
- Hung, Y.Y. Applications of digital shearography for testing of composite structures. Compos. B Eng. 1999, 30B, 765–773. [Google Scholar] [CrossRef]
- Creath, K. Phase-shifting speckle interferometry. Appl. Opt. 1985, 24, 3053. [Google Scholar] [CrossRef] [PubMed]
- Creath, K. V Phase-Measurement Interferometry Techniques. In Progress in Optics Volume 26; ELSEVIER: North-Holland, THe Netherlands, 1988; pp. 349–393. [Google Scholar]
- Sim, C.W.; Chau, F.S.; Toh, S.L. Vibration analysis and non-destructive testing with real time shearography. Opt. Laser Technol. 1995, 27, 45–49. [Google Scholar] [CrossRef]
- Pedrini, G.; Zou, Y.L.; Tiziani, H.J. Quantitative evaluation of digital shearing interferogram using the spatial carrier method. Pure Appl. Opt. 1996, 5, 313–321. [Google Scholar] [CrossRef]
- Steinchen, W.; Yang, L.X.; Kupfer, G.; Mackel, P. Non-destructive testing of aerospace composite materials using digital shearography. J. Aerosp. Eng. 1998, 212, 21–30. [Google Scholar] [CrossRef]
- Hung, Y.Y.; Rowlands, R.E.; Daniel, I.M. Speckle-shearing interferometric technique: A full-field strain gauge. Appl. Opt. 1975, 14, 618–622. [Google Scholar] [CrossRef] [PubMed]
- Carré, P. Installation et utilisation du comparateur photoélectrique et interférentiel du Bureau International des Poids et Mesures. Metrologia 1966, 2, 13–20. [Google Scholar] [CrossRef]
- Steinchen, W.; Yang, L.X. Digital Shearography: Theory and Application of Digital Speckle Pattern Shearing Interferometry; SPIE Press: Bellingham, WA, USA, 2003. [Google Scholar]
- Bi, H.B.; Zhang, Y.; Ling, K.V.; Wen, C.Y. Class of 4+1-phase algorithms with error compensation. Appl. Opt. 2004, 43, 4199–4207. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Chen, J.L.; Lu, H. Improved phase-shifted digital speckle shearography for time-dependent deformation measurement. Opt. Eng. 2008, 47, 8. [Google Scholar]
- Zhu, L.Q.; Wang, Y.H.; Xu, N.; Wu, S.J.; Dong, M.L.; Yang, L.X. Real-time monitoring of phase maps of digital shearography. Opt. Eng. 2013, 52, 8. [Google Scholar] [CrossRef]
- Smythe, R.; Moore, R. Instantaneous phase measuring interferometry. Opt. Eng. 1984, 23, 361–364. [Google Scholar] [CrossRef]
- Kranz, J.; Lamprecht, J.; Hettwer, A.; Schwider, J. Fiber optical single frame speckle interferometer for measuring industrial surfaces. Proc. Spie Int. Soc. Opt. Eng. 1998, 328–331. [Google Scholar]
- Hettwer, A.; Kranz, J.; Schwider, J. Three channel phase-shifting interferometer using polarization-optics and a diffraction grating. Opt. Eng. 2000, 39, 960–966. [Google Scholar] [CrossRef]
- Bhaduri, B.; Mohan, N.K.; Kothiyal, M.P.; Sirohi, R.S. Use of spatial phase shifting technique in digital speckle pattern interferometry (DSPI) and digital shearography (DS). Opt. Express 2006, 14, 11598–11607. [Google Scholar] [CrossRef] [PubMed]
- Bhaduri, B.; Mohan, N.K.; Kothiyal, M.P. Simultaneous measurement of out-of-plane displacement and slope using a multiaperture DSPI system and fast Fourier transform. Appl. Opt. 2007, 46, 5680–5686. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.J.; He, X.Y.; Yang, L.X. Enlarging the angle of view in Michelson-interferometer-based shearography by embedding a 4f system. Appl. Opt. 2011, 50, 3789–3794. [Google Scholar] [CrossRef] [PubMed]
- Xie, X.; Yang, L.X.; Xu, N.; Chen, X. Michelson interferometer based spatial phase shift shearography. Appl. Opt. 2013, 52, 4063–4071. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.X.; Xie, X. Spatial Phase Shift Shearography for Strain Measurement. In Digital Shearography: New Developments and Applications; SPIE: Washington, WA, USA, 2016. [Google Scholar]
- Huang, Y.H.; Janabi-Sharifi, F.; Liu, Y.S.; Hung, Y.Y. Dynamic phase measurement in shearography by clustering method and Fourier filtering. Opt. Express 2011, 19, 606–615. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.J.; Zhu, L.Q.; Feng, Q.B.; Yang, L.X. Digital shearography with in situ phase shift calibration. Opt. Lasers Eng. 2012, 50, 1260–1266. [Google Scholar] [CrossRef]
- Amar, S.; Bahich, M.; Dalimi, H.; Barj, E.; Afifi, M. Digital carrier superposition by Hilbert-Huang transform for optical phase recovery in speckle shearing interferometry. Opt. Eng. 2015, 54, 7. [Google Scholar] [CrossRef]
- Maeda, T.; Kadambi, A.; Schechner, Y.Y.; Raskar, R. Dynamic Heterodyne Interferometry. In Proceedings of the IEEE International Conference on Computational Photography, Pittsburgh, PA, USA, 8–10 April 2018. [Google Scholar]
- Albertazzi, A.; Fantin, A.V.; Willemann, D.P.; Benedet, M.E. Phase Maps Retrieval from Sequences of Phase Shifted Images with Unknown Phase Steps Using Generalized N-Dimensional Lissajous Figures-Principles and Applications. Int. J. Optomechat. 2014, 8, 340–356. [Google Scholar] [CrossRef]
- Xie, X.; Li, X.N.; Chen, X.; Yang, L.X. Review of Recent Developments of Spatial Phase-Shift Digital Shearography. In Proceedings of the International Conference on Experimental Mechanics, Singapore, 4 March 2015. [Google Scholar]
- Aranchuk, V.; Lal, A.K.; Hess, C.F.; Trolinger, J.D.; Scott, E. Pulsed spatial phase-shifting digital shearography based on a micropolarizer camera. Opt. Eng. 2018, 57, 6. [Google Scholar] [CrossRef]
- Kirkove, M.; Guerit, S.; Jacques, L.; Loffet, C.; Languy, F.; Vandenrijt, J.F.; Georges, M. Determination of vibration amplitudes from binary phase patterns obtained by phase-shifting time-averaged speckle shearing interferometry. Appl. Opt. 2018, 57, 8065–8077. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.X. Recent developments in digital shearography for nondestructive testing. Mater. Eval. 2006, 64, 704–709. [Google Scholar]
- Bhaduri, B.; Tay, C.J.; Quan, C.; Niu, H.; Sjodahl, M. Two wavelength simultaneous DSPI and DSP for 3D displacement field measurements. Opt. Commun. 2011, 284, 2437–2440. [Google Scholar] [CrossRef]
- Xie, X.; Xu, N.; Sun, J.F.; Wang, Y.H.; Yang, L.X. Simultaneous measurement of deformation and the first derivative with spatial phase-shift digital shearography. Opt. Commun. 2013, 286, 277–281. [Google Scholar] [CrossRef]
- Yang, L.X. Grundlagen und Anwendungen der phaserschieb shearografie zur zerstoerungsfreien werkstoffpruefung. In Proceedings of the VDI Fortschritt-Berichte Reihe 8: Mess-, Steuerungs- und Reqelungstechnik, VDI Verlag GmbH, Duesseldorf, Geremany, 1998. [Google Scholar]
- Xie, X.; Lee, C.P.; Li, J.R.; Zhang, B.Y.; Yang, L.X. Polarized digital shearography for simultaneous dual shearing directions measurements. Rev. Sci. Instrum. 2016, 87, 7. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.H.; Gao, X.Y.; Xie, X.; Wu, S.J.; Liu, Y.X.; Yang, L.X. Simultaneous Dual Directional Strain Measurement Using Spatial Phase-Shift Digital Shearography. Opt. Lasers Eng. 2016, 87, 197–203. [Google Scholar] [CrossRef]
- Barrera, E.S.; Fantin, A.V.; Willemann, D.P.; Benedet, M.E.; Gonçalves, A.A. Multiple-aperture one-shot shearography for simultaneous measurements in three shearing directions. Opt. Lasers Eng. 2018, 111, 86–92. [Google Scholar] [CrossRef]
- Xu, N.; Xie, X.; Chen, X.; Yang, L.X. Shearography for specular object inspection. Opt. Lasers Eng. 2014, 61, 14–18. [Google Scholar] [CrossRef]
- Yan, P.Z.; Wang, Y.H.; Sun, F.Y.; Lu, Y.; Liu, L.; Zhao, Q.H. Shearography for non-destructive testing of specular reflecting objects using scattered light illumination. Opt. Laser Technol. 2019, 112, 452–457. [Google Scholar] [CrossRef]
- Kurtz, R.M. Directed Acoustic Shearography. In Proceedings of the Photonics in the Transportation Industry: Auto to Aerospace III, International Society for Optics and Photonics, Orlando, FL, USA, 20 April 2010. [Google Scholar]
- Liu, H.; Guo, S.; Chen, Y.F.; Liu, H.; Tan, C.Y.; Ke, K.L.; Zhang, L. Shearography using wave-defect interactions for crack detection in metallic structures. In Proceedings of the 2017 IEEE International Ultrasonics Symposium, Washington, WA, USA, 5–9 September 2017. [Google Scholar]
- Liu, H.; Guo, S.; Chen, Y.F.; Tan, C.Y.; Zhang, L. Acoustic shearography for crack detection in metallic plates. Smart Mater. Struct. 2018, 27, 10. [Google Scholar] [CrossRef]
- Mahmud, M.S.; Naydenova, I.; Toal, V. Implementation of phase-only modulation utilizing a twisted nematic liquid crystal spatial light modulator. J. Opt. A Pure Appl. Opt. 2008, 10, 7. [Google Scholar] [CrossRef]
- Sun, F.Y.; Wang, Y.H.; Yan, P.Z.; Zhao, Q.H.; Yang, L.Y. The application of SLM in shearography detecting system. Opt. Lasers Eng. 2019, 114, 90–94. [Google Scholar] [CrossRef]
- Dhanotia, J.; Prakash, S. Phase Contrast Imaging of Small Transparent Objects using Digital Shearography. In Proceedings of the Conferene on Light and Its Interactions with Matter, Natl Inst Technol, Kerala, India, 19–21 March 2014. [Google Scholar]
- Sanati, H.; Reshadi, F.; Faraji, G.; Soltani, N.; Zalnezhad, E. Evaluation of residual stress in ultrafine-grained aluminum tubes using shearography. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2015, 229, 953–962. [Google Scholar] [CrossRef]
- Barmouz, M.; Behravesh, A.H.; Reshadi, F.; Soltani, N. Assessment of defect detection in wood-plastic composites via shearography method. J. Thermoplast. Compos. Mater. 2016, 29, 28–36. [Google Scholar] [CrossRef]
- Wang, X.; Gao, Z.; Yang, S.; Gao, C.; Sun, X.; Wen, X.; Feng, Z.; Wang, S.; Fan, Y. Application of digital shearing speckle pattern interferometry for thermal stress. Measurement 2018, 125, 11–18. [Google Scholar] [CrossRef]
- Feng, X.; He, X.Y.; Tian, C.P.; Zhou, H.H. Research on Inner Defect Detection of Pressure Vessels with Digital Shearography. In Proceedings of the International Conference on Experimental Mechanics, Singapore, 15–17 November 2014. [Google Scholar]
- Benedet, M.E.; Macedo, F.J.; Fantin, A.V.; Willemann, D.P.; Silva, F.A.A.; Soares, S.D.; Albertazzi, A. An endoscopic shearography system with radial sensitivity for inner inspection of adhesion faults in composite material pipes. In Proceedings of the Conference on Optical Measurement Systems for Industrial Inspection X part of the SPIE Optical Metrology Symposium, Munich, Germany, 25–29 June 2017. [Google Scholar]
- Buchta, D.; Heinemann, C.; Pedrini, G.; Krekel, C.; Osten, W. Lock-in-shearography for the detection of transport-induced damages on artwork. In Proceedings of the Conference on Optics for Arts, Architecture, and Archaeology VI, Munich, Germany, 25–29 June 2017. [Google Scholar]
- Pascual-Francisco, J.B.; Barragan-Perez, O.; Susarrey-Huerta, O.; Michtchenko, A.; Martinez-Garcia, A.; Farfan-Cabrera, L.I. The effectiveness of shearography and digital image correlation for the study of creep in elastomers. Mater. Res. Express 2017, 4, 11. [Google Scholar] [CrossRef]
- Pascual-Francisco, J.B.; Susarrey-Huerta, O.; Michtchenko, A.; Barragan-Perez, O. Measurement of creep strain in polymers by means of electronic speckle pattern shearing interferometry. In Proceedings of the Dimensional Optical Metrology and Inspection for Practical Applications VII, Orlando, FL, USA, 15–19 April 2018. [Google Scholar]

| Phase-shift step N | Algorithms | Formula | Feature |
|---|---|---|---|
| 3 | 3 + 3 | Good phase map quality, only for static measurements, and enough calculation. | |
| 4 | 4 + 4 | Good phase map quality, only for static measurements, and simpler calculation. | |
| 4 + 2 | Acceptable phase map quality for dynamic measurement at a low dynamic range. | ||
| 4 + 1 | Poor phase map quality and small measurement range for a real dynamic measurement. | ||
| 5 | 5 + 5 | Good phase map quality, only for static measurements, and more accurate calculation. |
| Phase-Shift Digital Shearography Method | Advantage | Disadvantage | ||
|---|---|---|---|---|
| TPS-DS | Easy to implement with high precision. | Generally cannot measure dynamic phase. | ||
| SPS-DS | Multichannel spatial phase shift | Ability to measure dynamic phase. | Position matching is needed between interferograms or can only measure information in one dimension. | |
| Carrier-frequency spatial phase shift | Mach–Zehnder based | No requirement for shearing amount. | Small measurement size, poor phase map quality, and poor stability. | |
| Double-aperture based | Good phase map quality. | Small measurement size and poor stability. | ||
| Michelson based | Easy to use due to its simple structure and good stability. | Large shearing amount required. | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Q.; Dan, X.; Sun, F.; Wang, Y.; Wu, S.; Yang, L. Digital Shearography for NDT: Phase Measurement Technique and Recent Developments. Appl. Sci. 2018, 8, 2662. https://doi.org/10.3390/app8122662
Zhao Q, Dan X, Sun F, Wang Y, Wu S, Yang L. Digital Shearography for NDT: Phase Measurement Technique and Recent Developments. Applied Sciences. 2018; 8(12):2662. https://doi.org/10.3390/app8122662
Chicago/Turabian StyleZhao, Qihan, Xizuo Dan, Fangyuan Sun, Yonghong Wang, Sijin Wu, and Lianxiang Yang. 2018. "Digital Shearography for NDT: Phase Measurement Technique and Recent Developments" Applied Sciences 8, no. 12: 2662. https://doi.org/10.3390/app8122662
APA StyleZhao, Q., Dan, X., Sun, F., Wang, Y., Wu, S., & Yang, L. (2018). Digital Shearography for NDT: Phase Measurement Technique and Recent Developments. Applied Sciences, 8(12), 2662. https://doi.org/10.3390/app8122662






