Impulse Noise Denoising Using Total Variation with Overlapping Group Sparsity and Lp-Pseudo-Norm Shrinkage
Abstract
Featured Application
Abstract
1. Introduction
2. Traditional TV Model
3. Proposed Method
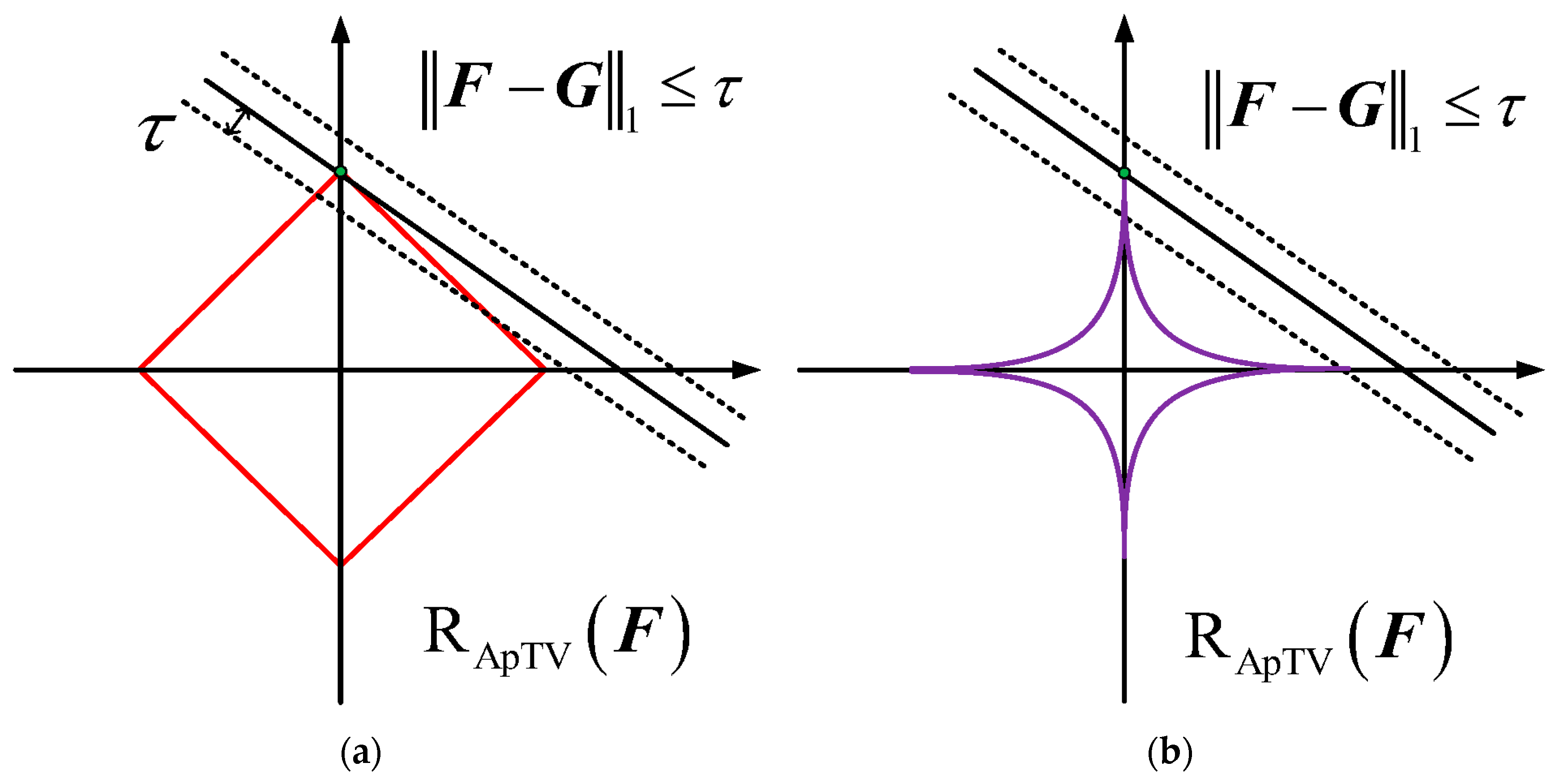
3.1. Overlapping Group Sparsity with L1 Norm (OGS-L1) Model
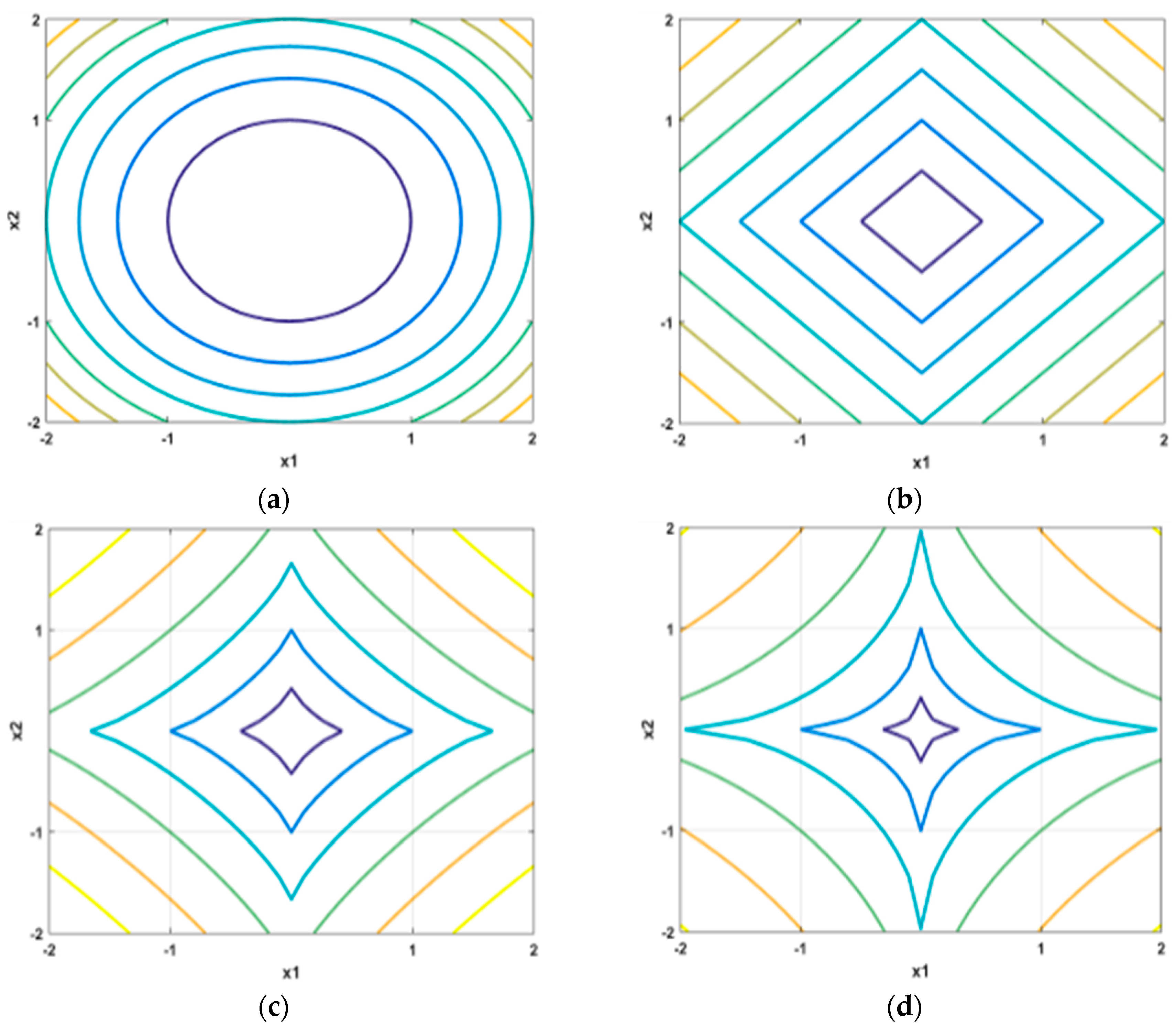
3.2. Overlapping Group Sparsity with Lp-Pseudo-Norm (OSG-Lp) Model
4. Solution
4.1. Solving the OSG-Lp Model
4.2. OGS-Lp-FAST Model
| Algorithm 1 OGS-Lp-FAST pseudo-code |
| Input: image G with noise Output: denoised image F Initialize: 1: for 2: If : 3: are updated with Equations (33) and (34) 4: are updated with Equation (35) 5: is updated with Equation (37) 6: are updated with Equation (39) 7: 8 Else 9: Restart as in Equation (38) 10: End If 11: If E < tol Break; 12: End For 13: Return F(k) as F |
5. Experimental Results and Analyses
5.1. Evaluation Method
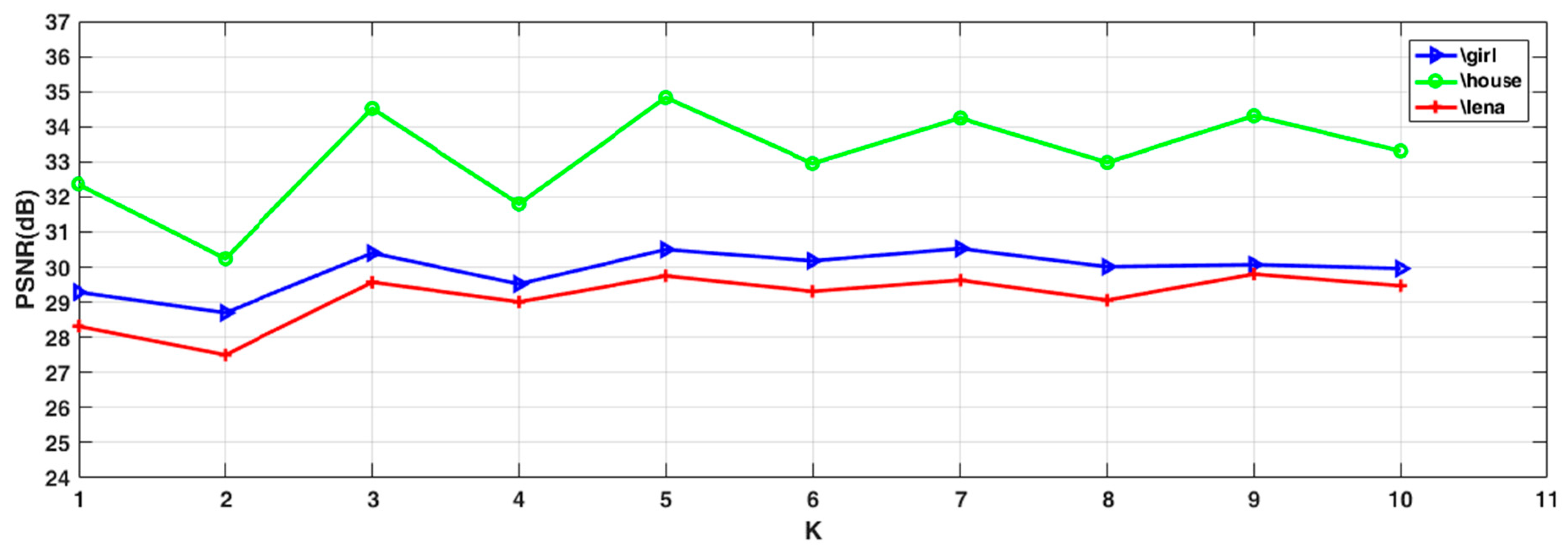
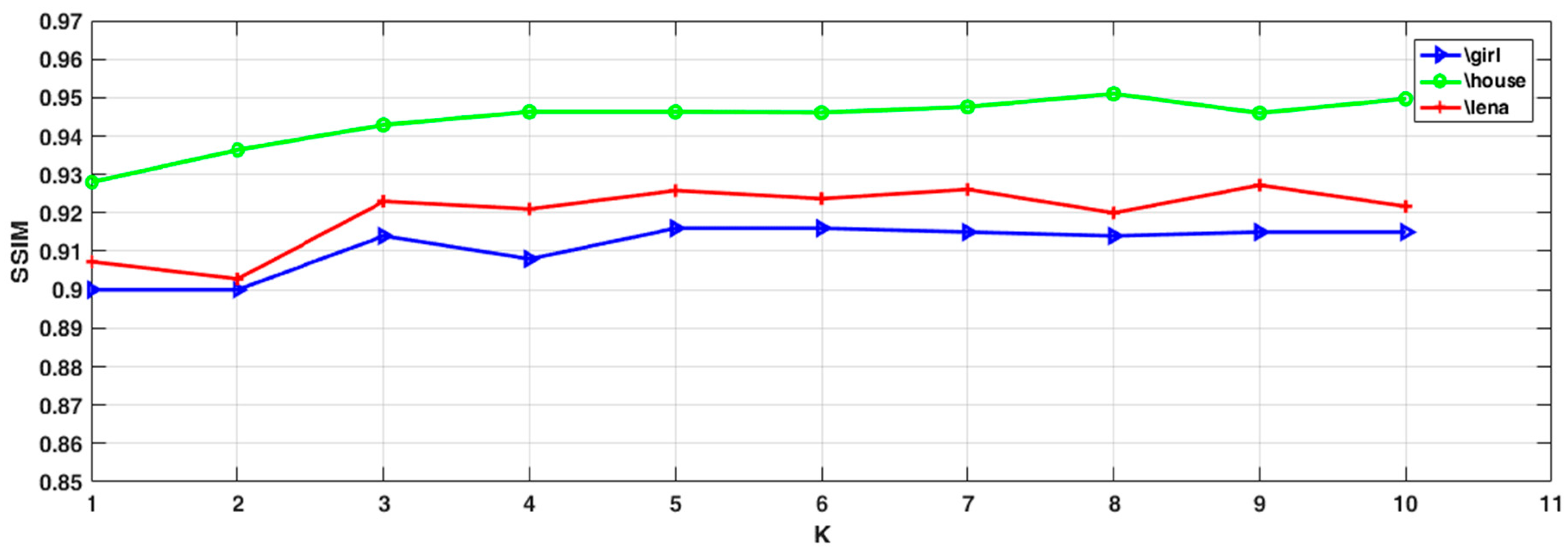
5.2. Sensitivity of the Parameters
5.3. Testing and Comparing the Denoising Performance of Different Algorithms
- With the introduction of different levels of noise to the images, our model generates higher PSNR and SSIM values for the reconstructed images than other methods, indicating its superior denoising effect. The recovered images also resemble the original ones more.
- The proposed model works better at lower noise levels. For example, at a 20% noise level, as shown in Table 2, the PSNR value of the “House” image (37.72 dB) given by our model is 5.91 dB higher than that given by the ITV model (31.81 dB) and 5.4 dB higher than that of the TGV model (32.32 dB). Even at high noise levels, our model still performs better than the others, which shows the clear advantages that total variation with overlapping group sparsity has over the classic anisotropic TV model.
- Compared to OGS-L1, our proposed method incorporates the Lp-pseudo-norm shrinkage, which adds another degree of freedom to the algorithm and improves the depiction of the gradient-domain sparsity of the images, achieving a better denoising effect. For example, at a 20% noise level, as shown in Table 2, the PSNR value of the “Girl” image (32.34 dB) given by our model is 1.67 dB higher than that given by the OGS-L1 model (30.67 dB). Even at a noise level of 50%, as shown in Table 5, the PSNR value of the “Girl” image (27.35 dB) given by our model is still 0.90 dB higher than that given by the OGS-L1 model (26.45 dB). This proves that the Lp-pseudo-norm is more suitable as a regularizer for describing the sparsity of images than the L1-norm.
- In terms of the runtime of the six models, the OGS-based method is more time consuming than ATV, ITV, and TGV. This is mainly because the OGS model considers the gradient information of the neighborhood in an image undergoing reconstruction, thus making the computation more complex.
- Comparing the values of PSNR and SSIM in Table 2, Table 3, Table 4 and Table 5, OGS-Lp-FAST and OGS-Lp have the same denoising effect. However, by observing the value of runtime of all testing images, we find that convergence is sped up in the OGS-LP-FAST method with the use of accelerated ADMM with a restart. For example, at a 20% noise level, as shown in Table 2, the time value of the “Woman” image (8.69 s) given by the OGS-Lp-FAST model is 7.53 s less than that given by the OGS-L1 model (16.22 s).
6. Discussion and Conclusions
- An overlapping group sparsity (OGS)-based regularizer is used to replace the anisotropic total variation (ATV), to describe the prior conditions of the image. OGS makes full use of the similarity among image neighborhoods and the dissimilarity in the surroundings of each point. It promotes the distinction between the smooth and edge regions of an image, thus enhancing the robustness of the proposed model.
- Lp-pseudo-norm shrinkage is used in place of the L1-norm regularization to describe the fidelity term of images with salt and pepper noise. With the inclusion of another degree of freedom, Lp-pseudo-norm shrinkage reflects the sparsity of the image better and greatly improves the denoising performance of the algorithm.
- The difference operator is used for convolution. Under the ADMM framework, the complex model is transformed into a series of simpler mathematical problems to solve.
- Appropriate K values could effectively improve the overall denoising performance of the model. In practice, this parameter needs to be adjusted. If it is too small, the neighborhood information is not utilized completely. If the value is too big, too many dissimilar pixel blocks will be included, impairing the denoising result.
- The adoption of accelerated ADMM with a restart accelerates the convergence of the algorithm. The running time is reduced.
- In this paper, we focus on impulse noise removal, but the model is also applicable to other types of noise removal that we will further study in future work.
Author Contributions
Funding
Conflicts of Interest
References
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-Variation-Regularized Low-Rank Matrix Factorization for Hyperspectral Image Restoration. IEEE Trans. Geosci. Remote Sens. 2015, 54, 178–188. [Google Scholar] [CrossRef]
- Cevher, V.; Sankaranarayanan, A.; Duarte, M.F.; Reddy, D.; Baraniuk, R.G.; Chellappa, R. Compressive Sensing for Background Subtraction; Springer: Berlin/Heidelberg, Germany, 2008; pp. 155–168. [Google Scholar]
- Huang, G.; Jiang, H.; Matthews, K.; Wilford, P. Lensless imaging by compressive sensing. In Proceedings of the IEEE International Conference on Image Processing, Melbourne, VIC, Australia, 15–18 September 2014; pp. 2101–2105. [Google Scholar]
- Chen, Y.; Peng, Z.; Cheng, Z.; Tian, L. Seismic signal time-frequency analysis basedon multi-directional window using greedy strategy. J. Appl. Geophys. 2017, 143, 116–128. [Google Scholar] [CrossRef]
- Lu, S.L.T.; Fang, L. Spectral–spatial adaptive sparse representation for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2016, 54, 373–385. [Google Scholar] [CrossRef]
- Zhao, W.; Lu, H. Medical Image Fusion and Denoising with Alternating Sequential Filter and Adaptive Fractional Order Total Variation. IEEE Trans. Instrum. Meas. 2017, 66, 1–12. [Google Scholar] [CrossRef]
- Knoll, F.; Bredies, K.; Pock, T.; Stollberger, R. Second order total generalized variation (TGV) for MRI. Magn. Reson. Med. 2011, 65, 480–491. [Google Scholar] [CrossRef] [PubMed]
- Kong, D.; Peng, Z. Seismic random noise attenuation using shearlet and total generalized variation. J. Geophys. Eng. 2015, 12, 1024–1035. [Google Scholar] [CrossRef]
- Zhu, Z.; Yin, H.; Chai, Y.; Li, Y.; Qi, G. A novel multi-modality image fusion method based on image decomposition and sparse representation. Inform. Sci. 2018, 432, 516–529. [Google Scholar] [CrossRef]
- Marquina, A.; Osher, S.J. Image super-resolution by TV-regularization and Bregman iteration. J. Sci. Comput. 2008, 37, 367–382. [Google Scholar] [CrossRef]
- Nikolova, M. A variational approach to remove outliers and impulse noise. J. Math. Imaging Vis. 2004, 20, 99–120. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Qin, Z. An Alternating Direction Method for Total Variation Denoising. Optim. Methods Softw. 2015, 30, 594–615. [Google Scholar] [CrossRef]
- Tai, X.C.; Wu, C. Augmented Lagrangian Method, Dual Methods and Split Bregman Iteration for ROF Model. In International Conference on Scale Space and Variational Methods in Computer Vision; Springer: Berlin/Heidelberg, Germany, 2009; pp. 502–513. [Google Scholar]
- Ng, M.; Wang, F.; Yuan, X.M. Fast Minimization Methods for Solving Constrained Total-Variation Superresolution Image Reconstruction. Multidimens. Syst. Signal Process. 2011, 22, 259–286. [Google Scholar] [CrossRef]
- Chan, T.; Marquina, A.; Mulet, P. High-order total variation-based image restoration. SIAM J. Sci. Comput. 2000, 22, 503–516. [Google Scholar] [CrossRef]
- Chan, T.F.; Esedoglu, S.; Park, F. A fourth order dual method for staircase reduction in texture extraction and image restoration problems. In Proceedings of the 2010 17th IEEE International Conference on Image Processing (ICIP), Hong Kong, China, 26–29 September 2010; pp. 4137–4140. [Google Scholar]
- Wu, L.; Chen, Y.; Jin, J.; Du, H.; Qiu, B. Four-directional fractional-order total variation regularization for image denoising. J. Electron. Imaging 2017, 26, 053003. [Google Scholar] [CrossRef]
- Bredies, K.; Kunisch, K.; Pock, T. Total generalized variation. SIAM J. Imaging Sci. 2010, 3, 492–526. [Google Scholar] [CrossRef]
- Feng, W.; Lei, H.; Gao, Y. Speckle reduction via higher order total variation approach. IEEE Trans. Image Process. 2014, 23, 1831–1843. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Chen, Y.; Wang, L.; Lin, F.; Wang, H.; Chen, Y. Four-Directional Total Variation Denoising Using Fast Fourier Transform and ADMM. In Proceedings of the IEEE 3rd International Conference on Image, Vision and Computing (ICIVC), Chongqing, China, 27–29 June 2018; pp. 379–383. [Google Scholar]
- Hajiaboli, M.R. An Anisotropic Fourth-Order Partial Differential Equation for Noise Removal; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Zhang, J.; Chen, K. A Total Fractional-Order Variation Model for Image Restoration with Non-homogeneous Boundary Conditions and its Numerical Solution. Siam J. Imaging Sci. 2015, 8, 2487–2518. [Google Scholar] [CrossRef]
- Chen, P.-Y.; Selesnick, I.W. Group-Sparse Signal Denoising: Non-Convex Regularization, Convex Optimization. arXiv 2013, arXiv:1308.5038. [Google Scholar] [CrossRef]
- Liu, J.; Huang, T.-Z.; Selesnick, I.W.; Lv, X.-G.; Chen, P.-Y. Image restoration using total variation with overlapping group sparsity. Inform. Sci. 2015, 295, 232–246. [Google Scholar] [CrossRef]
- Adam, T.; Paramesran, R. Image denoising using combined higher order non-convex total variation with overlapping group sparsity. Multidimens. Syst. Signal Process. 2018, 1–25. [Google Scholar] [CrossRef]
- Wu, Y.C.L.; Du, H. Efficient compressedsensing MR image reconstruction using anisotropic overlapping group sparsitytotal variation. In Proceedings of the 2017 7th International Workshop on Computer Science and Engineering, Beijing, China, 25–27 June 2017. [Google Scholar]
- Chen, Y.; Wu, L.; Peng, Z.; Liu, X. Fast Overlapping Group Sparsity Total Variation Image Denoising Based on Fast Fourier Transform and Split Bregman Iterations. In Proceedings of the 7th International Workshop on Computer Science and Engineering, Beijing, China, 25–27 June 2017. [Google Scholar]
- Chartrand, R. Exact Reconstruction of Sparse Signals via Nonconvex Minimization. IEEE Signal Process. Lett. 2007, 14, 707–710. [Google Scholar] [CrossRef]
- Parekh, A.; Selesnick, I.W. Convex Denoising using Non-Convex Tight Frame Regularization. IEEE Signal Process. Lett. 2015, 22, 1786–1790. [Google Scholar] [CrossRef]
- Li, S.; He, Y.; Chen, Y.; Liu, W.; Yang, X.; Peng, Z. Fast multi-trace impedance inversion using anisotropic total p-variation regularization in the frequency domain. J. Geophys. Eng. 2018, 15. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Liu, J.; Huang, T.-Z.; Liu, G.; Wang, S.; Lv, X.-G. Total variation with overlapping group sparsity for speckle noise reduction. Neurocomputing 2016, 216, 502–513. [Google Scholar] [CrossRef]
- Goldstein, T.; O’donoghue, B.; Setzer, S.; Baraniuk, R. Fast alternating direction optimization methods. SIAM J. Imaging Sci. 2014, 7, 1588–1623. [Google Scholar] [CrossRef]
- Chan, R.H.; Ho, C.-W.; Nikolova, M. Salt-and-pepper noise removal by median-type noise detectors and detail-preserving regularization. IEEE Trans. Image Process. 2005, 14, 1479–1485. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Q.; Wu, C.; Shu, Q.; Liu, R.W. Spatially adaptive total generalized variation-regularized image deblurring with impulse noise. J. Electron. Imaging 2018, 27, 053006. [Google Scholar] [CrossRef]
- Trivedi, M.C.; Singh, V.K.; Kolhe, M.L.; Goyal, P.K.; Shrimali, M. Patch-Based Image Denoising Model for Mixed Gaussian Impulse Noise Using L1 Norm. In Intelligent Communication and Computational Technologies; Springer: Singapore, 2018; pp. 77–84. [Google Scholar]
- Zheng, L.; Maleki, A.; Weng, H.; Wang, X.; Long, T. Does ℓp-minimization outperform ℓ1-minimization? IEEE Trans. Inform. Theory 2017, 63, 6896–6935. [Google Scholar] [CrossRef]
- Xie, Y.; Gu, S.; Liu, Y.; Zuo, W.; Zhang, W.; Zhang, L. Weighted Schatten $p$ -Norm Minimization for Image Denoising and Background Subtraction. IEEE Trans. Image Process. 2016, 25, 4842–4857. [Google Scholar] [CrossRef]
- Zhou, X.; Molina, R.; Zhou, F.; Katsaggelos, A.K. Fast iteratively reweighted least squares for lp regularized image deconvolution and reconstruction. IEEE Int. Conf. Image Process. 2015, 24, 1783–1787. [Google Scholar]
- Chen, F.; Zhang, Y. Sparse Hyperspectral Unmixing Based on Constrained lp—l2 Optimization. IEEE Geosci. Remote Sens. Lett. 2013, 10, 1142–1146. [Google Scholar] [CrossRef]
- Chen, Y.; Peng, Z.; Gholami, A.; Yan, J.; Li, S. Seismic Signal Sparse Time-Frequency Analysis by Lp-Quasinorm Constraint. arXiv 2018, arXiv:1801.05082. [Google Scholar]
- Woodworth, J.; Chartrand, R. Compressed Sensing Recovery via Nonconvex Shrinkage Penalties. Inverse Probl. 2016, 32, 075004. [Google Scholar] [CrossRef]
- Sidky, E.Y.; Chartrand, R.; Boone, J.M.; Pan, X. Constrained TpV Minimization for Enhanced Exploitation of Gradient Sparsity: Application to CT Image Reconstruction. IEEE J. Transl. Eng. Health Med. 2014, 2, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Tai, X.C. Augmented Lagrangian Method, Dual Methods, and Split Bregman Iteration for ROF, Vectorial TV, and High Order Models. Siam J. Imaging Sci. 2012, 3, 300–339. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]


| Image | House | Lena | Woman | Milk drop | Girl | Shoulder |
|---|---|---|---|---|---|---|
| Parameter | ||||||
| Level | ||||||
| 20% | 0.14/0.45 | 0.15/0.45 | 0.15/0.65 | 0.14/0.65 | 0.14/0.65 | 0.14/0.65 |
| 30% | 0.15/0.45 | 0.15/0.65 | 0.15/0.7 | 0.16/0.65 | 0.15/0.65 | 0.15/0.65 |
| 40% | 0.15/0.45 | 0.16/0.65 | 0.15/0.7 | 0.19/0.65 | 0.15/0.65 | 0.15/0.65 |
| 50% | 0.18/0.55 | 0.17/0.65 | 0.2/0.7 | 0.2/0.65 | 0.18/0.55 | 0.18/0.55 |
| Image | Method | The Output Seismic Signal | |||
|---|---|---|---|---|---|
| PSNR (dB) | SSIM | Time (s) | |||
| 20% | Lena | ATV | 28.71 | 0.8854 | 4.81 |
| ITV | 28.83 | 0.8936 | 2.45 | ||
| TGV | 28.63 | 0.8966 | 9.59 | ||
| OGS-L1 | 29.79 | 0.9115 | 16.34 | ||
| OGS-Lp | 31.47 | 0.9474 | 13.94 | ||
| OGS-Lp-FAST | 31.55 | 0.9482 | 8.64 | ||
| House | ATV | 32.31 | 0.8871 | 3.09 | |
| ITV | 31.81 | 0.8888 | 1.84 | ||
| TGV | 32.32 | 0.9135 | 8.38 | ||
| OGS-L1 | 33.04 | 0.9127 | 15.27 | ||
| OGS-Lp | 37.47 | 0.9667 | 12.45 | ||
| OGS-Lp-FAST | 37.72 | 0.9679 | 10.48 | ||
| Shoulder | ATV | 35.32 | 0.9636 | 5.42 | |
| ITV | 35.33 | 0.9649 | 3.56 | ||
| TGV | 35.29 | 0.9256 | 14.98 | ||
| OGS-L1 | 37.00 | 0.9719 | 17.77 | ||
| OGS-Lp | 38.89 | 0.9829 | 16.06 | ||
| OGS-Lp-FAST | 38.92 | 0.983 | 14.61 | ||
| Girl | ATV | 29.45 | 0.8868 | 4.53 | |
| ITV | 30.05 | 0.894 | 3.22 | ||
| TGV | 30.14 | 0.8907 | 9.58 | ||
| OGS-L1 | 30.67 | 0.8995 | 13.48 | ||
| OGS-Lp | 32.29 | 0.9365 | 14.17 | ||
| OGS-Lp-FAST | 32.34 | 0.9371 | 11.69 | ||
| Milk Drop | ATV | 32.32 | 0.8973 | 4.83 | |
| ITV | 31.02 | 0.9039 | 3.63 | ||
| TGV | 30.48 | 0.894 | 8.59 | ||
| OGS-L1 | 33.35 | 0.911 | 16.39 | ||
| OGS-Lp | 35.76 | 0.9533 | 13.42 | ||
| OGS-Lp-FAST | 35.87 | 0.9538 | 8.58 | ||
| Woman | ATV | 29.45 | 0.8868 | 4.53 | |
| ITV | 29.65 | 0.9015 | 3.73 | ||
| TGV | 29.84 | 0.8853 | 8.98 | ||
| OGS-L1 | 30.35 | 0.908 | 16.03 | ||
| OGS-Lp | 31.71 | 0.9395 | 16.22 | ||
| OGS-Lp-FAST | 31.7 | 0.9398 | 8.69 | ||
| Image | Method | The Output Seismic Signal | |||
|---|---|---|---|---|---|
| PSNR (dB) | SSIM | Time (s) | |||
| 30% | Lena | ATV | 27.08 | 0.829 | 5 |
| ITV | 27.06 | 0.837 | 2.88 | ||
| TGV | 27.23 | 0.8319 | 8.16 | ||
| OGS-L1 | 27.59 | 0.8543 | 9.56 | ||
| OGS-Lp | 29.19 | 0.9035 | 15.72 | ||
| OGS-Lp-FAST | 29.21 | 0.9039 | 7.48 | ||
| House | ATV | 30.4 | 0.8717 | 3.8 | |
| ITV | 30.16 | 0.8545 | 2.17 | ||
| TGV | 30.82 | 0.8862 | 11.61 | ||
| OGS-L1 | 31.5 | 0.8807 | 7.77 | ||
| OGS-Lp | 35.03 | 0.9432 | 13.8 | ||
| OGS-Lp-FAST | 35.13 | 0.9444 | 10.77 | ||
| Shoulder | ATV | 34.48 | 0.9551 | 4.95 | |
| ITV | 34.33 | 0.9556 | 3.94 | ||
| TGV | 34.74 | 0.9493 | 22 | ||
| OGS-L1 | 35.34 | 0.9599 | 16.97 | ||
| OGS-Lp | 36.5 | 0.9633 | 18.88 | ||
| OGS-Lp-FAST | 36.47 | 0.9628 | 5.88 | ||
| Girl | ATV | 28.17 | 0.8586 | 5.17 | |
| ITV | 28.53 | 0.8737 | 3.31 | ||
| TGV | 28.82 | 0.8422 | 8.84 | ||
| OGS-L1 | 29.11 | 0.8818 | 8.88 | ||
| OGS-Lp | 30.42 | 0.9155 | 15.64 | ||
| OGS-Lp-FAST | 30.41 | 0.9148 | 12.84 | ||
| Milk Drop | ATV | 30.24 | 0.8788 | 4.95 | |
| ITV | 30.1 | 0.8681 | 2.33 | ||
| TGV | 29.42 | 0.8878 | 11.45 | ||
| OGS-L1 | 31.08 | 0.8836 | 9.33 | ||
| OGS-Lp | 32.7 | 0.9261 | 16.88 | ||
| OGS-Lp-FAST | 33.19 | 0.9274 | 10.64 | ||
| Woman | ATV | 27.86 | 0.8534 | 4.27 | |
| ITV | 28.43 | 0.866 | 2.83 | ||
| TGV | 28.32 | 0.844 | 9.53 | ||
| OGS-L1 | 29.05 | 0.8725 | 11.59 | ||
| OGS-Lp | 30.15 | 0.9063 | 17.25 | ||
| OGS-Lp-FAST | 30.13 | 0.9047 | 10.89 | ||
| Image | Method | The Output Seismic Signal | |||
|---|---|---|---|---|---|
| PSNR (dB) | SSIM | Time (s) | |||
| 40% | Lena | ATV | 25.85 | 0.796 | 5 |
| ITV | 25.8 | 0.8009 | 3.11 | ||
| TGV | 26.2 | 0.8041 | 10.27 | ||
| OGS-L1 | 26.22 | 0.8151 | 11.25 | ||
| OGS-Lp | 27.64 | 0.8683 | 18.88 | ||
| OGS-Lp-FAST | 27.67 | 0.8675 | 9.81 | ||
| House | ATV | 28.5 | 0.8433 | 4.94 | |
| ITV | 28.69 | 0.8356 | 2.31 | ||
| TGV | 29.21 | 0.8284 | 9.48 | ||
| OGS-L1 | 29.31 | 0.8566 | 11.95 | ||
| OGS-Lp | 32.84 | 0.9182 | 13.77 | ||
| OGS-Lp-FAST | 32.92 | 0.9189 | 12.8 | ||
| Shoulder | ATV | 32.4 | 0.9328 | 4.86 | |
| ITV | 32.54 | 0.9357 | 3.86 | ||
| TGV | 32.8 | 0.9345 | 24.81 | ||
| OGS-L1 | 32.62 | 0.9310 | 16.36 | ||
| OGS-Lp | 33.25 | 0.9510 | 20.66 | ||
| OGS-Lp-FAST | 33.24 | 0.9509 | 17.61 | ||
| Girl | ATV | 27.19 | 0.8348 | 4.94 | |
| ITV | 27.33 | 0.8447 | 3.09 | ||
| TGV | 27.86 | 0.8135 | 12.11 | ||
| OGS-L1 | 27.88 | 0.8526 | 11.78 | ||
| OGS-Lp | 28.87 | 0.8861 | 18.05 | ||
| OGS-Lp-FAST | 28.86 | 0.8847 | 12.69 | ||
| Milk Drop | ATV | 27.51 | 0.8307 | 3.97 | |
| ITV | 28.1 | 0.8424 | 3.19 | ||
| TGV | 28.09 | 0.8521 | 12.97 | ||
| OGS-L1 | 29.34 | 0.8569 | 10.27 | ||
| OGS-Lp | 30.56 | 0.8938 | 16.94 | ||
| OGS-Lp-FAST | 30.46 | 0.8933 | 13 | ||
| Woman | ATV | 26.97 | 0.8338 | 4.67 | |
| ITV | 27.13 | 0.8366 | 3.63 | ||
| TGV | 27.34 | 0.7708 | 9.58 | ||
| OGS-L1 | 27.7 | 0.8483 | 13.13 | ||
| OGS-Lp | 28.27 | 0.8722 | 18.45 | ||
| OGS-Lp-FAST | 28.29 | 0.8716 | 13.11 | ||
| Image | Method | The Output Seismic Signal | |||
|---|---|---|---|---|---|
| PSNR (dB) | SSIM | Time (s) | |||
| 50% | Lena | ATV | 23.44 | 0.7353 | 6 |
| ITV | 23.56 | 0.7457 | 4.14 | ||
| TGV | 25.05 | 0.7631 | 13.44 | ||
| OGS-L1 | 25.08 | 0.7612 | 15.86 | ||
| OGS-Lp | 25.74 | 0.8264 | 19.06 | ||
| OGS-Lp-FAST | 25.72 | 0.8262 | 11.67 | ||
| House | ATV | 26.48 | 0.8046 | 3.61 | |
| ITV | 27.09 | 0.8139 | 2.88 | ||
| TGV | 27.88 | 0.8264 | 15.14 | ||
| OGS-L1 | 27.85 | 0.8245 | 10.05 | ||
| OGS-Lp | 31.24 | 0.8932 | 16.41 | ||
| OGS-Lp-FAST | 31.15 | 0.8923 | 14.61 | ||
| Shoulder | ATV | 30.99 | 0.9137 | 4.91 | |
| ITV | 31.07 | 0.9168 | 3.59 | ||
| TGV | 31.93 | 0.8954 | 24.31 | ||
| OGS-L1 | 30.99 | 0.9137 | 16.5 | ||
| OGS-Lp | 31.94 | 0.9161 | 19.45 | ||
| OGS-Lp-FAST | 32.05 | 0.9277 | 17.72 | ||
| Girl | ATV | 25.1 | 0.7761 | 5.58 | |
| ITV | 25.73 | 0.7977 | 3.3 | ||
| TGV | 26.75 | 0.814 | 15.67 | ||
| OGS-L1 | 26.45 | 0.811 | 14.16 | ||
| OGS-Lp | 27.32 | 0.846 | 19.28 | ||
| OGS-Lp-FAST | 27.35 | 0.8463 | 15.91 | ||
| Milk Drop | ATV | 26.19 | 0.8082 | 4.92 | |
| ITV | 26.51 | 0.8188 | 3.42 | ||
| TGV | 27.01 | 0.8349 | 19.05 | ||
| OGS-L1 | 27.61 | 0.8351 | 14.67 | ||
| OGS-Lp | 28.65 | 0.868 | 17.8 | ||
| OGS-Lp-FAST | 28.59 | 0.8682 | 14.11 | ||
| Woman | ATV | 25.84 | 0.8049 | 5.11 | |
| ITV | 25.24 | 0.7939 | 3.67 | ||
| TGV | 25.99 | 0.685 | 10.84 | ||
| OGS-L1 | 26.29 | 0.8143 | 13.95 | ||
| OGS-Lp | 26.56 | 0.8165 | 18.19 | ||
| OGS-Lp-FAST | 26.61 | 0.8169 | 14.02 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Chen, Y.; Lin, F.; Chen, Y.; Yu, F.; Cai, Z. Impulse Noise Denoising Using Total Variation with Overlapping Group Sparsity and Lp-Pseudo-Norm Shrinkage. Appl. Sci. 2018, 8, 2317. https://doi.org/10.3390/app8112317
Wang L, Chen Y, Lin F, Chen Y, Yu F, Cai Z. Impulse Noise Denoising Using Total Variation with Overlapping Group Sparsity and Lp-Pseudo-Norm Shrinkage. Applied Sciences. 2018; 8(11):2317. https://doi.org/10.3390/app8112317
Chicago/Turabian StyleWang, Lingzhi, Yingpin Chen, Fan Lin, Yuqun Chen, Fei Yu, and Zongfu Cai. 2018. "Impulse Noise Denoising Using Total Variation with Overlapping Group Sparsity and Lp-Pseudo-Norm Shrinkage" Applied Sciences 8, no. 11: 2317. https://doi.org/10.3390/app8112317
APA StyleWang, L., Chen, Y., Lin, F., Chen, Y., Yu, F., & Cai, Z. (2018). Impulse Noise Denoising Using Total Variation with Overlapping Group Sparsity and Lp-Pseudo-Norm Shrinkage. Applied Sciences, 8(11), 2317. https://doi.org/10.3390/app8112317




