Correlation for Condensation Heat Transfer in a 4.0 mm Smooth Tube and Relationship with R1234ze(E), R404A, and R290
Abstract
:1. Introduction
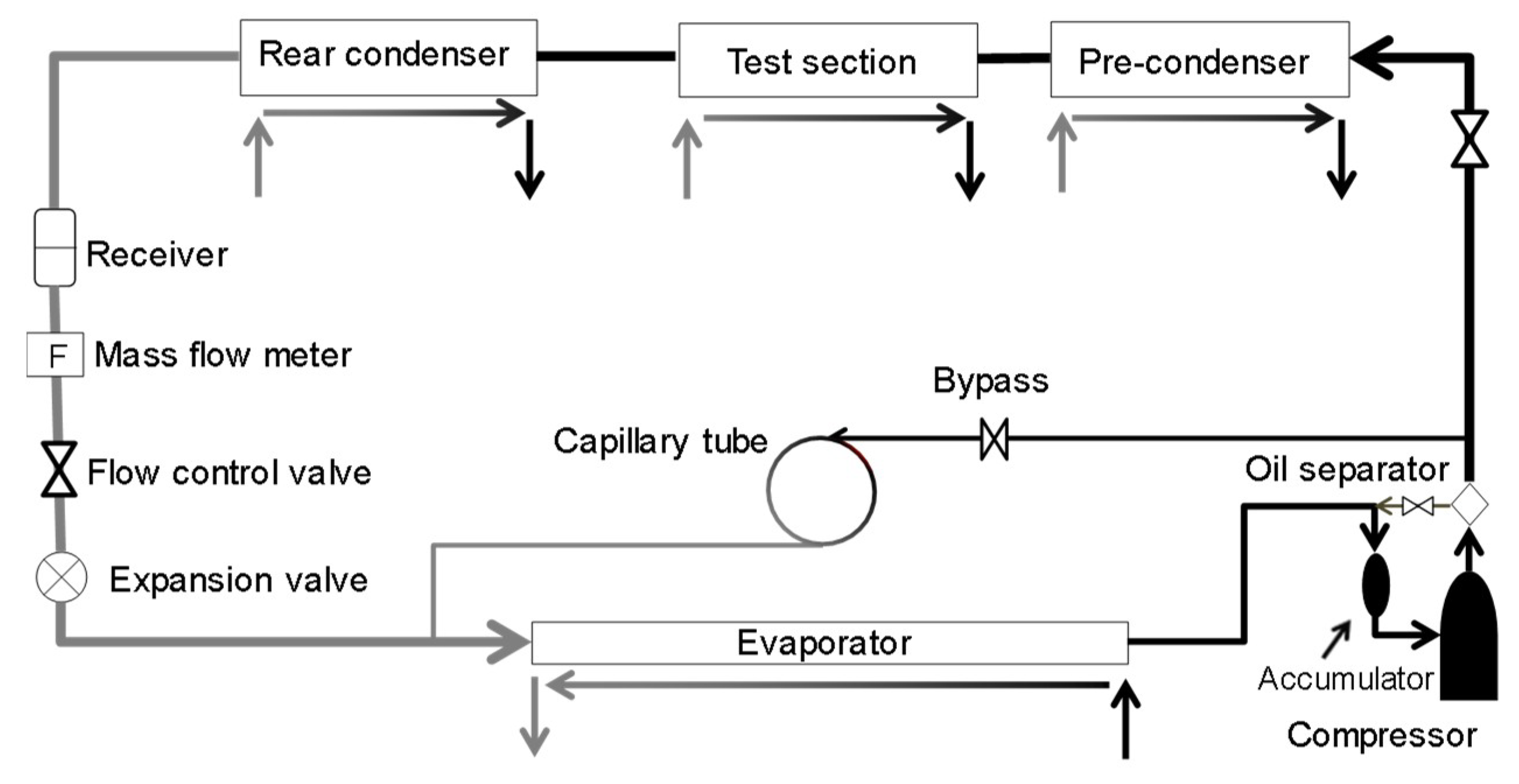
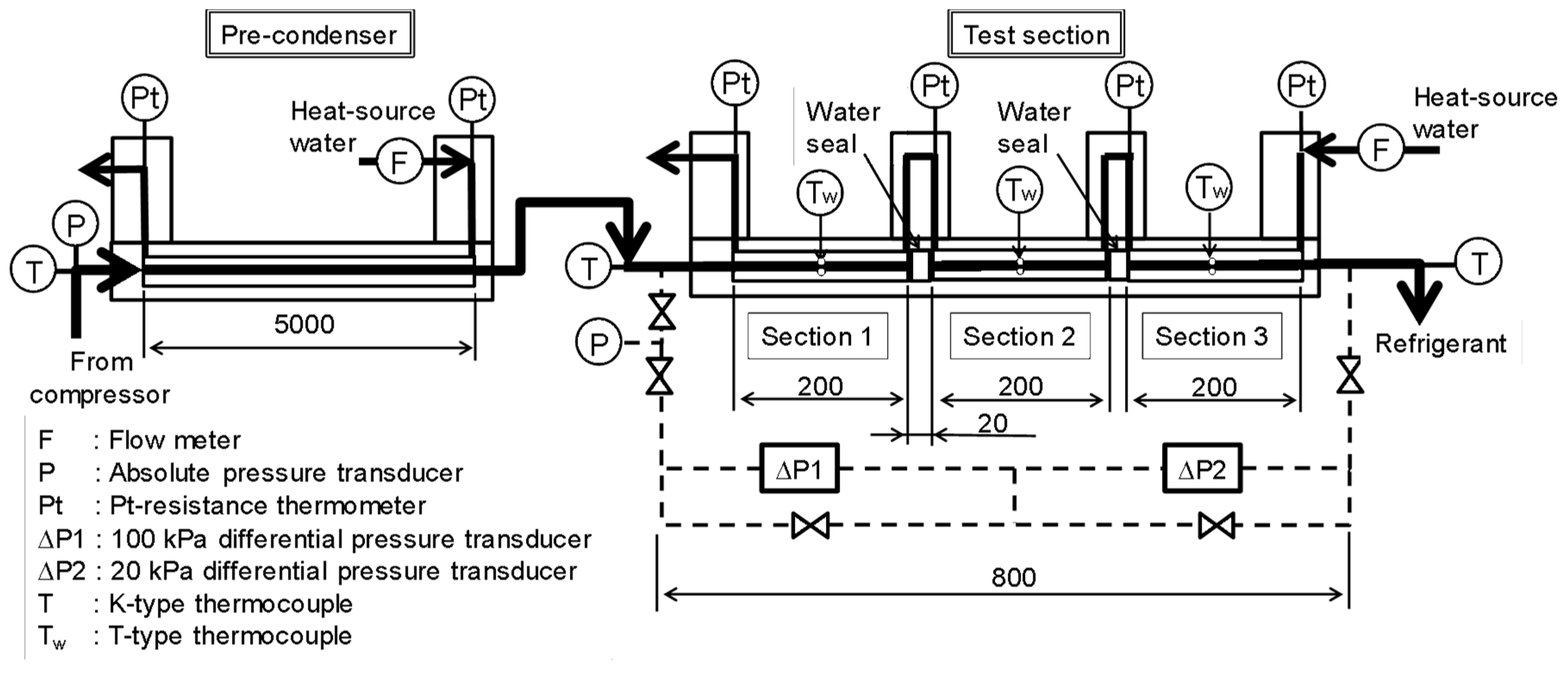
2. Experimental Setup and Procedure
3. Method of Experimental Data Analysis
4. Results and Discussion
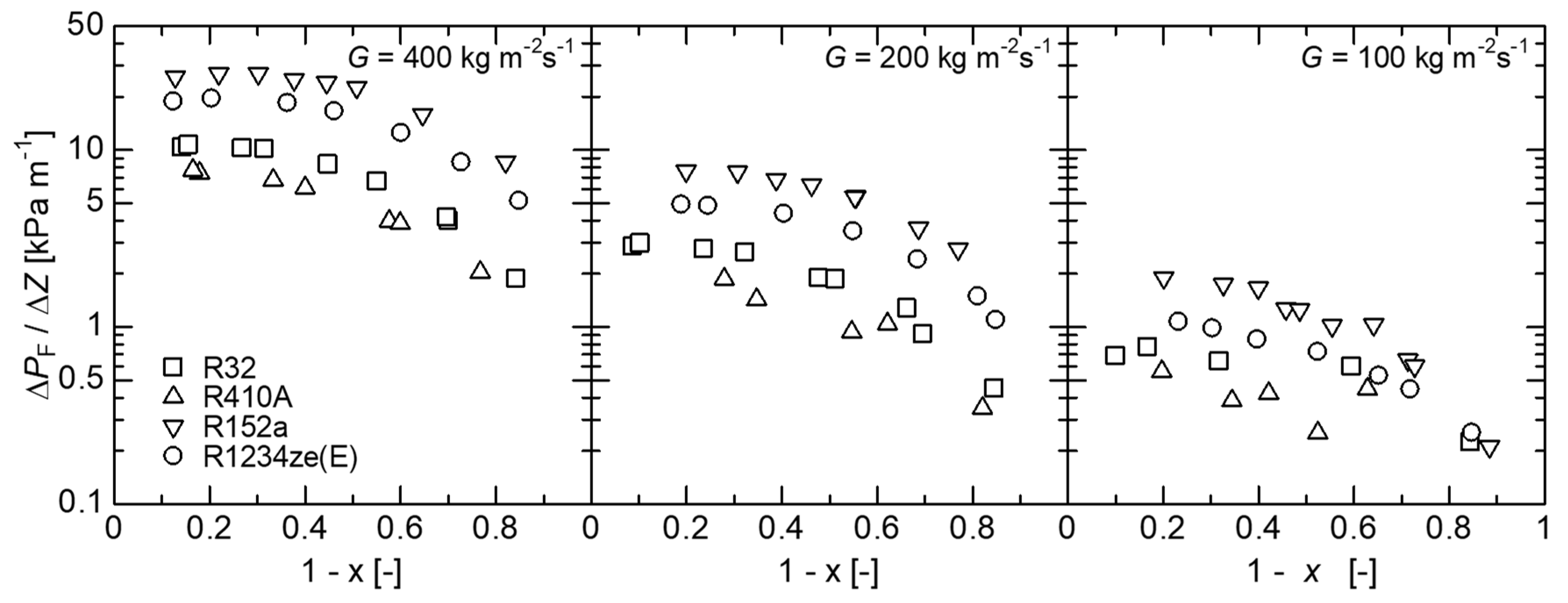
4.1. Pressure Drop in a Smooth Tube
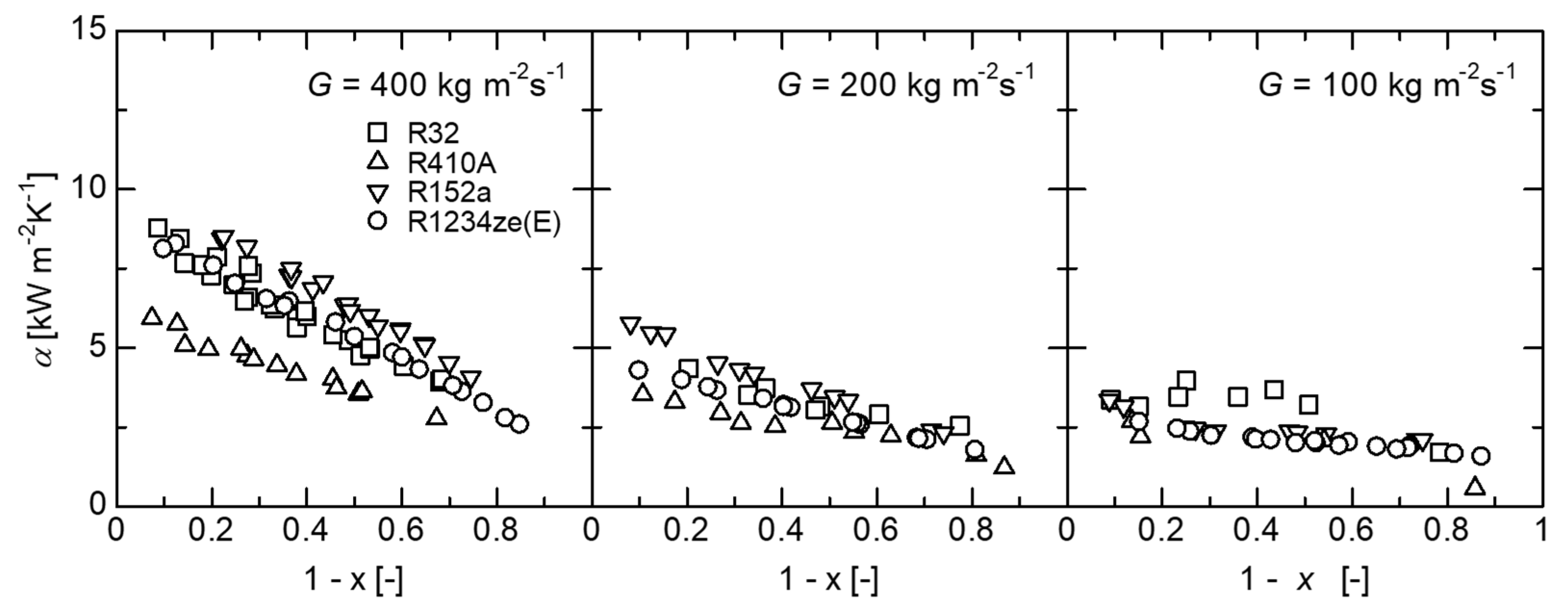
4.2. Condensation Heat Transfer Coefficient
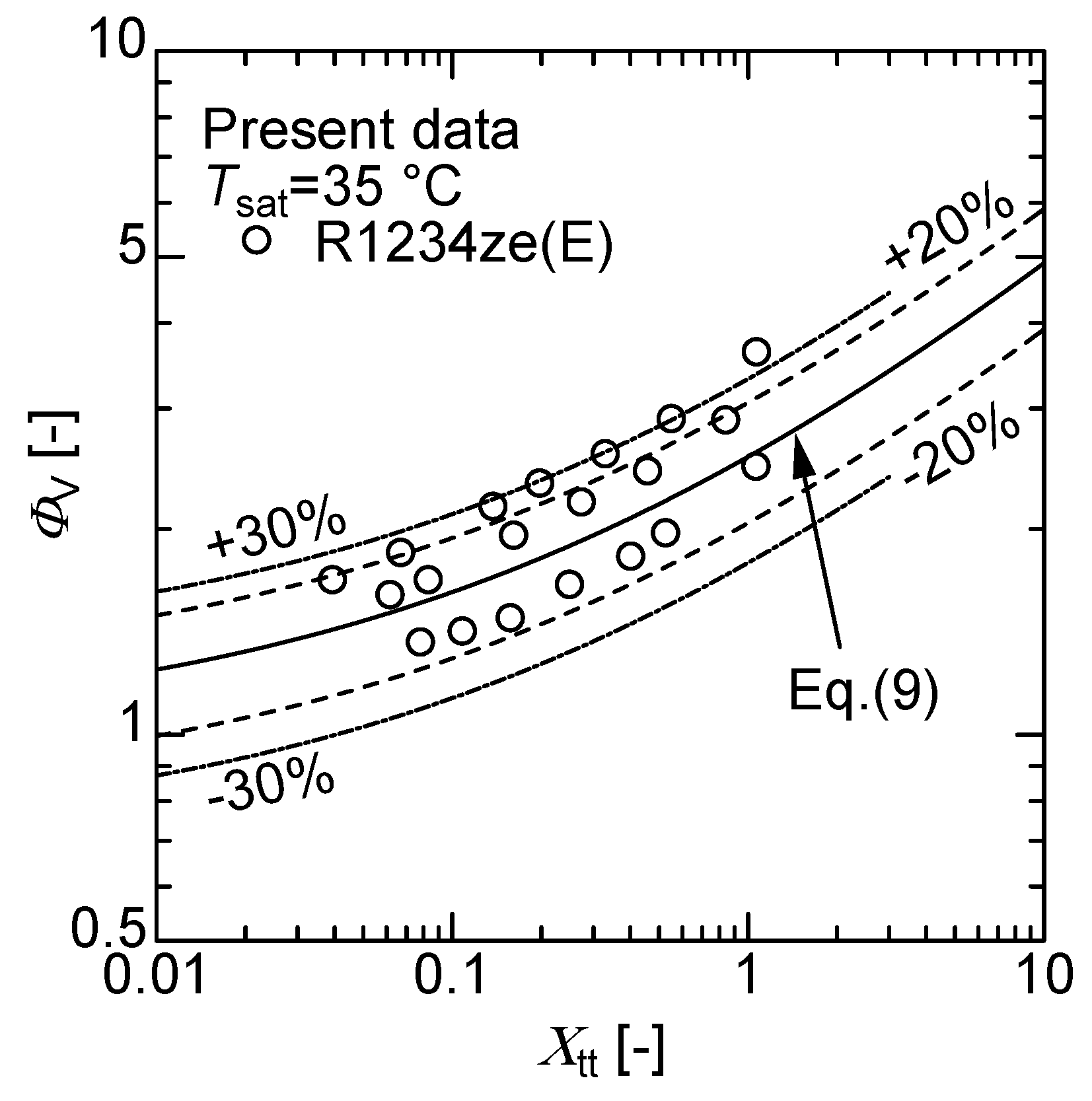
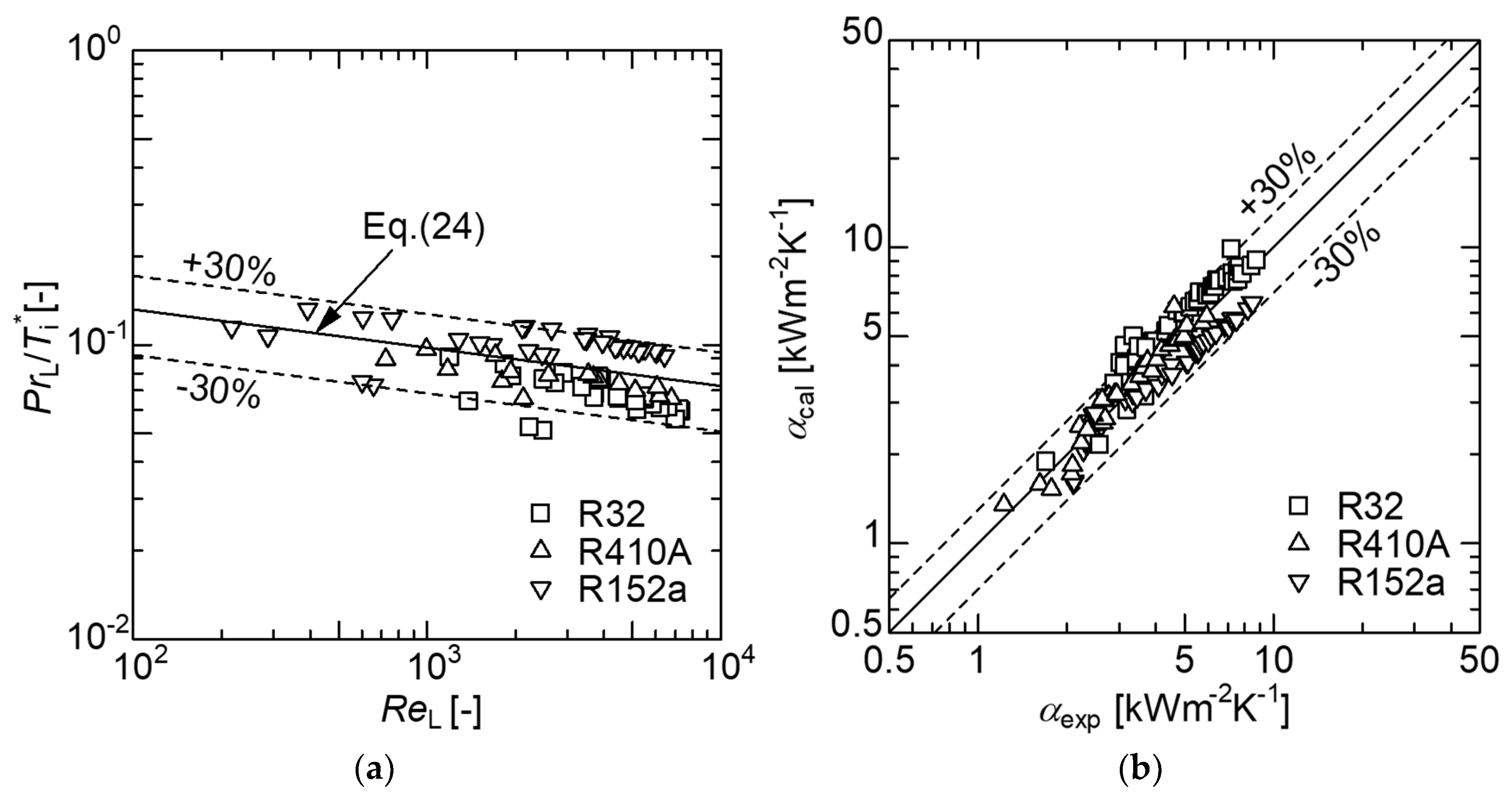
4.3. Derivation of the General Correlation for Condensation Heat Transfer in Small-Diameter Smooth Tube
5. Conclusions
- (1)
- The frictional pressure drop of R1234ze(E) can be correlated within ±30% by our previous general correlation of frictional pressure drop for the small-diameter smooth tube.
- (2)
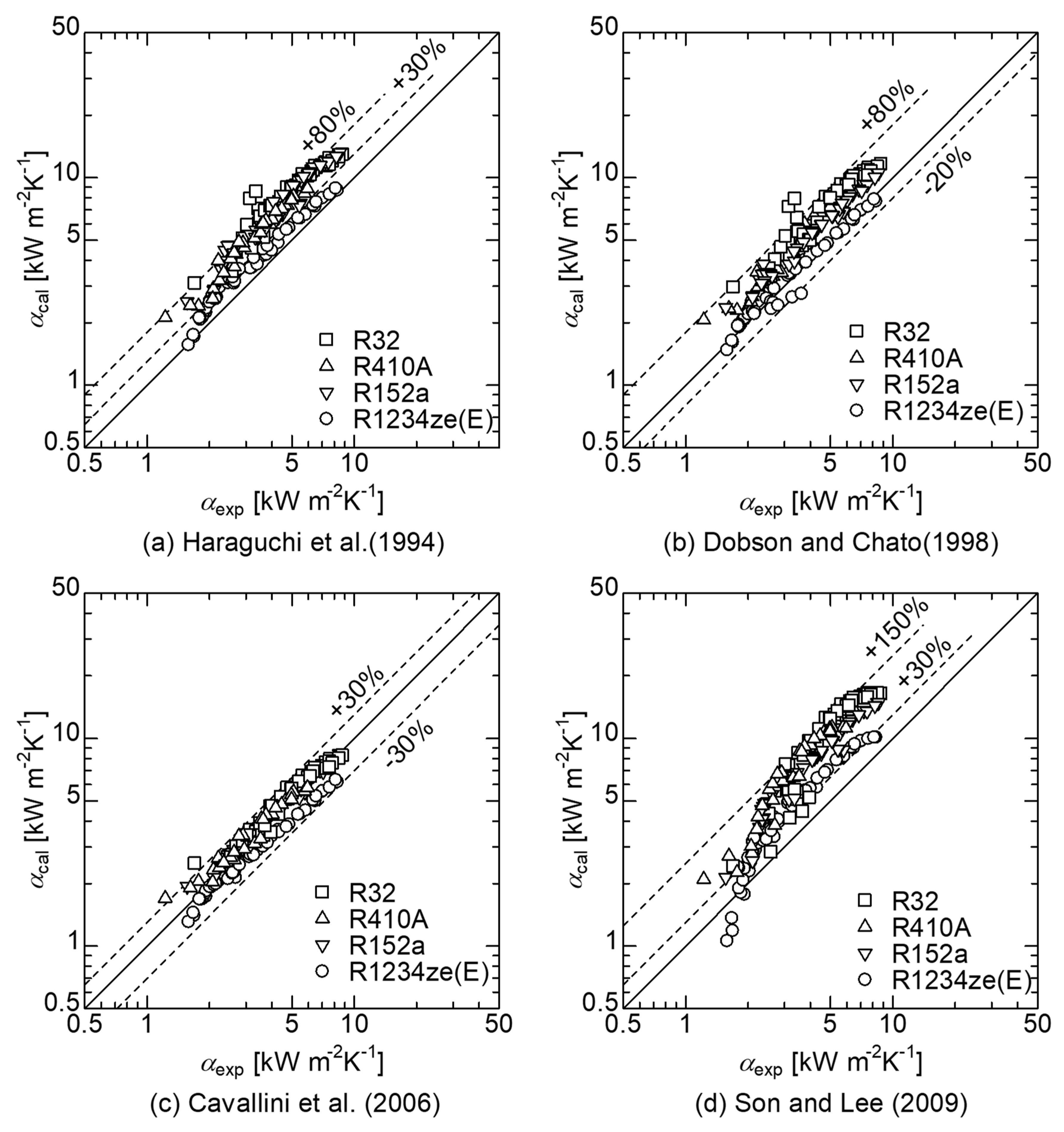
- For small-diameter smooth tubes, the condensation heat transfer coefficient can be predicted within ±30% by the correlation of Cavallini et al., which has the highest accuracy among the previously proposed correlations.
- (3)
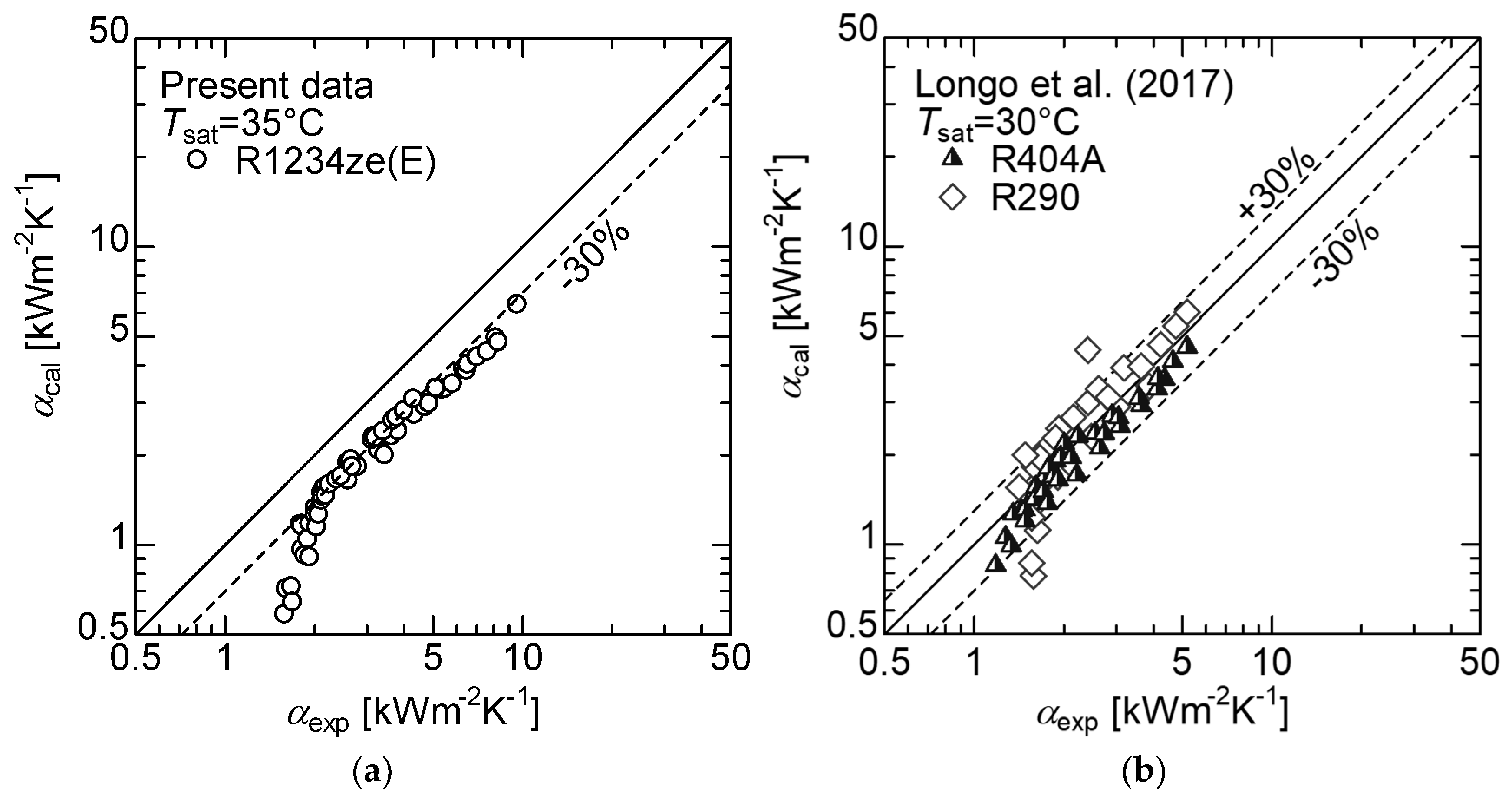
- A new general correlation, by a simple and convenient method for estimating the condensation heat transfer for small-diameter smooth tubes and several kinds of refrigerants, was proposed. The predicted trend agrees with the measured values of R1234ze(E); however, the predicted value underestimates the experimental values by approximately −30%, particularly in the low wetness region.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | heat transfer area (m2) |
| Bo | Bond number = |
| cP | isobaric specific heat (J kg−1 K−1) |
| d | tube diameter (m) |
| f | friction factor |
| FrSO | Solliman’s modified Froude number |
| G | refrigerant mass velocity (kg m−2s−1) |
| g | gravitational acceleration (m s−2) |
| Ga | Galileo number = |
| hfg | latent heat of condensation (J kg−1) |
| L | heat transfer length (m) |
| m | mass flow rate (kg s−1) |
| Nu | Nusselt number = |
| NuB | free convection Nusselt number |
| NuF | forced convection Nusselt number |
| P | pressure (Pa) |
| Ph | phase change number = |
| Pr | Prandtl number = |
| Q | heat transfer rate of each subsection (W) |
| ReL | liquid Reynolds number = |
| ReV | vapor Reynolds number = |
| T | temperature (K) |
| Ti* | dimensionless temperature difference |
| x | vapor quality |
| Greek Symbols | |
| α | heat transfer coefficient (W m−2 K−1) |
| total pressure drop (Pa) | |
| frictional pressure drop (Pa) | |
| acceleration pressure drop (Pa) | |
| λ | thermal conductivity (W m−1 K−1) |
| μ | viscosity (Pa s) |
| ξ | void fraction |
| ρ | density (kg m−3) |
| Φ | two-phase pressure drop multiplier |
| Lockhart–Martinelli parameter | |
| Subscripts | |
| cal | calculated value |
| c | heat-source water |
| exp | experiment |
| i | inside |
| L | liquid |
| n | subsection number |
| o | outside |
| pre | pre-condenser |
| r | refrigerant |
| sat | saturated |
| so | Soliman |
| V | vapor |
| W | wall |
References
- Haraguchi, H.; Koyama, S.; Fujii, T. Condensation of Refrigerants HCFC22, HFC134a and HCFC123 in a Horizontal Smooth Tube: 1st Report, Proposals of Empirical Expressions for Local Pressure Drop. J. Jpn. Soc. Mech. Eng. 1994, 60, 239–244. (In Japanese) [Google Scholar]
- Haraguchi, H.; Koyama, S.; Fujii, T. Condensation of Refrigerants HCFC22, HFC134a and HCFC123 in a Horizontal Smooth tube: 2nd report, Proposals of Empirical Expressions for Local Heat Transfer Coefficient. J. Jpn. Soc. Mech. Eng. 1994, 60, 245–252. (In Japanese) [Google Scholar]
- Dobson, M.; Chato, J. Condensation in Smooth Horizontal Tubes. J. Heat Transf. 1998, 120, 193–213. [Google Scholar] [CrossRef]
- Cavallini, A.; Del Col, D.; Doretti, L.; Matkovic, M.; Rossetto, L.; Zilio, C. Condensation in Horizontal Smooth Tubes: A New Heat Transfer Model for heat Exchanger Design. Heat Transf. Eng. 2006, 27–28, 31–38. [Google Scholar] [CrossRef]
- Hossain, M.A.; Onaka, Y.; Miyara, A. Experimental Study on Condensation Heat Transfer and Pressure drop in Horizontal Smooth Tube for R1234ze(E), R32 and R410A. Int. J. Refrig. 2012, 35, 927–938. [Google Scholar] [CrossRef]
- Han, B.; Liu, F.; Cai, D.; Tian, Q.; He, G. Experimental Study on Condensation Heat Transfer of R32/R290 Mixture in Horizontal Tubes. Appl. Therm. Eng. 2015. [Google Scholar] [CrossRef]
- Son, C.; Lee, H. Condensation Heat Transfer Characteristics of R-22, R-134a and R-410A in Small Diameter Tubes. Heat Mass Transf. 2009, 45, 1153–1166. [Google Scholar] [CrossRef]
- Matsumoto, T.; Arata, Y.; Miyata, K.; Hamamoto, Y.; Mori, H. Experiment on Condensation Heat Transfer of HFC134a in a Horizontal Single Rectangular Mini-channel. In Proceedings of the 9th Asian Conference on Refrigeration and Air-conditioning 2018, Sapporo, Japan, 10–13 June 2018. [Google Scholar]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C. R134a and Its Low GWP Substitutes R1234yf and R1234ze(E) Condensation inside a 4 mm Horizontal Smooth Tube. In Proceedings of the 17th International Refrigeration and Air Conditioning Conference at Purdue 2018, West Lafayette, IN, USA, 9–12 July 2018. [Google Scholar]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C. R410A and Its Low GWP Substitutes R32 Condensation inside a 4 mm Horizontal Smooth Tube. In Proceedings of the 16th International Heat Transfer Conference 2018, Beijing, China, 10–15 August 2018. [Google Scholar]
- Inoue, N.; Ichinose, J. Single-phase Heat Transfer and Pressure Drop inside Internally Helical-grooved Horizontal Small-diameter Tubes. Int. J. Air-Cond. Refrig. 2012, 20. [Google Scholar] [CrossRef]
- Ichinose, J.; Inoue, N. The Condensation Heat Transfer and Pressure Drop of R410A and R32 inside Horizontal Small-diameter Tubes-2nd Report: Empirical Correlation for Condensation Heat Transfer and Pressure Drop. Trans. JSRAE 2011, 28, 479–490. (In Japanese) [Google Scholar]
- Hirose, M.; Ichinose, J.; Inoue, N. Development of the general correlation for condensation heat transfer and pressure drop inside horizontal 4 mm small-diameter smooth and microfin tubes. Int. J. Refrig. 2018, 90, 238–248. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23, Reference Fluid Thermodynamic and Transport Properties REFPROP Ver. 9.1; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar]
- Smith, S.L. Void Fractions in Two-Phase Flow: A Correlation Based upon an Equal Velocity Head Model. Proc. Inst. Mech. Eng. 1969, 184, 647–664. [Google Scholar] [CrossRef]
- Longo, G.A.; Mancin, S.; Righetti, G.; Zilio, C. Saturated vapour condensation of HFC404A inside a 4 mm ID horizontal smooth tube: Comparison with the long-term low GWP substitutes HC290 (Propane) and HC1270 (Propylene). Int. J. Heat Mass Transf. 2017, 108, 2088–2099. [Google Scholar] [CrossRef]
| Instrument | Full Scale | Uncertainty |
|---|---|---|
| T-type thermocouple | - | 0.05 K |
| Coriolis mass flow meter | 43 kg h−1 | 0.2% |
| Absolute pressure transducer | 3 MPa | ±0.3 kPa |
| Differential pressure transducer | 100 kPa | ±0.2 kPa |
| Differential pressure transduscer | 20 kPa | ±0.04 kPa |
| Pt-resistance thermometer | - | ±0.04 K |
| Volumetric flow meter | 500 L h−1 | ±0.01 L h−1 |
| R410A | R32 | R152a | R1234ze(E) | R404A | R290 | |
|---|---|---|---|---|---|---|
| Global Warming Potential* | 1924 | 677 | 138 | <1 | 3942 | 3 |
| Pressure (MPa) | 2.14 | 2.19 | 0.79 | 0.67 | 1.61 | 1.22 |
| Dew point temp. (°C) | 35.0 | 35.0 | 35.0 | 35.0 | 35.0 | 35 |
| Boiling point temp. (°C) | 34.9 | 34.6 | ||||
| Vapor density (kg m−3) | 88.9 | 63.3 | 24.6 | 35.3 | 87.5 | 26.6 |
| Liquid density (kg m−3) | 1005 | 917.1 | 873.4 | 1129 | 995.0 | 476.1 |
| Vapor viscosity (μPa s) | 14.5 | 13.5 | 10.5 | 12.7 | 12.5 | 8.7 |
| Liquid viscosity (μPa s) | 103.2 | 101.0 | 145.3 | 177.2 | 119.4 | 87.4 |
| Vapor thermal cond. (mW m−1 K−1) | 17.7 | 17.2 | 16.1 | 14.5 | 17.7 | 20.5 |
| Liquid thermal cond. (mW m−1 K−1) | 83.6 | 118.3 | 93.8 | 70.9 | 60.0 | 89.1 |
| Latent heat (kJ kg−1) | 169 | 249 | 267 | 159 | 128 | 317 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inoue, N.; Hirose, M.; Jige, D.; Ichinose, J. Correlation for Condensation Heat Transfer in a 4.0 mm Smooth Tube and Relationship with R1234ze(E), R404A, and R290. Appl. Sci. 2018, 8, 2267. https://doi.org/10.3390/app8112267
Inoue N, Hirose M, Jige D, Ichinose J. Correlation for Condensation Heat Transfer in a 4.0 mm Smooth Tube and Relationship with R1234ze(E), R404A, and R290. Applied Sciences. 2018; 8(11):2267. https://doi.org/10.3390/app8112267
Chicago/Turabian StyleInoue, Norihiro, Masataka Hirose, Daisuke Jige, and Junya Ichinose. 2018. "Correlation for Condensation Heat Transfer in a 4.0 mm Smooth Tube and Relationship with R1234ze(E), R404A, and R290" Applied Sciences 8, no. 11: 2267. https://doi.org/10.3390/app8112267
APA StyleInoue, N., Hirose, M., Jige, D., & Ichinose, J. (2018). Correlation for Condensation Heat Transfer in a 4.0 mm Smooth Tube and Relationship with R1234ze(E), R404A, and R290. Applied Sciences, 8(11), 2267. https://doi.org/10.3390/app8112267




