An Efficient Automatic Midsagittal Plane Extraction in Brain MRI
Abstract
1. Introduction
2. Materials and Methods
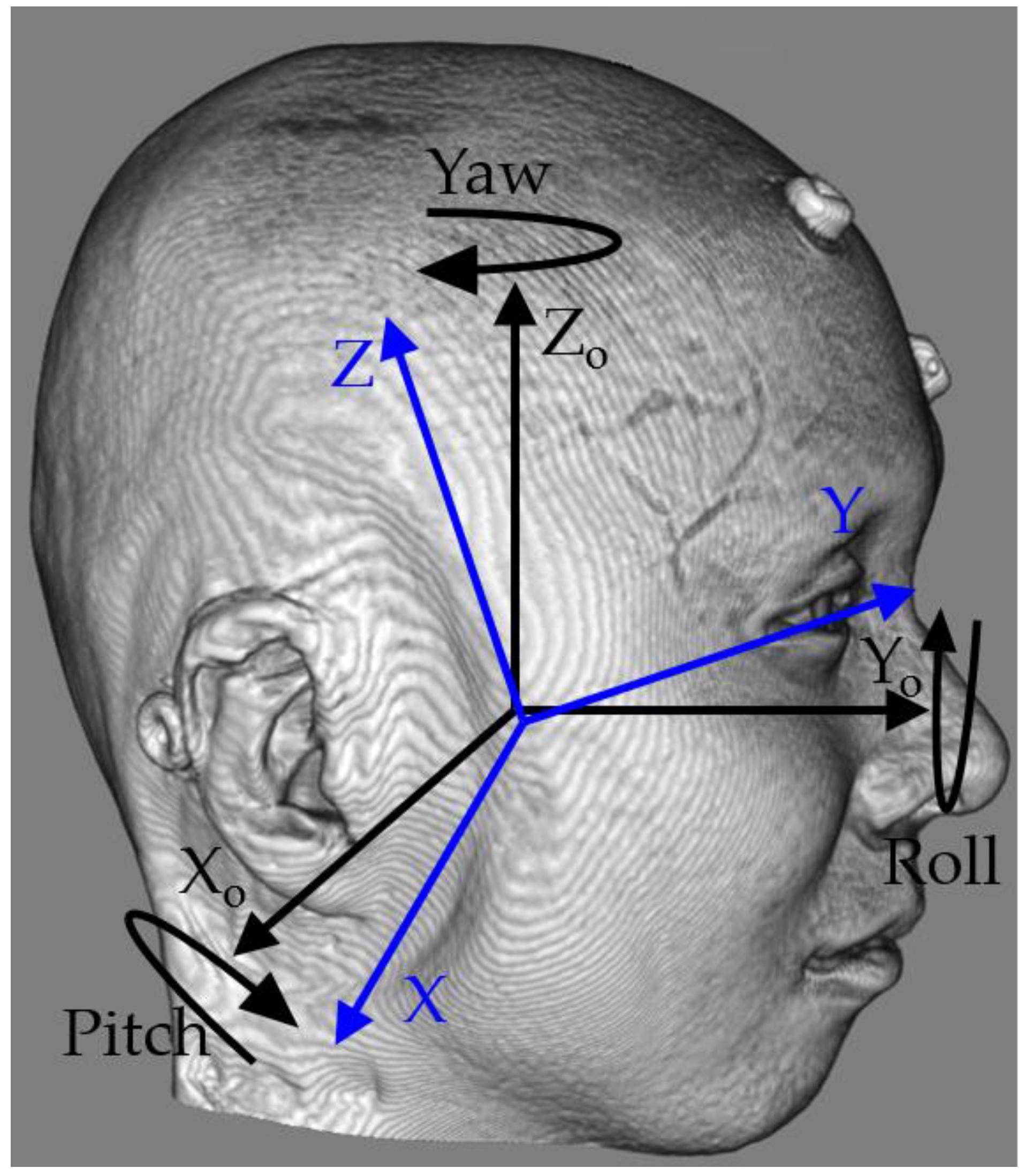
2.1. Geometry of MSP
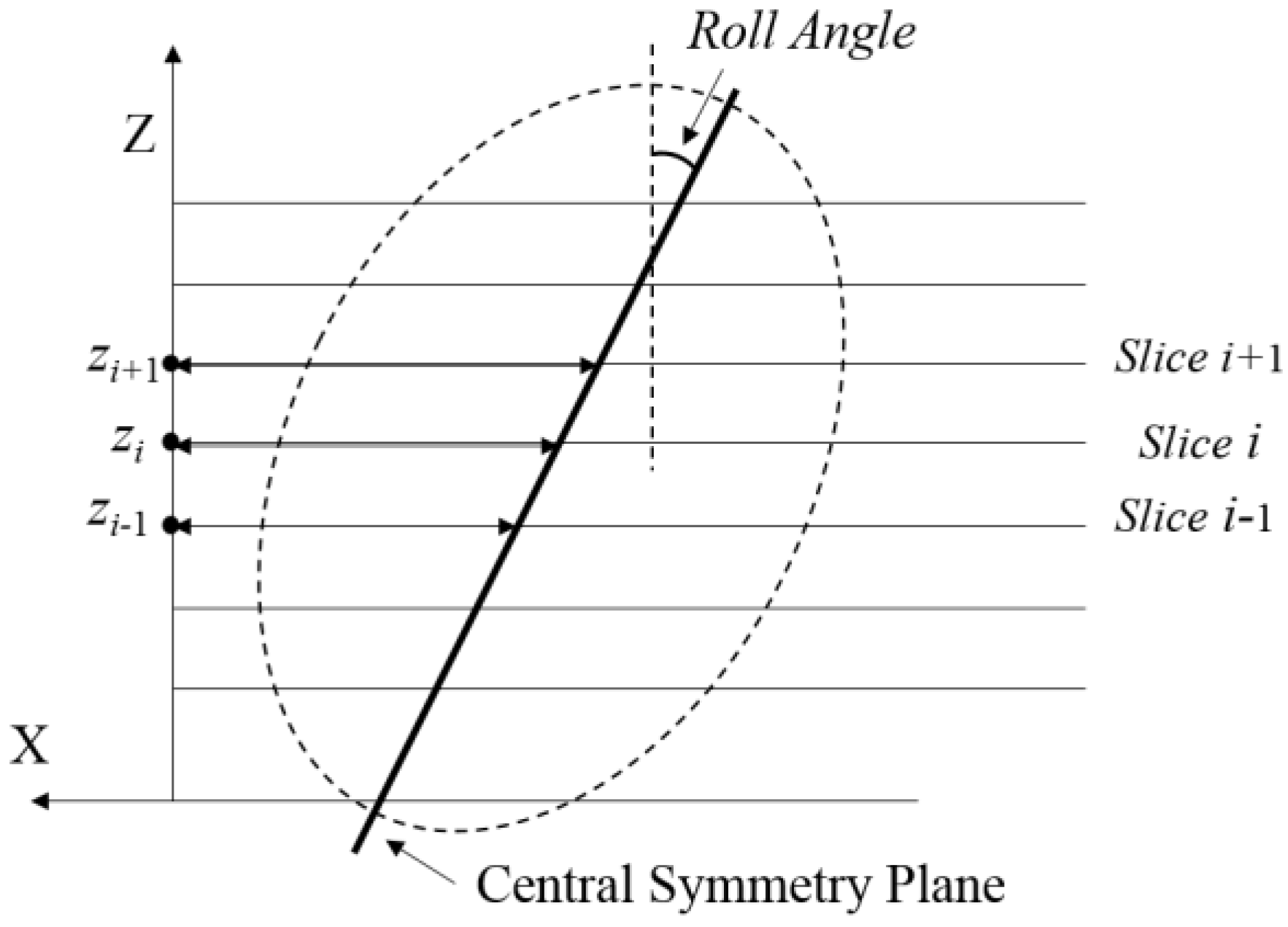
2.2. Estimation of Yaw Angle (θr)
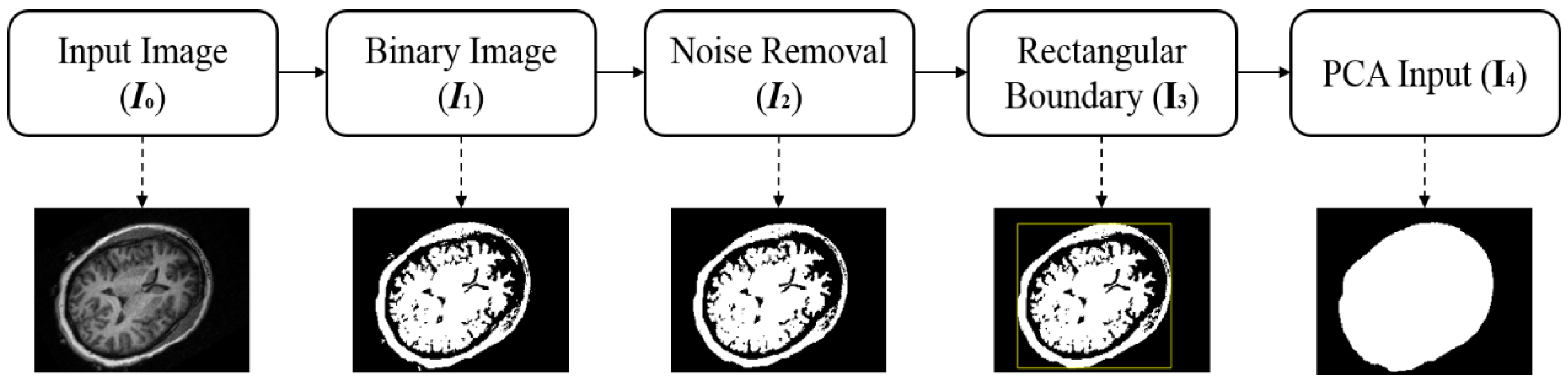
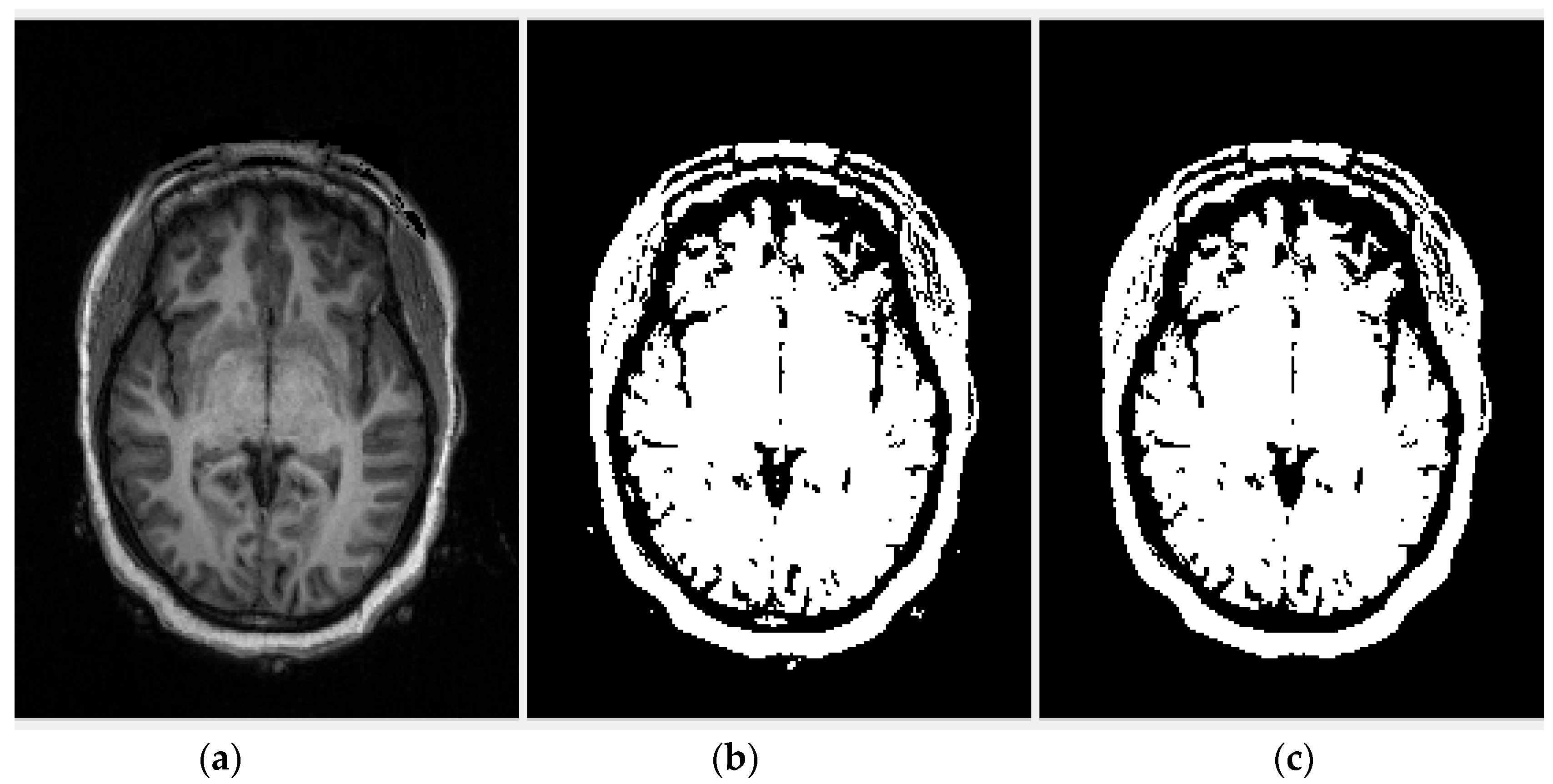
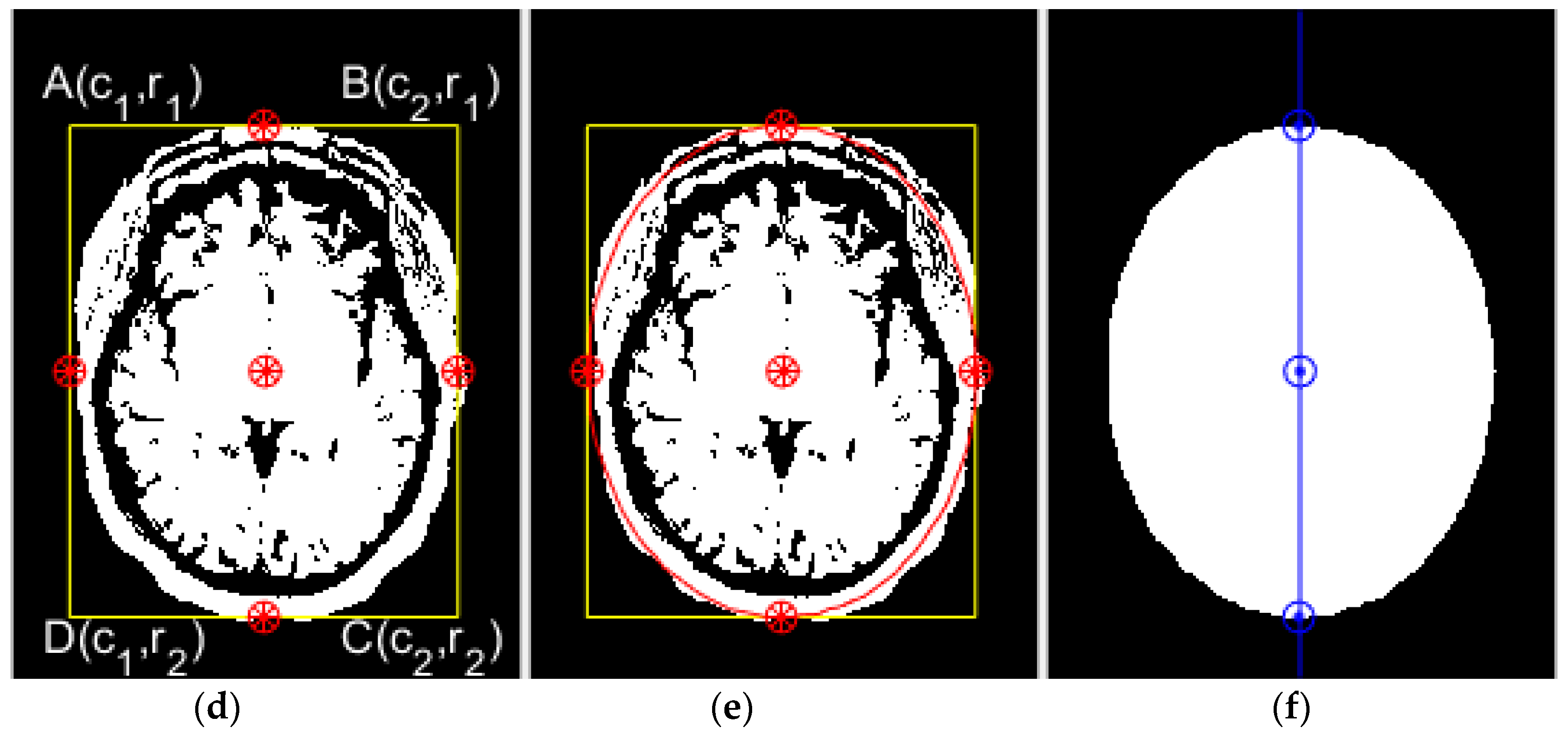
2.2.1. Region of Interest Extraction
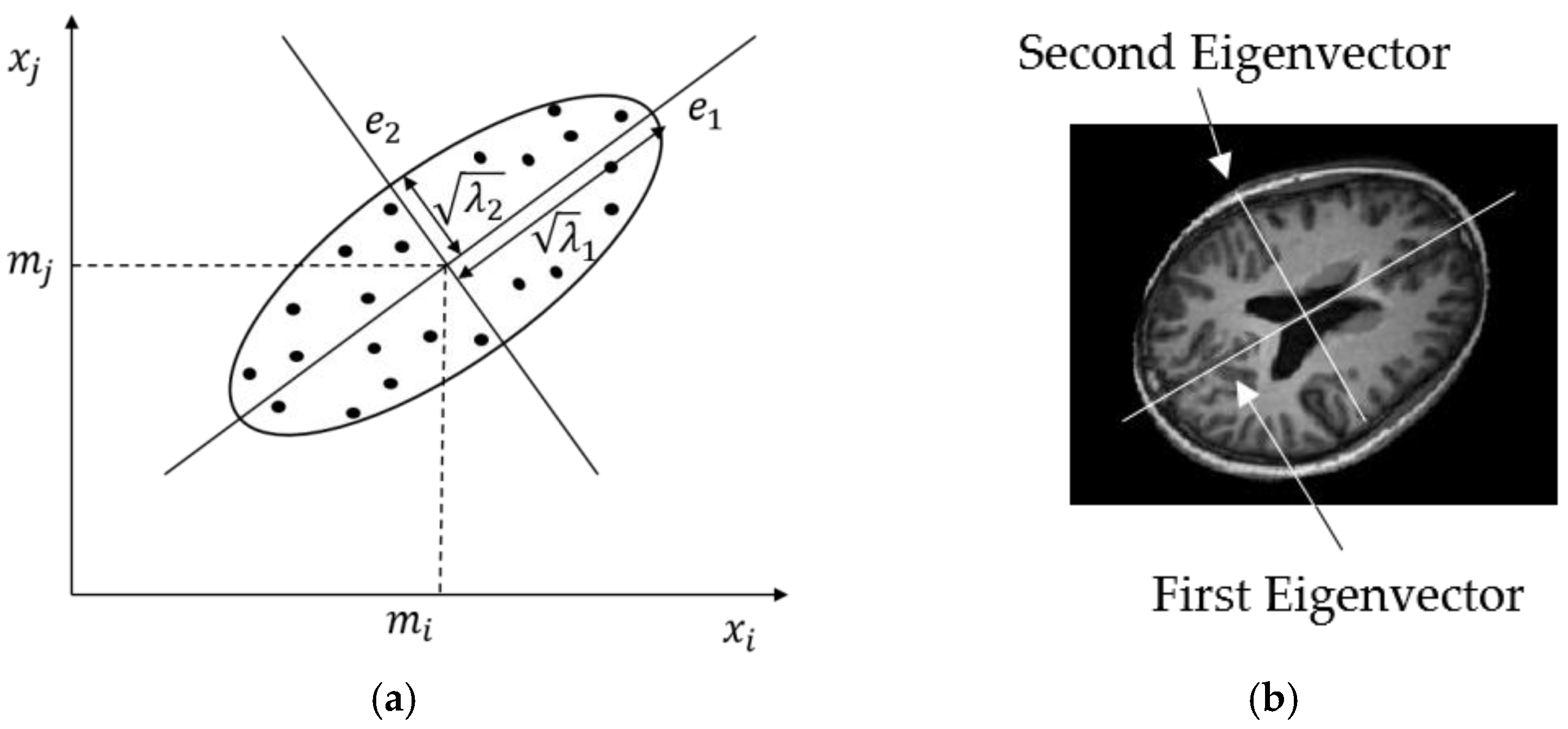
2.2.2. Principal Component Analysis
2.2.3. Cross-Correlation
2.3. Fitting of Plane in Three Dimensions
2.4. Transformation for Tilt Correction
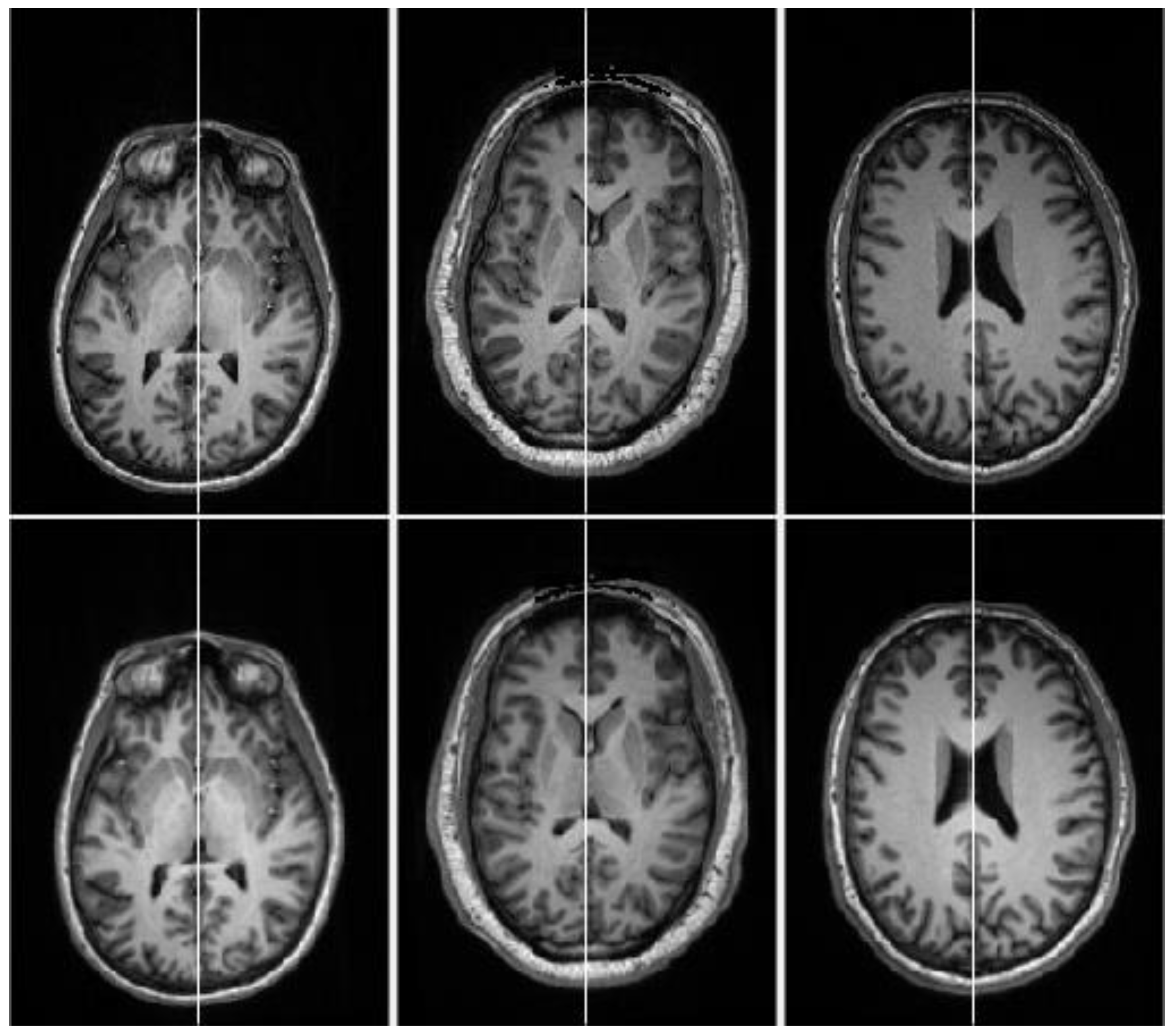
3. Results and Discussion
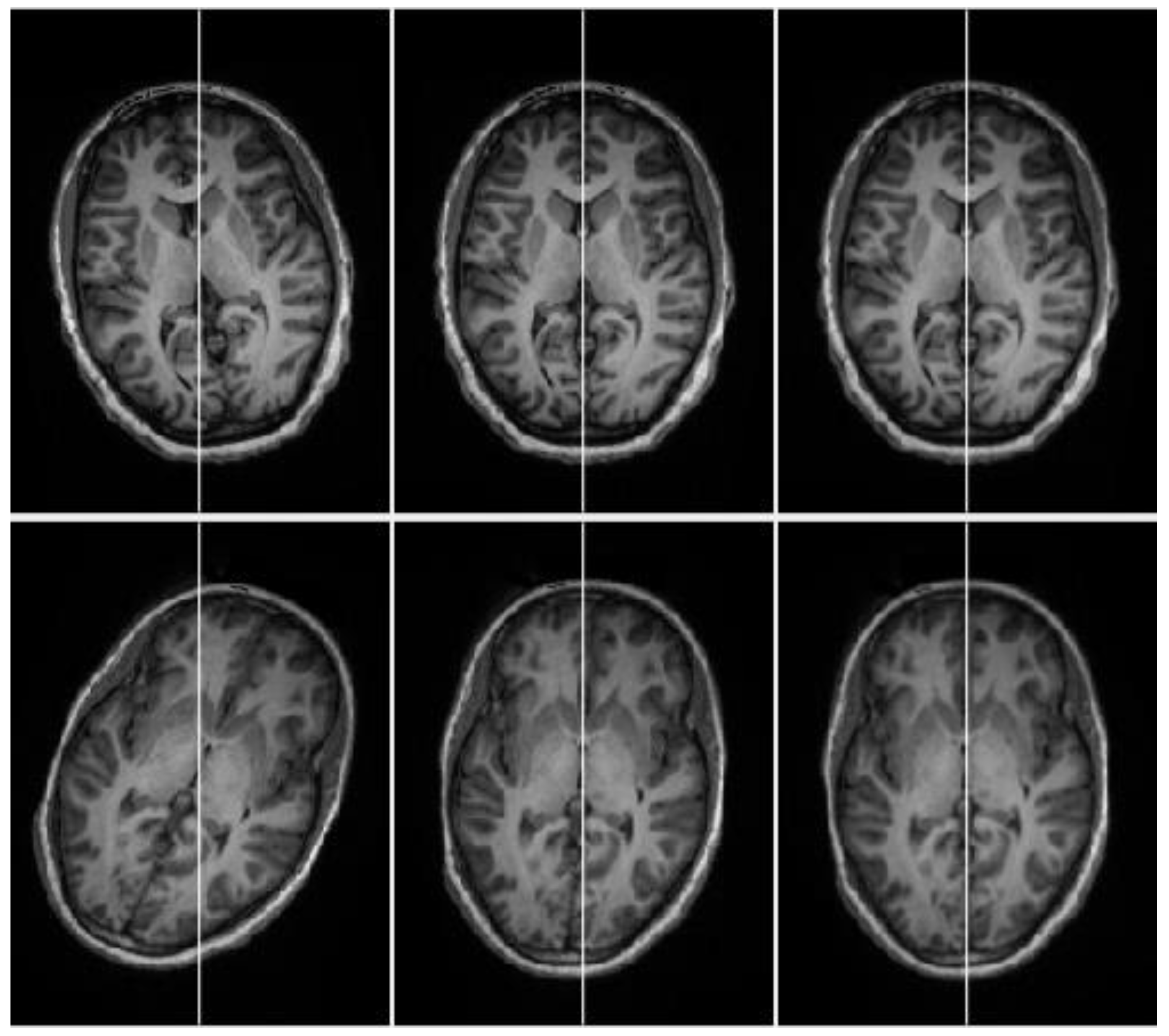
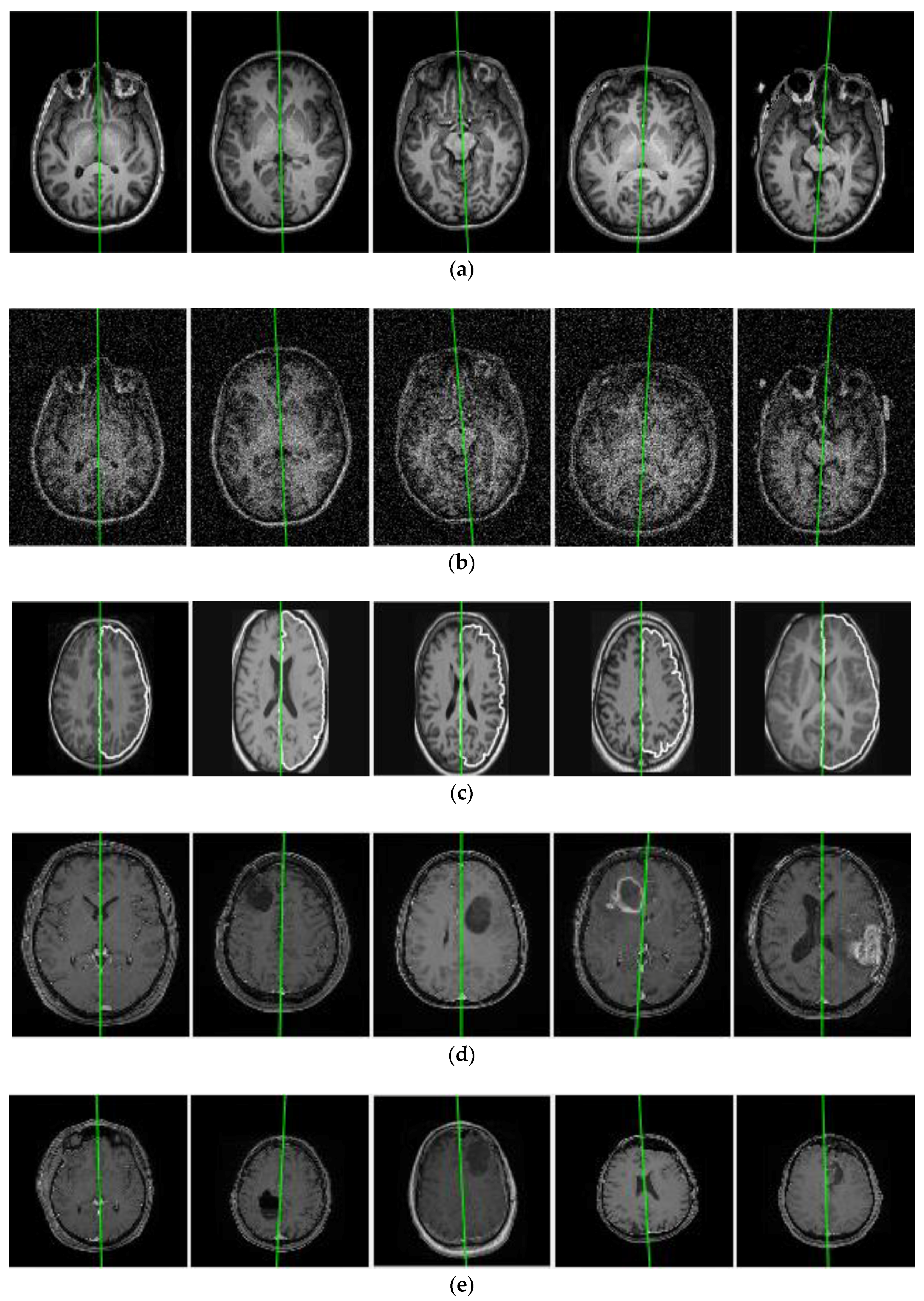
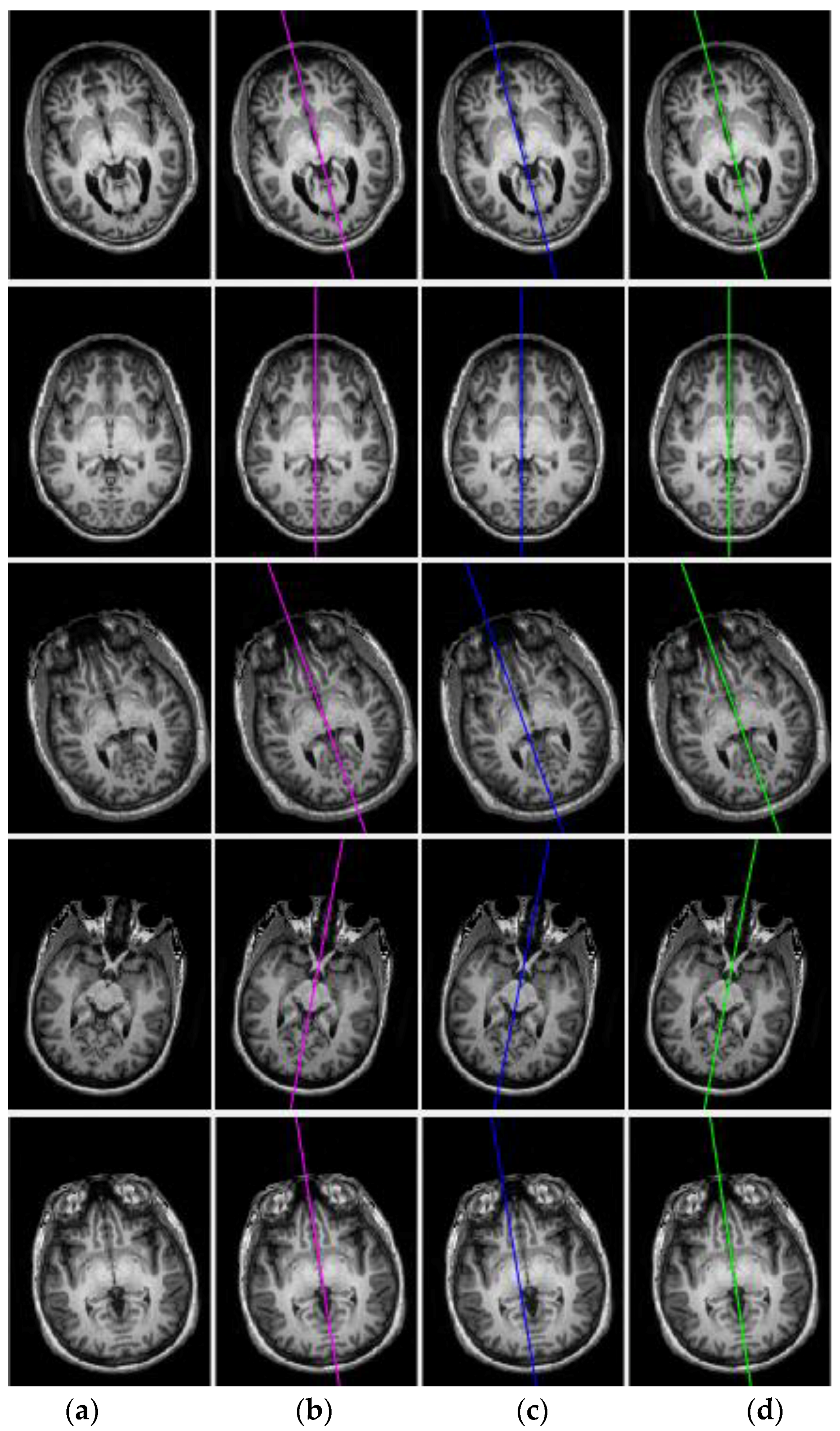
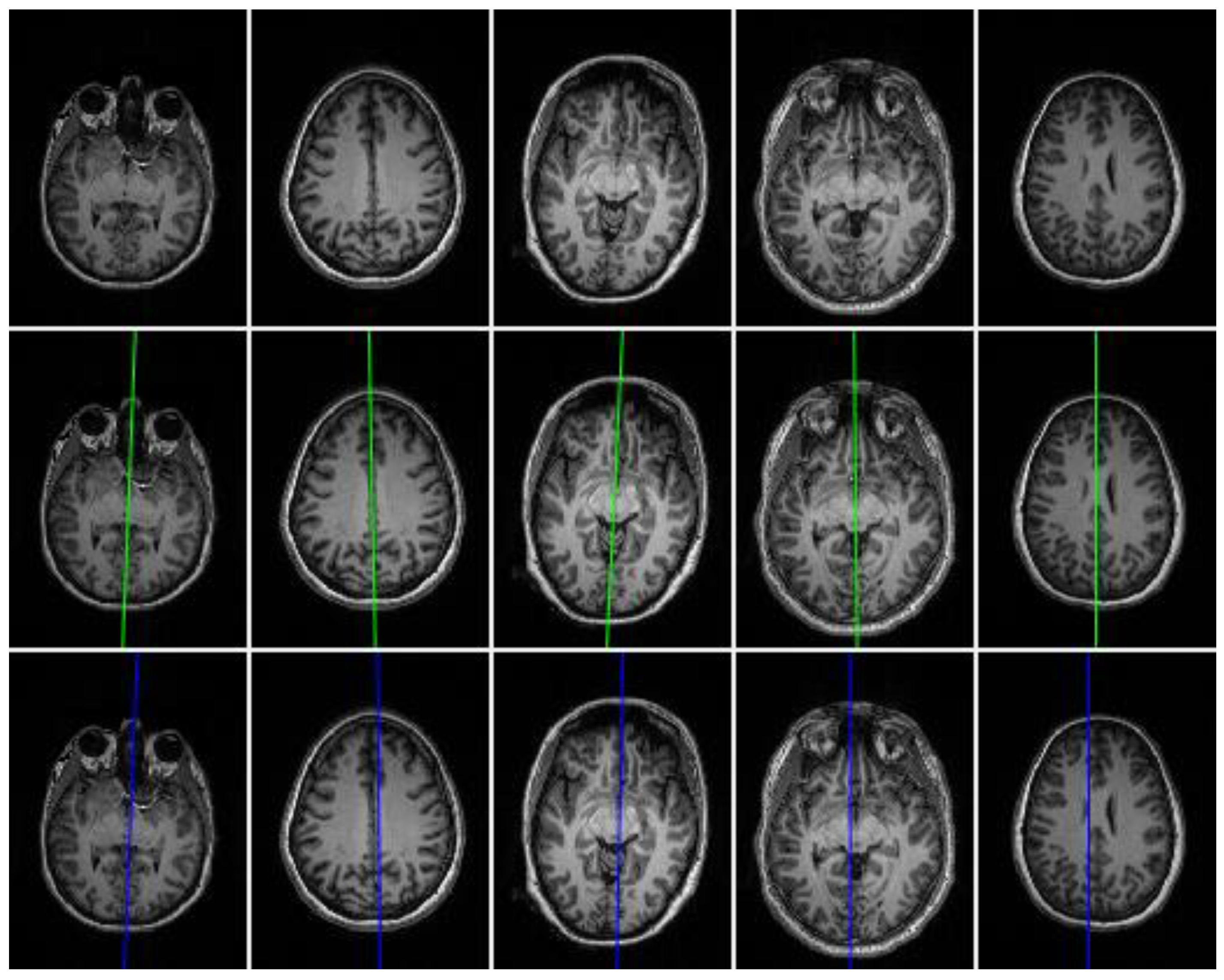
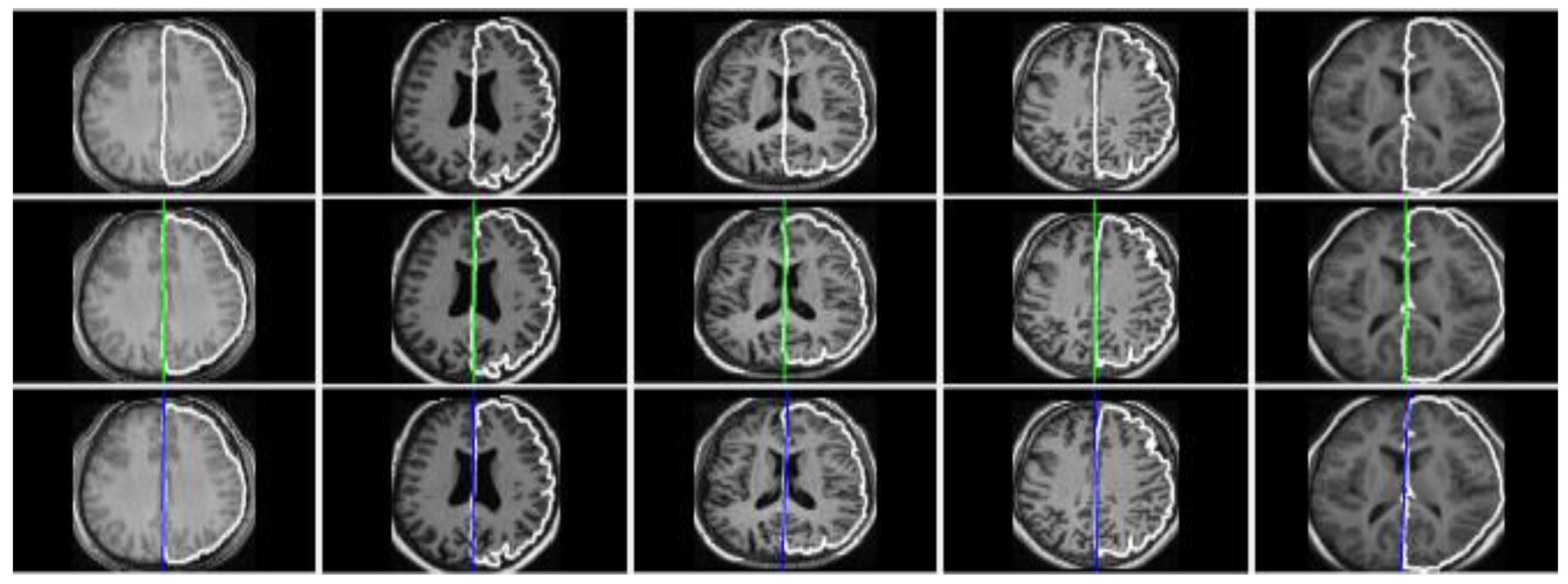
3.1. Evaluation on Real Datasets
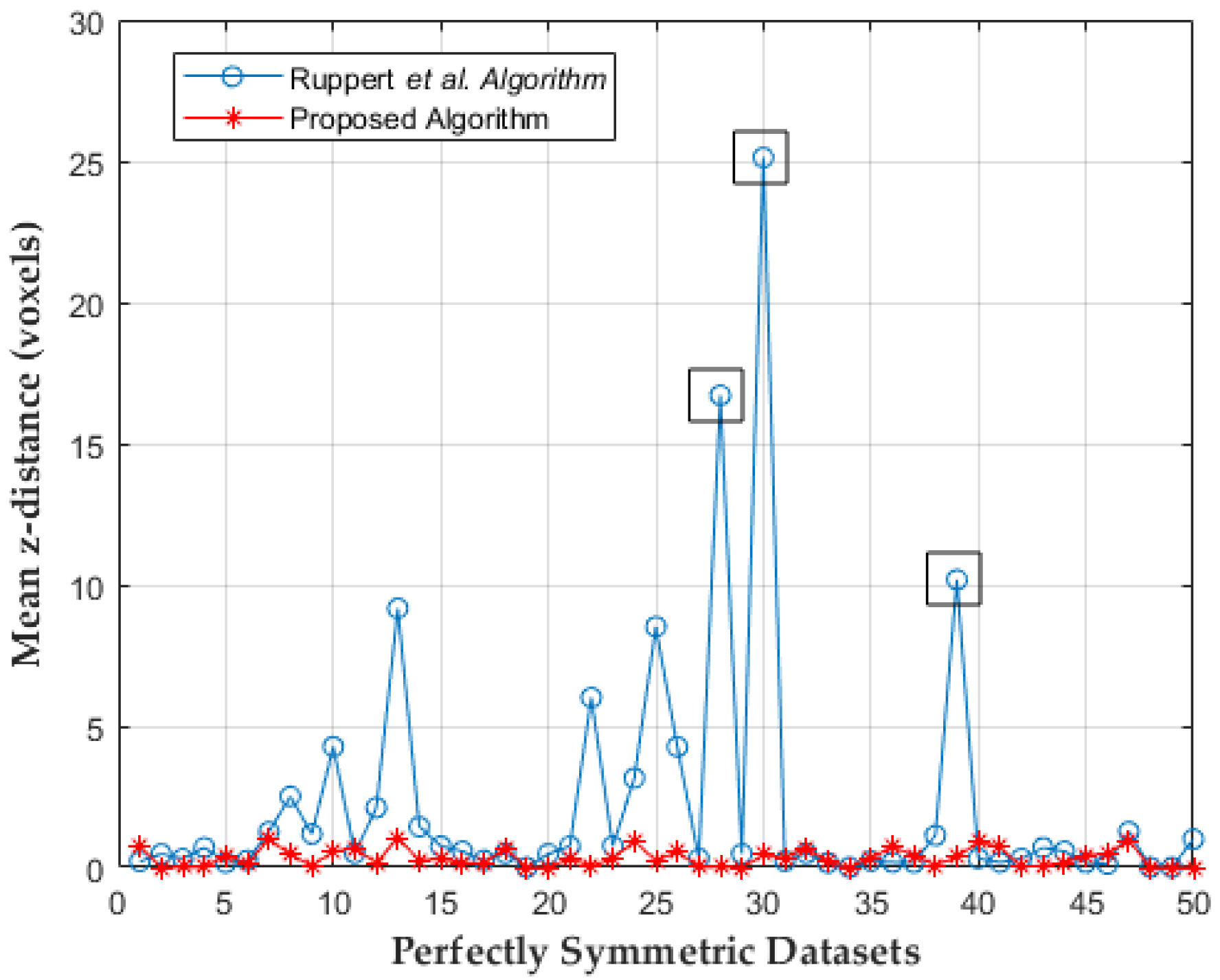
3.2. Evaluation and Comparison on Synthetic Datasets
3.3. Evaluation and Comparison on Real Datasets
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Davarpanah, S.H.; Liew, A.W.-C. Brain mid-sagittal surface extraction based on fractal analysis. Neural Comput. Appl. 2018, 30, 153–162. [Google Scholar] [CrossRef]
- Crow, T. Schizophrenia as an anomaly of cerebral asymmetry. In Imaging of the Brain in Psychiatry and Related Fields; Springer: Berlin, Germany, 1993; pp. 3–17. [Google Scholar]
- Oertel-Knochel, V.; Linden, D.E. Cerebral asymmetry in schizophrenia. Neuroscientist 2011, 17, 456–467. [Google Scholar] [CrossRef] [PubMed]
- Yu, C.-P.; Ruppert, G.C.; Nguyen, D.T.; Falcao, A.X.; Liu, Y. Statistical Asymmetry-based Brain Tumor Segmentation from 3D MR Images. Biosignals 2012, 15, 527–533. [Google Scholar]
- Roy, S.; Bandyopadhyay, S.K. Detection and Quantification of Brain Tumor from MRI of Brain and it’s Symmetric Analysis. Int. J. Inf. Commun. Technol. Res. 2012, 2, 477–483. [Google Scholar]
- Hermes, G.; Ajioka, J.W.; Kelly, K.A.; Mui, E.; Roberts, F.; Kasza, K.; Mayr, T.; Kirisits, M.J.; Wollmann, R.; Ferguson, D.J.P.; et al. Neurological and behavioral abnormalities, ventricular dilatation, altered cellular functions, inflammation, and neuronal injury in brains of mice due to common, persistent, parasitic infection. J. Neuroinflamm. 2008, 5, 48. [Google Scholar] [CrossRef] [PubMed]
- Schulte, T.; Muller-Oehring, E.M.; Rohlfing, T.; Pfefferbaum, A.; Sullivan, E.V. White Matter Fiber Degradation Attenuates Hemispheric Asymmetry When Integrating Visuomotor Information. J. Neurosci. 2010, 30, 12168–12178. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Schmidt, E.A.; Hiler, M.; Smielewski, P.; Pickard, J.D.; Czosnyka, M. Asymmetry of critical closing pressure following head injury. J. Neurol. Neurosurg. Psychiatry 2005, 76, 1570–1573. [Google Scholar] [CrossRef] [PubMed]
- Roussigné, M.; Blader, P.; Wilson, S.W. Breaking symmetry: The zebrafish as a model for understanding left-right asymmetry in the developing brain. Dev. Neurobiol. 2012, 72, 269–281. [Google Scholar] [CrossRef] [PubMed]
- Doi, K. Computer-aided diagnosis in medical imaging: Historical review, current status and future potential. Comput. Med. Imaging Graph. 2007, 31, 198–211. [Google Scholar] [CrossRef] [PubMed]
- Alves, R.S.; Tavares, J.M.R. Computer image registration techniques applied to nuclear medicine images. In Computational and Experimental Biomedical Sciences: Methods and Applications; Springer: Berlin, Germany, 2015; pp. 173–191. [Google Scholar]
- Lancaster, J.L.; Glass, T.G.; Lankipalli, B.R.; Downs, H.; Mayberg, H.; Fox, P.T. A modality-independent approach to spatial normalization of tomographic images of the human brain. Hum. Brain Mapp. 1995, 3, 209–223. [Google Scholar] [CrossRef]
- Minoshima, S.; Koeppe, R.A.; Frey, K.A.; Kuhl, D.E. Anatomic standardization: Linear scaling and nonlinear warping of functional brain images. J. Nucl. Med. 1994, 35, 1528–1537. [Google Scholar] [PubMed]
- Liu, S.X. Symmetry and asymmetry analysis and its implications to computer-aided diagnosis: A review of the literature. J. Biomed. Inform. 2009, 42, 1056–1064. [Google Scholar] [CrossRef] [PubMed]
- Prima, S.; Ourselin, S.; Ayache, N. Computation of the Mid-Sagittal Plane in 3D Medical Images of the Brain. In Proceedings of the 6th European Conference on Computer Vision-Part II, Dublin, Ireland, 26 June–1 July 2000; pp. 685–701. [Google Scholar]
- Liu, S.X.; Kender, J.; Imielinska, C.; Laine, A. Employing symmetry features for automatic misalignment correction in neuroimages. J. Neuroimaging 2011, 21, e15–e33. [Google Scholar] [CrossRef] [PubMed]
- Volkau, I.; Prakash, K.B.; Ananthasubramaniam, A.; Aziz, A.; Nowinski, W.L. Extraction of the midsagittal plane from morphological neuroimages using the Kullback–Leibler’s measure. Med. Image Anal. 2006, 10, 863–874. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Collins, R.T.; Rothfus, W.E. Robust midsagittal plane extraction from normal and pathological 3-D neuroradiology images. IEEE Trans. Med. Imaging 2001, 20, 175–192. [Google Scholar] [CrossRef] [PubMed]
- Kalavathi, P.; Senthamilselvi, M.; Prasath, V.B.S. Review of Computational Methods on Brain Symmetric and Asymmetric Analysis from Neuroimaging Techniques. Technologies 2017, 5, 16. [Google Scholar] [CrossRef]
- Brummer, M.E. Hough transform detection of the longitudinal fissure in tomographic head images. IEEE Trans. Med. Imaging 1991, 10, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Guillemaud, R.; Marais, P.; Zisserman, A.; Mc Donald, T.; Crow, B. A 3-Dimensional midsagittal plane for brain asymmetry measurement. Schizophr. Res. 1995, 18, 183–184. [Google Scholar] [CrossRef]
- Nowinski, W.L.; Prakash, B.; Volkau, I.; Ananthasubramaniam, A.; Beauchamp, N.J., Jr. Rapid and automatic calculation of the midsagittal plane in magnetic resonance diffusion and perfusion images. Acad. Radiol. 2006, 13, 652–663. [Google Scholar] [CrossRef] [PubMed]
- Kuijf, H.J.; van Veluw, S.J.; Geerlings, M.I.; Viergever, M.A.; Biessels, G.J.; Vincken, K.L. Automatic extraction of the midsagittal surface from brain MR images using the Kullback–Leibler measure. Neuroinformatics 2014, 12, 395–403. [Google Scholar] [CrossRef] [PubMed]
- Ardekani, B.A.; Kershaw, J.; Braun, M.; Kanno, I. Automatic detection of the mid-sagittal plane in 3-D brain images. IEEE Trans. Med. Imaging 1997, 16, 947–952. [Google Scholar] [CrossRef] [PubMed]
- Prima, S.; Ourselin, S.; Ayache, N. Computation of the mid-sagittal plane in 3-D brain images. IEEE Trans. Med. Imaging 2002, 21, 122–138. [Google Scholar] [CrossRef] [PubMed]
- Bergo, F.P.; Ruppert, G.C.; Pinto, L.F.; Falcao, A.X. Fast and Robust Mid-Sagittal Plane Location in 3D MR Images of the Brain. In Proceedings of the BIOSIGNALS, Madeira, Portugal, 28–31 January 2008; pp. 92–99. [Google Scholar]
- Ruppert, G.C.; Teverovskiy, L.; Yu, C.-P.; Falcao, A.X.; Liu, Y. A new symmetry-based method for mid-sagittal plane extraction in neuroimages. In Proceedings of the 2011 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Chicago, IL, USA, 30 March–2 April 2011; pp. 285–288. [Google Scholar]
- Wu, H.; Wang, D.; Shi, L.; Wen, Z.; Ming, Z. Midsagittal plane extraction from brain images based on 3D SIFT. Phys. Med. Biol. 2014, 59, 1367–1387. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Hu, Q. A PCA-based approach to the representation and recognition of MR brain midsagittal plane images. In Proceedings of the 30th Annual International Conference of the IEEEEngineering in Medicine and Biology Society, Vancouver, BC, Canada, 20–24 August 2008; pp. 3916–3919. [Google Scholar]
- Kalavathi, P.; Prasath, V.B.S. Automatic segmentation of cerebral hemispheres in MR human head scans. Int. J. Imaging Syst. Technol. 2016, 26, 15–23. [Google Scholar] [CrossRef]
- Ferrari, R.J.; Pinto, C.H.V.; Moreira, C.A.F. Detection of the midsagittal plane in MR images using a sheetness measure from eigenanalysis of local 3D phase congruency responses. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 2335–2339. [Google Scholar]
- Descoteaux, M.; Audette, M.; Chinzei, K.; Siddiqi, K. Bone enhancement filtering: Application to sinus bone segmentation and simulation of pituitary surgery. Comput. Aided Surg. 2006, 11, 247–255. [Google Scholar] [CrossRef] [PubMed]
- de Lima Freire, P.G.; da Silva, B.C.G.; Pinto, C.H.V.; Moreira, C.A.F.; Ferrari, R.J. Midsaggital Plane Detection in Magnetic Resonance Images Using Phase Congruency, Hessian Matrix and Symmetry Information: A Comparative Study. In Proceedings of the International Conference on Computational Science and Its Applications, Melbourne, Australia, 2–5 July 2018; pp. 245–260. [Google Scholar]
- Toro, C.; Gonzalo-Martín, C.; García-Pedrero, A.; Menasalvas Ruiz, E. Supervoxels-Based Histon as a New Alzheimer’s Disease Imaging Biomarker. Sensors 2018, 18, 1752. [Google Scholar] [CrossRef] [PubMed]
- Caggiano, A. Tool Wear Prediction in Ti-6Al-4V Machining through Multiple Sensor Monitoring and PCA Features Pattern Recognition. Sensors 2018, 18, 823. [Google Scholar] [CrossRef] [PubMed]
- Cristalli, C.; Grabowski, D. Multivariate Analysis of Transient State Infrared Images in Production Line Quality Control Systems. Appl. Sci. 2018, 8, 250. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, X.; Liu, X.; He, Y. Identification of Hybrid Okra Seeds Based on Near-Infrared Hyperspectral Imaging Technology. Appl. Sci. 2018, 8, 1793. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, X.; Xie, X.; Kuang, J. A Multi-Frame PCA-Based Stereo Audio Coding Method. Appl. Sci. 2018, 8, 967. [Google Scholar] [CrossRef]
- Maalek, R.; Lichti, D.D.; Ruwanpura, J.Y. Robust Segmentation of Planar and Linear Features of Terrestrial Laser Scanner Point Clouds Acquired from Construction Sites. Sensors 2018, 18, 819. [Google Scholar] [CrossRef] [PubMed]
- Solomon, C.; Breckon, T. Fundamentals of Digital Image Processing: A Practical Approach with Examples in Matlab; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 247–262. [Google Scholar]
- Mudrová, M.; Procházka, A. Principal component analysis in image processing. In Proceedings of the MATLAB Technical Computing Conference, Prague, Czech Republic, 4–8 July 2005. [Google Scholar]
- Petras, I.; Bednarova, D. Total Least Squares Approach to Modeling: A Matlab Toolbox. Acta Montan. Slovaca 2010, 15, 158–170. [Google Scholar]
- Minovic, P.; Ishikawa, S.; Kato, K. Symmetry Identification of a 3-D Object Represented by Octree. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 507–513. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Soille, P. Morphological Image Analysis: Principles and Applications, 2nd ed.; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Noble, B.; Daniel, J.W. Applied Linear Algebra; Prentice-Hall: Upper Saddle River, NJ, USA, 1988; Volume 3. [Google Scholar]
- Liu, Y.; Collins, R.T.; Rothfus, W.E. Automatic Extraction of the Central Symmetry (Mid-Sagittal) Plane from Neuroradiology Images; Carnegie Mellon University, The Robotics Institute: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Puccio, B.; Pooley, J.P.; Pellman, J.S.; Taverna, E.C.; Craddock, R.C. The preprocessed connectomes project repository of manually corrected skull-stripped T1-weighted anatomical MRI data. Gigascience 2016, 5, 45. [Google Scholar] [CrossRef] [PubMed]
- Internet Brain Segmentation Repository (IBSR). Massachusetts General Hospital. Available online: http://www.nitrc.org/projects/ibsr/ (accessed on 26 September 2018).
- Mercier, L.; Del Maestro, R.F.; Petrecca, K.; Araujo, D.; Haegelen, C.; Collins, D.L. Online database of clinical MR and ultrasound images of brain tumors. Med. Phys. 2012, 39, 3253–3261. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing (Global Edition), 4th ed.; Pearson: New York, NY, USA, 2018; pp. 747–750. [Google Scholar]
- Zhao, L.; Ruotsalainen, U.; Hirvonen, J.; Hietala, J.; Tohka, J. Automatic cerebral and cerebellar hemisphere segmentation in 3D MRI: Adaptive disconnection algorithm. Med. Image Anal. 2010, 14, 360–372. [Google Scholar] [CrossRef] [PubMed]



| Datasets | Detail of Images |
|---|---|
| NFBS [48] | There are 125 T1-weighted MRI scans, 77 females and 48 males in the 21–45 age range (average: 31) with a variety of clinical and subclinical psychiatric symptoms. The size of the individual scan is 256 × 256 × 192 and each voxel size is 1 × 1 × 1 mm3. The first two dimensions in each scan size indicate the individual image size (rows, columns) and the third dimension represents the number of images in the scan. |
| IBSR [49] | Eighteen volumes of T1-weighted brain MRI from all age groups from juvenile to adult are available online with ground truth. The size of the individual scan is 256 × 256 × 128 and each voxel size is 1.5 × 1.5 × 1.5 mm3. Most of the scans in this database have low-contrast images. |
| MNI BITE [50] | Real T1-weighted brain MRI of 14 patients with brain tumors (gliomas). We have used scans from Group 2 (pre-operative MRIs) and Group 3 (post-resection MRIs). The size of each scan in Group 2 is 394 × 466 × 378. Group 3 contains scans of different sizes and dimensions. |
| Ruppert et al. Algorithm | Proposed Algorithm | |||||
|---|---|---|---|---|---|---|
| z Score (Voxels) | Angle Difference (°) | Time (s) | z-Score (Voxels) | Angle Difference (°) | Time (s) | |
| Mean | 1.246 | 0.10 | 35.02 | 0.336 | 0.06 | 1.04 |
| Std. | 2.041 | 0.22 | 1.12 | 0.324 | 0.21 | 0.02 |
| Median | 0.50 | 0.00 | 34.86 | 0.250 | 0.00 | 1.01 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, H.Z.U.; Lee, S. An Efficient Automatic Midsagittal Plane Extraction in Brain MRI. Appl. Sci. 2018, 8, 2203. https://doi.org/10.3390/app8112203
Rehman HZU, Lee S. An Efficient Automatic Midsagittal Plane Extraction in Brain MRI. Applied Sciences. 2018; 8(11):2203. https://doi.org/10.3390/app8112203
Chicago/Turabian StyleRehman, Hafiz Zia Ur, and Sungon Lee. 2018. "An Efficient Automatic Midsagittal Plane Extraction in Brain MRI" Applied Sciences 8, no. 11: 2203. https://doi.org/10.3390/app8112203
APA StyleRehman, H. Z. U., & Lee, S. (2018). An Efficient Automatic Midsagittal Plane Extraction in Brain MRI. Applied Sciences, 8(11), 2203. https://doi.org/10.3390/app8112203






