Characterization of Asphalt Mixes Behaviour from Dynamic Tests and Comparison with Conventional Cyclic Tension–Compression Tests
Abstract
:Featured Application
Abstract
1. Introduction
2. Materials and Methods
3. Characterization of the Linear Viscoelastic (LVE) Behaviour
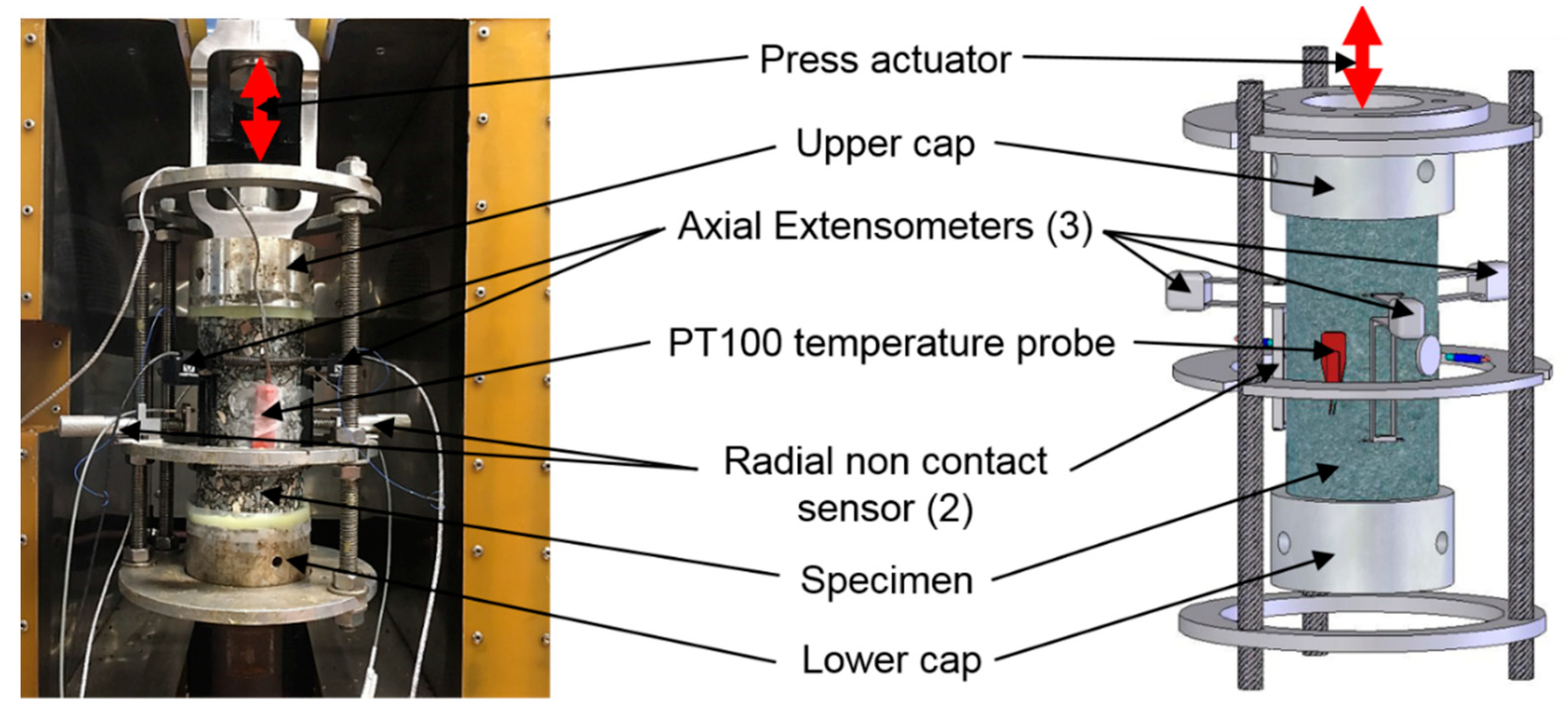
3.1. Cyclic Tension–Compression Tests
3.2. Modelling of the LVE Behaviour: 2S2P1D Rheological Model
4. Dynamic Tests
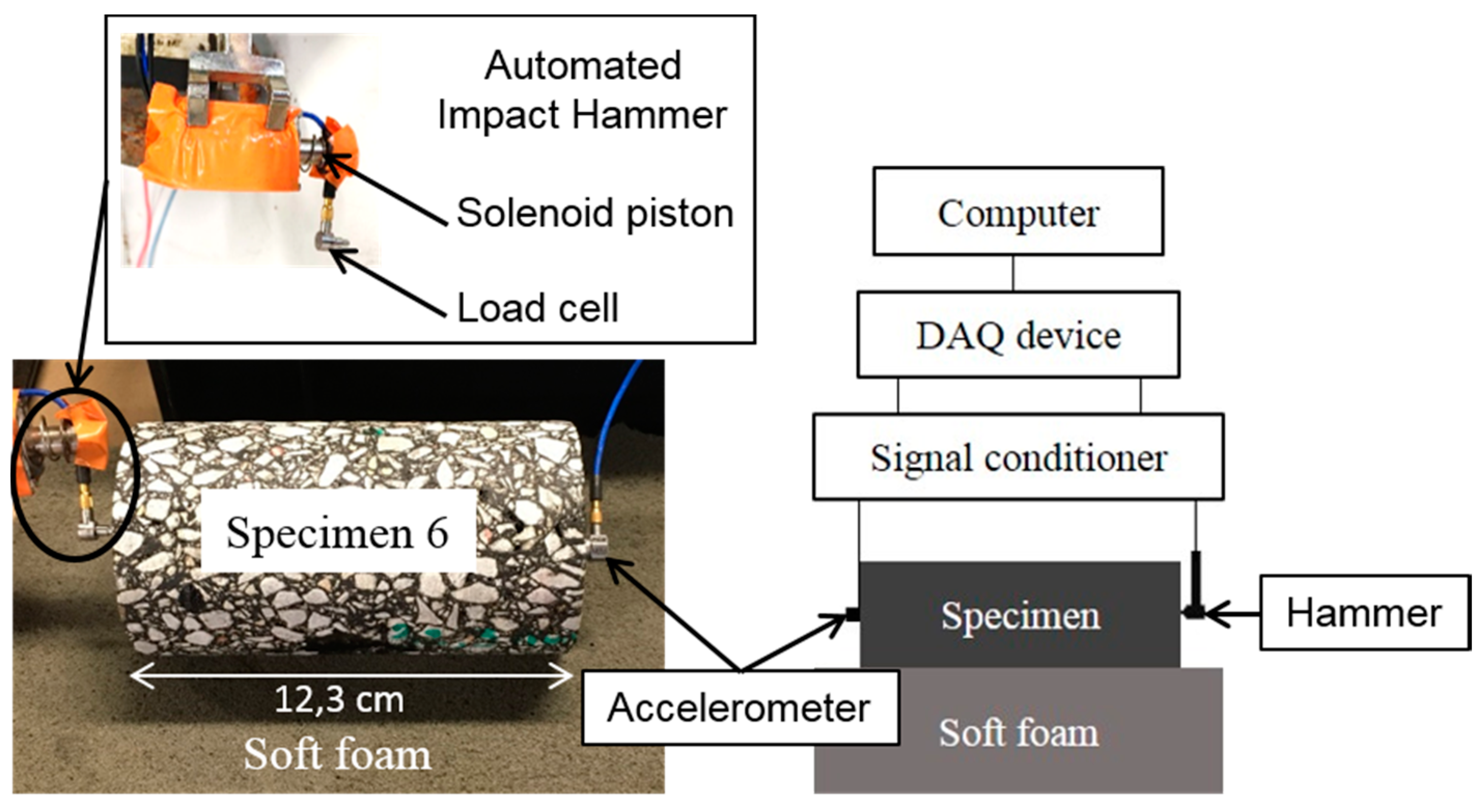
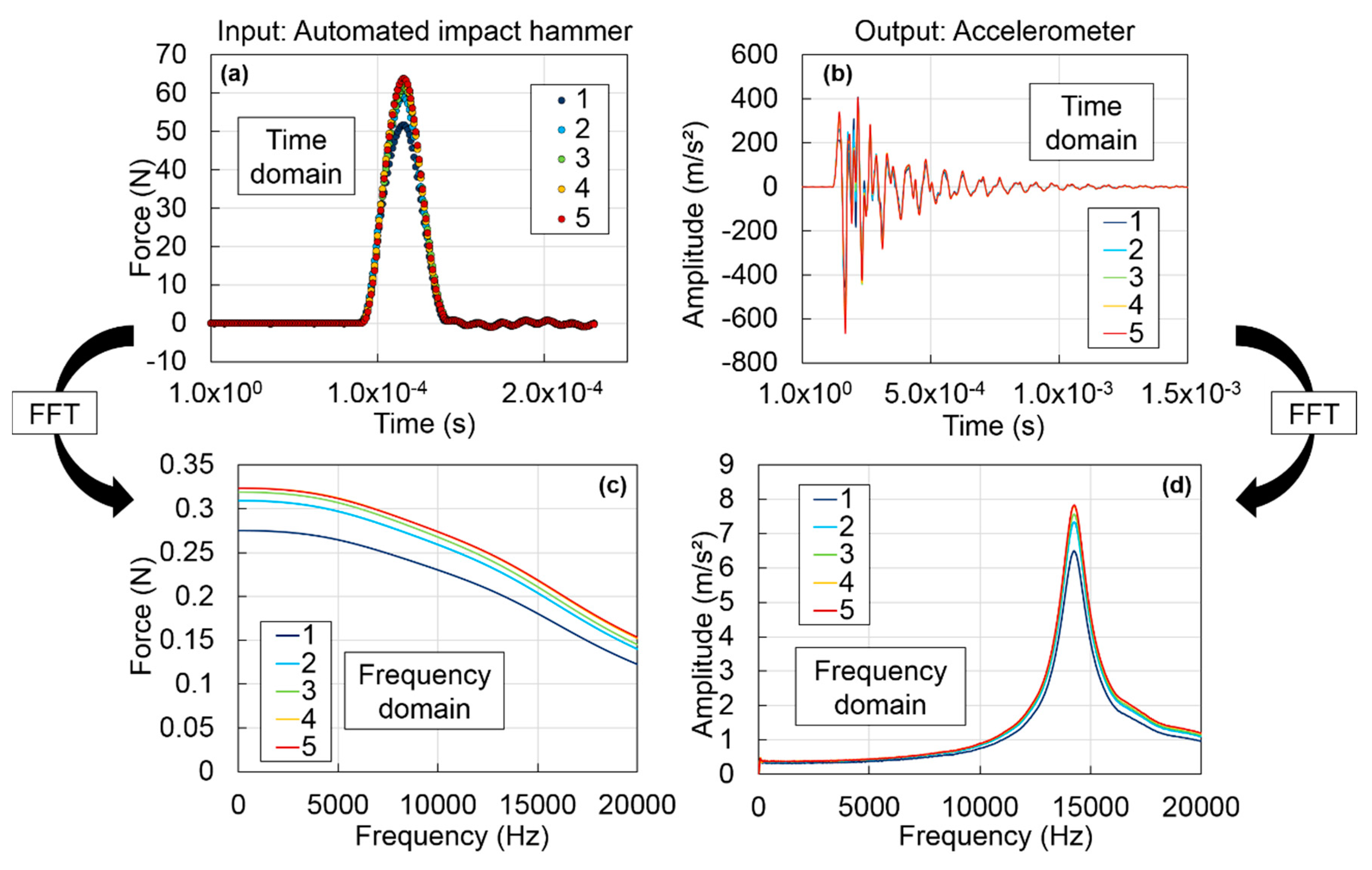
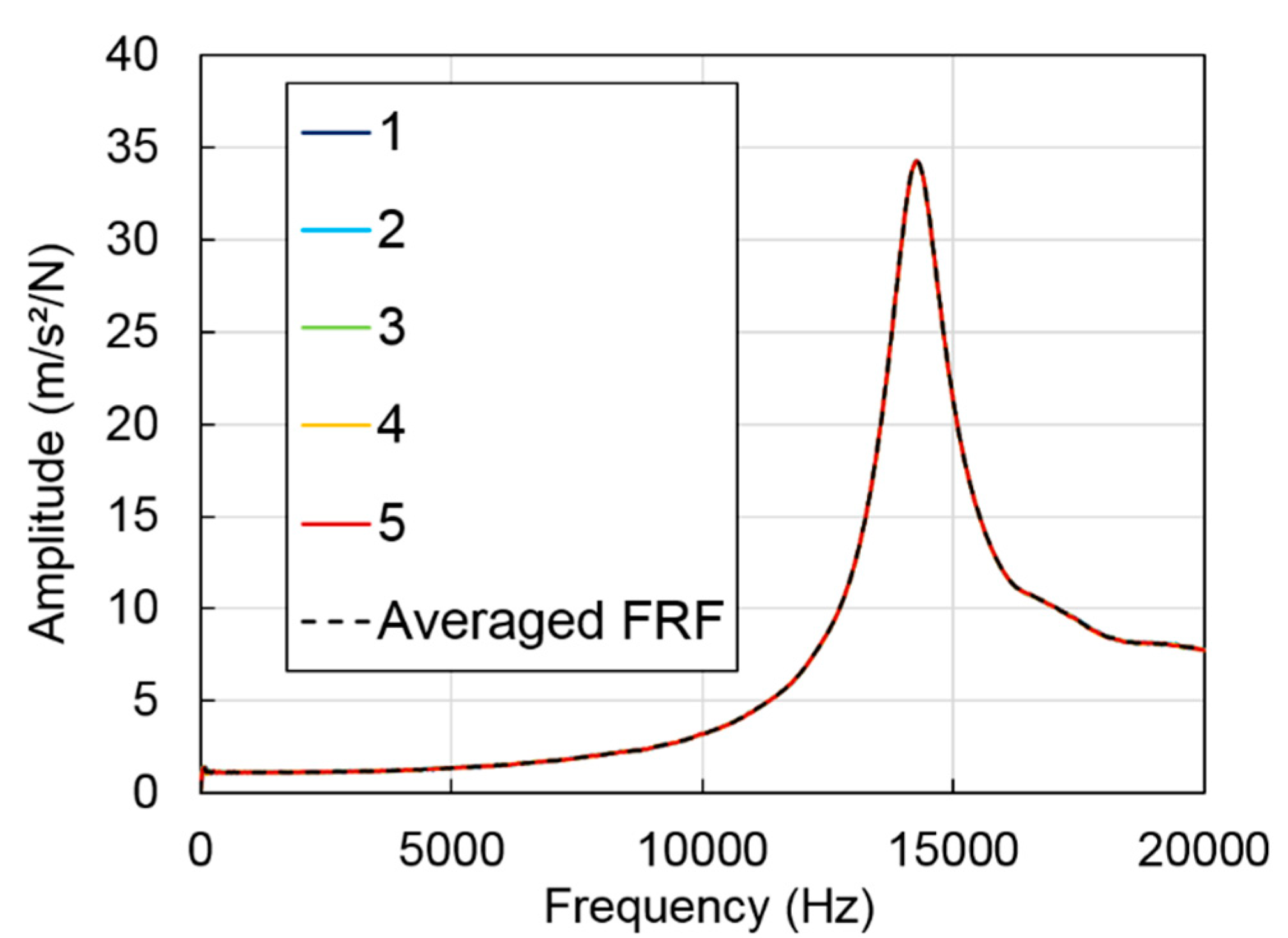
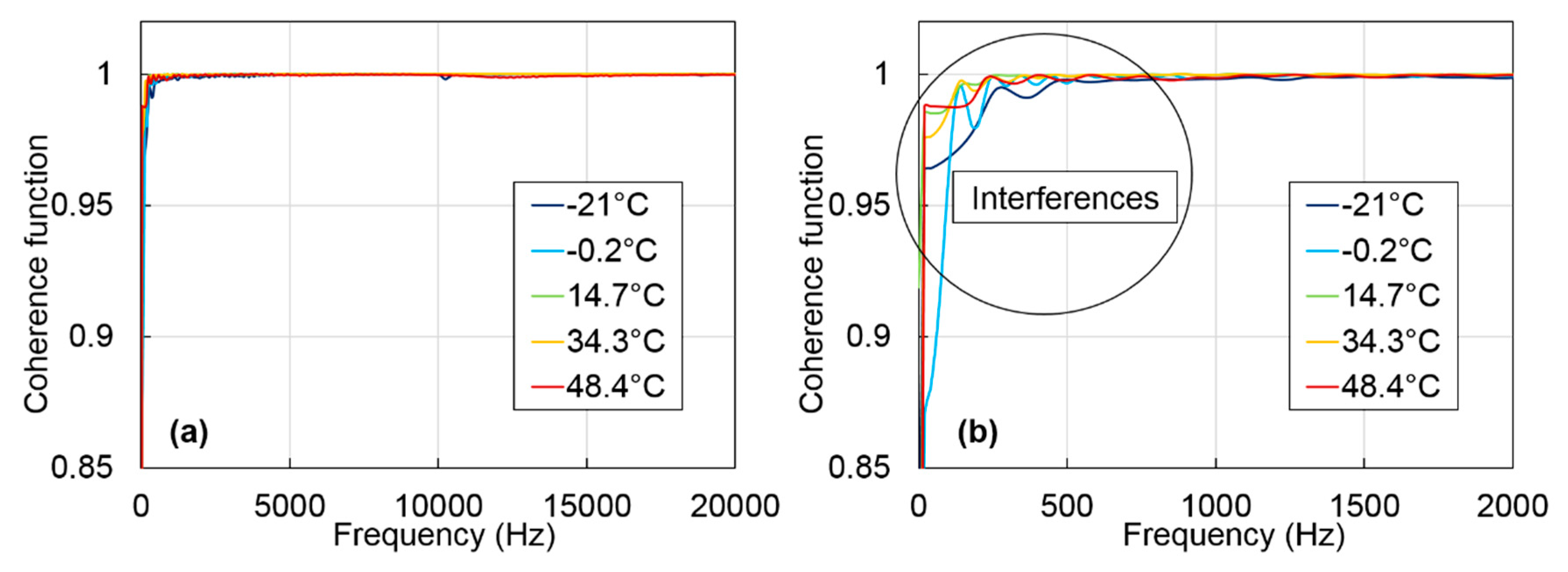
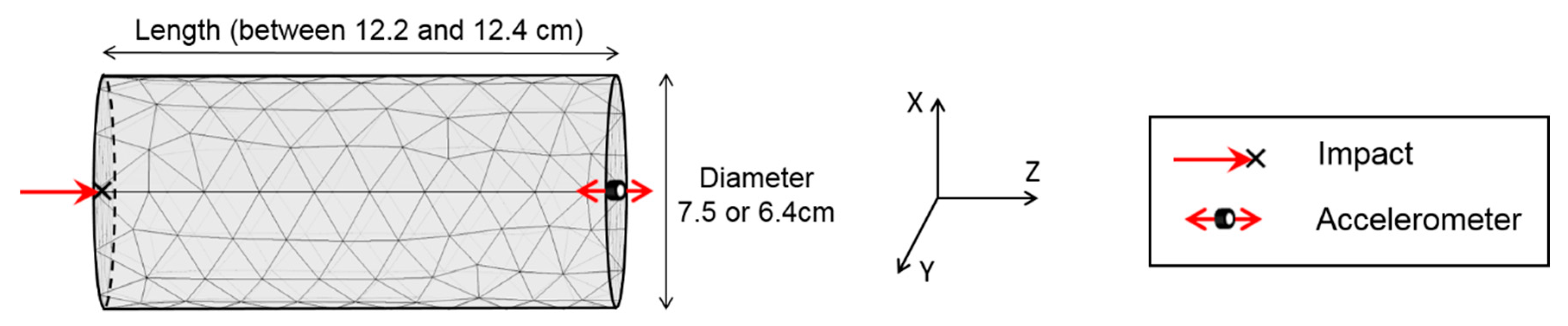
4.1. Measurement of the Frequency Response Functions (FRFs)
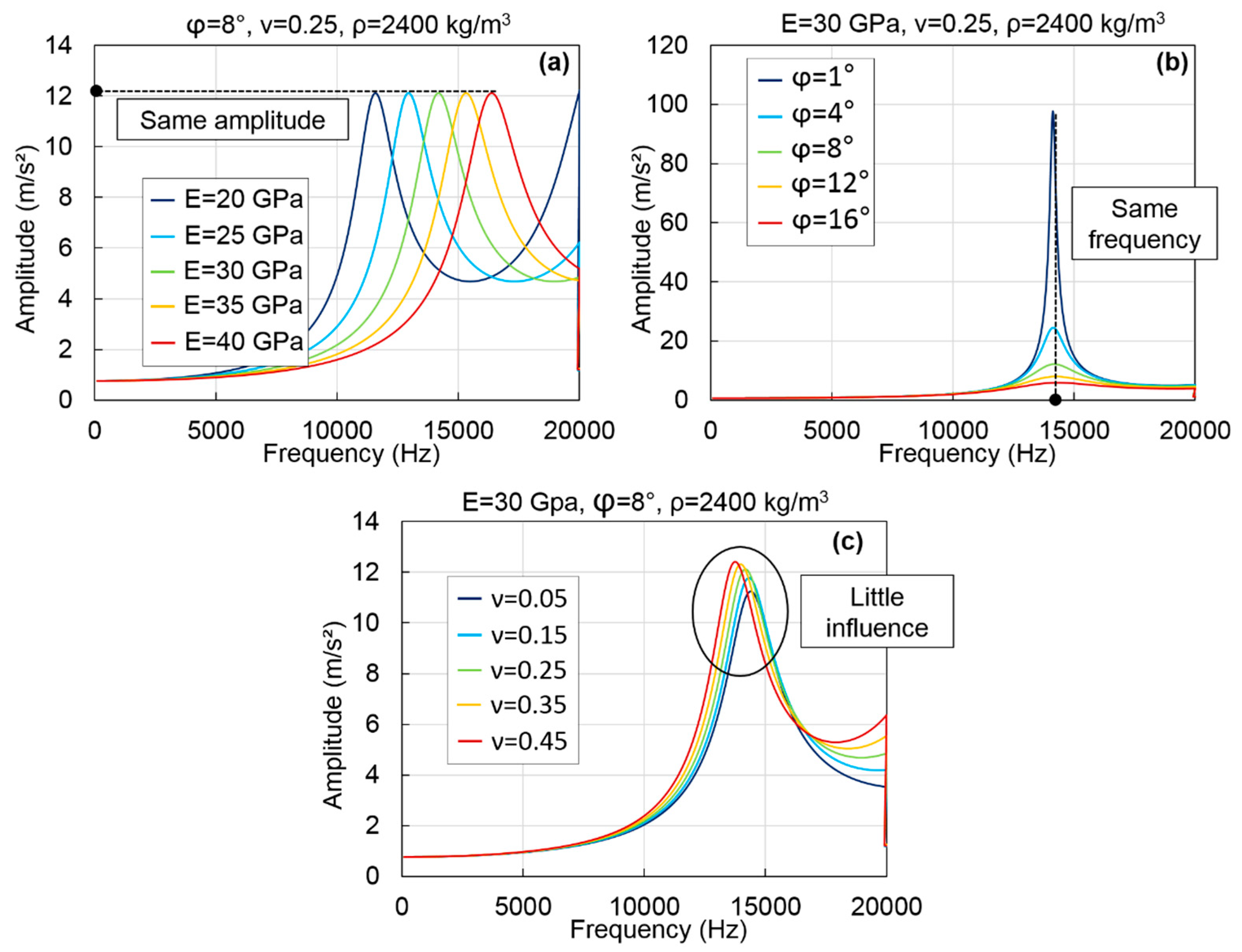
4.2. Calculation of FRFs with the Finite Element Method (FEM)
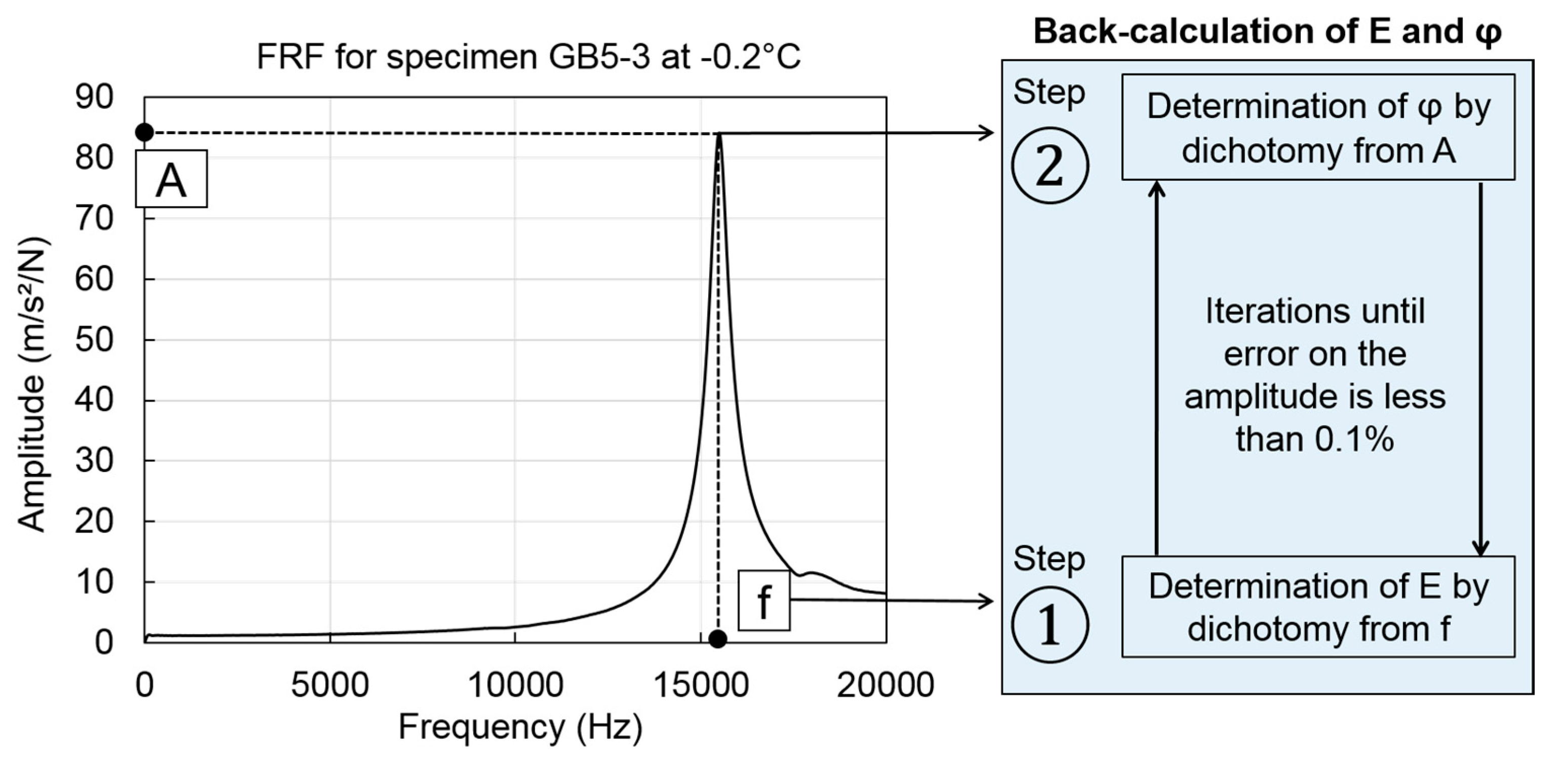
4.3. Determination of the Material LVE Properties from Dynamic Tests
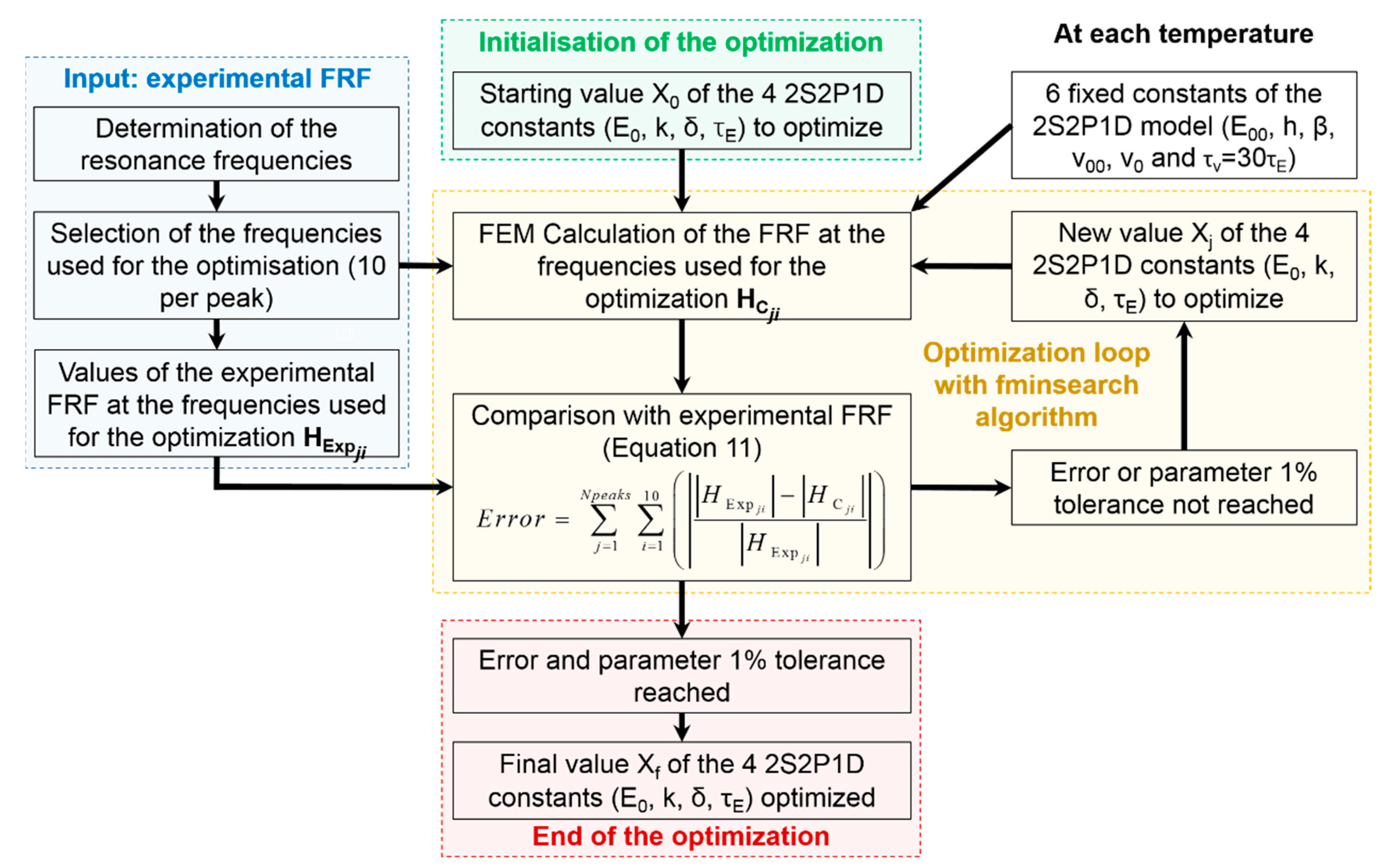
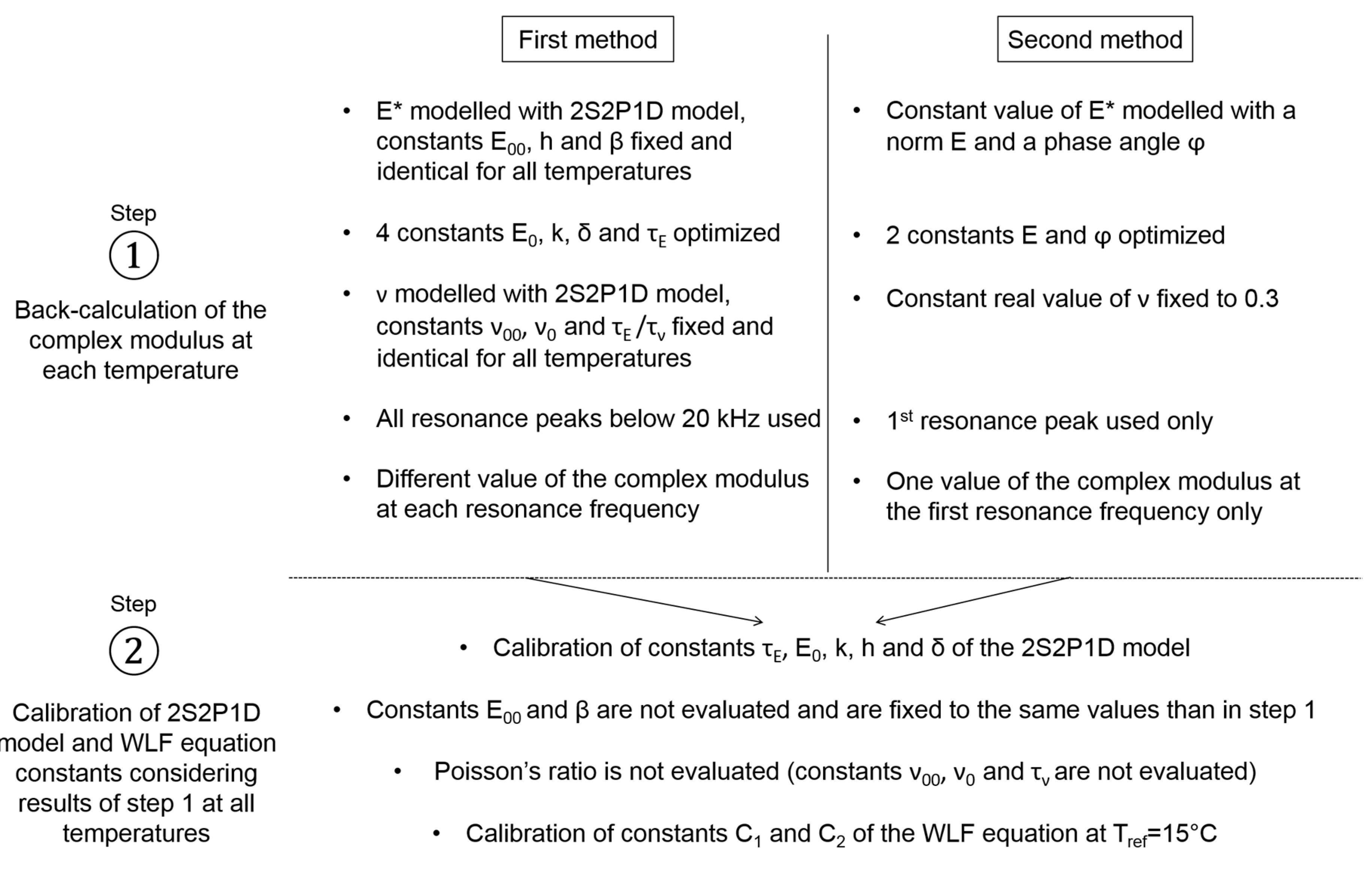
4.3.1. First Method: Optimization of the 2S2P1D Model Constants to Match Experimental FRFs
4.3.2. Second Method: Constant Complex Modulus Obtained from the First Resonance Peak Only
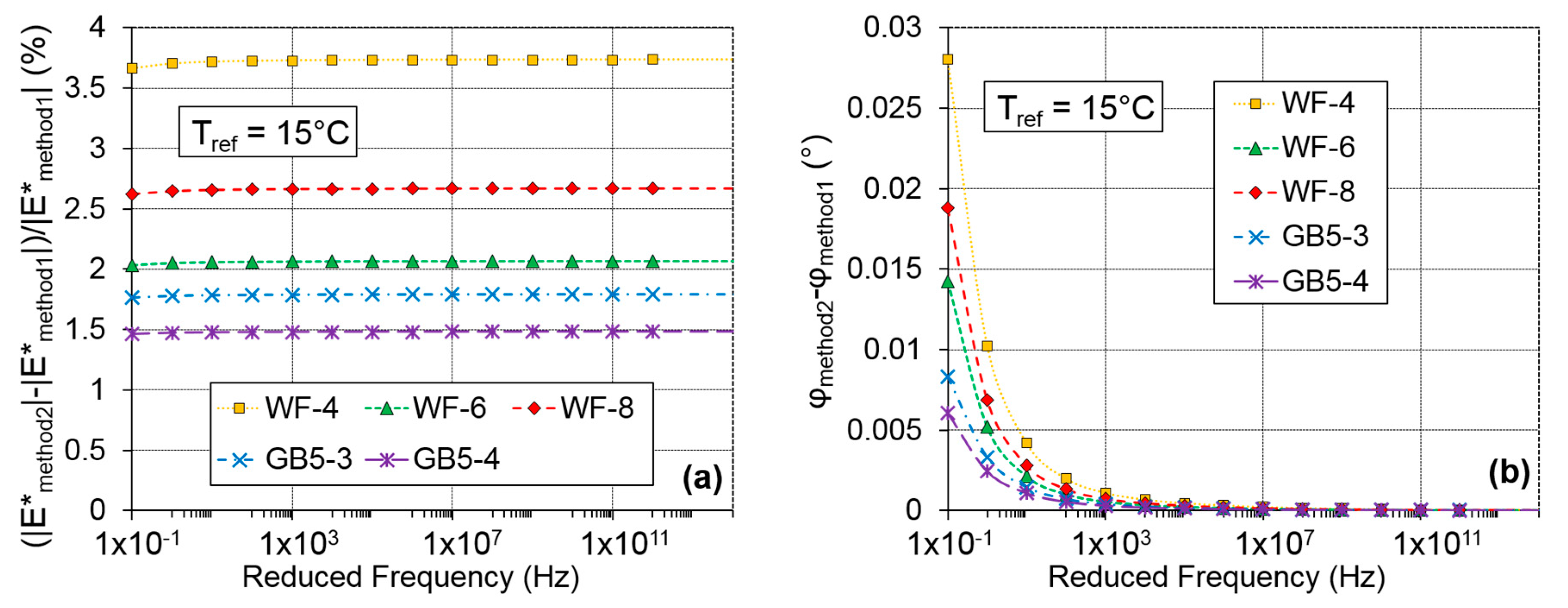
4.3.3. Summary and Remarks on the Two Methods
5. Results
5.1. Tension–Compression Tests Results
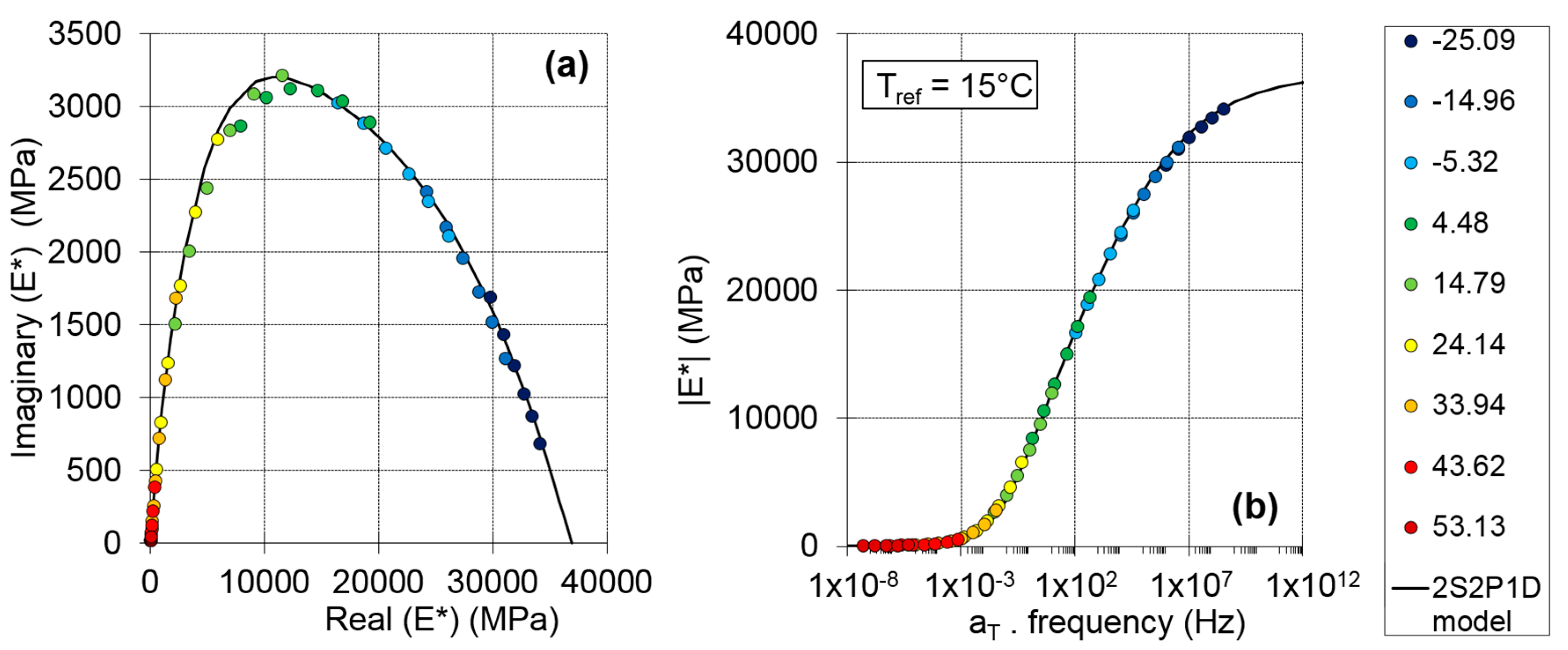
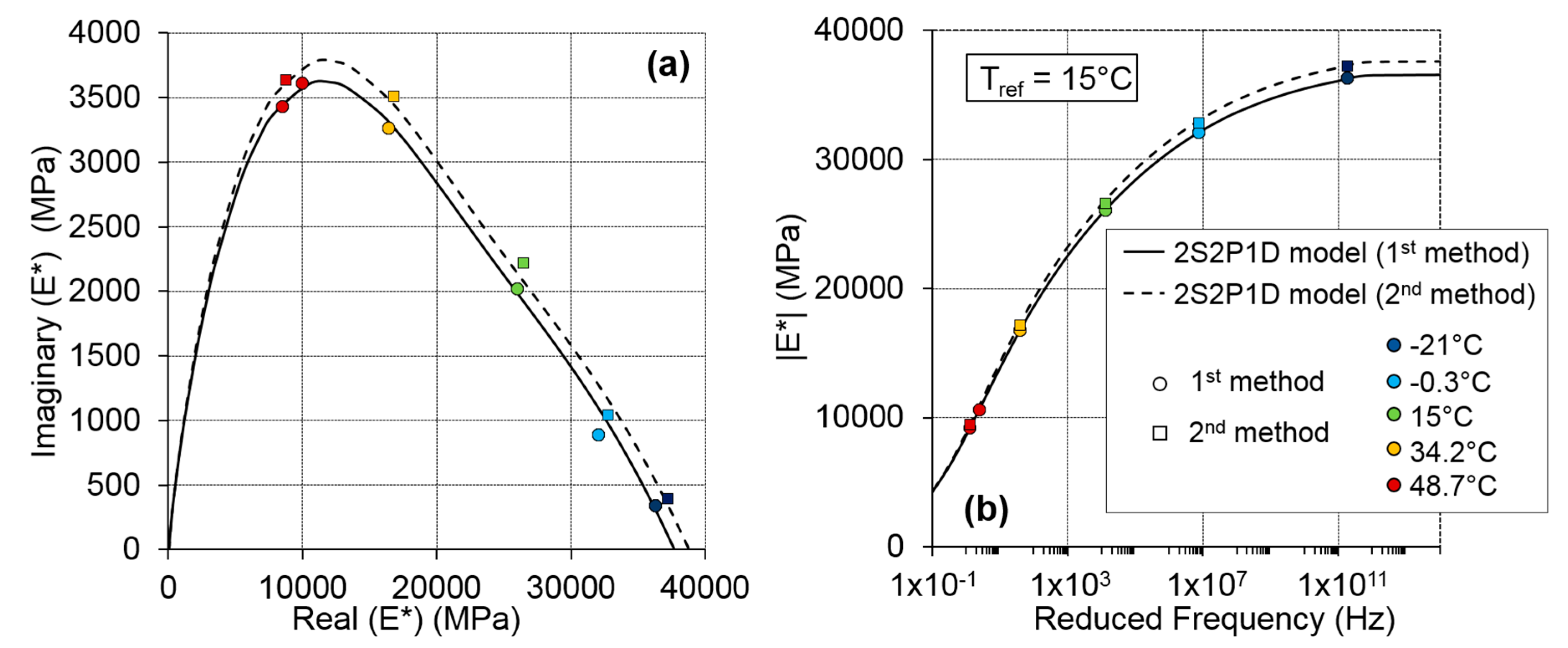
5.2. Dynamic Impact Tests Results
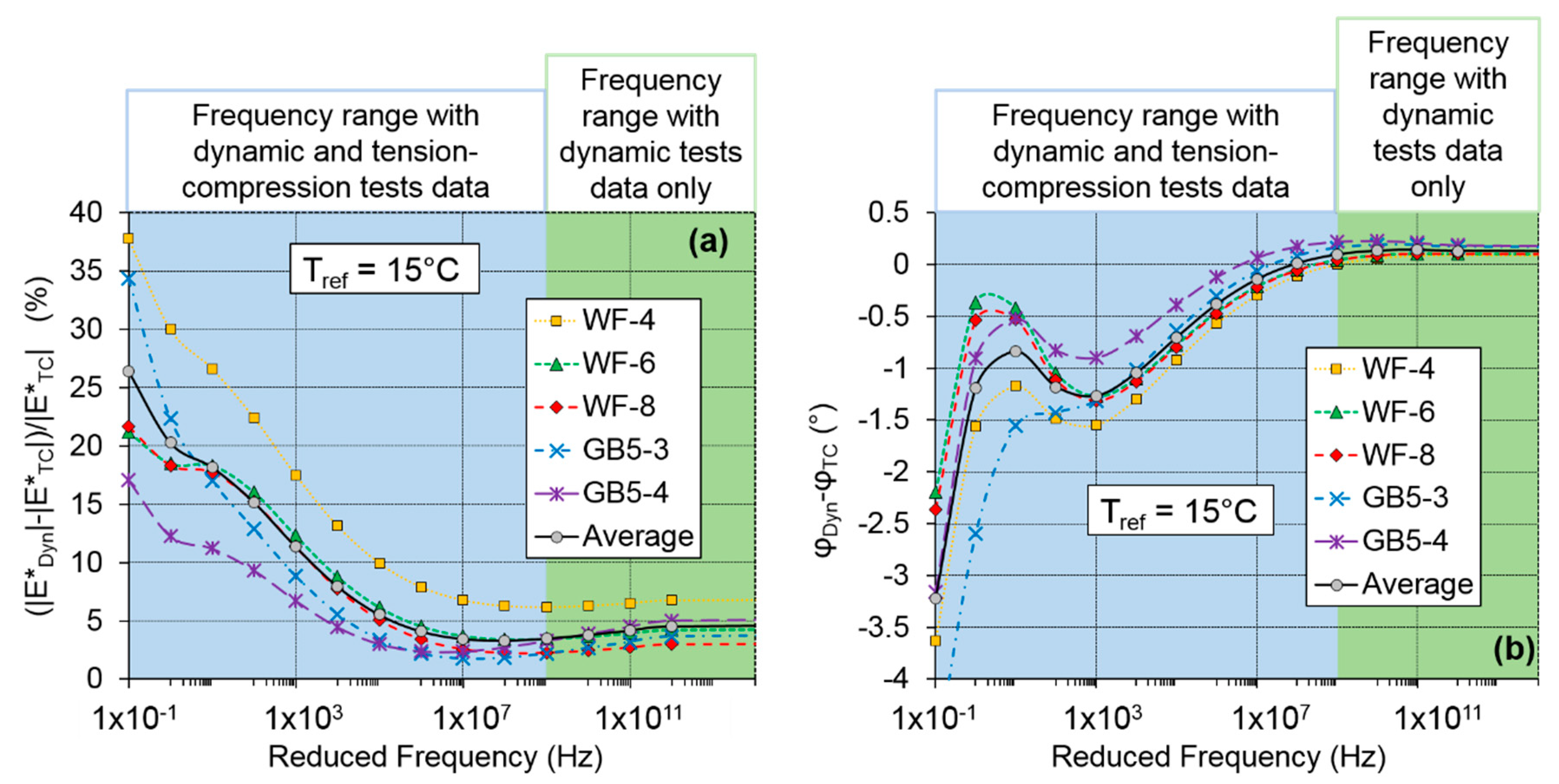
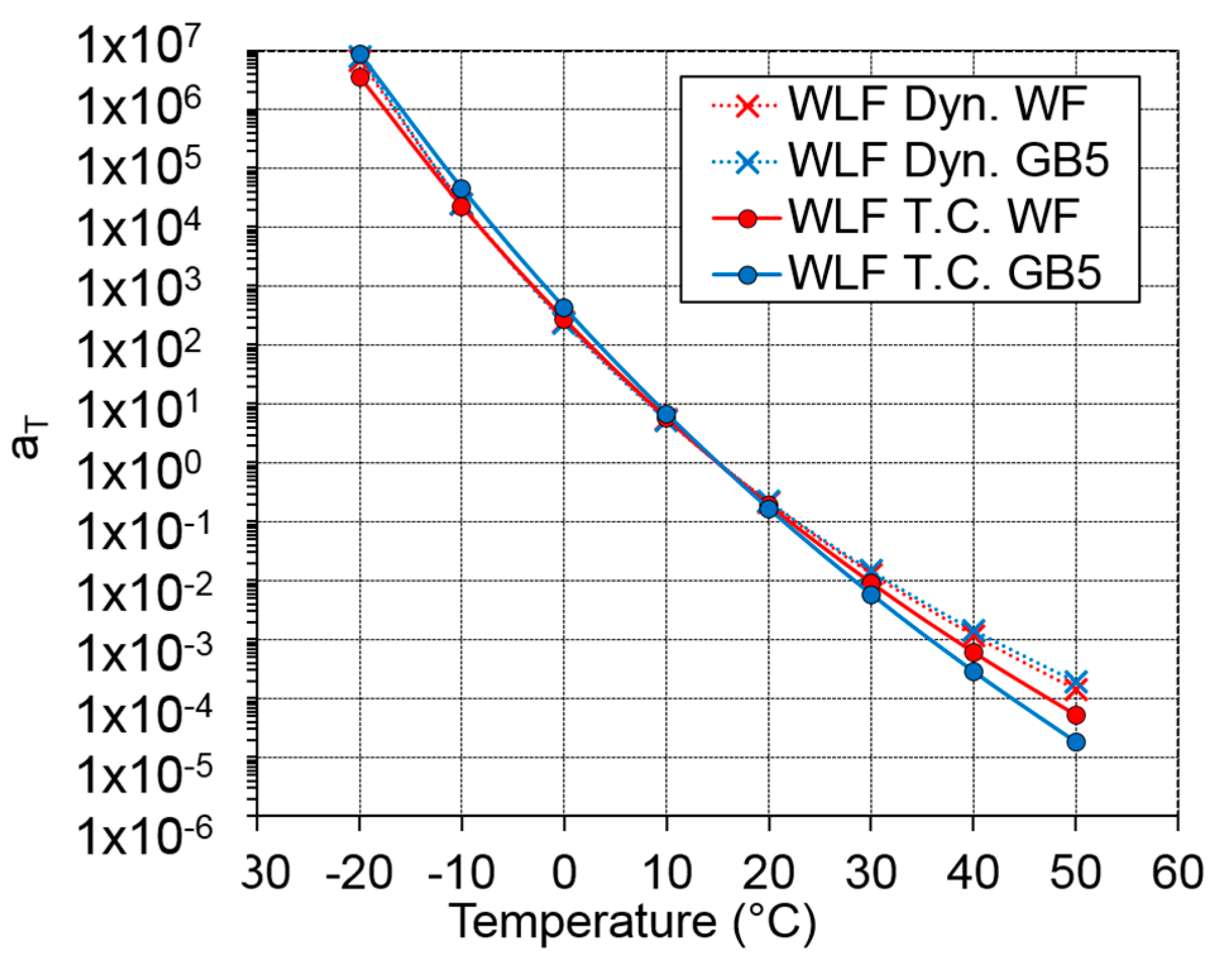
5.3. Comparison between Cyclic and Dynamic Tests Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Di Benedetto, H.; Corte, J.F. Matériaux Routiers Bitumineux 2: Constitution et Propriétés Thermomécaniques des Mélanges; Lavoisier: Paris, France, 2005; p. 288. (In French) [Google Scholar]
- Halvorsen, W.G.; Brown, D.L. Impulse technique for structural response frequency testing. J. Sound Vib. 1977, 11, 8–21. [Google Scholar] [CrossRef]
- ASTM: C215-08. Standard Test Method for Fundamental Transverse, Longitudinal and Torsional Frequencies of Concrete Specimens; ASCE: West Conshoshocken, PA, USA, 2008. [Google Scholar]
- Migliori, A.; Sarrao, J. Resonant Ultrasound Spectroscopy-Applications to Physics, Materials Measurements and Nondestructive Evaluation; Wiley-Interscience Publication: New York, NY, USA, 1997. [Google Scholar]
- Renault, A.; Jaouen, L.; Sgard, F. Characterization of elastic parameters of acoustical porous materials from beam bending vibrations. J. Sound Vib. 2010, 330, 1950–1963. [Google Scholar] [CrossRef]
- Di Benedetto, H.; Sauzéat, C.; Sohm, J. Stiffness of bituminous mixtures using ultrasonic wave propagation. Road Mater. Pavement Des. 2009, 10, 789–814. [Google Scholar] [CrossRef]
- Mounier, D.; Di Benedetto, H.; Sauzéat, C. Determination of bituminous mixtures linear properties using ultrasonic wave propagation. Constr. Build. Mater. 2012, 36, 638–647. [Google Scholar] [CrossRef]
- Norambuena-Contreras, J.; Castro-Fresno, D.; Vega-Zamanillo, A.; Celay, M.; Lombillo-Vozmediano, I. Dynamic modulus of asphalt mixture by ultrasonic direct test. NDT E Int. 2010, 43, 629–634. [Google Scholar] [CrossRef]
- Kweon, G.; Kim, Y.R. Determination of the complex modulus of asphalt concrete using the impact resonance test. J. Transp. Res. Board 2006, 1970, 151–160. [Google Scholar] [CrossRef]
- Lacroix, A.; Kim, Y.R.; Far, M.S.S. Constructing the dynamic modulus mastercurve using impact resonance testing. J. Assoc. Asphalt Paving Technol. 2009, 78, 67–102. [Google Scholar]
- Whitmoyer, S.L.; Kim, Y.R. Determining asphalt concrete properties via the impact resonant method. J. Test. Eval. 1994, 22, 139–148. [Google Scholar] [CrossRef]
- Gudmarsson, A.; Ryden, N.; Birgisson, B. Application of resonant acoustic spectroscopy to asphalt concrete beams for determination of the dynamic modulus. Mater. Struct. 2012, 45, 1903–1913. [Google Scholar] [CrossRef]
- Leisure, R.; Willis, F. Resonant ultrasound spectroscopy. J. Phys. Condens. Matter 1999, 9, 6001–6029. [Google Scholar] [CrossRef]
- Ostrovsky, L.; Lebedev, A.; Matveyev, A.; Popatov, A.; Sutin, A.; Soustova, I.; Johnson, P. Application of three-dimensional resonant acoustic spectroscopy method to rock and building materials. J. Acoust. Soc. Am. 2001, 110, 1770–1777. [Google Scholar] [CrossRef] [PubMed]
- Ryden, N. Resonant frequency testing of cylindrical asphalt samples. Eur. J. Environ. Civ. Eng. 2011, 15, 587–600. [Google Scholar] [CrossRef]
- Ren, Z.; Atalla, N.; Ghinet, S. Optimization based identification of the dynamic properties of linearly viscoelastic materials using vibrating beam techniques. ASME J. Vib. Acoust. 2011, 133, 041012. [Google Scholar] [CrossRef]
- Rupitsch, S.J.; Ilg, J.; Sutor, A.; Lerch, R.; Döllinger, M. Simulation based estimation of dynamic mechanical properties for viscoelastic materials used for vocal fold models. J. Sound Vib. 2011, 330, 4447–4459. [Google Scholar] [CrossRef]
- Gudmarsson, A.; Ryden, N.; Birgisson, B. Characterizing the low strain complex modulus of asphalt concrete specimens through optimization of frequency response functions. J. Acoust. Soc. Am. 2012, 132, 2304–2312. [Google Scholar] [CrossRef] [PubMed]
- Gudmarsson, A.; Ryden, N.; Di Benedetto, H.; Sauzéat, C.; Tapsoba, N.; Birgisson, B. Comparing Linear Viscoelastic Properties of Asphalt Concrete Measured by Laboratory Seismic and Tension-Compression Tests. J. Nondestruct. Eval. 2014, 33, 571–582. [Google Scholar] [CrossRef]
- Gudmarsson, A.; Ryden, N.; Di Benedetto, H.; Sauzéat, C. Complex modulus and complex Poisson’s ratio from cyclic and dynamic modal testing of asphalt concrete. Constr. Build. Mater. 2015, 88, 20–31. [Google Scholar] [CrossRef]
- Carret, J.-C.; Pedraza, A.; Di Benedetto, H.; Sauzéat, C. Comparison of the 3-dim linear viscoelastic behavior of asphalt mixes determined with tension-compression and dynamic tests. Constr. Build. Mater. 2018, 174, 529–536. [Google Scholar] [CrossRef]
- Carret, J.-C.; Di Benedetto, H.; Sauzéat, C. Multi-modal dynamic linear viscoelastic back analysis for asphalt mixes. J. Nondestruct. Eval. 2018, 37, 35. [Google Scholar] [CrossRef]
- Poirier, J.E.; Pouget, S.; Leroy, C.; Delaporte, B. Projets Mure et Improvmure: Bilan à mi-parcours. Revue Générale des Routes et de l’Aménagement 2016, 937, 38–41. (In French) [Google Scholar]
- Gayte, P.; Di Benedetto, H.; Sauzéat, C.; Nguyen, Q. Influence of transient effects for analysis of complex modulus tests on bituminous mixtures. Road Mater. Pavement Des. 2015, 17, 271–289. [Google Scholar] [CrossRef]
- Graziani, A.; Di Benedetto, H.; Perraton, D.; Sauzéat, C.; Hofko, B.; Poulikakos, L.; Pouget, S. Recommendation of RILEM TC 237-SIB on complex Poisson’s ratio characterization of bituminous mixtures. Mater. Struct. 2017, 50, 142. [Google Scholar] [CrossRef]
- Perraton, D.; Di Benedetto, H.; Sauzéat, C.; Hofko, N.; Graziani, A.; Nguyen, Q. 3 Dim experimental investigation of linear viscoelastic properties of bituminous mixtures. Mater. Struct. 2016, 49, 4813–4829. [Google Scholar] [CrossRef]
- Di Benedetto, H.; Olard, F.; Sauzéat, C.; Delaporte, B. Linear viscoelastic behavior of bituminous materials: From binders to mixtures. Road Mater. Pavement Des. 2004, 5, 163–202. [Google Scholar] [CrossRef]
- Olard, F.; Di Benedetto, H. General 2S2P1D model and relation between the linear viscoelastic behaviors of bituminous binders and mixes. Road Mater. Pavement Des. 2003, 4, 185–224. [Google Scholar] [CrossRef]
- Tiouajni, S.; Di Benedetto, H.; Sauzéat, C.; Pouget, S. Approximation of linear viscoelastic model in the 3 dimensional case with mechanical analogues of finite size—Application to bituminous materials. Road Mater. Pavement Des. 2011, 12, 897–930. [Google Scholar] [CrossRef]
- Di Benedetto, H.; Delaporte, B.; Sauzéat, C. Three dimensional linear behavior of bituminous materials: Experiments and modeling. ASCE Int. J. Geomech. 2007, 7, 149–157. [Google Scholar] [CrossRef]
- Nguyen, H.M.; Pouget, S.; Di Benedetto, H.; Sauzéat, C. Time-temperature superposition principle for bituminous mixtures. Eur. J. Environ. Civ. Eng. 2009, 13, 1095–1107. [Google Scholar] [CrossRef]
- Nguyen, M.L.; Sauzéat, C.; Di Benedetto, H.; Tapsoba, N. Validation of the time–temperature superposition principle for crack propagation in bituminous mixtures. Mater. Struct. 2013, 46, 1075–1087. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Di Benedetto, H.; Sauzéat, C.; Tapsoba, N. Time-temperature superposition principle validation for bituminous mixes in the linear and nonlinear domain. ASCE J. Mater. Civ. Eng. 2013, 25, 1181–1188. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1980. [Google Scholar]
- Brüggemann, T.; Biermann, D.; Zabel, A. Development of an automatic modal pendulum for the measurement of frequency responses for the calculation of stability charts. Procedia CIRP 2015, 33, 587–592. [Google Scholar] [CrossRef]
- Norman, P.E.; Jung, G.; Ratcliffe, C.; Crane, R.; Davis, C. Development of an Automated Impact Hammer for Modal Analysis of Structures; DSTO-TN-1062; DSTO Defence Science and Technology Organisation: Fishermans Bend, Australia, 2012. [Google Scholar]
- Mangiafico, S.; Di Benedetto, H.; Sauzéat, C.; Olard, F.; Pouget, S.; Planque, L. New method to obtain viscoelastic properties of bitumen blends from pure and RAP binder constituents. Road Mater. Pavement Des. 2014, 15, 312–329. [Google Scholar] [CrossRef]
- Pouget, S.; Sauzéat, C.; Di Benedetto, H.; Olard, F. Modeling of viscous bituminous wearing course materials on orthotropic steel deck. Mater. Struct. 2012, 45, 1115–1125. [Google Scholar] [CrossRef]
- Airey, G.; Rahimzadeh, B. Combined bituminous binder and mixture linear rheological properties. Constr. Build. Mater. 2004, 18, 535–548. [Google Scholar] [CrossRef]
- Nguyen, Q.T.; Di Benedetto, H.; Sauzéat, C. Linear and nonlinear viscoelastic behavior of bituminous mixtures. Mater. Struct. 2015, 48, 2339–2351. [Google Scholar] [CrossRef]
- Mangiafico, S.; Babadopoulos, L.; Di Benedetto, H.; Sauzéat, C. Nonlinearity of bituminous mixtures. Mech. Time-Depend. Mater. 2018, 22, 29–49. [Google Scholar] [CrossRef]
| Specimen | Mass (g) | Height (mm) | Diameter (mm) | Density (kg/m3) | Void Ratio (%) | Bitumen Content (%) | RAP Content (%) |
|---|---|---|---|---|---|---|---|
| WF-4 | 1293 | 0.123 | 75 | 2379 | 6.6 | 5.4 | 70 |
| WF-6 | 1320 | 0.123 | 75 | 2431 | 4.2 | 5.4 | 70 |
| WF-8 | 1330 | 0.123 | 75 | 2449 | 3.8 | 5.4 | 70 |
| GB5-3 | 941 | 0.152 | 64 | 2381 | 4.8 | 4.8 | 30 |
| GB5-4 | 951 | 0.152 | 64 | 2378 | 5.1 | 4.8 | 30 |
| Temperature (°C) | −20 | 0 | 15 | 35 | 50 |
|---|---|---|---|---|---|
| Number of peaks | 1 | 1 | 1 | 1 | 2 |
| E (GPa) | 20 | 25 | 30 | 35 | 40 | RSD (%) | |
|---|---|---|---|---|---|---|---|
| ϕ = 8° | f (Hz) | 11,580 | 12,940 | 14,180 | 15,320 | 16,380 | 13.5 |
| ν = 0.25 | Amplitude (m/s²) | 12.1 | 12.1 | 12.1 | 12.1 | 12.1 | 6 × 10−4 |
| ϕ (°) | 1 | 4 | 8 | 12 | 16 | RSD (%) | |
| E = 30 GPa | f (Hz) | 14,120 | 14,140 | 14,180 | 14,240 | 14,340 | 0.6 |
| ν = 0.25 | Amplitude (m/s²) | 97.7 | 24.4 | 12.1 | 8.0 | 5.9 | 130.8 |
| ν | 0.05 | 0.15 | 0.25 | 0.35 | 0.45 | RSD (%) | |
| E = 30 GPa | f (Hz) | 14,400 | 14,320 | 14,180 | 13,980 | 13,760 | 1.8 |
| ϕ = 8° | Amplitude (m/s²) | 11.2 | 11.8 | 12.1 | 12.3 | 12.4 | 4.0 |
| Specimen | E00 (MPa) | E0 (MPa) | δ | k | h | β | τE15°C (s) | C1 | C2 |
|---|---|---|---|---|---|---|---|---|---|
| WF-4 | 28 | 33,400 | 2.28 | 0.177 | 0.57 | 154 | 5.4 × 10−2 | 24.9 | 166.6 |
| WF-6 | 40 | 37,500 | 2.28 | 0.177 | 0.57 | 154 | 7.0 × 10−2 | 24.9 | 166.6 |
| WF-8 | 56 | 36,900 | 2.28 | 0.177 | 0.57 | 154 | 6.9 × 10−2 | 24.9 | 166.6 |
| GB5-3 | 65 | 39,100 | 1.80 | 0.180 | 0.60 | 350 | 7.5 × 10−2 | 24.7 | 165.9 |
| GB5-4 | 65 | 39,500 | 1.80 | 0.180 | 0.60 | 350 | 1.5 × 10−1 | 24.7 | 165.9 |
| Specimen | E00 (MPa) | E0 (MPa) | δ | k | h | β | τE15°C (s) | C1 | C2 |
|---|---|---|---|---|---|---|---|---|---|
| WF-4 | 100 | 34,800 | 1.39 | 0.142 | 0.49 | 250 | 4.0 × 10−2 | 18.9 | 133.2 |
| WF-6 | 100 | 38,700 | 1.39 | 0.142 | 0.49 | 250 | 7.0 × 10−2 | 18.9 | 133.2 |
| WF-8 | 100 | 37,500 | 1.39 | 0.142 | 0.49 | 250 | 4.0 × 10−2 | 18.9 | 133.2 |
| GB5-3 | 100 | 39,100 | 1.17 | 0.130 | 0.442 | 250 | 5.5 × 10−2 | 19.2 | 139.5 |
| GB5-4 | 100 | 40,500 | 1.17 | 0.130 | 0.442 | 250 | 7.0 × 10−2 | 19.2 | 139.5 |
| Specimen | E00 (MPa) | E0 (MPa) | δ | k | h | β | τE15°C (s) | C1 | C2 |
|---|---|---|---|---|---|---|---|---|---|
| WF-4 | 100 | 36,100 | 1.39 | 0.142 | 0.49 | 250 | 4.0 × 10−2 | 18.9 | 133.2 |
| WF-6 | 100 | 39,500 | 1.39 | 0.142 | 0.49 | 250 | 7.0 × 10−2 | 18.9 | 133.2 |
| WF-8 | 100 | 38,500 | 1.39 | 0.142 | 0.49 | 250 | 4.0 × 10−2 | 18.9 | 133.2 |
| GB5-3 | 100 | 39,800 | 1.17 | 0.130 | 0.442 | 250 | 5.5 × 10−2 | 19.2 | 139.5 |
| GB5-4 | 100 | 41,100 | 1.17 | 0.130 | 0.442 | 250 | 7.0 × 10−2 | 19.2 | 139.5 |
| GB5-4 | 100 | 40,500 | 1.17 | 0.130 | 0.442 | 250 | 7.0 × 10−2 | 19.2 | 139.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carret, J.-C.; Di Benedetto, H.; Sauzéat, C. Characterization of Asphalt Mixes Behaviour from Dynamic Tests and Comparison with Conventional Cyclic Tension–Compression Tests. Appl. Sci. 2018, 8, 2117. https://doi.org/10.3390/app8112117
Carret J-C, Di Benedetto H, Sauzéat C. Characterization of Asphalt Mixes Behaviour from Dynamic Tests and Comparison with Conventional Cyclic Tension–Compression Tests. Applied Sciences. 2018; 8(11):2117. https://doi.org/10.3390/app8112117
Chicago/Turabian StyleCarret, Jean-Claude, Hervé Di Benedetto, and Cédric Sauzéat. 2018. "Characterization of Asphalt Mixes Behaviour from Dynamic Tests and Comparison with Conventional Cyclic Tension–Compression Tests" Applied Sciences 8, no. 11: 2117. https://doi.org/10.3390/app8112117
APA StyleCarret, J.-C., Di Benedetto, H., & Sauzéat, C. (2018). Characterization of Asphalt Mixes Behaviour from Dynamic Tests and Comparison with Conventional Cyclic Tension–Compression Tests. Applied Sciences, 8(11), 2117. https://doi.org/10.3390/app8112117




