New Candidate Multicomponent Chalcogenide Glasses for Supercontinuum Generation
Abstract
1. Introduction
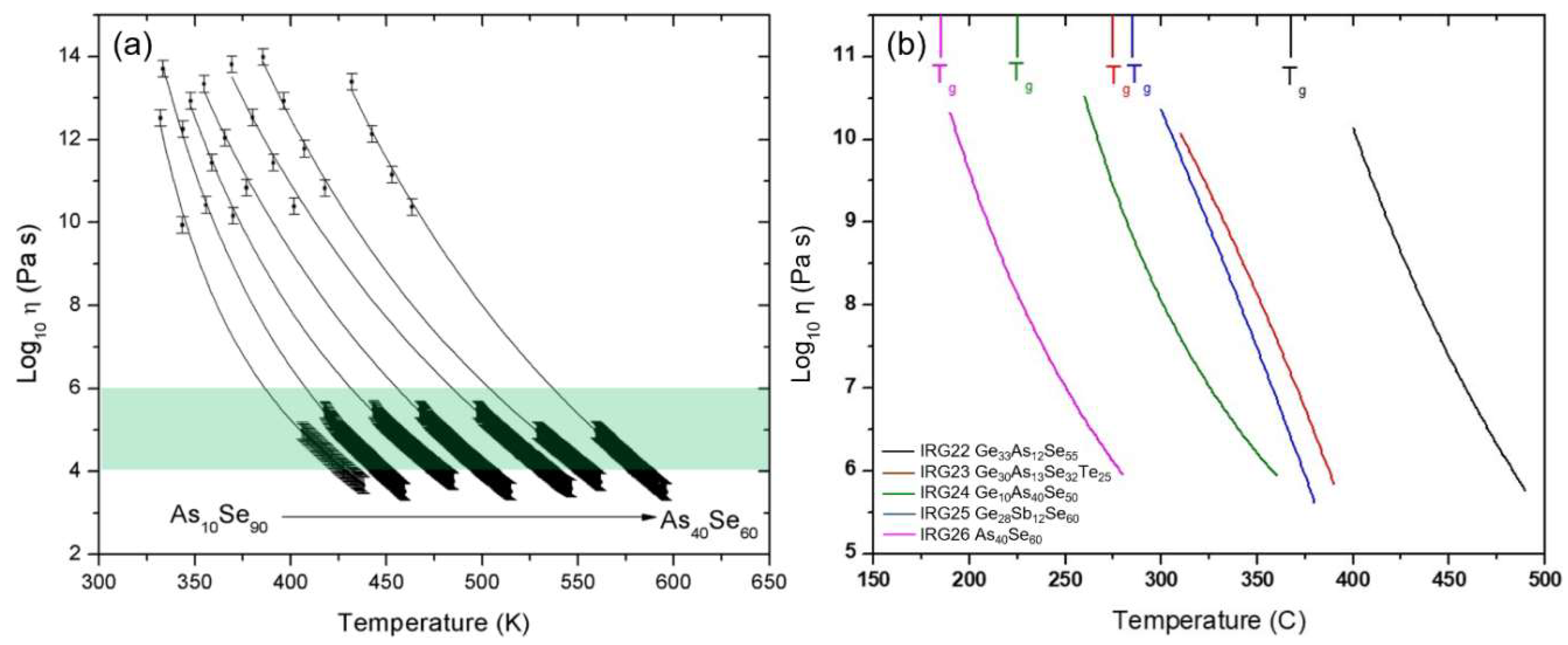
2. Optical and Physical Properties and Composition: Glasses
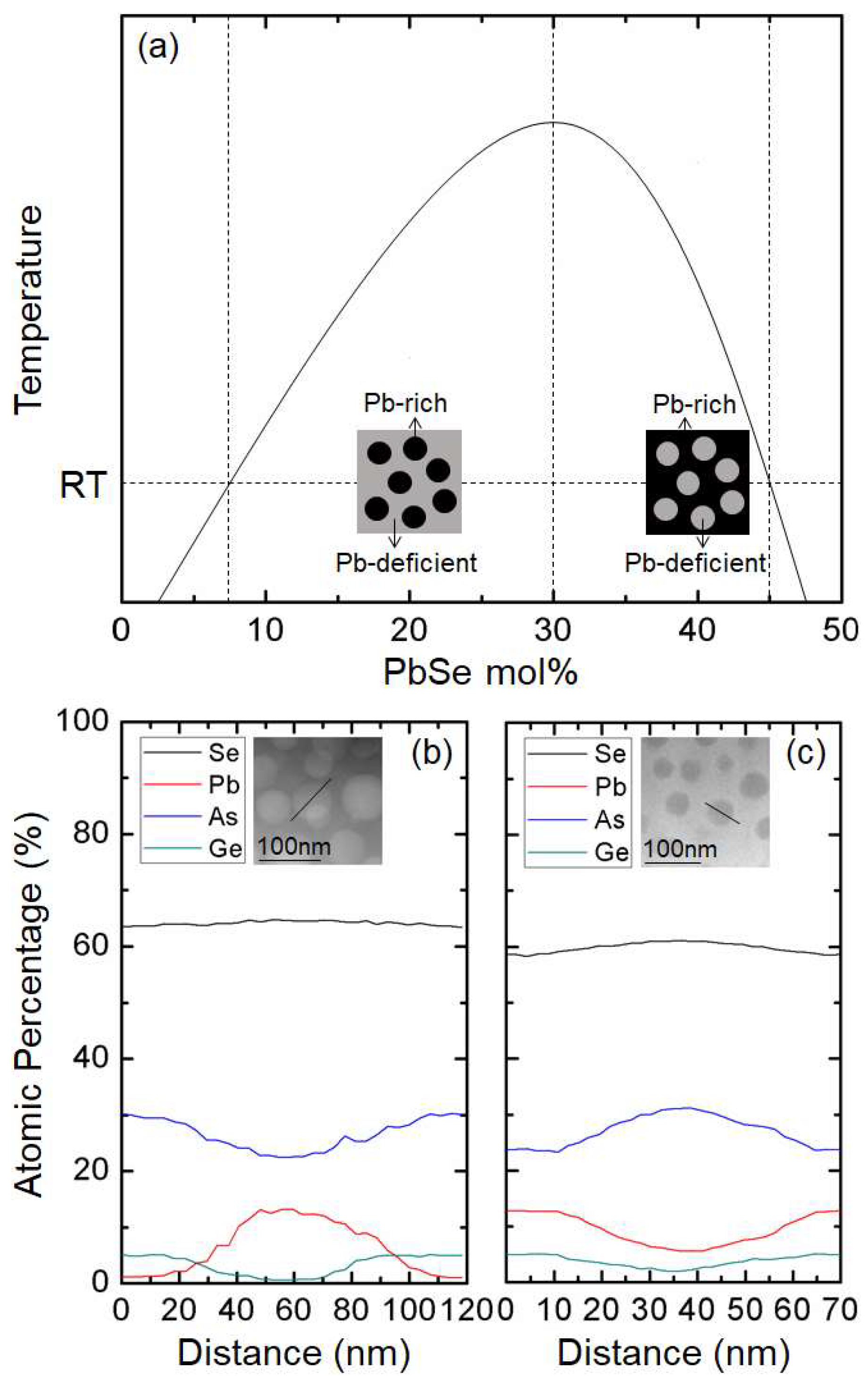
3. Composition, Morphology, and Optical Properties: Glasses Towards Glass Ceramics
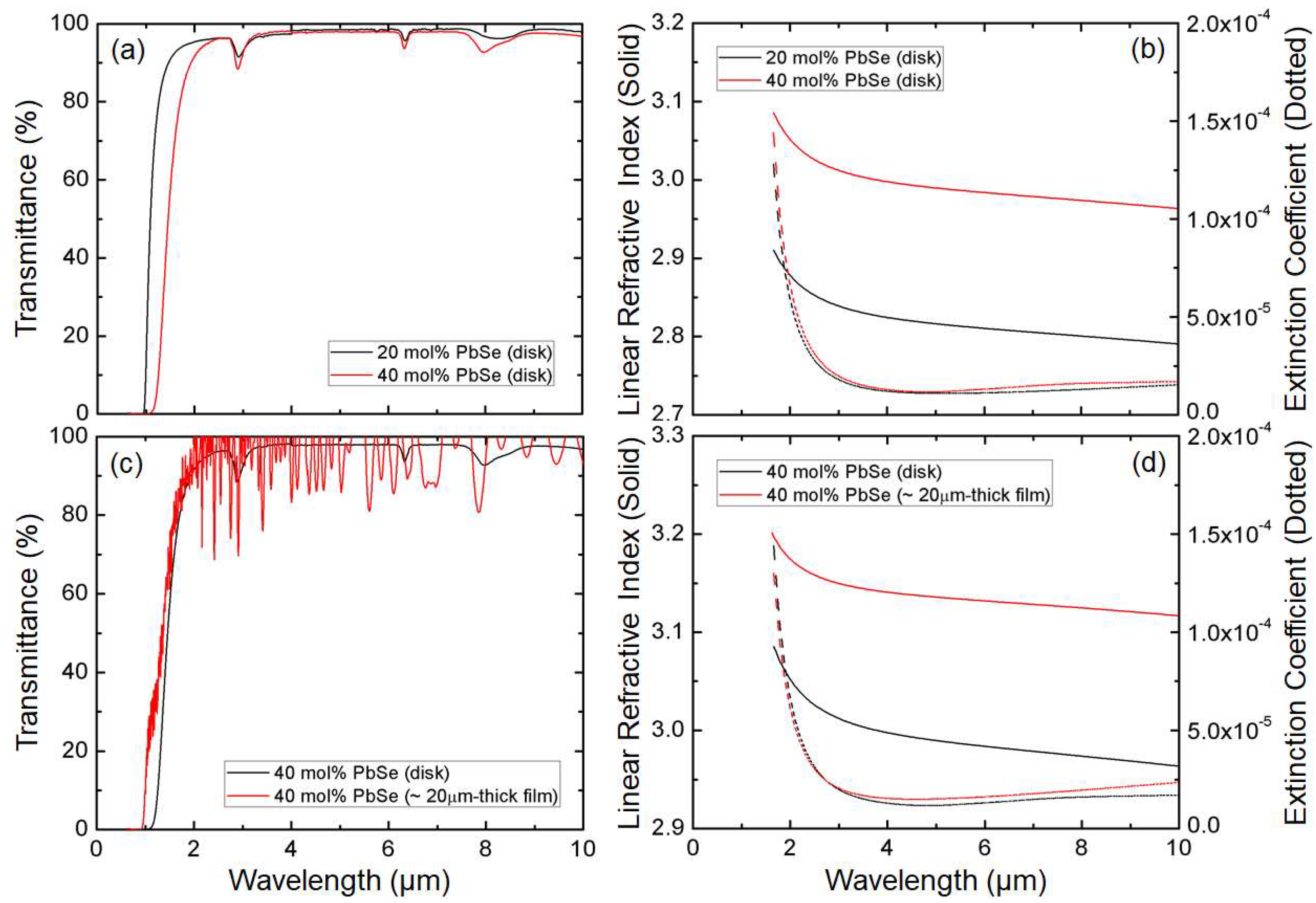
4. Linear Optical Property Variation
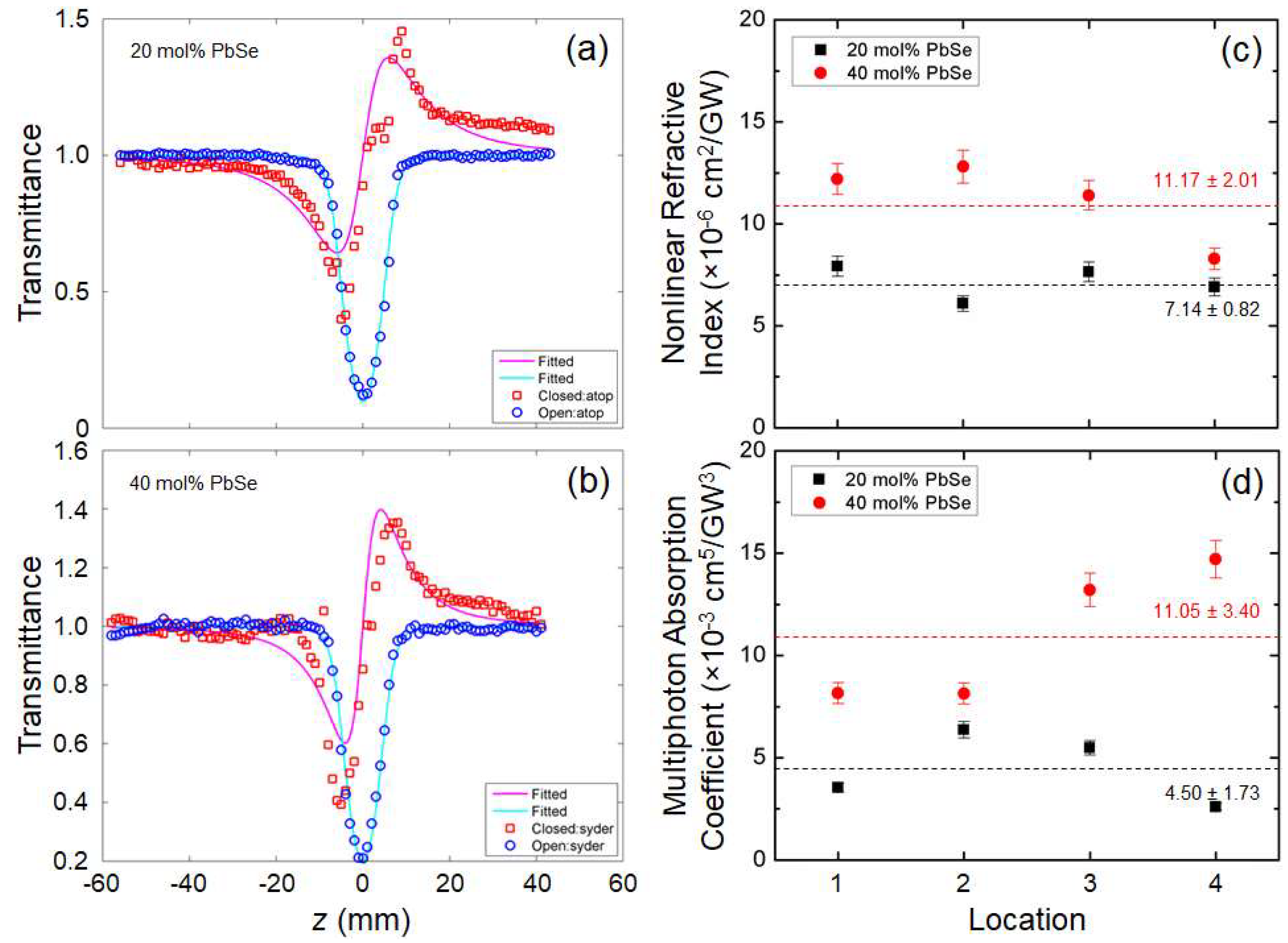
5. Nonlinear Optical Property Variation
6. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Du, Q.; Luo, Z.; Zhong, H.; Zhang, Y.; Huang, Y.; Du, T.; Zhang, W.; Gu, T.; Hu, J. Chip-scale broadband spectroscopic chemical sensing using an integrated supercontinuum source in a chalcogenide glass waveguide. Photon. Res. 2018, 6, 506–510. [Google Scholar] [CrossRef]
- Eggleton, B.; Luther-Davies, B.; Richardson, K. Chalcogenide photonics. Nat. Photonics 2011, 5, 141. [Google Scholar] [CrossRef]
- Mandon, J.; Sorokin, E.; Sorokina, I.; Guelachvili, G.; Picqué, N. Supercontinua for high-resolution absorption multiplex infrared spectroscopy. Opt. Lett. 2008, 33, 285–287. [Google Scholar] [CrossRef]
- Wang, T.; Ng, D.; Ng, S.; Toh, Y.; Chee, A.; Chen, G.; Wang, Q.; Tan, D. Supercontinuum generation in bandgap engineered, back-end CMOS compatible silicon rich nitride waveguides. Laser Photonics Rev. 2015, 9, 498–506. [Google Scholar] [CrossRef]
- Johnson, A.; Mayer, A.; Klenner, A.; Luke, K.; Lamb, E.; Lamont, M.; Joshi, C.; Okawachi, Y.; Wise, F.; Lipson, M.; et al. Octave-spanning coherent supercontinuum generation in a silicon nitride waveguide. Opt. Lett. 2015, 40, 5117–5120. [Google Scholar] [CrossRef]
- Hsieh, I.; Chen, X.; Liu, X.; Dadap, J.; Panoiu, N.; Chou, C.; Xia, F.; Green, W.; Vlasov, Y.; Osgood, R. Supercontinuum generation in silicon photonic wires. Opt. Express 2007, 15, 15242–15249. [Google Scholar] [CrossRef]
- Chen, L.; Chen, F.; Dai, S.; Tao, G.; Yan, L.; Shen, X.; Ma, H.; Zhang, X.; Xu, Y. Third-order nonlinearity in Ge–Sb–Se glasses at mid-infrared wavelengths. Mater. Res. Bull. 2015, 70, 204–208. [Google Scholar] [CrossRef]
- Zakery, A.; Elliott, S. Optical properties and applications of chalcogenide glasses: A review. J. Non-Cryst. Solids 2003, 330, 1–2. [Google Scholar] [CrossRef]
- Anashkina, E.; Shiryaev, V.; Snopatin, G.; Muraviev, S.; Kim, A. On the possibility of mid-IR supercontinuum generation in As-Se-Te/As-S core/clad fibers with all-fiber femtosecond pump source. J. Non-Cryst. Solids 2018, 480, 38–42. [Google Scholar] [CrossRef]
- Patrick, H.; Frédéric, S.; Vincent, C.; Johann, T.; Ludovic, G. Selenide glass single mode optical fiber for nonlinear optics. Opt. Mater. 2007, 29, 651–656. [Google Scholar] [CrossRef]
- Monro, T.; Ebendorff-Heidepriem, H. Progress in Microstructured Optical Fibers. Annu. Rev. Mater. Res. 2006, 36, 467–495. [Google Scholar] [CrossRef]
- Savelli, I.; Mouawad, O.; Fatome, J.; Kibler, B.; Désévédavy, F.; Gadret, G.; Jules, J.; Bony, P.; Kawashima, H.; Gao, W.; et al. Mid-infrared 2000-nm bandwidth supercontinuum generation in suspended-core microstructured Sulfide and Tellurite optical fibers. Opt. Express 2012, 20, 27083–27093. [Google Scholar] [CrossRef]
- Kohoutek, T.; Yan, X.; Shiosaka, T.; Yannopoulos, S.; Chrissanthopoulos, A.; Suzuki, T.; Ohishi, Y. Enhanced Raman gain of Ge-Ga-Sb-S chalcogenide glass for highly nonlinear microstructured optical fibers. JOSA B 2011, 28, 2284–2290. [Google Scholar] [CrossRef]
- Dantanarayana, H.; Abdel-Moneim, N.; Tang, Z.; Sojka, L.; Sujecki, S.; Furniss, D.; Seddon, A.; Kubat, I.; Bang, O.; Benson, T. Refractive index dispersion of chalcogenide glasses for ultra-high numerical-aperture fiber for mid-infrared supercontinuum generation. Opt. Mater. Express 2014, 4, 1444–1455. [Google Scholar] [CrossRef]
- Petersen, C.; Møller, U.; Kubat, I.; Zhou, B.; Dupont, S.; Ramsay, J.; Benson, T.; Sujecki, S.; Abdel-Moneim, N.; Tang, Z.; et al. Mid-infrared supercontinuum covering the 1.4–13.3 μm molecular fingerprint region using ultra-high NA chalcogenide step-index fibre. Nat. Photonics 2014, 8, 830. [Google Scholar] [CrossRef]
- Boudebs, G.; Cherukulappurath, S.; Leblond, H.; Troles, J.; Smektala, F.; Sanchez, F. Experimental and theoretical study of higher-order nonlinearities in chalcogenide glasses. Opt. Commun. 2003, 219, 427–433. [Google Scholar] [CrossRef]
- Gao, W.; Liao, M.; Yan, X.; Kito, C.; Kohoutek, T.; Suzuki, T.; El-Amraoui, M.; Jules, J.; Gadret, G.; Desevedavy, F.; et al. Visible Light Generation and Its Influence on Supercontinuum in Chalcogenide As2S3 Microstructured Optical Fiber. Appl. Phys. Express 2011, 4, 102601. [Google Scholar] [CrossRef]
- El-Amraoui, M.; Fatome, J.; Jules, J.; Kibler, B.; Gadret, G.; Fortier, C.; Smektala, F.; Skripatchev, I.; Polacchini, C.; Messaddeq, Y.; et al. Strong infrared spectral broadening in low-loss As-S chalcogenide suspended core microstructured optical fibers. Opt. Express 2010, 18, 4547–4556. [Google Scholar] [CrossRef]
- Troles, J.; Smektala, F.; Boudebs, G.; Monteil, A.; Bureau, B.; Lucas, J. Chalcogenide glasses as solid state optical limiters at 1.064 μm. Opt. Mater. 2004, 25, 231–237. [Google Scholar] [CrossRef]
- Choi, J.; Han, Z.; Sohn, B.; Chen, G.; Smith, C.; Kimerling, L.; Richardson, K.; Agarwal, A.; Tan, D. Nonlinear characterization of GeSbS chalcogenide glass waveguides. Sci. Rep. 2016, 6, 39234. [Google Scholar] [CrossRef]
- Olivier, M.; Tchahame, J.; Němec, P.; Chauvet, M.; Besse, V.; Cassagne, C.; Boudebs, G.; Renversez, G.; Boidin, R.; Baudet, E.; et al. Structure, nonlinear properties, and photosensitivity of (GeSe2)100-x(Sb2Se3)x glasses. Opt. Mater. Express 2014, 4, 525–540. [Google Scholar] [CrossRef]
- Liu, Q.; Zhao, X.; Tanaka, K.; Narazaki, A.; Hirao, K.; Gan, F. Second-harmonic generation in Ge-As-S glasses by electron beam irradiation and analysis of the poling mechanism. Opt. Commun. 2001, 198, 187–192. [Google Scholar] [CrossRef]
- Rozé, M.; Calvez, L.; Ledemi, Y.; Allix, M.; Matzen, G.; Zhang, X. Optical and Mechanical Properties of Glasses and Glass–Ceramics Based on the Ge-Ga-Se System. J. Am. Ceram. Soc. 2008, 91, 3566–3570. [Google Scholar] [CrossRef]
- Zhang, X.; Bureau, B.; Lucas, P.; Boussard-Pledel, C.; Lucas, J. Glasses for Seeing Beyond Visible. Chem. Eur. J. 2008, 14, 432–442. [Google Scholar] [CrossRef] [PubMed]
- Vigreux-Bercovici, C.; Ranieri, V.; Labadie, L.; Broquin, J.; Kern, P.; Pradel, A. Waveguides based on Te2As3Se5 thick films for spatial interferometry. J. Non-Cryst. Solids 2006, 352, 2416–2419. [Google Scholar] [CrossRef]
- Wang, T.; Gai, X.; Wei, W.; Wang, R.; Yang, Z.; Shen, X.; Madden, S.; Luther-Davies, B. Systematic z-scan measurements of the third order nonlinearity of chalcogenide glasses. Opt. Mater. Express. 2014, 4, 1011–1022. [Google Scholar] [CrossRef]
- Stegeman, R.; Stegeman, G.; Delfyett, P., Jr.; Petit, L.; Carlie, N.; Richardson, K.; Couzi, M. Raman gain measurements and photo-induced transmission effects of germanium- and arsenic-based chalcogenide glasses. Opt. Express. 2006, 14, 11702–11708. [Google Scholar] [CrossRef] [PubMed]
- Cerqua-Richardson, K.; McKinley, J.; Lawrence, B.; Joshi, S.; Villeneuve, A. Comparison of nonlinear optical properties of sulfide glasses in bulk and thin film form. Opt. Mater. 1998, 10, 155–159. [Google Scholar] [CrossRef]
- Serna, S.; Lin, H.; Alonso-Ramos, C.; Yadav, A.; Le Roux, X.; Richardson, K.; Cassan, E.; Dubreuil, N.; Hu, J.; Vivien, L. Nonlinear optical properties of integrated GeSbS chalcogenide waveguides. Photonics Res. 2018, 6, B37–B42. [Google Scholar] [CrossRef]
- Zou, L.E.; He, P.P.; Chen, B.X.; Iso, M. Nonlinear optical properties of As20S80 system chalcogenide glass using Z-scan and its strip waveguide under bandgap light using the self-phase modulation. AIP Adv. 2017, 7, 025003. [Google Scholar] [CrossRef]
- Almeida, J.M.P.; Barbano, E.C.; Arnold, C.B.; Misoguti, L.; Mendonca, C.R. Nonlinear optical waveguides in As2S3-Ag2S chalcogenide glass thin films. Opt. Mater. Express 2017, 7, 93–99. [Google Scholar] [CrossRef]
- Krogstad, M.R.; Ahn, S.; Park, W.; Gopinath, J. Nonlinear characterization of Ge28Sb12Se60 bulk and waveguide devices. Opt. Express 2015, 6, 7870–7878. [Google Scholar] [CrossRef]
- Yu, Y.; Gai, X.; Ma, P.; Choi, D.-Y.; Yang, Z.; Wang, R.; Debbarma, S.; Madden, S.J.; Luther-Davies, B. A broadband, quasi-continuous, mid-infrared supercontinuum generated in a chalcogenide glass waveguide. Laser Photonics Rev. 2014, 8, 792–798. [Google Scholar] [CrossRef]
- Yu, Y.; Gai, X.; Ma, P.; Vu, K.; Yang, Z.; Wang, R.; Choi, D.-Y.; Madden, S.; Luther-Davies, B. Experimental demonstration of linearly polarized 2–10 μm supercontinuum generation in a chalcogenide rib waveguide. Opt. Lett. 2016, 41, 958–961. [Google Scholar] [CrossRef]
- Tremblay, J.-E.; Malinowski, M.; Richardson, K.; Fathpour, S.; Wu, M.C. Picojoule-level octave-spanning supercontinuum generation in chalcogenide waveguides. Opt. Express 2018, 26, 21358–21363. [Google Scholar] [CrossRef]
- Miyashita, T.; Terunuma, Y. Optical transmission loss of As–S fiber in 1.0–55μm wavelength region. Jpn. J. Appl. Phys. 1982, 21, 75. [Google Scholar] [CrossRef]
- Hattori, H.; Sato, S.; Fujioka, T. High power CO laser transmission through As–S glass fibers. Electron. Lett. 1984, 20, 811–812. [Google Scholar] [CrossRef]
- Gattass, R.R.; Shaw, L.B.; Nguyen, V.Q.; Pureza, P.C.; Aggarwal, I.D.; Sanghera, J.S. All-fiber chalcogenide-based mid-infrared supercontinuum source. Opt. Fiber Technol. 2012, 18, 345–348. [Google Scholar] [CrossRef]
- Marandi, A.; Rudy, C.W.; Plotnichenko, V.G.; Dianov, E.M.; Vodopyanov, K.L.; Byer, R.L. Mid-infrared supercontinuum generation in tapered chalcogenide fiber for producing octave-spanning frequency comb around 3 μm. Opt. Express 2012, 20, 24218–24225. [Google Scholar] [CrossRef]
- Deng, D.; Liu, L.; Tuan, T.H.; Kanou, Y.; Matsumoto, M.; Tezuka, H.; Suzuki, T.; Ohishi, Y. Mid-infrared supercontinuum covering 3–10 μm using a As2Se3 core and As2S5 cladding step-index chalcogenide fiber. J. Ceram. Soc. Jpn. 2016, 124, 103–105. [Google Scholar] [CrossRef]
- Kedenburg, S.; Steinle, T.; Mörz, F.; Steinmann, A.; Giessen, H. High-power mid-infrared high repetition-rate supercontinuum source based on a chalcogenide step-index fiber. Opt. Lett. 2015, 40, 2668–2671. [Google Scholar] [CrossRef] [PubMed]
- Møller, U.; Yu, Y.; Kubat, I.; Petersen, C.R.; Gai, X.; Brilland, L.; Méchin, D.; Caillaud, C.; Troles, J.; Luther-Davies, B.; Bang, O. Multi-milliwatt mid-infrared supercontinuum generation in a suspended core chalcogenide fiber. Opt. Express 2015, 23, 3282–3291. [Google Scholar] [CrossRef] [PubMed]
- Cheng, T.; Nagasaka, K.; Tuan, T.H.; Xue, X.; Matsumoto, M.; Tezuka, H.; Suzuki, T.; Ohishi, Y. Mid-infrared supercontinuum generation spanning 2.0 to 15.1 μm in a chalcogenide step-index fiber. Opt. Lett. 2016, 41, 2117–2120. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Yu, Y.; Zhai, C.; Qi, S.; Wang, Y.; Yang, A.; Gai, X.; Wang, R.; Yang, Z.; Luther-Davies, B. High brightness 2.2–12 μm mid-infrared supercontinuum generation in a nontoxic chalcogenide step-index fiber. J. Am. Ceramic Soc. 2016, 99, 2565–2568. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, B.; Gai, X.; Zhai, C.; Qi, S.; Guo, W.; Yang, Z.; Wang, R.; Choi, D.-Y.; Madden, S.; et al. 1.8–10 μm mid-infrared supercontinuum generated in a step-index chalcogenide fiber using low peak pump power. Opt. Lett. 2015, 40, 1081–1084. [Google Scholar] [CrossRef] [PubMed]
- Karim, M.R.; Rahman, B.M.A.; Agrawal, G.P. Mid-infrared supercontinuum generation using dispersion-engineered Ge11.5As24Se64.5 chalcogenide channel waveguide. Opt. Express 2015, 23, 6903–6914. [Google Scholar] [CrossRef] [PubMed]
- Yeom, D.-I.; Mägi, E.C.; Lamont, M.R.E.; Roelens, M.A.F.; Fu, L.; Eggleton, B.J. Low-threshold supercontinuum generation in highly nonlinear chalcogenide nanowires. Opt. Lett. 2008, 33, 660–662. [Google Scholar] [CrossRef] [PubMed]
- Psaila, N.D.; Thomson, R.R.; Bookey, H.T.; Shen, S.X.; Chiodo, N.; Osellame, R.; Cerullo, G.; Jha, A.; Kar, A.K. Supercontinuum generation in an ultrafast laser inscribed chalcogenide glass waveguide. Opt. Express 2007, 15, 15776–15781. [Google Scholar] [CrossRef]
- Lamont, M.R.E.; Luther-Davies, B.; Choi, D.-Y.; Madden, S.; Eggleton, B.J. Supercontinuum generation in dispersion engineered highly nonlinear (γ = 10 /W/m) As2S3 chalcogenide planar waveguide. Opt. Express 2008, 16, 14938–14944. [Google Scholar] [CrossRef] [PubMed]
- Gai, X.; Choi, D.-Y.; Madden, S.; Yang, Z.; Wang, R.; Luther-Davies, B. Supercontinuum generation in the mid-infrared from a dispersion-engineered As2S3 glass rib waveguide. Opt. Lett. 2012, 37, 3870–3872. [Google Scholar] [CrossRef] [PubMed]
- Cherukulappurath, S.; Guignard, M.; Marchand, C.; Smektala, F.; Boudebs, G. Linear and nonlinear optical characterization of tellurium based chalcogenide glasses. Opt. Commun. 2004, 242, 313–319. [Google Scholar] [CrossRef]
- Belykh, A.V.; Efimov, O.M.; Glebov, L.B.; Matveev, Y.A.; Mekryukov, A.M.; Mikhailov, M.D.; Richardson, K.A. Photo-structural Transformation of Chalcogenide glasses under Nonlinear Absorption of Laser Radiation. J. Non-Cryst. Solids 1997, 213, 330–335. [Google Scholar] [CrossRef]
- Tanaka, K. Photoinduced Deformation in Chalcogenide Glasses. In Amorphous Chalcogenides, Advances and Applications; Wang, R., Ed.; Pan Stanford Publishing: Boca Raton, FL, USA, 2014. [Google Scholar]
- Buff, A. A Study of Crystallization Behavior in Phase Separated Chalcogenide Glasses. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2016. [Google Scholar]
- Fauvel, V. Synthesis and Mechanical Properties of Chalcogenide Glass-Ceramics. Master’s Thesis, ENSIL-ENSCI Ecole d’Ingénieurs de Limoges, Limoges, France, 2018. [Google Scholar]
- Kang, M.; Swisher, A.M.; Pogrebnyakov, A.V.; Liu, L.; Kirk, A.; Aiken, S.; Sisken, L.; Lonergan, C.; Cook, J.; Malendevych, T.; et al. Ultra-Low Dispersion Multicomponent Thin Film Chalcogenide Glass for Broadband Gradient Index Optics. Adv. Mater. 2018, 30, 1803628. [Google Scholar] [CrossRef] [PubMed]
- Yadav, A.; Kang, M.; Goncalves, C.; Sisken, L.; Blanco, C.; Arias, C.; Riveiro-Baleine, C.; Richardson, K. Index and Dispersion engineering of GeSe2-As2Se3-PbSe chalcogenide glasses through purification. 2018; submitted. [Google Scholar]
- Kang, M.; Sisken, L.; Cook, J.; Blanco, C.; Richardson, M.; Mingareev, I.; Richardson, K. Refractive Index Patterning of Infrared Glass Ceramics through Laser-Induced Vitrification. Opt. Mater. Express 2018, 8, 2722–2733. [Google Scholar] [CrossRef]
- Sisken, L. Laser-Induced Crystallization Mechanisms in Chalcogenide Glass Materials for Advanced Optical Functionality. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2017. [Google Scholar]
- Sisken, L.; Smith, C.; Buff, A.; Kang, M.; Chamma, K.; Wachtel, P.; Musgraves, J.; Rivero-Baleine, C.; Kirk, A.; Kalinowski, M.; et al. Evidence of spatially selective refractive index modification in 15GeSe2-45As2Se3-40PbSe glass through correlation of structure and optical property measurements for GRIN applications. Opt. Mater. Express 2017, 7, 3077–3092. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, X.; Ren, J.; Yunxia, Y.; Chen, G.; Ma, H.; Adam, J. Glass formation and properties of chalcogenide in a GeSe2-As2Se3-PbSe system. J. Am. Ceram. Soc. 2007, 90, 1500–1503. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, X.; Yang, G.; Xu, Y.; Ma, H.; Adam, J.; Gu, Z.; Chen, G. Micro-crystallization of the infrared transmitting chalcogenide glass in GeSe2-As2Se3-PbSe system. Ceram. Int. 2009, 35, 83–86. [Google Scholar] [CrossRef]
- Richardson, K.; Kang, M.; Sisken, L.; Yadav, A.; Blanco, C.; Antia, M.; Novak, S.; Gleason, B.; Smith, C.; Buff, A.; et al. Advances in infrared GRIN: A review of novel materials towards components and devices. Proc. SPIE 2018, 10627, 106270A. [Google Scholar]
- Richardson, K.; Buff, A.; Smith, C.; Sisken, L.; Musgraves, J.; Wachtel, P.; Mayer, T.; Swisher, A.; Pogrebnyakov, A.; Kang, M.; et al. Engineering novel infrared glass ceramics for advanced optical solutions. Proc. SPIE 2016, 9822, 982205. [Google Scholar]
- Yadav, A.; Kang, M.; Smith, C.; Lonergan, J.; Buff, A.; Sisken, L.; Chamma, K.; Blanco, C.; Caraccio, J.; Mayer, T.; et al. Influence of phase-separation on structure-property relationships in the (GeSe2-3As2Se3)1-xPbSex glass system. Phys. Chem. Glasses-B 2017, 58, 115–126. [Google Scholar] [CrossRef]
- Yadav, A.; Buff, A.; Kang, M.; Sisken, L.; Smith, C.; Lonergan, J.; Blanco, C.; Antia, M.; Driggers, M.; Kirk, A.; et al. Melt property variation in GeSe2-As2Se3-PbSe glass ceramics for infrared gradient refractive index (GRIN) applications. Int. J. Appl. Glass Sci. 2018. [Google Scholar] [CrossRef]
- Hu, J.; Feng, N.; Carlie, N.; Petit, L.; Wang, J.; Agarwal, A.; Richardson, K.; Kimerling, L. Demonstration of Low-Loss High-Index-Contrast Planar Glass Waveguides with Graded-Index Cladding Layers. Opt. Express 2007, 15, 14566–14572. [Google Scholar] [CrossRef] [PubMed]
- Lenz, G.; Zimmermann, J.; Katsufuji, T.; Lines, M.E.; Hwang, H.Y.; Spalter, S.; Slusher, R.E.; Cheong, S.-W.; Sanghera, J.S.; Aggarwal, I.D. Large Kerr effect in bulk Se-based chalcogenide glasses. Opt. Lett. 2000, 25, 254–256. [Google Scholar] [CrossRef] [PubMed]
- Prasad, A.; Zha, C.-J.; Wang, R.-P.; Smith, A.; Madden, S.; Luther-Davies, B. Properties of GexAsySe1-x-y glasses for all-optical signal processing. Opt. Express 2008, 16, 2804–2815. [Google Scholar] [CrossRef] [PubMed]
- Busse, L.E.; Moon, J.A.; Sanghera, J.S.; Aggarwal, I.D. Chalcogenide fibers deliver high IR power. Laser Focus World 1996, 32, 143–150. [Google Scholar]
- Aggarwal, I.D.; Sanghera, J.S. Development and applications of chalcogenide glass optical fibers at NRL. J. Optoelectron. Adv. Mater. 2002, 4, 665–678. [Google Scholar]
- Kulkarni, O.P.; Xia, C.; Lee, D.J.; Kumar, M.; Kuditcher, A.; Islam, M.N.; Terry, F.L.; Freeman, M.J., Jr.; Aitken, B.G.; Currie, S.; et al. Third order cascaded Raman wavelength shifting in chalcogenide fibers and determination of Raman gain coefficient. Opt. Express 2006, 14, 7924–7930. [Google Scholar] [CrossRef] [PubMed]
- Papagiakoumou, E.; Papadopoulos, D.N.; Serafetinides, A.A. Pulsed infrared radiation transmission through chalcogenide glass fibers. Opt. Commun. 2007, 276, 80–86. [Google Scholar] [CrossRef]
- Boudebs, G.; Sanchez, F.; Troles, J.; Smektala, F. Nonlinear optical properties of chalcogenide glasses: Comparison between Mach–Zehnder interferometry and Z-scan techniques. Opt. Commun. 2001, 199, 425–433. [Google Scholar] [CrossRef]
- Quémard, C.; Smektala, F.; Couderc, V.; Barthélémy, A.; Lucas, J. Chalcogenide glasses with high non linear optical properties for telecommunications. J. Phys. Chem. Solids 2001, 62, 1435–1440. [Google Scholar] [CrossRef]
- Kumar, P.; Kaur, J.; Tripathi, S.; Sharma, I. Effect of antimony (Sb) addition on the linear and non-linear optical properties of amorphous Ge-Te-Sb thin films. Indian J. Phys. 2017, 91, 1503–1511. [Google Scholar] [CrossRef]
- Waldmann, M.; Musgraves, J.D.; Richardson, K.; Arnold, C.B. Structural properties of solution processed Ge23Sb7S70 glass materials. J. Mater. Chem. 2012, 22, 17848–17852. [Google Scholar] [CrossRef]
- Sohn, B.-U.; Monmeyran, C.; Kimerling, L.C.; Agarwal, A.M.; Tan, D.T.H. Kerr nonlinearity and multi-photon absorption in germanium at mid-infrared wavelengths. Appl. Phys. Lett. 2017, 111, 091902. [Google Scholar] [CrossRef]
- Zou, Y.; Moreel, L.; Lin, H.; Zhou, J.; Li, L.; Danto, S.; Musgraves, J.D.; Richardson, K.; Dobson, K.D.; Birkmire, R.; et al. Solution Processing and Resist-Free Nanoimprint Fabrication of Thin Film Chalcogenide Glass Devices: Inorganic-Organic Hybrid Photonic Integration. Adv. Opt. Mater. 2014, 2, 759–764. [Google Scholar] [CrossRef]
- Li, C.; Novak, S.; Richardson, K.; Deng, W. Electrospray deposition of quantum dot-doped Ge23Sb7S70 chalcogenide glass films. Thin Solid Films 2017, 624, 194–199. [Google Scholar] [CrossRef]
- Novak, S.; Li, C.; Borodinov, N.; Han, Z.; Monmeyran, C.; Patel, N.; Du, Q.; Lumdee, C.; Kik, P.; Deng, W.; et al. Electrospray deposition of uniform thickness Ge23Sb7S70 and As40S60 chalcogenide glass films. J. Vis. Exp. 2016. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Rouxel, T.; Troles, J.; Bureau, B.; Boussard-Plédel, C.; Houizot, P.; Sangleboeuf, J.-C. Viscosity of As2Se3 glass during the fiber drawing process. J. Am. Ceram. Soc. 2011, 94, 2408–2411. [Google Scholar] [CrossRef]
- Musgraves, J.; Wachtel, P.; Novak, S.; Wilkinson, J.; Richardson, K. Composition dependence of the viscosity and other physical properties in the arsenic selenide glass system. J. Appl. Phys. 2011, 110, 063503. [Google Scholar] [CrossRef]
- Schott Advanced Optics. Available online: https://www.schott.com/advanced_optics/english/products/optical-materials/ir-materials/infrared-chalcogenide-glasses/index.html (accessed on 1 September 2018).
- Schott Zerodur. Available online: https://www.schott.com/d/advanced_optics/e532f55f-d6c1-4748-8c60-886eaca1daf5/1.2/schott-zerodur-general-may-2013-eng.pdf (accessed on 1 September 2018).
- Lin, C.; Calvez, L.; Ying, L.; Chen, F.; Song, B.; Shen, X.; Dai, S.; Zhang, X. External influence on third-order optical nonlinearity of transparent chalcogenide glass-ceramics. Appl. Phys. A 2011, 104, 615–620. [Google Scholar] [CrossRef]
- Hubert, M.; Delaizir, G.; Monnier, J.; Godart, C.; Ma, H.; Zhang, X.; Calvez, L. An innovative approach to develop highly performant chalcogenide glasses and glass-ceramics transparent in the infrared range. Opt. Express 2011, 19, 23513–23522. [Google Scholar] [CrossRef] [PubMed]
- Calvez, L.; Ma, H.; Lucas, J.; Zhang, X. Preparation and properties of glasses and glass-ceramics based on GeSe2-Sb2Se3 and halides. Phys. Chem. Glasses Eur. J. Glass Sci. Technol. Part B 2006, 47, 142–145. [Google Scholar]
- Calvez, L.; Ma, H.; Lucas, J.; Zhang, X. Selenium-Based Glasses and Glass Ceramics Transmitting Light from the Visible to the Far-IR. Adv. Mater. 2007, 19, 129–132. [Google Scholar] [CrossRef]
- Ghosh, G. Sellmeir coefficients and dispersion of thermo-optic coefficients for some optical glasses. Appl. Opt. 1997, 36, 1540–1546. [Google Scholar] [CrossRef] [PubMed]
- Gibson, D.; Bayya, S.; Nguyen, V.; Sanghera, J.; Kotov, M.; Drake, G. GRIN optics for multispectral infrared imaging. Proc. SPIE 2015, 9451, 94511P. [Google Scholar]
- Mizrahi, V.; Delong, K.; Stegeman, G.; Saifi, M.; Andrejco, M. 2-Photon Absorption as a Limitation to All-Optical Switching. Opt. Lett. 1989, 14, 1140–1142. [Google Scholar] [CrossRef] [PubMed]
- Devilliers, C.; Kroedel, M. CESIC: A new technology for lightweight and cost effective space instrument structures and mirrors. SPIE Proc. 2005, 5868, 58680F. [Google Scholar]
- Mirov, S.B.; Fedorov, V.V.; Martyshkin, D.; Moskalev, I.S.; Mirov, M.; Vasilyev, S. Progress in Mid-IR Lasers Based on Cr and Fe-Doped II-VI Chalcogenides. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 1601719. [Google Scholar] [CrossRef]
- Martyshkin, D.V.; Goldstein, J.T.; Fedorov, V.V.; Mirov, S.B. Crystalline Cr2+:ZnSe/chalcogenide glass composites as active mid-IR materials. Opt. Lett. 2011, 36, 1530–1532. [Google Scholar] [CrossRef] [PubMed]
- Karaksina, E.V.; Shiryaev, V.S.; Ketkova, L.A. Preparation of composite materials for fiber optics based on chalcogenide glasses containing ZnS(ZnSe):Cr(2+) crystals. J. Non-Cryst. Solids 2013, 377, 220–224. [Google Scholar] [CrossRef]
- Labadie, L.; Abel-Tiberini, L.; LeCoarer, E.; Vigreux-Bercovici, C.; Arezki, B.; Barillot, M.; Broquin, J.; Delboulbe, A.; Kern, P.; Kirschner, V.; et al. Recent progress in mid-infrared integrated optics for nulling interferometry. SPIE Proc. 2006, 6268, 62682E. [Google Scholar]
- O’Donnell, M.D.; Seddon, A.B.; Furniss, D.; Tikhomirov, V.K.; Rivero-Baleine, C.; Ramme, M.; Stegeman, R.; Stegeman, G.; Richardson, K.; Stolen, R.; et al. Tellurite and fluoro-tellurite glasses for fiberoptic Raman amplifiers: Glass characterization, optical properties, Raman gain, preliminary fiberization and fiber characterization. J. Am. Ceram. Soc. 2007, 90, 1448–1457. [Google Scholar] [CrossRef]
- O’Donnell, M.D.; Richardson, K.; Stolen, R.; Rivero-Baleine, C.; Cardinal, T.; Couzi, M.; Furniss, D.; Seddon, A.B. Raman gain of selected tellurite glasses for high power IR fiber lasers calculated from spontaneous scattering spectra. Opt. Mater. 2008, 30, 946–951. [Google Scholar] [CrossRef]
- Wang, T.; Venkatram, N.; Gosciniak, J.; Cui, Y.; Qian, G.; Ji, W.; Tan, D. Multi-photon absorption and third-order nonlinearity in silicon at mid-infrared wavelengths. Opt. Express 2013, 21, 32192–32198. [Google Scholar] [CrossRef] [PubMed]
- Bristow, A.; Rotenberg, N.; van Driel, H. Two-photon absorption and Kerr coefficients of silicon for 850–2200 nm. Appl. Phys. Lett. 2007, 90, 191104. [Google Scholar] [CrossRef]
- Kato, T.; Suetsugu, Y.; Takagi, M.; Sasaoka, E.; Nishimura, M. Measurements of the nonlinear refractive index in optical fiber by the cross-phase-modulation method with depolarized pump light. Opt. Lett. 1995, 20, 988–990. [Google Scholar] [CrossRef] [PubMed]
- Gholami, F.; Zlatanovic, S.; Simic, A.; Liu, L.; Borlaug, D.; Alic, N.; Nezhad, M.; Fainman, Y.; Radic, S. Third-order nonlinearity in silicon beyond 2350 nm. Appl. Phys. Lett. 2011, 99, 081102. [Google Scholar] [CrossRef]
| Form | Composition (mol%) | n1 at (λ) | λ = 1.06 µm | λ = 1.55 µm | Ref | ||
|---|---|---|---|---|---|---|---|
| n2 (×10−15 cm2/W) | α2 (cm/GW) | n2 (×10−15 cm2/W) | α2 (cm/GW) | ||||
| Bulk | As40Se60 | 2.38 (1.33 µm) | 4 | 28 | |||
| As40S40Se20 | 2.47 (1.33 µm) | 8 | <0.01 | 28 | |||
| As24S38Se38 | 2.32 (1.33 µm) | 15 (1.3 µm) | 0.06 | 17.5 | <0.05 | 28 | |
| Ge30As11Se49Te10 | 2.50 (1.33 µm) | 14 (1.3 µm) | 0.4 | 11 | 0.16 | 28 | |
| As30Se63Sb4Sn3 | 2.80 (1.33 µm) | 0.52 | 10 | 0.17 | 28 | ||
| Ge20Se80 | 0.372 | 6.01 × 10−6 | 7 | ||||
| Ge20Sb5Se75 | 0.429 | 3.14 × 10−6 | 7 | ||||
| Ge20Sb10Se70 | 0.622 | 4.78 × 10−6 | 7 | ||||
| As40Se60 | 1 | 16 × 10−6 | 7 | ||||
| As40S60 | 2.430 (1.55 µm) | 35 (1.35 µm) | 28.5 | 26,51 | |||
| Ge11.5As24Se64.5 | 2.634 (1.55 µm) | 88.3 (1.35 µm) | 79 | 26 | |||
| Ge15Sb10Se75 | 2.598 (1.55 µm) | 76.7 (1.35 µm) | 7.5 | 26 | |||
| Ge15Sb15Se70 | 2.690 (1.55 µm) | 137 (1.35 µm) | 10 | 26 | |||
| Ge20Se80 | 1.3 | 74 | |||||
| GeSe6 | 1.7 | 74 | |||||
| Ge11As11Se78 | 2.2 | 51,74 | |||||
| Ge10As10Se70Te10 | 1.9 | 51 | |||||
| Ge10As10Se60Te20 | 2.0 | 51 | |||||
| (GeSe2)90(Sb2Se3)10 | 2.51 (1.064 µm) | 8.9 | 10.7 | 21 | |||
| (GeSe2)60(Sb2Se3)40 | 2.85 (1.064 µm) | 14.8 | 12.4 | 21 | |||
| (GeSe2)40(Sb2Se3)60 | 2.51 (1.064 µm) | 21.2 | 21.5 | 21 | |||
| (GeSe4)0.5(AsSe3)0.5 | 2.2 | 2.7 | 19 | ||||
| GeAs2Se3 | 1.85 | 5.9 | 19 | ||||
| Ge10As10Se80 | 2.2 | 75 | |||||
| Ge10As20Se70 | 1.40 | 75 | |||||
| Ge20As40Se40 | 1.85 | 75 | |||||
| Composition (mol%) | n1 at λ = 4.515 µm | n2 at λ = 4.515 µm (×10−15 cm2/W) | α2 at λ = 4.515 µm (×10−3 cm5/W3) | Ref | |||
| GeSe2-As2Se3-PbSe(20 mol% PbSe) | ~ 2.85 | 7.14 | 4.50 | 54 | |||
| GeSe2-As2Se3-PbSe(40 mol% PbSe) | ~ 3.04 | 11.17 | 11.05 | 54,58–60 | |||
| Form | Composition (mol%) | n1 at λ = 1.55 µm | n2 at λ = 1.55 µm (×10−21 cm2/W) | α2 at λ = 1.55 µm (cm/GW) | Ref | ||
| Film | Ge20Te80 | 2.38 | 6.4 | 76 | |||
| Ge20Te78Sb2 | 2.43 | 7.5 | 76 | ||||
| Ge20Te76Sb4 | 2.48 | 8.7 | 76 | ||||
| Ge20Te70Sb10 | 2.62 | 12.3 | 76 | ||||
| Ge23Sb7S70 | 2.17 | 3710 | 0.01 | 20 | |||
| Ge23Sb7S70 | 9.3 (at 1.58 µm) | 77 | |||||
| Composition (mol%) | n1 at λ = 4.515 µm | n2 at λ = 4.515 µm | α2 at λ = 4.515 µm | Ref | |||
| GeSe2-As2Se3-PbSe (40 mol% PbSe) | ~ 3.14 | 56 | |||||
| Form | Composition (mol%) | Measurement λ ( µm) | Laser Damage (MW/cm2) | Ref |
|---|---|---|---|---|
| Bulk | Ge28Sb12Se60 | 1.5 | >1000 | 68 |
| GexAsySe1-x-y | 1.064 | 1000–4000 | 69 | |
| Ge23Sb7S70 | 1.06 | 7200 | 27 | |
| Ge18Ga5Sb7S70 | 1.06 | 6300 | 27 | |
| Ge18Ga5Sb7S68Se2 | 1.06 | 6000 | 27 | |
| Ge18Ga5Sb7S65Se5 | 1.06 | 5400 | 27 | |
| As24S38Se38 | 1.06 | 3500 | 27 | |
| As2S3 | 1.06 | 8400 * | 27 | |
| GeAs2Se2 | 1.064 | 5500–6000 | 19 | |
| Fiber | As2S3 | 3.5 | 200 | 70 |
| As2S3 | 5.4 | 1000 | 71 | |
| As2S3 | 1.5 | 1000 | 72 | |
| As2S3 | 1.064 | 1800 | 73 | |
| As-Se-Te | 1.064 | 130 | 73 | |
| As-Se-Te | 2.94 | 30.6 | 73 |
| Composition & FormOptical Constant | 20mol% PbSe | 40mol% PbSe | ||
|---|---|---|---|---|
| Bulk | Bulk | Film | ||
| Sellmeir coefficient [90] | A = −20.6611 B = 28.5635 C = 0.2312 D = 10.4782 E = 90.4186 | A = 4.1428 B = 4.7716 C = 0.5591 D = 41.6340 E = 168.4897 | A = −17.9359 B = 27.7528 C = 0.1949 D = 1.4171 E = 36.6873 | |
| MWIR (4 µm–6 µm) | Linear refractive index | 2.8387 at λ = 3 µm 2.8245 at λ = 4 µm 2.8164 at λ = 5 µm | 3.0118 at λ = 3 µm 2.9977 at λ = 4 µm 2.9897 at λ = 5 µm | 3.1495 at λ = 3 µm 3.1409 at λ = 4 µm 3.1358 at λ = 5 µm |
| Abbe Number [91] | ||||
| Nonlinear refractive index | 7.14 × 10−6 cm2/GW at λ = 4 µm | 11.17 × 10−6 cm2/GW at λ = 4 µm | In progress | |
| Four-photon absorption coefficient | 4.50 × 10−3 cm5/GW3 at λ = 4 µm | 11.05 × 10−3 cm5/GW3 at λ = 4 µm | In progress | |
| Nonlinear figure of merit [92] | 2.48 × 10−3 at λ = 4 µm | 1.58 × 10−3 at λ = 4 µm | In progress | |
| LWIR (8 µm–12 µm) | Linear refractive index | 2.8007 at λ = 8 µm 2.7906 at λ = 10 µm 2.7793 at λ = 12 µm | 2.9738 at λ = 8 µm 2.9634 at λ = 10 µm 2.9517 at λ = 12 µm | 3.1248 at λ = 8 µm 3.1168 at λ = 10 µm 3.1071 at λ = 12 µm |
| Abbe Number [91] | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goncalves, C.; Kang, M.; Sohn, B.-U.; Yin, G.; Hu, J.; Tan, D.T.H.; Richardson, K. New Candidate Multicomponent Chalcogenide Glasses for Supercontinuum Generation. Appl. Sci. 2018, 8, 2082. https://doi.org/10.3390/app8112082
Goncalves C, Kang M, Sohn B-U, Yin G, Hu J, Tan DTH, Richardson K. New Candidate Multicomponent Chalcogenide Glasses for Supercontinuum Generation. Applied Sciences. 2018; 8(11):2082. https://doi.org/10.3390/app8112082
Chicago/Turabian StyleGoncalves, Claudia, Myungkoo Kang, Byoung-Uk Sohn, Gufan Yin, Juejun Hu, Dawn T. H. Tan, and Kathleen Richardson. 2018. "New Candidate Multicomponent Chalcogenide Glasses for Supercontinuum Generation" Applied Sciences 8, no. 11: 2082. https://doi.org/10.3390/app8112082
APA StyleGoncalves, C., Kang, M., Sohn, B.-U., Yin, G., Hu, J., Tan, D. T. H., & Richardson, K. (2018). New Candidate Multicomponent Chalcogenide Glasses for Supercontinuum Generation. Applied Sciences, 8(11), 2082. https://doi.org/10.3390/app8112082




