Novel Common-Mode Current Suppression Method in Transformerless PV Grid-Connected System
Abstract
:1. Introduction
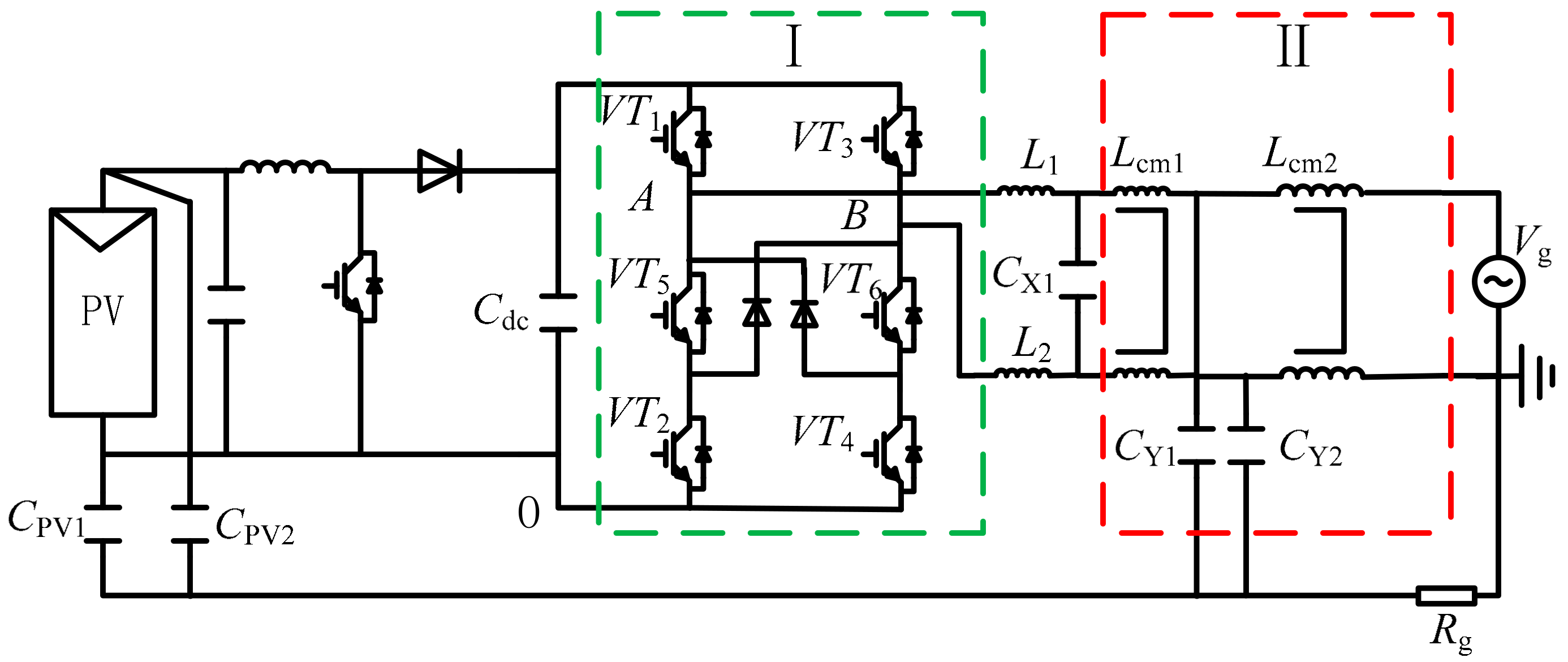
2. Analysis of the CM Current of Non-Isolated Grid-Connected PV System
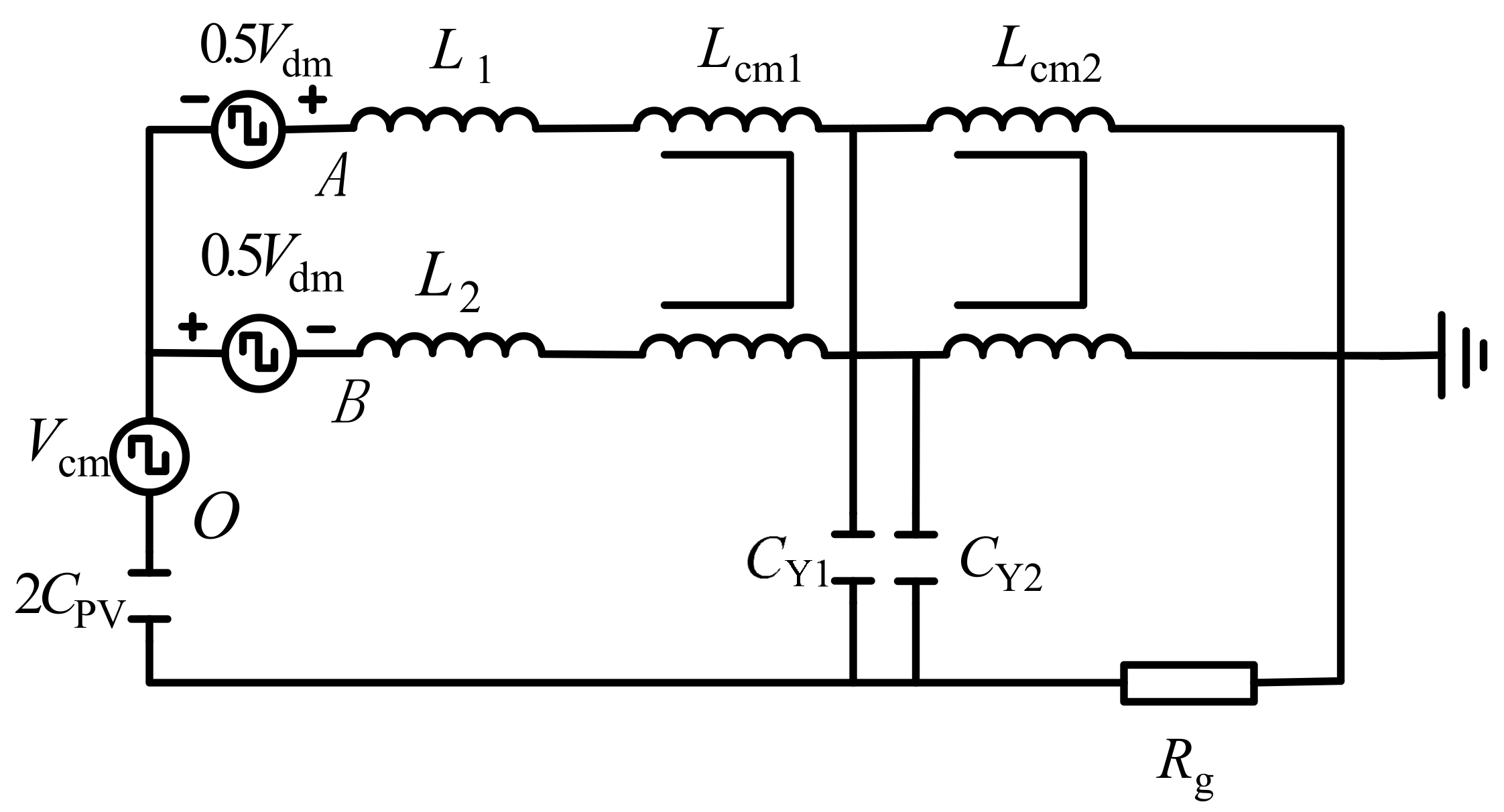
2.1. Analysis of CM Loop Models
2.2. Analysis of CM Current
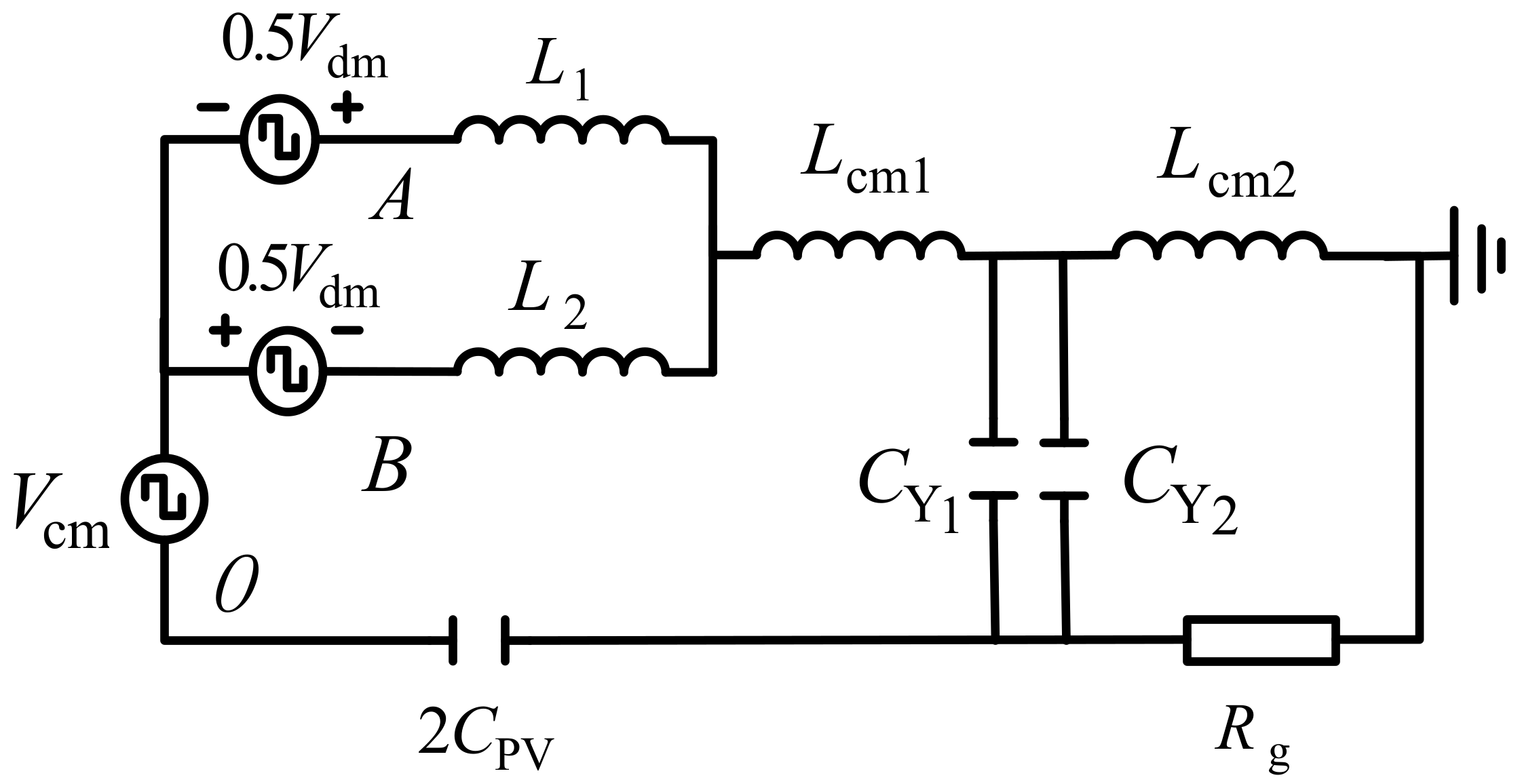
3. Proposed Novel CM Internal Loop Method to Suppression CM Current
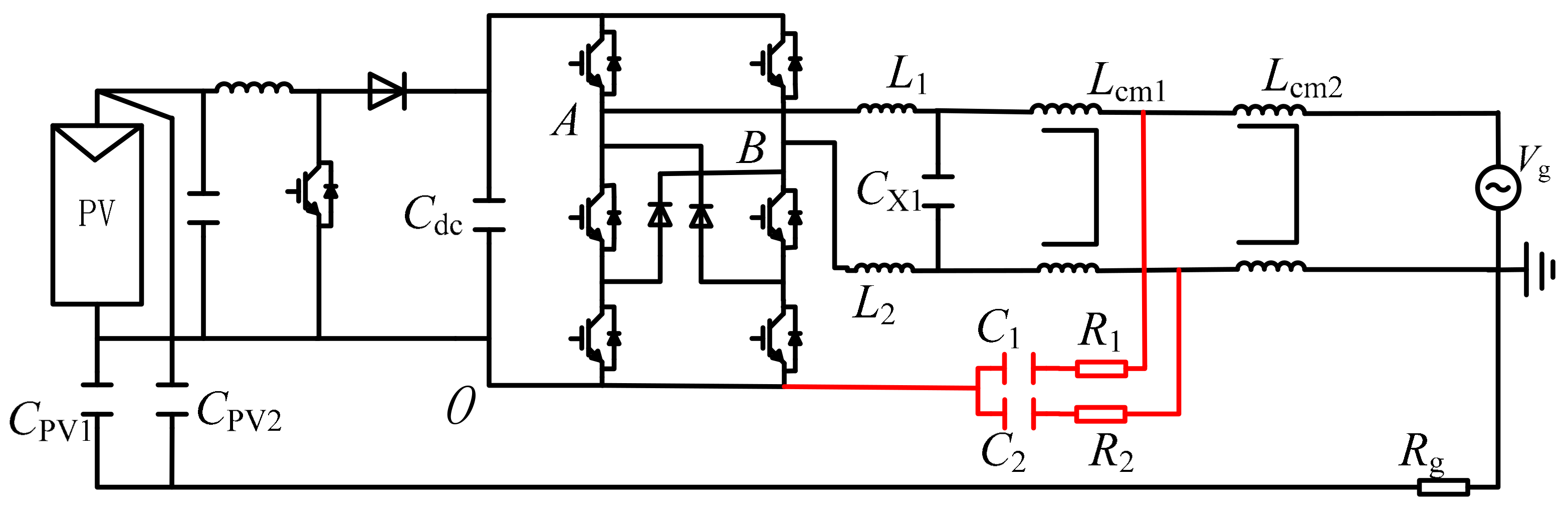
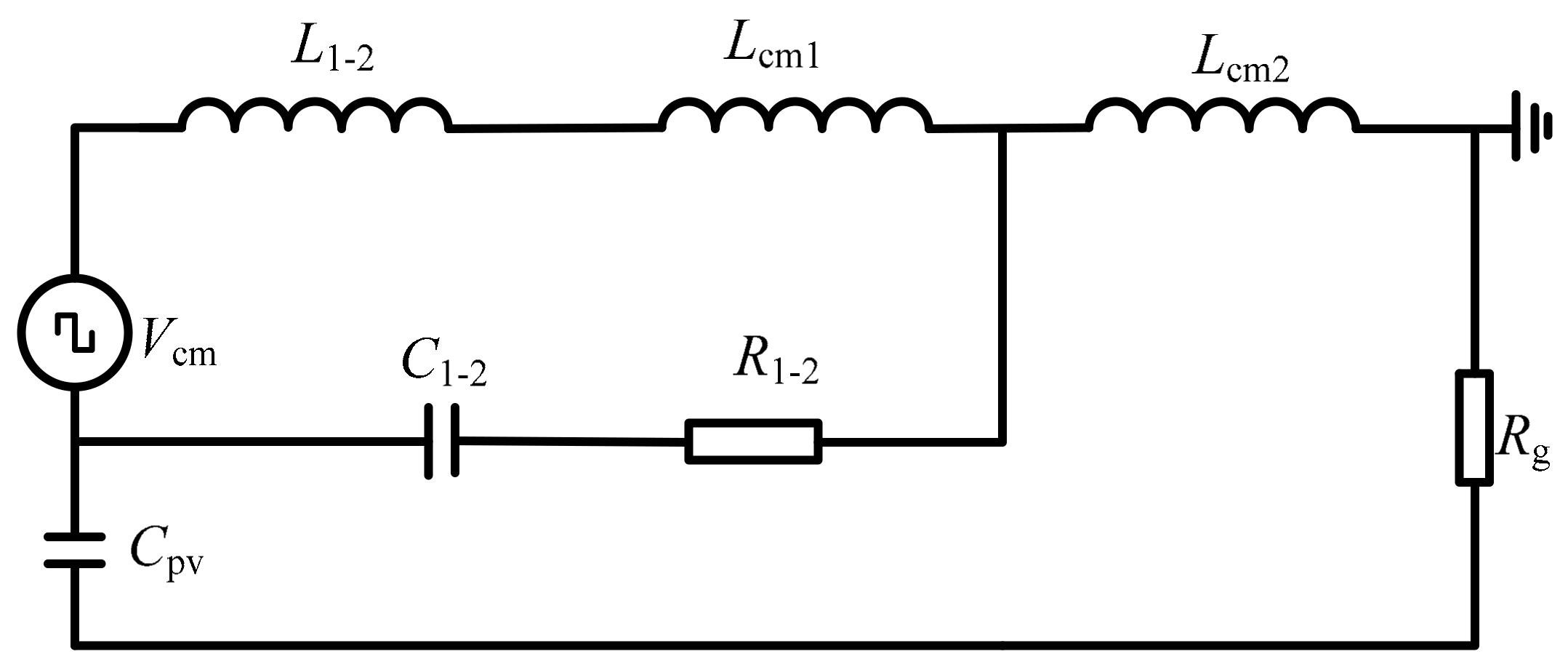
3.1. Traditional Construction of Single CM Internal Loop to Suppress CM Current
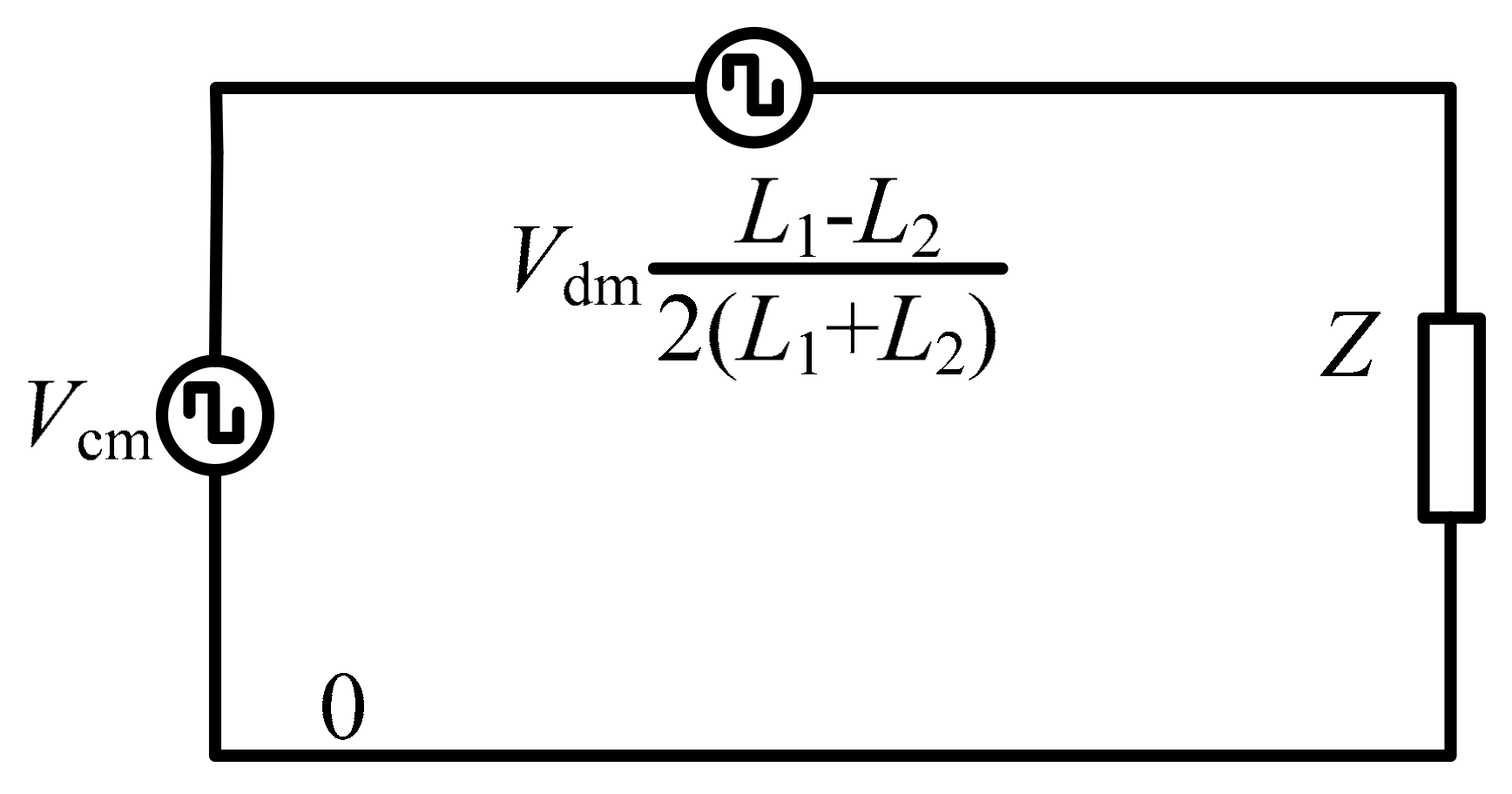
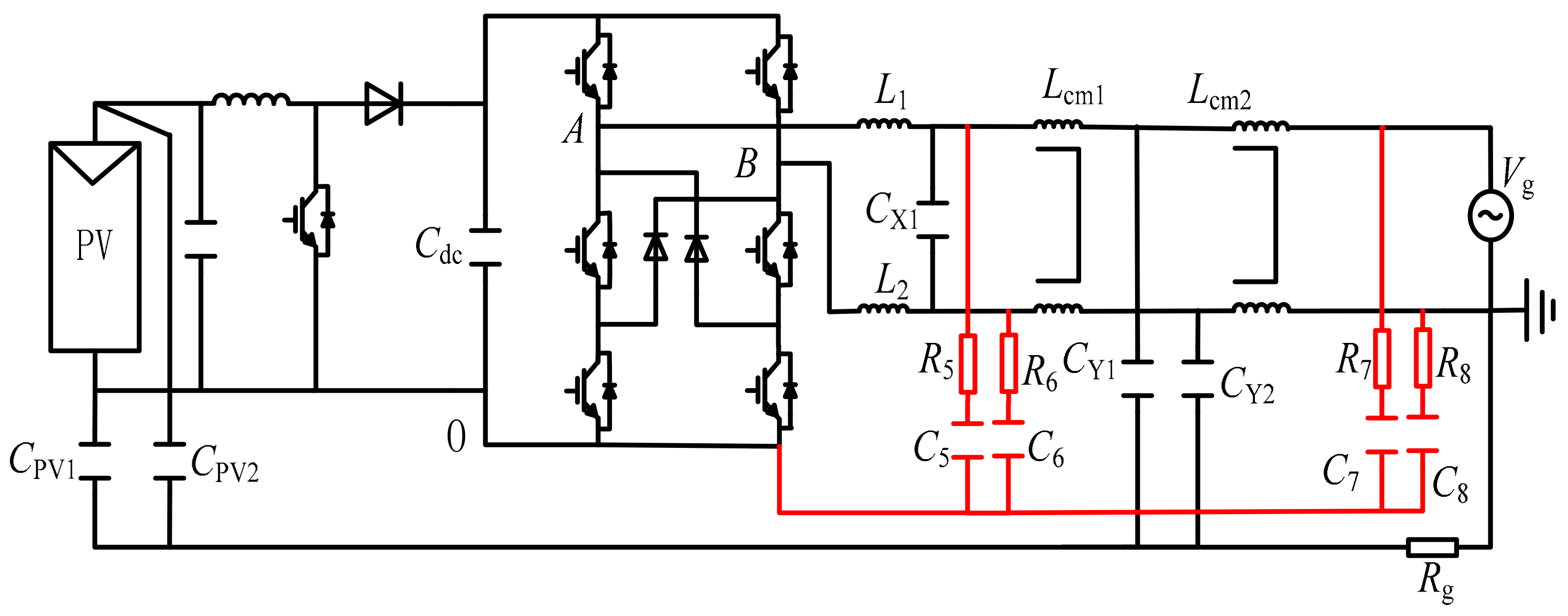
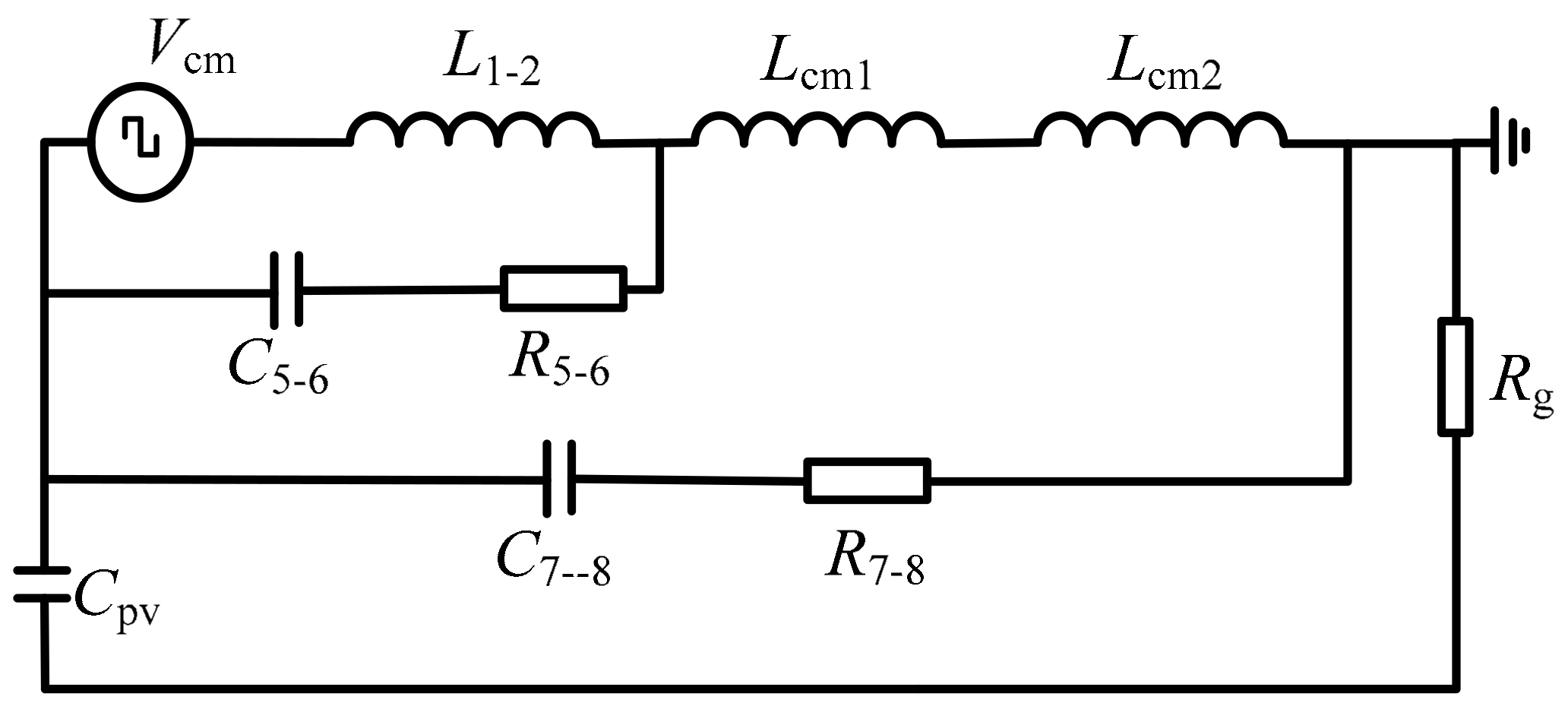
3.2. Proposed Novel Dual CM Internal Loop to Suppress CM Currents
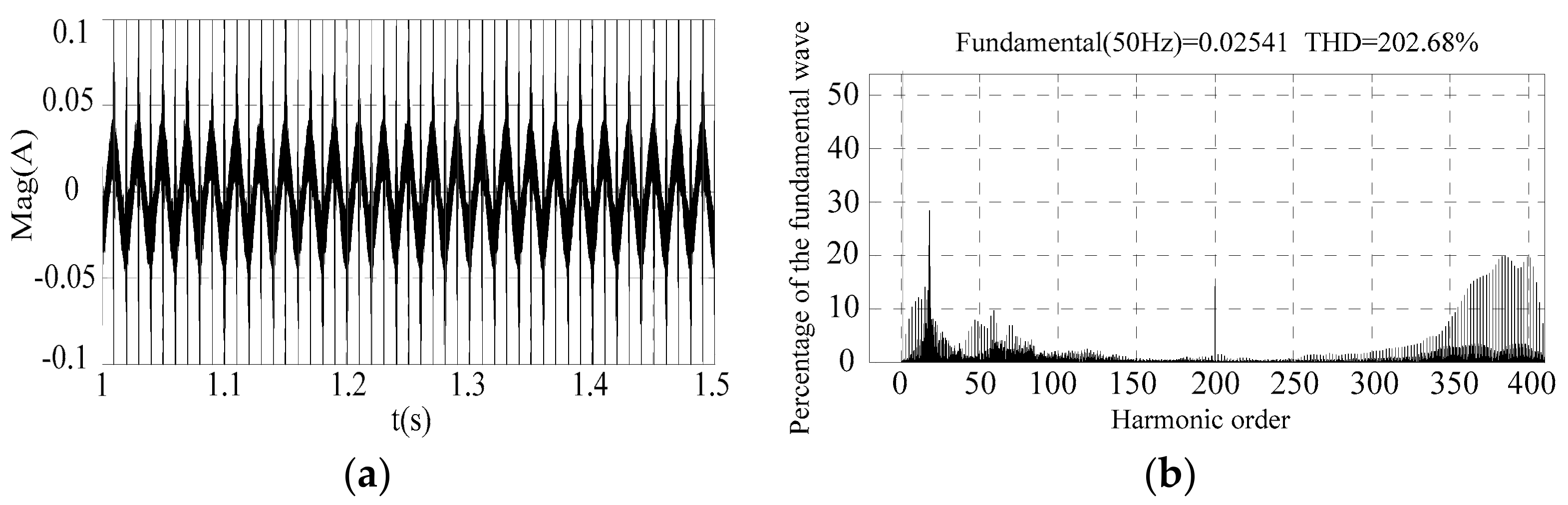
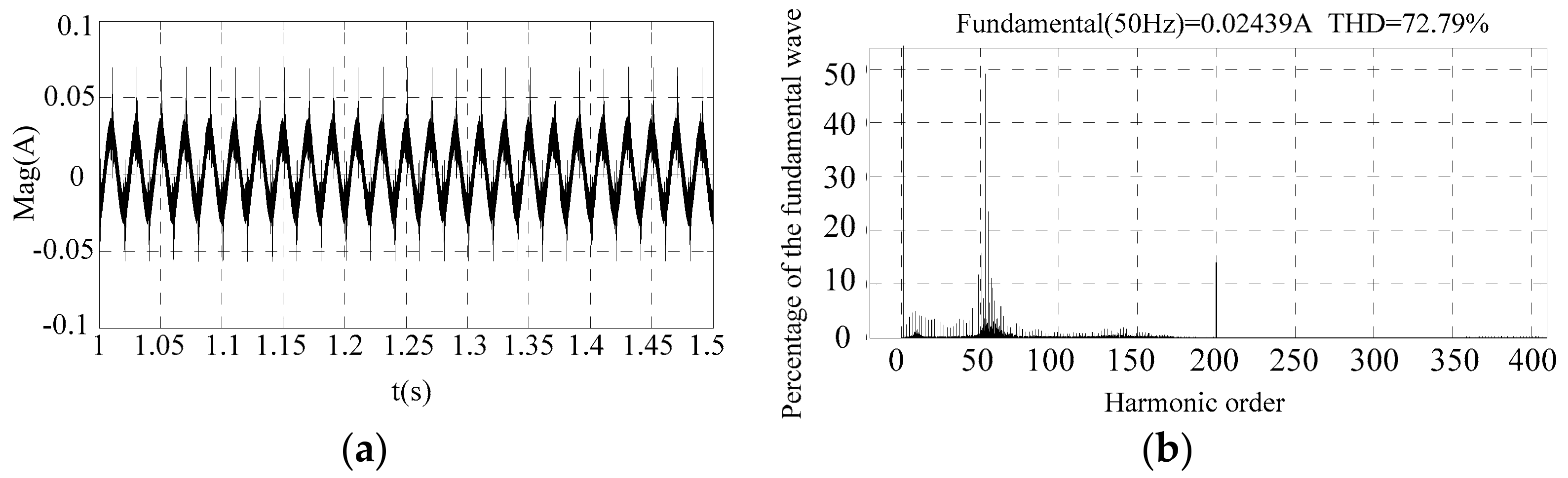
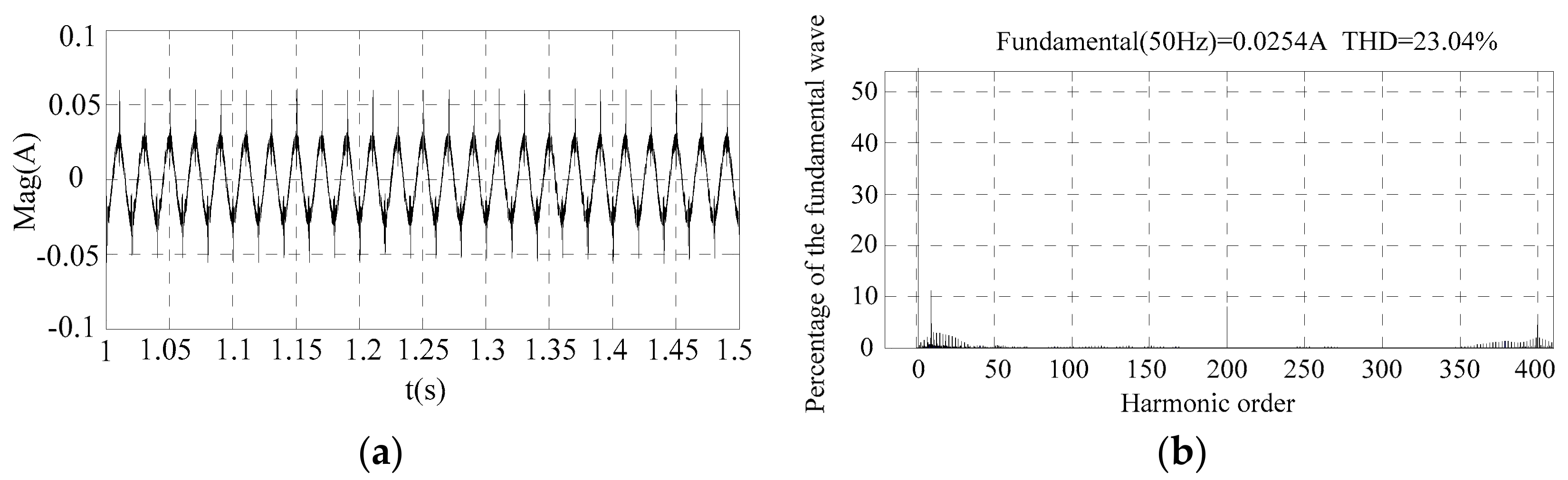
4. Simulation Analysis
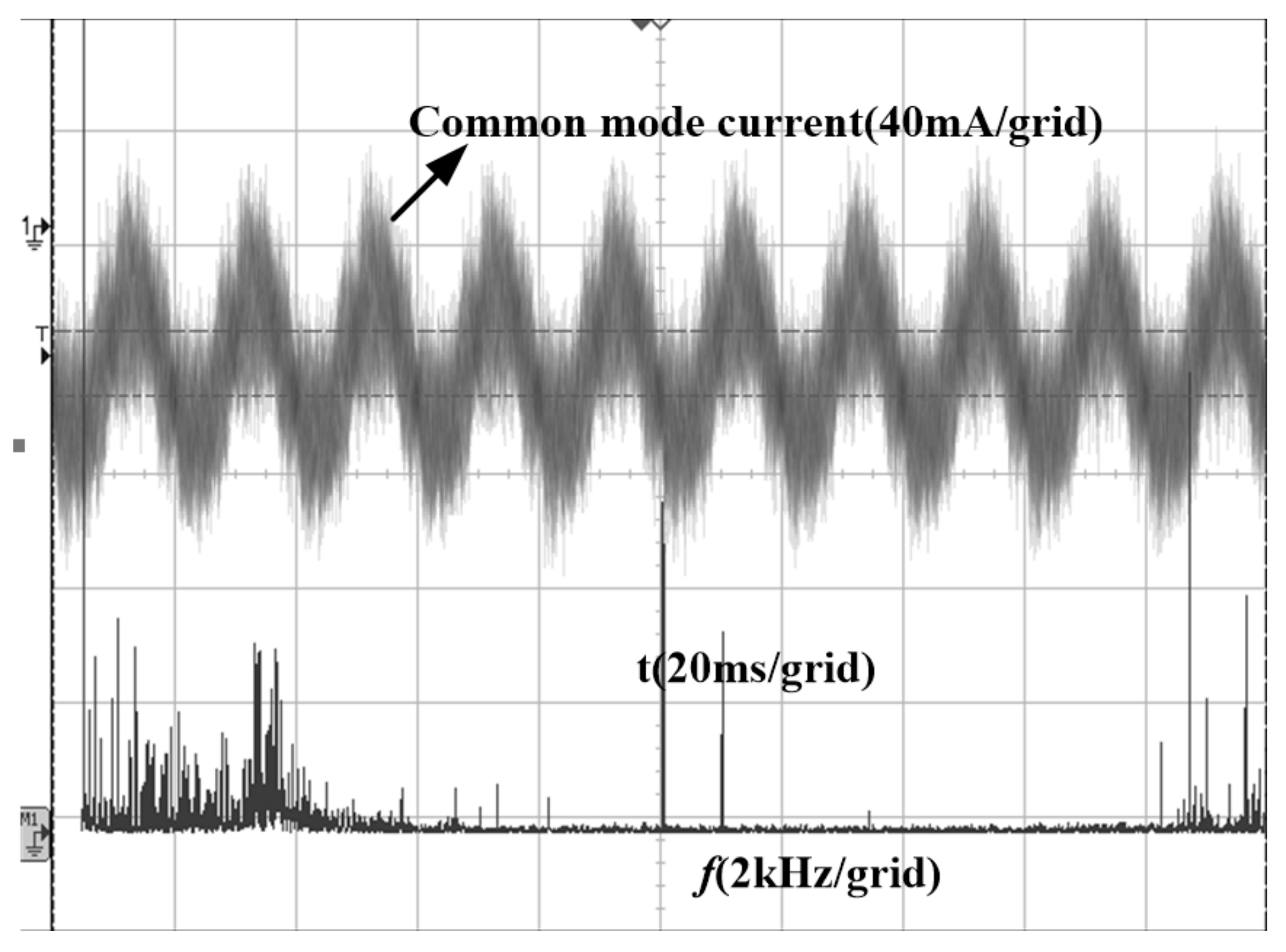
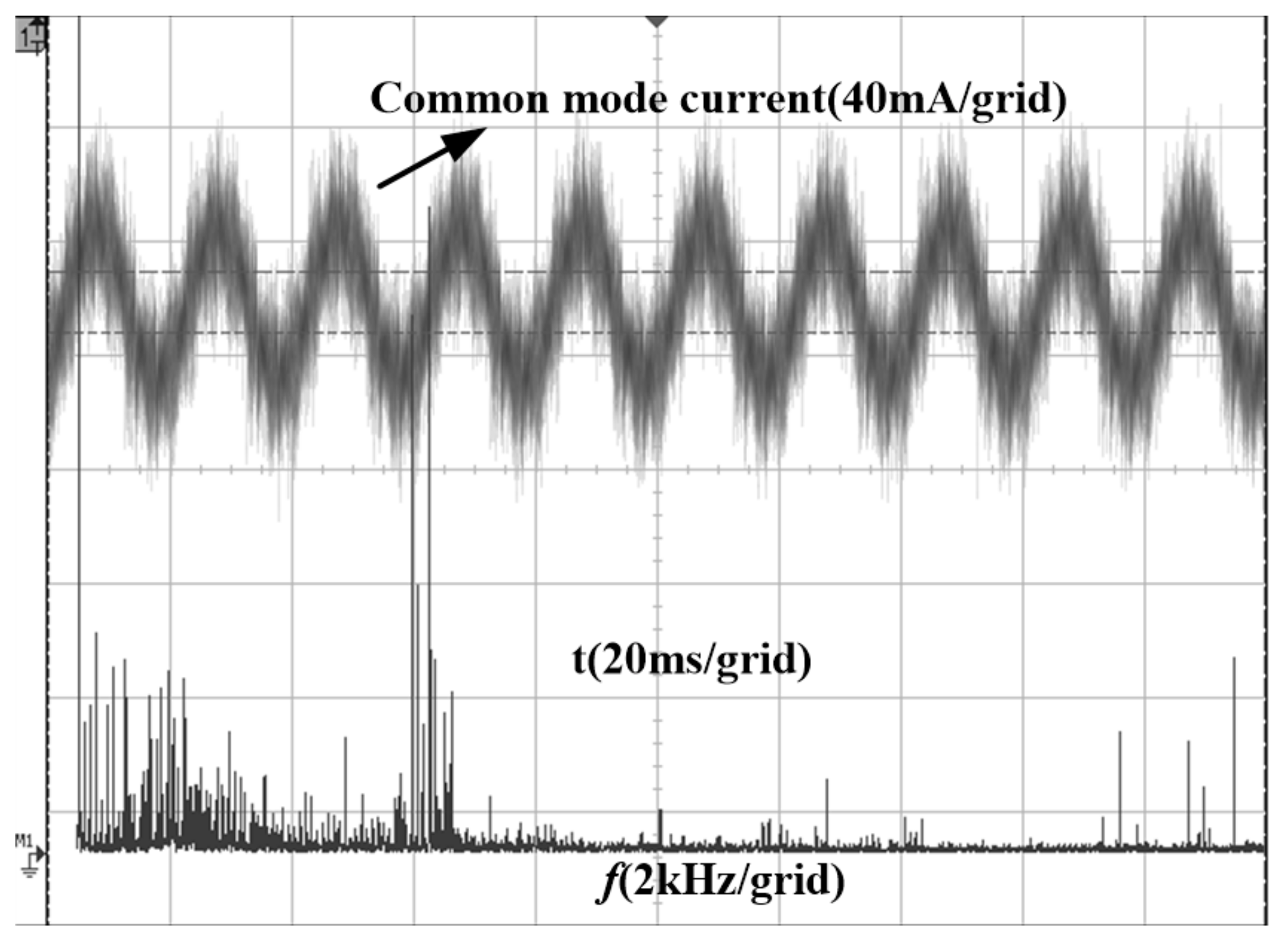
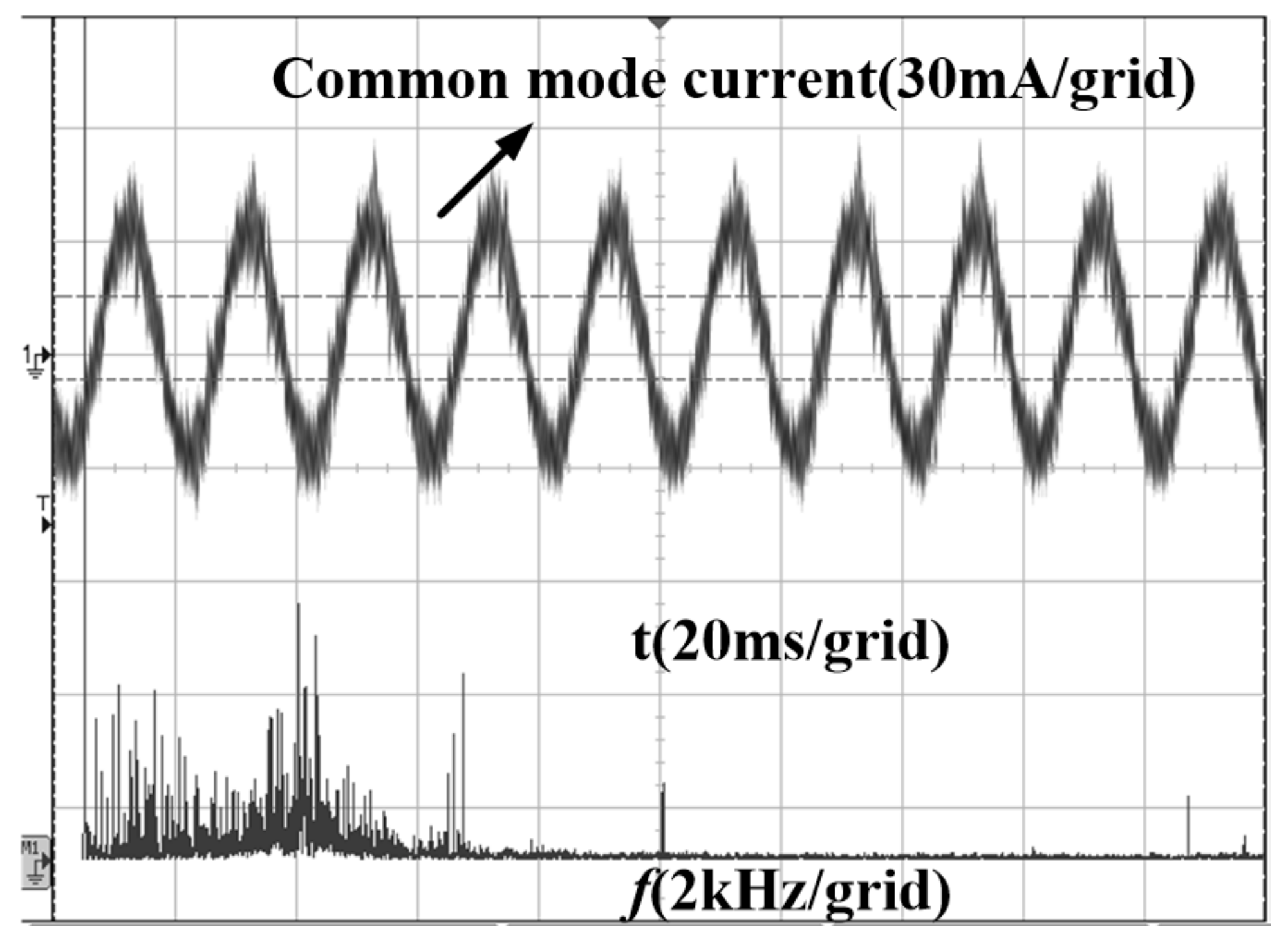
5. Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Khan, S.A.; Guo, Y.; Zhu, J. A High Efficiency Transformerless PV Grid-Connected Inverter with Leakage Current Suppression. In Proceedings of the 9th International Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 20–22 December 2016. [Google Scholar] [CrossRef]
- Grishanov, E.V.; Brovanov, S.V. Aspects of common-mode leakage current suppression in single-phase PV-generation systems. In Proceedings of the 2017 18th International Conference of Young Specialists on Micro/Nanotechnologies and Electron Devices (EDM), Erlagol, Russia, 29 June–3 July 2017; pp. 541–546. [Google Scholar] [CrossRef]
- Zhang, L.; Sun, K.; Xing, Y.; Xing, M. H6 Transformerless Full-Bridge PV Grid-Tied Inverters. IEEE Trans. Power Electron. 2014, 29, 1229–1238. [Google Scholar] [CrossRef]
- Kakosimos, P.; Sarigiannidis, A.; Beniakar, M.; Kladas, A. Investigation of transformerless topologies for renewable energy applications eliminating leakage currents. In Proceedings of the MedPower 2014, Athens, Greece, 2–5 November 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Araujo, S.V.; Zacharias, P.; Mallwitz, R. Highly Efficient Single-Phase Transformerless Inverters for Grid-Connected Photovoltaic Systems. IEEE Trans. Ind. Electron. 2010, 57, 3118–3128. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, D.; Chen, H.; Chen, G. An improved foster model of common-mode inductor and its application in EMI filter design. In Proceedings of the 2018 IEEE International Symposium on Electromagnetic Compatibility and 2018 IEEE Asia-Pacific Symposium on Electromagnetic Compatibility (EMC/APEMC), Singapore, 14–18 May 2018; pp. 461–465. [Google Scholar] [CrossRef]
- Kumar, D.; Pattanaik, A.; Singh, S.K. Comparative assessment of leakage current in a photovoltaic grid connected single phase transformerless inverter system. In Proceedings of the Recent Advances and Innovations in Engineering, Jaipur, India, 9–11 May 2014; pp. 1–7. [Google Scholar] [CrossRef]
- Figueredo, R.S.; de Carvalho, K.C.M.; Ama, N.R.N.; Matakas, L. Leakage current minimization techniques for single-phase transformerless grid-connected PV inverters—An overview. In Proceedings of the 2013 Brazilian Power Electronics Conference, Gramado, Brazil, 27–31 October 2013; pp. 517–524. [Google Scholar] [CrossRef]
- Zografos, D.; Koutroulis, E.; Yang, Y.; Blaabjerg, F. Minimization of leakage ground current in transformerless single-phase full-bridge photovoltaic inverters. In Proceedings of the 2015 17th European Conference on PowerElectronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Yang, B.; Li, W.; Gu, Y.; Cui, W.; He, X. Improved Transformerless Inverter with Common-Mode Leakage Current Elimination for a Photovoltaic Grid-Connected Power System. IEEE Trans. Power Electron. 2012, 27, 752–762. [Google Scholar] [CrossRef]
- Vázquez, N.; Vázquez, J.; Váquero, J.; Hernández, C.; Vázquez, E.; Osorio, R. Integrating Two Stages as a Common-Mode Transformerless Photovoltaic Converter. IEEE Trans. Ind. Electron. 2017, 64, 7498–7507. [Google Scholar] [CrossRef]
- Zarein, A.; Ghazizadeh, M.S.; Mosallanejad, A. An improved transformerless grid connected photovoltaic inverter with reduced leakage current and soft-switching technique. In Proceedings of the 2017 8th Power Electronics, Drive Systems & Technologies Conference (PEDSTC), Mashhad, Iran, 14–16 February 2017; pp. 466–471. [Google Scholar] [CrossRef]
- Ji, B.; Wang, J.; Zhao, J. A high efficiency non-isolated single-phase photovoltaic grid connected inverter with H6-type configuration. Proc. CSEE 2012, 32, 9–15. [Google Scholar]
- Dong, D.; Luo, F.; Boroyevich, D.; Mattavelli, P. Leakage Current Reduction in a Single-Phase Bidirectional AC–DC Full-Bridge Inverter. IEEE Trans. Power Electron. 2012, 27, 4281–4291. [Google Scholar] [CrossRef]
- Liu, S.; You, X.; Li, Y.; Zhang, Y.; Wang, J. Solution of restraining leakage current for single-phase non-isolated PV grid-connection inverters. Acta Energy Sol. Sin. 2014, 35, 2431–2437. [Google Scholar]
- Ridley, R.B. Secondary LC filter analysis and design techniques for current-mode controlled converters. IEEE Trans. Power Electron. 1988, 3, 499–507. [Google Scholar] [CrossRef]

| Parameters | Values |
|---|---|
| CPV1, CPV2/μF | 0.25 |
| L1, L2/mH | 1 |
| Cx1/μF | 47 |
| Lcm1, Lcm2/mH | 1.3 |
| CY1, CY2/nF | 10 |
| Pre-boost operating frequency/kHz | 10 |
| Post-level H6 bridge operating frequency/kHz | 20 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Zhu, H.; Zhao, R. Novel Common-Mode Current Suppression Method in Transformerless PV Grid-Connected System. Appl. Sci. 2018, 8, 2072. https://doi.org/10.3390/app8112072
Liu D, Zhu H, Zhao R. Novel Common-Mode Current Suppression Method in Transformerless PV Grid-Connected System. Applied Sciences. 2018; 8(11):2072. https://doi.org/10.3390/app8112072
Chicago/Turabian StyleLiu, Dongliang, Haoqi Zhu, and Ruiguang Zhao. 2018. "Novel Common-Mode Current Suppression Method in Transformerless PV Grid-Connected System" Applied Sciences 8, no. 11: 2072. https://doi.org/10.3390/app8112072
APA StyleLiu, D., Zhu, H., & Zhao, R. (2018). Novel Common-Mode Current Suppression Method in Transformerless PV Grid-Connected System. Applied Sciences, 8(11), 2072. https://doi.org/10.3390/app8112072





