A Method of Free-Space Point-of-Regard Estimation Based on 3D Eye Model and Stereo Vision
Abstract
Featured Application
Abstract
1. Introduction
2. Related Works
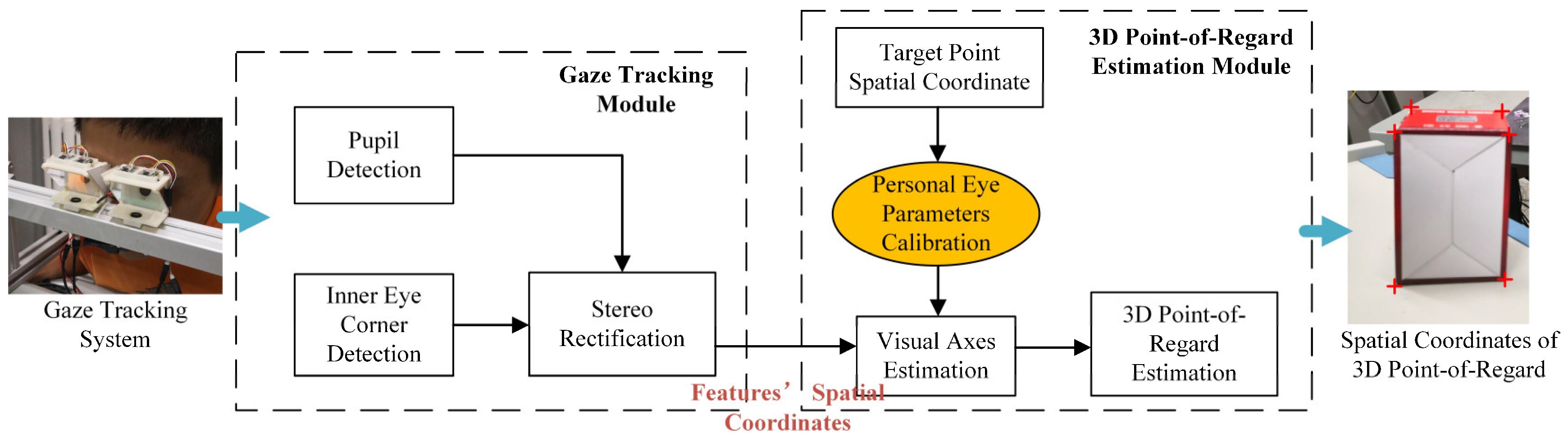
3. Methods
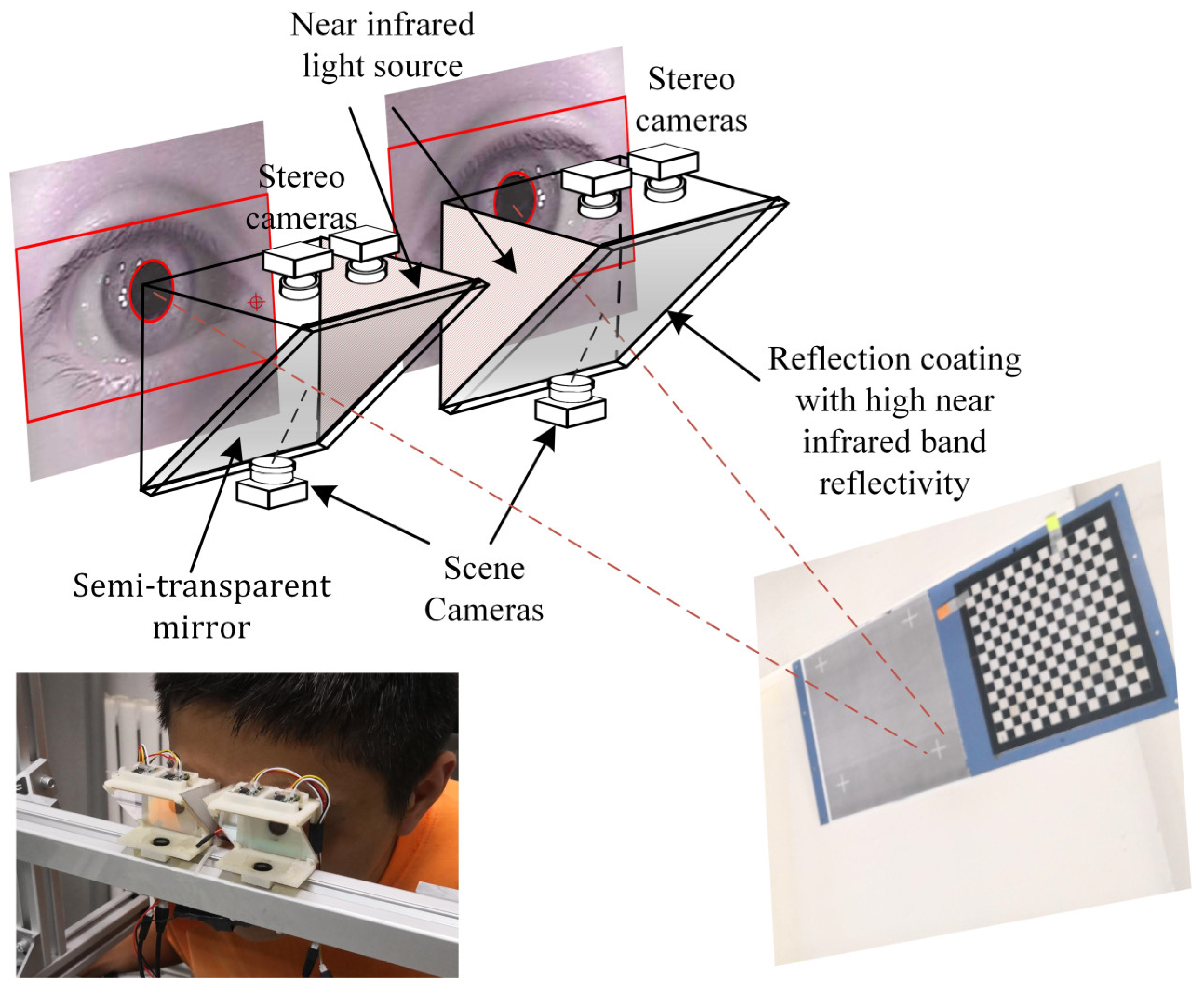
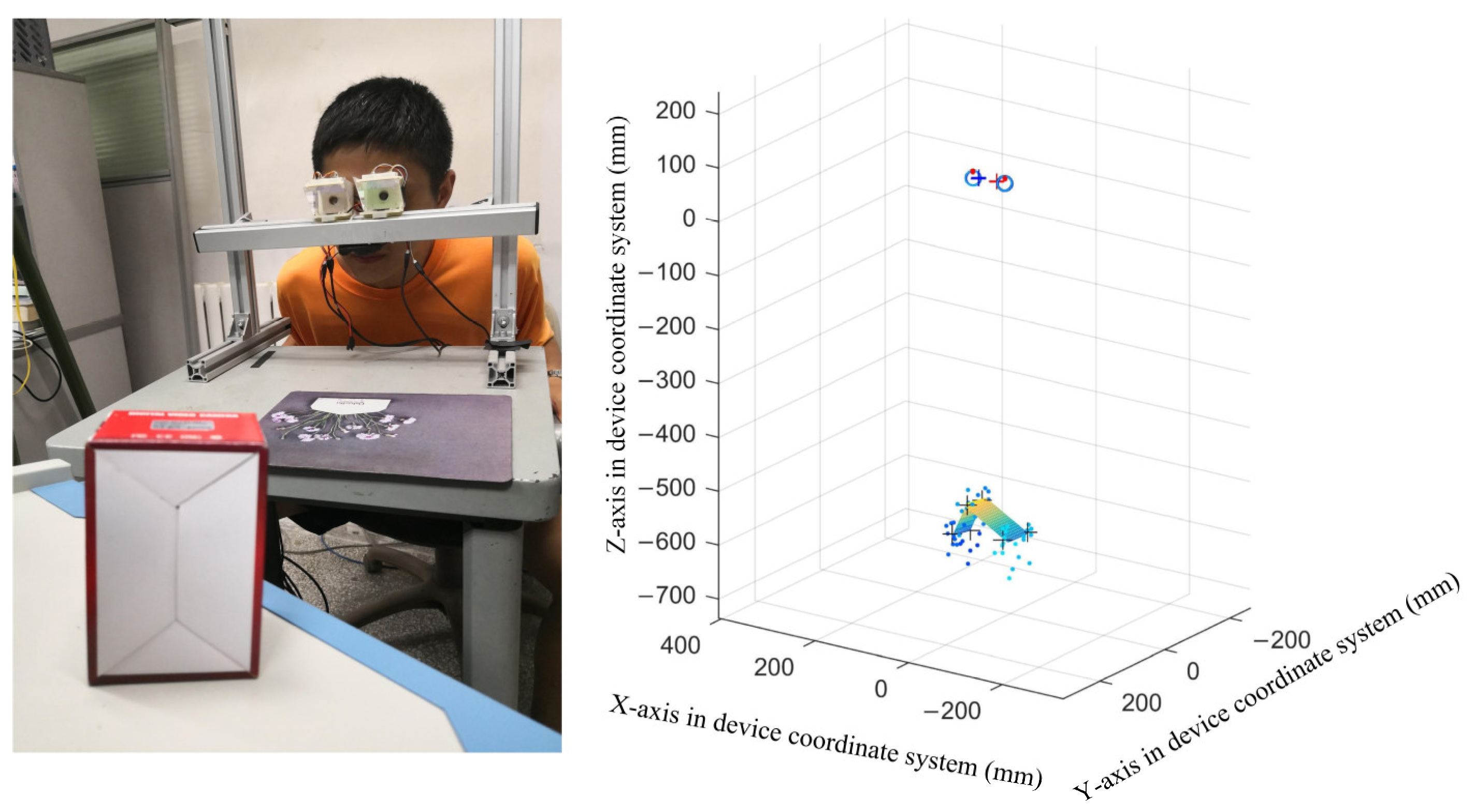
3.1. Customized Gaze Tracking System
- Ensure a large field of view;
- Reduce or avoid the influence of environment illumination on images; and
- The device should be miniaturized, light-weight, and low-cost.
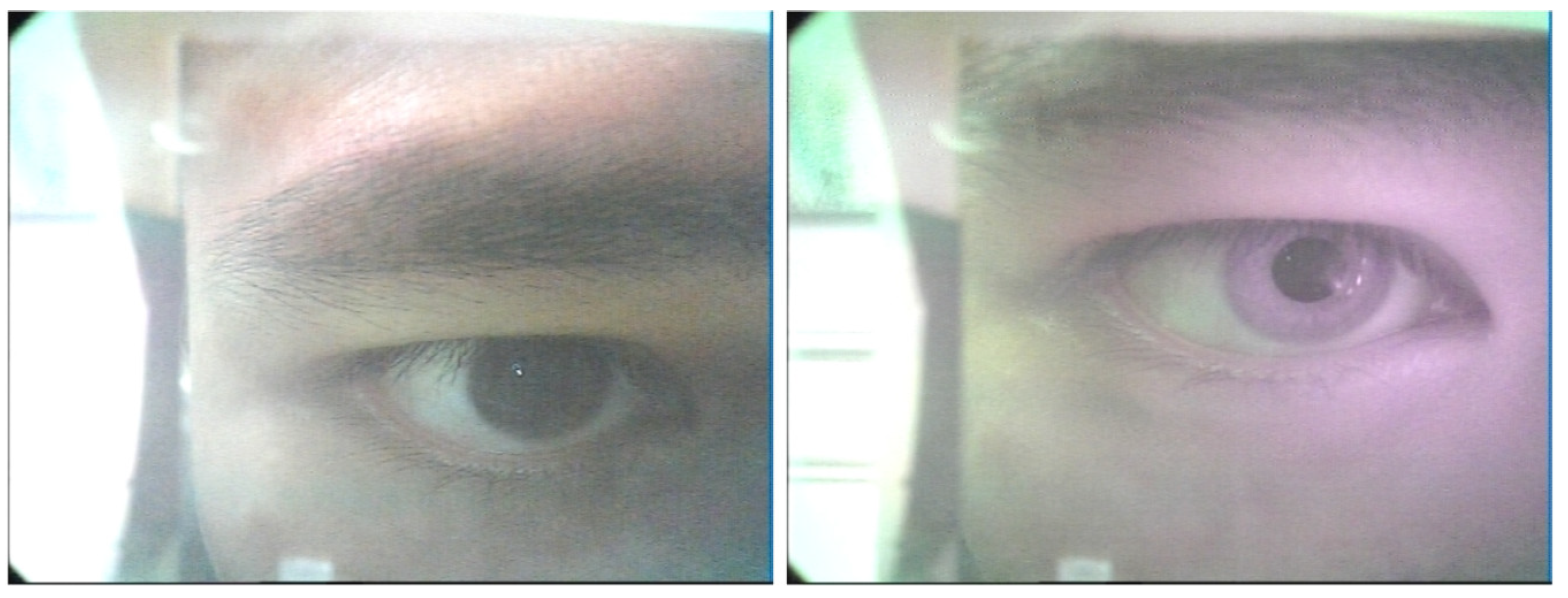
3.2. Eye Features Extraction
3.3. 3D Point-of-Regard Estimation
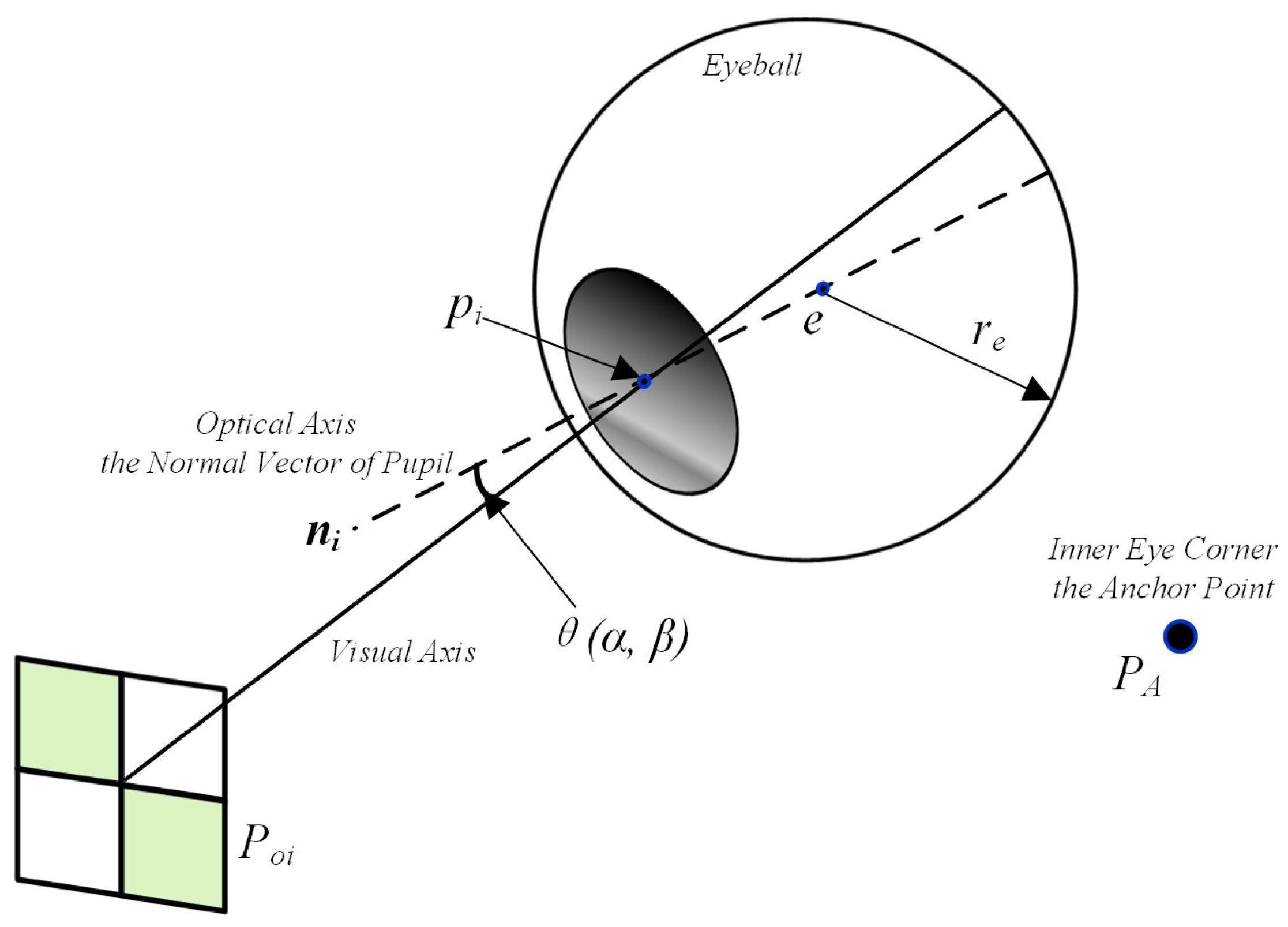
3.3.1. Eyeball Features and Personal Calibration
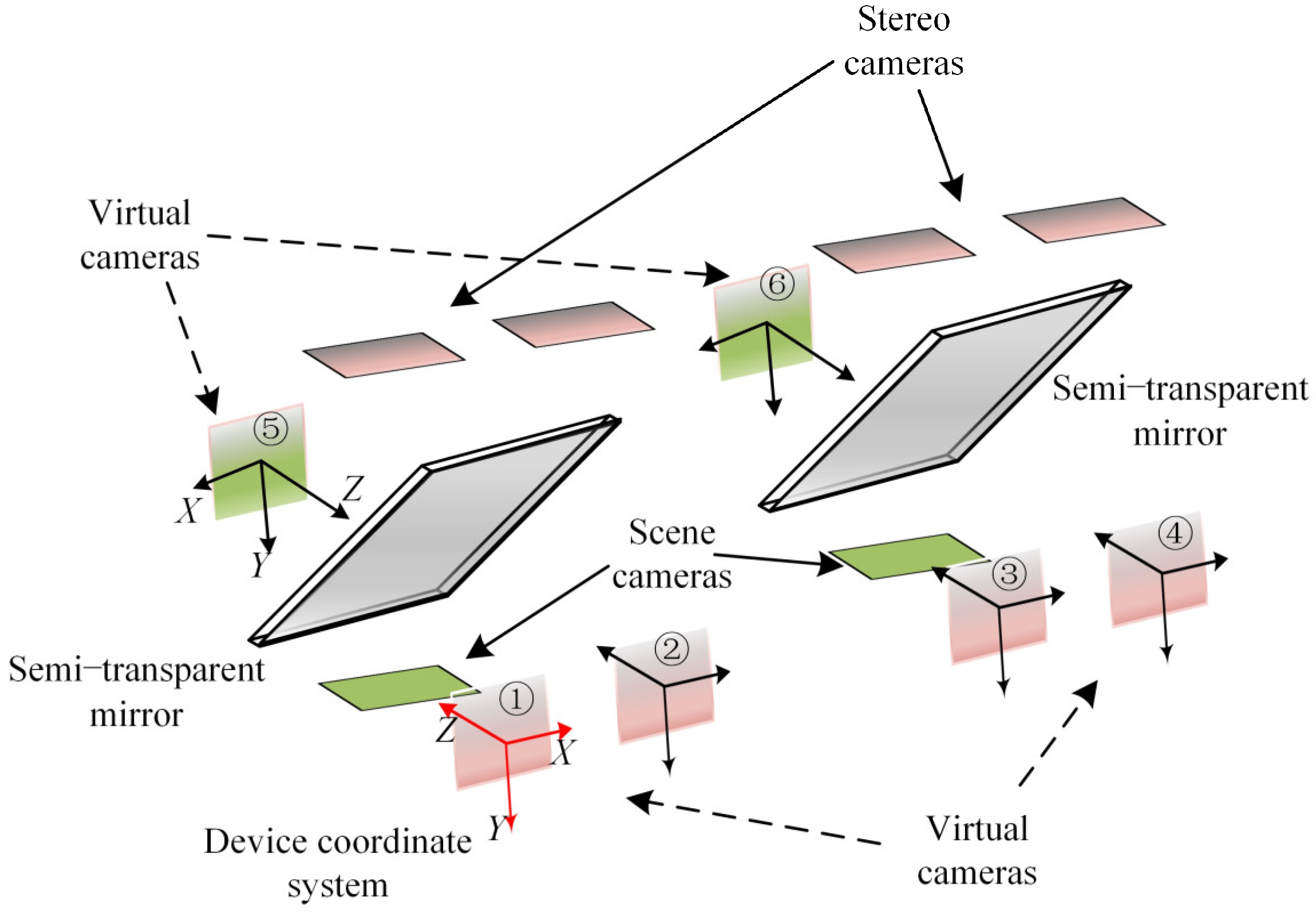
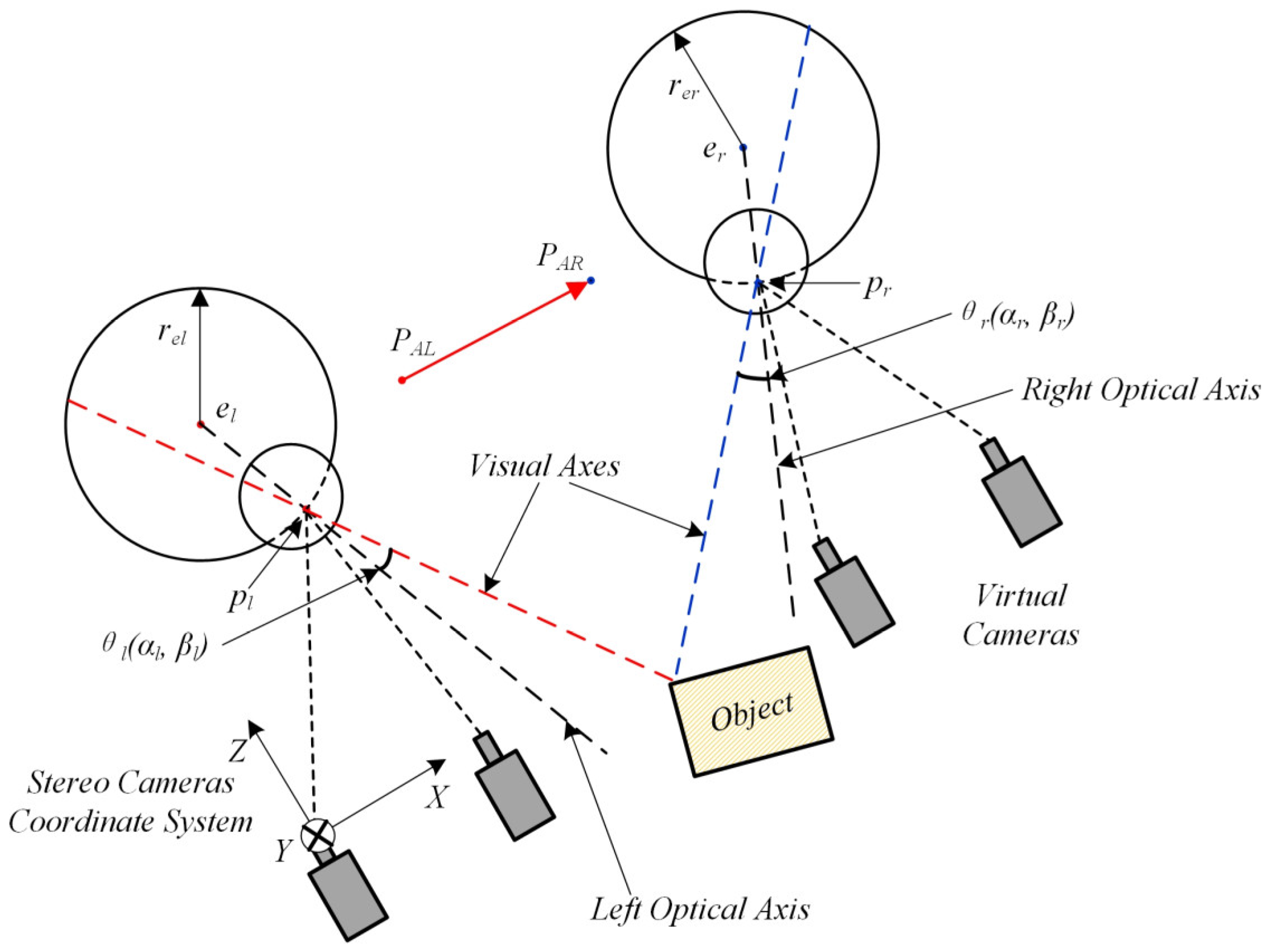
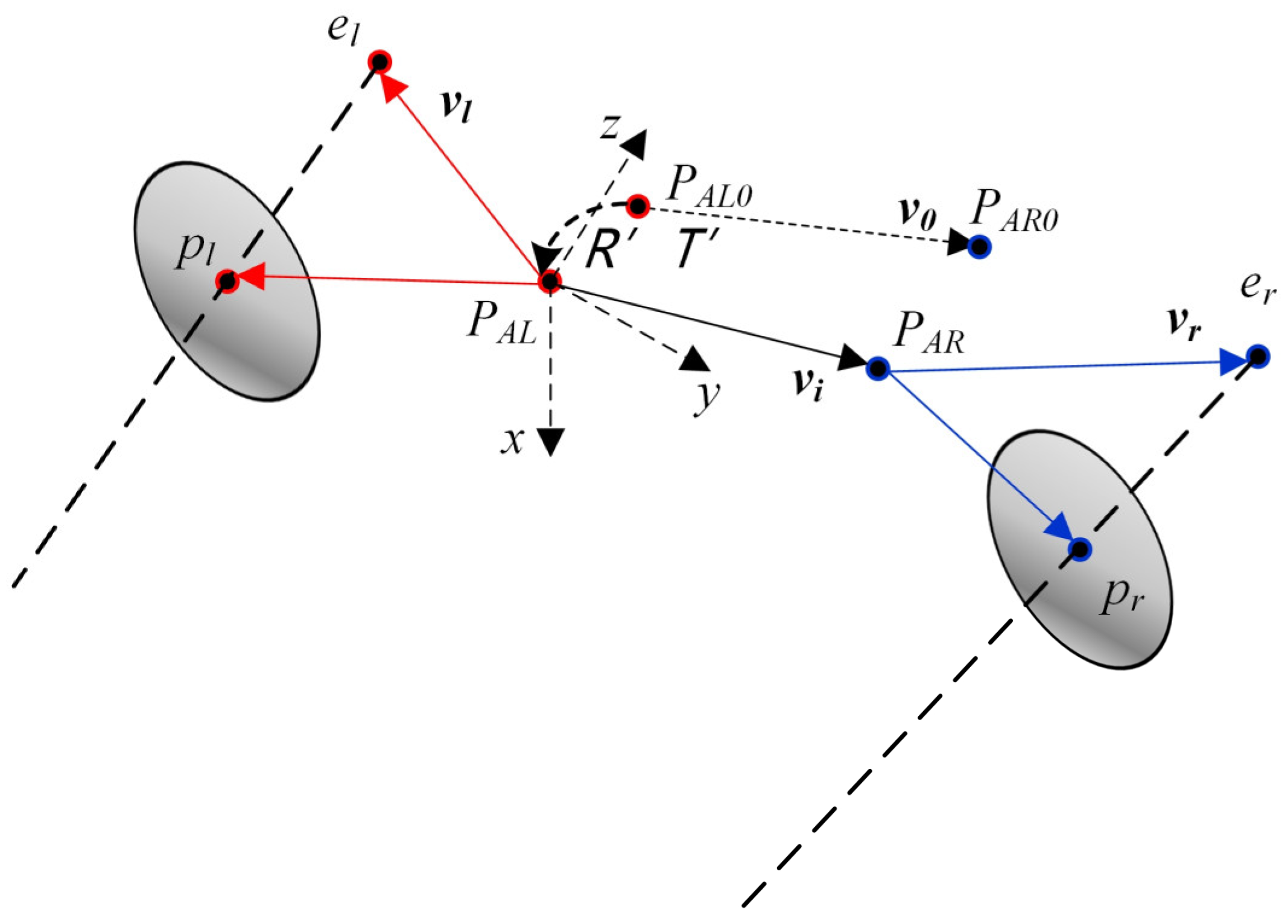
3.3.2. Eyeball Features Coordinate Alignment
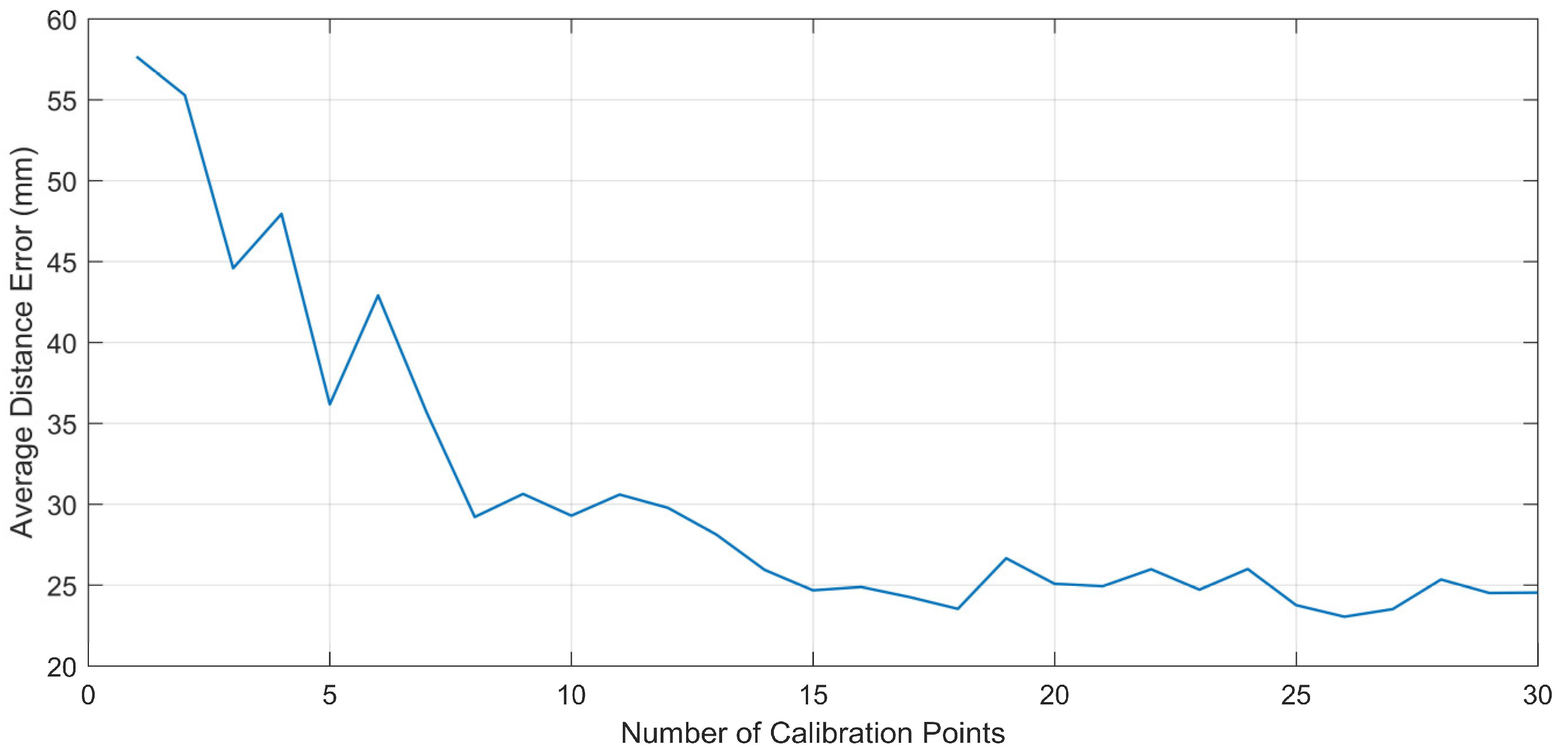
3.3.3. 3D Point-of-Regard Estimation and Calibration Experiment
4. Experiments
4.1. 3D Point-of-Regard Estimation Experiment in Free Space
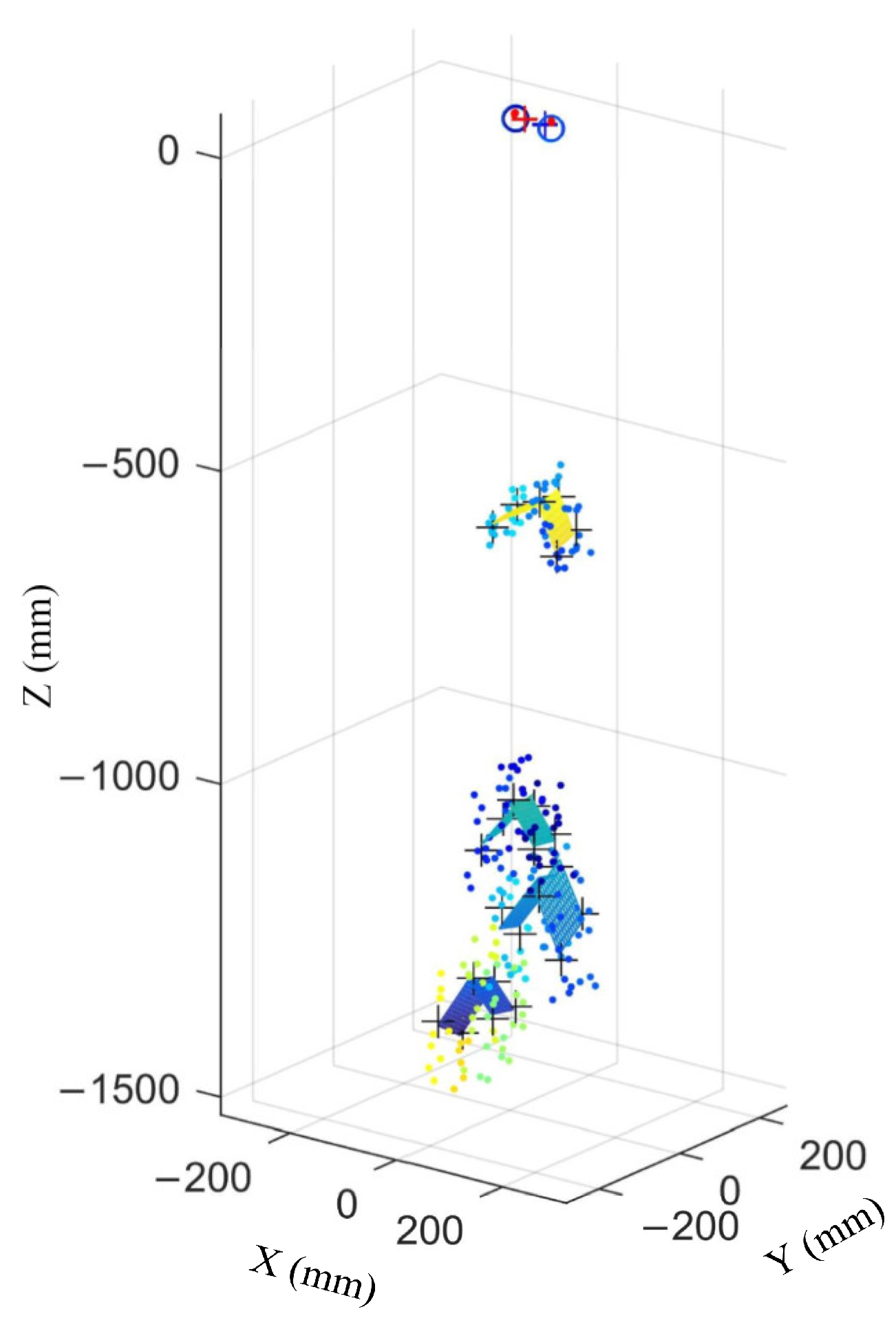
4.2. Error of the Method in Different Distances
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hansen, W.; Ji, Q. In the Eye of the Beholder: A Survey of Models for Eyes and Gaze. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 478–500. [Google Scholar] [CrossRef] [PubMed]
- Takemura, K.; Takahashi, K.; Takamatsu, J.; Ogasawara, T. Estimating 3-D Point-of-Regard in a Real Environment Using a Head-Mounted Eye-Tracking System. IEEE Trans. Hum. Mach. Syst. 2014, 44, 531–536. [Google Scholar] [CrossRef]
- Talmi, K.; Liu, J. Eye and gaze tracking for visually controlled interactive stereoscopic displays. Signal Process. Image Commun. 1999, 14, 799–810. [Google Scholar] [CrossRef]
- Kang, R.P.; Lee, J.J.; Kim, J. Gaze position detection by computing the three dimensional facial positions and motions. Pattern Recognit. 2002, 35, 2559–2569. [Google Scholar]
- Guestrin, E.D.; Eizenman, M. Remote point-of-gaze estimation requiring a single-point calibration for applications with infants. In Proceedings of the Symposium on Eye Tracking Research & Applications, Savannah, GA, USA, 26–28 March 2008; pp. 267–274. [Google Scholar]
- Wang, K.; Ji, Q. Real Time Eye Gaze Tracking with 3D Deformable Eye-Face Model. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 1003–1011. [Google Scholar]
- Guestrin, E.D.; Eizenman, M. General theory of remote gaze estimation using the pupil center and corneal reflections. IEEE Trans. Biomed. Eng. 2006, 53, 1124–1133. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Ji, Q. Novel eye gaze tracking techniques under natural head movement. IEEE Trans. Biomed. Eng. 2007, 54, 2246–2260. [Google Scholar] [PubMed]
- Villanueva, A.; Cabeza, R. A Novel Gaze Estimation System with One Calibration Point. IEEE Trans. Syst. Man Cybern. B Cybern. 2008, 38, 1123–1138. [Google Scholar] [CrossRef] [PubMed]
- Cho, D.C.; Yap, W.S.; Lee, H.; Kim, W. Long range eye gaze tracking system for a large screen. IEEE Trans. Consum. Electron. 2013, 58, 1119–1128. [Google Scholar] [CrossRef]
- Dong, H.Y.; Chung, M.J. A novel non-intrusive eye gaze estimation using cross-ratio under large head motion. Comput. Vis. Image Underst. 2005, 98, 25–51. [Google Scholar]
- Beymer, D.; Flickner, M. Eye gaze tracking using an active stereo head. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 16–22 June 2003; pp. 451–458. [Google Scholar]
- Cho, C.W.; Ji, W.L.; Shin, K.Y.; Lee, E.C.; Park, K.R.; Lee, H.; Cha, J. Gaze Detection by Wearable Eye-Tracking and NIR LED-Based Head-Tracking Device Based on SVR. ETRI J. 2012, 34, 542–552. [Google Scholar] [CrossRef]
- Model, D.; Eizenman, M. An Automatic Personal Calibration Procedure for Advanced Gaze Estimation Systems. IEEE Trans. Biomed. Eng. 2010, 57, 1031–1039. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Ji, Q. Probabilistic gaze estimation without active personal calibration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 609–616. [Google Scholar]
- Chi, J.N.; Xing, Y.Y.; Liu, L.N.; Gou, W. Calibration method for 3D gaze tracking systems. Appl. Opt. 2017, 56, 1536. [Google Scholar] [CrossRef]
- Zhang, X.; Sugano, Y.; Fritz, M.; Bulling, A. Appearance-based gaze estimation in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 4511–4520. [Google Scholar]
- Wang, K.; Ji, Q. 3D Gaze Estimation without Explicit Personal Calibration. Pattern Recognit. 2018, 79, 216–227. [Google Scholar] [CrossRef]
- Morimoto, C.H.; Mimica, M.R.M. Eye gaze tracking techniques for interactive applications. Comput. Vis. Image Underst. 2005, 98, 4–24. [Google Scholar] [CrossRef]
- Cheng, H.; Liu, Y.; Fu, W.; Ji, Y.; Yang, L.; Zhao, Y.; Yang, J. Gazing point dependent eye gaze estimation. Pattern Recognit. 2017, 71, 36–44. [Google Scholar] [CrossRef]
- Tan, K.H.; Kriegman, D.J.; Ahuja, N. Appearance-based Eye Gaze Estimation. In Proceedings of the IEEE Workshop on Applications of Computer Vision, Orlando, FL, USA, 3–4 December 2002; p. 191. [Google Scholar]
- Lu, F.; Chen, X.; Sato, Y. Appearance-Based Gaze Estimation via Uncalibrated Gaze Pattern Recovery. IEEE Trans. Image Process. 2017, 26, 1543–1553. [Google Scholar] [CrossRef] [PubMed]
- Durna, Y.; Ari, F. Design of a Binocular Pupil and Gaze Point Detection System Utilizing High Definition Images. Appl. Sci. 2017, 7, 498. [Google Scholar] [CrossRef]
- Sun, L.; Liu, Z.; Sun, M.T. Real time gaze estimation with a consumer depth camera. Inf. Sci. 2015, 320, 346–360. [Google Scholar] [CrossRef]
- Li, J.; Li, S. Gaze Estimation from Color Image Based on the Eye Model with Known Head Pose. IEEE Trans. Hum-Mach. Syst. 2016, 46, 414–423. [Google Scholar] [CrossRef]
- Cazzato, D.; Leo, M.; Distante, C. An investigation on the feasibility of uncalibrated and unconstrained gaze tracking for human assistive applications by using head pose estimation. Sensors 2014, 14, 8363–8379. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Song, M.; Liu, Z.; Sun, M. Real-time gaze estimation with online calibration. IEEE Multimedia 2014, 21, 28–37. [Google Scholar] [CrossRef]
- Funes-Mora, K.A.; Odobez, J.M. Gaze Estimation in the 3D Space Using RGB-D Sensors. Int. J. Comput. Vis. 2016, 118, 194–216. [Google Scholar] [CrossRef]
- Li, B.; Fu, H.; Wen, D.; LO, W. Etracker: A Mobile Gaze-Tracking System with Near-Eye Display Based on a Combined Gaze-Tracking Algorithm. Sensors 2018, 18, 1626. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.W.; Tan, W.C. An approach of head movement compensation when using a head mounted eye tracker. In Proceedings of the IEEE International Conference on Consumer Electronics-Taiwan 2016, Nantou, Taiwan, 27–29 May 2016. [Google Scholar]
- Su, D.; Li, Y.F. Toward flexible calibration of head-mounted gaze trackers with parallax error compensation. In Proceedings of the IEEE International Conference on Robotics and Biomimetics 2016, Qingdao, China, 3–7 December 2016; pp. 491–496. [Google Scholar]
- Pirri, F.; Pizzoli, M.; Rudi, A. A general method for the point of regard estimation in 3D space. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Colorado Springs, CO, USA, 20–25 June 2011; pp. 921–928. [Google Scholar]
- Wan, Z.; Wang, X.; Zhou, K.; Chen, X.; Wang, X. A Novel Method for Estimating Free Space 3D Point-of-Regard Using Pupillary Reflex and Line-of-Sight Convergence Points. Sensors 2018, 18, 2292. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, B.; Yang, D. A novel harris multi-scale corner detection algorithm. J. Electron. Inf. Technol. 2007, 29, 1735–1738. [Google Scholar]
- Haro, A.; Flickner, M.; Essa, I. Detecting and tracking eyes by using their physiological properties, dynamics, and appearance. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Hilton Head, SC, USA, 15 June 2000; pp. 163–168. [Google Scholar]

| Unit: cm | 0.8 m | 1.5 m | 2 m | 2.5 m | 3 m | 4 m |
|---|---|---|---|---|---|---|
| Error on X | 0.4 ± 0.4 | 0.6 ± 0.4 | 0.7 ± 0.6 | 0.9 ± 0.6 | 0.9 ± 0.5 | 1.3 ± 0.9 |
| Error on Y | 0.4 ± 0.3 | 0.6 ± 0.5 | 0.7 ± 0.4 | 0.8 ± 0.6 | 1.0 ± 0.6 | 1.3 ± 1.1 |
| Error on Z | 3.3 ± 2.7 | 4.2 ± 3.1 | 5.3 ± 4.0 | 7.6 ± 6.1 | 8.8 ± 6.3 | 10.7 ± 8.5 |
| Overall | 3.4 ± 2.7 | 4.3 ± 3.1 | 5.4 ± 4.1 | 7.8 ± 6.1 | 8.9 ± 6.4 | 10.8 ± 8.5 |
| Overall in [32] | 2.1 ± 0.3 | / | 3.6 ± 0.3 | / | 5.7 ± 0.5 | / |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, Z.; Wang, X.; Yin, L.; Zhou, K. A Method of Free-Space Point-of-Regard Estimation Based on 3D Eye Model and Stereo Vision. Appl. Sci. 2018, 8, 1769. https://doi.org/10.3390/app8101769
Wan Z, Wang X, Yin L, Zhou K. A Method of Free-Space Point-of-Regard Estimation Based on 3D Eye Model and Stereo Vision. Applied Sciences. 2018; 8(10):1769. https://doi.org/10.3390/app8101769
Chicago/Turabian StyleWan, Zijing, Xiangjun Wang, Lei Yin, and Kai Zhou. 2018. "A Method of Free-Space Point-of-Regard Estimation Based on 3D Eye Model and Stereo Vision" Applied Sciences 8, no. 10: 1769. https://doi.org/10.3390/app8101769
APA StyleWan, Z., Wang, X., Yin, L., & Zhou, K. (2018). A Method of Free-Space Point-of-Regard Estimation Based on 3D Eye Model and Stereo Vision. Applied Sciences, 8(10), 1769. https://doi.org/10.3390/app8101769





