Melodic Similarity and Applications Using Biologically-Inspired Techniques
Abstract
1. Introduction
1.1. From Bioinformatics to MIR
1.2. Contribution
2. Methods and Tools
2.1. Pairwise Alignment
2.2. Multiple Sequence Alignment
3. Melodic Sequence Data
3.1. Datasets
4. Multiple Sequence Alignment Quality for Melodic Sequences
AFFGABB-BBC AFFGABB-BBC ––––ABDDBBC A––––BDDBBC AFF-ABB–––– AFF-ABB––––
4.1. Motif Alignment Scoring
AFFGABB-BBC –AFFGABB-BBC ––––ABDDBBC –––––ABDDBBC –AFFABB–––– A-FF-ABB––––
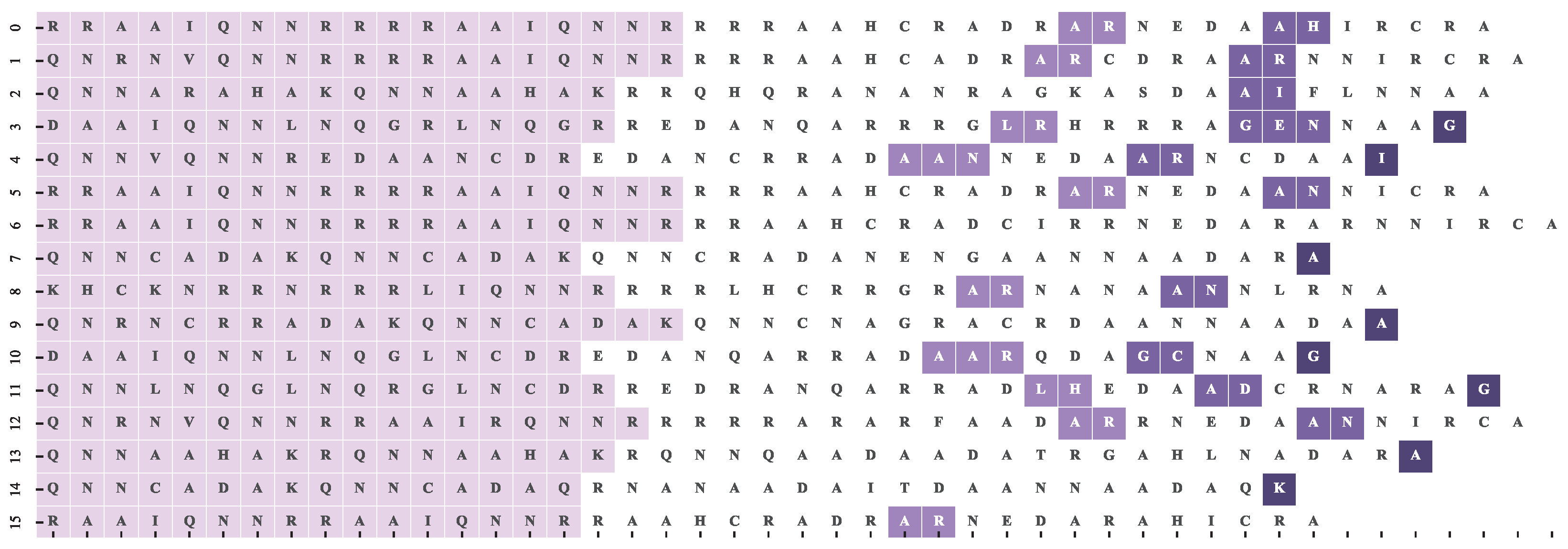
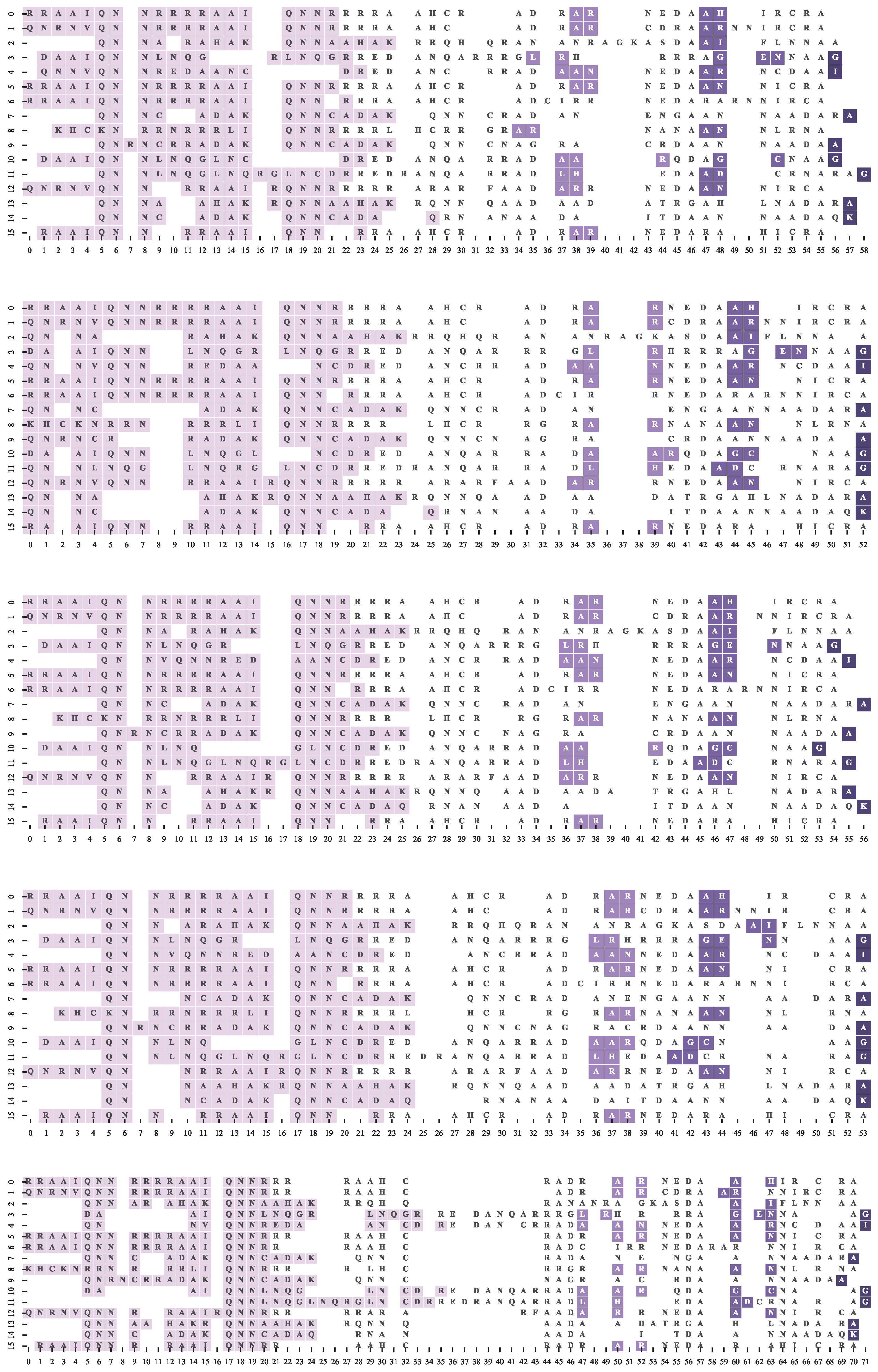
4.2. Dataset and Reference Motif Alignments
4.3. Multiple Sequence Alignment Algorithms and Settings
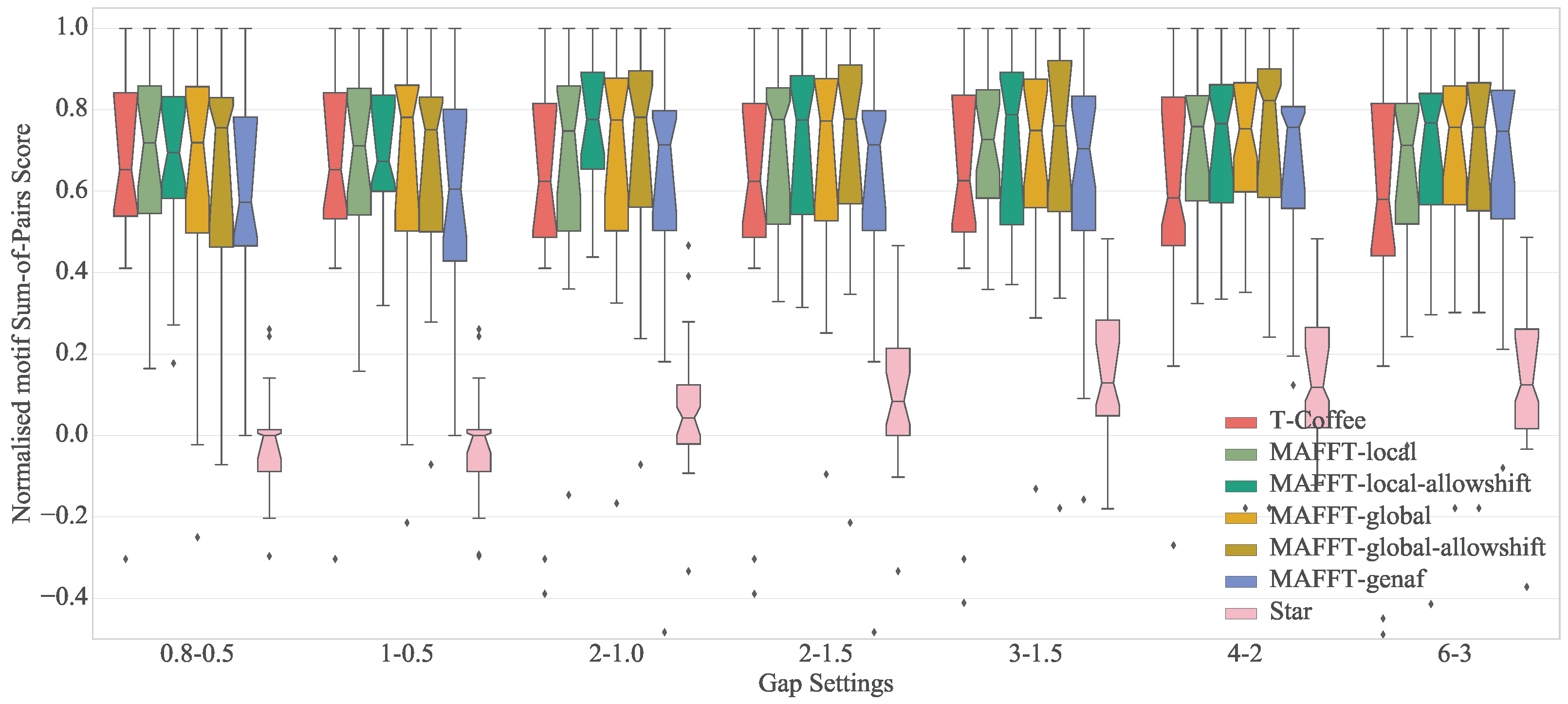
4.4. Results
4.5. Discussion
5. Analysis of Melodic Stability
5.1. Setup
5.2. Analysis
6. Data-Driven Modelling of Global Similarity
6.1. Generating Substitution Matrices
6.2. Computing the Alignments for Melodic and Intra-Song Motivic Similarity
––––XXABFXXXAGGXXXKLM XXABFXXXAGGXXXKLM– XXABFXXX–––––AGGXXXKLM LMXXXXABFXXXAGG––XK–– X–AGGXX–ABFX––AGGX ––AGGXXXKLMXXABFXXX–––
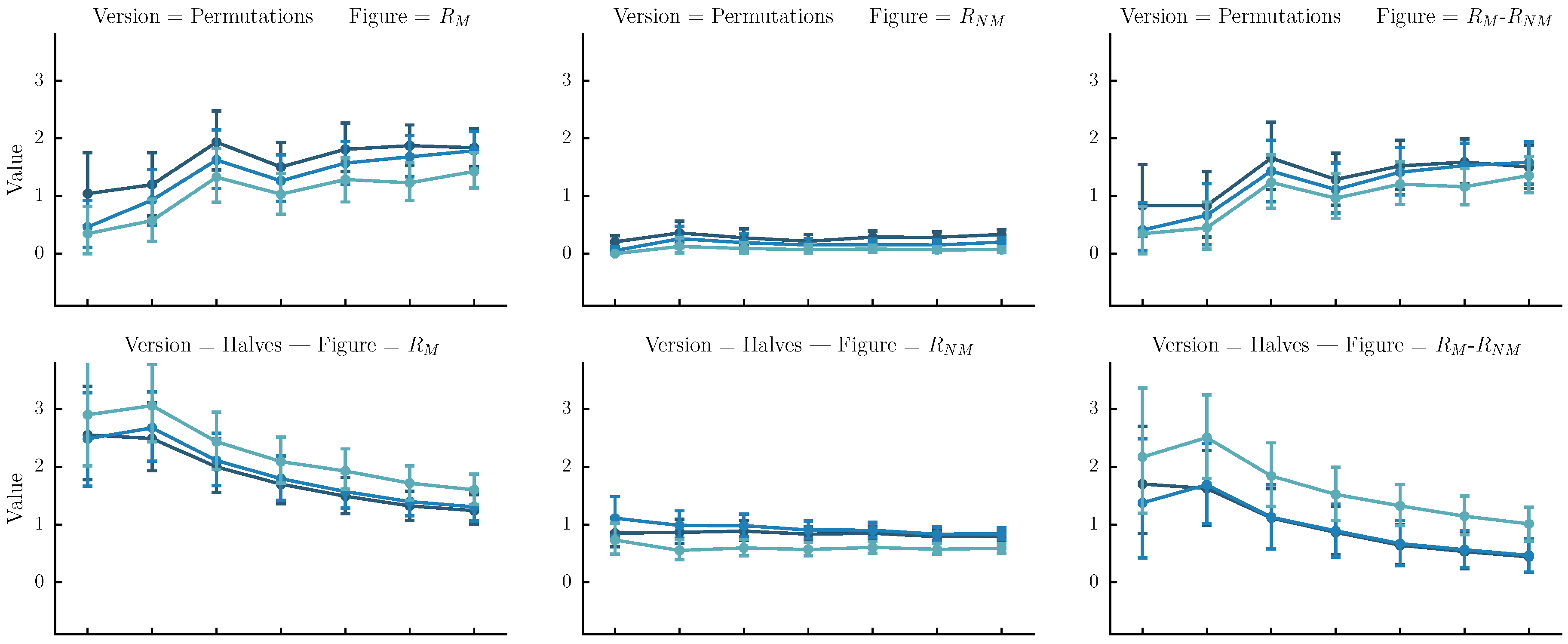
- Permutations: The original sequence is first split into n same-size segments. Each version is one of the rearrangements of the segments. In our case n is arbitrarily set to four. Although automatic melody segmentation algorithms could have been used, we decided to used a fixed number of segments for the sake of simplicity.
- Halves: The original sequence is iteratively split in subsequences of half size until their length is equal to four or their number is equal to . Each version is a sequence of length equal to the original, created by the concatenation of one of the subsequences.
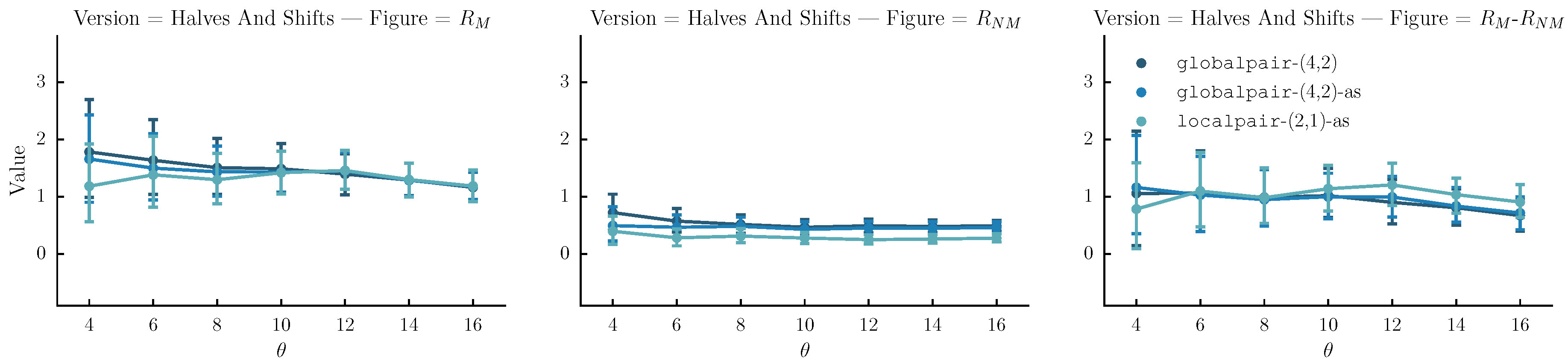
- Halves and shifts: A set of versions created by shifting the sequence by of its length to the right k times, resulting to k versions. The idea is to fuse the current set with the halves. We do that by randomly selecting versions from the halves method and versions from the current set.
6.3. Experimental Setup
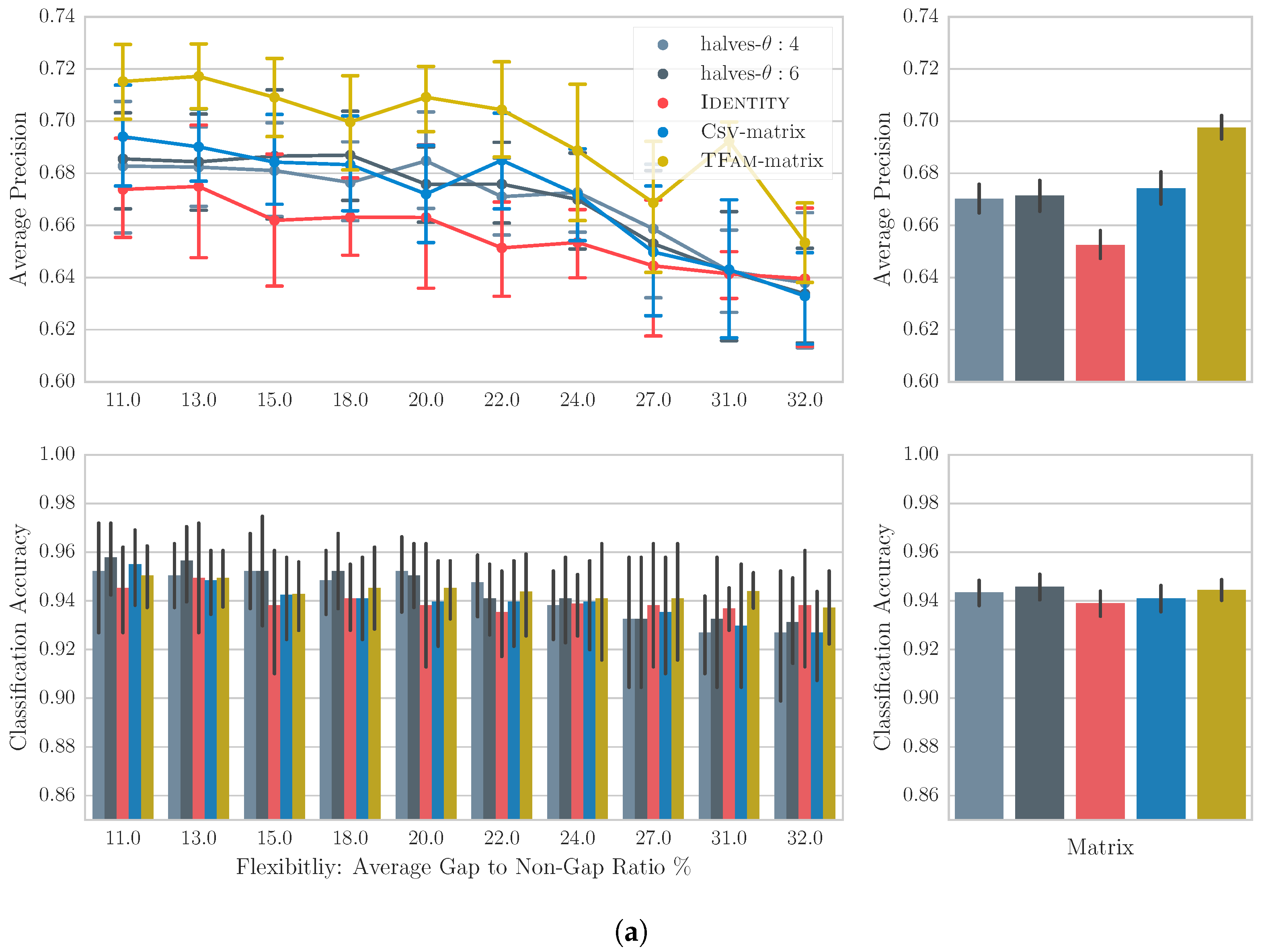
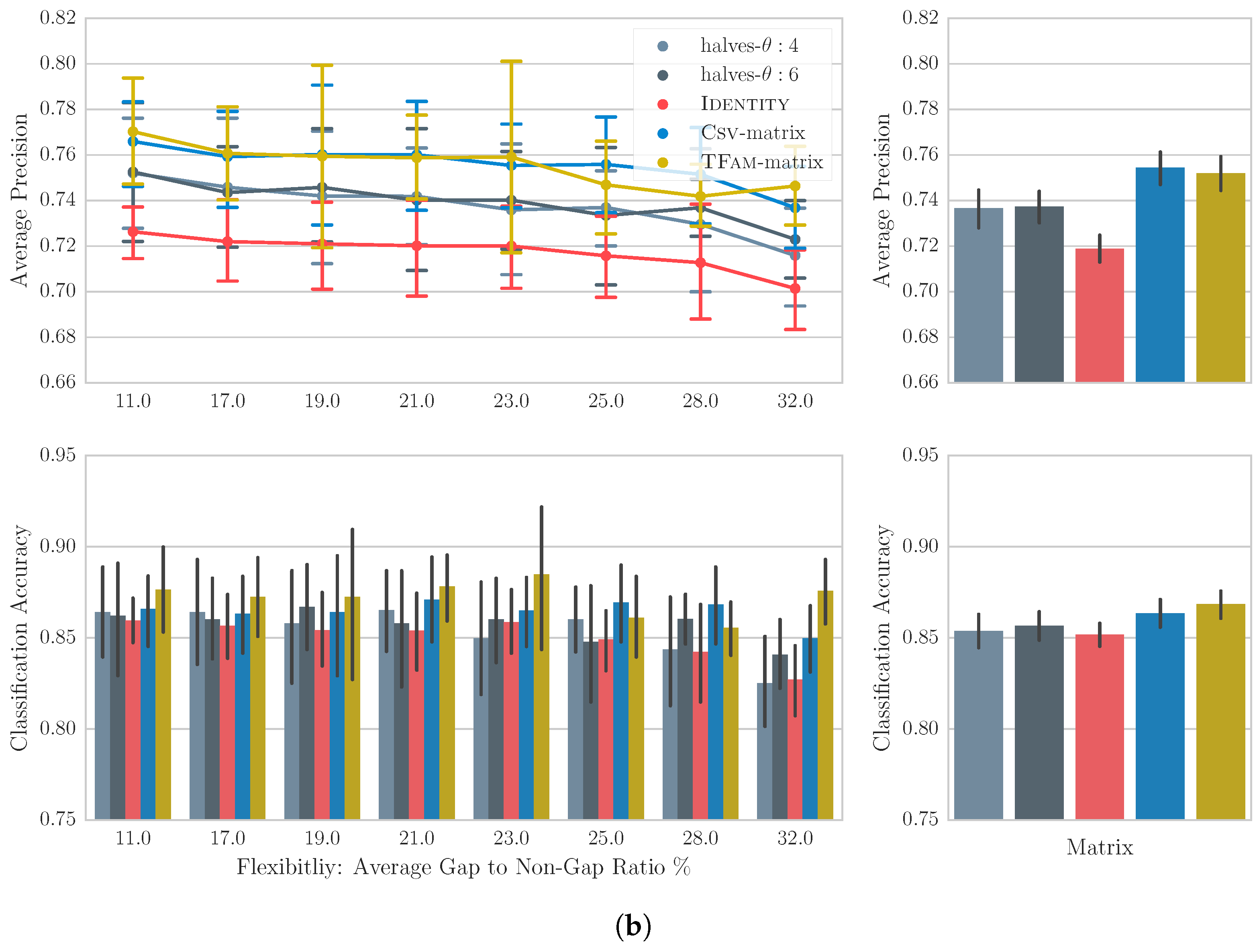
6.4. Results
6.5. Discussion
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Van Kranenburg, P. A Computational Approach to Content-Based Retrieval of Folk Song Melodies. Ph.D. Thesis, Utrecht University, Utrecht, The Netherlands, 2010. [Google Scholar]
- Volk, A.; Haas, W.; Kranenburg, P. Towards modelling variation in music as foundation for similarity. In Proceedings of the International Conference on Music Perception and Cognition, Thessaloniki, Greece, 23–28 July 2012; pp. 1085–1094. [Google Scholar]
- Pampalk, E. Computational Models of Music Similarity and Their Application to Music Information Retrieval. Ph.D. Thesis, Vienna University of Technology, Vienna, Austria, 2006. [Google Scholar]
- Volk, A.; Van Kranenburg, P. Melodic similarity among folk songs: An annotation study on similarity-based categorization in music. Music. Sci. 2012, 16, 317–339. [Google Scholar] [CrossRef]
- Marsden, A. Interrogating melodic similarity: A definitive phenomenon or the product of interpretation? J. New Music Res. 2012, 41, 323–335. [Google Scholar] [CrossRef]
- Ellis, D.P.; Whitman, B.; Berenzweig, A.; Lawrence, S. The quest for ground truth in musical artist similarity. In Proceedings of the International Society of Music Information Retrieval Conference, Paris, France, 13–17 October 2002; pp. 170–177. [Google Scholar]
- Deliège, I. Similarity perception categorization cue abstraction. Music Percept. 2001, 18, 233–244. [Google Scholar] [CrossRef]
- Novello, A.; McKinney, M.F.; Kohlrausch, A. Perceptual evaluation of music similarity. In Proceedings of the International Society of Music Information Retrieval, Victoria, BC, Canada, 8–12 October 2006; pp. 246–249. [Google Scholar]
- Jones, M.C.; Downie, J.S.; Ehmann, A.F. Human similarity judgements: Implications for the design of formal evaluations. In Proceedings of the International Society of Music Information Retrieval, Vienna, Austria, 23–30 September 2007; pp. 539–542. [Google Scholar]
- Tversky, A. Features of similarity. Psychol. Rev. 1977, 84, 327–352. [Google Scholar] [CrossRef]
- Lamere, P. Social tagging and music information retrieval. J. New Music Res. 2008, 37, 101–114. [Google Scholar] [CrossRef]
- Berenzweig, A.; Logan, B.; Ellis, D.P.; Whitman, B. A large-scale evaluation of acoustic and subjective music-similarity measures. Comput. Music J. 2004, 28, 63–76. [Google Scholar] [CrossRef]
- Hu, N.; Dannenberg, R.B.; Lewis, A.L. A probabilistic model of melodic similarity. In Proceedings of the International Computer Music Conference, Göteborg, Sweden, 16–21 September 2002. [Google Scholar]
- Hu, N.; Dannenberg, R.B. A comparison of melodic database retrieval techniques using sung queries. In Proceedings of the 2nd ACM/IEEE-Cs Joint Conference on Digital Libraries, Portland, OR, USA, 13–17 July 2002; pp. 301–307. [Google Scholar]
- Hanna, P.; Robine, M.; Rocher, T. An alignment based system for chord sequence retrieval. In Proceedings of the 9th ACM/IEEE-Cs Joint Conference on Digital Libraries, Austin, TX, USA, 14–19 June 2009; pp. 101–104. [Google Scholar]
- Bronson, B.H. Melodic stability in oral transmission. J. Int. Folk Music Counc. 1951, 3, 50–55. [Google Scholar] [CrossRef]
- Krogh, A. An introduction to hidden markov models for biological sequences. New Compr. Biochem. 1998, 32, 45–63. [Google Scholar]
- Bascom, W. The main problems of stability and change in tradition. J. Int. Folk Music Counc. 1959, 11, 7–12. [Google Scholar] [CrossRef]
- Drake, C.; Bertrand, D. The quest for universals in temporal processing in music. Ann. N. Y. Acad. Sci. 2001, 930, 17–27. [Google Scholar] [CrossRef] [PubMed]
- Gurney, E. The Power of Sound; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Casey, M.; Slaney, M. The importance of sequences in musical similarity. In Proceedings of the International Conference On Acoustics, Speech and Signal Processing, Toulouse, France, 14–19 May 2006; pp. 5–8. [Google Scholar]
- Capra, J.A.; Singh, M. Predicting functionally important residues from sequence conservation. Bioinformatics 2007, 23, 1875–1882. [Google Scholar] [CrossRef] [PubMed]
- Valdar, W.S. Scoring residue conservation. Proteins Struct. Funct. Bioinform. 2002, 48, 227–241. [Google Scholar] [CrossRef] [PubMed]
- Luscombe, N.M.; Greenbaum, D.; Gerstein, M. What is bioinformatics? A proposed definition and overview of the field. Methods Inf. Med. 2001, 40, 346–358. [Google Scholar] [PubMed]
- Bountouridis, D.; Wiering, F.; Brown, D.; Veltkamp, R.C. Towards polyphony reconstruction using multidimensional multiple sequence alignment. In Proceedings of the International Conference on Evolutionary and Biologically Inspired Music and Art, Amsterdam, The Netherlands, 19–21 April 2017; pp. 33–48. [Google Scholar]
- Bountouridis, D.; Brown, D.; Koops, H.V.; Wiering, F.; Veltkamp, R. Melody retrieval and classification using biologically-inspired techniques. In Proceedings of the International Conference on Evolutionary and Biologically Inspired Music and Art, Amsterdam, The Netherlands, 19–21 April 2017; pp. 49–64. [Google Scholar]
- Bountouridis, D.; Koops, H.V.; Wiering, F.; Veltkamp, R. A data-driven approach to chord similarity and chord mutability. In Proceedings of the International Conference on Multimedia Big Data, Taipei, Taiwan, 20–22 April 2016; pp. 275–278. [Google Scholar]
- Nguyen, K.; Guo, X.; Pan, Y. Multiple Biological Sequence Alignment: Scoring Functions, Algorithms and Evaluation; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Needleman, S.B.; Wunsch, C.D. A general method applicable to the search for similarities in the amino acid sequence of two proteins. J. Mol. Biol. 1970, 48, 443–453. [Google Scholar] [CrossRef]
- Durbin, R.; Eddy, S.R.; Krogh, A.; Mitchison, G. Biological Sequence Analysis: Probabilistic Models of Proteins and Nucleic Acids; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Smith, T.F.; Waterman, M.S. Identification of common molecular subsequences. J. Mol. Biol. 1981, 147, 195–197. [Google Scholar] [CrossRef]
- Mongeau, M.; Sankoff, D. Comparison of musical sequences. Comput. Humanit. 1990, 24, 161–175. [Google Scholar] [CrossRef]
- Ewert, S.; Müller, M.; Dannenberg, R.B. Towards reliable partial music alignments using multiple synchronization strategies. In Proceedings of the International Workshop on Adaptive Multimedia Retrieval, Madrid, Spain, 24–25 September 2009; pp. 35–48. [Google Scholar]
- Serra, J.; Gómez, E.; Herrera, P.; Serra, X. Chroma binary similarity and local alignment applied to cover song identification. Audio Speech Lang. Process. 2008, 16, 1138–1151. [Google Scholar] [CrossRef]
- Müllensiefen, D.; Frieler, K. Optimizing measures of melodic similarity for the exploration of a large folk song database. In Proceedings of the International Society of Music Information Retrieval, Barcelona, Spain, 10–15 October 2004; pp. 1–7. [Google Scholar]
- Müllensiefen, D.; Frieler, K. Cognitive adequacy in the measurement of melodic similarity: Algorithmic vs. human judgements. Comput. Musicol. 2004, 13, 147–176. [Google Scholar]
- Sailer, C.; Dressler, K. Finding cover songs by melodic similarity. In Proceedings of the Annual Music Information Retrieval Evaluation Exchange, Victoria, BC, Canada, 8–12 September 2006; Available online: www.music-ir.org/mirex/abstracts/2006/CS_sailer.pdf (accessed on 28 November 2017).
- Ross, J.C.; Vinutha, T.; Rao, P. Detecting melodic motifs from audio for hindustani classical music. In Proceedings of the International Society of Music Information Retrieval, Porto, Portugal, 8–12 October 2012; pp. 193–198. [Google Scholar]
- Salamon, J.; Rohrmeier, M. A quantitative evaluation of a two stage retrieval approach for a melodic query by example system. In Proceedings of the International Society of Music Information Retrieval, Kobe, Japan, 26–30 October 2009; pp. 255–260. [Google Scholar]
- Hu, N.; Dannenberg, R.B.; Tzanetakis, G. Polyphonic audio matching and alignment for music retrieval. In Proceedings of the Workshop in Applications of Signal Processing to Audio and Acoustics, New Paltz, NY, USA, 19–22 October 2003; pp. 185–188. [Google Scholar]
- Ewert, S.; Müller, M.; Grosche, P. High resolution audio synchronization using chroma onset features. In Proceedings of the International Conference On Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; pp. 1869–1872. [Google Scholar]
- Balke, S.; Arifi-Müller, V.; Lamprecht, L.; Müller, M. Retrieving audio recordings using musical themes. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 20–25 March 2016; pp. 281–285. [Google Scholar]
- Raffel, C.; Ellis, D.P. Large-scale content-based matching of midi and audio files. In Proceedings of the International Society of Music Information Retrieval, Malaga, Spain, 26–30 October 2015; pp. 234–240. [Google Scholar]
- Müller, M. Information Retrieval for Music and Motion; Springer: Berlin, Germany, 2007. [Google Scholar]
- Thompson, J.D.; Higgins, D.G.; Gibson, T.J. Clustal W: Improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice. Nucleic Acids Res. 1994, 22, 4673–4680. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Jiang, T. On the complexity of multiple sequence alignment. J. Comput. Biol. 1994, 1, 337–348. [Google Scholar] [CrossRef] [PubMed]
- Kemena, C.; Notredame, C. Upcoming challenges for multiple sequence alignment methods in the high-throughput era. Bioinformatics 2009, 25, 2455–2465. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.C. Towards automatic music performance comparison with the multiple sequence alignment technique. In Proceedings of the International Conference on Multimedia Modelling, Huangshan, China, 7–9 January 2013; pp. 391–402. [Google Scholar]
- Wang, S.; Ewert, S.; Dixon, S. Robust joint alignment of multiple versions of a piece of music. In Proceedings of the International Society of Music Information Retrieval, Taipei, Taiwan, 27–31 October 2014; pp. 83–88. [Google Scholar]
- Knees, P.; Schedl, M.; Widmer, G. Multiple lyrics alignment: Automatic retrieval of song lyrics. In Proceedings of the International Society of Music Information Retrieval, London, UK, 11–15 October 2005; pp. 564–569. [Google Scholar]
- Poliner, G.E.; Ellis, D.P.; Ehmann, A.F.; Gómez, E.; Streich, S.; Ong, B. Melody transcription from music audio: Approaches and evaluation. IEEE Trans. Audio Speech Lang. Process. 2007, 15, 1247–1256. [Google Scholar] [CrossRef]
- Kim, Y.E.; Chai, W.; Garcia, R.; Vercoe, B. Analysis of a contour-based representation for melody. In Proceedings of the International Society of Music Information Retrieval, Plymouth, MA, USA, 23–25 October 2000. [Google Scholar]
- Huron, D. The melodic arch in western folksongs. Comput. Musicol. 1996, 10, 3–23. [Google Scholar]
- Margulis, E.H. A model of melodic expectation. Music Percept. Interdiscip. J. 2005, 22, 663–714. [Google Scholar] [CrossRef]
- Salamon, J.; Gómez, E.; Ellis, D.P.; Richard, G. Melody extraction from polyphonic music signals: Approaches, applications, and challenges. IEEE Signal Process. Mag. 2014, 31, 118–134. [Google Scholar] [CrossRef]
- Suyoto, I.S.; Uitdenbogerd, A.L. Simple efficient n-gram indexing for effective melody retrieval. In Proceedings of the Annual Music Information Retrieval Evaluation Exchange, London, UK, 14 September 2005; Available online: pdfs.semanticscholar.org/4103/07d4f5398b1588b04d2916f0f592813a3d0a.pdf (accessed on 28 November 2017).
- Ryynanen, M.; Klapuri, A. Query by humming of midi and audio using locality sensitive hashing. In Proceedings of the International Conderence on Acoustics, Speech and Signal Processing, Las Vegas, NV, USA, 31 March–4 April 2008; pp. 2249–2252. [Google Scholar]
- Hillewaere, R.; Manderick, B.; Conklin, D. Alignment methods for folk tune classification. In Proceedings of the Annual Conference of the German Classification Society on Data Analysis, Machine Learning and Knowledge Discovery, Hildesheim, Germany, 1–3 August 2014; pp. 369–377. [Google Scholar]
- Gómez, E.; Klapuri, A.; Meudic, B. Melody description and extraction in the context of music content processing. J. New Music Res. 2003, 32, 23–40. [Google Scholar] [CrossRef]
- Van Kranenburg, P.; de Bruin, M.; Grijp, L.; Wiering, F. The Meertens Tune Collections; Meertens Online Reports; Meertens Institute: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Bountouridis, D.; Van Balen, J. The cover song variation dataset. In Proceedings of the International Workshop on Folk Music Analysis, Istanbul, Turkey, 12–13 June 2014. [Google Scholar]
- Raghava, G.; Barton, G. Quantification of the variation in percentage identity for protein sequence alignments. BMC Bioinform. 2006, 7, 415–419. [Google Scholar] [CrossRef] [PubMed]
- Ewert, S.; Müller, M.; Müllensiefen, D.; Clausen, M.; Wiggins, G.A. Case study “Beatles songs” what can be learned from unreliable music alignments? In Proceedings of the Dagstuhl Seminar, Dagstuhl, Germany, 15–20 March 2009. [Google Scholar]
- Prätzlich, T.; Müller, M. Triple-based analysis of music alignments without the need of ground-truth annotations. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing, Shanghai, China, 20–25 March 2016; pp. 266–270. [Google Scholar]
- Pei, J.; Grishin, N.V. Promals: Towards accurate multiple sequence alignments of distantly related proteins. Bioinformatics 2007, 23, 802–808. [Google Scholar] [CrossRef] [PubMed]
- Blackburne, B.P.; Whelan, S. Measuring the distance between multiple sequence alignments. Bioinformatics 2012, 28, 495–502. [Google Scholar] [CrossRef] [PubMed]
- Bountouridis, D.; Van Balen, J. Towards capturing melodic stability. In Proceedings of the Interdisciplinary Musicology Conference, Berlin, Germany, 4–6 December 2014. [Google Scholar]
- Cowdery, J.R. A fresh look at the concept of tune family. Ethnomusicology 1984, 28, 495–504. [Google Scholar] [CrossRef]
- Hogeweg, P.; Hesper, B. The alignment of sets of sequences and the construction of phyletic trees: An integrated method. J. Mol. Evol. 1984, 20, 175–186. [Google Scholar] [CrossRef] [PubMed]
- Berger, M.; Munson, P.J. A novel randomized iterative strategy for aligning multiple protein sequences. Comput. Appl. Biosci. Cabios 1991, 7, 479–484. [Google Scholar] [CrossRef] [PubMed]
- Gotoh, O. Optimal alignment between groups of sequences and its application to multiple sequence alignment. Comput. Appl. Biosci. Cabios 1993, 9, 361–370. [Google Scholar] [CrossRef] [PubMed]
- Notredame, C.; Higgins, D.G.; Heringa, J. T-coffee: A novel method for fast and accurate multiple sequence alignment. J. Mol. Biol. 2000, 302, 205–217. [Google Scholar] [CrossRef] [PubMed]
- Notredame, C.; Holm, L.; Higgins, D.G. Coffee: An objective function for multiple sequence alignments. Bioinformatics 1998, 14, 407–422. [Google Scholar] [CrossRef] [PubMed]
- Morgenstern, B.; Dress, A.; Werner, T. Multiple dna and protein sequence alignment based on segment-to-segment comparison. Proc. Natl. Acad. Sci. USA 1996, 93, 12098–12103. [Google Scholar] [CrossRef] [PubMed]
- Katoh, K.; Misawa, K.; Kuma, K.i.; Miyata, T. Mafft: A novel method for rapid multiple sequence alignment based on fast fourier transform. Nucleic Acids Res. 2002, 30, 3059–3066. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.F. Generalized affine gap costs for protein sequence alignment. Proteins Struct. Funct. Genet. 1998, 32, 88–96. [Google Scholar] [CrossRef]
- Carroll, H.; Clement, M.J.; Ridge, P.; Snell, Q.O. Effects of gap open and gap extension penalties. In Proceedings of the Biotechnology and Bioinformatics Symposium, Provo, Utah, 20–21 October 2006; pp. 19–23. [Google Scholar]
- Dannenberg, R.B.; Hu, N. Understanding search performance in query-by-humming systems. In Proceedings of the Conference of the International Society of Music Information Retrieval, Barcelona, Spain, 10–15 October 2004. [Google Scholar]
- Margulis, E.H. Musical repetition detection across multiple exposures. Music Percept. Interdiscip. J. 2012, 29, 377–385. [Google Scholar] [CrossRef]
- Bigand, E.; Pineau, M. Context effects on melody recognition: A dynamic interpretation. Curr. Psychol. Cogn. 1996, 15, 121–134. [Google Scholar]
- Klusen, E.; Moog, H.; Piel, W. Experimente zur mündlichen Tradition von Melodien. Jahrbuch Fur Volksliedforschung 1978, 23, 11–32. [Google Scholar]
- Bigand, E. Perceiving musical stability: The effect of tonal structure, rhythm, and musical expertise. J. Exp. Psychol. Hum. Percept. Perform. 1997, 23, 808–822. [Google Scholar] [CrossRef] [PubMed]
- Schmuckler, M.A.; Boltz, M.G. Harmonic and rhythmic influences on musical expectancy. Atten. Percept. Psychophys. 1994, 56, 313–325. [Google Scholar] [CrossRef]
- Janssen, B.; Burgoyne, J.A.; Honing, H. Predicting variation of folk songs: A corpus analysis study on the memorability of melodies. Front. Psychol. 2017, 8, 621. [Google Scholar] [CrossRef] [PubMed]
- Van Balen, J.; Bountouridis, D.; Wiering, F.; Veltkamp, R. Cognition-inspired descriptors for scalable cover song retrieval. In Proceedings of the International Society of Music Information Retrieval, Taipei, Taiwan, 27–31 October 2014. [Google Scholar]
- Schoenberg, A.; Stein, L. Fundamentals of Musical Composition; Faber: London, UK, 1967. [Google Scholar]
- De Haas, W.B.; Wiering, F.; Veltkamp, R. A geometrical distance measure for determining the similarity of musical harmony. Int. J. Multimed. Inf. Retr. 2013, 2, 189–202. [Google Scholar] [CrossRef]
- Henikoff, S.; Henikoff, J.G. Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. USA 1992, 89, 10915–10919. [Google Scholar] [CrossRef] [PubMed]
- Hirjee, H.; Brown, D.G. Rhyme analyser: An analysis tool for rap lyrics. In Proceedings of the International Society of Music Information Retrieval, Utrecht, The Netherlands, 9–13 August 2010. [Google Scholar]
- Hirjee, H.; Brown, D.G. Solving misheard lyric search queries using a probabilistic model of speech sounds. In Proceedings of the International Society of Music Information Retrieval, Utrecht, The Netherlands, 9–13 August 2010; pp. 147–152. [Google Scholar]
- Hertz, G.Z.; Stormo, G.D. Identifying dna and protein patterns with statistically significant alignments of multiple sequences. Bioinformatics 1999, 15, 563–577. [Google Scholar] [CrossRef] [PubMed]
- Yamada, K.; Tomii, K. Revisiting amino acid substitution matrices for identifying distantly related proteins. Bioinformatics 2013, 30, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Long, H.; Li, M.; Fu, H. Determination of optimal parameters of MAFFT program based on BAliBASE3.0 database. SpringerPlus 2016, 5, 736–745. [Google Scholar] [CrossRef] [PubMed]
- Amancio, D.R.; Comin, C.H.; Casanova, D.; Travieso, G.; Bruno, O.M.; Rodrigues, F.A.; da Fontoura Costa, L. A systematic comparison of supervised classifiers. PLoS ONE 2014, 9, e94137. [Google Scholar] [CrossRef] [PubMed]



| Music | Bioinformatics |
|---|---|
| Melodies, chord progressions | DNA, proteins |
| Oral transmission, cover songs | Evolution |
| Variations, covers | Homologues |
| Tune family, clique | Homology, family |
| Cover song identification, melody retrieval | Homologue detection |
| Stability | Conservation |
| Summary statistics | TuneFam-26 | Csv-60 |
|---|---|---|
| Number of cliques | 26 | 60 |
| Clique Size median (var) | 13.0 (4.016) | 4.0 (1.146) |
| Sequence Length median (var) | 43.0 (15.003) | 26.0 (10.736) |
| AUC PID | 0.84 | 0.94 |
| Alphabet Size | 22 | 22 |
| Algorithm | 0.8–0.5 | 1–0.5 | 2–1.0 | 2–1.5 | 3–1.5 | 4–2 | 6–3 |
|---|---|---|---|---|---|---|---|
| Mafft-genaf | 0.57 (0.95) | 0.61 (0.83) | 0.71 (0.68) | 0.71 (0.68) | 0.70 (0.61) | 0.76 (0.53) | 0.75 (0.80) |
| Mafft-global | 0.72 (0.60) | 0.78 (0.60) | 0.77 (0.49) | 0.77 (0.48) | 0.75 (0.50) | 0.75 (0.41) | 0.76 (0.25) |
| Mafft-global-allowshift | 0.76 (0.83) | 0.75 (0.70) | 0.78 (0.49) | 0.78 (0.47) | 0.76 (0.46) | 0.82 (0.40) | 0.76 (0.26) |
| Mafft-local | 0.72 (0.58) | 0.71 (0.57) | 0.75 (0.50) | 0.78 (0.45) | 0.73 (0.46) | 0.76 (0.38) | 0.71 (0.24) |
| Mafft-local-allowshift | 0.69 (0.68) | 0.67 (0.72) | 0.78 (0.60) | 0.77 (0.45) | 0.79 (0.45) | 0.77 (0.35) | 0.77 (0.29) |
| T-Coffee | 0.65 (0.72) | 0.65 (0.72) | 0.62 (0.78) | 0.62 (0.78) | 0.63 (0.80) | 0.58 (0.95) | 0.58 (1.04) |
| Star | 0.00 (0.49) | 0.00 (0.48) | 0.04 (0.33) | 0.08 (0.37) | 0.13 (0.37) | 0.12 (0.29) | 0.12 (0.24) |
| Algorithm | Mafft-genaf | Mafft-global | Mafft-global-a | Mafft-local | Mafft-local-a |
|---|---|---|---|---|---|
| Mafft-global | |||||
| Mafft-global-a | |||||
| Mafft-local | |||||
| Mafft-local-a | |||||
| T-Coffee |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bountouridis, D.; Brown, D.G.; Wiering, F.; Veltkamp, R.C. Melodic Similarity and Applications Using Biologically-Inspired Techniques. Appl. Sci. 2017, 7, 1242. https://doi.org/10.3390/app7121242
Bountouridis D, Brown DG, Wiering F, Veltkamp RC. Melodic Similarity and Applications Using Biologically-Inspired Techniques. Applied Sciences. 2017; 7(12):1242. https://doi.org/10.3390/app7121242
Chicago/Turabian StyleBountouridis, Dimitrios, Daniel G. Brown, Frans Wiering, and Remco C. Veltkamp. 2017. "Melodic Similarity and Applications Using Biologically-Inspired Techniques" Applied Sciences 7, no. 12: 1242. https://doi.org/10.3390/app7121242
APA StyleBountouridis, D., Brown, D. G., Wiering, F., & Veltkamp, R. C. (2017). Melodic Similarity and Applications Using Biologically-Inspired Techniques. Applied Sciences, 7(12), 1242. https://doi.org/10.3390/app7121242







