1. Introduction
Spatial audio aims to reproduce a believable illusion for a listener being in a real acoustic space by electronic means [
1]. Dozens of different ways exist to record or artificially create the spatial sound signals, which are further reproduced with an array of loudspeakers or with headphones [
2]. For good spatial resolution, a high number of reproduction loudspeakers are often used in research facilities or in special venues, but such arrays are impractical in domestic or other daily listening environments. Therefore, the headphone reproduction of spatial sound is gaining interest. Commonly, the headphone-based spatial sound is implemented by virtualizing the reproduction loudspeaker array with the Head-Related Transfer Functions (HRTFs) [
3]. In essence, HRTFs are applied to virtually position the sound sources around the listener. The resulting binaural rendering can sound very convincing at the best, but, for some users, the sound is localized inside the head. To achieve better externalization, head-tracking devices are often used to compensate the movement of the listener’s head and to keep the reproduced auditory environment stable [
4,
5].
This work studies the virtual loudspeaker positioning in headphone-based spatial sound reproduction. The sound rendering is based on the Spatial Decomposition Method (SDM) [
6], which in essence analyzes directional information in spatial room impulse responses (RIRs). In brief, the SDM uses a compact array of microphones in a RIR measurement. Based on the time difference of arrivals between microphone pairs in short time windows, it estimates the direction of arrival (DOA) for each audio sample in the captured RIR. Therefore, the SDM allows a wide range of perceptual room acoustics studies, and it has been recently applied to study concert halls [
7,
8], studio control rooms [
9], car cabins [
10,
11], as well as stage acoustics for musicians [
12].
To reproduce the spatial sound analyzed with the SDM, audio samples in RIR are assigned to the loudspeakers of a given reproduction array. The assignment yields a number of sparse impulse responses equal to the number of loudspeakers used. The spatial sound is finally rendered by convolving sound signals with each of these sparse impulse responses. That is, the measured RIR is distributed spatially as convolution reverberators for a defined reproduction loudspeaker array.
Although the direction of arriving sound is accurately estimated in the analysis, the practical limits in the real or virtual loudspeaker array introduce varying amounts of angular error to the spatial sound reproduction. In the worst case, the mismatch between original and synthesized DOA may change the spatial image of the acoustic space drastically. In theory, all angular errors could be avoided and the analyzed sound field could be reproduced perfectly by assigning each sample to its own loudspeaker. However, this kind of approach is physically infeasible to implement, especially for real room-acoustic conditions.
One popular method to reduce the angular error in spatial sound synthesis is the Vector Base Amplitude Panning (VBAP) [
13]. VBAP weights each sound sample between the three closest reproduction loudspeakers so that the resulting sound appears to arrive from the original direction. When applied to all samples in the RIR, the spatial image of the space is reproduced correctly. However, it is known that amplitude panning of samples corresponds to time-averaging of multiple HRTFs, leading to low-pass filter effect on the perceived sound [
14].
Earlier studies employing SDM [
7,
8,
9,
10,
11,
12] have utilized a more straightforward synthesis method, namely Nearest Loudspeaker Synthesis (NLS), partially to circumvent the potential spectral issues with VBAP. NLS distributes each audio sample of a single monaural RIR to the nearest reproduction loudspeaker based on the estimated DOA information. Since only one reproduction loudspeaker at a time is involved in reproducing the RIR sample, this approach is free from the effects of HRTF averaging, but at the cost of increased angular error.
The aforementioned studies have used predetermined physical loudspeaker arrays for reproduction. Similar studies could still benefit from increased fidelity of spatial sound reproduction either by increasing the number of loudspeakers or by using the existing loudspeakers more efficiently. However, in many cases, adding loudspeakers is less feasible than optimizing the existing physical setup. When the reproduction of spatial audio is substituted with headphone listening, as in this study, the optimization becomes even more sensible. In theory, headphones enable the use of practically an unlimited number of virtual loudspeakers in any given direction. However, since the computational cost is directly proportional to the number of spatial channels rendered for headphones, using a smaller number of virtual loudspeakers is preferred. This requirement justifies smarter allocation of resources, which, in this case, means optimized virtual loudspeaker positions.
This paper presents a method of determining a room-specific virtual loudspeaker array that reproduces spatial sound perceptually more efficiently than a predetermined conventional array. The proposed method aims to minimize the directional error of NLS as well as to enhance labor-to-quality ratio of the rendering. In other words, spatial sound can be reproduced either more accurately with the same number of virtual loudspeakers, or at the same quality with a reduced channel number. These so-called optimized loudspeaker setups are compared with uniformly distributed setups to measure how recognizable are the differences in reproduction.
The paper is structured as follows. First,
Section 2 outlines the structure of the position optimization system. Next,
Section 3 describes the listening test, followed by the results in
Section 4. Finally, more detailed analysis is presented with discussion in
Section 5 and wrapped up in
Section 6.
2. Virtual Loudspeaker Position Optimization
The sound reproduction system used in this paper is similar to one presented by Tervo et al. [
10]. The system performs SDM analysis and NLS reproduction as described in
Section 1, resulting in a sparse impulse response (IR) for each reproduction loudspeaker. Finally, those sparse IRs are convolved with the audio signals to create the spatial sound. The used version of the SDM also post-equalizes the loudspeaker IRs as the rapid channel changes of the IR cause whitening of the signal. It should be noted that the optimization of the reproduction loudspeaker positions is done for SDM data before the convolution step. In other words, the optimization requires a spatial sound reproduction technique that has information on the spatial IR for each sound source, and thus cannot be applied to an arbitrary spatial sound reproduction technique.
The NLS requires information on the reproduction loudspeaker positions in order to be able to distribute the samples properly. As mentioned in
Section 1, the positions are usually static and not changed according to the acoustics of the space being reproduced. The method presented in this section replaces these static loudspeaker positions with optimal ones that are calculated from the RIR of the room being reproduced. The system used in reproduction is therefore the same as described above except for the way the loudspeaker setup is determined.
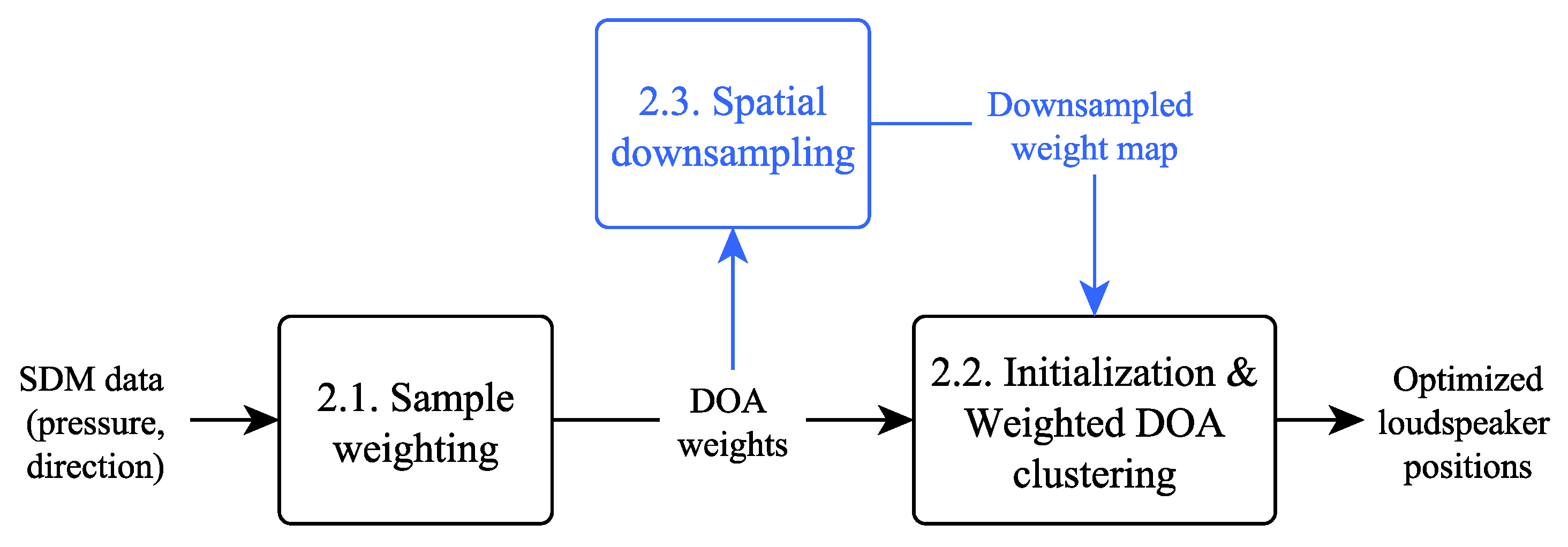
Figure 1 outlines the position optimization process which is done in two steps in its most basic form. First, SDM samples including RIR pressure and directional metadata (azimuth and elevation) are weighted according to their energy as well as their spatiotemporal properties. Then, loudspeaker positions are initialized based on the calculated weights and the final positions are obtained by clustering weighted DOAs iteratively until convergence. The clustering is computationally heavy by default due to a large number of RIR samples. To accelerate this process, the weighting data are reduced to a discrete number of equidistantly spaced points on the surface of a unit sphere, creating a downsampled spatial map of weights. Here, this operation is called spatial downsampling.
These steps are described in detail in the following subsections. First, the weighting and clustering operations are described, followed by the downsampling step.
2.1. Sample Weighting
Even though loudspeaker position optimization is calculated from the RIR, optimal results are not achieved with the pressure values of the IR alone. The early part of the RIR, which includes the direct sound and early reflections, can be assumed to contain the most important perceptual information about the acoustic space. As opposed to the late part, the central role of the early part is supported by its significance in the identification of the acoustic space [
15]. This is why it is reasonable to emphasize the early part of the response through directionally accurate reproduction. In addition, some of the DOAs calculated by the SDM describe the actual incoming direction of sound more accurately than others, which is discussed below in more detail. To take these presented properties into account in optimization, the first step in the process is to weight each pressure sample in the RIR accordingly.
The weighting is based on SDM data points—in other words, pressure and DOA of each audio sample in the RIR. As a whole, this information is called SDM data. The weighting
can be seen as a mapping of this data:
where
and
are the pressure and DOA values of the SDM data, respetively; and
N is the length of the IR in samples. In short, each SDM data point generates one scalar weight to be associated with itself.
Each weight consists of four distinct subweights named energy, delay, gradient and direction that are described in more detail below.
Energy weighting corresponds to the most traditional form of weighting. Each SDM data point is weighted according to its energy:
where
is the omnidirectional pressure value of the
nth data point. This gives more weight to data points with more incident energy.
Delay weighting emphasizes the SDM data points that locate in the earlier part of the RIR. Weighting is computed as a normalized backward Schroeder integral [
16] over the RIR:
This causes the direct sound and early reflections with distinctively more energy to be weighted more than samples in the later part of the response. This aspect is linked to psychocaoustics, as the early part of the RIR is perceptually more important than the late reverberation [
15].
Gradient weighting is used as a reliability measure to the SDM data points. The reliability of one SDM data point is dependent on the data points directly before and after it in time. If DOAs of the neighboring data points are close to the DOA of the current point, the point is given a large weight, and the greater the distance to its neighbors, the smaller the weight. The weight of one SDM data point is resolved as a mean of the distances between the DOA of the point and the DOAs of the previous and next data points:
where
h is the size of the time step between two SDM samples. The reasoning for this procedure is based on the fact that the SDM provides weighted average of the true DOAs in case of overlapping plane waves [
6,
10]. The set of samples over which the DOA changes can then be considered as spatially less accurate than samples with more steady DOA estimate.
Direction weighting emphasizes the data points that have a lot of energy arriving from their general direction regardless of the temporal information. The operation can be thought as a low-pass filter for directions; a single high-energy sample does not get a large weight unless there are more high energy samples in the same spherical sector. Conversely, the sectors with mainly low-energy samples are given a small weight. Perceptually, this operation can be thought as simulating the limits of perception. A single high energy sample cannot be heard separately but a longer period of time is needed to generate a perceivable acoustic event. Therefore, directions with more high-energy samples should be prioritized when searching for optimal loudspeaker positions. There is also a benefit in algorithmic means as the influence of high-energy sectors are spread, making it easier for the optimization algorithm to iterate to the directions with higher energy density. Similar to the spatial downsampling presented later in
Section 2.3, the general energy directions are approximated by calculating an energy map. First, an equidistant grid of points is created on the surface of the unit sphere, representing DOAs in the listener space. Then, each SDM data point is assigned to the closest point in this grid, measuring the distance from the DOA of the data point to the DOA of the grid point. When this nearest-neighbor search is ready, the energies of the assigned data points are accumulated grid point wise. The operation results in an energy map where the energy of different incoming directions has been approximated. Finally, the weight of the SDM data point is calculated from this map by interpolation:
where
is the DOA of
mth grid point,
M is the number of grid points and
is the energy value associated with the
ith closest grid point.
These four subweights form the final weight vector
through the following equation:
where
is a vector containing the values of one of the subweights described above and
is the corresponding mixing coefficient. As all
are equalized in range
, mixing coefficients practically adjust how much each partial weight vector reduces the resulting weights. Through the rest of the position optimization process, the weights are combined with their corresponding DOAs and used as a replacement for the pressure of the IR.
2.2. Initialization and Weighted DOA Clustering
As described before, NLS assigns each SDM data point to the closest loudspeaker in the reproduction array, resulting in a set of sparse IRs. However, the end result is not optimal as more important data points, for example early reflections, are allowed as much directional error as less direction-critical samples in the late reverberation. The weighting presented in the previous section solves the importance problem of different samples, but does not determine the actual virtual loudspeaker positions by itself. Therefore, weighted K-means clustering algorithm is used to find the most optimal loudspeaker positions based on the weighting data.
The aim of clustering is to find structure in the data iteratively, and the K-means algorithm is one of the most widely used clustering methods. The idea of the method is to minimize the Euclidean distance of the cluster data points by first assigning data vectors to cluster nodes and then update the node location according to the assigned vectors, most commonly to data mean. When these two operations are repeated, the result starts to converge towards the concentrations of data. However, the conventional K-means algorithm does not work in this case, as our data are not equally weighted. Instead, we use the weighted mean of the allocated samples to determine the cluster node position—or, as in this case, a new loudspeaker position. This causes the algorithm to position the node closer to the more weighted areas, effectively reducing the spatial error of directionally more important parts. The weights used by this algorithm are calculated as described in
Section 2.1.
The downside of the K-means algorithm is that the method is prone to find only a local optimum. To circumvent this problem, a good initialization of loudspeaker positions is required. Smart initialization not only boosts the probability of finding more optimal solution than a random one, but also helps the K-means to converge faster and find that solution in less time.
The initialization step is implemented in the presented system as follows. First, a weight map similar to the one used in direction weighting in
Section 2.1 is generated. There is one major difference: instead of using an equidistantly spaced point grid, the applied grid has equidistantly spaced points in the azimuth direction, but the elevation spacing is cosine-weighted. This procedure is applied to have every grid point to accumulate energy from approximately equally sized area. This kind of grid is also easier to sample from, as there is an equal number of azimuth points at each elevation angle. After equalizing the values of this map, it becomes a probability distribution function (pdf) which is later sampled from for new loudspeaker positions.
The initial loudspeaker positions are defined with Monte Carlo sampling. New positions are drawn from the weight distribution one-by-one and each new position is compared with all other positions already selected. If the new position is too close to any of the older locations, the sample is discarded and a new draw is made. If the new candidate is valid, it is stored and the sampling pdf is altered with Von Mises-Fisher distribution [
17] so that the proximity of the new position is picked less probably in the next iteration round. After drawing all the initial positions, the final positions are determined with weighted K-means clustering described above.
Occasionally, virtual loudspeaker positions tend to cluster during weighted K-means step iteration. In extreme cases, the final setup has two or more virtual loudspeakers positioned within a few degrees of each other. To eliminate such cases, each position has a repulsion area around itself. When two or more loudspeakers are moved too close to each other, the one with the most weight keeps its position while the others are relocated. The new positions are determined so that the relocated loudspeakers are as far from the other loudspeakers as possible. The repulsion area is gradually reduced to ensure that the algorithm converges even when there are lots of virtual loudspeakers to relocate.
Finally, the optimization algorithm described above is summarized in Algorithm 1. First, the initial loudspeaker positions are sampled from the weight map that is generated from the weights (
Section 2.3). The initial distances are controlled by rejecting the samples that are too close to previously sampled positions. When all the initial locations have been sampled successfully, the final positions are iterated by using weighted K-means clustering. Again, the distances of the iterated loudspeaker positions are monitored and loudspeakers with less weight are relocated in the case they come too close to more weighted ones. This relocation area is gradually reduced by the algorithm, which leads to convergence. The final result is then a set of virtual loudspeaker positions that are located close to the most weighted samples in their reproduction region.
| Algorithm 1 Virtual loudspeaker optimization by using weighted DOA clustering. |
| 1: | function OptimizeLoudspeakerPositions() |
| 2: | CalculateWeightMap() | ▹ Initialize loudspeaker positions |
| 3: | SampleWeightMap() |
| 4: | repeat | ▹ Calculate weighted K-means |
| 5: | |
| 6: | |
| 7: | for do |
| 8: | | ▹ find the closest loudspeaker to the SDM data point |
| 9: | end for |
| 10: | for do |
| 11: | | ▹ assign the data point to the ith loudspeaker |
| 12: | | ▹ weighted mean of the assigned DOAs |
| 13: | end for |
| 14: | | ▹ Apply repulsion area |
| 15: | for do |
| 16: | | ▹ distance to the closest neighbor |
| 17: | end for |
| 18: | for all , from smallest to largest do |
| 19: | vertices of a Voronoi diagram of | ▹ potential furthest points |
| 20: | | ▹ Select the furthest from all |
| 21: | end for |
| 22: | reduce |
| 23: | until all threshold |
| 24: | return |
| 25: | end function |
2.3. Spatial Downsampling
The optimization process described in
Section 2.1 and
Section 2.2 is already a working solution, which finds the optimized virtual loudspeaker positions from the SDM data. However, the process is slow due to the amount of data. The complexity of K-means algorithm is directly proportional to the number of data points clustered. As an IR of a regular concert hall is approximately two seconds long, there are 96,000 data points after SDM analysis when using 48 kHz sampling rate. Finding the optimal positions over the whole data is possible, but requires long computation time to complete. However, a considerable speedup is possible by reducing the number of data points. If the reduced data are used to find a coarse approximation of the positions, and the whole data are only used to fine-tune the result, a considerable speedup may be achieved. Here, this data reduction step is called spatial downsampling.
The implementation of spatial downsampling is similar to direction weighting and initialization of loudspeaker positions described before. The SDM data points are condensed to equidistant point grid on the unit sphere. The difference is that the energy of each data point is distributed between the three closest grid points in order to get more accurate approximation of the surrounding energy field. The distribution is calculated by determining barycentric coordinates of the data point with respect to those three closest grid points. The reduced point grid is then used instead of SDM data to initialize and optimize the virtual loudspeaker positions. After the optimization algorithm has converged, the reduced data are replaced by the original SDM data and the final optimized positions are fine-tuned from the reduced data optimum. The processing time is shortened due to reduced data, but the result is the same as without the reduction due to the fine-tuning step.
3. Perceptual Evaluation with a Listening Test
The performance of the virtual loudspeaker location optimization and its effect on the perceived spatial sound reproduction was evaluated with a subjective listening test. The aim of the listening test was to examine how perceivable the differences are in two typical use cases of the SDM-based spatial sound. The first case was a stereo music played in a dry studio control room and the second case was an orchestra music performance set to the acoustics of a concert hall. It should be noted that the first case has two sound sources in a small space and the second one has 24 sound sources in a large space.
3.1. Listening Test Setup and Sound Signals
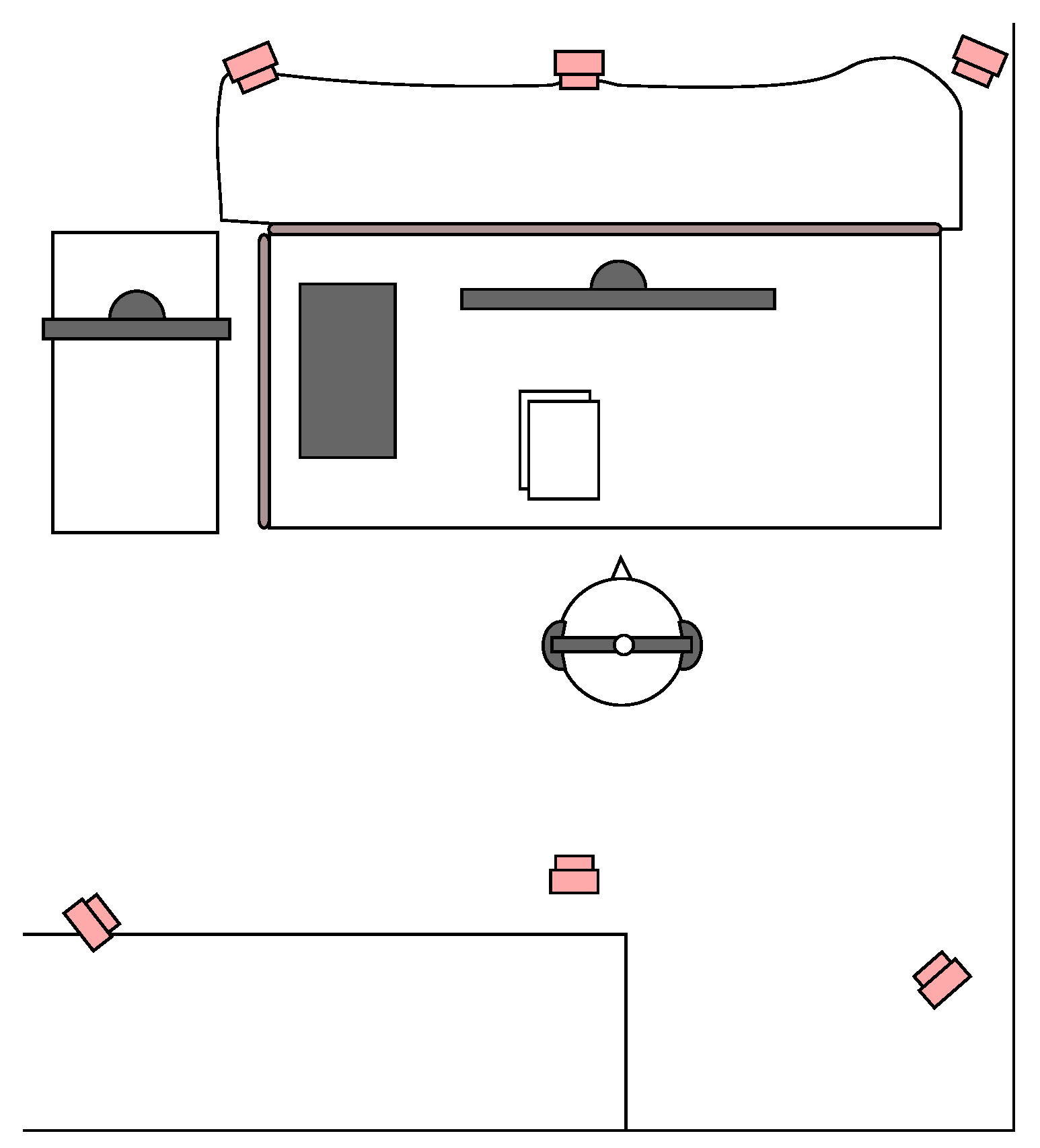
The listening test setup is illustrated in
Figure 2. The setup consisted of a desk, a computer and noise canceling headphones (Bose QuietComfort 25) and was located in the corner of a quiet open plan office. The listener’s head was tracked with a commercial tracking system (Optitrack V100 and TrackingTools software, version 2.5.3; 2012 by NaturalPoint Inc., Corvallis, OR, USA) that utilizes six infrared cameras surrounding the listening space. To reduce visual distractions, the front field of view of the subject was obscured with a curtain. The listening test program was built on the Unity engine and it utilized head tracking in six degrees of freedom. HRTFs were generated from a scanned human head with a fast boundary element method [
18] in far field. All the participants used the same HRTF set containing 836 directions. No interpolation was used between the HRTFs and the filter was swapped without cross-fading.
The experiment consisted of two test sets. Both sets introduced different listening conditions in order to compare loudspeaker optimization performance. The acoustic spaces were a studio control room in Helsinki, Finland and Musikverein concert hall, Vienna, Austria, later referred to as a “small room” and a “concert hall”, respectively. The small room RIRs had been measured with stereo pair of loudspeakers, whereas the acoustic response of the concert hall had been captured by using loudspeaker orchestra [
7]. Based on these prior measurements, the SDM analysis had been done for both rooms in advance.
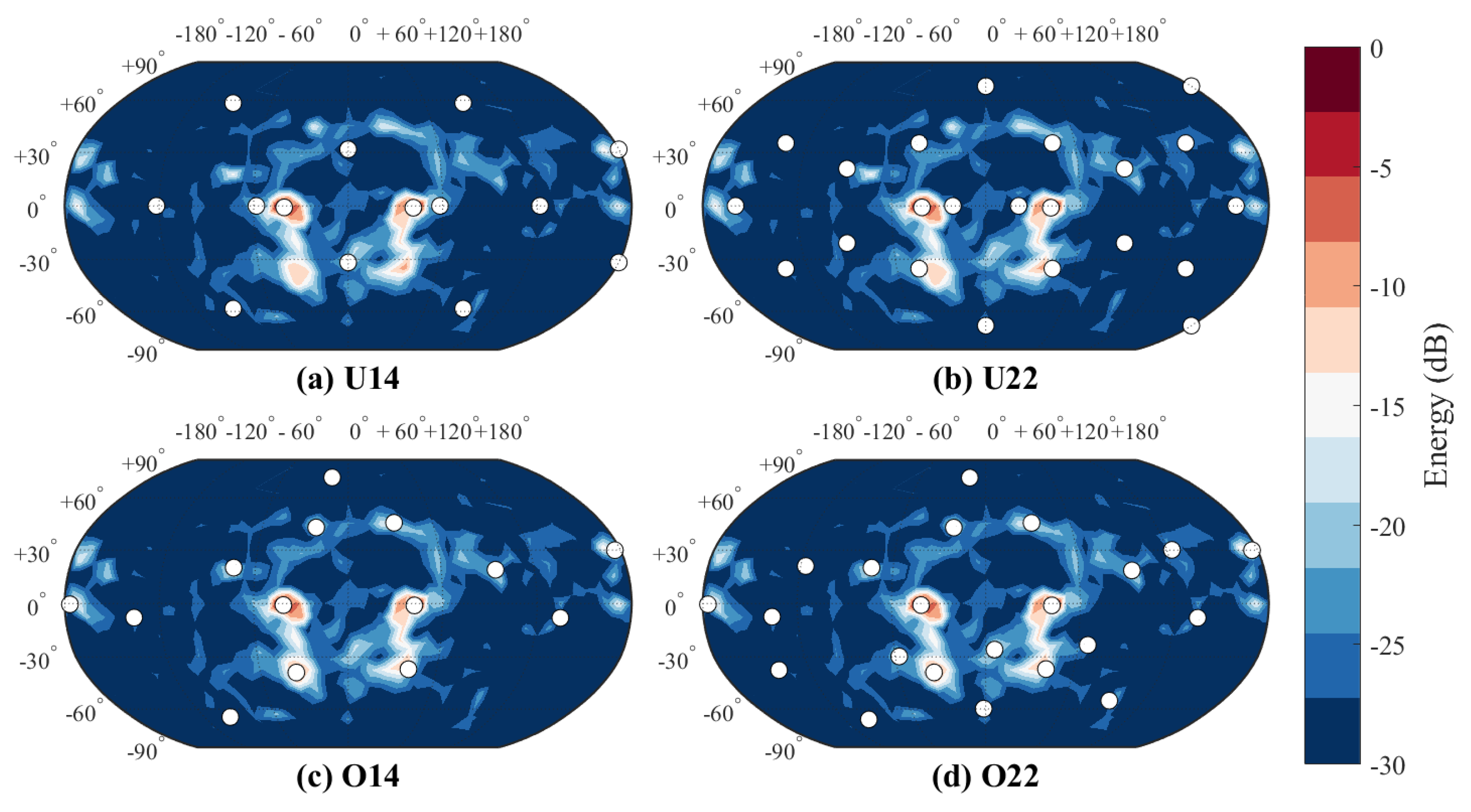
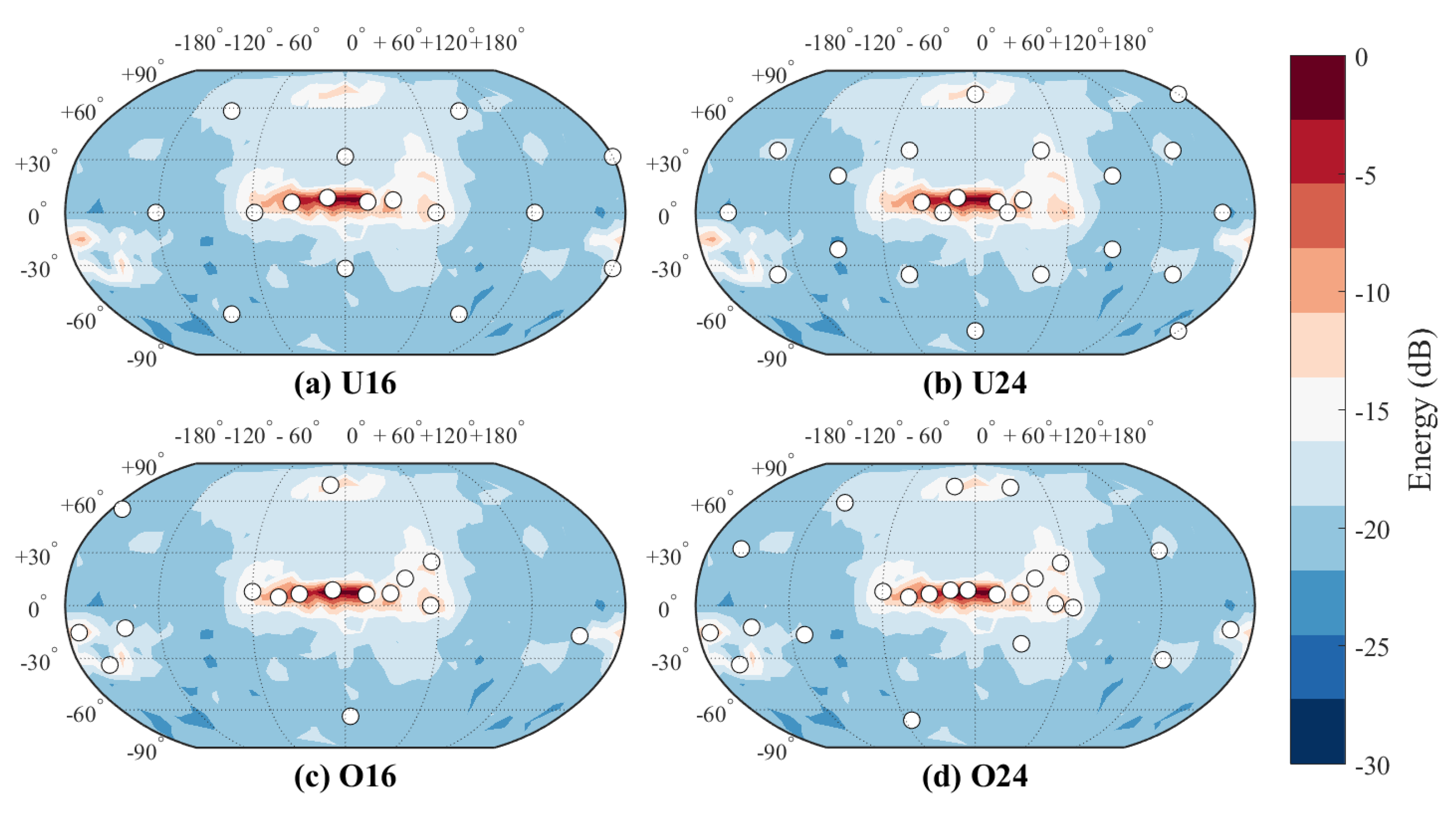
Both sets contained four different virtual loudspeaker setups; two position optimized setups and two uniformly distributed setups with fixed virtual loudspeaker positions for direct sounds. In
Figure 3 and
Figure 4, all these conditions have been illustrated for both spaces. The optimized loudspeaker setups were visually inspected for potential loudspeaker clusters, and uniform setups were based on Platonic solids.
The sound signals used were typical for both rooms. Since the small room was measured with traditional stereo setup, a stereo signal was used. In our case, a 34-s excerpt from the beginning of Céline Dion’s song “Because You Loved Me” was selected. For the concert hall, the music signal selected for the loudspeaker orchestra was Jean Sibelius’s Lemminkäinen suite, 1st part, 851–885 s. The orchestra signals were captured in professional recording with 21 close microphones for different instrument groups as quasi-anechoic material, which were then mapped to 24 measurement source channels in the loudspeaker orchestra.
The reproduction levels of all presented stimuli were equalized. This was accomplished by computing the equivalent level
of combined virtual loudspeaker channels as
where
M is the number of channels,
N is the length of one signal and
is the input signal of channel
i. This level was then used to calculate level alignment coefficient
:
where
dB was the target level. Finally, all output channels were multiplied by
to get the level aligned multichannel sound.
3.2. Listening Test Method
The listening test was executed as an ABX discrimination test. Subjects were asked to answer a question: “Which one of the samples A or B is the reference X?”. Moreover, they were asked to write down the criterion that they used to discriminate the reference from the odd sample. If they could not discriminate the samples from each other, they were asked to choose their answer at random. Full comparison between four conditions forms six pairs, which were repeated four times. Thus, a total of 24 stimulus triplets were presented for both rooms. A preference test was also considered as an option for the listening test. However, the differences between some of the samples were found to be small during preliminary tests, which made the asking for a preference unfeasible. Preference is also a matter of taste, which would have required more participants in the test, in case there would have been more than one preference group.
The listening test started with the participant reading and signing a paper of informed consent describing the test procedure, possible harm, and data policy. Then, the subject did both test sets in randomized order. Before each set, there were a training set of four ABX triplets, during which the listener was instructed to adjust the listening volume to a reasonable level. After the training set, the subject was asked to keep the volume at the same level during the test set. The subject was given an option to take a break between the test sets, and after completing the experiment, a small non-monetary compensation was offered to the subjects.
3.3. Statistical Analysis
The ABX test is designed to detect the small differences of the compared signals. Therefore the difference should not be detected by all the participants or otherwise the test loses its purpose. The contrary also holds: if the difference is too small, all participants have to guess and the result of the experiment is statistical noise. That being said, an approximation to the ability to distinguish the sound samples is needed to determine the expected detection rate over the listener population. In other words, the experimenter should decide how big portion of the subjects has truly heard the difference in the samples. When determining the threshold, one should also keep in mind the time and resources that can be used—smaller threshold needs more subjects and vice versa. The limit selected for this experiment is a compromise between distinction and the number of subjects; the expected detection threshold was set at one third of the population.
The determined threshold cannot be used directly to determine how large proportion of subjects has successfully discriminated the difference. Instead, the determined threshold needs to be adjusted to calculate the proportion
with the rearrangement of Abbot’s formula [
19]:
where
is the proportion of subjects that truly noticed the difference and
is the proportion of the population that got the test right by chance.
basically tells us the proportion of subjects that should score the sample pair right to prove the alternate hypothesis right.
After calculating the required observed proportion, the required number of subjects can be approximated with the following equation [
19]:
where
and
are the corresponding Z-scores of selected false positive and negative rates;
is the chance probability;
is the chosen probability for an alternate hypothesis; and
,
. However, required subject count becomes prohibitively large if our selected detection threshold is used for a simple ABX test setup. The reason for this is the chance of a subject guessing the correct sample—for the used test, the chance rate is 50 percent per evaluated pair. According to the Equation (
12), 94 participants would be needed to ensure the significance of the effect. To reduce the number of required subjects, replications of the same samples were used. The strategy was to make the participant evaluate the same sample pair multiple times. The subject was required to get all the replications right for the test case in order to count the sample as properly discriminated. The number of replications in this test was set at four times per sample pair, effectively reducing the chance rate to 6.25 percent and the number of required participants to 15 people.
To calculate Z-score for the results, the proportion of true discriminators should be calculated from the results. The equation for calculating the adjusted proportion
can be derived from Equation (
11):
From
, Z-score can be calculated with a binomial test for proportions [
19]:
where
N is the number of subjects. Finally, 95 percent confidence intervals were calculated [
19]:
where
is the Z-score for 95 percent confidence interval and
is the standard error for the adjusted proportion of discriminators [
19]:
4. Results
A total of 17 subjects participated in the listening test out of which 15 completed the whole experiment. The population consisted of acoustics experts and an audio engineer. Three people reported some kind of hearing defects: small dips, slight oversensitivity and 10 dB hearing threshold difference between right and left ears. However, these defects did not affect the test performance of these particular subjects, which is why their data was not excluded from the results. Both subjects that did not finish reported hearing clicking sounds during cross-fade, thus preventing them from focusedly discriminating the stimuli. However, only a few participants who finished the test reported observing this phenomenon or being distracted by it.
4.1. Discrimination
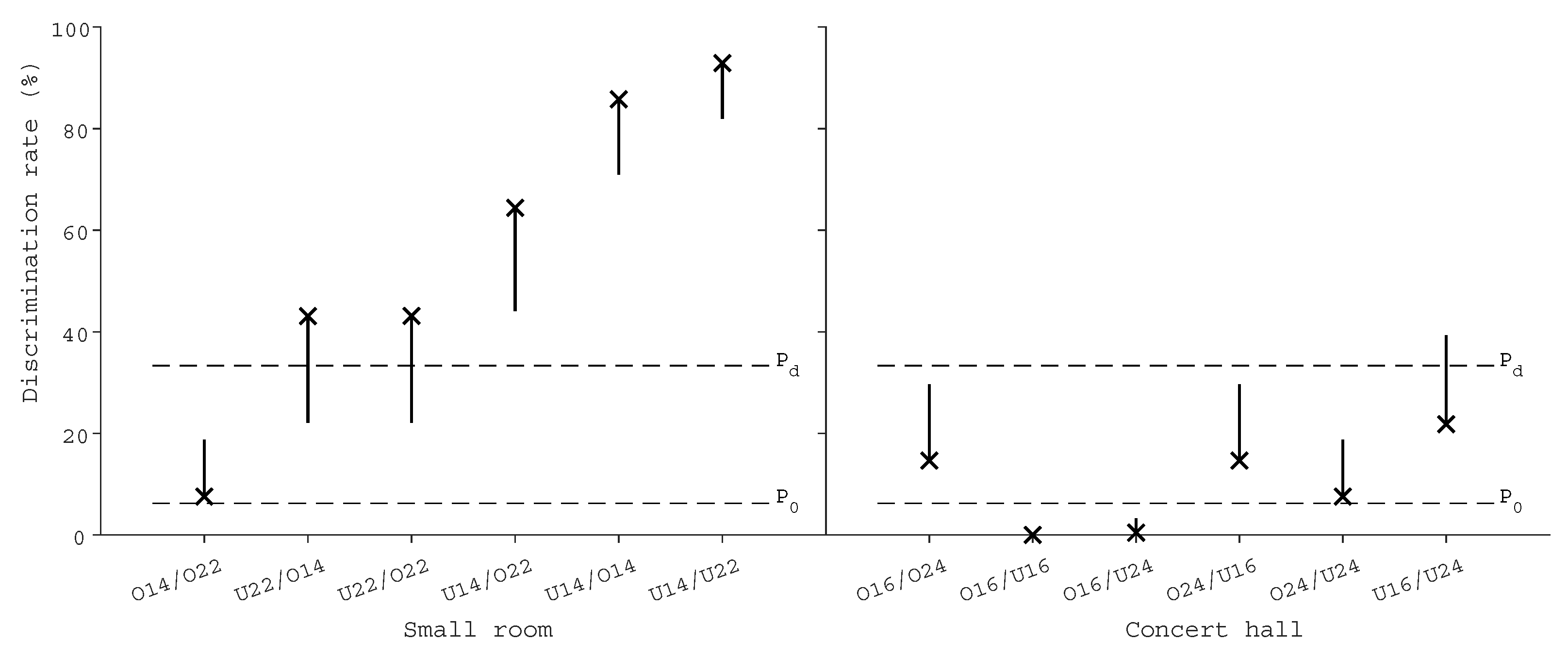
Discrimination results for all test cases are presented in
Figure 5, each case presenting the chance-corrected discrimination rate (a cross) and its one-tailed 95 percent Confidence Interval (CI). In addition, the selected detection threshold P
and chance rate P
have been visualized. The numerical values of the results are tabulated in
Table 1.
In the small room case, five out of six comparisons were significantly recognizable. Especially U14 has been clearly separated from the others. Both cases involving U22 were also recognized by a smaller margin; the cases are clearly over the chance rate, but may be heard less than third of the population within the limits of the confidence intervals. Comparison between optimized setups did not cross P, thus reaching significant similarity. In other words, less than one third of the population can ever discriminate the setups from each other.
On the contrary, none of the concert hall comparisons were significantly recognizable. Comparison of uniform setups appeared to be the most recognizable out of these setups, but further experiments are needed to conclude how recognizable the case is in the end. The rest of the comparisons and their CIs did not cross P, again reaching significant similarity. In particular, comparison between O16 and uniform setups could not be recognized, probably because the direct sound was reproduced similarly in all of them.
4.2. Discrimination Criteria
The discrimination criteria reported by subjects on a paper form were first encoded into electrical form. These answers were then interpreted and translated into English by using the wheel of concert hall acoustics [
20], each answer translating into one or more terms. Then, the resulting attributes were sorted and accumulated so that the frequencies of all individual attributes could be reported for every sample pair separately. Only those attributes were included in the analysis whose corresponding discrimination was correct.
The results of the analysis have been reported in order of frequency in
Table 1. The most frequent perceptual discriminating factors between conditions were image shift, reverberance, and width. The small room had also reported differences in spectral balance, spatial impression and timbre. In the concert hall renderings, loudness differences were reported in addition to the attributes used also for the small room.
Image shift was most frequently reported as the discriminating attribute in the small room. Uniform setup with 14 loudspeakers (U14) systematically collected the most reports, which reflects the high discrimination rate. In addition, the difference in reverberance made the discrimination of uniform setups (U14 vs. U22) even easier. Optimized setup with 14 loudspeakers (O14) had notable differences in spectral balance when compared with uniform setups. Most frequent reports on spatial impression concentrated in comparison of U22 to both O14 and U14.
The elicited attributes in concert hall pairs were not as distinct as in the case of the small room. The most evident differences were width in O16 vs. U16 and spectral balance in U16 vs. U24. Otherwise the distribution of answers was more uniform. In O16 vs. O24 loudness appeared the most frequent factor, as image shift and reverberance did in the case of O16 vs. U24. In the rest of the cases, there was no consensus on discriminative attributes.
5. Discussion
As the results show, the listening conditions drastically affect how well the differences in virtual loudspeaker positioning are noticed in binaural reproduction. The small room case appeared very susceptible to perceived image shifts and altered reverberance when the reproduction loudspeaker configuration was changed, whereas the changes in the setups were barely noticeable with the concert hall case.
As visualized in
Figure 3, perceived image shifts in the small room are explainable by the changes in the directions of early reflections. There are four strong reflections visible above the direct sounds, as well as reflections from the desk. The virtual loudspeakers of U14 that reproduce those directions are far from the reflections, whereas optimized setups have co-located loudspeakers for each of them. In U22, virtual loudspeakers are also off from those directions, but they are closer to them than in U14. This partly explains why U22 is as easy to discriminate from the optimized setups as U14 is. Visual inspection also suggests that O14 is a subset of O22, explaining why they are difficult to discriminate from each other. In short, strong early reflections affect the spatial image drastically, therefore requiring precise reproduction of their directions.
A notable aspect in the concert hall case is that the directions of early reflections did not play as large role as they did in the small room. The direct sound reproduction loudspeakers were positioned identically between O16 and uniform setups, making discrimination between the setups hard. O24 had more loudspeakers optimized to reproduce direct sounds, thus being more distinctive than O16 when compared with uniform setups. Finally, U16 and U24 could probably have been discriminated from each other because of the combined effect of differences in the reproduction of side, ceiling and back wall reflections. To summarize, direct sounds dominate the spatial impression, allowing more drastic changes in reflection directions before the difference is heard.
The small room case had only two sound sources with 60 degree separation. The reflections are then relatively scarce, therefore likely more audible and susceptible to changes in reproduction. The concert hall case in turn had 24 densely located sound sources, each having their own set of reflections and source signals. As the source positions are close to each other at the stage, most of the reflections are coming from adjacent directions. However, as these directions are not precisely the same, the reflections are spread over a larger area than in the two-channel case, therefore making the precise direction of the reflection fuzzier. However, more experiments are needed in different spaces to prove this theory.
Another difference between the cases is the strength of the reverberation. Small room has only little if any diffuse reverberation, whereas the concert hall has prominently longer and more diffuse reverberation. Strong reverberant field may reduce the importance of correct spatial reproduction of earliest reflections. This psychoacoustic factor remains hypothetical and also needs more research.
6. Conclusions
The aim of this study was to present a method of optimizing virtual loudspeaker positions for spatial sound reproduction with head-tracked headphones. The rendering of spatial sound was implemented with the Spatial Decomposition Method in combination with nearest loudspeaker synthesis to analyze and reproduce measured room impulse responses in perceptual room acoustics studies. These studies have earlier used a static loudspeaker array to synthesize spatial impulse responses convolved with sound signals. However, a static reproduction array is not an optimal way of reproduction when concerning the arbitrary directions of early reflections. This is especially the case with headphones where the loudspeakers are virtualized with the help of HRTFs.
The implementation was evaluated with a discriminative listening test, which consisted of one simple and one complex auditory scene. They were a small room with stereo loudspeaker audio and a concert hall with 24 channel orchestra music. The results implied that optimization of virtual loudspeaker positions is important in a small room. This is because misplaced early reflections cause image shifting and change perception of reverberance. However, this effect was not so large in the concert hall case. In any case, the number of virtual loudspeakers can be reduced to minimize the real-time computation required for HRTF processing, if the directions of direct sounds and early reflections are accurately reproduced. The study for the minimum number of virtual loudspeakers needed without deteriorating the sound quality is left for future work.