Exploring the Effects of Pitch Layout on Learning a New Musical Instrument †
Abstract
Featured Application
Abstract
1. Introduction
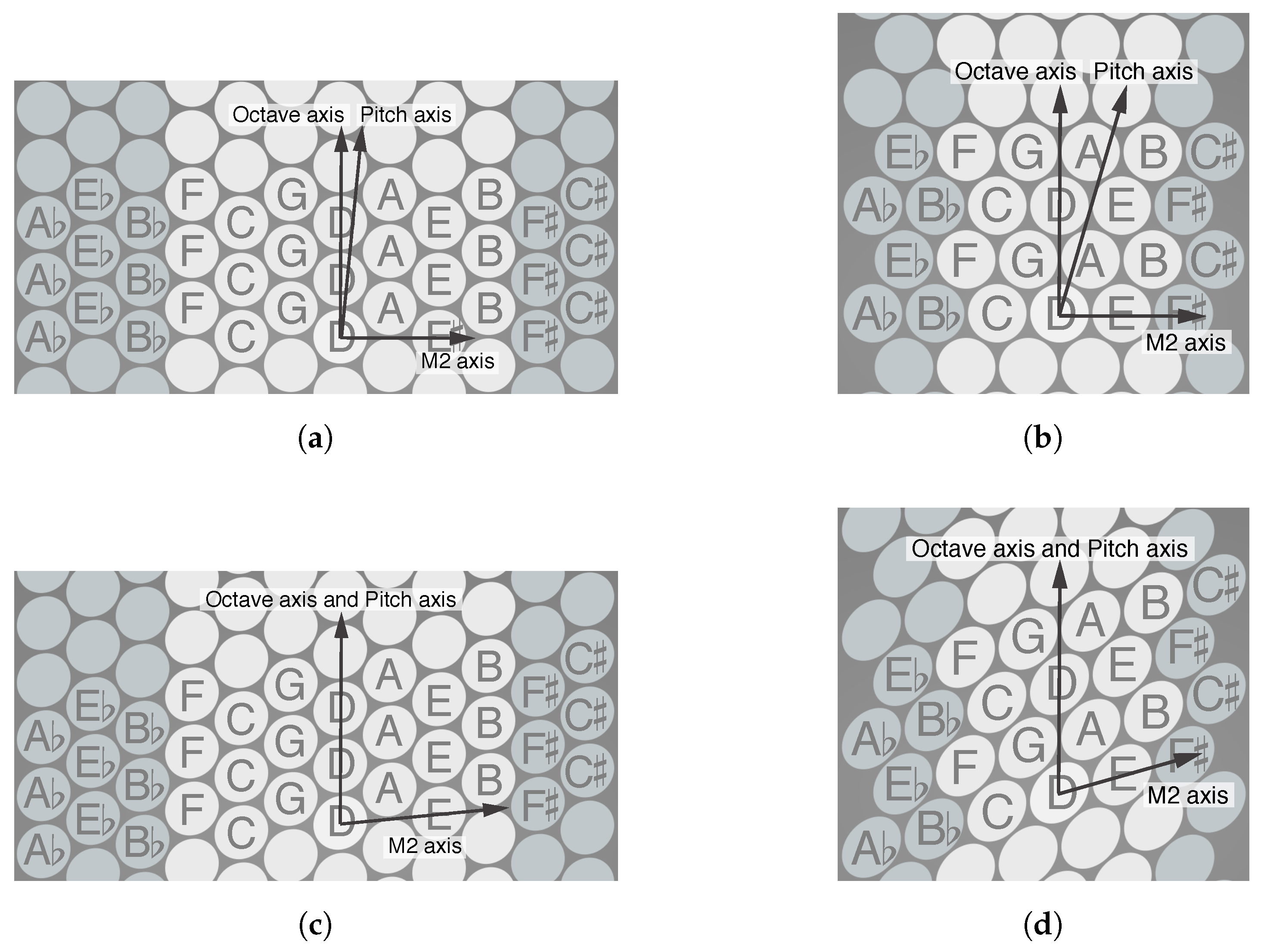
1.1. Isomorphic Layout Properties
- The octave axis is here defined as any axis that passes through the closest button centres that are an octave apart.
- The major second axis (M2 axis, for short) is here defined as any axis that passes through the closest button centres that are a major second apart.
1.1.1. Adjacent (A) or NonAdjacent () Seconds
1.1.2. Sheared (S) or Unsheared ()
1.2. Motor Skill Learning in Music Performance
- A cognitive stage, encompassing the processing of information and detecting patterns. Here, various motor solutions are tried out, and the performer finds which solutions are most effective.
- A fixation stage, when the general motor solution has been selected, and a period commences where the patterns of movement are perfected. This stage can last months, or even years.
- An autonomous stage, where the movement patterns do not require as much conscious attention on the part of the performer.
1.3. Study Design
- Adjacency , where 0 is the code for a layout with non-adjacent major seconds ( or ), and 1 is the code for a layout with adjacent major seconds ( or ).
- Shear , where 0 is the code for an unsheared layout ( or ), and 1 is the code for a sheared layout ( or ).
- LayoutNo , where 0 is the code for the first layout played by a participant, 1 is the code for the second layout they played, and 2 is the code for the third and final layout they played.
- PerfNo , where 0 is the code for their first performance of a given layout, 1 is the code for their second performance of a given layout, 2 is the code for their third performance of a given layout, 3 is the code for their fourth performance of a given layout. Note that participants gave three performances for the training, two performances for the immediate retention tasks, and four performances for the transfer task.
- then then
- then then
- then then
- then then .
2. Results
2.1. Modelling Approach
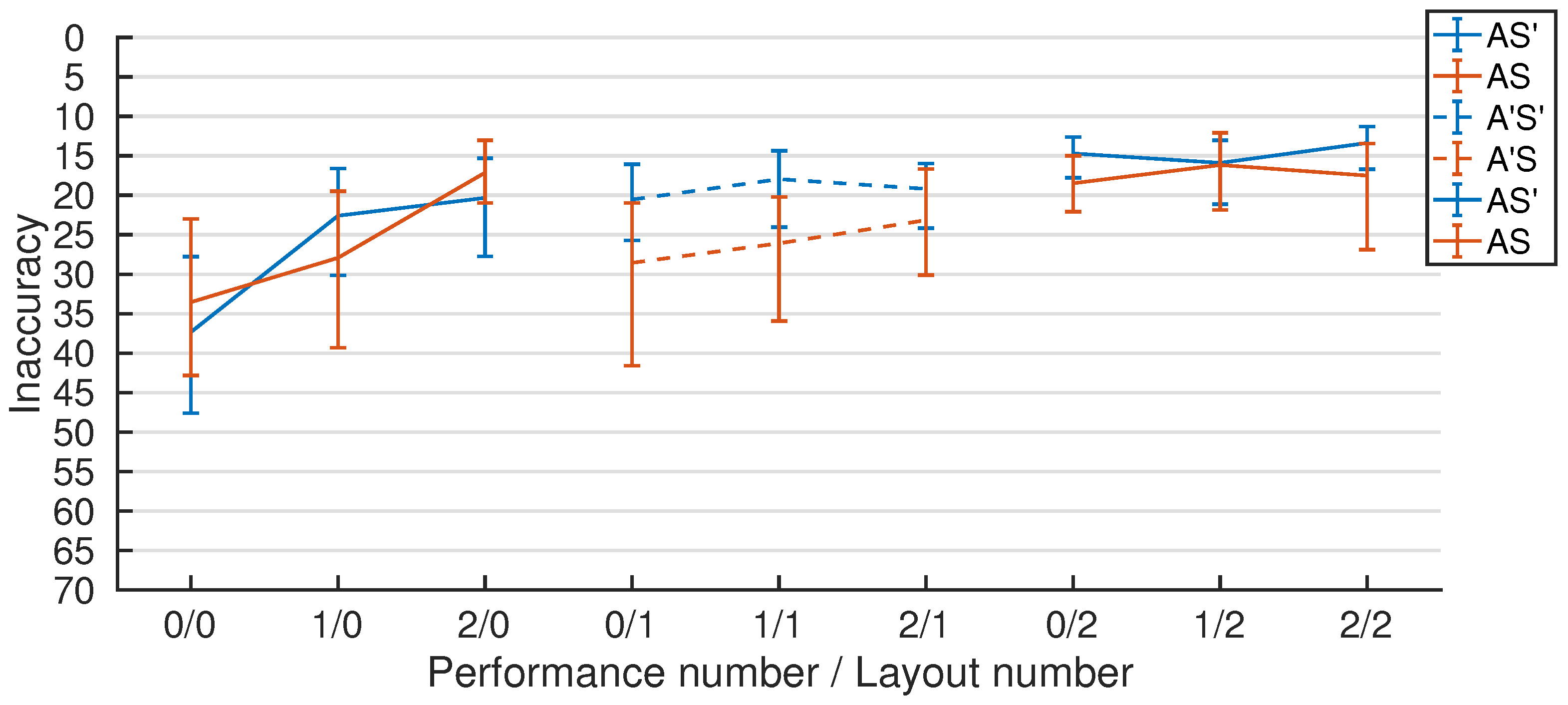
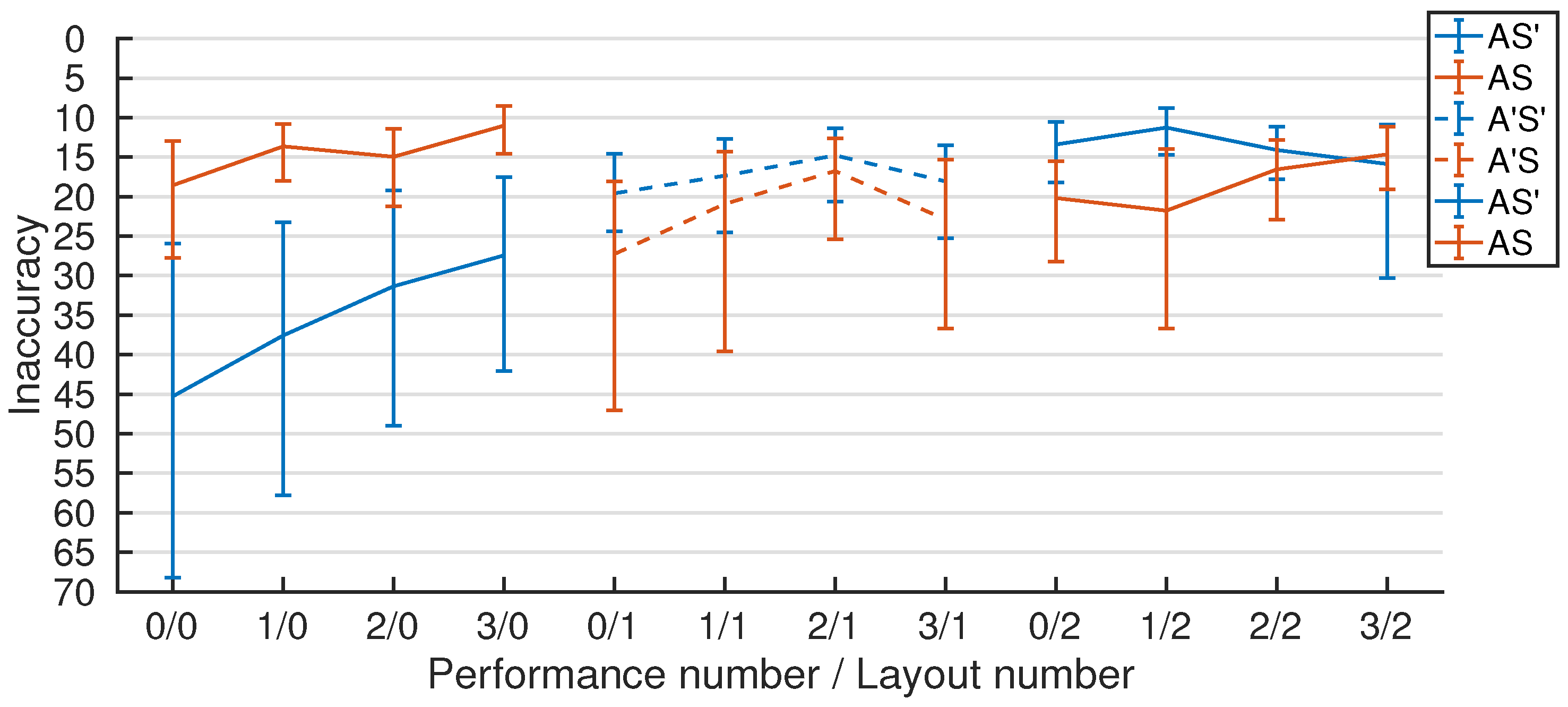
2.2. Training Performances
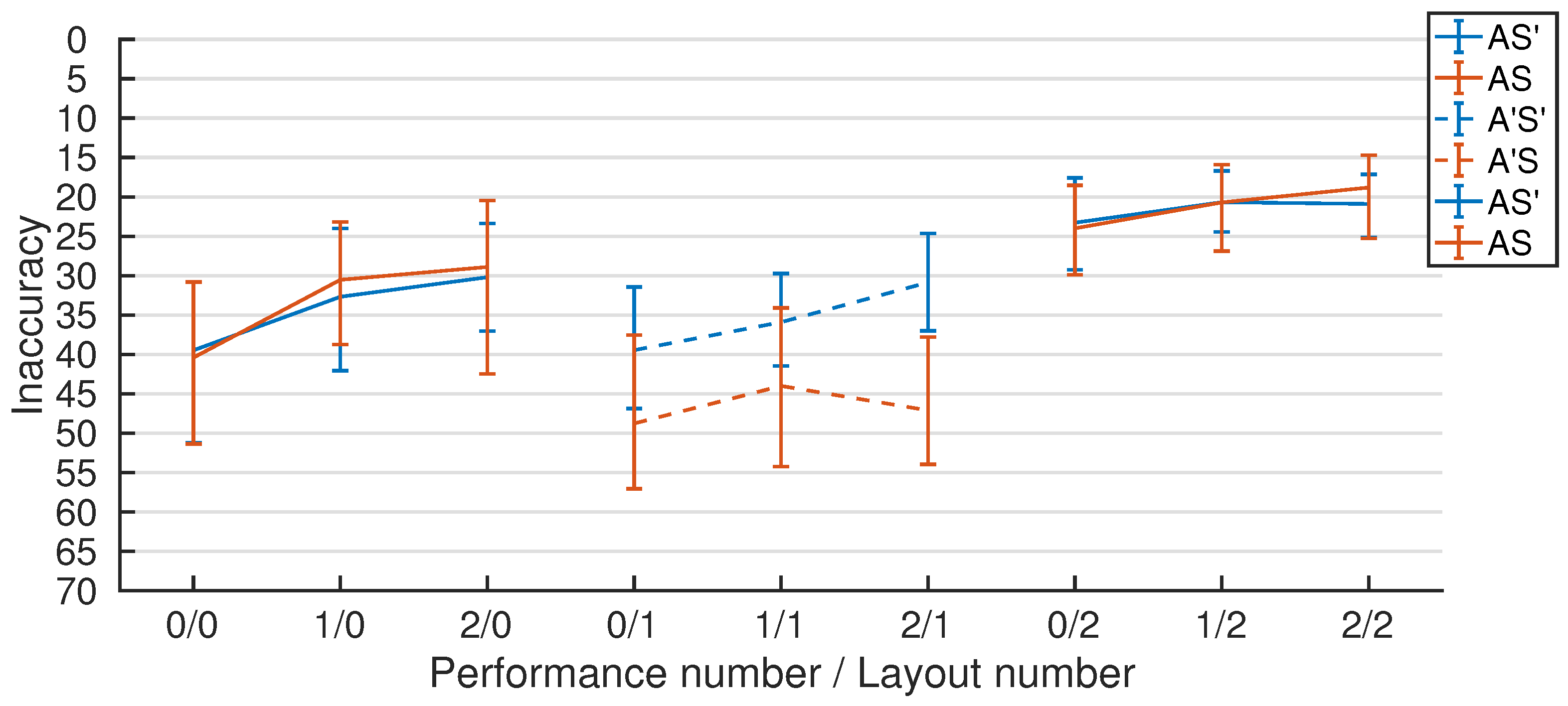
2.3. Immediate Retention
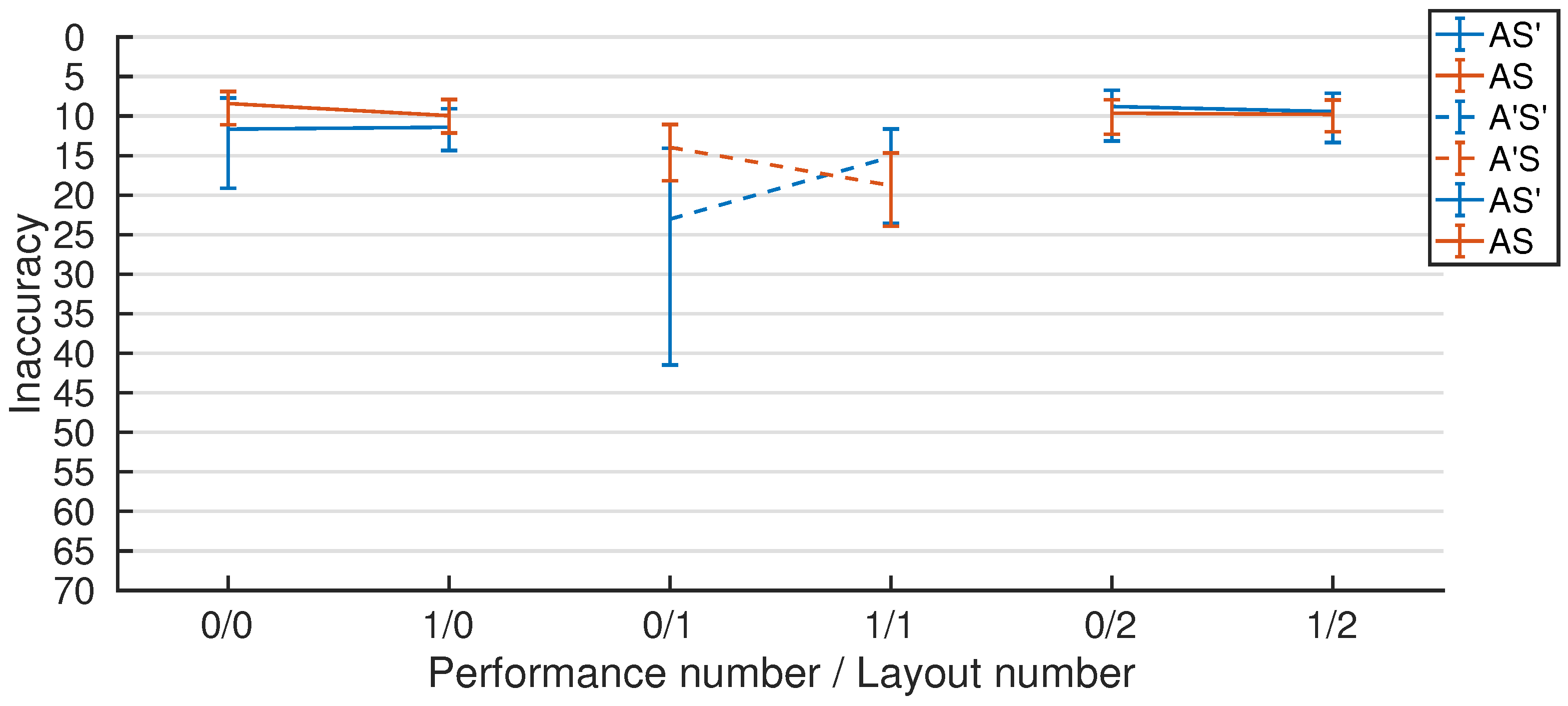
2.4. Transfer
3. Discussion
3.1. PerfNo and LayoutNo
3.2. Adjacency
3.3. Shear
3.4. Limitations
3.5. Summary
4. Methods
4.1. Participants
4.2. Materials
4.2.1. Hardware and Software
4.2.2. Musical Tasks
4.3. Procedure
4.3.1. Training Paradigm and Testing of Immediate Retention
- watching the sequence once as demonstrated by audiovisual highlighting
- playing along with the audiovisual highlighted sequence three times (training)
- reproducing the sequence in the absence of audiovisual highlighting, for two consecutive performances (immediate retention task)
4.3.2. Transfer Task
4.4. Measuring Performance Inaccuracy
4.4.1. Training Tasks
- N is the total number of notes in the target sequence
- is the time in milliseconds of nth target note
- is the time in milliseconds of first performed note within the time window that matches the pitch of the target note.
4.4.2. Retention and Transfer Tasks
- N is the total number of notes in the target sequence.
- C is the total number of notes in the corrected performance.
- is the time in milliseconds of the cth note in the corrected performance.
- is the time of the metronome beat closest to the performed note .
- E is the number of errors calculated as explained above.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- MacRitchie, J.; Milne, A.J. Evaluation of the Learnability and Playability of Pitch Layouts in New Musical Instruments. In Proceedings of the 14th Sound and Music Computing Conference, Espoo, Finland, 5–8 July 2017; pp. 450–457. [Google Scholar]
- Bosanquet, R.H.M. Elementary Treatise on Musical Intervals and Temperament; Macmillan: London, UK, 1877. [Google Scholar]
- Helmholtz, H.L.F. On the Sensations of Tone as a Physiological Basis for the Theory of Music; Dover: New York, NY, USA, 1877. [Google Scholar]
- Wicki, K. Tastatur für Musikinstrumente. Swiss Patent 13329, 30 October 1896. [Google Scholar]
- Keislar, D. History and principles of microtonal keyboards. Comput. Music J. 1987, 11, 18–28. [Google Scholar] [CrossRef]
- Array Instruments. The Array Mbira. Available online: http://www.arraymbira.com (accessed on 24 October 2017).
- Paine, G.; Stevenson, I.; Pearce, A. Thummer Mapping Project (ThuMP) Report. In Proceedings of the 2007 International Conference on New Interfaces for Musical Expression (NIME07), New York, NY, USA, 6–10 June 2007; pp. 70–77. [Google Scholar]
- C-Thru Music. The AXiS-49 USB Music Interface. Available online: http://www.c-thru-music.com/cgi/?page=prod_axis-49 (accessed on 24 October 2017).
- Park, B.; Gerhard, D. Rainboard and Musix: Building Dynamic Isomorphic Interfaces. In Proceedings of the International Conference on New Interfaces for Musical Expression, Daejeon, Korea, 25–31 May 2013; pp. 319–324. [Google Scholar]
- Roger Linn Design. LinnStrument: A Revolutionary Expressive Musical Performance Controller. Available online: http://www.rogerlinndesign.com/linnstrument.html (accessed on 24 October 2017).
- ROLI. ROLI | BLOCKS. Available online: https://roli.com/products/blocks (accessed on 24 October 2017).
- Terpstra, S.; Horvath, D. Terpstra Keyboard. Available online: http://terpstrakeyboard.com (accessed on 24 October 2017).
- Milne, A.J.; Sethares, W.A.; Plamondon, J. Isomorphic controllers and Dynamic Tuning: Invariant fingering over a tuning continuum. Comput. Music J. 2007, 31, 15–32. [Google Scholar] [CrossRef]
- Huygens Fokker Foundation. Microtonality - Scales. Available online: http://www.huygens-fokker.org/microtonality/scales.html (accessed on 24 October 2017).
- Prechtl, A.; Milne, A.J.; Holland, S.; Laney, R.; Sharp, D.B. A MIDI sequencer that widens access to the compositional possibilities of novel tunings. Comput. Music J. 2012, 36, 42–54. [Google Scholar] [CrossRef]
- Milne, A.J.; Sethares, W.A.; Plamondon, J. Tuning continua and keyboard layouts. J. Math. Music 2008, 2, 1–19. [Google Scholar] [CrossRef]
- Vos, P.G.; Troost, J.M. Ascending and descending melodic intervals: Statistical findings and their perceptual relevance. Music Percept. 1989, 6, 383–396. [Google Scholar] [CrossRef]
- Euler, L. Tentamen Novae Theoriae Musicae ex Certissismis Harmoniae Principiis Dilucide Expositae; Saint Petersburg Academy: Saint Petersburg, Russia, 1739. [Google Scholar]
- Zatorre, R.J.; Chen, J.L.; Penhune, V.B. When the brain plays music: Auditory-motor interactions in music perception and production. Nat. Rev. Neurosci. 2007. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, R.A.; Lee, T.D. Motor Control and Learning, 5th ed.; Human Kinetics: Champaign, IL, USA, 2011. [Google Scholar]
- Kunde, W.; Koch, I.; Hoffmann, J. Anticipated action effects affect the selection, initiation, and execution of actions. Q. J. Exp. Psychol. Sect. A 2004, 57, 87–106. [Google Scholar] [CrossRef] [PubMed]
- Rusconi, E.; Kwan, B.; Giordano, B.L.; Umiltà, C.; Butterworth, B. Spatial representation of pitch height: The SMARC effect. Cognition 2006, 99, 113–129. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, M. Non-musicians also have a piano in the head: Evidence for spatial–musical associations from line bisection tracking. Cogn. Process. 2017, 18, 75–80. [Google Scholar] [CrossRef] [PubMed]
- Pitteri, M.; Marchetti, M.; Priftis, K.; Grassi, M. Naturally together: Pitch-height and brightness as coupled factors for eliciting the SMARC effect in non-musicians. Psychol. Res. 2017, 81, 243–254. [Google Scholar] [CrossRef] [PubMed]
- Lega, C.; Cattaneo, Z.; Merabet, L.B.; Vecchi, T.; Cucchi, S. The effect of musical expertise on the representation of space. Front. Hum. Neurosci. 2014, 8, 250. [Google Scholar] [CrossRef] [PubMed]
- Stewart, L.; Verdonschot, R.G.; Nasralla, P.; Lanipekun, J. Action-perception coupling in pianists: Learned mappings or spatial musical association of response codes (SMARC) effect? Q. J. Exp. Psychol. 2013, 66, 37–50. [Google Scholar] [CrossRef] [PubMed]
- Keller, P.E.; Dalla Bella, S.; Koch, I. Auditory imagery shapes movement timing and kinematics: Evidence from a musical task. J. Exp. Psychol. Hum. Percept. Perform. 2010, 36, 508–513. [Google Scholar] [CrossRef] [PubMed]
- Keller, P.E.; Koch, I. The planning and execution of short auditory sequences. Psychon. Bull. Rev. 2006, 13, 711–716. [Google Scholar] [CrossRef] [PubMed]
- Pfordresher, P.Q. Musical training and the role of auditory feedback during performance. Ann. N. Y. Acad. Sci. 2012, 1252, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Shepard, R.N. Geometrical approximations to the structure of musical pitch. Psychol. Rev. 1982, 89, 305–333. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Gerhard, D. Appropriate Isomorphic Layout Determination Using 3-D Helix Lattices. In Proceedings of the 43rd International Computer Music Conference/The 6th Electronic Music Week, Shanghai, China, 16–20 October 2017. [Google Scholar]
- Barr, D.J.; Levy, R.; Scheepers, C.; Tilyc, H.J. Random effects structure for confirmatory hypothesis testing: Keep it maximal. J. Mem. Lang. 2013, 68, 255–278. [Google Scholar] [CrossRef] [PubMed]
- McCullagh, P.; Nelder, J.A. Generalized Linear Models, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 1989. [Google Scholar]
- Jayanthakumar, J.; Schubert, E.; de Graaf, D. NTPP (Note Time Playing Path) MIDI Performance Analyser; Version 0.1; University of New South Wales: Sydney, Australia, 2011. [Google Scholar]


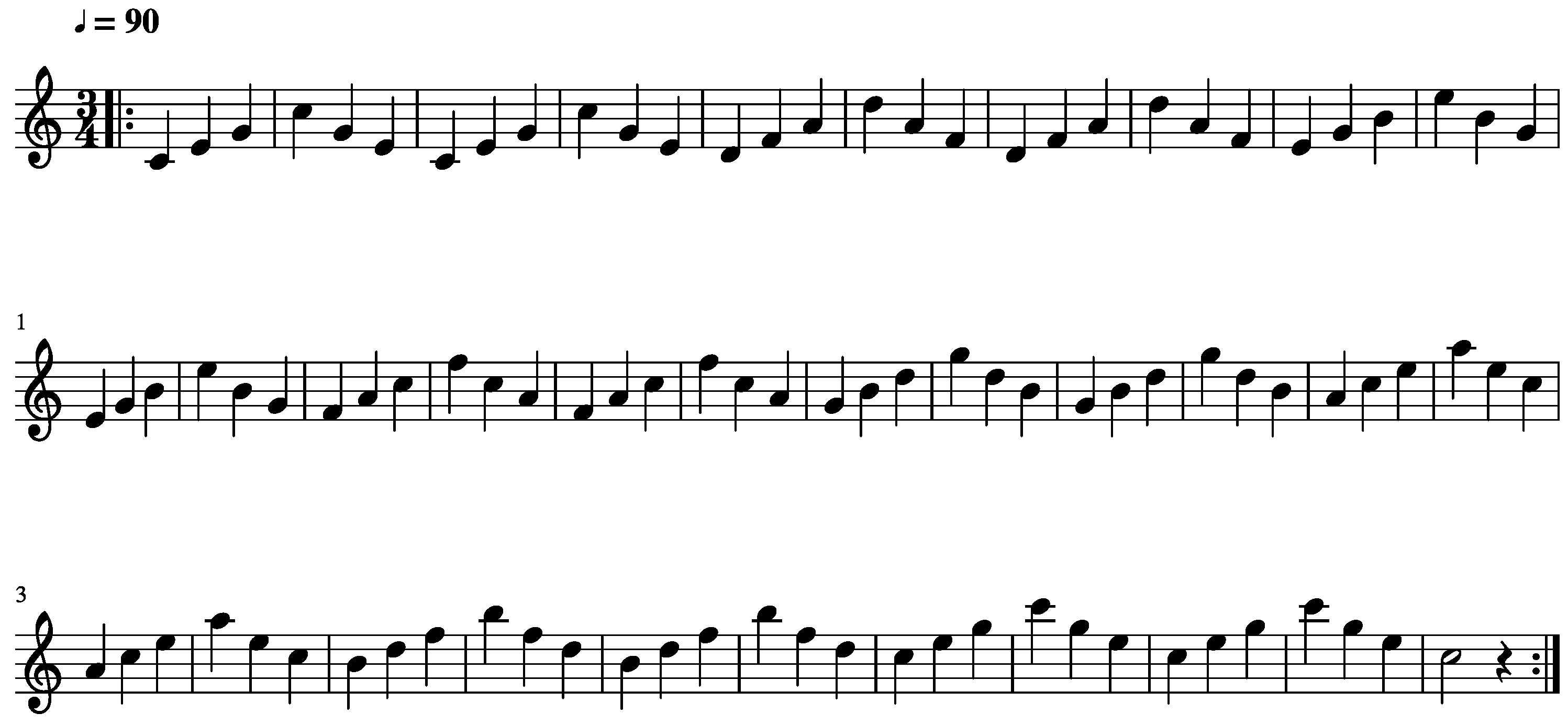
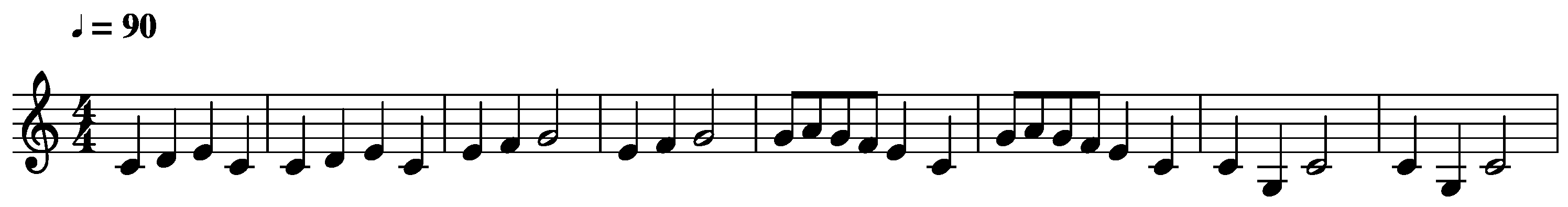
| Fixed Effect | Estimate | Factor | p-Value |
|---|---|---|---|
| (Intercept) | 3.48 | 32.61 | <0.001 *** |
| Adjacency | −0.06 | 0.94 | 0.263 |
| Shear | 0.13 | 1.14 | 0.026 * |
| LayoutNo | −0.37 | 0.69 | 0.001 *** |
| PerfNo | −0.27 | 0.77 | <0.001 *** |
| LayoutNo:PerfNo | 0.12 | 1.13 | 0.003 ** |
| Log Likelihood | −727.67 | ||
| Num. obs. | 208 | ||
| Num. groups: ID | 24 | ||
| Var: ID (Intercept) | 0.04 | ||
| Var: Residual | 0.17 | ||
| 0.44 |
| Fixed Effect | Estimate | Factor | p-Value |
|---|---|---|---|
| (Intercept) | 3.92 | 50.36 | <0.001 *** |
| Adjacency | −0.43 | 0.65 | <0.001 *** |
| Shear | 0.08 | 1.08 | 0.037 * |
| LayoutNo | −0.22 | 0.80 | <0.001 *** |
| PerfNo | −0.09 | 0.91 | <0.001 *** |
| Log Likelihood | −738.65 | ||
| Num. obs. | 209 | ||
| Num. groups: ID | 24 | ||
| Var: ID (Intercept) | 0.05 | ||
| Var: Residual | 0.08 | ||
| 0.78 |
| Fixed Effect | Estimate | Factor | p-Value |
|---|---|---|---|
| (Intercept) | 2.85 | 17.32 | <0.001 *** |
| Adjacency | −0.54 | 0.58 | <0.001 *** |
| Shear | −0.08 | 0.92 | 0.305 |
| LayoutNo | −0.04 | 0.96 | 0.412 |
| PerfNo | 0.04 | 1.04 | 0.581 |
| Log Likelihood | −437.37 | ||
| Num. obs. | 142 | ||
| Num. groups: ID | 24 | ||
| Var: ID (Intercept) | 0.06 | ||
| Var: Residual | 0.26 | ||
| 0.38 |
| Fixed Effect | Estimate | Factor | p-Value |
|---|---|---|---|
| (Intercept) | 3.43 | 30.85 | <0.001 *** |
| Adjacency | −0.05 | 0.96 | 0.408 |
| Shear | −0.50 | 0.61 | <0.001 *** |
| LayoutNo | −0.38 | 0.68 | <0.001 *** |
| PerfNo | −0.13 | 0.88 | <0.001 *** |
| LayoutNo:Shear | 0.33 | 1.39 | 0.002 ** |
| LayoutNo:PerfNo | 0.07 | 1.07 | 0.021 * |
| Log Likelihood | −996.89 | ||
| Num. obs. | 288 | ||
| Num. groups: ID | 24 | ||
| Var: ID (Intercept) | 0.11 | ||
| Var: Residual | 0.26 | ||
| 0.66 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
MacRitchie, J.; Milne, A.J. Exploring the Effects of Pitch Layout on Learning a New Musical Instrument. Appl. Sci. 2017, 7, 1218. https://doi.org/10.3390/app7121218
MacRitchie J, Milne AJ. Exploring the Effects of Pitch Layout on Learning a New Musical Instrument. Applied Sciences. 2017; 7(12):1218. https://doi.org/10.3390/app7121218
Chicago/Turabian StyleMacRitchie, Jennifer, and Andrew J. Milne. 2017. "Exploring the Effects of Pitch Layout on Learning a New Musical Instrument" Applied Sciences 7, no. 12: 1218. https://doi.org/10.3390/app7121218
APA StyleMacRitchie, J., & Milne, A. J. (2017). Exploring the Effects of Pitch Layout on Learning a New Musical Instrument. Applied Sciences, 7(12), 1218. https://doi.org/10.3390/app7121218






