Featured Application
A real-time physical model sound effect that can replicate the sound of a number of swinging objects, such as a sword, baseball bat and golf club, has great potential for dynamic environments within virtual reality or games. The properties exposed by the sound effects model could be automatically adjusted by a physics engine giving a wide corpus of sounds from one simple model, all based on fundamental fluid dynamics principles.
Abstract
A real-time physically-derived sound synthesis model is presented that replicates the sounds generated as an object swings through the air. Equations obtained from fluid dynamics are used to determine the sounds generated while exposing practical parameters for a user or game engine to vary. Listening tests reveal that for the majority of objects modelled, participants rated the sounds from our model as plausible as actual recordings. The sword sound effect performed worse than others, and it is speculated that one cause may be linked to the difference between expectations of a sound and the actual sound for a given object.
1. Introduction
The sound of an object swinging through the air has a very distinctive swoosh sound. We expect this sound when watching a sword fight in a movie or playing a golfing game. This is a common sound within films, TV programmes and games covering genres like sports, material arts or a swashbuckling yarn. These distinct sounds are all generated by a similar physical process as the objects move through the air.
When sounds are added into media to replicate or emphasise original sounds, like a sword swoosh, they are classed as sound effects. A sound effect is usually implemented as a pre-recorded sample or from sound synthesis. Pre-recorded samples have a drawback in media like games and virtual reality as they are unable to change or evolve with the environment, but they are often viewed as more perceptually accurate than synthesised effects. Synthesised effects have the advantage of being based on algorithms and hence have the potential to adapt with their environments.
Being able to replicate these sounds within a single synthesis model offers the opportunity to cover a wide variety of objects travelling through the air. This potentially gives a programmer the ability to obtain the results required without having to find a sample within a sound effects library or record the sound themselves. It also provides an audio programmer the ability to integrate parameters of the model into a game engine. Thus, the synthesis model can evolve with the environment, increasing immersion within a game or virtual reality. A video illustrating the model being used to synthesise a sword swing within the Unity game engine is shown at https://www.youtube.com/watch?v=zVvNthqKQIk.
This article is a revised and extended version of [1], which won the best paper award at the 14th Sound and Music Computing Conference 2017. It presents a new sound synthesis method illustrating the design, implementation and analysis of a real-time physically-derived model that can be used to produce sounds similar to those of an object swooshing through the air. The objects examined were a metal sword, a wooden sword, a baseball bat, a golf club and a broom handle, which represent different object geometries commonly heard swinging through the air. To our knowledge, this is the first synthesis model that replicates a wide variety of objects swinging through the air by using bona fide fluid dynamics equations to calculate the sound output in real time.
Section 2 describes the state of the art and related work, while Section 3 gives a detailed description of our method. The implementation is given in Section 4 followed by both subjective and objective evaluations of our model in Section 5. A discussion of the work is presented in Section 6 followed by conclusions in Section 7.
2. Background and Related Work
Sound synthesis techniques can be split into two broad approaches, signal-based and physical models [2]. Signal-based models aim to replicate the sound properties; matching frequency components, replicating the time envelope or similar. Physical models aim to replicate the processes behind the natural sound creation by mathematical models.
The advantage of a signal-based model is that it is relatively computationally inexpensive to replicate the spectrum of a sound using established techniques such as additive synthesis or noise shaping. A drawback of this approach is that it is rarely possible to relate changes in signal properties to the physical processes creating the sound. For example, an increase in speed of a sword not only changes the fundamental tone frequency, but also the gain. Therefore, changing one signal-based property could lose realism in another.
Physical models aim to replicate the physics behind the sound generation process. Sounds generated by these models have the advantage of possessing greater authenticity in the generated sounds, especially in relation to parameter adjustments. A potential drawback is that the computational cost required to produce sounds is often high, and the physical models typically cannot adapt quickly to parameter adjustments, making real-time operation challenging and often not possible.
In the middle of these traditional techniques lay physically-inspired models. These hybrid approaches replicate the signal produced, but add characteristics of the physics that are behind the sound creation. For a simple sword model, this might be noise shaping with a bandpass filter with centre frequency proportional to the speed of the swing. A variety of examples of physically-inspired models was given in [3]; the model for whistling wires being exactly the bandpass filter mentioned.
Four different sword models were evaluated in [4]. Here, the application was for interactive gaming, and the evaluation was focused on perception and preference rather than accuracy of sound. The user was able to interact with the sound effect through the use of a Wii Controller. One model was a band-filtered noise signal with the centre frequency proportional to the acceleration of the controller. A physically-inspired model replicated the dominant frequency modes extracted from a recording of a bamboo stick swung through the air. The amplitude of the modes was mapped to the real-time acceleration data.
The other synthesis methods in [4] both mapped acceleration data from the Wii Controller to different parameters; one using the data to threshold between two audio samples, the other a granular synthesis method mapping acceleration to the playback speed of grains. Tests revealed that the granular synthesis was the preferred method for expression and perception. One possible reason that the physical model was less popular could be the lack of correlation between speed and frequency pitch, which the band-filtered noise had. This may also be present in the granular model.
A signal-based approach to a variety of environmental sound effects, including sword whoosh, waves and wind sounds, was undertaken in [2]. Analysis and synthesis occur in the frequency domain using a sub-band method to produce narrow band coloured noise. In [5], a rapier sword sound was replicated, but this focused on the impact rather than the swoosh when swung through the air.
A physical model of sword sounds was explored in [6]. Here, offline sound textures were generated based on the physical dimensions of the sword. The sound textures were then played back with speed proportional to the movement. The sound textures were generated using computational fluid dynamics software (CFD), solving the Navier–Stokes equations and used Lighthill’s acoustic analogy [7] extended by Curle’s method [8]. In this model [6], the sword was split into a number of compact sound sources (discussed in Section 3.2), spaced along the length of the sword. As the sword was swept thought the air, each source moved at a different speed; therefore, the sound texture for each source was adjusted accordingly. The sounds from each source were summed and output to the listener.
An overview of the different synthesis methods and parameters available to a user are presented in table form in Table 1. It can be seen that the only model offering real-time operation with instantaneous variability of physical parameter was [1]. Outputs from [4,6] were used within our listening test, Section 5, to represent alternative synthesis methods.

Table 1.
Table highlighting different synthesis methods for swing sounds.
A Japanese katana sword was analysed in [9] by means of wind tunnel experiments. A number of harmonics from vortex shedding were observed along with additional harmonics from a cavity tone due to the shinogi or blood grooves in the profile of the sword.
3. Method
3.1. Aeroacoustics
When sound is generated by airflows or air interacting with objects, the process is labelled aeroacoustics. This falls under the wider body of research known as fluid dynamics, which describes the physical processes controlling the flow of fluids and enables the prediction of pressures, noises, strains on objects, etc. Understanding these processes enables better design of a wide number of objects including aircraft, cars, trains, ships, buildings, space vehicles and bridges.
Today, computers are able to solve the highly complex equations that govern these processes using techniques like finite difference or finite volume techniques and mapping out the domain of interest with complex mesh structures. Even with the advances in the computational power available, these processes can take hours and even days to complete depending on the level of detail required.
Prior to the availability of such processing power, engineers and scientists derived and defined simpler equations to allow them to calculate the approximate acoustic characteristics. These are labelled semi-empirical equations, where assumptions and generalisations have been made to simplify calculations or to yield results in accordance with observations. Although many of these equations may at first appear complicated, once all the relevant parameters are known, they produce exact results with errors only due to the approximations made during the equation derivation.
There is a number of fundamental aeroacoustic sounds that constitute the main focus of research. Figure 1 illustrates a number of these fundamental tones and gives examples of the types of objects that produce them. Each tone is generated by distinct fluid dynamics processes.
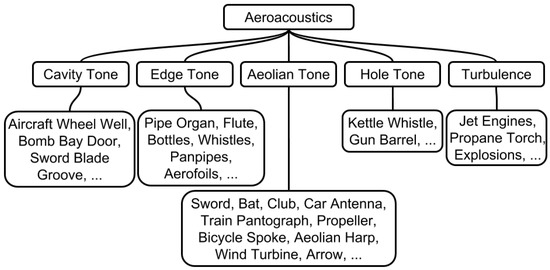
Figure 1.
A simplified taxonomy of aeroacoustic sounds.
3.2. Aeolian Tone
It can be seen from Figure 1 that the Aeolian tone is the fundamental tone produced when an object like a sword or bat is swung through the air. A brief overview of the Aeolian tone characteristics will be given here, including a number of fundamental equations. For greater depth, the reader is directed to [10].
3.2.1. Tone Frequency
Strouhal (1878) defined a useful relationship between the tone frequency , air speed and cylinder diameter d, Equation (1). The variable is known as the Strouhal number.
Rearranging to isolate the tone frequency gives:
As air flows around a cylinder, vortices are shed, causing a fluctuating lift force normal to the flow dominated by the fundamental frequency, . Simultaneously, a side axial fluctuating drag force is present with frequency , twice that of the lift frequency. It was noted in [11] that, “The amplitude of the fluctuating lift is approximately ten times greater than that of the fluctuating drag”.
It was shown in [8] and confirmed in [12] that aeroacoustic sounds in low flow speed situations could be modelled by the summation of compact sound sources, namely monopoles, dipoles and quadrupoles. An acoustic monopole can be described as a pulsating sphere, much smaller than the acoustic wavelength. A dipole is equivalent to two monopoles separated by a small distance, but of opposite phase. Quadrupoles are two dipoles separated by a small distance with opposite phases. A longitudinal quadrupole has the dipole axes in the same line, while a lateral quadrupole can be considered as four monopoles at the corners of a rectangle [13]. Aeolian tones can be represented by dipole sources, one for the lift fundamental frequency and one for the drag; each source can include a number of harmonics.
The turbulence around the cylinder affects the frequency and the bandwidth of the tone produced. A measure of this turbulence is given by a dimensionless variable, the Reynolds number , given by the relationship in Equation (3).
where and are the density and viscosity of air, respectively. An experimental study of the relationship between the Strouhal number and the Reynolds number was performed in [14], giving the following equation:
where and are constants and given in Table 1 of [14] (additional values were calculated in [10]). The different values represent the turbulence regions of the flow, starting at laminar up to sub-critical. With the Strouhal number obtained, diameter and air speed known, we can apply them to Equation (2) and obtain the fundamental frequency, , of the Aeolian tone, generated by the lift force.
3.2.2. Source Gain
The time-averaged acoustic intensity (W/m) of an Aeolian tone lift dipole source and the time-averaging period were given in [15]. The time-averaged acoustic intensity for low airspeeds is given as:
where b is the cylinder length; M is the Mach number; , where c is the speed of sound. The elevation angle, azimuth angle and distance between listener and source are given by , and r, respectively. is a numerical constant that lies somewhere between 0.5 and 2 [15]. The correlation length, l, has dimensionless units of diameter d and indicates the span-wise length that the vortex shedding is in phase; after this, the vortices become decorrelated. The work in [15] states that the exponent of Equation (5) can be neglected at low Mach numbers, in accordance with [16]. The gain for the drag dipole is obtained from its relationship to the lift gain given in [11] and the lift dipole harmonics values from similar relationships published in [17].
3.2.3. Wake Noise
As the Reynolds number increases, the vortices diffuse rapidly and merge into a turbulent wake. The wake produces wide band noise modelled by lateral quadrupole sources whose intensities vary with [18]. It was noted in [18] that there is very little noise content below the lift dipole fundamental frequency. Above the fundamental frequency, the roll off of the amplitude of the turbulent noise is .
The sound generated by jet turbulence was examined in [15,19,20]. The work in [15] states that the radiated sound pattern is greatly influenced by a Doppler factor of cos. The wake noise has less energy than a jet, and its intensity has been approximated by the authors to capture this relationship as shown in Equation (6):
where is a scaling factor between wake noise and lift dipole noise and B is an empirical constant. A value of B = 0.7 was found in [19] to match measured values.
4. Implementation
Our model was built using Pure Data, a real-time graphical data flow programming language. This was chosen due to the open source nature of the code and ease of repeatability rather than high performance computations.
4.1. Discrete Compact Sound Source
4.1.1. Fundamental Frequency Calculation
A uniform sampling of the continuous air flow speed , along with the given diameter d set by the user, permits the calculation of the Reynolds number from a discrete implementation of Equation (3). Using data published in [14] the discrete Strouhal number was calculated, Equation (4). Thereafter, a discrete implementation of Equation (2) was used to obtain the lift fundamental frequency .
4.1.2. Gain Calculations
The time-averaged intensity value calculated by Equation (5) pertains to the dipole associated with the fundamental lift frequency . Previous theoretical research [16] has set the constant and neglected the exponent. We set matching conditions used by [16], likewise neglecting the exponent, which has a negligible effect due to the low Mach numbers used in this implementation [15]. The correlation length l was obtained from a graph published in [21] showing the ratio of correlation length to diameter, , as a function of the Reynolds number. An equation replicating this relationship has been derived by the authors in Equation (7).
The discrete intensity value pertaining to the drag force was calculated using Equation (8).
where constant was added to the value of due to the 90 phase difference between the lift and drag forces.
4.1.3. Harmonic Content Calculations
In [10], the Aeolian tone was presented with two harmonics for the lift dipole and one for the drag dipole. Due to the additional computational complexity this adds, multiplied by the number of sources in each swinging object, the number of harmonics was reduced down to the most perceptually significant; the first lift dipole harmonic at .
Hardin [17] stated that this value was 60% of the fundamental SPL. This was implemented as shown below:
4.1.4. Tone Bandwidth Calculations
As stated in Section 3.2.1, there is a bandwidth around the tone, and this is related to the Reynolds number. Data available in [22] were limited to Reynolds numbers under 237,000. The relationship between the bandwidth and Reynolds number from 0–193,260 was found to be linear. This relationship was interpolated from the data as:
where is the tone bandwidth at −3 dB of the peak frequency. Above a Reynolds number of 193,260, a quadratic formula was found to fit the bandwidth data. This is shown in Equation (11).
4.1.5. Wake Calculations
A noise profile of is known as brown noise. This was approximated using white noise and the transfer function shown in Equation (12) [23].
In [23], has a value of 1, but this proved unstable in our implementation. A value of 0.99 was chosen, giving a stable implementation while producing a virtually identical magnitude spectrum. The required noise profile was generated using the transfer function given in Equation (13):
where is a white noise source and the output is a brown noise source. There is little wake contribution below the fundamental frequency [18]. Therefore, a high pass filter was applied to with the filter cut-off set at the lift dipole fundamental frequency, . This produces the turbulent noise profile required, :
where is the high pass filter transfer function. The inverse Z-transform of gives the wake output signal, . The wake gain was calculated by a discrete implementation of Equation (6). A value of was set perceptually based on sounds generated from experiments (Section 5), giving .
4.1.6. Final Output
To generate the correct output sound for the fundamental lift dipole, we used a white noise source filtered by a bandpass filter. The centre frequency of the bandpass filter was set to and the Q value as calculated in Section 4.1.4, giving the bandpass filter output . The same process was applied in relation to the fundamental drag dipole, using as a bandpass filter centre frequency, giving an output of . The lift dipole harmonic was computed in a similar way, giving output .
The gain values for the lift and drag dipole outputs were obtained from Equations (5) and (8). The appropriate gain value for the lift dipole harmonic was given in Equation (9). Finally, the wake output with gain was added. Note that a single white noise source was used for all fundamental and harmonic dipoles and for the wake noise as they were all part of a single compact source.
Combining the outputs from the lift dipole, drag dipole, harmonic and wake, it is possible to define a final output, Equation (15):
where is an absolute gain value allowing the user to increase the overall sound level depending on artistic requirements.
4.2. Swinging Model
The basic concept of all the models was to line up a number of the compact sources to replicate the sounds created as a cylindrical object swings through the air. The intensities given in Equation (15) were time averaged, which caused an issue for our model due to the swing time being shorter than the averaging process. Thus, the intensity was implemented as an instantaneous value.
For each of our models, eight Aeolian tone compact sound sources were used to replicate the sounds. The distance between each source depends on the correlation length, the distance given in diameters before the vortices being shed go out of phase or become decorrelated.
To increase the flexibility and ease of use of our swinging objects model, two modes of operation were available; one allowing the user to adjust the diameter of the top and bottom of the object with a linear interpolation between them and the second with preset objects based on actual physical measurements. Both modes of operation allow the user to predefine the top speed of the tip, start and end position of the object being swung, as well as the position of the observer. These parameters can be easily mapped to graphics or animation to have an exact match with visuals. The coordinate system used for the model is shown in Figure 2.
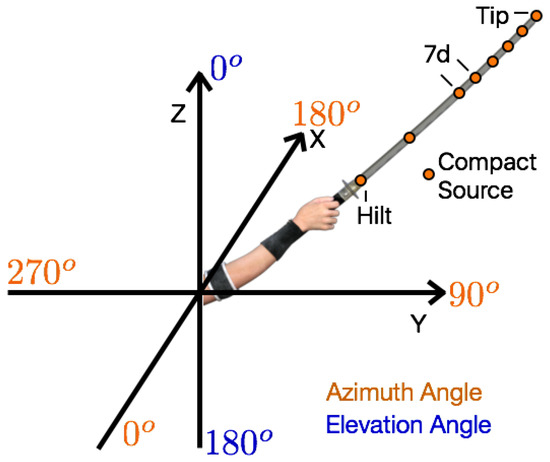
Figure 2.
Position of 8 compact sources and coordinates used in the sword model.
For ease of calculation, the swing action throughout was made to be an arc of constant radius and hence always tracing a line on the surface of a sphere. This allowed us to calculate the distance between the start and end position of the swing using the Haversine formula [24]. This formula calculates the length of a great circle on a sphere and is shown in Equation (16) below:
where and are the latitude of the start and finish points, respectively; and are the longitude values of the start and finish points. Latitude and longitude values are given in radians and determined from the start and end positions set by the user.
The radius r is the distance between the centre of the arc and tip of the object. This was set to be the length of the object with an additional 0.35 m to represent the length of the swinging arm. The top speed of the object being swung was set as the halfway distance of the arc, with linear acceleration and deceleration to and from rest.
In our implementation, the sword sweep created a two-dimensional plane in a three-dimensional environment with the observer taken as a point in that environment. Trigonometry identities were used to calculate the elevation and azimuth between each source and the observer.
Panning was included as the sound moves across the xy plane, as well as the Doppler effect. It was shown in [25] that the addition of the Doppler effect increases the natural perception. This effect was taken into account when the sword was moving towards or away from the observer and frequencies adjusted accordingly.
4.3. Variable Mode
This model gives the user the ability to vary the diameter of the object by setting the object diameter at the tip and the hilt. The user can also vary the length of the object. The position of the Aeolian tone compact sound sources depends on the choices made by the user when setting the diameter and length values.
Six of the eight compact sound sources were placed at the tip of the object. It is known from Equation (5) that the gain is proportional to , and the greatest speed will be at the tip of a sword, a golf club, etc., during a normal swing. The remaining sources were placed at the hilt and midway between the 6th source at the tip and the hilt. This is illustrated in Figure 2.
This positioning of the six sources at the tip was equivalent to each source having a set correlation length of 7d; see Section 3.2.2. A range of correlation values from 17–3d were given in [16] depending on the Reynolds number. A plot showing similar values was given in [21]. Since the position of the sources has to be chosen prior to calculation of the Reynolds number, the value 7d was chosen as a compromise, covering a reasonable length of the sword for a wide range of speeds (in [6], the correlation length of 3d was used; the number of sources set to match the length of the sword).
4.4. Preset Mode
A number of actual objects were measured; a metal sword, wooden sword, baseball bat, 3–wood golf club, 7–iron golf club and a broom handle. Exact measurements gave us the opportunity to set the position and diameter of each of the compact sound sources individually, giving a more accurate model. The correlation length at the tip of all objects was set to 5d for all objects except the baseball bat, which had a reduced correlation length of 2d due to its thickness. The exact values of the source position from the base of the object to the tip and the corresponding object diameter are shown in Table 2.

Table 2.
Diameter and radius of compact sound sources for the preset objects. All values in metres. Correlation length = 5d except for baseball bat, where correlation length = 2d.
4.5. Grooved Profile
In [26], a physically-derived sound synthesis model of a cavity tone was presented. This covers a separate fundamental aeroacoustic sound with a different set of fluid dynamics equations governing the generation of the tone. In [9], the sound generated by a grooved sword was found to contain a number of discrete frequencies, including those from the cavity tone. Thus, we added in cavity tone compact sound sources at the same location as the Aeolian tone compact sources to our model.
5. Evaluations and Results
5.1. Subjective Evaluation
The subjective evaluation was split into two different tests, a listening test and an object recognition test. A total of 26 participants undertook the test, 18 males, 7 females and 1 preferring not to say. Participants were aged between 17 and 71 with a median of 28 and standard deviation of 13. The order of the listening test and object recognition was split to examine if the order had any influence on the results. Working models of both versions of the swinging object model are available at https://code.soundsoftware.ac.uk/projects/physicallyderivedswingingobjects, which includes a copy of all sounds used in our listening test.
5.1.1. Listening Tests
A double-blind listening test was carried out to evaluate the effectiveness of our synthesis model. The Web Audio Evaluation Tool [27] was used to build and run listening tests in the browser. This allowed test page order and samples on each page to be randomised. All samples were loudness normalised in accordance with [28]. Headphones were used to administer the sounds to participants. These were either AKG K553 Pro Closed-Back Studio Headphones or Beyerdynamic DT150 closed back Isolating Studio Headphones.
Each participant was presented with five test pages, one for each of the preset sound effects. The wooden sword, baseball bat, golf club and broom handle pages contained two real samples, two samples from our physical model (PM), two samples generated by spectral modelling synthesis (SMS) [29] from a recording and an anchor. The metal sword page included two real samples, one synthesis sample from [4], one synthesis sample from [6], one SMS sample, one sample from our physical model and a sample from the physical model with cavity tone compact sound sources added.
All the sampled recordings were captured by the authors within the Listening Room, Electronic Engineering and Computer Science Department, Queen Mary University of London. They were recorded on a Neumann U87 microphone placed approximately 20 cm from the midpoint of the swing and at 90 degrees to the plane of the swing. The impulse response of the room was captured and applied to all other sounds in the listening test so that the natural reverb of the room would not influence the results (except samples from [4,6]).
The anchors were created from a real-time browser-based synthesis effect (http://c4dm.eecs.qmul.ac.uk/audioengineering/RTSFX/app/main-panel/whoosh.html), to allow a thorough comparison of how plausible the synthesis method is compared to the recorded sample. It was expected that a low pass filtered sample, as used in the MUltiple Stimuli with Hidden Reference and Anchor (MUSHRA) standard, would still be considered plausible, whereas a low-quality anchor would encourage the full use of the scale and allow for better understanding as to the effectiveness of the synthesis method.
Rating the plausibility of sound from a physical model was the preferred judgement in [30], stating a plausible sound as one that listeners thought “was produced in some physical manner”. Box plots for all five objects are shown in Figure 3. Our physical model outperforms the alternative synthesis methods on all of the objects except the metal sword. The metal sword performed poorly for plausibility in this test, with the model with added cavity tones performing slightly better.
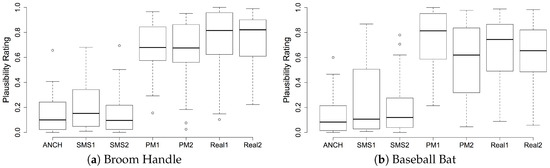
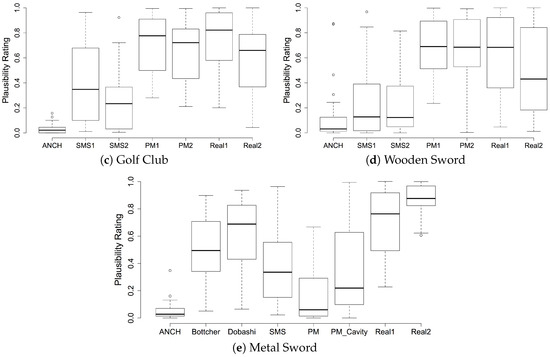
Figure 3.
Box plots showing plausibility results for the preset objects. (ANCH, Anchor; SMS, Spectral Modelling Synthesis; PM, Physical Model; PMCavity, physical model including cavity tone; Real, recorded sample).
We performed the Shapiro–Wilk test for the plausibility ratings to examine the distribution of the ratings. The results are shown in Table 3, which indicate that 29 out of 36 tests were not normally distributed. To examine similarity between the ratings between each audio source in the listening test, we performed the Mann–Whitney U-test. Results of these are shown in Table 4, Table 5, Table 6, Table 7 and Table 8.

Table 3.
Results for Shapiro–Wilk test for the plausibility ratings (**** ⇒ p < 0.0001, *** ⇒ p < 0.001, ** ⇒ p < 0.01, * ⇒ p < 0.05, - ⇒ p ≥ 0.05). SMS, spectral modelling synthesis; PM, physical model; PMCavity, physical model including cavity tone; Real, recorded sample.

Table 4.
The effect of different samples for a broom pole (**** ⇒ p < 0.0001, *** ⇒ p < 0.001, ** ⇒ p < 0.01, * ⇒ p < 0.05, - ⇒ p ≥ 0.05). SMS, spectral modelling synthesis; PM, physical model; Real, recorded sample.

Table 5.
The effect of different samples for a baseball bat (**** ⇒ p < 0.0001, *** ⇒ p < 0.001, ** ⇒ p < 0.01, * ⇒ p < 0.05, - ⇒ p ≥ 0.05). SMS, spectral modelling synthesis; PM, physical model; Real, recorded sample.

Table 6.
The effect of different samples for a golf club (**** ⇒ p < 0.0001, *** ⇒ p < 0.001, ** ⇒ p < 0.01, * ⇒ p < 0.05, - ⇒ p ≥ 0.05). SMS, spectral modelling synthesis; PM, physical model; Real, recorded sample.

Table 7.
The effect of different sample for a wooden sword (**** ⇒ p < 0.0001, *** ⇒ p < 0.001, ** ⇒ p < 0.01, * ⇒ p < 0.05, - ⇒ p ≥ 0.05). SMS, spectral modelling synthesis; PM, physical model; Real, recorded sample.

Table 8.
The effect of different samples for a metal sword (**** ⇒ p < 0.0001, *** ⇒ p < 0.001, ** ⇒ p < 0.01, * ⇒ p < 0.05, - ⇒ p ≥ 0.05). SMS, spectral modelling synthesis; PM, physical model; PMCavity, physical model including cavity tone; Real, recorded sample.
5.1.2. Object Recognition
For this test, participants were able to control the speed parameter of the physical model by use of a Wii controller and swinging the virtual object through the air. The five preset objects were presented in a pseudorandom order and the user asked to identify which object they were swinging from the list of presets. Fourteen participants completed the object recognition test prior to the listening test, and 12 completed it after the listening test. Each preset was presented twice giving 10 individual tests in total.
Table 9 and Table 10 give the results of how often participants correctly identified the object being modelled by our physical model. A clear difference can be seen between participants who completed the object recognition test prior to the listening test compared to those who completed the object recognition after. It is reasonable to conclude that completing the listening test first provides some level of training for the object recognition.

Table 9.
Objects identified from the Wii Controller; tested before the listening test.

Table 10.
Objects identified from Wii Controller; tested after the listening test.
Results presented in Table 9 show that participants were far less able to identify the object being modelled by our synthesis model when having to choose before the listening test. In fact, it was more common to choose one of the other objects being modelled rather than the correct one. The wooden sword model was never correctly identified, while the metal sword object was correctly identified more than any other object, but still less than 50% of the time.
On examination of those who completed the object recognition test after the listening test, shown in Table 10, it can be seen that there was an increase for all objects being correctly identified. Similar to results shown in Table 9, the metal sword object was correctly identified more often than the other objects and on this occasion, more often than not. Although the results for the other objects are higher than those presented in Table 9, it was still more common for participants to choose one of the other objects being modelled rather than the one being replicated by our synthesis model.
5.2. Objective Evaluation
The sound produced by katana swords was examined in [9]. One sword examined had a profile with grooves on either side, which produced a cavity tone along with the Aeolian tone. To replicate this, we added a cavity tone model [26] to the sword model, which allowed a wider range of sword and object profiles to be modelled.
The sword in [9] had a thickness of 0.005 m, and the tones were measured in a wind tunnel with airspeed 24 ms. Roger [9] observed a tone around 960 Hz due to vortex shedding (Aeolian tone) and a higher frequency sound around 6–9 kHz. The dimension of the groove in the sword was not published in [9], but it was possible for us to replicate this sound based on the published cavity tone peaks.
The magnitude spectrum output of a compact sound source, including the cavity tone, is shown in Figure 4. The parameters set were airspeed 24 ms, diameter m and cavity length m. The Aeolian tone frequency can be seen clearly at 969 Hz, with a harmonic at 2907 Hz. The cavity tone frequencies are seen at 3213 Hz, 7497 Hz, 11,780 Hz and 16,064 Hz. The length of the cavity was set to give the second cavity tone at 7497 Hz, approximately halfway between the 6 kHz and 9 kHz observed in [9].
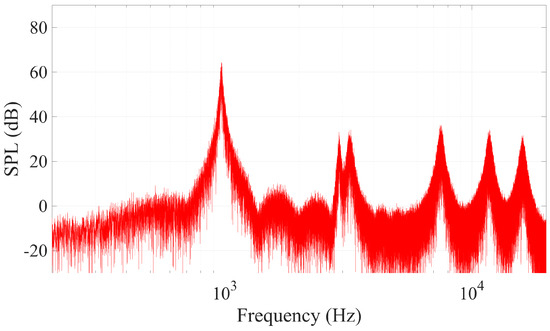
Figure 4.
Magnitude spectrum of the physical model of the grooved sword.
The Aeolian tone and second cavity tone are very similar to the details published in [9]. The peaks around 3 kHz from the Aeolian tone harmonic and first cavity tone are at a greater magnitude in the synthesis model than in [9]. The published data do not cover frequencies as high as the third and fourth cavity tone.
It was noted in [9] that two oscillating motions around a sword with a groove will modulate each other. In [9], wind tunnel experiments were given where the airspeed was ramped from 15 ms to 30 ms. Under these circumstances there were a number of extra harmonics found. The magnitude of individual modulated frequencies varies with airspeed. Our model does not produce any harmonics that relate to the interaction between the two oscillating tones. The addition of these may increase the authenticity of our model and is a possible area of future work.
6. Discussion
The results from the listening test indicate that overall, our model performs well compared to other synthesis models. It has exceptional performance for the broom handle, baseball bat, golf club and wooden sword objects, where participants found sounds generated by our model to be as plausible as real recordings. The exception to this was the metal sword physical model sound effect, which actually performed worse in this test compared to our previously published test [1]. During the previous listening test [1], we did not have the physical dimensions of the sword samples. In this test, we had the dimensions, as well as the impulse response of the room in which the samples were recorded, thus enabling a fairer comparison.
One possible reason for the poorer performance of the metal sword physical model was that all the other modelled objects were thicker than the metal sword. Thicker objects have higher Reynolds numbers, which results in lower Q values. Spectral modelling synthesis analyses a recording and extracts sinusoidal components. Thinner objects produce sounds closer to pure tones and hence are better synthesised using SMS than thicker objects.
Table 8 shows that our physical model was significantly different from all other sounds, especially the real sounds and those synthesised by other methods. Since only one physical model sound was compared with a number of others, it is believed that a further listening test would be necessary to investigate if this result would be repeated over the range of sword dimensions and speeds. Results given in [1] indicated that the lower quality physical model sounds were rated as more plausible. These sounds had a fixed Q value that gave the impression of a thicker object. The diameter used to generate sounds in [6] was 0.01 m, substantially thicker than the sword we were modelling. It may be the case that listeners perceive a thicker sound as more plausible even if not physically accurate. This could be revealed in future perceptual evaluations.
In the original paper [1], the value of in Equation (6) was set to . This was set perceptually as no exact relationship between dipole and wake noise had been identified. During the design of the listening test for this article, the value was again set perceptually, but this time, all objects were considered, including sounds generated using the Wii Controller. This resulted in the value of being set to , increasing the wake gain.
The broom handle, baseball bat and golf club objects were all cylindrical with thickness to width ratios of 1:1. For the wooden sword, this ratio decreases to approximately 0.37:1 and for a metal sword to approximately 0.14:1. The Aeolian tone model is designed around vortex shedding from cylindrical objects, and it is reasonable to assume that additional discrepancies may exist when there is a deviation from the thickness to width ratio of a cylinder.
Another possible reason for the poor rating of the metal sword object compared to the other objects is that the number of participants who have swung a real sword and heard the sound may well be less than those who have perhaps swung a golf club and the other objects. Memory plays an important role in perception [31]. If participants have heard a Foley sound effect for a sword more often than an actual sword sound, this may influence their perception of the physical model.
In contrast, it can be argued that participants will have more likely heard the actual sounds of a golf club at a live sporting event or within sporting broadcasts, and hence, their memory of these sounds would be closer to the physical model. Since all participants were from the U.K., the baseball bat would most likely not be as familiar to them as other objects, and hence, they might not have as strong a memory of the sound made by this object. This would make the difference between a memory of a Foley sound and an actual sound diminish.
It is clear from the object recognition that, with zero training, it was extremely difficult to identify an object from controlling the speed parameter from the swing of a Wii Controller. This is corroborated by the variation in results from those who did the object recognition test before the listening test to those who took the test after. Clearly, the listening tests provided participants with some form of informal training for the object recognition (it was found that the object recognition test provides negligible training for the listening test). This is in line with results from [32] where it was found that participant training was the dominant factor in determining whether or not similar tests produced significant results.
A common comment from participants when completing recognition tests was that they would like to have some visual stimulus to assist them with making their decision. It is anticipated that participants may have given more accurate choices if they were able to choose from pictures of the five objects being modelled rather than the names. The label of broom handle could produce a wide variety of images in the minds of participants, but a picture of the actual broom handle we were modelling would allow participants to focus on the same object. A further comment was that the participant would prefer a none of the above option when they believed the sound did not match any of the objects.
The use of a Wii Controller was an obvious interface for participants to swing and generate the sounds due to the sensors and ergonomic design. It was noted in a previous test as part of [1] that a participant would have liked some sense of weight in their hand to increase their sense of belief. This comment, along with the previous comment requesting visual stimulus, indicates that participants look for non-aural cues to assist in identifying sounds. Further research into which cues participants prefer and the effects on identification is required.
Since all sounds from the objects modelled were generated by the same physical model, it was understandable that there was some confusion between choices, possibly due to sonic similarities between the sound effects. The only differences between each synthesis model were the dimensions of the object being swung and the speed, either set as in the listening test or generated by each participant using the Wii Controller. A listening test that only provides a choice between a metal sword and a baseball bat would be expected to produce more clear-cut results.
The classification of different sound effects with sonic similarities was examined in [33] where nine categories of sound effects were identified. It is anticipated that objects modelled herein would be categorised into the same category in [33], but within weapons and sports in a traditional sound effect library.
Comparison with results published in [9] indicates that we have good agreement with the Aeolian tone frequency generated by vortex shedding. Wind tunnel results show the sword tested in [9] having an Aeolian tone peak at 960 Hz, while our model predicts the frequency at 969 Hz, a difference of 0.9%.
The inclusion of the cavity tone within the sword model provides the possibility to model more complex blade profiles. Listening tests indicate that it was found as plausible as the SMS sample, similar to Bottcher’s sample, but not as plausible as Dobashi’s sample and the real recordings. None of the other profiles are believed to include the cavity tone, but it was found that inclusion of it makes our model more plausible. It is difficult to draw overriding conclusions why this occurred, but it may be linked to Foley sword sound effects previously heard by participants.
Future research into the inclusion of the cavity tone compared to actual swords with known cavity profiles would be advantageous, enabling us to better judge how plausible the inclusion of this tone is in the generation of sword swoosh sounds. This would also assist in evaluating how the lack of modulation between the Aeolian tone and cavity tone in our model affects perception and if we need to extend our model to include this.
The range of sword profiles that we are able to model from using only the Aeolian tone and cavity tone is yet to be explored. Similarly, it is yet to be established if the sword material, bronze, steal, etc., plays an important role in the sound produced. It is known that when the vortex shedding frequency is approximately equal to a vibration frequency of the object, the sound is re-enforced. A physical model replicating this in the form of an Aeolian harp was given in [34]. Adding some of the physical properties implemented in this model would allow for consideration of the mass density of the metal and damping of the construction to be considered. Whether this would have an influence on perception is another area for further research.
Further objective evaluation would include obtaining exact velocity data for known object swings and comparing the physical model using these data and a recording of the swing from which these data were captured. This may involve wind tunnel measurements as in [9].
It is recognised that the swing sounds recorded for the listening tests were mono, and the output from the physical model includes basic stereo panning. The listener position within the virtual space of the physical model was set to replicate the microphone position when the other sounds were recorded. Although we believe this would not have a strong affect on plausible ratings, examination of spatialisation should be undertaken within future evaluation, and recording swing sounds binaurally would be preferred.
Additional models could be developed to replicate other sporting equipment, for example hockey sticks, cricket bats or even tennis racquets or lacrosse sticks, which have meshed faces. A physical model of a ball travelling through the air may also be possible although the fluid dynamics will differ from that of a cylinder, and the spinning of the ball may add other sounds not possible from our model. Authenticity may also be increased if the swinging arc of the objects was not restricted to great circles on the surface of a sphere. Normal swings often have the arms extending at the elbow, creating more elliptical arcs.
7. Conclusions
This article has presented a physically-derived synthesis model for objects swinging through the air. Adjustable parameters allow the user to approximate objects or to predefine the dimensions of objects. It is possible to match the object dimensions to graphics and for them to be morphed in real time.
Listening tests indicated that for all objects, except the very thinnest, participants found our model as plausible as real-world recordings. We have also highlighted that recognising an object from hearing the sound only was extremely difficult without any form of training.
An initial evaluation of extending the shape of profiles by adding the cavity tone has been carried out. Further evaluation is required in relation to this, examining the profiles of known objects that contain cavities and the interaction between the two fundamental aeroacoustic tones.
Acknowledgments
Rod Selfridge is funded by ESPRC, Grant EP/G03723X/1. David Moffat is funded by EPSRC Studentship—Award Reference No. 1513645.
Author Contributions
Rod Selfridge was responsible for researching relevant fluid dynamics equations, design and implementations of the synthesis model. He was also involved in devising and running the tests, analysing results and evaluation of the synthesis model. He drafted the article, critically reviewed and implemented revisions. David Moffat was involved in generating alternative synthesis sounds for comparison, devising and running of the tests, collating the data as well as analysis and evaluation of the synthesis model. He contributed to presentation of results, critical reviewing and redrafting this article. Joshua D. Reiss supervised all aspects of the research, implementation, testing and analysis. He critically reviewed and redrafted the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Selfridge, R.; Moffat, D.; Reiss, J.D. Real-time Physical Model for Synthesis of Sword Swing Sounds. In Proceedings of the 14th Sound and Music Computing: Best Paper Award, Espoo, Finland, 5–8 July 2017. [Google Scholar]
- Marelli, D.; Aramaki, M.; Kronland-Martinet, R.; Verron, C. Time-frequency synthesis of noisy sounds with narrow spectral components. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 1929–1940. [Google Scholar] [CrossRef]
- Farnell, A. Designing Sound; MIT Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Böttcher, N.; Serafin, S. Design and evaluation of physically inspired models of sound effects in computer games. In Proceedings of the 35th International Conference: Audio for Games, London, UK, 11–13 February 2009. [Google Scholar]
- Mengual, L.; Moffat, D.; Reiss, J.D. Modal Synthesis of Weapon Sounds. In Proceedings of the 61st International Conference: Audio for Games, London, UK, 10–12 February 2016. [Google Scholar]
- Dobashi, Y.; Yamamoto, T.; Nishita, T. Real-time rendering of aerodynamic sound using sound textures based on computational fluid dynamics. ACM Trans. Graph. 2003, 22, 732–740. [Google Scholar] [CrossRef]
- Lighthill, M.J. On sound generated aerodynamically. I. General theory. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Curle, N. The influence of solid boundaries upon aerodynamic sound. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 231, 505–514. [Google Scholar] [CrossRef]
- Roger, M. Coupled oscillations in the aeroacoustics of a Katana blade. J. Acoust. Soc. Am. 2008, 123, 3023. [Google Scholar] [CrossRef]
- Selfridge, R.; Reiss, J.; Avital, E.; Tang, X. Physically Derived Synthesis Model of an Aeolian Tone. In Proceedings of the 141st Audio Engineering Society Convention: Best Student Paper Award, Audio Engineering Society, Los Angeles, CA, USA, 29 October–1 November 2016. [Google Scholar]
- Cheong, C.; Joseph, P.; Park, Y.; Lee, S. Computation of aeolian tone from a circular cylinder using source models. Appl. Acoust. 2008, 69, 110–126. [Google Scholar] [CrossRef]
- Gerrard, J. Measurements of the sound from circular cylinders in an air stream. Proc. Phys. Soc. Sect. B 1955, 68, 453. [Google Scholar] [CrossRef]
- Russell, D.A.; Titlow, J.P.; Bemmen, Y.J. Acoustic monopoles, dipoles, and quadrupoles: An experiment revisited. Am. J. Phys. 1999, 67, 660–664. [Google Scholar] [CrossRef]
- Fey, U.; König, M.; Eckelmann, H. A new Strouhal-Reynolds-number relationship for the circular cylinder in the range 47 < Re < 2 × 105. Phys. Fluids 1998, 10, 1547–1549. [Google Scholar]
- Goldstein, M.E. Aeroacoustics; McGraw-Hill International Book Co.: New York, NY, USA, 1976; Volume 1. [Google Scholar]
- Phillips, O.M. The intensity of Aeolian tones. J. Fluid Mech. 1956, 1, 607–624. [Google Scholar] [CrossRef]
- Hardin, J.C.; Lamkin, S.L. Aeroacoustic Computation of Cylinder Wake Flow. AIAA J. 1984, 22, 51–57. [Google Scholar] [CrossRef]
- Etkin, B.; Korbacher, G.; Keefe, R. Acoustic radiation from a stationary cylinder in a fluid stream (Aeolian tones). J. Acoust. Soc. Am. 1957, 29, 30–36. [Google Scholar] [CrossRef]
- Musafir, R. On The Sound Field of Organized Vorticity in Jet Flows. In Proceedings of the 13th International Congress on Acoustics, Belgrade, Serbia, 24–31 August 1989. [Google Scholar]
- Avital, E.; Alonso, M.; Supontisky, V. Computational aeroacoustics: The low speed jet. Aeronaut. J. 2008, 112, 405–414. [Google Scholar] [CrossRef]
- Norberg, C. Flow around a circular cylinder: Aspects of fluctuating lift. J. Fluids Struct. 2001, 15, 459–469. [Google Scholar] [CrossRef]
- Norberg, C. Effects of Reynolds Number and a Low-Intensity Freestream Turbulence on the Flow around a Circular Cylinder; Chalmers University of Technology: Goteborg, Sweden, 1987. [Google Scholar]
- Kasdin, N. Discrete simulation of colored noise and stochastic processes and 1/f α power law noise generation. Proc. IEEE 1995, 83, 802–827. [Google Scholar] [CrossRef]
- Mahmoud, H.; Akkari, N. Shortest Path Calculation: A Comparative Study for Location-Based Recommender System. In Proceedings of the World Symposium on Computer Applications & Research, Cairo, Egypt, 12–14 March 2016. [Google Scholar]
- Morrell, M.J.; Reiss, J.D. Inherent Doppler properties of spatial audio. In Proceedings of the 129th Audio Engineering Society Convention, San Francisco, CA, USA, 4–7 November 2010. [Google Scholar]
- Selfridge, R.; Reiss, J.; Avital, E. Physically Derived Synthesis Model of a Cavity Tone. In Proceedings of the 20th Digital Audio Effects Conference, Edinburgh, UK, 5–9 September 2017. [Google Scholar]
- Jillings, N.; De Man, B.; Moffat, D.; Reiss, J.D. Web Audio Evaluation Tool: A Browser-Based Listening Test Environment. In Proceedings of the 12th Sound and Music Computing, Maynooth, Ireland, 26 July–1 August 2015. [Google Scholar]
- Recommendation ITU_R BS.1534-3. Method for the Subjective Assessment of Intermediate Quality Level of Audio Systems; Technical Report; International Telecommunication Union Radiocommunication Assembly: Geneva, Switzerland, 2015. [Google Scholar]
- Amatriain, X.; Bonada, J.; Loscos, A.; Serra, X. Spectral processing. In DAFX: Digital Audio Effects; Wiley: Chichester, UK, 2002. [Google Scholar]
- Castagné, N.; Cadoz, C. 10 criteria for evaluating physical modelling schemes for music creation. In Proceedings of the 6th Digital Audio Effects Conference, London, UK, 8–11 September 2003. [Google Scholar]
- Gaver, W.W.; Norman, D.A. Everyday Listening and Auditory Icons. Ph.D. Thesis, University of California, San Diego, CA, USA, 1988. [Google Scholar]
- Reiss, J.D. A Meta-Analysis of High Resolution Audio Perceptual Evaluation. J. Audio Eng. Soc. 2016, 64, 364–379. [Google Scholar] [CrossRef]
- Moffat, D.; Ronan, D.; Reiss, J.D. Unsupervised Taxonomy of Sound Effects. In Proceedings of the 20th Digital Audio Effects Conference, Edinburgh, UK, 5–9 September 2017. [Google Scholar]
- Selfridge, R.; Moffat, D.; Reiss, J.D.; Avital, E. Real-Time Physical Model of an Aeolian Harp. In Proceedings of the 24th International Congress on Sound and Vibration, London, UK, 23–27 July 2017. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).