SymCHM—An Unsupervised Approach for Pattern Discovery in Symbolic Music with a Compositional Hierarchical Model
Abstract
1. Introduction
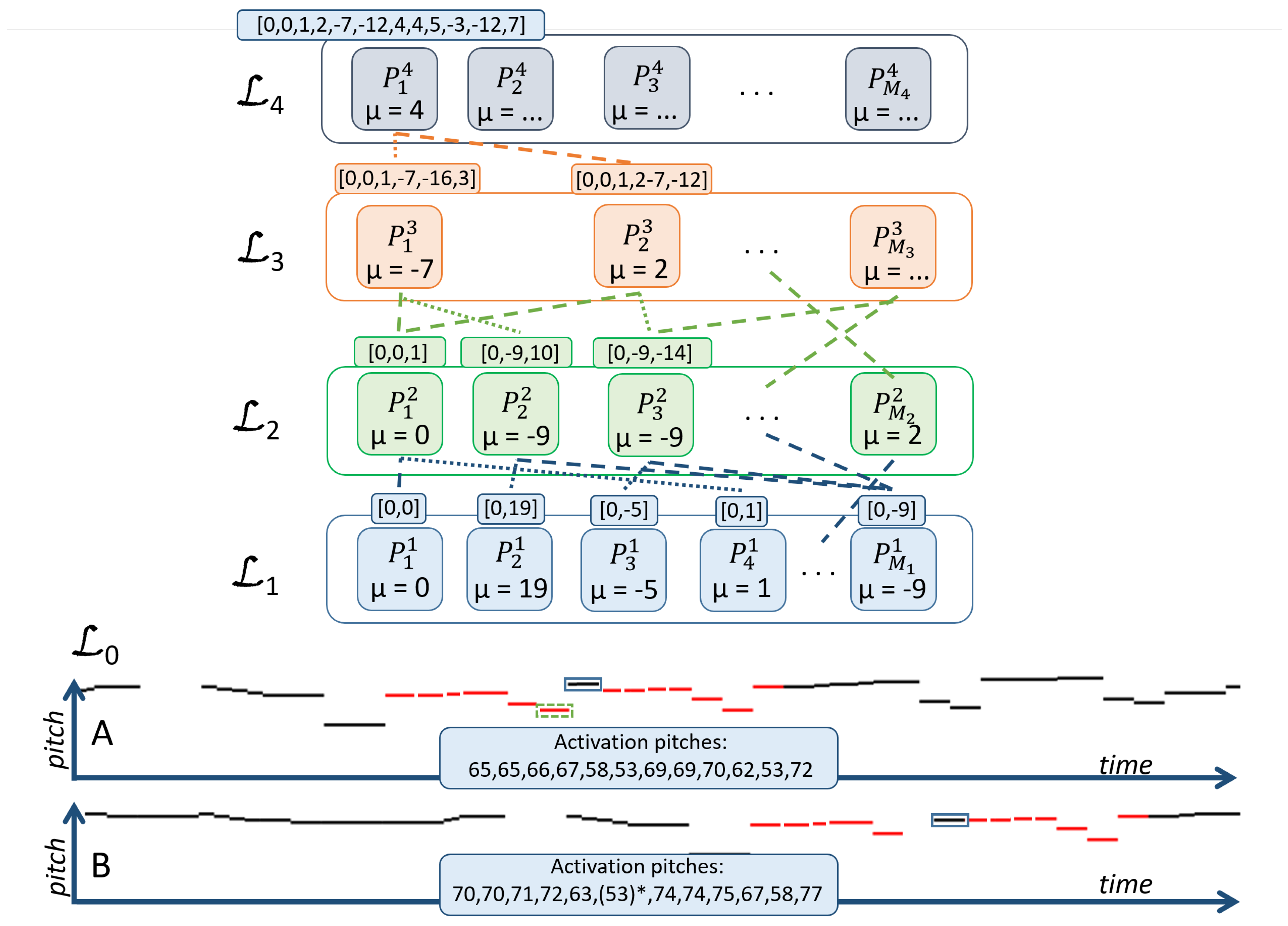
2. The Symbolic Compositional Hierarchical Model
2.1. Model Description
2.1.1. Compositional Layers
2.1.2. Activations: Occurrences of Patterns
2.1.3. The Input Representation and Input Layer
2.2. Constructing a Hierarchy of Parts
- the coverage of each part from is calculated as a union of events in the training data covered by all activations of the part,
- parts are iteratively added to the new layer by choosing the part that adds most to the coverage of the entire training set in each iteration. This ensures that only compositions that provide enough coverage of new data with regard to the currently selected set of parts will be added,
- the algorithm stops when the additional coverage falls below the learning threshold .
2.3. Inferring Patterns
2.3.1. Hallucination
2.3.2. Inhibition
3. Pattern Selection with SymCHM
3.1. Basic Selection
3.2. SymCHMMerge: Improved Pattern Selection
3.2.1. Merging Redundant Patterns
3.2.2. Increasing Diversity
4. Evaluation
- Bach’s Prelude and Fugue in A minor (BWV(Bach-Werke-Verzeichnis) 889): 731 note events, 3 patterns, 21 pattern occurrences,
- Beethoven’s Piano Sonata in F minor (Opus 2, No. 1), third movement: 638 note events, 7 patterns, 22 pattern occurrences,
- Chopin’s Mazurka in B flat minor (Opus 24, No. 4): 747 note events, 4 patterns, 94 pattern occurrences,
- Gibbons’ “The Silver Swan”: 347 note events, 8 patterns, 33 pattern occurrences,
- Mozart’s Piano Sonata in E flat major, K. 282-2nd movement: 923 note events, 9 patterns, 38 pattern occurrences.
4.1. Evaluation Metrics
- : the number of patterns in a ground truth
- : a set of ground truth patterns
- —occurrences of pattern
- : the number of patterns in the algorithm’s output
- : a set of patterns returned by the algorithm
- —occurrences of pattern .
- k: the number of ground truth patterns identified by the algorithm
4.2. Performance
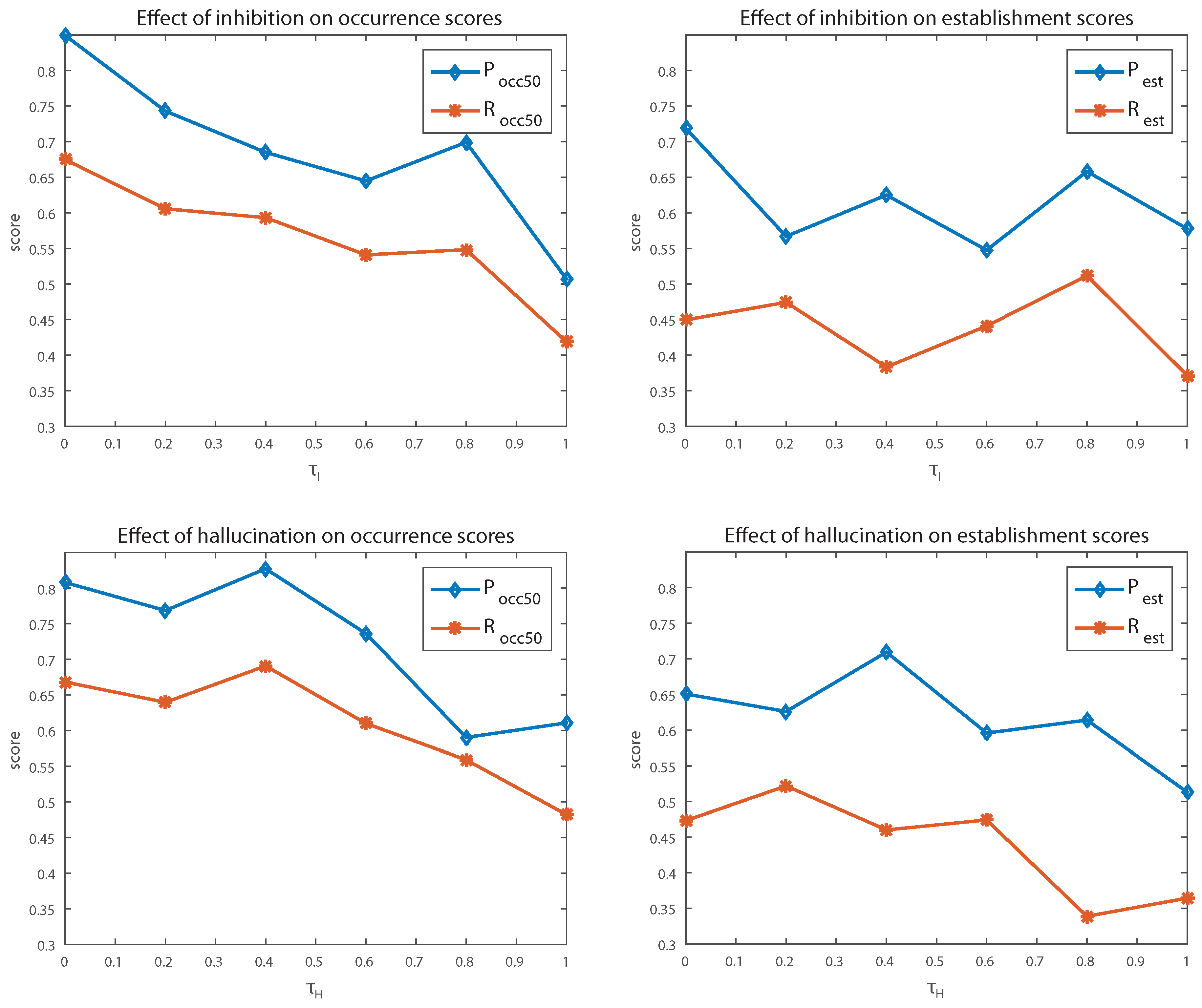
4.3. Sensitivity to Parameter Values
4.3.1. Inhibition
4.3.2. Hallucination
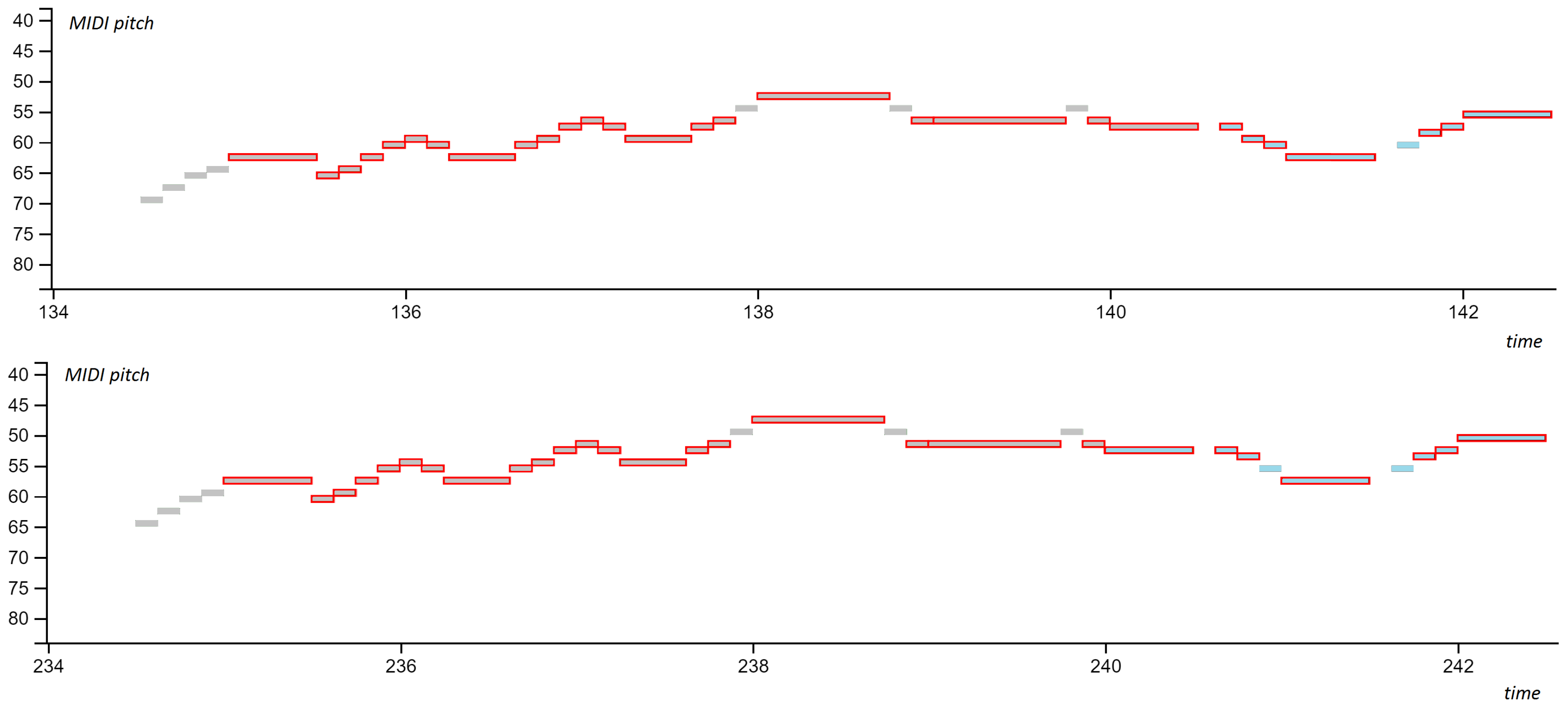
4.4. Error Analysis
4.4.1. Incomplete Matches
4.4.2. Unidentified Patterns
4.5. Drawbacks of the Evaluation
5. Conclusions
Author Contributions
Conflicts of Interest
Abbreviations
| CHM | Compositional Hierarchical Model |
| SymCHM | Compositional Hierarchical model for Symbolic music representations |
| SymCHMMerge | An extension of the SymCHM using a pattern merging technique |
References
- Lerdahl, F.; Jackendoff, R. A Generative Theory of Tonal Music; MIT Press: Cambridge, MA, USA, 1983. [Google Scholar]
- Hamanaka, M.; Hirata, K.; Tojo, S. Implementing “A Generative Theory of Tonal Music”. J. New Music Res. 2006, 35, 249–277. [Google Scholar] [CrossRef]
- Hirata, K.; Tojo, S.; Hamanaka, M. Techniques for Implementing the Generative Theory of Tonal Music. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Vienna, Austria, 23–30 September 2007. [Google Scholar]
- Marsden, A. Schenkerian Analysis by Computer: A Proof of Concept. J. New Music Res. 2010, 39, 269–289. [Google Scholar] [CrossRef]
- Todd, N. A Model of Expressive Timing in Tonal Music. Music Percept. Interdiscip. J. 1985, 3, 33–57. [Google Scholar] [CrossRef]
- Farbood, M. Working memory and the perception of hierarchical tonal structures. In Proceedings of the International Conference of Music Perception and Cognition, Seattle, WA, USA, 23–27 August 2010; pp. 219–222. [Google Scholar]
- Balaguer-Ballester, E.; Clark, N.R.; Coath, M.; Krumbholz, K.; Denham, S.L. Understanding Pitch Perception as a Hierarchical Process with Top-Down Modulation. PLoS Comput. Biol. 2009, 4, 1–15. [Google Scholar] [CrossRef] [PubMed]
- McDermott, J.H.; Oxenham, A.J. Music perception, pitch and the auditory system. Curr. Opin. Neurobiol. 2008, 18, 452–463. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, E.J.; Bello, J.P.; LeCun, Y. Moving beyond feature design: Deep architectures and automatic feature learning in music informatics. In Proceedings of the 13th International Conference on Music Information Retrieval (ISMIR), Porto, Portugal, 8–12 October 2012. [Google Scholar]
- Rigaud, F.; Radenen, M. Singing Voice Melody Transcription using Deep Neural Networks. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), New York, NY, USA, 7–11 August 2016; pp. 737–743. [Google Scholar]
- Jeong, I.Y.; Lee, K. Learning Temporal Features Using a Deep Neural Network and its Application to Music Genre Classification. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), New York, NY, USA, 7–11 August 2016; pp. 434–440. [Google Scholar]
- Schluter, J.; Bock, S. Musical Onset Detection with Convolutional Neural Networks. In Proceedings of the 6th International Workshop on Machine Learning and Music, held in Conjunction with the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases, ECML/PKDD 2013, Prague, Czech Republic, 23–27 September 2013. [Google Scholar]
- Battenberg, E.; Wessel, D. Analyzing Drum Patterns using Conditional Deep Belief Networks. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Porto, Portugal, 8–12 October 2012; pp. 37–42. [Google Scholar]
- Deng, J.; Kwok, Y.K. A Hybrid Gaussian-Hmm-Deep-Learning Approach for Automatic Chord Estimation with Very Large Vocabulary. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), New York, NY, USA, 7–11 August 2016; pp. 812–818. [Google Scholar]
- Campilho, A.; Kamel, M. (Eds.) Image Analysis and Recognition; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Gemany, 2012; Volume 7324. [Google Scholar]
- Coward, E.; Drabløs, F. Detecting periodic patterns in biological sequences. Bioinformatics 1998, 14, 498–507. [Google Scholar] [CrossRef] [PubMed]
- Margulis, E.H. On Repeat: How Music Plays the Mind; Oxford University Press: Oxford, UK, 2014; p. 224. [Google Scholar]
- Downie, J.S. The music information retrieval evaluation exchange (2005–2007): A window into music information retrieval research. Acoust. Sci. Technol. 2008, 29, 247–255. [Google Scholar] [CrossRef]
- Meredith, D.; Lemstrom, K.; Wiggins, G.A. Algorithms for discovering repeated patterns in multidimensional representations of polyphonic music. J. New Music Res. 2002, 31, 321–345. [Google Scholar] [CrossRef]
- The MIREX Discovery of Repeated Themes & Sections Task. Available online: http://www.music-ir.org/mirex/wiki/2015:Discovery_of_Repeated_Themes_%26_Sections (accessed on 19 June 2015).
- Collins, T.; Thurlow, J.; Laney, R.; Willis, A.; Garthwaite, P.H. A Comparative Evaluation of Algorithms for Discovering Translational Patterns in Baroque Keyboard Works. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Utrecht, Netherlands, 9–13 August 2010; pp. 3–8. [Google Scholar]
- Wang, C.I.; Hsu, J.; Dubnov, S. Music Pattern Discovery with Variable Markov Oracle: A Unified Approach to Symbolic and Audio Representations. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Malaga, Spain, 26–30 October 2015; pp. 176–182. [Google Scholar]
- Cambouropoulos, E.; Crochemore, M.; Iliopoulos, C.S.; Mohamed, M.; Sagot, M.F. A Pattern Extraction Algorithm for Abstract Melodic Representations that Allow Partial Overlapping of Intervallic Categories. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), London, UK, 11–15 September 2005; pp. 167–174. [Google Scholar]
- Conklin, D.; Bergeron, M. Feature Set Patterns in Music. Comput. Music J. 2008, 32, 60–70. [Google Scholar] [CrossRef]
- Conklin, D.; Anagnostopoulou, C. Representation and Discovery of Multiple Viewpoint Patterns. In Proceedings of the 2001 International Computer Music Conference, Havana, Cuba, 18–22 September 2001; pp. 479–485. [Google Scholar]
- Conklin, D. Melodic analysis with segment classes. Mach. Learn. 2006, 65, 349–360. [Google Scholar] [CrossRef]
- Rolland, P.Y. Discovering Patterns in Musical Sequences. J. New Music Res. 1999, 28, 334–350. [Google Scholar] [CrossRef]
- Owens, T. Charlie Parker: Techniques of Improvisation; Number Let. 1 in Charlie Parker: Techniques of Improvisation; University of California: Los Angeles, CA, USA, 1974. [Google Scholar]
- Cambouropoulos, E. Musical Parallelism and Melodic Segmentation. Music Percept. Interdiscip. J. 2006, 23. [Google Scholar] [CrossRef]
- Meredith, D. Music Analysis and Point-Set Compression. J. New Music Res. 2015, 44, 245–270. [Google Scholar] [CrossRef]
- Meredith, D. COSIATEC and SIATECCompress: Pattern Discovery by Geometric Compression. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Curitiba, Brazil, 4–8 November 2013; pp. 1–6. [Google Scholar]
- Velarde, G.; Meredith, D. Submission to MIREX Discovery of Repeated Themes and Sections. In Proceedings of the 10th Annual Music Information Retrieval eXchange (MIREX’14), Taipei, Taiwan, 27–31 October 2014; pp. 1–3. [Google Scholar]
- Velarde, G.; Weyde, T.; Meredith, D. An approach to melodic segmentation and classification based on filtering with the Haar-wavelet. J. New Music Res. 2013, 42, 325–345. [Google Scholar] [CrossRef]
- Lartillot, O. Submission to MIREX Discovery of Repeated Themes and Sections. In Proceedings of the 10th Annual Music Information Retrieval eXchange (MIREX’14), Taipei, Taiwan, 27–31 October 2014; pp. 1–3. [Google Scholar]
- Lartillot, O. In-depth motivic analysis based on multiparametric closed pattern and cyclic sequence mining. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Taipei, Taiwan, 27–31 October 2014; pp. 361–366. [Google Scholar]
- Ren, I.Y. Closed Patterns in Folk Music and Other Genres. In Proceedings of the 6th International Workshop on Folk Music Analysis, Dublin, Ireland, 15–17 June 2016; pp. 56–58. [Google Scholar]
- Nieto, O.; Farbood, M. MIREX 2014 Entry: Music Segmentation Techniques And Greedy Path Finder Algorithm To Discover Musical Patterns. In Proceedings of the 10th Annual Music Information Retrieval eXchange (MIREX’14), Taipei, Taiwan, 27–31 October 2014; pp. 1–2. [Google Scholar]
- Nieto, O.; Farbood, M.M. Identifying Polyphonic Patterns From Audio Recordings Using Music Segmentation Techniques. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Taipei, Taiwan, 27–31 October 2014; pp. 411–416. [Google Scholar]
- Reber, A.S. Implicit Learning and Tacit Knowledge : An Essay on the Cognitive Unconscious; Oxford University Press: Oxford, UK, 1993. [Google Scholar]
- Pesek, M.; Leonardis, A.; Marolt, M. A compositional hierarchical model for music information retrieval. In Proceedings of the International Conference on Music Information Retrieval (ISMIR), Taipei, Taiwan, 27–31 October 2014; pp. 131–136. [Google Scholar]
- Pesek, M.; Leonardis, A.; Marolt, M. Robust Real-Time Music Transcription with a Compositional Hierarchical Model. PLoS ONE 2017, 12. [Google Scholar] [CrossRef] [PubMed]
- Fidler, S.; Boben, M.; Leonardis, A. Learning Hierarchical Compositional Representations of Object Structure. In Object Categorization: Computer and Human Vision Perspectives; Cambridge University Press: Cambridge, UK, 2009; pp. 196–215. [Google Scholar]
- Meredith, D. Method of Computing the Pitch Names of Notes in MIDI-Like Music Representations. US Patent US 20040216586 A1, 4 November 2004. [Google Scholar]
- Collins, T. JKU Patterns Development Database. August 2013. Available online: https://dl.dropbox.com/u/11997856/JKU/JKUPDD-Aug2013.zip (accessed on 13 September 2017).
- Meredith, D. COSIATEC and SIATECCompress: Pattern Discovery by Geometric Compression. In Proceedings of the 9th Annual Music Information Retrieval eXchange (MIREX’13), Curitiba, Brazil, 4–8 November 2013. [Google Scholar]
- Temperley, D. The Cognition of Basic Musical Structures; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
| Parameter | Description | Value |
|---|---|---|
| Hallucination parameter retaining the activation of a part in an incomplete presence of the events in the input signal | 0.5 | |
| Inhibition parameter reducing the number of competing activations | 0.4 | |
| Redundancy parameter determining the the necessary amount of overlapping pattern occurrences in order for the occurrences to be merged | 0.5 | |
| Merging parameter determining the amount of redundant pattern occurrences needed for two patterns to be merged into one | 0.5 | |
| Learning threshold for added coverage which needs to be exceeded in order for a candidate composition to be retained while learning the model | 0.005 | |
| Window limiting the time span of activations, defined per layer |
| Algorithm | |||||||
| SymCHM MIREX 2015 | 53.36 | 41.40 | 42.32 | 81.34 | 59.84 | 67.92 | |
| NF1 MIREX 2014 | 50.06 | 54.42 | 50.22 | 59.72 | 32.88 | 40.86 | |
| DM1 MIREX 2013 | 52.28 | 60.86 | 54.80 | 56.70 | 75.14 | 62.42 | |
| OL1 MIREX 2015 | 61.66 | 56.10 | 49.76 | 87.90 | 75.98 | 80.66 | |
| VM2 MIREX 2015 | 65.14 | 63.14 | 62.74 | 60.06 | 58.44 | 57.00 | |
| SymCHM JKU PDD | 67.92 | 45.36 | 51.01 | 93.90 | 82.72 | 86.85 | |
| SymCHMMerge JKU PDD | 67.96 | 50.67 | 56.97 | 88.61 | 75.66 | 80.02 | |
| SymCHM MIREX 2015 | 37.78 | 73.34 | 62.48 | 67.24 | 10.64 | 6.50 | 5.12 |
| NF1 MIREX 2014 | 33.28 | 54.98 | 33.40 | 40.80 | 1.54 | 5.00 | 2.36 |
| DM1 MIREX 2013 | 43.28 | 47.20 | 74.46 | 56.94 | 2.66 | 4.50 | 3.24 |
| OL1 MIREX 2015 | 42.72 | 78.78 | 71.08 | 74.50 | 16.0 | 23.74 | 12.36 |
| VM2 MIREX 2015 | 42.20 | 46.14 | 60.98 | 51.52 | 6.20 | 6.50 | 6.2 |
| SymCHM JKU PDD | 51.75 | 78.53 | 72.99 | 75.41 | 25.00 | 13.89 | 17.18 |
| SymCHMMerge JKU PDD | 52.89 | 83.23 | 68.86 | 73.88 | 35.83 | 20.56 | 25.63 |
| Piece | |||||||||
| bach | 3 | 2 | 100.00 | 66.67 | 80.00 | 100.00 | 45.65 | 62.68 | |
| beet | 7 | 7 | 65.81 | 60.02 | 62.78 | 80.71 | 80.71 | 80.71 | |
| chop | 4 | 5 | 47.95 | 49.81 | 48.86 | 62.36 | 51.96 | 56.69 | |
| gbns | 8 | 3 | 78.16 | 35.49 | 48.81 | 100.00 | 100.00 | 100.00 | |
| mzrt | 9 | 8 | 47.88 | 41.39 | 44.40 | 100.00 | 100.00 | 100.00 | |
| Average | 6.2 | 5 | 67.96 | 50.67 | 56.97 | 88.61 | 75.66 | 80.02 | |
| Piece | |||||||||
| bach | 62.96 | 41.97 | 50.37 | 100.00 | 45.65 | 62.68 | 100.00 | 66.67 | 80.00 |
| beet | 77.38 | 64.95 | 70.62 | 79.24 | 72.44 | 75.69 | 0.00 | 0.00 | 0.00 |
| chop | 46.96 | 39.92 | 43.15 | 57.00 | 46.29 | 51.09 | 0.00 | 0.00 | 0.00 |
| gbns | 81.82 | 34.33 | 48.37 | 100.00 | 100.00 | 100.00 | 66.67 | 25.00 | 36.36 |
| mzrt | 57.21 | 47.54 | 51.93 | 79.92 | 79.92 | 79.92 | 12.50 | 11.11 | 11.77 |
| Average | 65.27 | 45.74 | 52.89 | 83.23 | 68.86 | 73.88 | 35.83 | 20.56 | 25.63 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pesek, M.; Leonardis, A.; Marolt, M. SymCHM—An Unsupervised Approach for Pattern Discovery in Symbolic Music with a Compositional Hierarchical Model. Appl. Sci. 2017, 7, 1135. https://doi.org/10.3390/app7111135
Pesek M, Leonardis A, Marolt M. SymCHM—An Unsupervised Approach for Pattern Discovery in Symbolic Music with a Compositional Hierarchical Model. Applied Sciences. 2017; 7(11):1135. https://doi.org/10.3390/app7111135
Chicago/Turabian StylePesek, Matevž, Aleš Leonardis, and Matija Marolt. 2017. "SymCHM—An Unsupervised Approach for Pattern Discovery in Symbolic Music with a Compositional Hierarchical Model" Applied Sciences 7, no. 11: 1135. https://doi.org/10.3390/app7111135
APA StylePesek, M., Leonardis, A., & Marolt, M. (2017). SymCHM—An Unsupervised Approach for Pattern Discovery in Symbolic Music with a Compositional Hierarchical Model. Applied Sciences, 7(11), 1135. https://doi.org/10.3390/app7111135







