Review of the Remaining Useful Life Prognostics of Vehicle Lithium-Ion Batteries Using Data-Driven Methodologies
Abstract
:1. Introduction
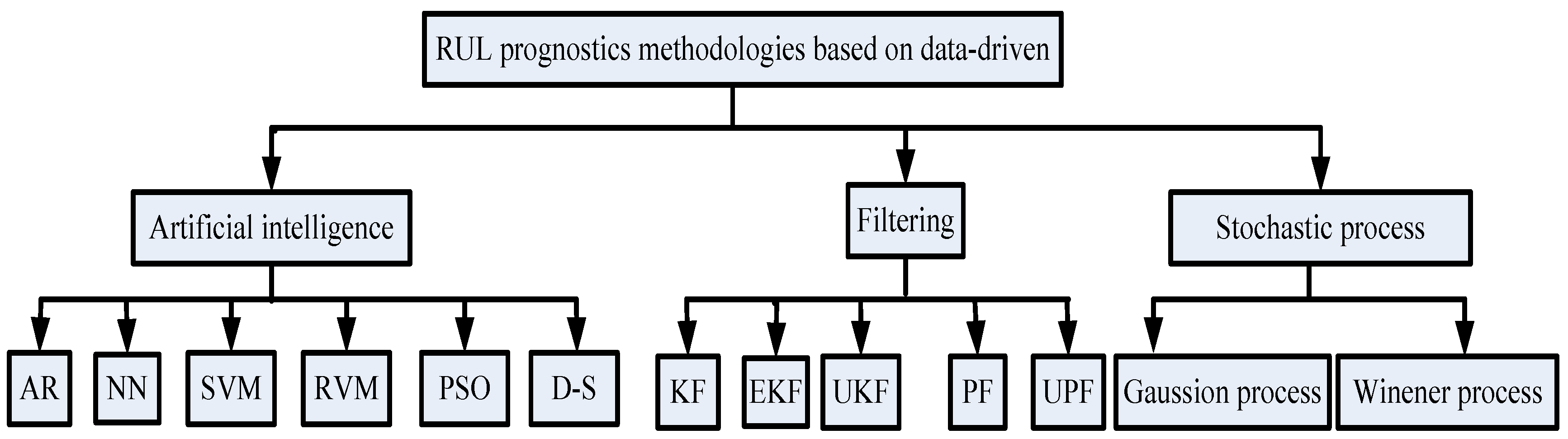
2. Remaining Useful Life (RUL) Prognostics Methodologies
2.1. RUL Prognostics Methodologies Based on Artificial Intelligence
2.2. RUL Prognostics Methodologies Based on Filtering Techniques
2.3. RUL Prognostics Methodologies Based on the Stochastic Degradation Process
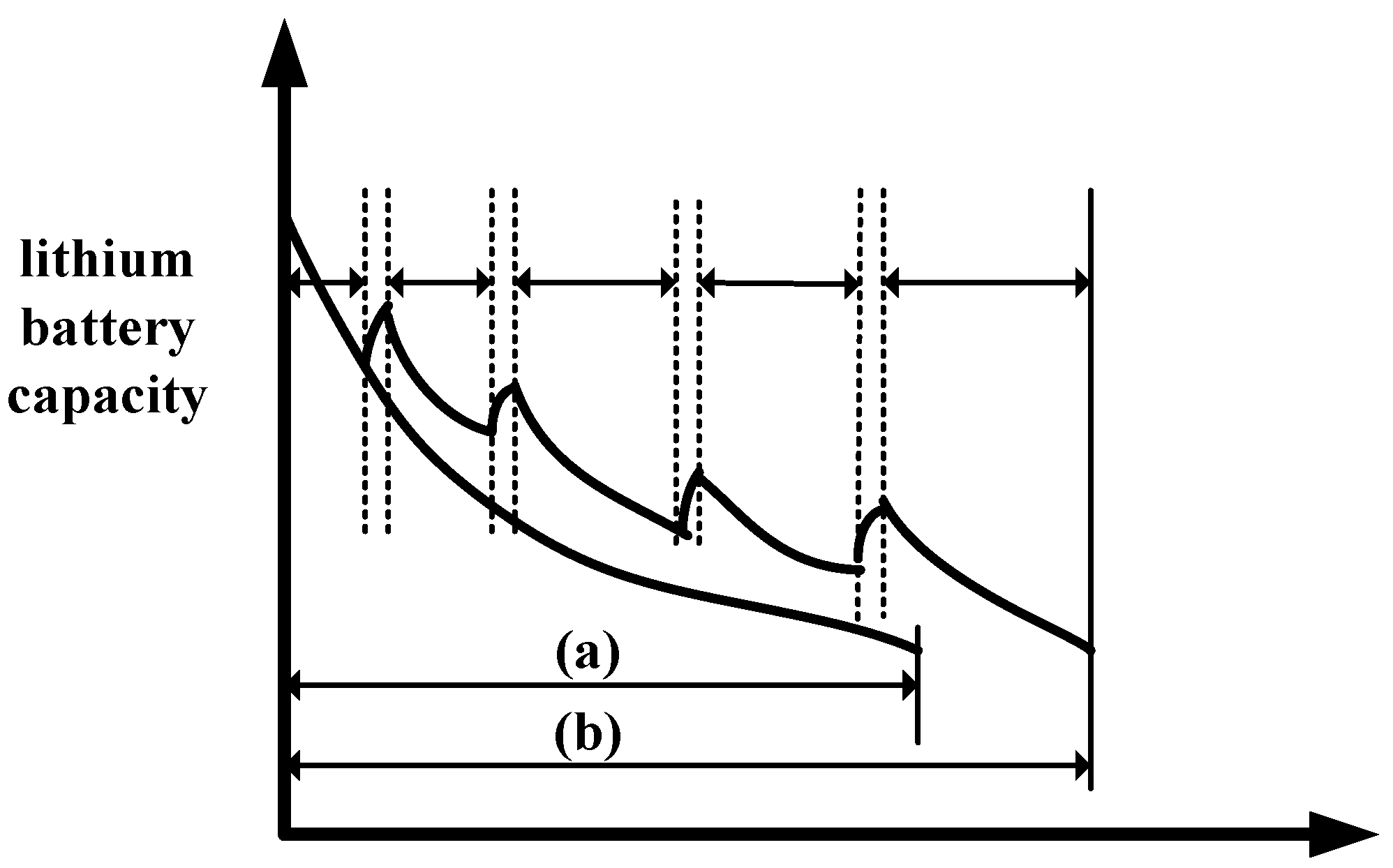
3. Problem Analysis
- (1)
- Degradation modeling and RUL prediction methods for vehicle lithium-ion batteries with time-varying ambient temperature
- (2)
- Degradation modeling and RUL prediction methods for vehicle lithium-ion batteries with a random variable current
- (3)
- Degradation modeling and RUL prediction methods for vehicle lithium-ion batteries considering self-recharge characteristics
- (4)
- Denoising of random signals for vehicle lithium-ion batteries considering the system configuration of the cars
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hu, J.; Morais, H.; Sousa, T.; Lind, M. Electric vehicle fleet management in smart grids: A review of services, optimization and control aspects. Renew. Sustain. Energy Rev. 2016, 56, 1207–1226. [Google Scholar] [CrossRef] [Green Version]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S.; Wild, M. A review on electric vehicle battery modeling: From Lithium-ion toward Lithium–Sulphur. Renew. Sustain. Energy Rev. 2016, 56, 1008–1021. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Dubé, Y. A comprehensive review of lithium-ion batteries used in hybrid and electric vehicles at cold temperatures. Appl. Energy 2016, 164, 99–114. [Google Scholar] [CrossRef]
- Battery Defect Is the Biggest Hidden Trouble of Pure Electric Vehicles. Available online: http://finance.sina.com.cn/roll/20150429/113022073040.shtml (accessed on 29 April 2015).
- Self ignition electric vehicle. Available online: http://www.diandong.com/news/201508312701.shtml (accessed on 31 August 2015).
- Tesla Model S Catches Fire at Supercharger Station in Norway. Available online: http://blog.caranddriver.com/tesla-model-s-catches-fire-at-supercharger-station-in-norway (accessed on 4 January 2016).
- Escobar, L.A.; Meeker, W.Q.; Luis, A.; William, E.; Meeker, Q. A review of accelerated test models. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef]
- Chen, C.; Pecht, M. Prognostics of Lithium-Ion Batteries Using Model Based and Data-Driven Methods. In Proceedings of the 2012 Prognostics & System Health Management Conference, Beijing, China, 23–25 May 2012.
- Lin, C.; Tang, A.; Wang, W. A review of SOH estimation methods in Lithium-ion batteries for electric vehicle applications. Energy Proc. 2015, 75, 1920–1925. [Google Scholar] [CrossRef]
- Liu, D.; Luo, Y.; Liu, J.; Peng, Y.; Guo, L.; Pecht, M. Lithium-ion battery remaining useful life estimation based on fusion nonlinear degradation AR model and RPF algorithm. Neural Comput. Appl. 2013, 25, 557–572. [Google Scholar] [CrossRef]
- Si, X.S.; Wang, W.; Hu, C.H.; Zhou, D.H. Remaining useful life estimation-A review on the statistical data driven approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Long, B.; Xian, W.; Jiang, L.; Liu, Z. An improved autoregressive model by particle swarm optimization for prognostics of lithium-ion batteries. Microelectr. Reliab. 2013, 53, 821–831. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Bertrand, N.; Delétage, J.Y.; Vinassa, J.M. Behavior and state-of-health monitoring of Li-ion batteries using impedance spectroscopy and recurrent neural networks. Int. J. Electr. Power Energy Syst. 2012, 42, 487–494. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Cho, B.H. Complementary cooperation algorithm based on DEKF combined with pattern recognition for SOC/Capacity estimation and SOH prediction. IEEE Trans. Power Electr. 2012, 27, 436–451. [Google Scholar] [CrossRef]
- Bai, G.; Wang, P.; Hu, C.; Pecht, M. A generic model-free approach for lithium-ion battery health management. Appl. Energy 2014, 135, 247–260. [Google Scholar] [CrossRef]
- Min, W. Lithium battery remaining capacity prediction method. Rural. Electr. 2008, 7, 15–16. [Google Scholar]
- Wu, Z.Y.; Cao, L.-H.; Chao, T.; Li, T.; Zeng, L.-B.; Hu, B. Research of Modified Elman Neural Network in the Lithium-ion Battery Capacity Prediction Method. J. Southwest Univ. Sci. Technol. 2012, 27, 65–69. [Google Scholar]
- Liu, J.; Saxena, A.; Goebel, K. An adaptive recurrent neural network for remaining useful life prediction of lithimion batteries. In Proceedings of the Annual Conference of Prognostics and Health Management Society, Portland, OR, USA, 10–16 October 2010; pp. 1–9.
- Wang, S.; Zhao, L.-L.; Su, X.-H.; Ma, P.-J. Prognostics of Lithium-Ion batteries based on battery performance analysis and flexible support vector regression. Energies 2014, 7, 6492–6508. [Google Scholar] [CrossRef]
- Dong, H.-C.H.; Jin, X.-N.; Lou, Y.-B. Lithium-ion battery state of health monitoring and remaining useful life prediction based on support vector regression-particle filter. J. Power Sources 2014, 271, 114–123. [Google Scholar] [CrossRef]
- Klass, V.; Behm, M.; Lindbergh, G. A support vector machine-based state-of-health estimation method for lithium-ion batteries under electric vehicle operation. J. Power Sources 2014, 270, 262–272. [Google Scholar] [CrossRef]
- Nuhic, A.; Terzimehic, T.; Soczka-Guth, T.; Buchholz, M.; Dietmayer, K. Health diagnosis and remaining useful life prognostics of lithium-ion batteries using data-driven methods. J. Power Sources 2013, 239, 680–688. [Google Scholar] [CrossRef]
- Chen, X.-Z.; Yu, J.-S.; Tang, D.-Y.; Wang, Y.-X. Probabilistc Residual life prediction for lithium-ion batteries based on Bayesian LS-SVR. Atca Aeronaut. Astron. Sin. 2013, 34, 2219–2229. [Google Scholar]
- Zhang, J.; Lee, J. A review on prognostics and health monitoring of Li-ion battery. J. Power Sources 2011, 196, 6007–6014. [Google Scholar] [CrossRef]
- Hu, C.; Jain, G.; Schmidt, C.; Strief, C.; Sullivan, M. Online estimation of lithium-ion battery capacity using sparse Bayesian learning. J. Power Sources 2015, 289, 105–113. [Google Scholar] [CrossRef]
- Ng, S.S.Y.; Xing, Y.; Tsui, K.L. A naive Bayes model for robust remaining useful life prediction of lithium-ion battery. Appl. Energy 2014, 118, 114–123. [Google Scholar] [CrossRef]
- Wang, D.; Miao, Q.; Pecht, M. Prognostics of lithium-ion batteries based on relevance vectors and a conditional three-parameter capacity degradation model. J. Power Sources 2013, 239, 253–264. [Google Scholar] [CrossRef]
- Liu, D.-T.; Zhou, J.-B.; Liao, H.-T. A health indicator extraction and optimization framework for lithium-ion battery degradation modeling and prognostics. IEEE Trans. Syst. Man Cybern. Syst. 2015, 45, 915–928. [Google Scholar]
- Widodo, A.; Shim, M.C.; Caesarendra, W.; Yang, B.S. Intelligent prognostics for battery health monitoring based on sample entropy. Expert Syst. Appl. 2011, 38, 11763–11769. [Google Scholar] [CrossRef]
- Zhou, J.; Ma, Y.; Peng, Y.; Peng, X. Remaining Useful Life Estimation with Dynamic Grey Relevance Vector Machine for Lithium-ion Battery. Int. J. Adv. Comput. Technol. 2013, 5, 460–469. [Google Scholar]
- Miao, Q.; Viliam, M. Condition monitoring of rotating machinery hidden markov models. Acta Aeronaut. Astron. Sin. 2005, 26, 641–646. [Google Scholar]
- Yuan, Y.; Zhuo, D.-F. Application of Hidden Semi—Markov Model in Prediction of Residual Life. Comput. Technol. Dev. 2014, 24, 184–191. [Google Scholar]
- Zhang, C.-L.; He, Y.-G.; Yuan, L.-F. Prognostics of lithium-Ion batteries based on wavelet denoising and DE-RVM. Comput. Intell. Neurosci. 2015, 2015, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Tseng, K.-H.; Liang, J.-W.; Chang, W.-C. Regression models using fully discharged voltage and internal resistance for state of health estimation of Lithium-Ion batteries. Energies 2015, 8, 2889–2907. [Google Scholar] [CrossRef]
- Orchard, M.E.; Hevia-Koch, P.; Zhang, B.; Tang, L. Risk measures for particle-filtering-based state-of-charge prognosis in Lithium-Ion batteries. IEEE Trans. Ind. Electr. 2013, 60, 5260–5269. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Chao, H.; Gaurav, J.; Zhang, P.-Q. Data-driven method based on particle swarm optimization and k-nearest neighbor regression for estimating capacity of lithium-ion battery. Appl. Energy 2014, 129, 49–55. [Google Scholar]
- Chen, Y.; Miao, Q.; Zheng, B.; Wu, S.; Pecht, M. Quantitative Analysis of Lithium-Ion Battery Capacity Prediction via Adaptive Bathtub-Shaped Function. Energies 2013, 6, 3082–3096. [Google Scholar] [CrossRef]
- Wang, S.; Shang, L.; Li, Z.; Deng, H.; Ma, Y. Lithium-ion battery security guaranteeing method study based on the state of charge estimation. Int. J. Electrochem. Sci. 2015, 10, 5130–5151. [Google Scholar]
- Sepasi, S.; Ghorbani, R.; Liaw, B.Y. Inline state of health estimation of lithium-ion batteries using state of charge calculation. J. Power Sources 2015, 299, 246–254. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for electric vehicle batteries using unscented kalman filtering. Microelectr. Reliab. 2013, 53, 840–847. [Google Scholar] [CrossRef]
- Zheng, X.-J.; Fang, H.-J. An integrated unscented kalman filter and relevance vector regression approach for lithium-ion battery remaining useful life and short-term capacity prediction. Reliab. Eng. Syst. Saf. 2015, 144, 74–82. [Google Scholar] [CrossRef]
- Yu, J.-B. State-of-health monitoring and prediction of lithium-ion battery using probabilistic indication and state-space model. IEEE Trans. Instrum. Meas. 2015, 64, 2937–2949. [Google Scholar]
- Miao, Q.; Cui, H.-J.; Zhou, X. Remaining useful life prediction of the lithium-ion battery using particle filtering. J. Chongqing Univ. 2013, 36, 47–52, 60. [Google Scholar]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. An Ensemble Model for Predicting the Remaining Useful Performance of Lithium-ion Batteries. Microelectr. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
- Liu, D.-T.; Pang, J.-Y.; Zhou, J.-B.; Peng, Y.; Pecht, M. Prognostics for state of health estimation of lithium-ion batteries based on combination Gaussian process functional regression. Microelectr. Reliab. 2013, 53, 832–839. [Google Scholar] [CrossRef]
- Li, F.; Xu, J.-P. A new prognostics method for state of health estimation of lithium-ion batteries based on a mixture of Gaussian process models and particle filter. Microelectr. Reliab. 2015, 55, 1035–1045. [Google Scholar] [CrossRef]
- Yi, J.; Shen, J.N.; Shen, J.-F. State of health estimation of lithium-ion batteries: A multiscale Gaussian process regression modeling approach. Aiche J. 2015, 61, 1589–1600. [Google Scholar]
- Tang, S.; Yu, C.; Wang, X.; Guo, X.; Si, X. Remaining useful life prediction of Lithium-Ion batteries based on the Wiener process with measurement error. Energies 2014, 7, 520–547. [Google Scholar] [CrossRef]
- Dalal, M.; Ma, J.; He, D. Lithium-ion battery life prognostic health management system using particle filtering framework. Proc. Inst. Mech. Eng. Part J. Risk Reliab. 2011, 225, 81–90. [Google Scholar] [CrossRef]
- Walker, E.; Rayman, S.; White, R.E. Comparison of a particle filter and other state estimation methods for prognostics of lithium-ion batteries. Diss. Theses Gradworks 2013, 287, 1–12. [Google Scholar] [CrossRef]
- Pola, D.; Navarrete, H.F.; Orchard, M.E.; Rabie, R.S.; Cerda, M.A.; Olivares, B.E.; Silva, J.F.; Espinoza, P.A.; Perez, A. Particle-Filtering-Based Discharge Time Prognosis for Lithium-Ion Batteries With a Statistical Characterization of Use Profiles. IEEE Trans. Reliab. 2015, 64, 1–11. [Google Scholar] [CrossRef]
- Wang, D.; Yang, F.; Tsui, K.L.; Zhou, Q.; Bae, S.J. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Spherical Cubature Particle Filter. IEEE Trans. Instrum. Meas. 2016, in press. [Google Scholar] [CrossRef]
- Miao, Q.; Xie, L.; Cui, H.; Liang, W.; Pecht, M. Remaining useful life prediction of lithium-ion battery with unscented particle filter technique. Microelectr. Reliab. 2013, 53, 805–810. [Google Scholar] [CrossRef]
- Goebel, K.; Saha, B.; Saxena, A.; Celaya, J.R.; Christophersen, J.P. Prognostics in battery health management. IEEE Instrum. Meas. Mag. 2008, 11, 33–40. [Google Scholar] [CrossRef]
- Lei, Z.-G.; Zhang, C.-N.; Li, J.-Q. Research on Thermal Characteristics of EVs Lithium—Ion Battery. J. Power Supply 2014, 5, 83–87. [Google Scholar]
- Li, P.; An, F.-Q.; Zhang, J.-B.; Wang, H.-R. Temperature sensitivity of lithium-ion battery: A review. J Automot. Saf. Energy 2014, 5, 224–237. [Google Scholar]
- Selman, J.R.; Hallaj, S.A.; Uchida, I.; Hirano, Y. Cooperative research on safety fundamentals of lithium batteries. J. Power Sources 2001, 97–98, 726–732. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. Battery management systems in electric and hybrid vehicles. Energies 2011, 4, 1840–1857. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Cycle Life of Commercial Lithium-Ion Batteries with Lithium Titanium Oxide Anodes in Electric Vehicles. Energies 2014, 7, 4895–4909. [Google Scholar] [CrossRef]
- Ma, Z.-Y.; Jiang, J.-C.; Zhang, W.-G.; Wang, Z.-G.; Zheng, L.-F.; Shi, W. Research on Path Dependence of Large Format LiMn2O4 Battery Degradation in Thermal Aging. Trans. China Electrotech. Soc. 2014, 29, 221–227. [Google Scholar]
- Li, Y.; Hu, Y.; Liu, Q.-G. Influence of discharge rate on cycling performance of lithium-ion battery. Chin. J. Power Sources 2006, 6, 488–491. [Google Scholar] [CrossRef]
- Xue, Y. A car-following model with stochastically considering the relative velocity in a traffic flow. Acta Phys. Sin. 2003, 52, 2750–2756. [Google Scholar]
- Yang, Q.; Liu, Y.-S. Robust Adaptive Observer for the Charge of Battery with Charging and Discharging Uncertainties. J. Chongqing Univ. 2015, 47, 1009–3087. [Google Scholar]
| Methodology | Advantages | Disadvantages | Main Relevant References |
|---|---|---|---|
| Artificial intelligence | (a) Does not need a data model (b) The algorithms are simple and feasible (c) The algorithms are the best solution for non-linear systems | (a) The point estimated value of RUL (b) Does not describe the uncertainty of measurement results | [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33] |
| Filtering techniques | (a) Can be used in any form of state-space model (b) best solution for non-linear, Gaussian, and non-Gaussian systems | (a) Needs data mode (state-space model) (b) The point estimated value of RUL | [34,35,36,37,38,39,40,41,42,43,44,45] |
| Stochastic process | (a) Considers the time-dependence of the degradation process (b) Describes the uncertainty of predictable results | (a) Higher calculation complexity (b) Considers uncertain factors | [46,47,48,49] |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, L.; Fu, X.; Guan, Y. Review of the Remaining Useful Life Prognostics of Vehicle Lithium-Ion Batteries Using Data-Driven Methodologies. Appl. Sci. 2016, 6, 166. https://doi.org/10.3390/app6060166
Wu L, Fu X, Guan Y. Review of the Remaining Useful Life Prognostics of Vehicle Lithium-Ion Batteries Using Data-Driven Methodologies. Applied Sciences. 2016; 6(6):166. https://doi.org/10.3390/app6060166
Chicago/Turabian StyleWu, Lifeng, Xiaohui Fu, and Yong Guan. 2016. "Review of the Remaining Useful Life Prognostics of Vehicle Lithium-Ion Batteries Using Data-Driven Methodologies" Applied Sciences 6, no. 6: 166. https://doi.org/10.3390/app6060166
APA StyleWu, L., Fu, X., & Guan, Y. (2016). Review of the Remaining Useful Life Prognostics of Vehicle Lithium-Ion Batteries Using Data-Driven Methodologies. Applied Sciences, 6(6), 166. https://doi.org/10.3390/app6060166





