Determination of Optimal Initial Weights of an Artificial Neural Network by Using the Harmony Search Algorithm: Application to Breakwater Armor Stones
Abstract
:1. Introduction
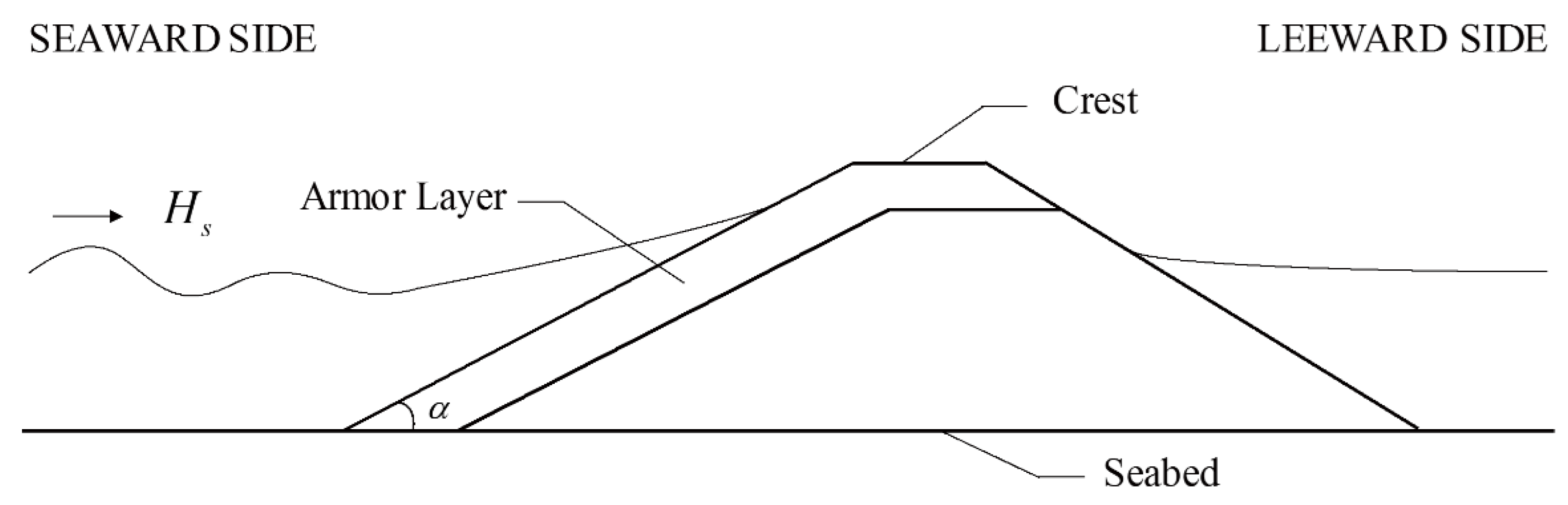
2. Previous Studies for Estimation of Stability Number
3. Development of an HS-ANN Hybrid Model
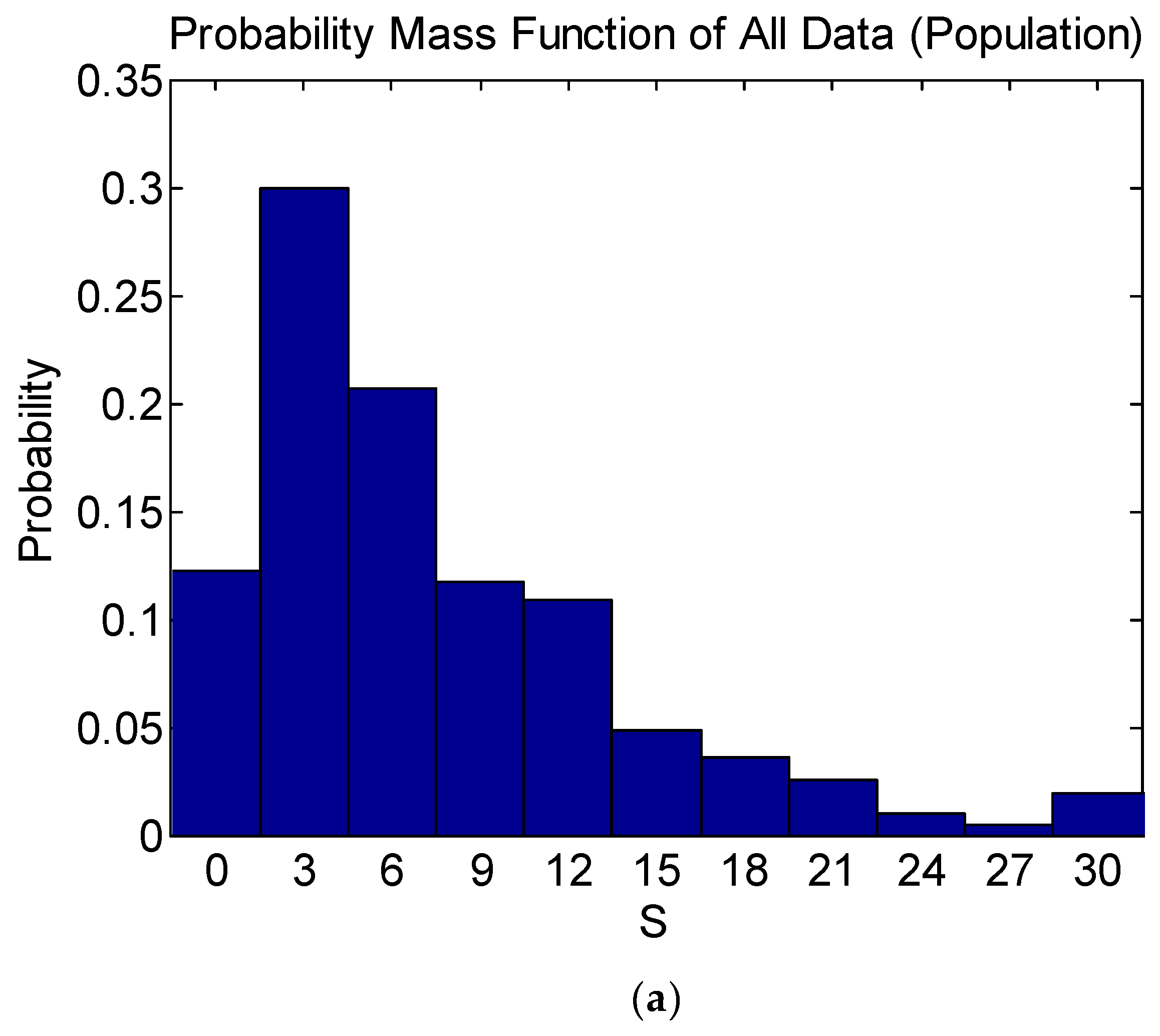
3.1. Sampling of Training Data of ANN Model
3.2. ANN Model
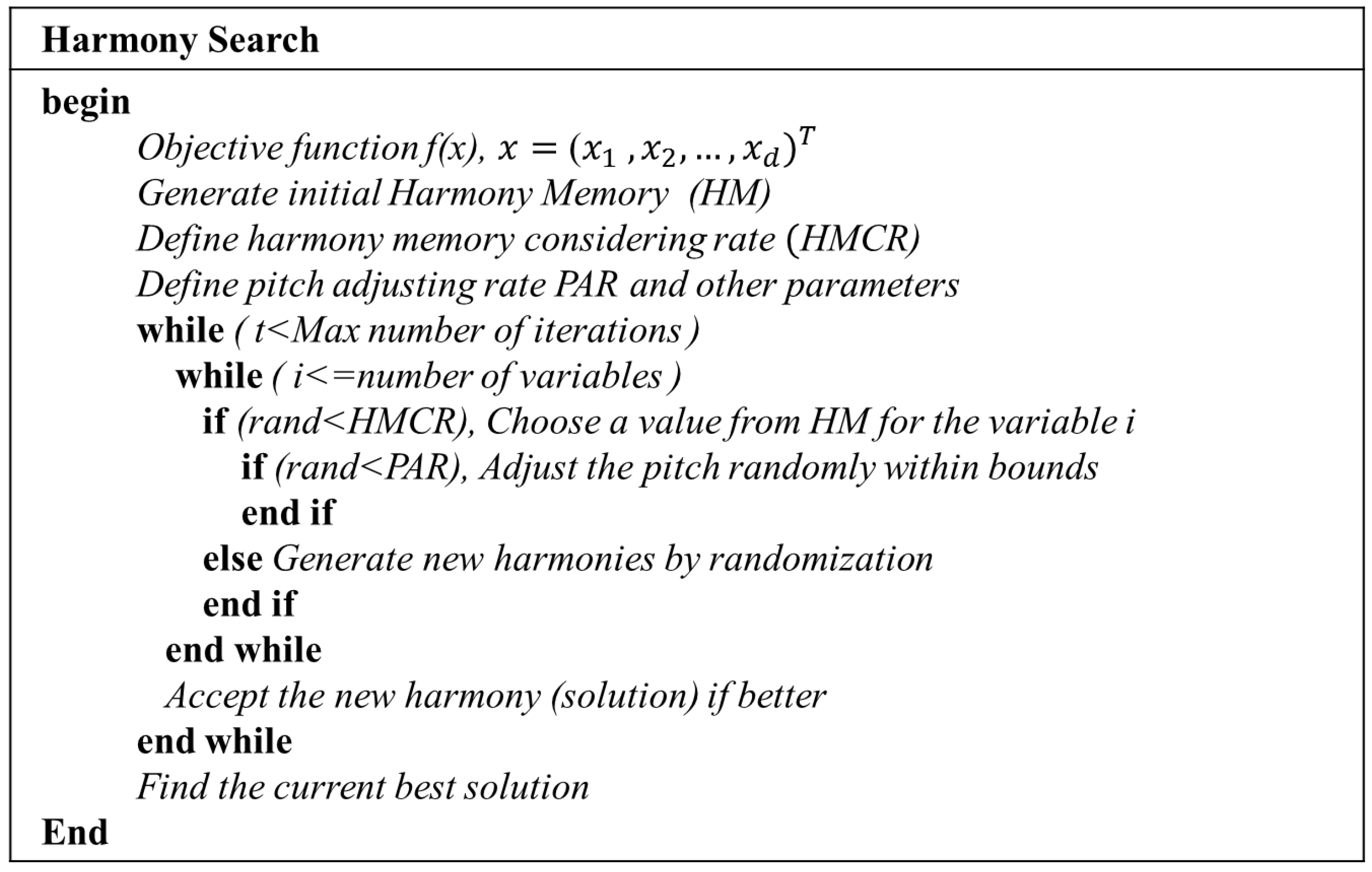
3.3. HS-ANN Hybrid Model
Step 1. Initialization of the algorithm parameters
Step 2. Initialization of harmony memory
Step 3. Improvise a new harmony from the HM
Step 4. Evaluate new harmony and update the HM
Step 5. Repeat Steps 3 and 4 until the termination criterion is satisfied
4. Result and Discussion
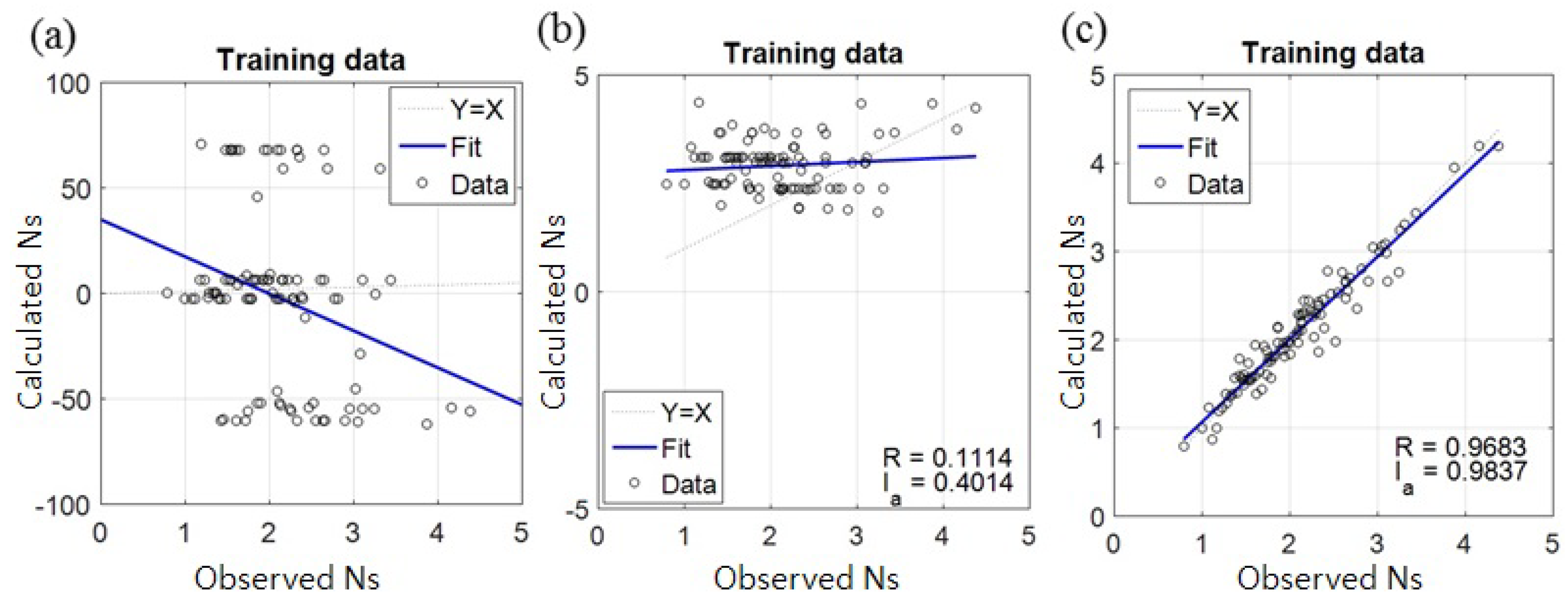
4.1. Assessment of Accuracy and Stability of the Models
4.2. Aspect of Transition of Weights
4.3. Computational Time
5. Conclusion
- The correlation coefficients of the present study were greater than those of previous studies probably because of the use of stratified sampling.
- In terms of the index of agreement, the HS-ANN model gave the most excellent predictive ability and stability with HMCR = 0.7 and PAR = 0.5 or HMCR = 0.9 and PAR = 0.1, which correspond to Geem [33] who suggested the optimal ranges of HMCR = 0.7–0.95 and PAR = 0.1–0.5 for the HS algorithm.
- The statistical analyses showed that the HS-ANN model with proper values of HMCR and PAR can give much better and more stable prediction than the conventional ANN model.
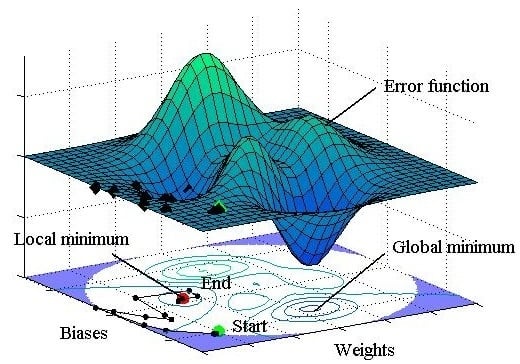
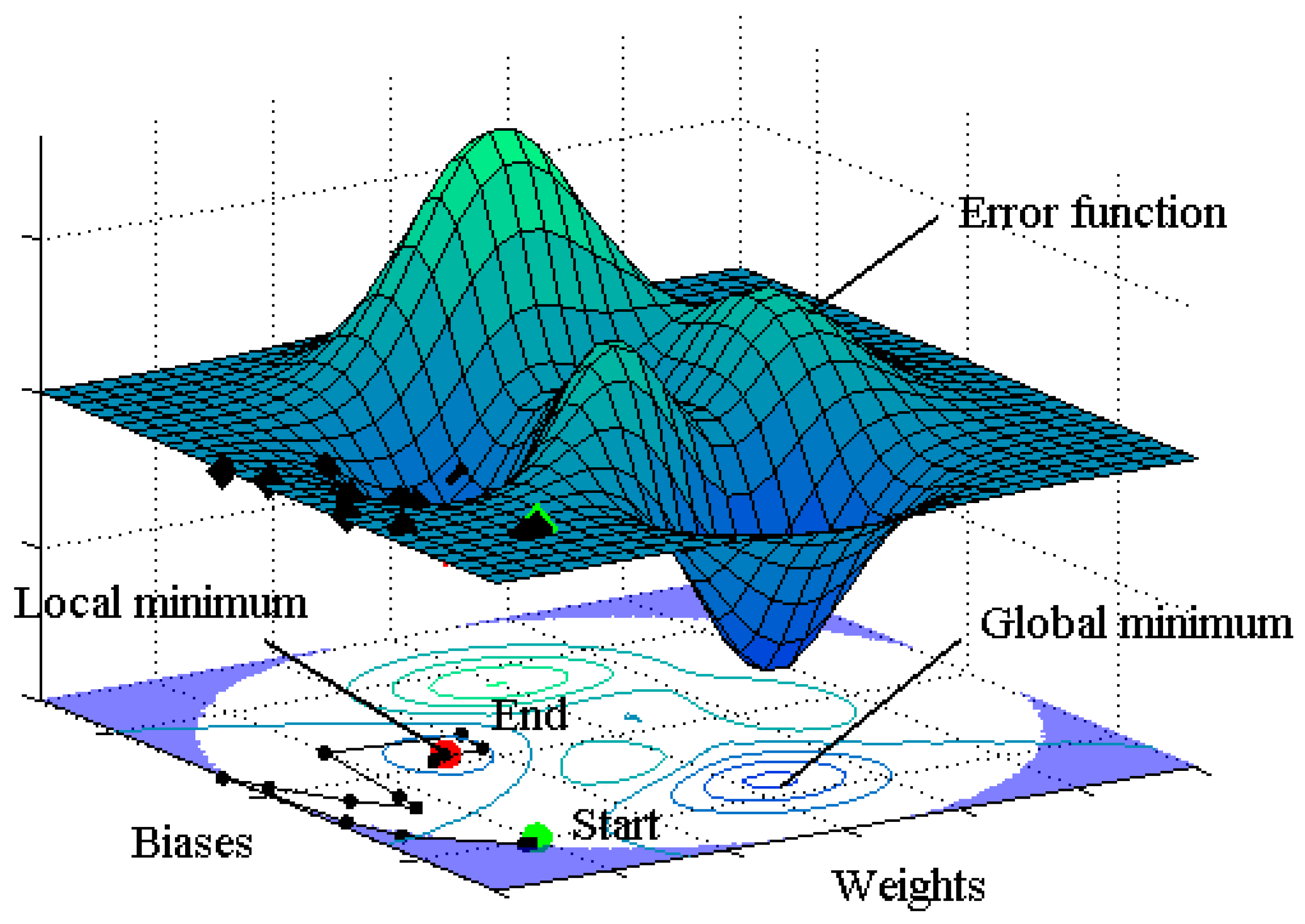
- The HS algorithm was found to be excellent in finding the global minimum of an error function. Therefore, the HS-ANN hybrid model would solve the local minimization problem of the conventional ANN model using a Monte Carlo simulation, and thus could be used as a robust and reliable ANN model not only in coastal engineering but also other research areas.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 1990, 52, 99–115. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Mase, H.; Sakamoto, M.; Sakai, T. Neural network for stability analysis of rubble-mound breakwaters. J. Waterway Port Coast. Ocean Eng. 1995, 121, 294–299. [Google Scholar] [CrossRef]
- Tsai, C.P.; Lee, T. Back-propagation neural network in tidal-level forecasting. J. Waterway Port Coast. Ocean Eng. 1999, 125, 195–202. [Google Scholar] [CrossRef]
- Cox, D.T.; Tissot, P.; Michaud, P. Water level observations and short-term predictions including meteorological events for entrance of Galveston Bay, Texas. J. Waterway Port Coast. Ocean Eng. 2002, 128, 1–29. [Google Scholar] [CrossRef]
- Kim, D.H.; Park, W.S. Neural network for design and reliability analysis of rubble mound breakwaters. Ocean Eng. 2005, 32, 1332–1349. [Google Scholar] [CrossRef]
- Van Gent, M.R.A.; Van den Boogaard, H.F.P.; Pozueta, B.; Medina, J.R. Neural network modeling of wave overtopping at coastal structures. Coast. Eng. 2007, 54, 586–593. [Google Scholar] [CrossRef]
- Browne, M.; Castelle, B.; Strauss, D.; Tomlinson, R.; Blumenstein, M.; Lane, C. Near-shore swell estimation from a global wind–wave model: Spectral process, linear and artificial neural network models. Coast. Eng. 2007, 54, 445–460. [Google Scholar] [CrossRef]
- Balas, C.E.; Koc, M.L.; Tür, R. Artificial neural networks based on principal component analysis, fuzzy systems and fuzzy neural networks for preliminary design of rubble mound breakwaters. Appl. Ocean Res. 2010, 32, 425–433. [Google Scholar] [CrossRef]
- Yoon, H.D.; Cox, D.T.; Kim, M.K. Prediction of time-dependent sediment suspension in the surf zone using artificial neural network. Coast. Eng. 2013, 71, 78–86. [Google Scholar] [CrossRef]
- Rabunal, J.R.; Dorado, J. Artificial Neural Networks in Real-Life Applications; Idea Group Publishing: Hershey, PA, USA, 2006. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Rocha, M.; Cortez, P.; Neves, J. Evolutionary neural network learning. In Progress in Artificial Intelligence; Pires, F.M., Abreu, S., Eds.; Springer Berlin Heidelberg: Heidelberg, Germany, 2003; Volume 2902, pp. 24–28. [Google Scholar]
- Krenker, A.; Bester, J.; Kos, A. Introduction to the artificial neural networks. In Artificial Neural Networks—Methodological Advances and Biomedical Applications; Suzuki, K., Ed.; InTech: Rijeka, Croatia, 2011; pp. 15–30. [Google Scholar]
- Kolen, J.F.; Pollack, J.B. Back Propagation Is Sensitive to Initial Conditions. In Proceedings of the Advances in Neural Information Processing Systems 3, Denver, CO, USA, 26–29 November 1990; Lippmann, R.P., Moody, J.E., Touretzky, D.S., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1990; pp. 860–867. [Google Scholar]
- Yam, Y.F.; Chow, T.W.S. Determining initial weights of feedforward neural networks based on least-squares method. Neural Process. Lett. 1995, 2, 13–17. [Google Scholar] [CrossRef]
- Venkatesan, D.; Kannan, K.; Saravanan, R. A genetic algorithm-based artificial neural network model for the optimization of machining processes. Neural Comput. Appl. 2009, 18, 135–140. [Google Scholar] [CrossRef]
- Chang, Y.-T.; Lin, J.; Shieh, J.-S.; Abbod, M.F. Optimization the initial weights of artificial neural networks via genetic algorithm applied to hip bone fracture prediction. Adv. Fuzzy Syst. 2012, 2012, 951247. [Google Scholar] [CrossRef]
- Mulia, I.E.; Tay, H.; Roopsekhar, K.; Tkalich, P. Hybrid ANN-GA model for predicting turbidity and chlorophyll-a concentration. J. Hydroenv. Res. 2013, 7, 279–299. [Google Scholar] [CrossRef]
- Krogh, A.; Vedelsby, J. Neural network ensembles, cross validation and active learning. Adv. Neural Inf. Process. Syst. 1995, 7, 231–238. [Google Scholar]
- Boucher, M.A.; Perreault, L.; Anctil, F. Tools for the assessment of hydrological ensemble forecasts obtained by neural networks. J. Hydroinf. 2009, 11, 297–307. [Google Scholar] [CrossRef]
- Zamani, A.; Azimian, A.; Heemink, A.; Solomatine, D. Wave height prediction at the Caspian Sea using a data-driven model and ensemble-based data assimilation methods. J. Hydroinf. 2009, 11, 154–164. [Google Scholar] [CrossRef]
- Kim, S.E. Improving the Generalization Accuracy of ANN Modeling Using Factor Analysis and Cluster Analysis: Its Application to Streamflow and Water Quality Predictions. Ph.D. Thesis, Seoul National University, Seoul, Korea, 2014. [Google Scholar]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Hudson, R.Y. Laboratory investigation of rubble-mound breakwaters. J. Waterways Harbors Div. 1959, 85, 93–121. [Google Scholar]
- Van der Meer, J.W. Rock Slopes and Gravel Beaches under Wave Attack; Delft Hydraulics Communication No. 396: Delft, The Netherlands, 1988. [Google Scholar]
- Van der Meer, J.W. Stability of breakwater armor layers—Design formulae. Coast. Eng. 1987, 11, 93–121. [Google Scholar] [CrossRef]
- Smith, W.G.; Kobayashi, N.; Kaku, S. Profile Changes of Rock Slopes by Irregular Waves. In Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, 4–9 October 1992; Edge, B.L., Ed.; American Society of Civil Engineers: Reston, VA, USA, 1992; pp. 1559–1572. [Google Scholar]
- Haldar, A.; Mahadevan, S. Reliability Assessment Using Stochastic Finite Element Analysis; John Wiley & Sons: New York, NY, USA, 2000. [Google Scholar]
- Hoel, P.G. Introduction to Mathematical Statistics, 3rd ed.; Wiley & Sons: New York, NY, USA, 1962. [Google Scholar]
- Lee, A. Determination of Near-Global Optimal Initial Weights of Artificial Neural Networks Using Harmony Search Algorithm: Application to Breakwater Armor Stones. Master’s Thesis, Seoul National University, Seoul, Korea, 2016. [Google Scholar]
- Lee, K.S.; Geem, Z.W. A new structural optimization method based on the harmony search algorithm. Comput. Struct. 2004, 82, 781–798. [Google Scholar] [CrossRef]
- Geem, Z.W. Music-Inspired Harmony Search Algorithm; Springer: Berlin, Germany, 2009. [Google Scholar]
- Willmott, C.J. On the validation of models. Phys. Geol. 1981, 2, 184–194. [Google Scholar]
- Whitley, D.; Starkweather, T.; Bogart, C. Genetic algorithms and neural networks: Optimizing connections and connectivity. Parallel Comput. 1990, 14, 347–361. [Google Scholar] [CrossRef]
- Hozjan, T.; Turk, G.; Fister, I. Hybrid artificial neural network for fire analysis of steel frames. In Adaptation and Hybridization in Computational Intelligence; Fister, I., Ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 149–169. [Google Scholar]
- Zhang, J.R.; Zhang, J.; Lok, T.; Lyu, M.R. A hybrid particle swarm optimization–back-propagation algorithm for feedforward neural network training. Appl. Math. Comput. 2007, 185, 1026–1037. [Google Scholar] [CrossRef]
- Nikelshpur, D.; Tappert, C. Using Particle Swarm Optimization to Pre-Train Artificial Neural Networks: Selecting Initial Training Weights for Feed-Forward Back-Propagation Neural Networks. In Proceedings of the Student-Faculty Research Day, CSIS, Pace University, New York, NY, USA, 3 May 2013.
- Nawi, N.M.; Khan, A.; Rehman, M.Z. A New Back-Propagation Neural Network Optimized with Cuckoo Search Algorithm. In Computational Science and Its Applications–ICCSA 2013, Proceedings of the 13th International Conference on Computational Science and Its Applications, Ho Chi Minh City, Vietnam, 24–27 June 2013; Part I. Murgante, B., Misra, S., Carlini, M., Torre, C., Nguyen, H.-Q., Taniar, D., Apduhan, B.O., Gervasi, O., Eds.; Springer Berlin Heidelberg: Heidelberg, Germany, 2013; Volume 7971, pp. 413–426. [Google Scholar]




| Author | Correlation Coefficient | Number of Data | Remarks |
|---|---|---|---|
| Van der Meer [27] | 0.92 (Mase et al. [3]) | 579 | Empirical formula, Equation (3) in this paper |
| Mase et al. [3] | 0.91 | 609 | Including data of Smith et al. [28] |
| Kim and Park [6] | 0.902 to 0.952 | 641 | Including data of low-crested structures |
| Balas et al. [9] | 0.906 to 0.936 | 554 | ANN-PCA hybrid models |
| Input Variables | Output Variable |
|---|---|
| Range | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.09 | 0.26 | 0.03 | 0.42 | 0.13 | 0.06 | - | - | 0.31 |
| 2 | 0.00 | - | - | 0.03 | - | 0.00 | - | 1.74 | - |
| 3 | 0.00 | - | - | 0.01 | 0.00 | 1.24 | - | 0.00 | - |
| 4 | 0.00 | - | - | 0.01 | - | 0.14 | 0.84 | 0.17 | - |
| 5 | 0.05 | - | - | 0.12 | 0.47 | 0.11 | 0.00 | 0.08 | 0.00 |
| 6 | 0.10 | - | - | 0.14 | - | 0.02 | 0.02 | 0.02 | - |
| 7 | 0.04 | - | - | 0.11 | - | 1.24 | 0.00 | 0.06 | - |
| 8 | 0.07 | 0.35 | - | 0.06 | - | - | 0.02 | 0.00 | - |
| 9 | 0.14 | - | - | 0.90 | - | - | 0.38 | - | - |
| 10 | 1.50 | 0.04 | 0.03 | 0.45 | 0.08 | - | - | 0.14 | 0.37 |
| 11 | - | - | - | 0.43 | - | - | 0.52 | - | - |
| 1.99 | 0.64 | 0.06 | 2.67 | 0.68 | 2.81 | 1.77 | 2.20 | 0.69 | |
| 9 | 2 | 1 | 10 | 3 | 6 | 6 | 7 | 2 | |
| 16.8 | 5.99 | 3.84 | 18.3 | 7.86 | 12.6 | 12.6 | 14.1 | 5.99 |
| HS-ANN | HMCR\PAR | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 |
| 0.1 | 0.957 | 0.971 | 0.961 | 0.9731 | 0.964 | |
| 0.3 | 0.959 | 0.967 | 0.970 | 0.9723 | 0.960 | |
| 0.5 | 0.961 | 0.954 | 0.961 | 0.957 | 0.968 | |
| 0.7 | 0.968 | 0.9732 | 0.959 | 0.967 | 0.970 | |
| 0.9 | 0.9715 | 0.970 | 0.9724 | 0.970 | 0.960 | |
| ANN | 0.971 | |||||
| Average | ||||||
|---|---|---|---|---|---|---|
| HS-ANN | HMCR\PAR | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 |
| 0.1 | 0.885 | 0.926 | 0.872 | 0.843 | 0.905 | |
| 0.3 | 0.934 | 0.910 | 0.913 | 0.914 | 0.912 | |
| 0.5 | 0.913 | 0.929 | 0.929 | 0.934 | 0.929 | |
| 0.7 | 0.881 | 0.929 | 0.9481 | 0.9443 | 0.9404 | |
| 0.9 | 0.9482 | 0.935 | 0.913 | 0.9375 | 0.892 | |
| ANN | 0.804 | |||||
| Standard Deviation | ||||||
| HS-ANN | HMCR\PAR | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 |
| 0.1 | 0.205 | 0.120 | 0.245 | 0.277 | 0.158 | |
| 0.3 | 0.137 | 0.175 | 0.155 | 0.183 | 0.189 | |
| 0.5 | 0.178 | 0.101 | 0.104 | 0.073 | 0.138 | |
| 0.7 | 0.224 | 0.130 | 0.0211 | 0.0313 | 0.0425 | |
| 0.9 | 0.0232 | 0.110 | 0.168 | 0.0314 | 0.200 | |
| ANN | 0.317 | |||||
| Minimum Value | ||||||
| HS-ANN | HMCR\PAR | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 |
| 0.1 | 0.001 | 0.216 | 0.001 | 0.001 | 0.002 | |
| 0.3 | 0.002 | 0.001 | 0.029 | 0.004 | 0.002 | |
| 0.5 | 0.003 | 0.319 | 0.254 | 0.468 | 0.003 | |
| 0.7 | 0.001 | 0.051 | 0.8891 | 0.8523 | 0.7105 | |
| 0.9 | 0.8852 | 0.196 | 0.013 | 0.8014 | 0.005 | |
| ANN | 0.001 | |||||
| Maximum Value | ||||||
| HS-ANN | HMCR\PAR | 0.1 | 0.3 | 0.5 | 0.7 | 0.9 |
| 0.1 | 0.978 | 0.985 | 0.980 | 0.9871 | 0.981 | |
| 0.3 | 0.979 | 0.983 | 0.985 | 0.986 | 0.979 | |
| 0.5 | 0.980 | 0.977 | 0.980 | 0.978 | 0.984 | |
| 0.7 | 0.984 | 0.9862 | 0.979 | 0.983 | 0.985 | |
| 0.9 | 0.985 | 0.985 | 0.986 | 0.985 | 0.980 | |
| ANN | 0.985 | |||||
| Algorithm | HS-ANN Model | Conventional ANN Model | ||
|---|---|---|---|---|
| Average | SD | Average | SD | |
| HS | 285.6 | 7.8 | - | - |
| BP | 102.9 | 55.2 | 68.6 | 95.0 |
| Total | 385.5 | 55.7 | 68.6 | 95.0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, A.; Geem, Z.W.; Suh, K.-D. Determination of Optimal Initial Weights of an Artificial Neural Network by Using the Harmony Search Algorithm: Application to Breakwater Armor Stones. Appl. Sci. 2016, 6, 164. https://doi.org/10.3390/app6060164
Lee A, Geem ZW, Suh K-D. Determination of Optimal Initial Weights of an Artificial Neural Network by Using the Harmony Search Algorithm: Application to Breakwater Armor Stones. Applied Sciences. 2016; 6(6):164. https://doi.org/10.3390/app6060164
Chicago/Turabian StyleLee, Anzy, Zong Woo Geem, and Kyung-Duck Suh. 2016. "Determination of Optimal Initial Weights of an Artificial Neural Network by Using the Harmony Search Algorithm: Application to Breakwater Armor Stones" Applied Sciences 6, no. 6: 164. https://doi.org/10.3390/app6060164
APA StyleLee, A., Geem, Z. W., & Suh, K.-D. (2016). Determination of Optimal Initial Weights of an Artificial Neural Network by Using the Harmony Search Algorithm: Application to Breakwater Armor Stones. Applied Sciences, 6(6), 164. https://doi.org/10.3390/app6060164